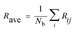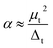Probing the properties of size dependence and correlation for tantalum clusters: geometry, stability, vibrational spectra, magnetism, and electronic structure

Abstract

A comprehensive investigation on the equilibrium geometry, relative stability, vibrational spectra, and magnetic and electronic properties of neutral tantalum clusters (Ta_n, n = 2–17) was performed using density functional theory (DFT). We perform a study of the size dependence and correlations among those descriptors of parameters, and showed these could provide a novel way to confirm and predict experimental results. Some new isomer configurations that have never been reported before for tantalum clusters were found. The growth behaviors revealed that a compact geometrical growth route is preferred and develops a body-centered-cubic (BCC) structure with the cluster size increasing. The perfectly fitted functional curve, strong linear evolution, and obvious odd–even oscillation behavior proved their corresponding properties depended on the cluster size. Multiple demonstrations of the magic number were confirmed through the correlated relationships with the relative stability, including the second difference in energy, maximum hardness, and minimum polarizability. An inverse evolution trend between the energy gap and electric dipole moment and strong linear correlation between ionization potentials and polarizability indicated the strong correlation between the magnetic and electronic properties. Vibrational spectroscopy as a fingerprint was used to distinguish the ground state among the competitive geometrical isomers close in energy. The charge density difference isosurface, density of states, and molecular orbitals of selected representative clusters were analyzed to investigate the difference and evolutional trend of the relative stability and electronic structure. In addition, we first calculated the ionization potential and magnetic moment and compared these with the current available experimental data for tantalum clusters.

---

1 Introduction

Clusters are aggregates of a finite number of atoms or molecules, bridging the gap between isolated atoms/molecules and the macroscopic solid state of matter.¹ Transition metal (TM) clusters have attracted considerable attention and showed promise in various applications, such as nanoelectronics, catalysis, biological and chemical sensing, molecular imaging, biological labeling, and biomedicine.^2,3 The ionization enhancement behavior has been investigated for tantalum clusters by strong-field ionization and in a Coulomb exposition study.⁴ Gas-phase clusters represent an ideal model system to study quantum coherent phenomena at practically macroscopic scales.⁵ Most recently, Kramers blocking of spin–lattice relaxation in clusters of vanadium-group elements have been studied, and this relaxation of the quantum phenomenon was clearly found to be more efficient for larger nuclear mass tantalum clusters.⁵ Tantalum clusters and their oxide complexes have also gained attention for their enhanced oxygen reduction reaction as catalysts,^6–8 ferroelectric state, and spin uncoupling property related to their superconductivity characteristics.⁹

Both experimental and theoretical studies have been carried out to investigate the characteristic parameters of neutral and charged tantalum clusters. Sakurai et al. observed the magic numbers by time-of-flight (TOF) mass spectrometry.¹⁰ The ionization potentials were measured by threshold laser photoionization spectroscopy.¹¹ The magnetic moments were measured by a magnetic deflection method and discussed by Kramers degeneracy theorem.⁵ The gas-phase infrared (IR) spectra of tantalum cations and Ta_nO_0,1,2⁺ (n = 6–11) clusters were experimentally observed by Fielicke et al.^12,13 The IR vibrational spectra of tantalum cation Ta_n⁺ clusters were simulated using density functional theory (DFT) by Du et al. with comparison to the experimental ones, while a high-stability icosahedral cluster (Ta₁₂²⁺) with spherical aromaticity was also investigated.^14,15

The geometric and electronic structures of clusters can vary for different charge states, especially in terms of their vibrational pattern and structural fingerprint.¹⁶ Some experimental studies concentrated on the electronic properties of neutral clusters were only based on the limited geometry of charged clusters by using mass-selected methods.^17–19 More recently, a two-color IR-UV spectroscopy method was used to directly probe the electronic density of states (DOS) and vibrational spectra for isolated neutral cobalt clusters.²⁰ Neutral Tm and Pr clusters were produced successfully in a cryogenically cooled laser vaporization source, and their size-dependent electric dipole, polarizability, and magnetic moments were investigated by experiment.²¹ The geometrical structure of a cluster also plays an important role in the determination of its properties, and this structural information may be obtained from a comparison of measured experimental vibrational spectra with theoretical calculations, as has been done successfully for vanadium and niobium clusters.^22–24 The existing theoretical studies on neutral tantalum clusters, however, are not sufficient as they are limited to either selected sizes or only examine simple geometries. For example, theoretical studies for tantalum clusters are limited to dimer, trimer, and tetrahedral clusters,^25–33 while several available DFT studies for larger neutral tantalum clusters only plotted and concentrated on their lowest-energy structures.^9,34,35

Polarizability is very sensitive to the delocalization of valence electrons as well as to the cluster structure and shape, and therefore, it represents one of the most important observables for understanding the electronic properties of clusters. Specifically, the experimentally measurable static dipole polarizabilities can provide information on the bonding and geometrical features of clusters.^36–39 The electronic polarizabilities can be measured by passing a collimated beam of neutral clusters through an inhomogeneous electric field.¹ Electric dipole polarizabilities for many neutral TMs clusters have been investigated by molecular beam deflection experiments,⁴⁰ such as aluminum, nickel, niobium, noble metals, pure and mixed alkali metals. But until now, no measurements of static electric polarizabilities for tantalum clusters has been available. In addition, there are no theoretical investigations in the literature on the ionization potential in order to compare the existing experimental measurements.¹¹ Since we demonstrated a strong linear correlation between the ionization potential and polarizability for scandium and yttrium clusters in our previous reports,^40,41 we were interested to know whether this principle could also serve as one criterion of this relation for tantalum clusters. Thus, the polarizabilities of tantalum clusters then could be predicted by the correlation with the measured ionization potential, and the ionization potential could serve as a bridge between them.

With this in mind, we performed an extensive and systematic study, first using a hybrid DFT functional to investigate neutral tantalum clusters. In consideration of the computational time, which can be explained clearly by the cluster properties of size dependence and correlation, our study was performed for Ta_n clusters with sizes up to n = 17. We aimed to determine their low-lying geometrical isomers, structural evolution, and relatively stability. We explored a compact geometrical growth route for neutral tantalum clusters, and present herein some new isomer configurations that have never been reported before or that are different from those reported in previous studies of tantalum clusters. We also performed an analysis of the charge density and DOS to gain insights into the electronic structure for selected lowest-energy geometries of the clusters. The magnetic and electronic structural properties, including magnetic moment, electric dipole moment and HOMO–LUMO gap, static dipole polarizabilities, electron affinity, ionization potentials, and their relationships between relative stability with each other were also predicted. We first compared the ionization potential and magnetic moment by theory with available experimental data for tantalum clusters. The main purpose of this work was to confirm and interpret the size dependence and correlation for different properties and the reactivity of tantalum clusters. This includes the correlation between equilibrium geometry, relative stability, vibrational spectra, magnetic and electronic properties, followed by the theoretical and experimental predictions based on size-dependent evolution. It is hoped that our work would be beneficial to gaining a greater understanding of the physical and chemical properties of small TM clusters, and could act as powerful guidelines for future theoretical and experimental research.

2 Computational method

All geometry optimizations, vibrational frequency analyses, and electronic structure calculations of tantalum clusters up to 17 atoms were carried out using DFT within the Gaussian 03 programs.⁴² The exchange-correlation functional B3LYP and the relativistic effective core potential (RECP) basis set LANL2DZ were used for all of the computations. The accuracy of the theoretical level was checked by calculations on a tantalum dimer and trimer. The results are summarized in the ESI† of this paper. Comparisons between our calculated results of Ta₂ and Ta₃ and measurements as well as the results of previous theoretical calculations showed that DFT is adequate for calculating their bond lengths, relative energetic, and electronic properties. Therefore, the selected B3LYP/LANL2DZ DFT level can be reliably used to investigate properties for larger tantalum clusters. The finite field approach⁴³ implemented within the GAUSSIAN 03 package was used to calculate the static electric polarizability and dipole moments of natural tantalum clusters. The detail computational method and definition for the reactivity descriptors can be referenced from the section titled “Computational detail” in the ESI.†

3 Results and discussion

3.1 Equilibrium geometry and growth behavior

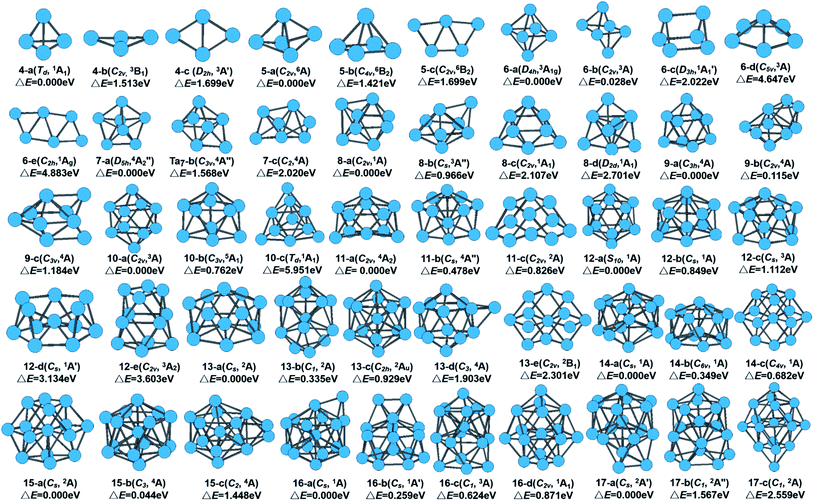
The global minimum as well as all metastable configurations together with their symmetry, electronic states, and the relative energies from the ground state of neutral Ta_n (n = 4–17) clusters are displayed in Fig. 1. A detailed analysis of the geometrical information and energy difference for those isomers of tantalum clusters was performed and is detailed in the in ESI.† Also, in Table S1 in the ESI,† we have listed all information on the structure and energy for all the calculated stable geometries of the neutral Ta_n (n = 2–17) clusters, including their symmetry, spin multiplicity, total energy, average binding energy per atom, and zero-point vibrational energies.

Fig. 1 Calculated stable geometries of neutral Ta_n (n = 4–17) clusters.

Similar to niobium clusters,⁴⁴ the turnover point of the planar to 3D geometry also undergoes an early transition, which occurs with the size of 4 atoms for tantalum clusters. Thus, a 3D compact shape of geometrical evolution is favored generally for tantalum clusters. Starting from seven-atom tantalum clusters, the planar configurations were not selected to search for the stable structures. The initial 3D geometries based on capping different faces of the pentagonal bipyramid (PBP), prism, octahedron, and antiprism structures were considered instead. Their optimized ground state structures can be regarded as adding orderly one atom or single capping. Several different isomers and their competitive candidates of Ta₈, Ta₉, and Ta₁₀ cluster are depicted in Table S1† and Fig. 1. For Ta₈, the bicapped distorted octahedron with a C_2v symmetry and spin single state (¹A) (8-a) was found to be the lowest-energy structure. This structure can be viewed as the one obtained from the capping of a PBP, or from bicapping of the Ta₆ structure. A similar structure was obtained for the Ta₈ cluster by Fa et al.⁹ For Ta₉, a tricapped prism structure with a C_3h symmetry (9-a) was found to be the ground state geometry. Another view of this structure is that of a triangle capping a pentagonal pyramid or a rhombus capping a rectangle that evolved from the lowest-energy structure of Ta₈ by capping one atom on the top of a bicapped octahedron. This lowest-energy structure for Ta₉ is different with the result in ref. 9, which is for a hexagon with cappings of one and two atoms on the two faces (9-b, another view of this structure is that of two fused pentagonal bipyramids) obtained within the Dmol³ program using the GGA method, which lies 0.115 eV higher in total energy. However, Kumar et al.⁴⁴ and Grönbeck et al.⁴⁵ obtained a tricapped prism as the lowest energy for a Nb₉ cluster when using BLYP and an ab initio ultrasoft pseudopotential method, respectively. For Ta₁₀, the bicapped antiprism structure with a C_2v symmetry (10-a) and spin triplet state (³A) was found to be most stable. This structure could also be considered to arise from the capping of a prism. Thus, for the smaller size range of n ≤ 10 clusters, the growth behavior showed competition between the tetrahedral- and prism-based growth.

Three competitive candidates for the ground state of Ta₁₁ were found, which nearly degenerated with the same energy. Similar to the results by Grönbeck et al.⁴⁵ for Nb₁₁ and Fa et al.⁹ for Ta₁₁, our calculated four-capped pentagonal bipyramid was the lowest-energy structure and the three-capped hexagonal bipyramid structure was the first close-lying isomer for the Ta₁₁ cluster. Two competitive candidates, which were formed by adding one atom to Ta₁₁ for the close-lying state of Ta₁₂, appeared. They all evolved by capping one atom on the distorted pentagonal bipyramid and hexagonal bipyramid structure of Ta₁₁, respectively. Fig. 1 shows that our calculation obtained two isomers (12-d and 12-e) that have never been found for V, Nb, and Ta clusters before. In the previous study using the GGA method,⁹ the lowest-energy structure of Ta₁₂ was predicted to be a relaxed icosahedron missing one surface atom (12-b). However, for the Ta₁₂⁺ cluster cations, a slightly distorted icosahedron was considered to be the lowest energy structure in the recent study by Du et al.¹⁴

A quasilayer-like growth mode based on a hexagonal bipyramid unit was observed from Ta₁₃ to Ta₁₇ clusters, as indicated in Fig. 1. Their optimized ground state structures could be regarded as orderly adding one atom or single capping. The 13-atom cluster is one of the most studied clusters because it is considered as the seed for different cluster growth patterns. The ground state of the Ta₁₃ cluster was found to be a distorted five-capped hexagonal bipyramid (HBP) structural pattern (13-a) based on the ground states of Ta₁₁. It is a spin double state (²A) with C_s symmetry. 13-atom clusters of many transition metals have been found to have an icosahedral structure. However, it is not even a local minimum for Ta₁₃ according to our calculated result. It should be noticed that the capped icosahedron isomer relaxes significantly and lies highest in energy for Ta₁₄. From the growth behavior of Ta₁₂–Ta₁₄, it can be concluded that tantalum clusters do not favor icosahedral growth, just like niobium clusters.⁴⁶ For Ta₁₅, two competitive candidates for the ground state were found. The Ta₁₅ cluster prefers a fragment structure of the BCC bulk tantalum as the lowest energy structure (15-a), which agrees with previous theoretical studies on neutral Ta₁₅ clusters.^9,35 However, there is a slight distortion and the symmetry with C_s is not fully cubic. This structure shows another view of a hexagonal layer with the center atom capped with a rhombus above and below. The capped BCC geometry also shows the highest stability in other TM 15-atom clusters, such as Nb₁₅,⁴⁶ W₁₅,⁴⁷ and Cr₁₅ (ref. 48) clusters. It is generally known that the crystal structure of Ta bulk is a BCC structure. The lowest-energy structures were found to favor the BCC unit geometry, which means it can be obtained easily in experiment.

Continuing the growth trend of hexagonal structures, Ta₁₆ and Ta₁₇ were based on the capping of hexagonal bipyramid structure of Ta₁₅ (15-b) with a dimer and a trimer on one of the hexagonal faces. The next isomer of Ta₁₆ and Ta₁₇ clusters were formed by adding one atom on the face of the pentagonal bipyramid structure. Though the capped icosahedral isomer was separated from the ground state by a large energy gap, a capped decahedron was found as the first close-lying isomer of Ta₁₇, lying 1.567 eV higher in energy. The ground-state structures of Ta₁₆ and Ta₁₇ showed a trend of hexagonal-based growth. These results suggest that clusters with hexagonal isomers in which a bulk BCC type structure possess the lowest energy become favorable, and the icosahedral growth is never favored for larger tantalum clusters. The optimal structure of a tantalum cluster is not simply built up from the smaller size cluster by adding one atom randomly, otherwise the preferred growth route tends to yield a compact structure.

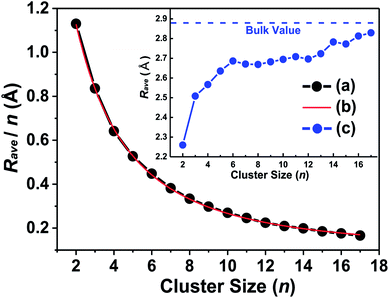
The electronic and magnetic structures of clusters strongly depend on their geometric quantity and sensitivity to finite size effects. For example, Tb clusters exhibit irregular oscillatory ferromagnetic and antiferromagnetic exchange interactions between their moments and the interatomic distance of the clusters.⁴⁹ In the present, the average bonding distance (R_ave) between atoms is defined as:

where R_ij is the nearest-neighbor distance less than 15% of the minima distance and N_b is the number of bonds of cluster. As shown in Fig. 2, R_ave increases with some local oscillations during the cluster growth process. The bulk limit for the tantalum BCC lattice⁵⁰ is indicated in Fig. 2 by a horizontal dashed blue line. The average bond length was 2.829 Å for Ta₁₇, slightly smaller than the bulk nearest-neighbor distance (2.880 Å).⁵⁰ It is interesting that the average bonding distance per atom parameter, which is defined as R_ave/n (n being the number of Ta atoms in the cluster), decreased monotonically and coincided perfectly with the curve of the Lorentz functional with increasing the cluster size numbers. The calculated and fitting curves together present a very useful tool to predict the geometrical structure information related to the bonding radius for small clusters.

Fig. 2 Calculated average bonding distance (R_ave) as a function of cluster size: (a) average bonding distance per atom (R_ave/n), (b) Lorentz fitting curve of (a), (c) the average bonding distance with their evolution tendency and comparison with bulk tantalum (inset figure).

3.2 Binding energy and relative stability

In order to understand the size dependence and relationship between the binding energy and relative stability of Ta_n clusters, we calculated the total binding energy (E_b), binding energy per atom (E_b/n), and second-order difference of energies [Δ₂E(n)] based on the total energies of the lowest-energy structures, based on the total energies and evaluated by using the following expressions:

E_b = nE(Ta) − E(Ta_n)

E_b/n = [nE(Ta) − E(Ta_n)]/n

Δ₂E(n) = [E(Ta_n+1) + E(Ta_n−1) − 2E(Ta_n)]

where E(Ta_n) and E(Ta) are the energies of a Ta_n cluster and a free Ta atom [state: ⁴A_1G, E(Ta) = −57.638 a.u. calculated by the B3LYP/LANL2DZ DFT method] with zero-point energy corrections, respectively. The calculated total binding energy linearly increased with the cluster size, as shown in the inset of Fig. 3, and therein the red line is the linear fitting result (the function can be found in the figure). However, the binding energy cannot always increase with the increasing cluster size. This linear correlation is only limited to the calculated finite atoms number for small tantalum clusters.

Fig. 3 Average bonding energy per atom (E_b/n) of the ground state structures of Ta_n (n = 2–17) clusters vs. the inverse of the cluster size (1/n); inset figure is the total binding energy (E_b) as a function of cluster size (n).

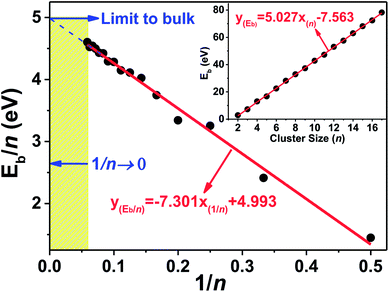
Alternatively, we plotted the binding energy per atom versus the inverse of cluster size (1/n) in Fig. 3, which also shows that there conformably exists a strong linear relationship between them. The binding energy per atom converges to the cohesive energy of bulk Ta when the cluster size n grows to an infinite value (lim 1/n → 0). By simply linear fitting our calculated binding energies of Ta_n (n = 2–17) clusters, one intercept of the line with a value of 4.993 eV was obtained, which is far from the experimental cohesive energy per atom of Ta bulk (8.10 eV per atom)⁵⁰ These results imply that the compact icosahedron growth patterns will be invalid for larger tantalum clusters and it will change to a BCC crystal structure finally.⁵¹ This conclusion is coincident with the above discussed geometrical result in which the BCC structure is energetically preferred for neutral tantalum clusters.

As shown in Fig. 4, the E_b/n values of the ground state fit a curve of the Exp-Assoc. nonlinear function [y_(Eb/n) = −3.21 + 1.740 × (1 − exp(−x_(n)/8.407)) + 6.299 × (1 − exp(−x_(n)/1.747))], and increase monotonically with increasing cluster size numbers (n). The binding energy per atom of tantalum clusters increases rapidly with the cluster size up to n = 7. Then, the curve becomes smoother in the size range of n = 8–17. The small humps in the E_b/n curve only indicate a large stability for some specific clusters, which cannot obviously reveal the stability for all tantalum clusters. Further, the second difference in the energy of ground state was analyzed to investigate the stabilities and magic numbers of tantalum clusters.

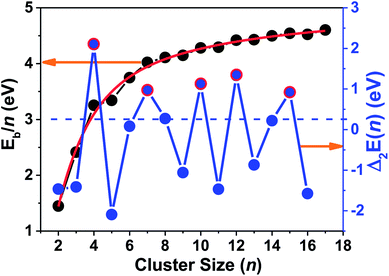Fig. 4 Binding energy per atom (E_b/n) and second differences in total energy [Δ₂E(n)] for the most stable neutral tantalum clusters vs. cluster size.

The understanding of the variation in the second differences in the energy properties of clusters is important for catalysis and can provide a good way to show the relative local stability of small clusters.^52,64 From our definition of Δ₂E(n) by eqn (4) in the ESI,† we can estimate that the relative stabilities that have positive values are more stable than their neighboring sizes. The particular peaks and valleys corresponding to n = 4, 7, 10, 12, and 15 (highlighted by the red circles in Fig. 4) indicate that these clusters are the magic numbers for local stability maxima compared with their neighbors. Being coincident with the measured TOF mass spectra and a previous DFT study, the magic numbers of neutral Ta_n clusters were obtained at n = 4, 7, 10, and 15.^9,10 Our present work also indicates that the Ta₁₂ cluster corresponding with a distorted empty cage icosahedron shows a very prominent stability. Similar to the Ta₁₂⁺ cluster cation,¹⁴ the highly compact icosahedron geometry with S₁₀ symmetry of neutral Ta₁₂ cluster may be responsible for the enhanced stability. The positively charged tantalum clusters cations,¹⁴ with one electron missing from the neutral cluster, still follow a similar pattern in the compact growth of the ground-state geometry and the relative stability order.

Our current conclusion for the magic cluster Ta₁₂ is inconsistent with the experimental results from TOF mass spectrometry,¹⁰ in which the Ta₁₃ cluster is one of the magic number clusters. Also the neutral Ta₁₂ cluster was not found to be magic in a previous DFT study.⁹ It would useful, therefore, to explore the nature of chemical bonds via the changes in electronic charge density during the cluster and molecule formation. In this study, the deformation charge density (Δρ) is defined as:

Δρ = ρ_{(Tan cluster)} − nρ_{(Ta atom)}

where ρ is the charge density of the cluster and atom, i.e., the deformation charge density isosurface is the cluster's charge density after bonding minus the individual free atoms' charge density on their isosurface. Through the deformation charge density, one can obviously obtain the properties of charge moving and the direction of polarization during the process of bonding and electron coupling. The charge density difference isosurface in Fig. 5 indicates that the structure of the Ta₁₂ cluster with an empty cage distorted icosahedron (ICO) and S₁₀ symmetry shows a very prominent stability, in which the steric hindrance effects and charge interactions are the smallest. Its high stability is attributed to the high-symmetry geometries and compact atomic arrangements of the clusters. The ground state of the Ta₁₃ cluster was found to be a distorted five-capped hexagonal bipyramid structural pattern, which can help reduce the steric hindrance effect and the charge rejection. Compared with several previous studies for 13-atom materials,³⁴ we conclude that the icosahedral growth is not favored for tantalum clusters. Although the distorted slightly icosahedral structure doped with one atom to the ground state of Ta₁₂ is not a local minimum for Ta₁₃ clusters, to the ground-state structure of Ta₁₃ with empty space is added two extra atoms to form a compact hexagonal ICO structure with 15 atoms, which is the magic number of clusters and it has a higher stability.

Fig. 5 Deformation charge density isosurface from top-down view for the lowest energy geometry of Ta₁₂, Ta₁₃, and Ta₁₅ clusters, where the blue lines indicate charge accumulation and the purple lines are charge depletion.

3.3 Vibrational spectra

As discussed above, there are always one or two competitive candidates of the ground state for certain species of neutral tantalum cluster sizes. The energy difference of those degenerated isomers is so tiny that it can be hard to distinguish which one is the ground state structure. In Table S1,† we have listed all the vibrational peaks or their most clear six peaks for the ground state structure and their isomers of neutral Ta_n (n = 3–17) clusters. For the purpose of comparison, the calculated IR spectra of both states of the lowest-lying and first close-lying for some selected structures of Ta_n (n = 3–17) clusters are also plotted in Fig. 6. The frequency range is shown from 0 to 300 cm⁻¹, as no signals were found at higher photon energy. By comparing the previous experimental and theoretical spectra for tantalum cluster cations,^12,14 a significant change in vibrational spectra of neutral tantalum clusters could be found by removing one electron.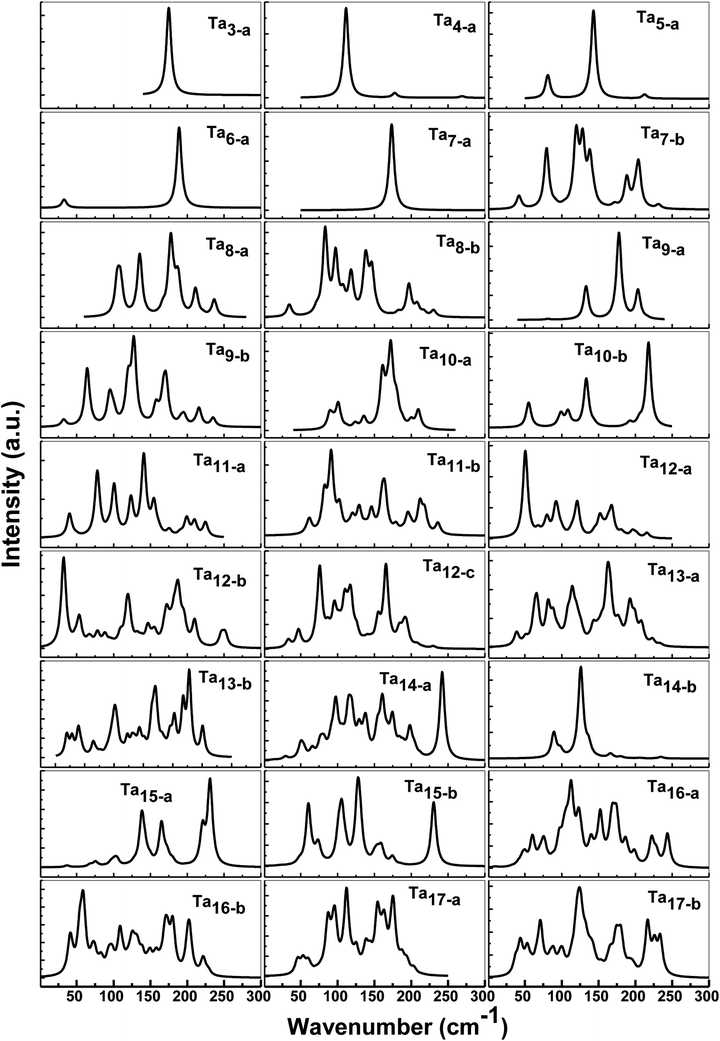

Fig. 6 Predicted IR spectra for the low-lying and selected close-lying states and isomers of neutral Ta_n (n = 3–17) clusters.

As depicted in Fig. 6, the vibrational spectra for the ground state of Ta₃ and Ta₇ are relatively simple with a very high intense peak, centered at about 175 cm⁻¹ and 173 cm⁻¹ with degenerate modes, respectively. Neutral Ta₄ and Ta₆ mainly presented two obvious peaks: a very high and a very low intensity peak, respectively. Three resonances could be observed for the neutral spectrum of Ta₅ and Ta₉ clusters. For Ta₈ and Ta_n (n = 10–17) clusters, their IR spectra in their ground state and first close-lying state are much more complicated with a rich spectral structure, including the presence of at least four intense peaks in the range of 0–300 cm⁻¹. The IR spectra of the competitive candidates for the ground states of Ta₇ and Ta₉ are more complicated than their ground states. However, for Ta₁₃ and Ta₁₄ clusters, their predicted spectra of the competitive candidates for the ground state are simpler than their lowest-energy state’. For the Ta₁₂ cluster, two competitive candidates (12-b and 12-c) for the close-lying state are also plotted in Fig. 6. The slightly distorted icosahedron (12-a) with the lowest energy and those two isomers all show more than six clear peaks, mainly in the range 50–200 cm⁻¹. However, in some cases, appropriate structures fitting well with the experimental spectra may be not obtained for some clusters by the theoretical calculations.¹⁴ The entire different vibrational spectroscopy results for three isomers and their clear peaks can be used to compare the results with the experimental spectrum. It may require a selective method to distinguish which one is the ground state structure that can be measured experimentally among those isomers close in energy.

Vibrational spectroscopy is a preferred method to obtain information on the structure and bonding of clusters. It depends sensitively on the cluster size and geometrical and electronic structure. Even the same isomer but with different spin states has its own individual ‘‘fingerprint’’ spectrum. As shown in Fig. 6, it is clear that the calculated spectra of both the ground state and the close-lying state are completely different. However, up to now, no experimental IR data have actually been available to allow comparisons for neutral tantalum clusters species. A comparison between the calculated and experimental values of vibrational frequency is a sensitive benchmark for testing the performance of different computational models in order to judge their accuracy and to apply them to larger or more complex systems.^53,54 Thus, to obtain structural information and to distinguish those competitive candidates for the ground state that are nearly degenerate with an approximate energy, we hope that further experimental research on vibrational spectra will be performed in the future to compare with our theoretical spectra.

3.4 Magnetic moments, electric dipole moment, and HOMO–LUMO gap

A reduced atomic coordination induces the asymmetric charge distribution, which leads to stronger electron localization and unequivalent interatomic distances, which then enhances the ferroelectricity and ferromagnetism for tantalum clusters.⁹ As shown in Fig. 7, our calculated atomic magnetic moments ranged from 0 to 5 μ_B for the lowest energy structures and oscillatory decreased with increasing cluster size, displaying remarkable size dependence with an odd–even oscillation. An interesting atomic-like behavior, which is a direct indication of the absence of spin–lattice interaction, indicated various quantum relaxation processes for the tantalum clusters.⁵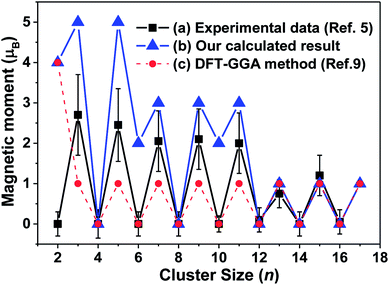

Fig. 7 The magnetic moments of for neutral tantalum clusters presented as a function of cluster size: (a) experimental measured values obtained by a magnetic deflection method (ref. 5); (b) our calculated result for the lowest energy structure based on the B3LYP/LANL2DZ DFT level, (c) previous theoretical report based on the GGA DFT method (ref. 9).

By comparing the experimental results with magnetic deflection measurements, although they exhibited a similar oscillation trend and agreed well for larger Ta_n (n = 12–16) clusters, our calculated magnetic moments were generally higher. The measured value for those smaller tantalum clusters were between our calculated results based on the B3LYP/LANL2DZ level and those previously reported by the GGA functional DFT method.⁹ The previous reports in theory for the magnetic moments of tantalum clusters showed that even- and odd-numbered clusters have the same spin moment of 0 and 1 μ_B for neutral clusters,⁹ or 1 μ_B and 2 μ_B for their cations,¹⁴ respectively. The magnetic moments of tantalum clusters change discontinuously with geometrical structure for the lowest-energy structure and their degenerated isomers. Stern–Gerlach molecular beam deflection experiments cannot distinguish those energetically close isomers.⁵⁵ For example, as listed in Table S1,† the most stable Ta₄, Ta₈, and Ta₁₄ clusters exhibit nonmagnetic ground states. However, 4-b, 8-b, and 14-b, which are the second-lowest competitive candidates, have 2 μ_B magnetic moments. Thus, in this paper, we obtained many geometrical isomers for different cluster sizes that could be used to confirm and interpret the experimental data.

To further investigate the ferroelectricity and ferromagnetism of tantalum clusters, the electric dipole moments (EDMs) were calculated and demonstrated their relationship with geometrical structure. The obtained dipole moments for the ground state of Ta_n (n = 2–9) clusters with highly symmetry were generally very low with almost zero value approximately, except for the Ta₄ cluster. A similar result appeared in our previous investigation for scandium clusters.⁴¹ The larger Ta_n (n ≥ 10) clusters exhibit nonzero EDM, therefore they become multiferroic or magnetoelectric clusters because of the unpaired spin and symmetric structure. Compared with charged clusters, most of the Ta_n⁺ clusters correspond to moderate dipole moments,¹⁴ while neutral clusters show very different dipole moments, as plotted in Fig. 8 and listed in Table S1.† We should emphasize that the calculated dipole moment of Ta₁₆ and Ta₁₇ clusters are obviously larger than their preceding cluster sizes, with values of 2.248 and 3.116 Debye, respectively. The gap between the highest occupied and the lowest unoccupied molecular orbitals (HOMO–LUMO gap, E_gap) can be used to analyze the stability and their transition to metallicity with increasing cluster size. As presented in Fig. 8, the energy gaps of tantalum clusters gradually decreased with the increasing cluster size, which indicates a trend of nonmetallic–metallic transition and therefore they should be more reactive.

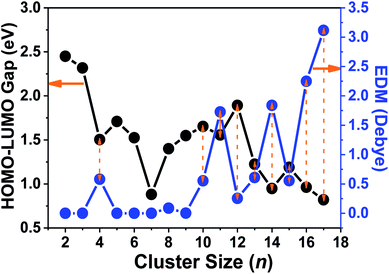Fig. 8 The HOMO–LUMO gaps and electric dipole moments (EDM) of Ta_n (n = 2–17) clusters vs. cluster size.

An interesting size dependence and correlation with the electronic properties should be noted, in which a small HOMO–LUMO gap corresponds generally to a high nonzero dipole moment for neutral tantalum clusters (indicated by orange arrows in Fig. 8). However, the relationships for scandium and yttrium clusters are reversed with tantalum clusters,^40,41 which follow the same evolutionary trend as the cluster size increases, owing to the energy gap of a cluster precisely depending on the eigenvalues of the HOMO and LUMO energy levels. In the perturbation theory, static dipole polarizability (α) is expressed as a sum of contributions from all excited states.⁶⁵ A clear correlation between the polarizability and HOMO–LUMO gap holds if the dominant excited state is mainly described by the HOMO-to-LUMO transition.⁵⁶ This also can be easily rationalized using the two-level model:⁶⁶

where α is the polarizability, μ_t² is the transition dipole moment from the ground state to the first dipole-allowed excited state, and Δ_t is the corresponding transition energy. Approximately, Δ_t can be replaced with the HOMO–LUMO energy gap. From this model, we can see that the cluster with a large (or small) HOMO–LUMO gap and low (high) dipole moment will lead to a small (large) polarizability. As discussed in this paper and presented in Fig. 11, the polarizabilities of Ta_n (n = 2–17) clusters exhibit local minima at their magic number (n = 4, 7, 10, 12, and 15), all of which have relatively smaller polarizabilities in comparison with their neighbors in cluster size. For example, for the Ta₁₂ cluster, an inverse correlation between the HOMO–LUMO gap (large) and dipole moment (low) leads to a local minima static dipole polarizability as a magic number cluster. Thus, a large HOMO–LUMO gap corresponds generally to a smaller nonzero dipole moment for the magic number tantalum clusters, except for Ta₄, while a relatively small HOMO–LUMO gap corresponds generally to a high nonzero dipole moment for other tantalum clusters, except for Ta₁₃. The Ta₄ and Ta₁₃ clusters exhibit relatively lower dipole moments, leading to them not fitting the above analysis result. For some semiconductor and transition metal (TM) clusters, a higher symmetry and compact geometrical structure often lead to a relatively low dipole moment.^36,56,57 According to our results of geometrical optimization, the lowest energy structure is a tetrahedron with T_d symmetry for the Ta₄ cluster and a five-capped hexagonal bipyramid (HBP) compact structure for the Ta₁₃ cluster. In addition, as listed in Table S1,† the different isomers have different EDMs, which shows that the geometrical structure of a tantalum cluster has a very important effect on its EDM, even when they are energetically close. With an increase in the number of atoms, there exist some metastable isomers close to the lowest-energy structure in most of the neutral tantalum clusters, and whose EDM amplitudes may have a larger fluctuation. The correlation between the geometrical structure and its ferroelectricity, shows the similar geometrical origin of the ferroelectric properties as that of Nb clusters.^58,59

3.5 Density of states and molecular orbitals

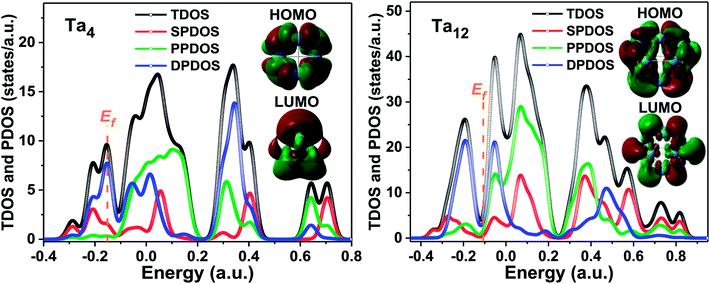
The s-, p-, d-projected partial and total DOS for the most stable configurations of representative Ta_n clusters with n = 4, 7, 10, 12, 13, and 15 are plotted in Fig. 9 and S1,† respectively. The Fermi level (E_f) is presented as a dashed vertical line, in which all the DOS cross the Fermi level, indicating that the metallicity of these clusters corresponded with the above analysis of the HOMO–LUMO gap. The energy levels for s, p, and d peaks are distinctly separated, and gradually broaden and non-localized as the cluster sizes increase. The total DOS of these selected clusters is mainly contributed from the d-projected DOS together with an amount of the p-projected DOS near the Fermi level, implying the hybridization states of p with d electrons. The valence bands are principally formed by overlaps of the atomic orbitals 5d and 6s. The total DOS is dominated by the contributions of d and p electrons below and above the energy of zero, respectively. However, the contribution of the s-projected DOS cannot be neglected in the whole energy level regions for tantalum clusters. As evidenced by the diagram, complex s and p–d hybridization states are revealed in the atomic orbit projected DOS curve. This means that a strong hybridization occurred between the s, p, and d states, especially for the p–d hybridization, which was mainly responsible for the electronic structure characterization of the tantalum clusters.

Fig. 9 The s-, p-, d-projected partial density of states and total density of states for the lowest energy structure of representative Ta₄ and Ta₁₂ clusters along with the corresponding HOMO and LUMO orbitals surfaces (the dashed orange lines refer to the Fermi level).

There exist four significant isolated peaks near the Fermi level in DOS of ground state geometry for representative cases of the Ta₁₂ magic number cluster. The selected ground state Ta₇, Ta₁₀, Ta₁₂, Ta₁₃, and Ta₁₅ show similar electronic bands due to their similar geometry based on the BCC structure, which is energetically preferred in our structure optimizations. The corresponding active HOMO and LUMO orbital isosurfaces of these clusters are also depicted in the inset figure of Fig. 9, from which one can obtain that both the HOMO and LUMO states of these clusters exhibit delocalized behavior. Besides, a deeper analysis of the molecular orbitals also show that the HOMO and LUMO orbitals are mostly contributed to by the 5d and 6s atomic orbitals. This indicates that 5d and 6s valence electrons in the atom shell play a dominant role in the chemical activities of tantalum clusters.

3.6 Electron affinity, ionization potential, and chemical hardness

Vertical electron affinity (VEA) and vertical ionization potential (VIP) are important properties that reflect the size-dependent evolution of an electronic structure, and are defined by formulas given in the ESI.† The VEA is evaluated by adding one electron to a cluster in its equilibrium geometry and then taking the difference between their binding energies. The VIP is the energy difference between neutral and cationic clusters. The ionization potentials for Ta_3–64 were obtained from their photoionization efficiency spectra by Collings et al.¹¹ Their results showed that the ionization potentials of small tantalum clusters containing less than 60 atoms decrease with size more rapidly than the results predicted by spherical droplet model. However, no accurate theoretical study has been performed to compare the results with experimental VIP values for neutral tantalum clusters. Here, we calculated the VEA and VIP versus cluster size from n = 2 to 17 for the Ta_n cluster using a more accurate DFT method combined with RECP and a corresponding valence basis set. Comparing with the available experimental values in ref. 11, there is a remarkably good agreement with our calculated results as presented in Fig. 10, which implies that the used accurate DFT determination is appropriate and the atomic structures for the ground state of tantalum clusters are reliable. Consequently, our theoretical results confirmed the experimental observation.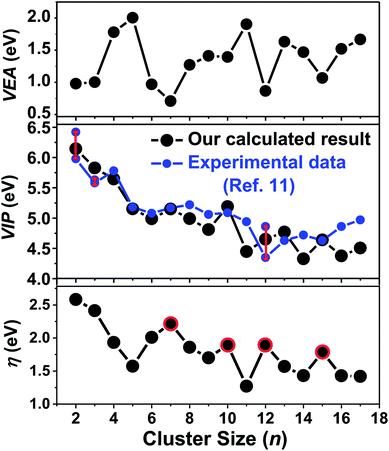

Fig. 10 Size dependence of the calculated vertical electron affinity (VEA), vertical ionization potential (VIP), and chemical hardness (η) of the lowest-energy tantalum clusters.

The calculated values of VEA for all the calculated clusters were much lower than their VIP values, which indicated that these clusters can easily accept one electron. The VIP decreased gradually as the cluster size increased, implying that the large number tantalum cluster will exhibit a high metallic character, and can more easily lose one electron comparatively to clusters with a smaller size. This trend of covalent–metallic transition and chemical reactivity is consistent with the above analysis of gradually decreasing HOMO–LUMO gaps for tantalum clusters. As shown in Fig. 10, both the VEA and VIP curves of tantalum clusters exhibit oscillatory behavior roughly, but do not exhibit odd–even alternations as those of Na_n, Cu_n, Ag_n, and Au_n clusters.⁶⁰ The absence of an electronic shell effect means that the contribution to the stability of tantalum clusters relies on a geometric closed shell rather than an electronic closed shell. An important aspect of metal clusters has been the finding of magic clusters with closed electronic shells.⁶⁷ As an example, for Au clusters,⁶⁰ the even–odd oscillation in cluster stability and electronic properties predicted that non-compact structures with even numbers of atoms were more stable than neighboring clusters with odd numbers of atoms.⁶⁸ The stability of such magic clusters is even more pronounced if they also have a geometrically closed shell of atoms.³⁵ In the case of this paper, an empty cage icosahedral structure of Ta₁₂ was special because of the special structures having a geometric shell. As discussed in this paper, the Ta₁₂ cluster showed very prominent stability, and has a geometrically closed shell but not necessarily a closed electronic shell.

Chemical hardness has been established as an electronic quantity that may be used to characterize the relative stability of molecules and aggregates, in many cases by the principle of maximum hardness (PMH). Structures with large values of hardness are often considered to be harder, namely, less reactive and more stable.⁶¹ The chemical hardness (η) values can be approximated through the equation η = (VIP − VEA)/2 using the VIP and VEA values; its detail definition can be found in the ESI† of this paper. The PMH is concerned with the study of the rationalizing of chemical reactions, and it also asserts that molecular systems present the highest value of hardness at equilibrium.⁶² Assuming that the PMH holds in the system of neutral tantalum clusters, the chemical hardness could be expected to present a behavior with a local maximum at the number of magic clusters. As plotted in Fig. 10, the cluster size with n = 7, 10, 12, 15 (highlighted by red circles in Fig. 10) of Ta_n present higher hardness values than their neighboring clusters. This also means that the stable magic number clusters are harder than their neighboring systems, while at the same time they are less reactive, confirming that the stability of neutral tantalum clusters is a manifestation of the PMH.

3.7 Static dipole polarizability

The static dipole polarizabilities of neutral tantalum clusters with up to 17 atoms were investigated using the numerically finite field method in the framework of DFT. The finite field approach implemented within the GAUSSIAN 03 package can be used to calculate the dipole moment and static electric polarizability components at the B3LYP/LANL2DZ level.⁴⁰ The measured data in most experiments are usually the mean polarizabilities (〈α〉); as presented in the ESI,† this is calculated from the polarizability tensor by 〈α〉 = (α_xx + α_yy + α_zz)/3, in which α_xx, α_yy, and α_zz are the diagonal components (α_ii) of the polarizability tensor. The variation of the calculated values for the mean static dipole polarizabilities (〈α〉) and its average for per atom (〈α〉/n) with the cluster size are plotted in Fig. 11 and listed in Table S1 (ESI†), respectively.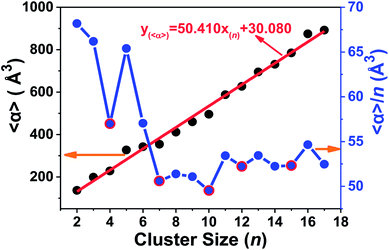

Fig. 11 The static electric polarizability and its average per atom of the lowest-energy structure of Ta_n (n = 2–17) clusters.

It is important to remark that a strong correlation exists in which polarizabilities increases monotonically and linearly with cluster size. This important observation provides a way to estimate the polarizability for larger size clusters. This linear relationship farther suggest that the electrons are more strongly attracted by the nuclei in the tantalum clusters, and their electronic structure will be more compact. Fig. 11 also shows that the static polarizability per atom decreases slowly with increasing cluster size, accompanied with some local oscillations. By increasing the cluster size, the polarizabilities of Ta_n (n = 2–17) clusters exhibit local minima at n = 4, 7, 10, 12, and 15 (highlighted by red circles in Fig. 11), all of which have relatively smaller polarizabilities in comparison with their neighbors in cluster size. The minimum polarizability principle (MPP) states that any system evolves naturally toward a state of minimum polarizability.⁶³ By applying the MPP to chemical reactivity, we can conclude that those clusters with the local minimum polarizability are more stable than the neighboring clusters. This is also in agreement with the discussion above on the stability of neutral tantalum clusters according to their energy difference and hardness analysis. In addition, by comparing the polarizability data of different geometrical isomers listed for the same cluster size in Table S1 (ESI†), we also could find that the static polarizabilities per atom for most stable geometries of Ta_n clusters (except Ta₁₆) were all lower than their close-lying competitive candidates and isomers.

Van Dijk et al. tried to compare the magnetic properties of Tm and Pr clusters with their electric properties experimentally,²¹ and found that there was little correlation between the polarizability, electric dipole, and magnetic properties, which implied that the changes seen from one size to another in the magnetic moment were not of electric origin. An inverse relationship between the ionization potential and polarizability has been proved generally for neutral atomic systems. In this paper, valuable information for neutral tantalum clusters has been achieved by the strong correlation between ionization potentials and static dipole polarizabilities. As displayed in Fig. 12, the cube root of the polarizability per atom (〈α〉^1/3/n) is directly proportional to the inverse of the vertical ionization energy per atom (VIP⁻¹/n) for tantalum clusters. The ionization potentials and electric dipole polarizabilities of clusters can be measured experimentally with laser photoionization spectroscopy and molecular beam deflection, respectively. This strong linear correlation in here-reported theoretical prediction can be used to estimate the ionization potentials and electric dipole polarizabilities. It also provides a way to determine in the future experimental measurements of the atomic geometrical structure for neutral tantalum clusters.

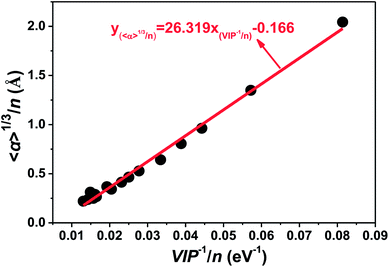Fig. 12 Relationship between polarizability (〈α〉^1/3/n) and the inverse of vertical ionization potential (VIP⁻¹/n) for the most stable geometries of tantalum clusters.

4 Conclusions

We reported a comprehensive investigation into neutral tantalum clusters Ta_n (n = 2–17) by using DFT at the B3LYP/LANL2DZ level. The optimal geometries of tantalum clusters preferred a compact growth route, leading to a BCC structure. The presented size dependence properties could be used to predict evolutional trends as the cluster size increased. This includes perfectly fitting functional curves for the average bonding distance and binding energy per atom, the strong linear evolution for the binding energy and static dipole polarizability, and the obvious odd–even oscillation behavior for magnetic moments. The correlations between the relative stability with the second differences total energy, chemical hardness, and static electric polarizability, respectively, were coincident with each other when used to characterize those more reliable assignments of the global minima. Combined with the analysis of the charge density difference isosurface, the Ta₁₂ cluster showed very prominent stability; although this was not found in the experiment using mass spectrometry. Vibrational spectroscopy as a fingerprint can distinguish those competitive candidates that are the ground state structure among isomers close in energy. The calculated ionization potential and magnetic moments were reliable at a reasonable level compared with the available experimental data. Also, the HOMO and LUMO states exhibited delocalized behavior, and a strong hybridization occurred between s, p, and d states. For neutral tantalum clusters, the ionization potentials and static dipole polarizabilities were linearly related, while an inverse relationship was achieved between the HOMO–LUMO gap and the electric dipole moment. The investigated size dependence and correlations among the different descriptor parameters were shown to provide a way to confirm and predict experimental results.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the Natural Nature Science Foundation of China (Project No. 11375159).

References

1. R. L. Johnston, Atomic and Molecular Clusters, Taylor & Francis, London, 2002.
2. K. D. Sattler, Handbook of Nanophysics: Clusters and Fullerenes, CRC Press, FL, US, 2011.
3. W. Chen and S. Chen, Functional Nanometer-Sized Clusters of Transition Metals: Synthesis, Properties and Applications, The Royal Society of Chemistry, Cambridge, UK, 2014.
4. D. E. Blumlinga, S. G. Sayresa, M. W. Rossa and A. W. Castleman Jr, Strong-field ionization of small niobium and tantalum clusters, Int. J. Mass Spectrom., 2013, 333, 55–58.
5. A. Diaz-Bachs, M. I. Katsnelson and A. Kirilyuk, Kramers degeneracy and relaxation in vanadium, niobium and tantalum clusters, New J. Phys., 2018, 20, 043042.
6. D. Neuwirth, J. F. Eckhard, B. R. Visser, M. Tschurl and U. Heiz, Two reaction regimes in the oxidation of larger cationic tantalum clusters (Ta_n⁺, n = 13–40) under multi-collision conditions, Phys. Chem. Chem. Phys., 2016, 18, 8115.
7. J. F. Eckhard, D. Neuwirth, C. Panosetti, H. Oberhofer, K. Reuter, M. Tschurl and U. Heiza, Consecutive reactions of small, free tantalum clusters with dioxygen controlled by relaxation dynamics, Phys. Chem. Chem. Phys., 2017, 19, 5985.
8. G. Zwaschka, M. Rondelli, M. Krause, M. D. Rötzer, M. N. Hedhili, U. Heiz, J.-M. Basset, F. F. Schweinberger and V. D'Elia, Supported sub-nanometer Ta oxide clusters as model catalysts for the selective epoxidation of cyclooctene, New J. Chem., 2018, 42, 3035.
9. W. Fa, C. Luo and J. Jinming Dong, Coexistence of ferroelectricity and ferromagnetism in tantalum clusters, J. Chem. Phys., 2006, 125, 114305.
10. M. Sakurai, K. Watanabe, K. Sumiyama and K. Suzuki, Magic numbers in transition metal (Fe, Ti, Zr, Nb, and Ta) clusters observed by time-of-flight mass spectrometry, J. Chem. Phys., 1999, 111, 235–238.
11. B. A. Collings, D. M. Rayner and P. A. Hackett, Ionization potentials of tantalum clusters with three to 64 atoms, Int. J. Mass Spectrom. Ion Processes, 1993, 125, 207–214.
12. P. Gruene, A. Fielicke and G. Meijer, Experimental vibrational spectra of gas-phase tantalum cluster cations, J. Chem. Phys., 2007, 127, 234307.
13. A. Fielicke, P. Gruene, M. Haertelt, J. H. Dan and G. Meijer, Infrared Spectroscopy and Binding Geometries of Oxygen Atoms Bound to Cationic Tantalum Clusters, J. Phys. Chem. A, 2010, 114, 9755–9761.
14. J. Du, X. Sun and G. Jiang, A theoretical study on Ta_n⁺ cluster cations: Structural assignments, stability, and electronic properties, J. Chem. Phys., 2012, 136, 094311.
15. J. Du, X. Sun, J. Chen, L. Zhang and G. Jiang, An icosahedral Ta₁₂²⁺ cluster with spherical aromaticity, Dalton Trans., 2014, 43, 5574.
16. P. Gruene, D. M. Rayner, B. Redlich, A. F. G. van der Meer, J. T. Lyon, G. Meijer and A. Fielicke, Structures of Neutral Au₇, Au₁₉, and Au₂₀ Clusters in the Gas Phase, Science, 2008, 321, 674–676.
17. D. G. Leopold and W. C. Lineberger, A Study of the Low-Lying Electronic States of Fe₂ and Co₂ by Negative Ion Photoelectron Spectroscopy, J. Chem. Phys., 1986, 85, 51–55.
18. S.-R. Liu, H.-J. Zhai and L.-S. Wang, s–d Hybridization and Evolution of the Electronic and Magnetic Properties in Small Co and Ni Clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 113401.
19. C. Bartels, C. Hock, J. Huwer, R. Kuhnen, J. Schwöbel and B. von Issendorff, Probing the Angular Momentum Character of the Valence Orbitals of Free Sodium Nanoclusters, Science, 2009, 323, 1323–1327.
20. J. Jalink, J. M. Bakker, T. Rasing and A. Kirilyuk, Channeling Vibrational Energy To Probe the Electronic Density of States in Metal Clusters, J. Phys. Chem. Lett., 2015, 6, 750–754.
21. C. v. Dijk, J. Bowlan, W. A. de Heer, T. Rasing and A. Kirilyuk, Unusual Temperature Dependence of Magnetization and Possible Magnetic Noncollinearity in Tm and Pr Clusters, J. Phys. Chem. C, 2015, 119, 11153–11159.
22. A. Fielicke, A. Kirilyuk, C. Ratsch, J. Behler, M. Scheffler, G. von Helden and G. Meijer, Structure Determination of Isolated Metal Clusters via Far-Infrared Spectroscopy, Phys. Rev. Lett., 2004, 93, 023401.
23. C. Ratsch, A. Fielicke, A. Kirilyuk, J. Behler, G. Helden, G. Meijer and M. Scheffler, Structure determination of small vanadium clusters by density-functional theory in comparison with experimental far-infrared spectra, J. Chem. Phys., 2005, 122, 124302.
24. A. Fielicke, C. Ratsch, G. von Helden and G. Meijer, Isomer selective infrared spectroscopy of neutral metal clusters, J. Chem. Phys., 2005, 122, 091105.
25. Z. Hu, B. Shen, J. R. Lombardi and D. M. Lindsay, Spectroscopy of mass-selected tantalum dimers in argon matrices, J. Chem. Phys., 1992, 96, 8757–8760.
26. L. Fang, X. Shen, X. Chen and J. R. Lombardi, Raman spectra of ruthenium and tantalum trimers in argon matrices, Chem. Phys. Lett., 2000, 332, 299–302.
27. J. L. Jules and J. R. Lombardi, Transition Metal Dimer Internuclear Distances from Measured Force Constants, J. Phys. Chem. A, 2003, 107, 1268–1273.
28. D. Michael, Morse, Clusters of Transition-Metal Atoms, Chem. Rev., 1986, 86, 1049–1109.
29. X. Sun, J. Du, P. Zhang and G. Jiang, A Systemic DFT Study on Several 5d-Electron Element Dimers: Hf₂, Ta₂, Re₂, W₂, and Hg₂, J. Cluster Sci., 2010, 21, 619–636.
30. B. Wang, H.-J. Zhai, X. Huang and L.-S. Wang, On the Electronic Structure and Chemical Bonding in the Tantalum Trimer Cluster, J. Phys. Chem. A, 2008, 112, 10962–10967.
31. M. W. Heaven, G. M. Stewart, M. A. Buntine and G. F. Metha, Neutral Tantalum-Carbide Clusters: A Multiphoton Ionization and Density Functional Theory Study, J. Phys. Chem. A, 2000, 104, 3308–3316.
32. Z. J. Wu, Y. Kawazoe and J. Meng, Geometries and electronic properties of Ta_n, Ta_nO and TaO_n (n=1–3) clusters, J. Mol. Struct.: THEOCHEM, 2006, 764, 123–132.
33. V. Dryza, M. A. Addicoat, J. R. Gascooke, M. A. Buntine and G. F. Metha, Ionization Potentials of Tantalum–Carbide Clusters: An Experimental and Density Functional Theory Study, J. Phys. Chem. A, 2005, 109, 11180–11190.
34. A. S. Chaves, M. J. Piotrowski, L. Juarez and F. Da Silva, Evolution of the structural, energetic, and electronic properties of the 3d, 4d, and 5d transition-metal clusters TM_n systems for n = 2–15: a density functional theory investigation, Phys. Chem. Chem. Phys., 2017, 19, 15484.
35. V. Kumar, High symmetry Nb_n and Ta_n (n = 12, 15, and 17) clusters: High magnetic moments and the finding of superatoms with doping, Comput. Theor. Chem., 2013, 1021, 149–154.
36. J. Wang, M. Yang, G. Wang and J. Zhao, Dipole polarizabilities of germanium clusters, Chem. Phys. Lett., 2003, 367, 448–454.
37. K. Deng, J. Yang and C. T. Chan, Calculated polarizabilities of small Si clusters, Phys. Rev. A, 2000, 61, 025201.
38. E. M. Fernández, J. M. Soler and L. C. Balbás, Planar and cagelike structures of gold clusters: Density-functional pseudopotential calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235433.
39. J. C. Idrobo, W. Walkosz, S. F. Yip, S. Öğüt, J. Wang and J. Jellinek, Static polarizabilities and optical absorption spectra of gold clusters (Au_n, n=2–14 and 20) from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 205422.
40. X.-B. Li, H.-Y. Wang, R. Lv, W.-D. Wu, J.-S. Luo and Y.-J. Tang, Correlations of the Stability, Static Dipole Polarizabilities, and Electronic Properties of Yttrium Clusters, J. Phys. Chem. A, 2009, 113, 10335–10342.
41. X.-B. Li, H.-Y. Wang, J.-S. Luo, Y.-D. Guo, W.-D. Wu and Y.-J. Tang, Static dipole polarizabilities of Sc_n (n≤15) clusters, Chin. Phys. B, 2009, 18, 3414–3421.
42. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin and J. C. Burant, et al., Gaussian 03, Revision D. 01, Gaussian, Inc., Pittsburgh, PA, 2003.
43. H. A. Kurtz, J. James, P. Stewart and K. M. Dieter, Calculation of the nonlinear optical properties of molecules, J. Comput. Chem., 1990, 11, 82–87.
44. V. Kumar and Y. Kawazoe, Atomic and electronic structures of niobium clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 125403.
45. H. Grönbeck, A. Rosén and W. Andreoni, Structural, electronic, and vibrational properties of neutral and charged Nb_n (n=8, 9, 10) clusters, Phys. Rev. A, 1998, 58, 4630.
46. P. V. Nhat and M. T. Nguyen, Structures, Spectra, and Energies of Niobium Clusters from Nb₁₃ to Nb₂₀, J. Phys. Chem. A, 2012, 116, 7405–7418.
47. J. Du, X. Sun, D. Meng, P. Zhang and G. Jiang, Geometrical and electronic structures of small W_n (n=2–16) clusters, J. Chem. Phys., 2009, 131, 044313.
48. H. Cheng and L.-S. Wang, Dimer Growth, Structural Transition, and Antiferromagnetic Ordering of Small Chromium Clusters, Phys. Rev. Lett., 2009, 77, 51–54.
49. L. Peters, S. Ghosh, B. Sanyal, Chris van Dijk, J. Bowlan, W. de Heer, D. Anna, I. Di Marco, O. Eriksson, I. K. Mikhail, B. Johansson and A. Kirilyuk, Magnetism and exchange interaction of small rare-earth clusters; Tb as a representative, Sci. Rep., 2016, 6, 19676.
50. C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, Inc., New York, 1996.
51. A. Jiang, T. A. Tyson and A. Lisa, The structure of small Ta clusters, J. Phys.: Condens. Matter, 2005, 17, 6111–6121.
52. D.-B. Zhang and S. Jiang, Ground state, growth, and electronic properties of small lanthanum clusters, J. Chem. Phys., 2004, 120, 5104.
53. V. Chernyy, R. Logemann, A. Kirilyuk and J. M. Bakker, Direct IR Spectroscopic Detection of a Low-Lying Electronic State in a Metal Carbide Cluster, ChemPhysChem, 2018, 19, 1424–1427.
54. R. A. Knut, Structure characterization of metal oxide clusters by vibrational spectroscopy: possibilities and prospects, Phys. Chem. Chem. Phys., 2012, 14, 9270–9281.
55. J. Wang, Structural, electronic, and magnetic properties of Sc_n (n=2–18) clusters from density functional calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 155422.
56. J. Wang, M. Yang, J. Jellinek and G. Wang, Dipole polarizabilities of medium-sized gold clusters, Phys. Rev. A, 2006, 74, 023202.
57. J. Wang and Ju-G. Han, A computational investigation of copper-doped germanium and germanium clusters by the density-functional theory, J. Chem. Phys., 2005, 123, 244303.
58. R. Moro, X. Xu, S. Yin and A. W. de Heer, Ferroelectricity in Free Niobium Clusters, Science, 2003, 300, 1265–1269.
59. R. Moro, S. Yin, X. Xu and A. W. de Heer, Spin Uncoupling in Free Nb Clusters: Support for Nascent Superconductivity, Phys. Rev. Lett., 2004, 93, 086803.
60. X.-B. Li, H.-Y. Wang, X.-D. Yang, Z.-H. Zhu and Y.-J. Tang, Size dependence of the structures and energetic and electronic properties of gold clusters, J. Chem. Phys., 2007, 126, 084505.
61. R. G. Parr and R. G. Pearson, Absolute Hardness: Companion Parameter to Absolute Electronegativity, J. Am. Chem. Soc., 1983, 105, 7512–7516.
62. R. G. Pearson, Chemical Hardness: Applications from Molecules to Solids, Wiley-VCH Verlag GMBH, Weinheim, Germany, 1997.
63. K. C. Pratim, P. Fuentealba, P. Jaque and A. T. Labbé, Validity of the Minimum Polarizability Principle in Molecular Vibrations and Internal Rotations: An ab initio SCF Study, J. Phys. Chem. A, 1999, 103, 9307–9312.
64. F. Viñes, R. B. G. José and F. Illas, Understanding the reactivity of metallic nanoparticles: beyond the extended surface model for catalysis, Chem. Soc. Rev., 2014, 43, 4922.
65. B. J. Orr and J. F. Ward, Perturbation theory of the non-linear optical polarization of an isolated system, Mol. Phys., 1971, 20, 513–526.
66. J. L. Oudar, Optical nonlinearities of conjugated molecules. Stilbene derivatives and highly polar aromatic compounds, J. Chem. Phys., 1977, 67, 446–457.
67. V. Kumar, K. Esfarajani and Y. Kawazoe, Ab initio computer simulations on microclusters: structures and electronic properties, Springer-Verlag, Berlin, Germany, 2002.
68. B. Yoon, P. Koskinen, B. Huber, O. Kostko, B. von Issendorff, H. Häkkinen, M. Moseler and U. Landman, Size-dependent structural evolution and chemical reactivity of gold clusters, ChemPhysChem, 2007, 8, 157–161.

---

Footnote

† Electronic supplementary information (ESI) available: The computational details including DFT method, definition of reactivity descriptors, and finite field treatment method; the analysis of geometrical isomers and their energy difference; the calculated parameters of neutral Ta_n (n = 2–17) clusters for all relative stable geometrical isomers (Table S1); the DOS of representative Ta_n (n = 7, 10, 13 and 15) clusters (Fig. S1). See DOI: 10.1039/c8ra09240k

---