Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of sp2 and sp3 hybridized bonds on the structural, mechanical, and electronic properties in a hard BN framework
Hongxia Bu *a,
Haibin Zheng*a,
Hongcai Zhoub,
Hongyu Zhangc,
Zaifa Yanga,
Zhie Liua,
Hui Wang
*a,
Haibin Zheng*a,
Hongcai Zhoub,
Hongyu Zhangc,
Zaifa Yanga,
Zhie Liua,
Hui Wang a and
Qi Xua
a and
Qi Xua
aCollege of Physics and Electronic Engineering, Qilu Normal University, Jinan, Shandong 250200, China. E-mail: buhx666@163.com; haibin_zheng@126.com; Tel: +86-531-66778300
bScience and Information College, Qingdao Agricultural University, Qingdao, Shandong 266109, China
cDepartment of Physics, East China University of Science and Technology, Shanghai 200237, China
First published on 21st January 2019
Abstract
A first-principles approach is used to systematically investigate the role of sp2 and sp3 hybridized bonds on the structural, mechanical, and electronic properties in a new BN phase (denoted Hex-(BN)12). Hex-(BN)12 has the same number of sp2 and sp3 hybridized atoms. The calculated cohesion energy, phonon frequencies, and elastic constants unambiguously confirm the structural stability of this compound. Due to the different types of hybridization and B–N covalent bonds with ionic characteristics, Hex-(BN)12 has unequal bond lengths and bond angles in these hybrid orbitals. These cause the relative energetic stability to be slightly lower than c-BN and w-BN. The hardness of Hex-(BN)12 is estimated to range from 33 to 40 GPa. The bond-breaking order under stress is sp3–sp3, sp2–sp3, and sp2–sp2. DFT calculations with the gradient approximation (GGA) and HSE06 functional indicate the electronic structure contains an indirect band gap at 3.21 and 4.42 eV, respectively. The electronic states in the region near the Fermi level primarily arise from the 2p orbitals in sp2-hybridized atoms. In general, sp3 bonded B and N atoms guarantee higher mechanical properties, and sp2 bonded atoms ensure ductility and even conductivity, although all changes vary with spatial structure. Hex-(BN)12 can be obtained from multilayer yne-BN, and BN nanosheets, nanotubes and nanoribbons under pressure.
Introduction
Boron nitride (BN) is a group III–V compound that can theoretically exhibit a variety of frameworks because B and N atoms can form chemical bonds by means of sp, sp2, and sp3 hybridizations or combinations. It is an intriguing compound that has been studied for many years, and numerous BN structures were theoretically proposed or experimentally synthesized in the past few decades. Examples include sp and sp2 graphyne-BN (yne-BN) and graphdiyne-BN (diyne-BN);1–5 sp2-hybridized nanocages,6–8 nanotubes,9–12 nanoribbons13,14 and nanosheets;15–18 sp2 and sp3 porous BN networks,19 M-BN,20 HBNFs,21 and 3D BN allotropes from compressed single-walled BN nanotubes (BNNTs);22 sp3-hybridized c-BN, bct-BN, Z-BN,23 and O-BN.24 They usually have high thermal conductivity, chemical stability, excellent mechanical properties, and unique electronic and optical properties, facilitating practical applications in the many fields related to hydrogen energy,19,25,26 advanced abrasives,27 ultraviolet laser devices,28,29 nanoscale spintronic devices,30 nanomedicine,31,32 and flexible resistive memory devices.33Meanwhile, it is worth noting these BN phases exhibit unique physical and chemical properties. For example, they form many crystal structures, ranging from zero to three dimensional. The mechanical properties of these reported BN phases are different. c-BN and w-BN are typical superhard materials; M-BN is hard, while h-BN formed from sp2-hybridized atoms is more ductile and is widely used as a lubricant. Furthermore, given the same fundamental sp2 and sp3 hybridized bonds, their electronic structures are also different. The metallicity of T-B3N3 originates from sp2 hybridized B atoms,34 while M-BN is metallic with one-dimensional metallicity from sp2 B/N atoms.20 However, dz2-BN, lz2-BN, 3D(n,0)-I (n = 6, 8, 10, 12), and Na-HBNFs are semiconductors.19,21,22 All these characteristics indicate that the properties of BN are highly dependent on the crystalline structure, including the type of hybridization. However, fewer studies have focused on the influence from sp2 and sp3 hybridized bonds in 3D multiporous BN polymorphs. Moreover, the influence of sp2 and sp3 hybridization on stability, hardness, and electronic properties is an interesting issue that is worth studying.
In this work, we present a 3D hard BN skeleton consisting of both sp2 and sp3 hybridized bonds. This BN phase has hexagonal structure with 12 pairs of BN in a conventional unit cell. Thus, we have denoted this BN phase as Hex-(BN)12. The structure of Hex-(BN)12 is composed of narrow BN nanoribbons (BNNRs) interconnected by ultrathin BNNTs. Hex-(BN)12 is energetically, dynamically, and mechanically stable, and it is energetically more favorable than yne-BN. Calculations with the gradient approximation (GGA) and HSE06 functional show the presence of an indirect band gap of 3.21 and 4.42 eV at the Brillouin zone in Hex-(BN)12, respectively. We conducted a systematic first-principles study on the effect of sp2 and sp3 hybridizations on the structural, mechanical, and electronic properties of Hex-(BN)12.
Computational methods
First-principles calculations were performed using the CASTEP code, which is based on density functional theory (DFT).35,36 Electron–electron interactions were modeled using a generalized gradient approximation (GGA) according to Perdew, Burke, and Ernzerhof.37 The cutoff energy was set to 400 eV for the plane-wave basis within an ultrasoft pseudopotential.38 The k-point separation for Brillouin zone sampling was set to 0.02 Å−1 in accordance with the Monkhorst–Pack method.39 Lattice constants and internal coordinates were optimized within the Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization scheme.40 Phonon dispersion spectra were calculated using linear response and finite displacement theories in the CASTEP code. The standard GGA functional always underestimates the band gap in semiconductors, thus the band structure was calculated with a more accurate HSE06 hybrid functional41 as implemented in the CASTEP code within a norm-conserving pseudopotential.42 The convergence plane wave cutoff energy was set to 700 eV.The elastic constants (Cij) were theoretically calculated using Hooke's law (σi = Cijεj) for small stresses (σ) and strains (ε).43 Young's, bulk, and shear moduli were estimated using the Voigt–Reuss–Hill approximation.44 Vickers hardness was calculated using Chen's45 and Gao's46 hardness models.
On the basis of the equilibrium structure, a series of incremental stress were applied to the structure in order to determine its structural response to stress. At each step, a desired target stress component was defined along particular directions. The final structure and the corresponding strain were defined as lattice vectors and the atomic positions were fully relaxed simultaneously. In this way, the stress and strain relationship for tensile and shear deformation and the ideal strength were obtained as the structure collapsed.
Results and discussion
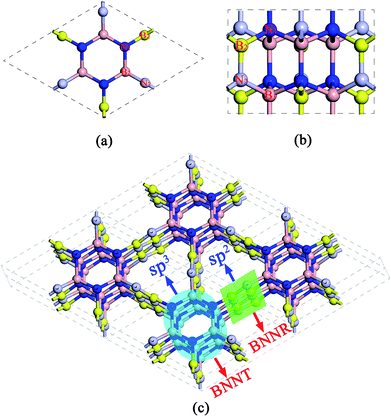
The predicted crystal structure is shown in Fig. 1 from different views. B and N atoms in the basal plane alternately bind to two adjacent layers through the polar B–N covalent bond. The structure has hexagonal symmetry with P63cm space group (C6V3, no. 185). It contains 12 BN pairs per primitive cell, thus the compound is referred to as Hex-(BN)12 hereafter. The fully relaxed lattice constants are a = b = 6.995 Å and c = 4.288 Å. Two inequivalent B atoms and two inequivalent N atoms are present in each primitive cell. B atoms occupy the 6c (0, 0.588, 1.143), 6c (0.216, 0, 1.164) Wyckoff positions, while N atoms occupy the 6c (0, 0.214, 0.793), 6c (0.586, 0, 0.811) Wyckoff positions. The framework of Hex-(BN)12 is composed of sp2- and sp3-hybridized B and N atoms, thus it can be thought of as a superlattice of ultrathin BNNTs and narrow BNNRs, as shown in Fig. 1c. The sp3-hybridized B and N atoms form ultrathin BNNTs, while sp2-hybridized atoms form narrow BNNRs. Notably, the BNNT in this framework differs significantly from the isolated BNNT because B and N atoms in the former are sp3-hybridized.The density of Hex-(BN)12 is 2.72 g cm−3 as the ratio of sp2 BN pairs to sp3 BN pairs is 6/6. The density was theoretically calculated using ρ = m/V, where ρ is the density, and m and V are the mass and volume of the primitive cell, respectively. This density value lies between the values for pure sp2-hybridized h-BN (2.27 g cm−3) and pure sp3-hybridized c-BN (3.47 g cm−3).
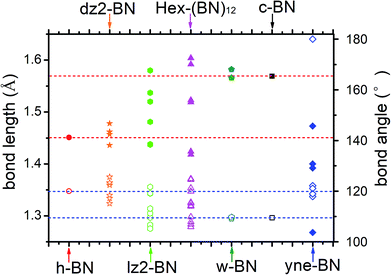
The optimized bond lengths and angles are shown in Fig. 2. There exists six distinct bonds and twelve bond angles. The lengths of two distinct sp2–sp2 bonds in the BNNR component are 1.418 and 1.424 Å; these values are slightly shorter than in h-BN (1.451 Å) and in a pristine BN sheet (1.452 Å).47 The lengths of the sp3–sp3 bonds in the BNNT component are 1.592 and 1.604 Å, which is slightly longer than the calculated value for c-BN's (1.569 Å). The lengths of the sp2–sp3 bonds connecting BNNTs and BNNRs are 1.519 and 1.523 Å. The bond angles deviate slightly from the corresponding standard values in c-BN (109.5°) and in an h-BN monolayer (120°). For example, ∠B–N–B and ∠N–B–N in the sp2–sp2 bonds in BNNRs have slightly different angles of 119.91° and 121.1° (listed in Fig. 2), respectively, which differs slightly from the angle in an h-BN monolayer (120°). The same applies to other bond angels located at different positions. The different bond patterns and angles can be attributed to two possible explanations. First, different hybrid orbitals of B and N atoms have an important influence on the bond lengths and angles. Second, although B–N bonds in this phase are covalent in nature, they have ionic characteristics. The ionic characteristics have little influence on the bond lengths and angles. We think the significant differences in bond lengths and angles result from the former explanation, while small differences result from the latter. Moreover, Mulliken analysis further verifies the polarity of these B–N bonds, and the results are reasonably consistent with results published in the literature.1
To evaluate the relative stability of the predicted porous BN phase, we calculated the cohesive energy and compared it with several known BN phases. The cohesive energy is defined by the following equation:
| Ecoh = (nEB + nEN − E(BN)n)/n |
| Stru. | Sys | Groups | Rsp2 | Rsp3 | ρ ours/ref. | Ecoh | Eg ours/ref. |
|---|---|---|---|---|---|---|---|
| a Reference HSE result.b Reference experimental result.48 | |||||||
| h-BN | Hex | P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2/187 m2/187 |
100 | 0 | 2.27/2.270 (ref. 21) | 17.33 | 4.68/4.778 (ref. 21) |
| dz2-BN | Orth | Imm2/44 | 100 | 0 | 2.547 | 16.87 | 3.33/3.42 (ref. 19) |
| lz2-BN | Orth | Ima2/46 | 80 | 20 | 1.917 | 17.09 | 2.04/1.53 (ref. 19) |
| Hex-(BN)12 | Hex | P63cm/185 | 50 | 50 | 2.722 | 17.02 | 3.25/4.42a |
| 3D(6,0)-I | Tetra | P42mc/105 | 33.33 | 66.67 | 3.34/3.21 (ref. 22) | 16.81 | 3.34/3.21 (ref. 22) |
| c-BN | Cub | F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m/216 3m/216 |
0 | 100 | 3.47/3.48b | 17.18 | 4.45/4.440 (ref. 21) |
| bct BN | Tetra | P42/mnm/136 | 0 | 100 | 3.31/3.688 (ref. 21) | 16.98 | 4.77/4.782 (ref. 21) |
| w-BN | Hex | P63mc/186 | 0 | 100 | 3.46/3.49b | 17.15 | 5.20/5.207 (ref. 21) |
| yne-BN | Hex | P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) 2m/189 2m/189 |
— | — | — | 16.26 | 4.21 |
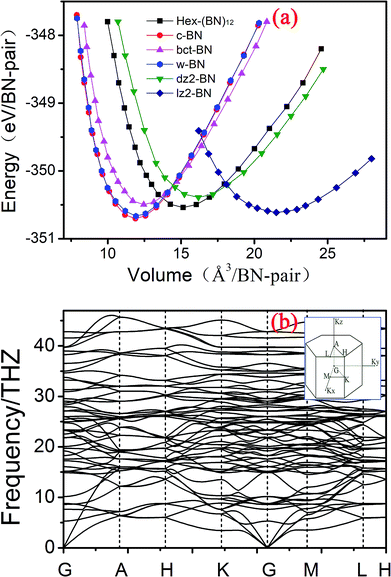 | ||
| Fig. 3 (a) Total energy as a function of volume per BN pair in Hex-(BN)12 compared with previously reported BN phases. (b) Phonon band structure in Hex-(BN)12. | ||
The dynamic stability of Hex-(BN)12 was also checked by calculating phonon dispersion along the high symmetry orientation in the Brillouin zone. We used linear response and finite displacement theories (shown in Fig. 3b) in the DFT framework to calculate the phonon spectrum in Hex-(BN)12. No imaginary frequencies were observed throughout the Brillouin zone, thus confirming the dynamic stability of this novel BN phase.
In addition, we calculated the elastic constants in order to test the mechanical stability of Hex-(BN)12. This phase has five independent elastic constants that correspond to its symmetric structure: C11, C33, C44, C12, and C13 are 498.084, 852.849, 222.766, 155.877, and 80.668 GPa, respectively. Obviously, these elastic constants satisfy the Born criteria for a hexagonal crystal:49 C44 > 0, C11 >|C12|, (C11 + 2C12) × C33 > 2C132. On the other hand, the mechanical stability confirms the plausibility of forming Hex-(BN)12.
The elastic constants of Hex-(BN)12 exhibit clear anisotropy. The elastic constant (C33) along the Z-direction (axial-direction) is slightly larger than the corresponding value in c-BN, while the elastic constants (C11 and C22) along the radial direction (X- and Y-directions) are about 35% smaller than that in c-BN. Nevertheless, the large magnitude of C33 indicates that the material has high resistance to linear compression along the axial direction.
In order to better understand the mechanical properties of this phase, Young's modulus was obtained along the three axes (Yx, Yy and Yz), and the net Young's modulus (E) was estimate from the following equation:44
| E = 9BG/(3B + G) |
The bulk modulus (B) and shear modulus (G) were then estimated from the elastic constants using Voigt–Reuss–Hill (VRH) approximations;44 these values are listed in Table 2. It is worth noting that Young's modulus along the Z-direction is comparable to the corresponding values from c-BN and w-BN, while Young's moduli along the X- and Y-directions are only about half the values in c-BN.
| Stru. | dz2-BN | lz2-BN | Hex-(BN)12 | 3D(6,0)-I | c-BN | bct BN | w-BN | Ref. |
|---|---|---|---|---|---|---|---|---|
| a Chen's result.b Gao's result. | ||||||||
| Yx | 699.68 | 687.13 | 445.64 | 570.28 | 719.25 | 711.97 | 910.27 | Our work |
| Yy | 81.28 | 90.48 | Our work | |||||
| Yz | 443.59 | 50.61 | 832.95 | 768.36 | 934.74 | 1004.92 | Our work | |
| E | 309.43 | 259.07 | 516.32 | 440.10 | 854.40 | 730.25 | 858.49 | Our work |
| 326.60 | 246.40 | 856 | 749 | 19, 50 and 51 | ||||
| B | 182.75 | 168.10 | 271.67 | 249.79 | 368.06 | 345.54 | 368.05 | Our work |
| 212.40 | 175.50 | 258.40 | 376.19 | 348.35 | 375.24 | 19, 22 and 23 | ||
| G | 127.04 | 104.19 | 218.181 | 182.41 | 383.61 | 318.12 | 386.273 | Our work |
| 131.30 | 97.30 | 156.10 | 381.52 | 309.44 | 384.17 | 19, 22 and 23 | ||
| k | 0.70 | 0.62 | 0.80 | 0.73 | 1.04 | 0.92 | 1.05 | Our work |
| Hv | 19.24 | 14.32 | 33.13 | 26.11 | 65.18 | 49.85 | 66.01 | Our worka |
| 62.40 | 49.14 | 59.59 | 53.39 | 64.25 | 61.13 | 63.62 | Our workb | |
| 56.10 | 46–80 | 58.77 | 50–60 | 22, 51 and 52 | ||||
| Beh | Bri | Bri | Bri | Bri | Bri | Bri | Bri | Our work |
Modulus and hardness are often discussed together, even though the underlying deformations are fundamentally different.45,53–55 Here, considering the fact this phase is highly anisotropic and has a porous structure, we calculated the theoretical Vickers hardness (Hv) using two different semi-empirical models. In the model of Chen et al.,45 the hardness is defined in terms of G and B using the following equation:
| Hv = 2(k2G)0.585 − 3 |
| Hv = 350 × Ne2/3 × e−1.191fi/d2.5 |
The factors affecting total hardness are complex and include the type of elastic modulus, bond length, bond density, bond strength, and degree of covalent bonding. Remarkably, strength and hardness are often positively correlated. Ideal strength represents the maximum stress at which a perfect crystal becomes unstable and is more accurate for describing the mechanical strength than elastic constants.56–58 In this work, we evaluated the ideal tensile strengths of Hex-(BN)12 along the [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0], [
0], [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2
2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0], and [0001] directions, as shown in Fig. 4. The corresponding tensile stresses of Hex-(BN)12 were found to be 49.00, 48.72, and 51.53 GPa with strains of 0.16, 0.17, and 0.11, respectively. Using the same strategy, the calculated ideal strength data for c-BN along the [111] direction was found to be 64.80 GPa, which agrees well with theoretical results from the literature57,58 and validates the computational methods used in this study. Clearly, Hex-(BN)12 has the lowest ideal tensile strength of 48.72 GPa at a strain of 0.17 along the [
0], and [0001] directions, as shown in Fig. 4. The corresponding tensile stresses of Hex-(BN)12 were found to be 49.00, 48.72, and 51.53 GPa with strains of 0.16, 0.17, and 0.11, respectively. Using the same strategy, the calculated ideal strength data for c-BN along the [111] direction was found to be 64.80 GPa, which agrees well with theoretical results from the literature57,58 and validates the computational methods used in this study. Clearly, Hex-(BN)12 has the lowest ideal tensile strength of 48.72 GPa at a strain of 0.17 along the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2
2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] radial direction in the (0001) surface, similar to monolayer graphyne.59,60 The shear strength in the (0001)[10
0] radial direction in the (0001) surface, similar to monolayer graphyne.59,60 The shear strength in the (0001)[10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0], (10
0], (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)[
0)[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2
2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] and (0001)[
0] and (0001)[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2
2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] slip systems are 38.44, 37.42, and 34.00 GPa at strains of 0.29, 0.21, and 0.19, respectively. The strength of the materials depends on the weakest strength component. All these results are consistent with the Hv values evaluated from Chen's semi-empirical model. We attribute the notable differences between the results from the two semi-empirical models to a large void network with large interstitial spacer. This fact results that the covalent bonds in the phase distributed ununiformly. Even though the sp2 and sp3 hybridized covalent bonds in this phase are strong, the large void reduces its mechanical properties. This is similar to previous research results on highly anisotropic, highly porous compounds.61,62 Therefore, we deduce that the hardness of Hex-(BN)12 should be approximately 33–40 GPa, which is close to the value for a β-SiC crystal, but the density of Hex-(BN)12 is lower than that of β-SiC by about 17%. Hard materials are those with hardness ranging from 20 to 40 GPa, while superhard materials are defined as materials with Hv exceeding 40 GPa.63,64 Both hardness values exceed 20 GPa, suggesting that Hex-(BN)12 at least is a hard material.
0] slip systems are 38.44, 37.42, and 34.00 GPa at strains of 0.29, 0.21, and 0.19, respectively. The strength of the materials depends on the weakest strength component. All these results are consistent with the Hv values evaluated from Chen's semi-empirical model. We attribute the notable differences between the results from the two semi-empirical models to a large void network with large interstitial spacer. This fact results that the covalent bonds in the phase distributed ununiformly. Even though the sp2 and sp3 hybridized covalent bonds in this phase are strong, the large void reduces its mechanical properties. This is similar to previous research results on highly anisotropic, highly porous compounds.61,62 Therefore, we deduce that the hardness of Hex-(BN)12 should be approximately 33–40 GPa, which is close to the value for a β-SiC crystal, but the density of Hex-(BN)12 is lower than that of β-SiC by about 17%. Hard materials are those with hardness ranging from 20 to 40 GPa, while superhard materials are defined as materials with Hv exceeding 40 GPa.63,64 Both hardness values exceed 20 GPa, suggesting that Hex-(BN)12 at least is a hard material.
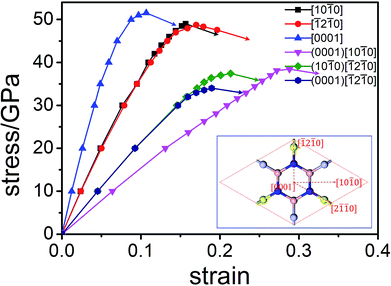 | ||
| Fig. 4 Orientation-dependent stress–strain relations for tensile and shear deformation in Hex-(BN)12. | ||
Table 2 shows that E, B, G, and Hv basically increase while the ductility decreases as the ratio of sp3-bonding atoms increases; lz2-BN and 3D(6,0)-I are exceptions. For instance, the ratio of sp3-hybridized atoms in orthorhombic lz2-BN is higher than in dz2-BN, but the corresponding E, B, G, Hv, and brittleness values are lower than those in dz2-BN. This shows that the relative mechanical properties of BN materials are sensitive to hybridization and spatial structure. Nevertheless, sp3-hybridized B and N atoms are greater determinants of E, B, G, Hv, and brittleness, while the ductility arises from the sp2-hybridized network. These mechanical values and density exhibit similar trends. Density often scales with mechanical properties,65 thus these density values are indicators of mechanical properties from another perspective. High density is consistent with superior mechanical properties,65 which again justifies its classification as a hard material.
In order to know more about this behavior of sp2- and sp3-hybridized B and N atoms under stress, Fig. 5 shows the critical and final states under different stress paths for Hex-(BN)12. We can see that sp3–sp3 bonds in the BNNT component are more vulnerable to rupture than the sp2–sp3 bonds connecting BNNTs and BNNRs, and the sp2–sp2 bonds connecting BNNRs. This result agrees with the bond length results, where the sp3–sp3 bond lengths are longer than the sp2–sp3 bond lengths (by 0.07 Å) and sp2–sp2 bond lengths (by 0.17 Å). This is unlike the case of Hex-C24, where the sp2–sp3 bond is more vulnerable to rupture than sp3–sp3 and sp2–sp2 bonds, although it has a shorter bond length than the sp3–sp3 bond.66 From the critical state along the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2
2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction, one can see that the sp3–sp3 bond ruptures first, followed by the sp2–sp3 bond. We can deduce that covalent bonds between sp2 and sp3-hybridized B/N atoms behave differently under stress, where the sp3–sp3 bond breaks first, followed by the sp2–sp3 bond and sp2–sp2 bond. This conclusion also can be supported by the ductility of the BN materials. c-BN, w-BN, and bct-BN are composed of tetrahedral sp3-hybridized B and N atoms, which cannot tolerate large deformations and are extremely brittle. Meanwhile, h-BN formed from sp2-hybridized atoms can sustain large distortions and is more ductile. These findings are similar to results from carbon. Therefore, Hex-(BN)12 consisting of sp2- and sp3-hybridized B/N atoms is quite interesting. Here, the Pugh modulus ratio (k) is used to separate brittle (above 0.57) and ductile (below 0.57) behavior.67 Our calculations show that k in Hex-(BN)12 is 0.80 (see Table 2), indicating that it is brittle. We attribute the brittleness of Hex-(BN)12 to sp3–sp3 covalent bonds. Moreover, the final states show that Hex-(BN)12 can be broken into BNNRs, BNNTs, BN nanosheets, and yne-BN due to tensile and shear forces.
0] direction, one can see that the sp3–sp3 bond ruptures first, followed by the sp2–sp3 bond. We can deduce that covalent bonds between sp2 and sp3-hybridized B/N atoms behave differently under stress, where the sp3–sp3 bond breaks first, followed by the sp2–sp3 bond and sp2–sp2 bond. This conclusion also can be supported by the ductility of the BN materials. c-BN, w-BN, and bct-BN are composed of tetrahedral sp3-hybridized B and N atoms, which cannot tolerate large deformations and are extremely brittle. Meanwhile, h-BN formed from sp2-hybridized atoms can sustain large distortions and is more ductile. These findings are similar to results from carbon. Therefore, Hex-(BN)12 consisting of sp2- and sp3-hybridized B/N atoms is quite interesting. Here, the Pugh modulus ratio (k) is used to separate brittle (above 0.57) and ductile (below 0.57) behavior.67 Our calculations show that k in Hex-(BN)12 is 0.80 (see Table 2), indicating that it is brittle. We attribute the brittleness of Hex-(BN)12 to sp3–sp3 covalent bonds. Moreover, the final states show that Hex-(BN)12 can be broken into BNNRs, BNNTs, BN nanosheets, and yne-BN due to tensile and shear forces.
 | ||
| Fig. 5 Critical and final states under different stress paths in Hex-(BN)12. Columns (a)–(c) show the critical state, stress paths (as labeled in Fig. 4), and final states when the stress exceed the critical tensile or shear force. | ||
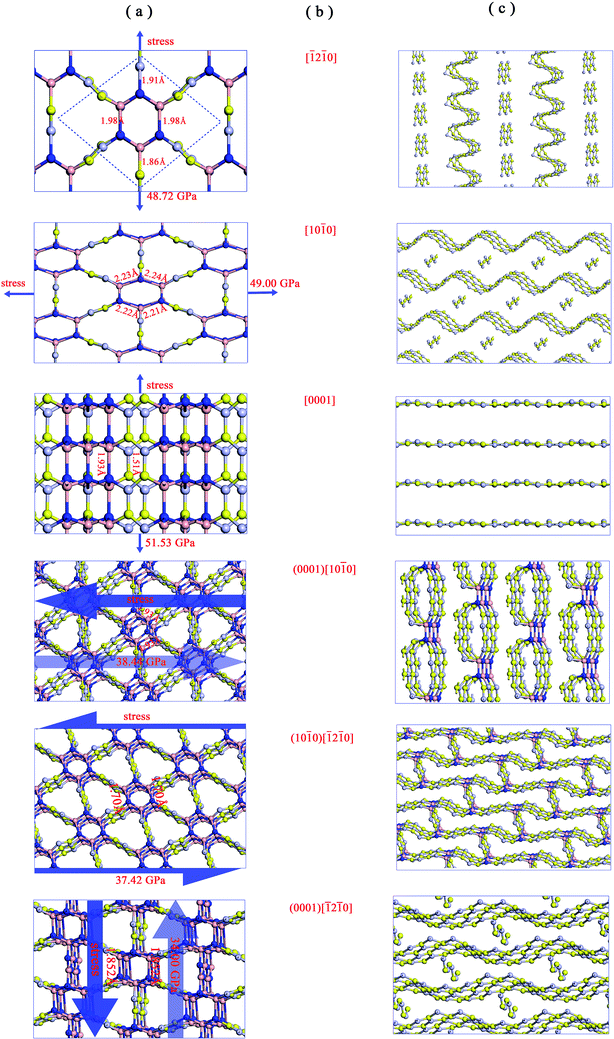
We then examined the electronic structure of Hex-(BN)12. The electronic band lines of Hex-(BN)12 obtained with the PBE functional are shown in Fig. 6a. Obviously, Hex-(BN)12 is a semiconductor with an indirect-band-gap of 3.21 eV at equilibrium. In light of the fact that the PBE functional always underestimates the band gap of semiconducting materials, we conducted more accurate DFT calculations with an HSE hybrid functional; the band gap was found to be approximately 4.42 eV.
 | ||
| Fig. 6 (a) Electronic band structures of Hex-(BN)12 along the high symmetry direction in the Brillouin zone. (b) Electron density of states (PDOS) projected on the s- and p-orbitals in B and N atoms with different hybridization as labeled in Fig. 1a. The energy at the Fermi level was set to zero. All results were obtained from DFT calculations with the PBE functional. | ||
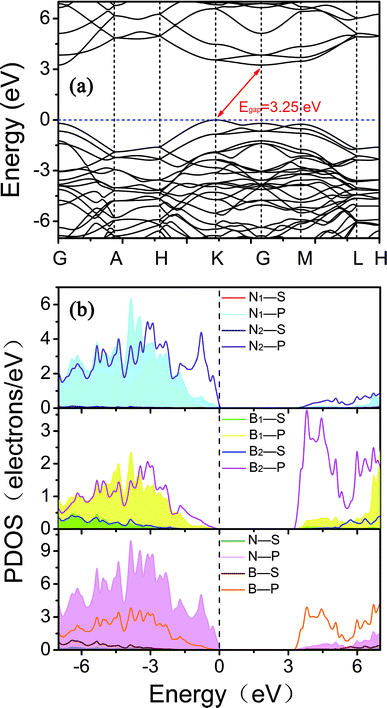
To explain the origins of the electronic band structures, the electron density of states (PDOS) projected on the s- and p-orbitals in B and N atoms (as labelled in Fig. 1) are shown in Fig. 6b. Clearly, the electronic states in the region near the Fermi level originate primarily from the 2p orbitals in the sp2-hybridized B and N atoms in the BNNR component, whereas the contribution from the sp3-hybridized atoms is very small. These features can also be visualized using isosurfaces of the Kohn–Sham wavefunctions for the valence band maximum (VBM) and conduction band minimum (CBM), as shown in Fig. 7. The spatial distribution of the wavefunction implies that sp2-hybridized B and N atoms can gain electrons more easily than sp3-hybridized atoms in Hex-(BN)12. One can conclude that sp2 bonded atoms readily conduct electricity in BN materials with sp2 and sp3 hybridization based on results in the literature.20,34 This result agrees well with the effects of sp2- and sp3-hybridized B and N atoms on strength and ductility.
 | ||
| Fig. 7 Isosurfaces of the Kohn–Sham wavefunctions of the (a) VBM and (b) CBM states in Hex-(BN)12. The isovalue was set to 0.05. Top and side views are plotted in the left and right columns. | ||
A number of results from experiments and theoretical calculations show that using precursors to seek new BN materials is feasible. Dai et al. predicted two types of porous BN networks that can be obtained with BNNRs.19 Xiong et al. and Hao et al. reported phase transitions of BNNT bundles under pressure.22,68 Inspired by the process of computing ideal strengths, we assumed two methods for synthesizing this new material based on the work of the aforementioned authors. First, Hex-(BN)12 can be obtained from direct compression of multilayer yne-BN. We then tentatively studied the structural transition of AB stacking in yne-BN to form Hex-(BN)12. The interlayer spaces are gradually compressed, and the yne-BN layers begin to buckle and bind together, finally converting into stable Hex-(BN)12. No transition state is found for this transition path. In addition, the transformation of yne-BN into Hex-(BN)12 is an exothermic process. The exothermic feature implies that fabrication of Hex-(BN)12 from yne-BN can be achieved under less rigorous conditions. Second, Hex-(BN)12 can be obtained from nanosheets, BNNTs, and BNNRs under pressure.19,22,34,68,69 Note that the major obstacle preventing new BN materials from being obtained is the limitation of a high-quality BN precursor. Today, successful preparation of BN nanosheets,15,70 single-walled BN nanotubes (SWBNNT),71,72 multi-walled BNNTs,73,74 and BNNRs75,76 provides fundamental building blocks for 3D BN polymorphs. A few new BN structures built using either BN nanosheets, nanotubes, or nanoribbons were reported in the literature.19,22,34,68,69,77,78 There is reason to believe that the special properties of Hex-(BN)12 will arouse further experimental efforts in producing this novel family of BN compounds.
Conclusions
First-principles calculations were used to examine a new, hard, and semiconductive BN phase called Hex-(BN)12. The Hex-(BN)12 has equal numbers of sp2− and sp3− hybridized B and N atoms. Its energetic, dynamic, and mechanical stability was also unambiguously confirmed from calculations of the cohesive energy, phonon spectrum, and elastic constants. It can be obtained from multilayer yne-BN, nanosheets, BNNTs, and BNNRs under pressure. Hex-(BN)12 has unequal bond lengths and bond angles in these hybrid orbitals due to its structural characteristics, which reduce its relative energetic stability. The hardness of Hex-(BN)12 was estimated to range from 33 to 40 GPa. The calculated ideal tensile and shear strengths along highly symmetric directions are greater than 48.72 and 34.00 GPa, respectively. The covalent bonds between sp2- and sp3-hybridized B and N atoms behave differently under stress and can be broken into BNNRs, BNNTs, BN nanosheets, or yne-BN when tensile and shear forces are applied. The electronic states in the region near the Fermi level primarily arise from 2p orbitals in the sp2-hybridized atoms. In addition, we can deduce from the present and prior results that sp3-bonded B and N atoms guarantee higher mechanical properties, while sp2-bonded atoms ensure ductility and even conductivity in the BN family, although all these properties will change as the spatial structure changes. We expect that the results presented here will provide a new understanding of the structural, mechanical, and electronical properties of BN materials containing sp2- and sp3-hybridized B and N atoms.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by National Natural Science Foundation of China (No. 11604170), Scientific Research in Universities of Shandong Province (No. J16LJ06), the Natural Science Foundation of Shandong Province, China (No. ZR2014AQ018, ZR2014FL029), National Natural Science Foundation of China (No. 11747132), and Foundation of Qilu Normal University (No. BS2017002, 2017005, 2017L0604).References
- X. Li and X. Cheng, Chem. Phys. Lett., 2018, 694, 102 CrossRef CAS.
- X. Cao, Y. Li, X. Cheng and Y. Zhang, Chem. Phys. Lett., 2011, 502, 217 CrossRef CAS.
- J. Zhou, K. Lv, Q. Wang, X. Chen, Q. Sun and P. Jena, J. Chem. Phys., 2011, 134, 174701 CrossRef PubMed.
- Z. Sun, Z. Shao, C. Wang and L. Yang, Carbon, 2016, 110, 313 CrossRef CAS.
- A. Ruiz-Puigdollers and P. Gamallo, Carbon, 2017, 114, 301 CrossRef CAS.
- D. Golberg, Y. Bando, O. Stéphan and K. Kurashima, Appl. Phys. Lett., 1998, 73, 2441 CrossRef CAS.
- M. Monajjemi and J. E. Boggs, J. Phys. Chem. A, 2013, 117, 1670 CrossRef CAS.
- V. Barone, A. Koller and G. E. Scuseria, J. Phys. Chem. A, 2006, 110, 10844 CrossRef CAS PubMed.
- N. G. Chopra, R. J. Luyken, K. Cherrey, V. H. Crespi, M. L. Cohen, S. G. Louie and A. Zettl, Science, 1995, 269, 966 CrossRef CAS PubMed.
- D. Golberg, Y. Bando, C. Tang and C. Zhi, Adv. Mater., 2007, 19, 2413 CrossRef CAS.
- C. Zhi, Y. Bando, C. Tang and D. Golberg, Mater. Sci. Eng., R, 2010, 70, 92 CrossRef.
- A. Siria, P. Poncharal, A. Biance, R. Fulcrand, X. Blase, S. T. Purcell and L. Bocquet, Nature, 2013, 494, 455 CrossRef CAS PubMed.
- W. Chen, Y. Li, G. Yu, C. Li, S. B. Zhang, Z. Zhou and Z. Chen, J. Phys. Chem. Lett., 2010, 132, 1699 CAS.
- H. Zeng, C. Zhi, Z. Zhang, X. Wei, X. Wang, W. Guo, Y. Bando and D. Golberg, Nano Lett., 2010, 10, 5049 CrossRef CAS.
- C. Zhi, Y. Bando, C. Tang, H. Kuwahara and D. Golberg, Adv. Mater., 2009, 21, 2889 CrossRef CAS.
- Y. Lin, T. V. Williams and J. W. Connell, J. Phys. Chem. Lett., 2010, 1, 277 CrossRef CAS.
- K. H. Lee, H. Shin, J. Lee, I. Lee, G. Kim, J. Choi and S. Kim, Nano Lett., 2012, 12, 714 CrossRef CAS PubMed.
- L. H. Li, J. Cervenka, K. Watanabe, T. Taniguchi and Y. Chen, ACS Nano, 2014, 8, 1457 CrossRef CAS PubMed.
- J. Dai, X. Wu, J. Yang and X. C. Zeng, J. Phys. Chem. Lett., 2014, 5, 393 CrossRef CAS PubMed.
- M. Xiong, K. Luo, Y. Pan, L. Liu, G. Gao, D. Yu, J. He, B. Xu and Z. Zhao, J. Alloys Compd., 2018, 731, 364 CrossRef CAS.
- J. Shang, J. Xiong, X. Xu and Y. Cai, Mater. Chem. Phys., 2018, 217, 5 CrossRef CAS.
- M. Xiong, C. Fan, Z. Zhao, Q. Wang, J. He, D. Yu, Z. Liu, B. Xu and Y. Tian, J. Mater. Chem. C, 2014, 2, 7022 RSC.
- C. He, L. Sun, C. Zhang, X. Peng, K. Zhang and J. Zhong, Phys. Chem. Chem. Phys., 2012, 14, 10967 RSC.
- Q. Huang, D. Yu, Z. Zhao, S. Fu, M. Xiong, Q. Wang, Y. Gao, K. Luo, J. He and Y. Tian, J. Appl. Phys., 2012, 112, 053518 CrossRef.
- Q. Weng, X. Wang, C. Zhi, Y. Bando and D. Golberg, ACS Nano, 2013, 7, 1558 CrossRef CAS PubMed.
- Y. Cai, J. Xiong, Y. Liu and X. Xu, J. Alloys Compd., 2017, 724, 229 CrossRef CAS.
- S. Klimenko, Y. A. Mukovoz, V. Lyashko, A. Vashchenko and V. Ogorodnik, Wear, 1992, 157, 1 CrossRef CAS.
- K. Watanabe, T. Taniguchi and H. Kanda, Nat. Mater., 2004, 3, 404 CrossRef CAS PubMed.
- Y. Kubota, K. Watanabe, O. Tsuda and T. Taniguchi, Science, 2007, 317, 932 CrossRef CAS PubMed.
- S. Hao, G. Zhou, W. Duan, J. Wu and B. Gu, J. Am. Chem. Soc., 2006, 128, 8453 CrossRef CAS PubMed.
- G. Ciofani, V. Raffa, A. Menciassi and A. Cuschieri, Nano Today, 2009, 4, 8 CrossRef CAS.
- G. Ciofani, S. Danti, G. G. Genchi, B. Mazzolai and V. Mattoli, Small, 2013, 9, 1672 CrossRef CAS PubMed.
- K. Qian, R. Y. Tay, V. C. Nguyen, J. Wang, G. Cai, T. Chen, E. H. T. Teo and P. S. Lee, Adv. Funct. Mater., 2016, 26, 2176 CrossRef CAS.
- S. Zhang, Q. Wang, Y. Kawazoe and P. Jena, J. Am. Chem. Soc., 2013, 135, 18216 CrossRef CAS PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567 CAS.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- D. Vanderbilt, Phys. Rev. B, 1990, 41, 7892 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188 CrossRef.
- B. G. Pfrommer, M. Côté, S. G. Louie and M. L. Cohen, J. Comput. Phys., 1997, 131, 233 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- D. R. Hamann, M. Schlüter and C. Chiang, Phys. Rev. Lett., 1979, 43, 1494 CrossRef CAS.
- N. W. Ashcroft and N. D. Mermin, Solid State Phys, Holt Saunders, Philadelphia, 1976, 113 Search PubMed.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef.
- X. Chen, H. Niu, D. Li and Y. Li, Intermetallics, 2011, 19, 1275 CrossRef CAS.
- F. Gao, J. He, E. Wu, S. Liu, D. Yu, D. Li, S. Zhang and Y. Tian, Phys. Rev. Lett., 2003, 91, 015502 CrossRef PubMed.
- M. Topsakal, E. Aktürk and S. Ciraci, Phys. Rev. B, 2009, 79, 115442 CrossRef.
- F. P. Bundy and R. H. Wentorf, J. Chem. Phys., 1963, 38, 1144 CrossRef CAS.
- J. F. Nye, Physical Properties of Crystals, Oxford University Press, Oxford, 1985 Search PubMed.
- H. Yao, L. Ouyang and W. Ching, J. Am. Ceram. Soc., 2007, 90, 3194 CrossRef CAS.
- X. Jiang, J. Zhao and R. Ahuja, J. Phys.: Condens. Matter, 2013, 25, 122204 CrossRef PubMed.
- V. V. Brazhkin, A. G. Lyapin and R. J. Hemley, Philos. Mag. A, 2002, 82, 231 CAS.
- H. Bu, M. Zhao, A. Wang and X. Wang, Carbon, 2013, 65, 341 CrossRef CAS.
- D. M. Teter, MRS Bull., 1998, 123, 27 Search PubMed.
- A. P. GERK, J. Mater. Sci., 1997, 12, 735 CrossRef.
- D. Roundy and M. L. Cohen, Phys. Rev. B, 2001, 64, 212103 CrossRef.
- Y. Zhang, H. Sun and C. Chen, Phys. Rev. Lett., 2004, 93, 195504 CrossRef PubMed.
- Y. Zhang, H. Sun and C. Chen, Phys. Rev. Lett., 2005, 94, 145505 CrossRef PubMed.
- S. W. Cranford and M. J. Buehler, Carbon, 2011, 49, 4111 CrossRef CAS.
- S. W. Cranford, D. B. Brommer and M. J. Buehler, Nanoscale, 2012, 4, 7797 RSC.
- H. Bu, M. Zhao, Y. Xi, X. Wang, H. Peng, C. Wang and X. Liu, EPL-Europhys. Lett., 2012, 100, 56003 CrossRef.
- X. Chen, H. Niu, C. Franchini, D. Li and Y. Li, Phys. Rev. B, 2011, 84, 121405 CrossRef.
- C. Sung and M. Sung, Mater. Chem. Phys., 1996, 43, 1 CrossRef CAS.
- J. Qin, D. He, J. Wang, L. Fang, L. Lei, Y. Li, J. Hu, Z. Kou and Y. Bi, Adv. Mater., 2008, 20, 4780 CrossRef CAS.
- Q. Zhu, A. R. Oganov, M. A. Salvadó, P. Pertierra and A. O. Lyakhov, Phys. Rev. B, 2011, 83, 193410 CrossRef.
- H. Bu, M. Zhao, W. Dong, S. Lu and X. Wang, J. Mater. Chem. C, 2014, 2, 2751 RSC.
- S. F. Pugh, Philos. Mag., 1954, 45, 823 CAS.
- S. Hao, G. Zhou, W. Duan, J. Wu and B. Gu, J. Am. Chem. Soc., 2008, 130, 5287 CrossRef PubMed.
- J. Dai, X. Wu, J. Yang and X. C. Zeng, J. Phys. Chem. Lett., 2013, 4, 3484 CrossRef CAS.
- W. Han, L. Wu, Y. Zhu, K. Watanabe and T. Taniguchi, Appl. Phys. Lett., 2008, 93, 223103 CrossRef.
- D. P. Yu, X. S. Sun, C. S. Lee, I. Bello, S. T. Lee, H. D. Gu, K. M. Leung, G. W. Zhou, Z. F. Dong and Z. Zhang, Appl. Phys. Lett., 1998, 72, 1966 CrossRef CAS.
- E. Bengu and L. D. Marks, Phys. Rev. Lett., 2001, 86, 2385 CrossRef CAS PubMed.
- C. Tang, Y. Bando and D. Golberg, J. Solid State Chem., 2004, 177, 2670 CrossRef CAS.
- C. Tang, Y. Bando, T. Sato and K. Kurashima, Chem. Commun., 2002, 1290 RSC.
- L. Li, L. H. Li, Y. Chen, X. J. Dai, P. R. Lamb, B. M. Cheng, M. Y. Lin and X. Liu, Angew. Chem., Int. Ed., 2013, 52, 4212 CrossRef CAS PubMed.
- Z. G. Chen, J. Zou, G. Liu, F. Li, Y. Wang, L. Wang, X. L. Yuan, T. Sekiguchi, H. M. Cheng and G. Q. Lu, ACS Nano, 2008, 2, 2183 CrossRef CAS PubMed.
- S. Xu, L. Wang, X. Qiao, X. Xu and Y. Cai, Comput. Mater. Sci., 2015, 110, 241 CrossRef CAS.
- M. Xiong, K. Luo, D. Yu, Z. Zhao, J. He and G. Gao, J. Appl. Phys., 2017, 121, 165106 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |