Open Access Article
Open Access ArticleControlling the shear thickening behavior of suspensions by changing the surface properties of dispersed microspheres
Yi. Chen *ab,
Yueyun Zhoua,
Hejie Piab and
Guangsheng Zeng*bc
*ab,
Yueyun Zhoua,
Hejie Piab and
Guangsheng Zeng*bc
aHunan Provincial Key Laboratory of Comprehensive Utilization of Agricultural and Animal Husbandry Waste Resources, College of Urban and Environmental Sciences, Hunan University of Technology, Zhuzhou, 412007, China. E-mail: yiyue514@aliyun.com; 290427057@qq.com
bHunan Provincial Engineering Laboratory of Key Technique of Non-metallic Packaging Waste Resources Utilization, Hunan University of Technology, Zhuzhou 412007, China. E-mail: guangsheng_zeng@126.com
cHunan Provincial Key Laboratory of Biomass Fiber Functional Materials, Hunan University of Technology, Zhuzhou 412007, China
First published on 25th January 2019
Abstract
To investigate the effect of the surface properties of dispersed particles on the shear thickening behavior of their corresponding suspensions and further control this characteristic, three kinds of suspensions were prepared by mixing SiO2, SiO2–NH2, and SiO2–COOH microspheres with a poly(ethylene glycol) fluid medium, and their rheological behavior was analyzed carefully. Compared to the SiO2 microsphere suspension, the SiO2–NH2 and SiO2–COOH microsphere suspensions show a weaker thickening behavior and a greater critical shear rate due to the aggregation tendency caused primarily by the organic chains. Moreover, the rheological behavior of the three suspensions display different dependencies on the pH value, which is comprehensively determined by the interaction between the microspheres and the medium. Moreover, the critical shear stress of suspensions with different pH values could be predicted by the Wagner model, which basically proves that the interaction between the particles significantly influences the beginning of thickening. The thickening degree could be interpreted by friction theory. The critical volume fraction corresponding to the onset of discontinuous shear thickening is determined by the friction coefficient between the particles, which is greatly affected by the pH value.
1 Introduction
The rheology of dense suspensions is of significant theoretical and technological importance due to its great potential in energy absorption, physical protection, magnetic damping and so on.1–3 However, shear rheology of even the simplest case of a suspension composed of hard spheres and Newtonian fluid is incompletely understood. Based on different particle suspensions, many attempts were made to explain how shear thickening happens, and some important mechanisms were advanced successively. Typically, the order–disorder transition theory, linking shear thickening to the breaking of ordered alignment of the layered structure above a critical shear rate,4,5 the dilatancy theory, regarding the thickening as a tendency of granular materials to expand underflow,6,7 the “hydroclusters” theory, in which the thickening is ascribed to the formation of jamming clusters by hydrodynamic lubrication forces,8,9 have been proven to be reasonable by experiments and simulations in special research systems.In addition to mechanistic exploration, a more pertinent question is whether this kind of special rheological behavior can meet the demands of practical applications.
For example, in self-protection and magnetic damping systems, there are various application demands, including the kind of impact or shear that needs to be resisted, the intensity of the magnetic field leading to the shear thickening, the degree of thickening for suitable energy absorption and so on.
In a colloidal suspension, the shape, size and surface structure of the particles and the viscosity and chemical structure of the media impact the rheological behavior significantly.10,11 However, alteration of the composition and material of the suspensions generally leads to an uncontrollable change of rheological behavior and other properties; thus, adjusting the thickening behavior in a controllable and simple method remains a great challenge. In shear thickening behavior, the most important feature is when the thickening happens and to what degree the thickening occurs, both of which are considered as important control objectives.
Focusing on the onset of thickening, analysis of the different mechanisms and prediction models related to the critical shear rate or critical shear stress was built up with a focus on different suspension systems. Based on hard sphere suspensions, including the mutual repulsion between the particles, Melrose and Ball established a model to predict the critical shear rate by hypothesizing that the time required for the conservative forces to separate a particle pair is equal to the time scale of the flow when shear thickening occurs.12 By modifying the model, Wagner and Maranzano established a new model to predict the critical shear stress of hard sphere suspensions by considering the particles size, concentration, surface potential and ionic strength.13,14 Based on the electrically-stabilized colloidal suspensions in which the micro-interactions such as the van der Waals attraction is non-negligible. Kaldasch et al. established the model for predicting the critical stress by using DLVO theory to analyze the two-particle interaction. Moreover, they proved that sterically stabilized colloidal suspensions such as polymeric brush coating colloidal particles could also adopt this activation model.15,16 Obviously, in these models, the balance between the applied stress and the interaction of the particles determines the onset of shear thickening.
For the degree of thickening, in contrast to continuous shear-thickening (CST) which is a continuous viscosity increase at any applied rate, discontinuous shear-thickening (DST) is an order of magnitude jump in the stationary stress when the strain rate crosses some threshold value. This CST to DST transition is observed when the volume fraction of the flowing suspension increases above a critical value near the random close packing, which depends on the system properties, e.g. polydispersity or shape, and on the flow geometry. DST is a kind of thickening form which could show a better effect for energy absorption and physical protection. Some theoretical approaches have attempted to understand this abrupt viscosity increase. Holmes et al. suggested that DST could be interpreted as a shear-induced glass transition based on an ad hoc mode-coupling theory.17–19 Brown gave the mechanism explanation that DST is related to the existence of an underlying jamming transition due to the frustration of the granular-like dilatancy by the confining stress.20–22 More recently, friction leading to the DST became the mainstream explanation of this phenomenon, that is, at low shear stress, the neighbouring particles are separated by a gap filled with solvent and interacts via hydrodynamic forces, which leads to a CST. While, at high shear stress, the repulsive force between the particles is overcome and thereby results in a frictional contact network and shear thickening behavior.23–26 Many other theoretical and experimental attempts were carried out to understand this effect. For example, new granular-like models where the additional frictional forces act between particles have been established to reproduce DST; frictional contact dynamics are expected to dominate especially at large volume fractions, close to the jamming transition, and is responsible for DST.27,28 Seto et al. introduced a numerical scheme including both relevant hydrodynamic interactions and granular-like contact, a critical shear stress associated with a critical shear rate where DST occurs, which separated the frictionless state and the frictional shear jammed state.29 Fernandez et al. identify a local Sommerfeld number that determines the transition from Newtonian to shear-thickening flows, and then showed that the suspension's volume fraction and the boundary lubrication friction coefficient controls the CST or DST transition.30 Wyart's assumptions about the contact proliferation predict two distinct types of DST in the absence of inertia.31 Comprehensively, the CST and DST behavior could be adjusted by altering the friction character of the particles.
Based on the foundation of previous research, it could be concluded that altering the short-range interactions can adjust the characteristics of shear thickening significantly. Though there have been many methods to change the shear thickening behavior of the suspensions, altering the interaction between components is considered as a simple and controllable approach. Applying an extra electric or magnetic field as an exogenous force to change the particle surface interactions has proved effective to control the rheological behavior of suspensions.32,33 Similarly, the endogenous force appearing inside the systems should also work to cause the same effect. In this research, we tried to introduce different groups into the surface of the SiO2 microsphere so as to alter the surface characteristics of the microspheres and adjust the interaction inside the systems. Taking into account the electron donor and electron acceptor characteristic of the introduced groups, an aqueous solution with different pH values were added into the suspensions to modulate the interaction further due to the inductive and ionization effects. All these changes should relate to the onset and the degree of thickening. By doing this, it is hoped that shear thickening behavior could be controlled more effectively, and the effects of particle interactions on the thickening process could be understood in depth.
2 Experimental
2.1 Materials
The SiO2 microsphere used here was prepared by the stöber sol–gel method in our lab,34 the radius of the microsphere is about 120 ± 10 nm, as shown in Fig. 1a, the density is 2.24 g cm−3. γ-aminopropyl-triethoxysilane, methylbenzene, butanedioic anhydride, dimethylformamide was supplied by Aladdin Co., Ltd, China, polyethylene glycol with molecular weights of 200 g mol−1 (PEG200) on average was supplied by Sigma-Aldrich Chemical GmbH, Düsseldorf, Germany, and is a low viscosity Newtonian media having, under 25 °C, a viscosity of 25 mPa s−1 and a density of 1.13 g cm−3.2.2 The synthesis of SiO2–NH2 microspheres
The SiO2–NH2 microspheres were prepared by surface modification of the SiO2 microspheres, the scheme is shown in Fig. 1d. To describe it briefly, the prepared SiO2 particles were vacuum dried at 110 °C for 5 h as an activation process, the activated SiO2 particles and methylbenzene solution with 5% wt γ-aminopropyl-triethoxysilane were added into a three-necked flask, the suspensions were heated to 110 °C and kept 8 h with magnetic stirring and reflux for reaction. Throughout the experiments, oxygen was eliminated from the system. After the reaction, the suspensions were extraction filtrated with a buchner funnel, the final modified SiO2 particles product was vacuum dried at 110 °C for 5 h and preserved in the vacuum drying oven. The grafting ratio of –NH2 could be adjusted by controlling the mass ratio of γ-aminopropyltriethoxysilane and the SiO2 particles. In this research, the content of NH2 in the surface of the SiO2 microsphere is 0.416 mmol g−1, which is measured by chemical titration. The size of the modified microsphere is basically equal to that of the unmodified microsphere, as shown in Fig. 1b.2.3 The synthesis of SiO2–COOH microspheres
The scheme of SiO2–COOH microspheres preparation is shown in Fig. 1e. To briefly describe, equimolar γ-aminopropyl-triethoxysilane and butanedioic anhydride were dispersed into dimethylformamide in a flask to form a 20 wt% solution, the solution was heated to 80 °C for 3 h with magnetic stirring and reacted under reflux. Then, the homogeneous dispersed SiO2/dimethylformamide suspension and a small quantity of deionized water were added into the system and stirred sequentially at 80 °C for 5 h. The solid modified SiO2 particles were separated using ultracentrifugation, the final SiO2–COOH microspheres were obtained by washing several times with ethanol and centrifugation. In this research, the content of COOH in the surface of SiO2 microsphere is 0.402 mmol g−1, which is measured by chemical titration. The size of the modified microsphere is equal to that of the unmodified microsphere basically, as shown in Fig. 1c.2.4 Preparation of suspension samples
The suspensions were prepared by adding fully dried SiO2 and modified SiO2 microspheres into the liquid medium in a blender and mixing for 2 h in order to obtain a uniform distribution of particles within the suspension. The samples were sonicated for an hour and then placed in a vacuum chamber for 30 min to remove air bubbles and ensure that the particles were not aggregated. Afterwards, the suspensions were dispersed for 40 min by a superfine homogenizer (F6/10, Fluko Equipment Germany) at high speed (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm). The suspensions were allowed to rest for 12 h in an air tight plastic bottle, the final high concentration suspensions of SiO2 and modified SiO2 microspheres in PEG200 with various volume fractions were prepared. In this research, the volume fraction was calculated by the mass and density of the dispersed particles and the media, the density of the modified SiO2 microspheres is considered the same as the unmodified SiO2 microspheres. When the effect of the pH value on the rheological behavior was investigated, a small amount of aqueous solution (diluted solutions of HCl or NaOH) with various pH values was added into the suspensions by a ratio of 1
000 rpm). The suspensions were allowed to rest for 12 h in an air tight plastic bottle, the final high concentration suspensions of SiO2 and modified SiO2 microspheres in PEG200 with various volume fractions were prepared. In this research, the volume fraction was calculated by the mass and density of the dispersed particles and the media, the density of the modified SiO2 microspheres is considered the same as the unmodified SiO2 microspheres. When the effect of the pH value on the rheological behavior was investigated, a small amount of aqueous solution (diluted solutions of HCl or NaOH) with various pH values was added into the suspensions by a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 to 1
15 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 in weight to that of the media.
25 in weight to that of the media.
2.5 Friction measurements
The friction between the microspheres cannot be directly and accurately measured due to their size and complex shape, a similar system was designed and measured by an universal micro-tribotester to simulate the actual situation. In test, a quartz sphere with a radius of 6 mm slides on a quartz disk in rotational mode was used to investigate the frictional properties between the microsphere surface. The rotational speed of the quartz disk was 100 rpm, and the radius of the track was 15 mm. Throughout the tests, the load was kept constant at 1 N. For simulating the real microspheres in suspensions, the special treatment was carried out in all test materials. For simulating the SiO2 microsphere, both the sphere and disk were treated using a piranha solution (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 concentrated H2SO4/30% H2O2) for 20 min to form –OH groups on the surface as that of the SiO2 microsphere. In order to simulate the SiO2–NH2 and SiO2–COOH microspheres further, the mixed solution A (methylbenzene solution with 5 wt% γ-aminopropyl-triethoxysilane) and mixed solution B (dimethylformamide solution with 20 wt% equimolar γ-aminopropyl-triethoxysilane and butanedioic anhydride, reacting at 80 °C for 5 h), as the reaction solutions used in surface modification of the microsphere, was coated on the surface of the piranha solution treated sphere and disk respectively. After that, the coated sphere and disk were kept at 80 °C for 5 h and then vacuum dried for 2 h. Through the treatment, the thickness of the surface covering layer of the sphere and disk reached 0.2–0.5 mm (the scheme is shown in Fig. 2). When testing the friction of the microspheres in q special medium, the corresponding medium was dropped on the surface of the disk and spheres to wrap the test interface for a better simulation of the real situation.
3 concentrated H2SO4/30% H2O2) for 20 min to form –OH groups on the surface as that of the SiO2 microsphere. In order to simulate the SiO2–NH2 and SiO2–COOH microspheres further, the mixed solution A (methylbenzene solution with 5 wt% γ-aminopropyl-triethoxysilane) and mixed solution B (dimethylformamide solution with 20 wt% equimolar γ-aminopropyl-triethoxysilane and butanedioic anhydride, reacting at 80 °C for 5 h), as the reaction solutions used in surface modification of the microsphere, was coated on the surface of the piranha solution treated sphere and disk respectively. After that, the coated sphere and disk were kept at 80 °C for 5 h and then vacuum dried for 2 h. Through the treatment, the thickness of the surface covering layer of the sphere and disk reached 0.2–0.5 mm (the scheme is shown in Fig. 2). When testing the friction of the microspheres in q special medium, the corresponding medium was dropped on the surface of the disk and spheres to wrap the test interface for a better simulation of the real situation.
 | ||
| Fig. 2 The schematic representation for measuring the frictional properties of different microspheres. | ||
2.6 Rheological tests
Steady-shear rheological experiments on the suspensions were conducted using a rheometer TA Instruments ARES-G2 rheometer (supplied by TA. Instruments, USA). To prevent adhesive slip between the sample and the rheometer plates, parallel plates with a 25 mm diameter were covered with emery cloth (NORTON, K224) using double sided tape. The gaps explored were fixed at 0.8 mm. Before the rheological test, a steady pre-shear was applied in the sample at a shear rate of 0.1 s−1 for 60 s in order to erase the shear history and an equilibrium time of 120 s was given at each shear rate to allow the system to reach a steady state. All the experiments were repeated at least three times.3 Results and discussion
3.1 The effect of surface property of microspheres on the shear thickening behavior
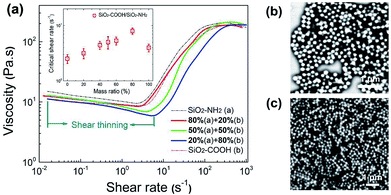
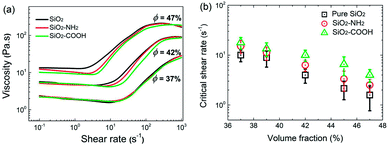
In colloidal suspensions, the properties of the dispersed particles including size, shape, and softness have a significant effect on their rheological behavior. Especially, in some systems with small colloidal particles, the surface chemical structure of the particles is also important for the shear thickening due to the relatively stronger interaction between the particles. Based on this, the nano-sized SiO2 microsphere and its surface modified products, the SiO2–NH2 and SiO2–COOH microspheres were used to investigate the effect of the surface properties on shear thickening by comparing their rheological behavior.Fig. 3 shows the shear rate versus the apparent viscosity curves of the suspensions. As shown in figure, for the different suspensions with the same volume fraction (ϕ), although the curves are approximately similar, the important features including the critical shear rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) defined as the shear rate at which the viscosity starts to increase significantly from the original decreasing or unchanged status, and the maximum viscosity still exhibits obvious differences, revealing the non-negligible effects of the surface groups. The detailed
) defined as the shear rate at which the viscosity starts to increase significantly from the original decreasing or unchanged status, and the maximum viscosity still exhibits obvious differences, revealing the non-negligible effects of the surface groups. The detailed ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) data is listed in Fig. 3b, from which it could be seen that, the rule
data is listed in Fig. 3b, from which it could be seen that, the rule ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) SiO2 <
SiO2 < ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) SiO2–NH2 <
SiO2–NH2 < ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) SiO2–COOH is tenable for suspensions with the same ϕ, the gap between them becomes greater at high ϕ. It could be concluded that the grafted surface chains lead to a stronger occurrence of shear thickening, especially for suspensions with a high ϕ.
SiO2–COOH is tenable for suspensions with the same ϕ, the gap between them becomes greater at high ϕ. It could be concluded that the grafted surface chains lead to a stronger occurrence of shear thickening, especially for suspensions with a high ϕ.
 | ||
| Fig. 3 The shear rate versus viscosity curves of three different suspensions with various volume fractions and the corresponding critical shear rate. | ||
Furthermore, the suspensions with mixed SiO2–NH2 and SiO2–COOH particles were prepared and their rheological curves are shown in Fig. 4. As shown in the figure, with an increased ratio of SiO2–COOH particles to the mixed particles, the ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) of the suspensions increases significantly, and the first shear thinning becomes stronger, when the ratio of the SiO2–COOH particles passes 50% of the total mass, the
of the suspensions increases significantly, and the first shear thinning becomes stronger, when the ratio of the SiO2–COOH particles passes 50% of the total mass, the ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is greater than that of the pure SiO2–COOH particle suspensions, and the maximum viscosity decreases considerably, revealing a weaker shear thickening behavior.
is greater than that of the pure SiO2–COOH particle suspensions, and the maximum viscosity decreases considerably, revealing a weaker shear thickening behavior.
Obviously, the surface grafted groups influence ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) of the suspensions and leads to the significantly harder jamming. This change caused by the surface modification was analyzed. First, according to previous research, due to the amount of hydroxyls between the SiO2 particles and the dispersion media, a special solvation layer formed by hydrogen bonding appears near the surface, where the density of the oligomeric chains is higher than that of the bulk. This high density solvation layer is helpful to prevent the media fluid from flowing through the gap between the two spheres and acts as a “barrier”, which promotes an earlier onset of shear thickening.35 Moreover, the thickness of this “strongly anchored” solvation layer could be approximately estimated. For SiO2 suspensions with a water and ethylene glycol (EG) media, the formed solvation layer thickness is 4.4 nm and 1.5 nm, respectively.36,37 Taking account the similarity, the solvation layer of SiO2 microsphere in PEG is on the order of 1 nm. While, after modification, the macromolecule chains cover the surface of the sphere and inhibit the formation of a solvation layer due to the destruction of the hydrogen bonding combination. However, this effect may be not large in this system due to the relatively small thickness of the solvation layer to the radius of the sphere (120 nm). Moreover, in the modified microspheres, the introduced groups both include low polarity organic chains, the similar polarity should lead to the slight aggregation of the microspheres and thereby result in a higher critical shear rate. This reason was proved further by the rheological behavior of the suspensions with the mixed particles.
of the suspensions and leads to the significantly harder jamming. This change caused by the surface modification was analyzed. First, according to previous research, due to the amount of hydroxyls between the SiO2 particles and the dispersion media, a special solvation layer formed by hydrogen bonding appears near the surface, where the density of the oligomeric chains is higher than that of the bulk. This high density solvation layer is helpful to prevent the media fluid from flowing through the gap between the two spheres and acts as a “barrier”, which promotes an earlier onset of shear thickening.35 Moreover, the thickness of this “strongly anchored” solvation layer could be approximately estimated. For SiO2 suspensions with a water and ethylene glycol (EG) media, the formed solvation layer thickness is 4.4 nm and 1.5 nm, respectively.36,37 Taking account the similarity, the solvation layer of SiO2 microsphere in PEG is on the order of 1 nm. While, after modification, the macromolecule chains cover the surface of the sphere and inhibit the formation of a solvation layer due to the destruction of the hydrogen bonding combination. However, this effect may be not large in this system due to the relatively small thickness of the solvation layer to the radius of the sphere (120 nm). Moreover, in the modified microspheres, the introduced groups both include low polarity organic chains, the similar polarity should lead to the slight aggregation of the microspheres and thereby result in a higher critical shear rate. This reason was proved further by the rheological behavior of the suspensions with the mixed particles.
In details, it was found that ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) SiO2–COOH is always higher than
SiO2–COOH is always higher than ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) SiO2–NH2, and is not a coincidence. Though both surface grafted chains have organic groups, the grafted chains in the SiO2–COOH microsphere is longer than that of the SiO2–NH2 microsphere, leading to a denser surface layer. Moreover, the interaction between the grafted chains themselves and between the grafted chains and media also has a significant effect on the shear thickening behavior, which will be discussed in the following section.
SiO2–NH2, and is not a coincidence. Though both surface grafted chains have organic groups, the grafted chains in the SiO2–COOH microsphere is longer than that of the SiO2–NH2 microsphere, leading to a denser surface layer. Moreover, the interaction between the grafted chains themselves and between the grafted chains and media also has a significant effect on the shear thickening behavior, which will be discussed in the following section.
Another significant difference is the initial rheological behavior under a low shear rate. An obvious shear thinning was observed in the mixed particles suspensions, meaning a kind of relaxation or disentanglement behavior. In the modified microsphere, the introduced groups include a low polarity chain and a polar end group with an electron donor or electron acceptor, the aggregation should be intensified by charge attraction, and could be observed in the SEM images of the freeze dried (−80 °C) suspensions, by which the original status of the particles was basically maintained. As shown in Fig. 4, in comparison to the pure SiO2–NH2 particles, the mixed particles show micro-aggregation, the uniformity of the dispersion decreases. Moreover, the mixing ratio of the particles corresponding to the greatest ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and strongest shear thinning is consistent, which is SiO2–COOH
and strongest shear thinning is consistent, which is SiO2–COOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2–NH2 = 8
SiO2–NH2 = 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, instead of 1-to-1. This special ratio may be related to the highest aggregation degree, which is determined by the ratio and the nature of the introduced groups.
2, instead of 1-to-1. This special ratio may be related to the highest aggregation degree, which is determined by the ratio and the nature of the introduced groups.
3.2 The effects of pH value on the shear thickening behavior of suspensions
The introduced grafted chains have a tendency for ionization in aqueous solutions due to their NH2 and COOH end groups, and therefore their interaction could be adjusted by altering the pH value. For this goal, a small amount of aqueous solution (5% mass of suspensions) with different pH values were added into the suspensions. It is noteworthy that the actual pH of the suspensions is not consistent with that of the added solution, the measured pH value of the dilute silica microspheres aqueous dispersion without any addition is about 5.84, the neutralization effect decreases the acidity and alkalinity of the solution in a small range. For a convenient comparison, the discussed pH value in the following analysis is that of the added aqueous solution instead of the actual value of the suspensions. The viscosity of the media changes from 25 mPa to 21.6 mPa s−1 after adding solution to whatever the pH value of the solution. The shear rate versus viscosity curves of the suspensions with different pH values are shown in Fig. 5. As shown in the figure, when the pH value changes, the rheological character of the suspensions including the![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , the maximum viscosity, the thinning and thickening degree exhibits different changes.
, the maximum viscosity, the thinning and thickening degree exhibits different changes.
A similar tendency was found in curves for the SiO2 and SiO2–NH2 suspensions, that is, with the increase of pH, the ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and maximum viscosity increases considerably and the initial thinning and followed thickening becomes stronger. While, for the SiO2–COOH suspensions, the effect is reversed.
and maximum viscosity increases considerably and the initial thinning and followed thickening becomes stronger. While, for the SiO2–COOH suspensions, the effect is reversed.
The reason for the diverse effects could be attributed to which one in the added solution is inclined to combine, the medium or the microsphere. This is determined by the interaction comparison. When the added solution is inclined to combine with the media, the thinning becomes more significant, which is ascribed to the added aqueous solution working as a lubricant, the ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) shifts to higher rate due to the decreased total viscosity, the thickening becomes more abrupt because of the lower effect of the added solution. When the added solution is inclined to combine with the microsphere, the result reverses.
shifts to higher rate due to the decreased total viscosity, the thickening becomes more abrupt because of the lower effect of the added solution. When the added solution is inclined to combine with the microsphere, the result reverses.
The selective combination of the added solution may also be explained by the alkalinity or acidity of the materials in the system. In the SiO2 and SiO2–NH2 suspensions, SiO2 and PEG show weak acidity due to the –OH groups, the SiO2–NH2 particles exhibit a weak alkalinity due to the dissociation of the –NH2 groups in aqueous solution. When an alkali solution was added into the suspensions, it was easier for it to combine with PEG than the microspheres. As well, the microspheres adsorbed less solution which leads to a slight effect on the degree of shear thickening. When adding an acid solution, more solution is combined with the alkaline microspheres which brings about a weaker shear thickening and nearly unchanged shear thinning behavior. In the SiO2–COOH suspensions, the particles show a relatively stronger acidity in the aqueous solution than that of the SiO2 microsphere, the rule with regards to the selective combination becomes reversed to that of the SiO2 and SiO2–NH2 suspensions and thereby results in a different rheological behavior.
Based on the above results, it was found that the rheological behavior of the suspensions could be adjusted by changing their pH value. The key point we considered is the combined ability of the aqueous solution with the microspheres. For proving this point further, the mass of the added aqueous solution was adjusted in order to observe the change of the rheological behavior in detail. A significant distinction was found in the degree of thinning and thickening.
Taking a typical example, three masses of alkali solution(1/25, 1/20 and 1/15 mass of suspensions) were added into the SiO2–C OOH suspensions, respectively, the viscosity of the pure media changes to 23.2, 21.6, and 20.2 mPa s−1, respectively, regardless of what the pH value of the solution is. The shear rate versus shear stress curves is exhibited in Fig. 6a for a more direct observation. As shown in the figure, the effect of added solution mass on the line slope (shear stress/shear rate) was different in the shear thinning and shear thickening region, the slope in the shear thinning region is basically unchanged with the change of the solution mass, while the slope in shear thickening region increases with the decreasing mass of added solution. The greater effect occurring in the shear thickening region proves that the alkali solution tends to combine more with the SiO2–COOH microspheres than the media. Moreover, the same test was carried out in other kinds of suspensions, the slope in the shear thinning and thickening regions is shown in Fig. 6b and c, When the solution is easier to combine with media (such as adding an acidic solution into the SiO2–COOH suspensions or adding an alkali solution into SiO2–NH2 suspensions), the shear thinning becomes stronger and the shear thickening degree becomes weaker, when the solution is easier to combine with the microspheres (such as adding alkali solution into the SiO2–COOH suspensions or adding acidic solution into SiO2–NH2 suspensions), the phenomenon is the inverse. From the slope change, the analysis above with respect to the selective combination could be demonstrated further.
We also note that, for the SiO2 suspensions, increasing the added aqueous solution always brings about a considerable decrease of the slope in the shear thickening region regardless of what the pH value of the added solution is, meaning that the SiO2 microspheres have a good ability to combine with the aqueous solution due to the existence of hydroxyls. By contrast, the surface grafted chains play the role of a hydrophobe to some degree.
3.3 The mechanism analysis of the rheological behavior affected by pH value
In the above analysis, it was found that the rheological behavior of the suspensions, especially its two main features, the beginning and the degree of thickening, could be influenced significantly by the changing the conditions due to the altered interaction between the particles. To figure out its mechanism, we tried to use the Wagner model which is suitable in hard sphere systems to predict the start of shear thickening. In this model, the critical shear stress (τc) could be calculated by the surface potential and the radius of the particles, which is expressed by the following equation:where lb is the Bjerrum length defined by lb ≡ e2/(4πεε0kBT), a is the radius of the particle, and Ψ = ψse/kBT is the dimensionless surface potential, (κa) is the relative double layer thickness. κ−1 is the Debye length, which could be calculated by hm = 1.453/κ.38 hm is the characteristic separation distance in the incipient hydrocluster state.
In this research, the media, the size of the particles and other conditions of the three suspensions is similar, the main impact on τc could be ascribed to the changed interaction between the particles. As we know, the zeta potential of the particles could represent the dimensionless surface potential to some degree. Using this substitution, the τc and zeta potential of the particles in different pH condition were measured and is shown in Fig. 7. It was found that the absolute value of the zeta potential exhibits a similar changing tendency as that of τc. For the SiO2 and SiO2–COOH suspensions, the τc increases with the increase of pH value. For the SiO2–NH2 suspensions, the τc decreases monotonously. Moreover, for the suspensions with the mixed particles, the same correlation between them was also found, which proves that the τc closely links with the zeta potential of particles. The zeta potential could represent the stability of the particles in the system, regardless of whether it is the SiO2 or modified SiO2 microsphere, higher stability between the particles brings about higher τc.
Moreover, the actual value and predicted value of τc calculated by using the Wagner equation are listed in Table 1, though the change tendency between the actual value and the predicted value is consistent, a discrepancy in the value still exists. Basically, the actual value is lower than the predicted value. For SiO2 microspheres, the effect of the solvation layer on the surface of the microspheres may be ignored in theoretical calculation, the existence of a solvation layer leads to the decreased separation distance between microspheres, which makes the thickening happen more easily under lower stress. For the modified microspheres, there exist low-polarity surface organic groups, these groups interact with each other or interact with the molecular chains of the media, this kind of extra force is not included in the theoretical model.
| pH | SiO2 | SiO2–COOH | SiO2–NH2 | Mixed particles | |||||
|---|---|---|---|---|---|---|---|---|---|
| A-v | P-v | A-v | P-v | A-v | P-v | MR (COOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OH) OH) |
A-v | P-v | |
| a A-v is actual measured value, P-v is the predicted value, MR is the mass ratio. | |||||||||
| 2 | 20.2 | 1.1 | 24.5 | 6.5 | 102.2 | 219.8 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
36.6 | 85.5 |
| 4 | 52.5 | 131.8 | 20.4 | 17.3 | 73.4 | 123.8 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
27.7 | 26.7 |
| 7 | 104.1 | 296.8 | 36.1 | 77.2 | 46.4 | 85.5 | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 50 |
24.4 | 5.4 |
| 9 | 157.8 | 340.3 | 52.1 | 125.6 | 34.8 | 6.7 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 60 |
25.4 | 6.6 |
| 11 | 192.8 | 405.4 | 76.3 | 140.5 | 17.4 | 3.1 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 80 |
24.3 | 19.4 |
CST and DST, linked to the different viscosity increase degree, both appear in this research system. The intrinsic factor determining the kind of shear thickening is a meaningful problem. Here, we tried to analyze it by using theory based on the friction coefficient between the particles.
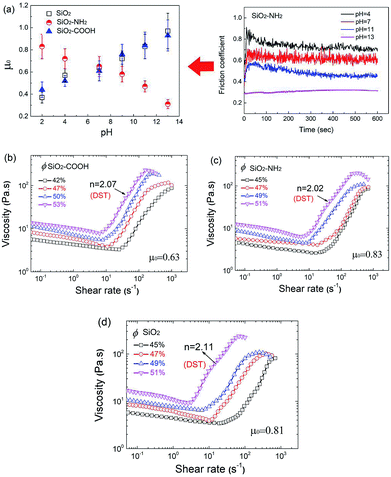
Until now, it has been commonly accepted that the lubrication status between the particles was separated into two typical regimes which are determined by a characteristic number, the Sommerfeld number s (s = ηfvRp/N), where ηf is the fluid viscosity, ν is the sliding speed between the two solid surfaces, Rp is the radius of the spheres and N is the normal load. For high s, corresponding to the rheological status called the “hydrodynamic lubrication” regime (HD regime), the two sliding surfaces are fully separated by a fluid film and the friction coefficient (μ) depends on s. For low s, a “boundary lubrication” regime (BL regime) appears, in which the lubrication film breaks down and contacts between the microscopic asperities on each surface support most of the load, and μ exhibits only very weak dependency on s. The boundary of s is about the order of 10−5. In some flow status, the “mixed regime” with both HD and BL also exists.
In the HD regime, the jamming volume fraction (ϕHDmax) is at a random close packing ϕRCP, regardless of the boundary friction coefficient. Conversely, the jamming volume fraction in the BL regime (ϕBLmax) changes with changed μ. When ϕ ≤ ϕBLmax, the suspension exhibits CST, and when ϕBLmax < ϕ≤ ϕHDmax, the system undergoes DST. As a consequence, ϕBLmax is the critical volume fraction for DST and therefore it can be tuned by changing the particle friction coefficient.
In this research, the shear thickening behavior of suspensions undergoes a transition from CST to DST with an increase of the volume fraction. This corresponding “s” calculated by using the physical parameter of the materials and the rheological character (Rp = 120 nm, ηf = 25 mPa s−1, ν could be substituted by the shear rate, which is between 0.1–100 s−1 corresponding to the shear thickening region, the corresponding N measured by rheometer is 0.01–1 N) is in the range of 10−7 to 10−8. We could reasonably consider that the systems are in boundary lubrication. Accordingly, the boundary lubrication between two rough particles could be described using the Amontons–Coulomb friction, the friction coefficient μ0 being independent of the load, speed and apparent contact area, corresponds to a special critical volume fraction that happens in DST. Here, the μ0 of the particles under different pH conditions was measured by using a special method, the value is shown in Fig. 8a. As shown in the figure, the pH value has a significant influence on the μ0 of the particles. The μ0 of the SiO2 and SiO2–COOH microspheres increases considerably with an increase of the pH value, while the μ0 of the SiO2–NH2 decreases. Obviously, the increased dissociation degree of the end groups advances μ0 between the particles. Fig. 8b–d provides several actual examples with regard to how suspensions with the special particle μ0 changes from CST to DST (n ≥ 2, n is Oswald-De Waele power law: τ = Kγn, when n is higher than 2, the thickening is discontinuous) with the increased volume fraction and the critical volume fraction (ϕBLmax).
It is worth noting that the measured μ0 exhibits some correlation with the test load and speed. The test load affects μ0 more significantly, the test with the higher load could get a higher μ0. The test speed only has a slight effect on it. However, under the same test conditions, the relative magnitude of μ0 belonging to different suspensions is unchanged. Therefore, the test value could be used in qualitative analysis.
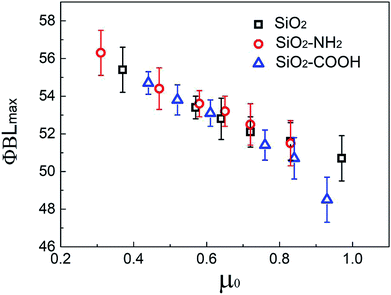
The μ0 and corresponding ϕBLmax for all suspensions with different pH value is shown in Fig. 9. Obviously, the ϕBLmax decreases gradually with the increase of μ0, the ϕBLmax for the same μ0 is similar even for different suspensions regardless of the surface chemical structure of the microsphere. It was proved further that the thickening behavior could be adjusted by changing the friction character of the particles, changing the pH value is a possible method for particles with polar or ionizable groups.
 | ||
| Fig. 9 The measured μ0 of three kinds of suspensions (ϕ = 53%) at various pH conditions and their ϕBLmax corresponding to the happen of DST. | ||
In order to quantify ϕBLmax, the viscosity versus shear rate curves in the thickening regime for different suspensions were fitted by the Oswald-De Waele power law: τ ∝ γn. It was found that the relationship of n and ϕ is nonlinear. A uniform expression obtained using ϕmax corresponds to a strong thickening (n = 4) for three kinds of suspensions (pH = 7) as a standard, the deviation of ϕ from the standard was normalized using (ϕmax − ϕ)/ϕmax. As shown in Fig. 10a, the n of the different suspensions collapse onto a single master curve as a function of a reduced volume fraction which does not depend on the surface chemical property. Furthermore, the exponential form of the same data was fitted in Fig. 10b, all the data disperse around the fitted line well, meaning an exponential relation of n with the volume fraction change. This understanding is helpful to predict and adjust the thickening degree by controlling the volume fraction of the suspensions.
4 Conclusion
To investigate the influence of the surface properties of the dispersed particles on the shear thickening behavior of the suspensions and find a convenient method to adjust the character of shear thickening, organic chains with COOH and NH2 end groups were grafted into the surface of SiO2 microspheres. The suspensions were prepared by matching prepared SiO2, SiO2–NH2 and SiO2–COOH microspheres with a PEG medium, respectively, their rheological behavior was measured and compared in detail.Obvious differences in the rheological behavior were observed for the three types of suspensions. By contrast, for the same ϕ, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) SiO2 <
SiO2 < ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) SiO2–NH2 <
SiO2–NH2 < ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) SiO2–COOH is always valid, and their gap becomes larger with increased ϕ, while the maximum viscosity displays the reverse, all of which reveals the large effects caused by the changed surface character of the microspheres. Though the grafted NH2 and COOH groups could strongly interact with the PEG medium by the hydroxyl groups, the introduced organic chains still destroy the solvation layer on the surface of the SiO2 microsphere formed by hydrogen bond interactions between the OH groups, and the particles slight aggregation more easily occurs due to the interaction of the macromolecular chains, both factors are against the occurrence of shear thickening. Moreover, the suspensions with mixed SiO2–NH2 and SiO2–COOH particles show higher
SiO2–COOH is always valid, and their gap becomes larger with increased ϕ, while the maximum viscosity displays the reverse, all of which reveals the large effects caused by the changed surface character of the microspheres. Though the grafted NH2 and COOH groups could strongly interact with the PEG medium by the hydroxyl groups, the introduced organic chains still destroy the solvation layer on the surface of the SiO2 microsphere formed by hydrogen bond interactions between the OH groups, and the particles slight aggregation more easily occurs due to the interaction of the macromolecular chains, both factors are against the occurrence of shear thickening. Moreover, the suspensions with mixed SiO2–NH2 and SiO2–COOH particles show higher ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , lower maximum viscosity and stronger shear thinning than that of suspensions with the single particle. This intensified weakening of thickening is attributed to the stronger aggregation tendency between the particles due to electron acceptor and donor characteristics the of –NH2 and –COOH groups, respectively.
, lower maximum viscosity and stronger shear thinning than that of suspensions with the single particle. This intensified weakening of thickening is attributed to the stronger aggregation tendency between the particles due to electron acceptor and donor characteristics the of –NH2 and –COOH groups, respectively.
For controlling the rheological behavior more effectively, a certain amount of aqueous solution with various pH values was added to the suspensions to adjust the interactions in the system. For the three kinds of suspensions, the effect of the pH value on their rheological behavior is different. For the SiO2 and SiO2–NH2 suspensions, the increased pH leads to a higher ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and larger maximum viscosity, the initial shear thinning becomes weaker and the shear thickening behavior is more abrupt. While the influence of the pH value on the SiO2–COOH suspensions is inverse. It fully proves that the rheological behavior of the suspensions could be adjusted by changing the micro-environment of the microspheres. The rule is summarized as follows: when the aqueous solution tends to combine with the microspheres, the shear thickening exhibits a greater weakening, whereas when the aqueous solution combines with the media more easily, the shear thinning exhibits a more obvious change, all of which is determined by the competing interaction between the components in the suspension. Changing the mass of the added aqueous solution should only change the degree of the effect but not the original trend.
and larger maximum viscosity, the initial shear thinning becomes weaker and the shear thickening behavior is more abrupt. While the influence of the pH value on the SiO2–COOH suspensions is inverse. It fully proves that the rheological behavior of the suspensions could be adjusted by changing the micro-environment of the microspheres. The rule is summarized as follows: when the aqueous solution tends to combine with the microspheres, the shear thickening exhibits a greater weakening, whereas when the aqueous solution combines with the media more easily, the shear thinning exhibits a more obvious change, all of which is determined by the competing interaction between the components in the suspension. Changing the mass of the added aqueous solution should only change the degree of the effect but not the original trend.
Based on the above test results, two theory models were used to analyze the related mechanism. Focusing on the start of shear thickening, the τc was analyzed by using the Wagner model, in which, the measured zeta potential was used to stand for the surface potential of particles. It was found that the measured τc and predicted τc both maintain a similar tendency as that of the absolute value of the zeta potential which directly depends on the pH value, indicating that the interaction between the particles affects the onset of shear thickening significantly. Though the value of the measured and predicted τc is similar, a gap between them still exists due to the more complex interactions in the actual system. Furthermore, friction theory was used to analyze the degree of shear thickening. Based on the calculated Sommerfeld number s of this researched system, it could be inferred that the suspensions are in the “boundary lubrication” regime, in which the fixed coefficient of friction μ0 is independent of the load, speed and apparent contact area. Here, the independent friction coefficients μ0 of each particle at different pH was estimated using a designed similar friction test system. For each suspension with a special μ0, there exists a critical volume fraction (ϕBLmax) corresponding to the onset of DST. With the increase of μ0, the ϕBLmax decreases significantly, the rule is independent of the kind of particle in the suspension. This phenomenon reveals that μ0 is the key factor to determine the degree of shear thickening. Moreover, an exponential relationship between the decreased ϕ and n − 1 (n is index τ ∝ γn) was found, indicating that the effect of ϕ on the thickening degree is reduced gradually with the decrease of ϕ.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial supports of the National Natural Science Foundation of China (11502077), The Key Research and Development Plan of Hunan (2016SK2077).Notes and references
- S. R. Waitukaitis and H. M. Jaeger, Nature, 2012, 487, 205–209 CrossRef CAS PubMed.
- M. van Hecke, Nature, 2012, 487, 174–175 CrossRef CAS PubMed.
- O. E. Petel, S. Ouellet and J. Loiseau, Appl. Phys. Lett., 2013, 120, 064103 CrossRef.
- R. L. Hoffman, J. Colloid Interface Sci., 1974, 46, 491–506 CrossRef CAS.
- R. L. Hoffman, J. Rheol., 1998, 42, 111–123 CrossRef CAS.
- E. Brown and H. M. Jaeger, J. Rheol., 2012, 56, 875–923 CrossRef CAS.
- A. Fall, N. Huang, F. Bertrand, G. Ovarlez and D. Bonn, Phys. Rev. Lett., 2008, 100, 018301 CrossRef PubMed.
- N. J. Wagner and J. F. Brady, Phys. Today, 2009, 62, 27–32 CrossRef CAS.
- X. Cheng, J. H. McCoy, J. N. Israelachvili and I. Cohen, Science, 2011, 333, 1276–1279 CrossRef CAS PubMed.
- W. Q. Jiang, Y. Q. Sun, Y. L. Xu, C. Peng, X. L. Gong and Z. Zhang, Rheol. Acta, 2010, 49, 1157–1163 CrossRef CAS.
- S. S. Shenoy and N. J. Wagner, Rheol. Acta, 2005, 44, 360–371 CrossRef CAS.
- J. Melrose and R. Ball, J. Rheol., 2004, 48, 961–978 CrossRef CAS.
- B. J. Maranzano and N. J. Wagner, J. Rheol., 2001, 45, 1205–1222 CrossRef CAS.
- B. J. Maranzano and N. J. Wagner, J. Chem. Phys., 2001, 114, 10514–10527 CrossRef CAS.
- J. Kaldasch, B. Senge and J. Laven, Rheol. Acta, 2008, 47, 319–323 CrossRef CAS.
- J. Kaldasch and B. Senge, Colloid Polym. Sci., 2009, 287, 1481–1485 CrossRef CAS.
- C. B. Holmes, M. Fuchs and M. E. Cates, Europhys. Lett., 2003, 63, 240 CrossRef CAS.
- C. B. Holmes, M. E. Cates, M. Fuchs and P. Sollich, J. Rheol., 2005, 49, 237–269 CrossRef CAS.
- M. Sellitto and J. Kurchan, Phys. Rev. Lett., 2005, 95, 236001 CrossRef PubMed.
- E. Brown and H. M. Jaeger, J. Rheol., 2010, 56, 875–923 CrossRef.
- A. Fall, N. Huang, F. Bertrand, G. Ovarlez and D. Bonn, Phys. Rev. Lett., 2008, 100, 018301 CrossRef PubMed.
- A. Fall, F. Bertrand, G. Ovarlez and D. Bonn, J. Rheol., 2012, 56, 575–591 CrossRef CAS.
- E. Brown and H. M. Jaeger, Rep. Prog. Phys., 2014, 77, 046602 CrossRef.
- D. Bi, J. Zhang, B. Chakraborty and R. P. Behringer, Nature, 2011, 480, 355–358 CrossRef CAS PubMed.
- N. Y. C. Lin, B. M. Guy, M. Hermes, C. Ness, J. Sun, W. C. K. Poon and I. Cohen, Phys. Rev. Lett., 2015, 115, 228304 CrossRef PubMed.
- B. M. Guy, M. Hermes and W. C. Poon, Phys. Rev. Lett., 2015, 115, 088304 CrossRef CAS PubMed.
- R. Mari, R. Seto, J. F. Morris and M. M. Denn, J. Rheol., 2014, 58, 1693–1724 CrossRef CAS.
- J. R. Royer, D. L. Blair and S. D. Hudson, Phys. Rev. Lett., 2016, 116, 188301 CrossRef PubMed.
- R. Seto, R. Mari, J. F. Morris and M. M. Denn, Phys. Rev. Lett., 2013, 111, 218301 CrossRef PubMed.
- N. Fernandez, R. Mani, D. Rinaldi, D. Kadau, M. Mosquet, H. Lombois-Burger, J. Cayer-Barrioz, H. J. Herrmann, N. D. Spencer and L. Isa, Phys. Rev. Lett., 2013, 111, 108301 CrossRef PubMed.
- M. Wyart and M. E. Cates, Phys. Rev. Lett., 2014, 112, 098302 CrossRef CAS PubMed.
- E. Brown, N. A. Forman, C. S. Orellana, H. J. Zhang, B. W. Maynor, D. E. Betts, J. M. DeSimone and H. M. Jaeger, Nat. Mater., 2010, 9, 220–224 CrossRef CAS PubMed.
- S. Wang, W. Q. Jiang, W. F. Jiang, F. Ye, Y. Mao, S. H. Xuan and X. L. Gong, J. Mater. Chem. C, 2014, 34, 7133–7140 RSC.
- T. Yokoi, Y. Sakamoto, O. Terasaki, Y. Kubota, T. Okubo and T. Tatsumi, J. Am. Chem. Soc., 2006, 128, 13664–13665 CrossRef CAS PubMed.
- J. Warren, S. Offenberger, H. Toghiani, C. U. Pittman Jr, T. E. Lacy and S. Kundu, ACS Appl. Mater. Interfaces, 2015, 7, 18650–18661 CrossRef CAS PubMed.
- T. Jiang and C. F. Zukoski, Macromolecules, 2012, 45, 9791–9803 CrossRef CAS.
- T. Glomann, A. Hamm, J. Allgaier, E. G. Hübner, A. Radulescu, B. Farago and G. J. Schneider, Soft Matter, 2013, 9, 10559–10571 RSC.
- Y. S. Lee and N. J. Wagner, Rheol. Acta, 2003, 42, 199–208 CAS.
| This journal is © The Royal Society of Chemistry 2019 |