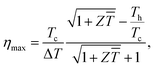Enhanced room-temperature thermoelectric performance of p-type BiSbTe by reducing carrier concentration

Abstract

Improving room-temperature thermoelectric performance of p-type (Bi,Sb)₂Te₃ is essential for its practical application. However, the usual doping or alloying methods increase the carrier concentration and result in enhanced thermoelectric properties at high temperatures but not room temperature. In this work, we find that Ti is a promising dopant to shift the optimum thermoelectric properties of p-type (Bi,Sb)₂Te₃ to room temperature by reducing its carrier concentration. p-type Bi_0.5Sb_1.5−xTi_xTe₃ samples with various Ti contents have been prepared using a simple melting method. The carrier concentration of Bi_0.5Sb_1.5−xTi_xTe₃ is reduced by partially replacing Sb with Ti, leading to not only a significantly increased Seebeck coefficient but also an improved power factor near room temperature. Moreover, the total thermal conductivity near room temperature also decreases owing to the combined effect of decreased electrical conductivity and an anisotropic microstructure. An optimal zT value of ∼1.2 is achieved near room temperature for the sample containing 6 at% Ti, and its average zT value below 150 °C increases to ∼1.1, demonstrating the great potential of this material for room-temperature thermoelectric devices.

---

Introduction

Thermoelectric materials, which can directly convert heat into electricity,¹ have recently attracted intensive attention. Thermoelectric devices have no moving parts, produce no noise, have a long service life, and are environmentally friendly, leading to their application in various fields, such as the aerospace industry, commercial power generation, and refrigeration.^2–4 The thermoelectric properties of a material are assessed by the thermoelectric figure of merit zT, where z is defined as z = S²σ/(κ_e + κ_L + κ_b) (S is the Seebeck coefficient, σ is the electrical conductivity, κ_e is the electronic thermal conductivity, κ_L is the lattice thermal conductivity, κ_b is the bipolar thermal conductivity, and T is the absolute temperature).⁵ Because of the mutual restriction of each parameter in the above formula, optimization of the material performance is a key issue in improving the efficiency of a thermoelectric device.

Bi₂Te₃ is one of the most promising materials in the temperature range of 250–500 K.^6,7 Today, commercial refrigeration devices are mostly made of Bi₂Te₃-based materials with a peak zT value near 1.^8,9 The thermoelectric properties of Bi–Sb–Te-based solid solutions have been effectively improved through the alloying effect.^10–13 Because the Seebeck coefficient S, electrical conductivity σ, and thermal conductivity κ in zT are all highly dependent on the carrier concentration,^14,15 optimization of the carrier concentration is crucial to achieve improved thermoelectric performance. The optimal carrier concentration of good thermoelectric materials is normally in the range of 10¹⁹ to 10²⁰ cm⁻³.^16–18 The carrier-concentration-dependent thermoelectric properties of Bi_2−xSb_xTe₃ were systematically investigated by Zhao et al.,¹⁹ with the optimal electrical transport performance achieved for a carrier concentration of 1.4 × 10¹⁹ cm⁻³. According to recent reports by Zheng and Deng,^20,21 Bi_0.5Sb_1.5Te₃ exhibits the best thermoelectric performance (zT = 1.1 at 87 °C) for a carrier concentration of approximately 2.5 × 10¹⁹ cm⁻³.

Atomic doping in p-type Bi_0.5Sb_1.5Te₃ is generally performed to increase the carrier concentration,^22–26 thereby improving the electrical conductivity to achieve enhanced thermoelectric properties. For instance, the substitution of Ag⁺,^22,23,26 Cu⁺ (ref. 24) and Cd²⁺ (ref. 25) for Bi³⁺/Sb³⁺ results in an increased hole concentration which suppresses the bipolar effect, leading to improved thermoelectric properties at high temperature. However, the thermoelectric properties near room temperature are not usually optimized because the material is overdoped in the low temperature range. As Bi₂Te₃-based materials are mainly used at room temperature, it is essential to regulate the carrier concentration to reach the peak zT value and corresponding highest average zT value near room temperature.

It is essential to reduce the carrier concentration of p-type Bi_0.5Sb_1.5Te₃ in order to optimize its room-temperature thermoelectric performance. According to our detailed survey and analysis, Ti is a non-toxic and earth-abundant element which has astable +4 valence state in a compound. Thus, reduced hole concentration in p-type Bi_0.5Sb_1.5Te₃ could be realized by the substitution of Ti for Bi/Sb, which is different from the previously reported doping strategy. In this work, the room-temperature thermoelectric properties of p-type Bi_0.5Sb_1.5Te₃ were improved by partially replacing Sb with Ti. The substitution of Ti for Sb results in decreased carrier concentration, electrical conductivity, and thermal conductivity but increased Seebeck coefficient. A maximum zT value of ∼1.2 was achieved at 75 °C for the sample containing 6 at% Ti.

Experimental

High-purity powders of Bi (Aladdin 99.99%), Sb (Aladdin 99.99%), Te (Aladdin 99.999%), and Ti (Aladdin 99.9%) were weighed to achieve a nominal composition of Bi_0.5Sb_1.5−xTi_xTe₃ and placed into a graphite crucible. The mixture was then sealed in an evacuated quartz tube at 10⁻⁴ torr and melted at 950 °C for 4 days. The obtained ingots were crushed into fine powders using an agate mortar. The powders were then hot pressed at 350 °C under a pressure of 75 MPa for 30 min in a vacuum to obtain pellets for measurement of the thermoelectric properties.

X-ray powder diffraction (XRD; PANalytical, Netherlands) was performed with Cu Kα radiation (λ = 0.1541854 nm) using the continuous scanning method. The morphologies of the samples were examined using scanning electron microscopy (SEM; Zeiss Gemini 300, Germany). An ULVAC-RIKO ZEM-3 thermoelectric measurement system was used to simultaneously measure the Seebeck coefficient and electrical resistivity. The thermal diffusivity of the sample was determined using the laser flash diffusivity method with a Netzsch laser flash apparatus (LFA 457). The total thermal conductivity κ was calculated using the equation κ = DρC_p, where D, ρ, and C_p are the thermal diffusivity, mass density, and volumetric specific heat capacity, respectively. The C_p value of the pure sample was determined using a Netzsch differential scanning calorimetry (201F1) instrument, and ρ was determined using the Archimedes method.

Results and discussion

Fig. 1a presents XRD patterns of the Ti_xBi_0.5Sb_1.5−xTe₃ powder samples after hot pressing and sintering. All the samples crystallized into a rhombohedral structure with space group R3̄m, and no obvious impurity diffraction peaks were detected. As observed in Fig. 1b, with increasing Ti content, the (1010) diffraction peak gradually shifted to high angle, indicating that the lattice constant decreased with the addition of Ti (see also Table 1 and Fig. S1†). The decrease of the lattice constant is attributed to the partial replacement of Sb³⁺ with Ti⁴⁺ ions, as the radius of Ti⁴⁺ (0.56 Å) is smaller than that of Sb³⁺ (0.76 Å). In addition, the variation in the lattice constant shown in Fig. S1† indicates that the solid solubility of Ti in Bi_0.5Sb_1.5Te₃ is approximately 10 at%. EDS analysis confirms that the measured composition of our sample is very close to its nominal composition (Fig. S2 and Table S1†).

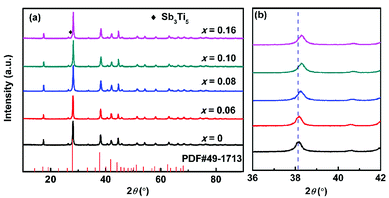Fig. 1 (a) XRD patterns and (b) enlarged (1010) diffraction peak for Ti_xBi_0.5Sb_1.5−xTe₃ (x = 0, 0.06, 0.08, 0.10, 0.16) samples.

Table 1 Lattice constants a and c of Ti_xBi_0.5Sb_1.5−xTe₃ samples

Ti content	a (Å)	c (Å)
x = 0	4.3013 (12)	30.5040 (06)
x = 0.06	4.2921 (15)	30.4450 (06)
x = 0.08	4.2893 (22)	30.4430 (10)
x = 0.10	4.2880 (04)	30.4310 (13)
x = 0.16	4.2901 (05)	30.4480 (11)

---

Fig. 2 shows the temperature dependence of the electrical conductivity, Seebeck coefficient, and power factor (PF) of the Ti_xBi_0.5Sb_1.5−xTe₃ samples. Because bismuth telluride has an anisotropic layered structure,^27,28 its thermoelectric performance is anisotropic (Fig. S3†). Therefore, the electrical and thermal transport properties in our works were measured along the same direction (parallel to the hot-pressing direction) to eliminate the anisotropic effect. As observed in Fig. 2a and 3a, both the electrical and thermal transport properties were measured parallel to the direction of applied pressure for the hot pressing. As bismuth telluride is a typical degenerate semiconductor, the electrical conductivity σ of the sample monotonically decreased with increasing T at low temperatures. At high temperatures, σ began to increase with increasing temperature because of the mixed electron and hole conduction originating from the intrinsic excitation. With increasing Ti content from x = 0 to x = 0.16, the room-temperature σ monotonically decreased from ∼75 000 to 40 000 S m⁻¹. Because a Ti atom provides one extra electron compared with the host Sb atom, the substitution of Ti for Sb leads to decreased hole carrier concentration and electrical conductivity in p-type Bi_0.5Sb_1.5Te₃.

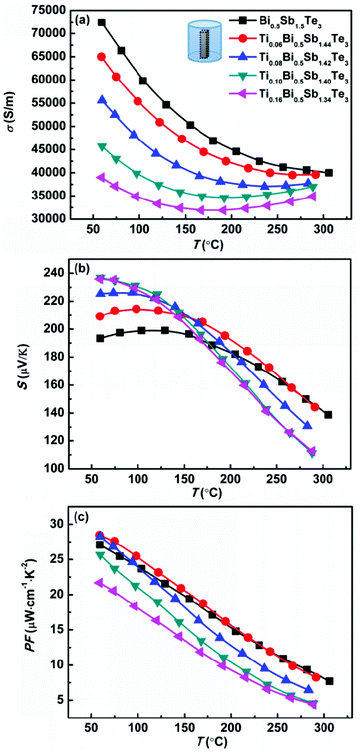Fig. 2 Temperature dependences of (a) electrical conductivity, (b) Seebeck coefficient, and (c) power factor for Bi_0.5Ti_xSb_1.5−xTe₃ samples.

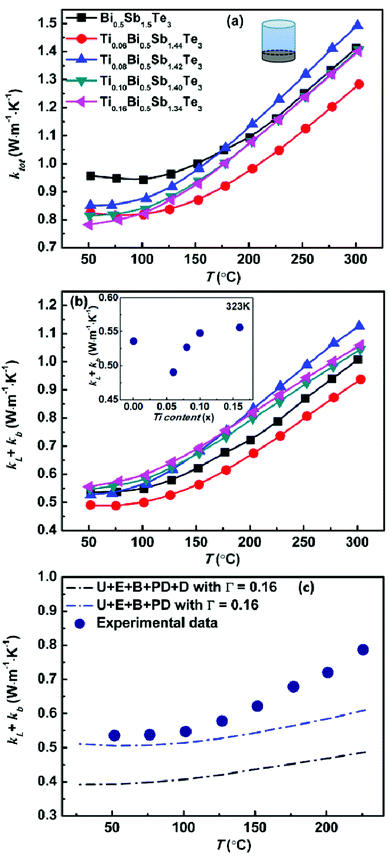Fig. 3 (a) Temperature dependence of total thermal conductivity, (b) sum of the lattice and bipolar thermal conductivity for Bi_0.5Ti_xSb_1.5−xTe₃ samples and (c) measured κ_L + κ_b data points for Bi_0.5Sb_1.5Te₃ pellet compared with calculated κ_L determined by different models.²⁹ The inset of (b) shows the κ_L + κ_b as a function of the Ti concentration at 323 K.

As observed in Fig. 2b, the Seebeck coefficients of all the samples were positive, demonstrating the hole-dominant p-type conduction. The Seebeck coefficient first increased and then decreased with increasing temperature, which is consistent with the temperature-dependent electrical conductivity. The decrease of the Seebeck coefficient at high temperature is attributed to the bipolar conduction. With increasing Ti content, the room-temperature Seebeck coefficient increases because of the decreased hole carrier concentration. As shown in Table 2, the carrier concentration decreased from 2.6 × 10¹⁹ to 1.1 × 10¹⁹ cm⁻³ as the Ti content x increased from x = 0 to x = 0.16. The substitution of Ti for Sb led to a reduction in the hole concentration and shifted the onset temperature of bipolar conduction to lower temperature; however, the Seebeck coefficient near room temperature increased, thereby enhancing the room-temperature thermoelectric performance.

Table 2 Carrier concentration (n) and mobility (μ) of Ti_xBi_0.5Sb_1.5−xTe₃ samples

Ti content	n (10^19 cm^−3)	μ (cm^2 V^−1 s^−1)
x = 0	2.6	201
x = 0.06	2.4	213
x = 0.08	1.9	216
x = 0.10	1.4	230
x = 0.16	1.1	238

---

The Seebeck coefficients of the samples with x = 0.10 and x = 0.16 were almost the same because the solid solubility limit of Ti is approximately x = 0.10. The effective mass of the charge carrier was calculated using the single-parabolic band model. According to our calculation, the substitution of Ti for Sb has little effect on the carrier effective mass (Fig. S4†), indicating that the band degeneracy of Bi_0.5Sb_1.5Te₃ was not altered by substituting Ti for Sb. Therefore, the increase of the Seebeck coefficient mainly resulted from the decrease in the hole concentration.

As shown in Fig. 2c, the power factors of all the samples monotonically decreased with increasing temperature. For the sample without Ti, the maximum power factor was approximately 27.5 μW cm⁻¹ K⁻². By replacing a small amount of Sb with Ti (x = 0.06), the maximum power factor increased to ∼29 μW cm⁻¹ K⁻² because of the increased Seebeck coefficient. The sample with x = 0.08 also exhibited a maximum power factor of approximately 29 μW cm⁻¹ K⁻²; however, its power factor above 100 °C was smaller than that of the sample without Ti because of the further reduced hole concentration and more prominent bipolar conduction. For the samples with higher Ti contents (x = 0.10 and x = 0.16), the increase in the Seebeck coefficient could not compensate for the decreased electrical conductivity, and their power factors were thus smaller than that of the sample without Ti over the entire measured temperature range. Our experimental results clearly indicate that the addition of Ti is effective in increasing the low-temperature (near room temperature) Seebeck coefficient of Bi_0.5Sb_1.5Te₃. The carrier concentration of our sample with x = 0.06 was very close to the optimal carrier concentration reported in the literature;^20,21 therefore, this sample exhibited the maximum power factor.

Fig. 3 shows the temperature dependences of the thermal transport properties for the Ti_xBi_0.5Sb_1.5−xTe₃ samples. The density of all samples was higher than 96%. Because the bipolar diffusion thermal conductivity could not be neglected, the total thermal conductivity κ_tot consisted of three parts: the electron thermal conductivity κ_e, lattice thermal conductivity κ_L, and bipolar diffusion thermal conductivity κ_b(κ_tot = κ_e + κ_L + κ_b). κ_e can be calculated using the Wiedemann–Franz law, κ_e = LσT, where L is the Lorenz constant. For semiconductor thermoelectric materials, the Lorenz constant can be expressed as a function of the Seebeck coefficient. In this work, an averaged L value of 1.75 × 10⁻⁸ V² K⁻² was used for our samples based on the variation range of their Seebeck coefficients. As shown in Fig. 3a, the total thermal conductivity decreased with increasing Ti content, especially at low temperature. Because of the addition of Ti, several factors could affect the thermal transport properties of our samples: (i) the decrease of the electrical conductivity σ with increasing Ti content leads to decreased electronic thermal conductivity κ_e (Fig. 2a); (ii) the differences in the size and mass of heterogeneous atoms result in stress and mass fluctuations, which could scatter the phonons and lead to a decrease of the lattice thermal conductivity κ_L; the inset of Fig. 3b shows the variation of κ_L + κ_b with respect to the Ti concentration around room temperature. The value of κ_L + κ_b first decreases with the increasing of Ti content because of the intensified point defect phonon scattering from mainly the mass difference between Ti (M_Ti = 47.9) and Sb (M_Sb = 121.8). With the further increase of Ti content, the temperature of bipolar diffusion shifts to the lower temperature, leading to the increase of κ_L + κ_b. (iii) The onset temperature of intrinsic excitation shifts to lower temperature and the bipolar diffusion thermal conductivity κ_b increases at high temperatures; Fig. 3c shows calculated κ_L of Bi_0.5Sb_1.5Te₃ by considering U + E + B + PD and U + E + B + PD + D (phonon–phonon umklapp (U), electron–phonon (E), grain boundary (B), point defect (PD) and dislocation (D) scatterings) according to the report of Hong et al.²⁹ The U + E + B + PD + D (blue curve) model matchs well with our experimental κ_L + κ_b before the appearance of the bipolar effect. The increasing divergence with the temperature can be ascribed to κ_b. (iv) The anisotropic feature of the microstructure becomes less prominent with increasing Ti content (Fig. S5†), thus causing the thermal conductivity to increase because the thermal conductivity perpendicular to the layer structure is the lowest. The combined effect of these competing factors resulted in decreased total thermal conductivity with increasing Ti content according to our experiments.

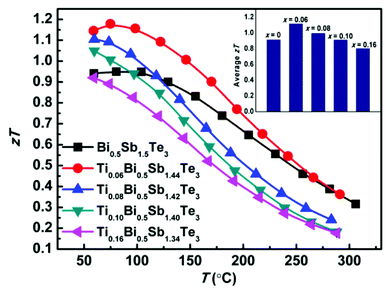
Fig. 4 shows the temperature-dependent thermoelectric figure of merit zT of the Ti_xBi_0.5Sb_1.5−xTe₃ samples. The room-temperature zT values of the samples with x = 0.06, 0.08, and 0.10 were all higher than that of the sample without Ti. The zT value of the sample with x = 0.16 was comparable to that of the sample without Ti, which can be attributed to the presence of the Sb₃Ti₅ impurity. The sample with x = 0.06 exhibited the best thermoelectric performance with a maximum zT value of approximately 1.2. The enhanced thermoelectric performance mainly originates from the optimized carrier concentration and reduced thermal conductivity achieved by partially replacing Sb with Ti.

Fig. 4 zT values of Ti_xBi_0.5Sb_1.5−xTe₃ samples.

Because thermoelectric devices made of bismuth-telluride-based materials are generally used near room temperature, the average zT value near room temperature is critical. The efficiency of a thermoelectric device also depends on other factors in addition to the maximum zT of the material.³⁰ For a Peltier cooler, the maximum efficiency (ƞ_max) is expressed as

where ZT̄ is the device thermoelectric figure of merit (a device composed of p- and n- type thermoelectric legs), T_h is the hot-side temperature, T_c is the cold-side temperature, 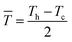and ΔT is the temperature difference between the hot and cold sides.³¹ To maximize the efficiency across a large temperature drop, it is imperative to maximize the device ZT̄ and not only the peak material zT. One method to achieve this objective is to tune the material properties to provide a large average zT in the working temperature range.^1,32 The average zT values of all our samples were calculated in the temperature range of 50–150 °C, and the corresponding results are presented in the inset of Fig. 4. The average zT values were 0.9 and 1.1 for the samples with x = 0 and x = 0.06, respectively. Thus, our results indicate that the device efficiency near room temperature can be significantly improved by partially substituting Sb with Ti in p-type Bi_0.5Sb_1.5Te₃. Moreover, our samples exhibit a good repeatability (Fig. S6†) which is fundamental important for a mature commercial thermoelectric material.

Conclusions

In this work, p-type Ti_xBi_0.5Sb_1.5−xTe₃ was first prepared using a simple and conventional melting method. The substitution of Ti for Sb introduced extra electrons, leading to a dramatically reduced hole carrier concentration. Consequently, the Seebeck coefficient near room temperature increased with increasing Ti content; however, the onset temperature of intrinsic excitation shifted to lower temperature. The partial substitution of Ti for Sb resulted in decreased electrical conductivity, prominent bipolar conduction, enhanced alloy scattering, and a less anisotropic microstructure, which had a complex effect on the thermoelectric transport properties. According to our experiments, the competition between these complex influencing factors resulted in reduction of the total thermal conductivity. The sample with x = 0.06 exhibited the optimal thermoelectric performance with a maximum zT of ∼1.2 near room temperature and an average zT ∼ 1.1 in the temperature range of 50–150 °C. Our experiments clearly demonstrate that the room-temperature thermoelectric properties of p-type Bi_0.5Sb_1.5Te₃ can be further improved by reducing its hole carrier concentration, which is critical for the commercial application of this material near room temperature.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 51772186, 51632005, and 51371194) and a research grant (No. 16DZ2260601) from the Science and Technology Commission of Shanghai Municipality.

Notes and references

1. L. E. Bell, Science, 2008, 321, 1457.
2. B. C. Sales, Science, 2002, 295, 1249.
3. T. M. Tritt, Science, 1996, 272, 1276–1277.
4. S. B. Riffat and X. Ma, Appl. Therm. Eng., 2003, 23, 913–935.
5. A. Majumdar, Materials science, 2004, 303, 777–778.
6. Z. Aabdin, N. Peranio and O. Eibl, Adv. Mater., 2012, 24, 4605–4608.
7. M. Scheele, N. Oeschler, K. Meier, A. Kornowski, C. Klinke and H. Weller, Adv. Funct. Mater., 2009, 19, 3476–3483.
8. R. Venkatasubramanian, E. Siivola, T. Colpitts and B. O'Quinn, Nature, 2001, 413, 597–602.
9. G. Zhang, B. Kirk, L. A. Jauregui, H. Yang, X. Xu, Y. P. Chen and Y. Wu, Nano Lett., 2012, 12, 56–60.
10. W. Xie, X. Tang, Y. Yan, Q. Zhang and T. M. Tritt, Appl. Phys. Lett., 2009, 94, 102111.
11. R.-S. Zhai, Y.-H. Wu, T.-J. Zhu and X.-B. Zhao, Rare Met., 2018, 37, 308–315.
12. Z. Xu, H. Wu, T. Zhu, C. Fu, X. Liu, L. Hu, J. He, J. He and X. Zhao, NPG Asia Mater., 2016, 8, e302.
13. S. Hwang, S.-I. Kim, K. Ahn, J. W. Roh, D.-J. Yang, S.-M. Lee and K.-H. Lee, J. Electron. Mater., 2012, 42, 1411–1416.
14. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
15. M. S. Dresselhaus, G. Chen, M. Y. Tang, R. G. Yang, H. Lee, D. Z. Wang, Z. F. Ren, J. P. Fleurial and P. Gogna, Adv. Mater., 2007, 19, 1043–1053.
16. M. R. Dirmyer, J. Martin, G. S. Nolas, A. Sen and J. V. Badding, Small, 2009, 5, 933–937.
17. Y. Pei, Z. M. Gibbs, A. Gloskovskii, B. Balke, W. G. Zeier and G. J. Snyder, Adv. Energy Mater., 2014, 4, 1400486.
18. Y. Pei, A. D. Lalonde, N. A. Heinz, X. Shi, S. Lwanaga, H. Wang, L. Chen and G. J. Snyder, Adv. Mater., 2011, 23, 5674–5678.
19. Y. Zhao, J. S. Dyck, B. M. Hernandez and C. Burda, J. Am. Chem. Soc., 2010, 132, 4982–4983.
20. G. Zheng, X. Su, H. Xie, Y. Shu, T. Liang, W. Liu, Y. Yan, Q. Zhang, C. Uher, M. G. Kanatzidis and X. Tang, Energy Environ. Sci., 2017, 10, 2638–2652.
21. R. Deng, X. Su, T. Luo, J. Li, W. Liu, Y. Yan and X. Tang, J. Solid State Chem., 2018, 264, 141–147.
22. J. K. Lee, S. D. Park, B. S. Kim, M. W. Oh, S. H. Cho, B. K. Min, H. W. Lee and M. H. Kim, Electron. Mater. Lett., 2010, 6, 201–207.
23. I. J. Vera-Marun, J. J. van den Berg, F. K. Dejene and B. J. van Wees, Nat. Commun., 2016, 7, 11525.
24. Z. Wei, C. Wang, L. You, S. Zhao, K. Yang, H. Chen, J. Luo and X. Chen, RSC Adv., 2017, 7, 41111–41116.
25. F. Hao, P. Qiu, Y. Tang, S. Bai, T. Xing, H.-S. Chu, Q. Zhang, P. Lu, T. Zhang, D. Ren, J. Chen, X. Shi and L. Chen, Energy Environ. Sci., 2016, 9, 3120–3127.
26. S. Seo, K. Lee, Y. Jeong, M. W. Oh and B. Yoo, J. Mater. Chem. C, 2015, 119, 18038–18045.
27. S. Chen, K. F. Cai, F. Y. Li and S. Z. Shen, J. Electron. Mater., 2013, 43, 1966–1971.
28. Y. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. Dai, Z. Fang, S. C. Zhang, I. R. Fisher, Z. Hussain and Z. X. Shen, Science, 2009, 325, 178–181.
29. M. Hong, Z. G. Cheng, L. Yang and J. Zou, Nano Energy, 2016, 20, 144–155.
30. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
31. T. M. Tritt and M. A. Subramanian, MRS Bull., 2011, 31, 188–198.
32. S. Wang, W. Xie, H. Li and X. Tang, Intermetallics, 2011, 19, 1024–1031.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra09771b

---