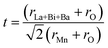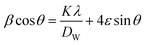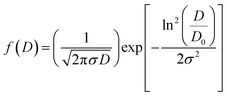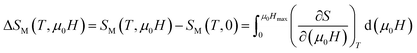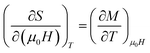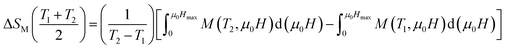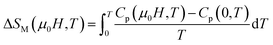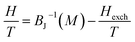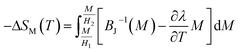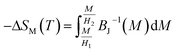Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Large magnetocaloric effect in manganese perovskite La0.67−xBixBa0.33MnO3 near room temperature
Ah. Dhahri *ab,
E. Dhahri
*ab,
E. Dhahri a and
E. K. Hlilc
a and
E. K. Hlilc
aLaboratoire de Physique Appliquée, Faculté des Sciences de Sfax, Université de Sfax, BP 1171, 3000, Tunisia. E-mail: dhahridhahri14@gmail.com; Tel: +216 20 20 45 55
bFaculté des Sciences de Monastir, Avenue de l'environnement 5019, Monastir, Tunisia
cInstitut Néel, CNRS et Université J. Fourier, BP 166, 38042 Grenoble, France
First published on 13th February 2019
Abstract
La0.67−xBixBa0.33MnO3 (x = 0 and 0.05) ceramics were prepared via the sol–gel method. Structural, magnetic and magnetocaloric effects have been systematically studied. X-ray diffraction shows that all the compounds crystallize in the rhombohedral structure with the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group. By analyzing the field and temperature dependence of magnetization, it is observed that both samples undergo a second order magnetic phase transition near TC. The value of TC decreases from 340 K to 306 K when increasing x from 0.00 to 0.05, respectively. The reported magnetic entropy change for both samples was considerably remarkable and equal to 5.8 J kg−1 K−1 for x = 0.00 and 7.3 J kg−1 K−1 for x = 0.05, respectively, for μ0H = 5 T, confirming that these materials are promising candidates for magnetic refrigeration applications. The mean-field theory was used to study the magnetocaloric effect within the thermodynamics of the model. Satisfactory agreement between experimental data and the mean-field theory has been found.
c space group. By analyzing the field and temperature dependence of magnetization, it is observed that both samples undergo a second order magnetic phase transition near TC. The value of TC decreases from 340 K to 306 K when increasing x from 0.00 to 0.05, respectively. The reported magnetic entropy change for both samples was considerably remarkable and equal to 5.8 J kg−1 K−1 for x = 0.00 and 7.3 J kg−1 K−1 for x = 0.05, respectively, for μ0H = 5 T, confirming that these materials are promising candidates for magnetic refrigeration applications. The mean-field theory was used to study the magnetocaloric effect within the thermodynamics of the model. Satisfactory agreement between experimental data and the mean-field theory has been found.
1 Introduction
Over the past few years, the perovskite manganites with ABO3-type compounds Tr1−xMxMnO3 (where Tr stands for a trivalent rare-earth element such as Bi3+, La3+ or Pr3+, and M for the divalent alkaline earth ions such as Sr2+, Ca2+ or Ba2+), have been extensively studied due to their extraordinary magnetic and electronic properties as well as their promise for potential technological applications.1,2 A prominent feature of the mixed-valence perovskite manganite materials is an insulator–metal (IM) transition accompanied simultaneously by the paramagnetic–ferromagnetic (PM–FM) transition giving rise to a colossal magnetoresistance (CMR) effect.3 The existence of the observed CMR near the transition temperature was due to the mixed valence state of Mn, evolving from Mn3+ (t32g↑e1g↑, S = 2) in the parent atom LaMnO3 to Mn4+ (t32g↑e0g, S = 3/2) to the doped element SrMnO3.4 The double exchange interaction of the neighboring spin moment of (Mn3+, Mn4+) coupled through oxygen ions (O2+), the small polaron theory and the Jahn–Teller (JT) effect have been proposed to explain the CMR phenomenon near the transition temperature.5 In addition, when a field is applied to this material, the unpaired spins are aligned parallel to the field. Since the total entropy of spins plus the lattice remains constant, the magnetic entropy change (−ΔSM) is removed from the spin system and goes into the lattice, which lowers the magnetic entropy and produces a net heat. On the contrary, when an applied field is removed from a magnetic sample, the spin tends to become random, leading to increment of the entropy and causing the material to cool down. As well known, the maximum of the magnetic entropy change in this kind of material always occurs around its magnetic ordering temperature (i.e., Curie temperature, TC). Nowadays, there is a need of new advanced magnetics materials with a second order magnetic phase transition, showing a large reversible (−ΔSM) at low applied fields. Some theoretical works have focused on this subject, for second order phase transition via the molecular mean field theory.6 For this it is important to know the field dependence of a given magnetic refrigerant sample. The study of the magnetocaloric effect is not only important from the point of view of potential applications; it also provides a tool to understand the intrinsic properties of a material. In Bi based manganites, the lone pair electrons of Bi3+ ion hybridize with oxygen 2p orbitals, which in turn reduces the bond length of dBi–O and bond angle of θMn–O–Mn and increases the bond length of dMn–O.7From this viewpoint, this paper reports the structural, magnetic and magnetic entropy change of Bi-substituted perovskite manganites La0.62Bi0.05Ba0.33MnO3. It is found that these materials show quite large magnetic entropy changes induced by low magnetic field changes.
2 Experimental details
Powders of La0.67−xBixBa0.33MnO3 (x = 0 and 0.05) were prepared via sol–gel route. In this process, La(NO3)3·6H2O, Ba(NO3)2, Bi(NO3)2·5H2O and Mn(NO3)2·6H2O precursors, all with purity of 99.9%, were weighed in the desired proportions and dissolved with small amounts of water. Ethylene glycol (EG) and citric acid (CA) were used as polymerization/complexation agents, respectively, forming a stable solution. 100 cm3 of metallic salts solution was added to 300 cm3 of a solution containing a mixture of citric acid (60 g) and ethylene glycol (13 mL). This solution was then heated on a thermal plate under constant stirring, where polymerization occurs in the liquid solution and leads to a homogeneous sol. When the sol is further heated to remove the excess of solvent, an intermediate resin is formed. Calcination of the resin at 573 K in air was performed and sintering at 1073 K for 10 hours. These procedures are outlined in the flow chart of Fig. 1.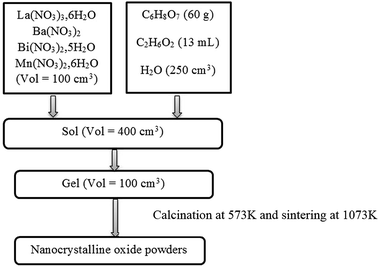 | ||
| Fig. 1 A flow chart illustrating the processing procedure for La0.67−xBixBa0.33MnO3 powders preparation. | ||
The phase purity and structure of sample were identified by X-ray powder diffraction at room temperature using a Siemens D5000 X-ray diffractometer with a graphite monochromatized CuKα radiation (λCuKα = 1.5406 Å) and 20° ≤ 2θ ≤ 90° with steps of 0.02° and a counting time of 18 s per step. According to our measurements, this system is able to detect up to a minimum of 3% of impurities. The structure analysis was carried out using the Rietveld method with FULLPROF software (version 0.2-Mars 1998-LLB-JRC).8 Scanning electron microscopy (SEM) using a Philips XL30 equipped with a field emission gun at 20 kV was used to characterize La0.67−xBixBa0.33MnO3 morphologies.
Magnetization (M) versus temperature (T) and magnetization versus magnetic field (μ0H) were performed by using BS1 and BS2 magnetometers developed in Louis Neel Laboratory at Grenoble. The isothermal curves were determined in the magnetic field range of 0–5 T. The temperature interval is fixed to 2 K in the vicinity of the Curie temperature (TC). The temperature steps were smaller near TC and larger further away.
3 Results and discussion
3.1 X-ray diffraction and microstructure analysis
The X-ray diffraction pattern for the samples (x = 0.00 and 0.05) is shown in Fig. 2. The samples of La0.67−xBixBa0.33MnO3 are a single phase without detectable secondary phase, within the sensitivity limits of the experiment (a few percent). The Rietveld refinements was successful considering the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c (no. 167) rhombohedral and centro symmetric space group (inset (a) of Fig. 2, for x = 0.0 for example). Standard hexagonal setting of the R
c (no. 167) rhombohedral and centro symmetric space group (inset (a) of Fig. 2, for x = 0.0 for example). Standard hexagonal setting of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group (with aH and cH cell parameters) was used. The manganite structure (LaAlO3 type) is described in this hexagonal setting, with (La/Bi/Ba) atoms at 6a (0, 0, 1/4) position, Mn at 6b (0, 0, 0) and O at 18e (x, 0, 1/4) position. This distorted manganite is characterized by ā
c space group (with aH and cH cell parameters) was used. The manganite structure (LaAlO3 type) is described in this hexagonal setting, with (La/Bi/Ba) atoms at 6a (0, 0, 1/4) position, Mn at 6b (0, 0, 0) and O at 18e (x, 0, 1/4) position. This distorted manganite is characterized by ā![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ā
ā![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ā antiphase oxygen octahedral tilt system (Glazer notation9) corresponding to rotations along the three pseudo cubic directions of the manganite. Detailed results of the structural refinements are regrouped in Table 1. It can be observed from the inset (b) in Fig. 2 that the position of the most intense peak shows a slight shift towards low angles with the increase of Bi, indicating that the cell volume of the La0.67−xBixBa0.33MnO3 specimens increases.
ā antiphase oxygen octahedral tilt system (Glazer notation9) corresponding to rotations along the three pseudo cubic directions of the manganite. Detailed results of the structural refinements are regrouped in Table 1. It can be observed from the inset (b) in Fig. 2 that the position of the most intense peak shows a slight shift towards low angles with the increase of Bi, indicating that the cell volume of the La0.67−xBixBa0.33MnO3 specimens increases.
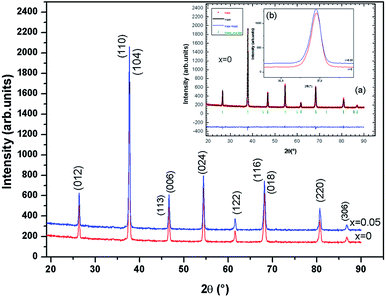 | ||
| Fig. 2 X-ray powder diffraction patterns and Rietveld refinement for the compounds La0.67−xBixBa0.33MnO3 (x = 0 and 0.05) at room temperature. | ||
| Crystallographic data | Refinement conditions | Average crystallite size | Strain ε (%) | Average grain size D (nm) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lattice parameters | Cell volume | Discrepancy factors | Debye–Scherrer technique Ds (nm) | Williamson–Hall technique Dw (nm) | ||||||
| a = b (Å) | c (Å) | V (Å3) | Rwp % | Rp % | RF % | χ2 % | ||||
| a a and c: hexagonal cell parameters; V: cell volume; Rwp, Rp; RF: the residuals for, respectively, the weighted pattern, the pattern and the Bragg structure factor; χ2: the goodness of fit. The numbers in parentheses are estimated standard deviations to the last significant digit. | ||||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| x = 0 | ||||||||||
| 5.5160 (3) | 13.5023(1) | 355.78(2) | 4.12 | 3.43 | 2.78 | 1.85 | 38 | 49 | 0.16 | 220 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| x = 0.05 | ||||||||||
| 5.50184 (2) | 13.5141(4) | 356.40(1) | 5.23 | 3.42 | 3.42 | 1.25 | 35 | 40 | 0.14 | 260 |
In order to quantitatively discuss the ionic match between A and B sites in perovskite compounds, a geometrical quantity, noted Goldschmidt tolerance factor (t), is usually introduced and is defined as:10
The value of average crystallite size was estimated from the full width at half maximum (FWHM) of X-ray diffraction peaks. The effects of synthesis, instruments and processing conditions were taken into consideration while making the calculation of crystallite size. The dependence of the size effect is given by Scherrer's formula: 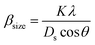 , where λ is the wavelength of CuKα radiation (λ = 1.5406 Å), K is grain shape factor (=0.89) and Ds is the thickness of the crystal. Using the Williamson–Hall (W–H) method,13 the average values of both Dw and lattice strain (ε) can be obtained from the intercept and the slope of the following relation, respectively,
, where λ is the wavelength of CuKα radiation (λ = 1.5406 Å), K is grain shape factor (=0.89) and Ds is the thickness of the crystal. Using the Williamson–Hall (W–H) method,13 the average values of both Dw and lattice strain (ε) can be obtained from the intercept and the slope of the following relation, respectively,
Fig. 3 shows the SEM photograph of the compounds. The samples contained connected particles with hexagonal shape and clear grain boundaries. These particles are largely agglomerated with a broad size distribution. The average value of thickness of both compounds is listed in Table 1.
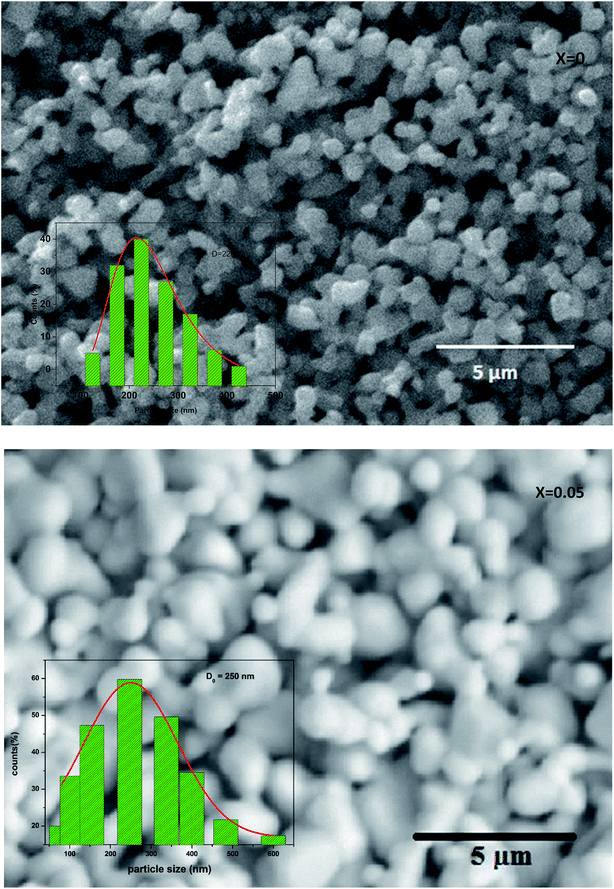 | ||
| Fig. 3 Scanning electron micrograph for La0.67−xBixBa0.33MnO3 (x = 0 and 0.05) manganite. The inset: dispersion histogram. | ||
After measuring the diameters of all the particles in SEM image, the size distribution histogram is fitted with the log-normal function expressed as:
〈D〉 = D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(σ2/2) exp(σ2/2) |
| σD = 〈D〉[exp(σ2) − 1]1/2 |
The results analysis showed 〈D〉 ≥ 397.48 μm and σD = 291.53 μm.
3.2 Bulk magnetization
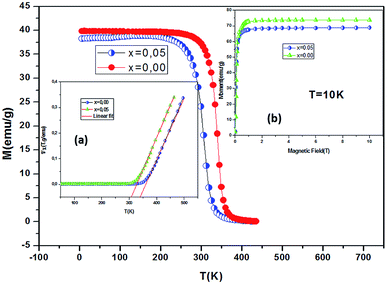
Low-field magnetization (M) versus temperature was first measured for the samples, in order to have an estimation of the transition temperature (TC). The result is presented in Fig. 4. The M(T) curve reveals that when increasing temperature, the samples exhibit a magnetic transition from paramagnetic (PM) state to ferromagnetic (FM) one. This transition occurs at the Curie temperature (TC) which is obtained from the peak of dM/dT curve. The Curie temperature decreases from 340 K to 306 K when increase x from 0.00 to 0.05, respectively for μ0H = 0.05 T. The Curie temperature of the Bi-doped compound was found to be lower than that of the undoped sample. This indicates that Bi substitution appears to weaken the magnetic interaction in the sample. Theoretical calculation has shown that off-center shifts of the ions with ns2 electronic configuration results in the structural distortion and minimization of the Coulombic energy.17 An orientation of the 6s2 lone pair toward a surrounding anion (O-2p) can produce a local distortion or even hybridization between Bi-6s-orbitals and O-2p orbitals,18 leading to the block of the movement of eg electrons through the Mn–O– Mn bridges (stronger localization).The inset of Fig. 4 shows the temperature dependence of the inverse magnetic susceptibility of x = 0 and x = 0.05. It could be fitted to the Curie–Weiss law just above TC (the PM region): χ = C/T − θCW, where θCW is the Weiss temperature and C is the Curie constant defined as: 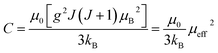 , where μ0 = 107 H m−1 is the permeability, g is the Landé factor, μB = 9.27 × 1024 J T−1 is the Bohr magneton, kB = 1.38 × 1023 J K−1 is the Boltzmann constant, J = L + S is the total moment and μeff is the effective paramagnetic moment. We can determine the effect of paramagnetic moment (μexpeff) from the curie constant. The theoretical μcalceff is estimated using the following expression:
, where μ0 = 107 H m−1 is the permeability, g is the Landé factor, μB = 9.27 × 1024 J T−1 is the Bohr magneton, kB = 1.38 × 1023 J K−1 is the Boltzmann constant, J = L + S is the total moment and μeff is the effective paramagnetic moment. We can determine the effect of paramagnetic moment (μexpeff) from the curie constant. The theoretical μcalceff is estimated using the following expression: 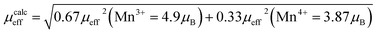 . The parameters μexpeff and μcalceff are summarized in Table 2. It is found that the μexpeff is greater as compared to μcalceff. This discrepancy validates the formation of ferromagnetic spin clusters within the paramagnetic state.19 A linear fit yields positive Curie–Weiss temperature θCW = 312 K (x = 0.05). This result confirms a mean FM interaction between spins for all samples (Table 2). Moreover, this value is higher than TC, which may be due to the existence of short range FM ordering.19
. The parameters μexpeff and μcalceff are summarized in Table 2. It is found that the μexpeff is greater as compared to μcalceff. This discrepancy validates the formation of ferromagnetic spin clusters within the paramagnetic state.19 A linear fit yields positive Curie–Weiss temperature θCW = 312 K (x = 0.05). This result confirms a mean FM interaction between spins for all samples (Table 2). Moreover, this value is higher than TC, which may be due to the existence of short range FM ordering.19
| x | TC (K) | W/W0 (10−2) | θCW (K) | θMn–O–Mn (°) | dMn–O (Å) | μexpeff (μB) | μcalceff (μB) |
|---|---|---|---|---|---|---|---|
| 0 | 340 | 4.73 | 348 | 165.32 | 1.959 | 5.32 | 4.586 |
| 0.05 | 306 | 4.66 | 312 | 165.12 | 1.965 | 5.81 | 4.586 |
The structure analysis shows that the unit cell becomes slightly larger as the 6s2 lone pair character becomes dominant, it has been shown that the Bi–O bond is shorter than the La–O, despite of the similar ionic radius of La3+ and Bi3+ ions.20 This can be interpreted as arising from the rather covalent character of the Bi–O bonds. The electronegativity of Bi enhances hybridisation between 6s2 of Bi3+ orbitals and 2p of O2− orbitals and this hybridisation produces a local distortion. It is observed that transition temperature TC decreases with increase in Bi ratio. This is presumably due to tilts the MnO6 octahedra, resulting in a reduced overlap between the Mn-3d and O-2p orbitals.21 It should also be noted that the La0.67Ba0.33MnO3 sample is ferromagnetic while Bi0.67Ba0.33MnO3 is antiferromagnetic, indicating a competition between the double exchange and the antiferromagnetic super exchange in these compounds can decrease TC. This phenomenon has been observed in the compound Bi0.6−xLaxCa0.4MnO3.22
3.3 Effect of Bi on magnetocaloric properties
The change of magnetic entropy of magnetic compounds has the largest value near a phase transition. According to the classical thermodynamic theory, the isothermal magnetic entropy change (–ΔSM) produced by the variation of a magnetic field from zero to μ0Hmax is given by:23,24The magnetic entropy is related to the magnetization M, magnetic field strength μ0H and absolute temperature T through the Maxwell relation:
In the case of magnetization measurement in small discrete magnetic fields and temperature interval ΔT, ΔSM can be approximated to:
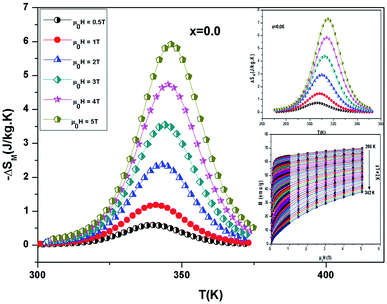
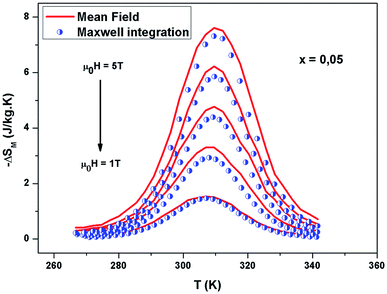
The −ΔSM(T) data calculated from the M(μ0H) curves (inset in Fig. 5) at different magnetic fields for the La0.67−xBixBa0.33MnO3 (x = 0 and 0.05) are plotted in Fig. 5. The compounds exhibit large changes in magnetic entropy around Curie temperature (TC), which is a characteristic property of simple ferromagnets due to the efficient ordering of magnetic spins at the temperature induced by magnetic field.25 Large magnetic entropy changes ΔSmaxM are reported for all the samples and are summarized in Table 3. The magnitude of (−ΔSmaxM(T)) for all samples increases with increasing the applied magnetic field (inset of Fig. 5). For example, the maximum magnetic-entropy value increases from 2.37 J kg−1 K−1 for x = 0.00 to 2.8 J kg−1 K−1 (2T) and 5.8 J kg−1 K−1 for x = 0.00 to 7.3 J kg−1 K−1 for x = 0.05 respectively (5T). Guo et al.26 indicated that the large magnetic entropy change in perovskite compounds could originate from the spin–lattice coupling in the magnetic ordering process. Strong coupling between spin and lattice is corroborated by the observed significant lattice change accompanying magnetic transition in perovskite manganites.27 The lattice structural change in the Mn–O bond distance as well as in the 〈Mn–O–Mn〉 bond angle would in turn favor the spin ordering. Thus a more abrupt variation of magnetization near Curie temperature (TC) occurs, resulting in a large magnetic entropy change as a large MCE.
| Composition | TC (K) | (−ΔSmaxM)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (J kg−1 K−1) (J kg−1 K−1) |
RCP (J kg−1) | μ0H (T) | Ref. |
|---|---|---|---|---|---|
| Gd5(Sr2Ge2) | 275 | 18.5 | 535 | 5 | 24 |
| Gd | 294 | 10.2 | 410 | 5 | 25 |
| La0.5Sm0.1Sr0.4Mn0.95In0.05O3 | 308 | 4.50 | 193.48 | 5 | 26 |
| La0.67Sr0.33Mn0.9Cr0.1O3 | 328 | 5 | — | 5 | 27 |
| La0.67Ba0.33MnO3 | 346 | 5.80 | 151 | 5 | This work |
| La0.62Bi0.05Ba0.33MnO3 | 310 | 7.30 | 209 | 5 | This work |
| Gd | 297 | 4 | 120 | 2 | 28 |
| MnFeP0.45As0.5 | 300 | 14.5 | 188 | 2 | 28 |
| La0.7Sr0.3Mn0.95Ti0.05O3 | 308 | 2.2 | 90 | 2 | 29 |
| La0.7Sr0.3Mn0.9Fe0.1O3 | 260 | 1.7 | 83 | 2 | 30 |
| La0.67Ba0.33MnO3 | 343 | 2.37 | 39 | 2 | This work |
| La0.62Bi0.05Ba0.33MnO3 | 308 | 2.80 | 80 | 2 | This work |
The change of magnetic entropy can be also calculated from the field dependence of the specific heat by the following integration:
From this equation, it determine the change of specific heat induced by the external magnetic field zero to μ0H as: 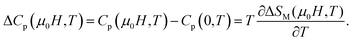
Fig. 6 shows the temperature dependence of ΔCp(μ0H, T) under different field variations for the samples (for example x = 0.05) calculated from the ΔSM(μ0H, T). The ΔCp(μ0H, T) undergoes a sudden change from positive to negative around TC with a positive value above TC and a negative value below TC. The maximum/minimum value of ΔCp(μ0H, T) observed at 320/300 K, exhibits an increasing trend with applied field and is obtained to be 122.4/−115.43 J kg−1 K−1 for x = 0.05 at 5 T.
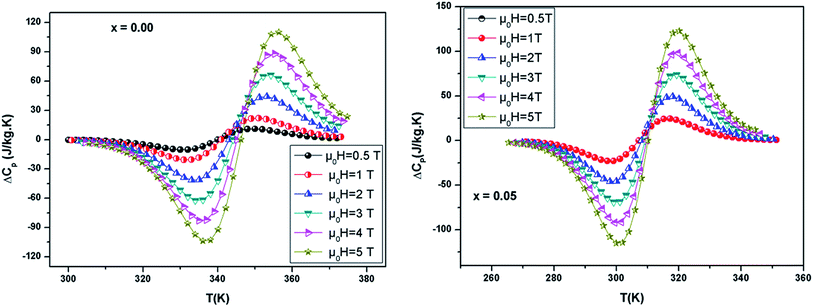 | ||
| Fig. 6 Change of specific heat of the samples as a function of temperature at different magnetic field. | ||
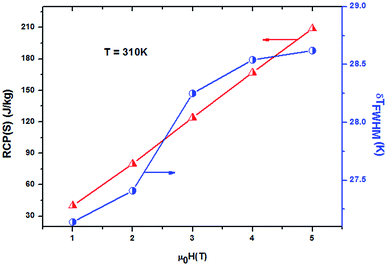
It should be noted that (−ΔSmaxM) is not the only parameter deciding about an applicability of material. To estimate if a material can be a good candidate for magnetic refrigeration (MR), Gschneidner and Pecharsky28 defined the relative cooling power (RCPS), which is the important index which is used to evaluate the cooling efficiency of a magnetic refrigerant. It is defined as the product between the maximum values of the magnetic entropy change (−ΔSmaxM) and the full width at half maximum δTFWHM of the magnetic entropy change curve (RCP(S) = −ΔSmaxM × δTFWHM).29 This parameter corresponds to the amount of heat that can be transferred between the cold and hot parts of the refrigerator in one ideal thermodynamic cycle. The results are summarized in Table 3. Fig. 7 shows the absolute value of RCPS and δTFWHM for the sample (x = 0.05) versus applied field at 310 K. It can be seen from this figure that RCPS (δTFWHM) increases monotonically as the field increases. The value of RCP is about 51% of Gd at 294 K for μ0H = 5 T.30 To evaluate the applicability of ours samples as a magnetic refrigerant, the obtained values of ΔSM in our study are compared in Table 3 with those reported in the literature for several other magnetic compounds.31–37
3.4 Modeling the magnetic properties
The Weiss molecular mean field model is a standard model in magnetism. Because of its simplicity, this model is still used in current research for a wide range of magnetic materials, although its limitations are well known. This concept of a molecular field assumes that the magnetic interaction between magnetic moments is equivalent to the existence of an exchange interaction depending on the magnetization M:38| Heff = H + Hexch = H + λM |
Amaral et al. proposed a model based on mean field theory and presented an approach of applying this method scenario to isotherm magnetization M(T, H) measurements.39 In our study, it consider the general mean field law:40 M(H, T) = BJ[(H + Hexch)/T], the Brillouin function BJ is written as: 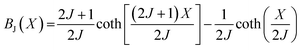 , where
, where 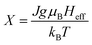 , J is the total angular momentum in the lattice, g is the gyromagnetic factor (landé factor), μB is the Bohr magnetron and kB is the Boltzmann's constant. The mean field exchange parameter λ is not predetermined. Then for corresponding values with the same (H + Hexch)/T, M is also the same, the value of the inverse BJ−1(M) function,41
, J is the total angular momentum in the lattice, g is the gyromagnetic factor (landé factor), μB is the Bohr magnetron and kB is the Boltzmann's constant. The mean field exchange parameter λ is not predetermined. Then for corresponding values with the same (H + Hexch)/T, M is also the same, the value of the inverse BJ−1(M) function,41
The study of the exchange field induced by the magnetization change makes it possible to find the value of the average field exchange parameter λ. Fig. 8 shows H/T versus 1/T for some of the values of M (5 emu per g per step) from 266 K to 342 K for x = 0.05. According to the mean scaling method such H/T versus 1/T curves should show a series of straight lines at different temperature. The linear relationship between H/T and 1/T is kept. Linear fits are then easily made to each isomagnetic line. Typically, the interpolation step was of 1 emu g−1. The slope of this isomagnetic line, will then give the exchange field (Hexch).
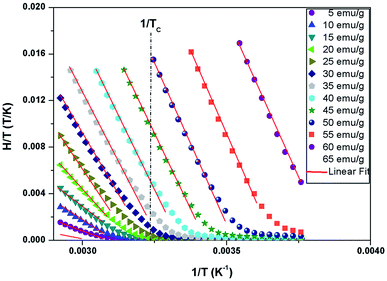 | ||
| Fig. 8 H/T versus 1/T curves with constant values of magnetization per curve for La0.62Bi0.05Ba0.33MnO3 compound. | ||
For all compounds in the paramagnetic domain or the materials of domain ordered such as anti-ferromagnetic, it can always expand increasing M in powers of H, or H in powers of M. In this latter approach it stop at the third order and considering that the magnetization is an odd function of field, it can write:42
| Hexch = λ1M + λ3M3 |
Fig. 9 shows the evolution of the exchange field versus the magnetization for the La0.67−xBixBa0.33MnO3 (x = 0.05 for example). The experimental data should be included for the fit by eqn (Hexch = λ1M + λ3M3). The results show a very small dependence on M3 (λ3 = −1.3984 × 10−5 (T g emu−1)3), is found for this second order transition system, thus Hexch = λ1M with λ1 = 1.25 T g emu−1. After obtaining the mean field exchange parameter the next step of this method consists on building the scaling plot of M vs. (H + Hexch)/T (Fig. 10). It has successfully fitted the scaled magnetization data with the Brillouin function. From the scaling plot and the subsequent fit with the saturation magnetization equal to 72 emu g−1 (this value is close to the experimental one (Ms = 69 emu g−1 at 10 K) (inset b of Fig. 4), and the value of the total angular momentum of the manganite is J = 1.9.
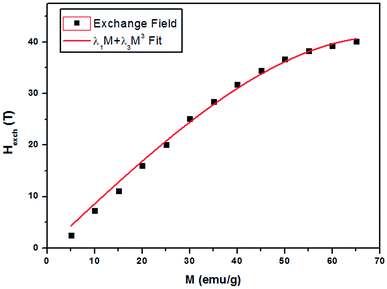 | ||
| Fig. 9 Exchange field versus magnetization for La0.62Bi0.05Ba0.33MnO3 sample, with the function λ1M + λ3M3 fit. | ||
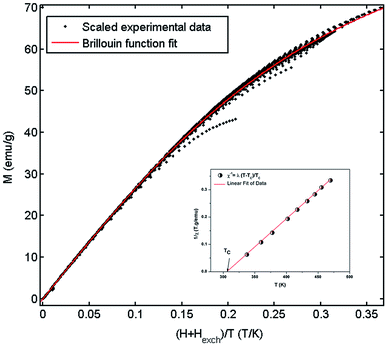 | ||
| Fig. 10 Mean-field scaling plot and Brillouin function fit. Inset 1/χ versus T of La0.62Bi0.05Ba0.33MnO3 compound. | ||
The magnetization measurements in the law temperature range show that the saturation magnetization is about Mtheors = JgμB = 3.67μB/f.u. This value is close to the experimental value Mexpers = 3.7μB at 10 K. The value of Mtheors per formula unit is given by: Mtheors = (nMn3+)MsMn3+ + (nMn4+)MsMn4+, where MsMn3+ = 4μB and MsMn4+ = 3μB are the magnetic moments, nMn3+ = 0.67 and nMn4+ = 0.33 are the contents of Mn3+ and Mn4+ ions respectively. It deduce that the total angular momentum of the compound is J = 1.835 (it was assumed that g = 2).
From a linear approximation of the susceptibility 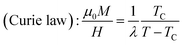 . Inset of the Fig. 10 shows the evolution of the inverse susceptibility (1/χ) versus temperature for the La0.62Bi0.05Ba0.33MnO3 compound. The straight line represents the Curie–Weiss law with λ = 1.25 T g emu−1 and TC = 306 K. The intersection is obtained at a temperature value equals to the critical one. At this point, the susceptibility becomes infinite, which corresponds to the ferromagnetic–paramagnetic transition. Fig. 11 shows how experimental data can be described using the mean-field method. A good agreement between the experimental M(T, μ0H) curves and the mean-field generated curves with the obtained parameters, except near the paramagnetic-ferromagnetic transition (TC), which are not adequately described. This result is probably due to the formation of magnetic domains and critical effects.
. Inset of the Fig. 10 shows the evolution of the inverse susceptibility (1/χ) versus temperature for the La0.62Bi0.05Ba0.33MnO3 compound. The straight line represents the Curie–Weiss law with λ = 1.25 T g emu−1 and TC = 306 K. The intersection is obtained at a temperature value equals to the critical one. At this point, the susceptibility becomes infinite, which corresponds to the ferromagnetic–paramagnetic transition. Fig. 11 shows how experimental data can be described using the mean-field method. A good agreement between the experimental M(T, μ0H) curves and the mean-field generated curves with the obtained parameters, except near the paramagnetic-ferromagnetic transition (TC), which are not adequately described. This result is probably due to the formation of magnetic domains and critical effects.
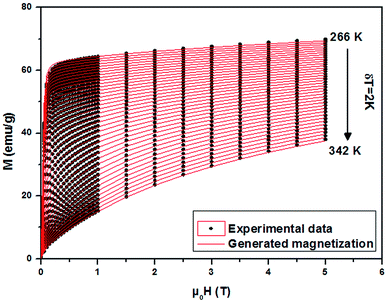 | ||
| Fig. 11 Experimental magnetization versus μ0H (black symbols) of La0.62Bi0.05Ba0.33MnO3 sample and the interpolation using the mean field method (red lines). | ||
3.5 Estimating the magnetocaloric effect (MCE)
The mean field approach allows us to estimate magnetic entropy variation ΔSM within the thermodynamics of the model and without using the usual numerical integration of a Maxwell relation.43 Within the mean field approach, ΔSM between magnetic fields H1 and H2 can be calculated using the following general expression, which also accounts for a possible dependence of λ on T:The linearity relation between H/T and 1/T in Fig. 8 improves that the mean field exchange parameter λ is independent of the temperature T. So the following equation will be simplified:
Fig. 12 shows the evolution of the magnetic entropy change (−ΔSM) data as a function of temperature at several magnetic applied fields for the La0.62Bi0.05Ba0.33MnO3 compound, by using the Maxwell relation and that basing on mean field theory. Both results are in good agreement, except close to TC, here an excepted small difference appears, due to the formation of magnetic domains and critical effects.
4 Conclusion
In summary, single phase La0.67−xBixBa0.33MnO3 (x = 0.00 and 0.05) compounds were prepared by the sol–gel technic. Using the magnetization measurements, magnetic and magnetocaloric effect have been studied. These compounds show second order ferromagnetic–paramagnetic phase transition, with a large magnetic entropy change. It have studied the mean-field scaling method for these samples. The insight that can be gained from the use of this methodology for a given magnetic system can be of great interest. In a simplistic approach, it can say that if this scaling method does not follow a molecular mean-field behavior, other methods must be pursued in order to interpret the magnetic behavior of the system. The mean-field scaling method is able to determine the exchange parameters J, λ and g of ours samples. These factors allow estimating some magnetic properties.Conflicts of interest
There are no conflicts to declare.References
- M. Khlifi, E. Dhahri and E. K. Hlil, J. Alloys Compd., 2014, 587, 771–777 CrossRef CAS.
- G. F. Wang, L. R. Li, Z. R. Zhao, X. Q. Yu and X. F. Zhang, Ceram. Int., 2014, 40, 16449–16454 CrossRef CAS.
- E. Dagotto, T. Hotta and A. Moreo, Phys. Rep., 2001, 344, 1 CrossRef CAS.
- A. Dhahri, E. Dhahri and E. K. Hlil, J. Alloys Compd., 2017, 700, 169–174 CrossRef CAS.
- R. Von Helmolt, J. Wecker, B. Holzapfel, L. Schultz and K. Samwer, Phys. Rev. Lett., 1993, 71, 2331 CrossRef CAS PubMed.
- C. P. Bean and D. S. Rodbell, Phys. Rev., 1962, 126, 104–115 CrossRef CAS; D. Rodbell, Phys. Rev. Lett., 1961, 7, 1 CrossRef.
- G. Lalitha and P. Venugopal Reddy, J. Alloys Compd., 2010, 494, 476–482 CrossRef CAS.
- J. Rodriguez Carvajal, FULLPROF, Laboratoire Leon Brillouin (CEACNRS), 2000–2005 Search PubMed.
- A. M. Glazer, Acta Crystallogr., 1972, B28, 3384 CrossRef.
- V. M. Goldschmidt, Geochemistry, Oxford University Press, 1958, p. 730 Search PubMed.
- R. D. Shannon, Acta Crystallogr., 1976, A32, 751 CrossRef CAS.
- G. Lalitha and P. Venugopal Reddy, J. Alloys Compd., 2010, 494, 476–482 CrossRef CAS.
- G. K. Williamson and W. H. Hall, Acta Metall., 1953, 1, 22–31 CrossRef CAS.
- A. G. Mohamed, S. Ghodhbane, A. Dhahri, J. Dhahri and E. K. Hlil, J. Alloys Compd., 2016, 681, 547–554 CrossRef.
- B. Aslibeiki, P. Kameli and M. H. Ehsani, Ceram. Int., 2016, 42, 12789–12795 CrossRef CAS.
- C. Lavorato, E. Lima Jr, D. Tobia, D. Fiorani, H. E. Troiani, R. D. Zysler and E. L. Winkler, Nanotechnology, 2014, 25, 355704 CrossRef PubMed.
- F. Sugawara, S. Iida, Y. Syono and S. Akimoto, J. Phys. Soc. Jpn., 1968, 25, 1553 CrossRef CAS.
- N. A. Hill and K. M. Rabe, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8759 CrossRef CAS.
- A. Dhahri, M. Jemmali, K. Taibi, E. Dhahri and E. K. Hlil, J. Alloys Compd., 2015, 618, 488–496 CrossRef CAS.
- M. Barandiarana, J. Gutierrez, L. Righi, M. Amboage, A. Pena, T. Hernandez, M. Insausti and T. Rojo, Physica B, 2001, 299, 286–292 CrossRef.
- Colossal magneto-resistance oxides, ed. Y. Tokura, Gordon and Breach, London, 2000 Search PubMed.
- R. R. Zhang, G. L. Kuang, L. H. Yin and Y. P. Sun, J. Appl. Phys., 2010, 108, 103903 CrossRef.
- M. Dhahri, A. Zaidi, K. Cherif, J. Dhahri and E. K. Hlil, J. Alloys Compd., 2017, 715, 266–274 CrossRef.
- Ah. Dhahri, E. Dhahri and E. K. Hlil, Appl. Phys. A, 2014, 116, 2077–2085 CrossRef CAS.
- A. Bhattacharyya, S. Chatterjee, S. Giri and S. Majumdar, Eur. Phys. J. B, 2009, 70, 347 CrossRef CAS.
- Z. B. Guo, Y. M. Du, J. S. Zhu, H. Huang, W. P. Ding and D. Feng, Phys. Rev. Lett., 1997, 78, 1142 CrossRef CAS.
- P. G. Radaelli, D. E. Cox, M. Marezio, S. W. Cheong, P. E. Schiffer and A. P. Ramirez, Phys. Rev. Lett., 1995, 75, 4488 CrossRef CAS PubMed.
- V. K. Pecharsky and K. A. Gschneidner Jr, J. Appl. Phys., 1999, 86, 565 CrossRef CAS.
- E. L. T. França, A. O. dos Santos, A. A. Coelho and L. M. da Silva, J. Magn. Magn. Mater., 2016, 401, 1088–1092 CrossRef.
- V. K. Pecharsky, K. A. Gschneidner and A. O. Tsokol, Rep. Prog. Phys., 2005, 68, 1479 CrossRef.
- K. A. Gschneidner Jr, V. K. Pecharsky and A. O. Tsokol, Rep. Prog. Phys., 2005, 68, 1479 CrossRef.
- M. H. Phan and S. C. Yu, Magn. Magn. Mater., 2007, 308, 325 CrossRef CAS.
- M. Dhahri, A. Zaidi, K. Cherif, J. Dhahri and E. K. Hlil, J. Alloys Compd., 2017, 691, 578–586 CrossRef CAS.
- Y. Sun, W. Tong and Y. Zhang, J. Magn. Magn. Mater., 2001, 232, 205–208 CrossRef CAS.
- O. Tegus, E. Bruck, K. H. J. Buschow and F. R. de Boer, Nature, 2002, 415, 150 CrossRef CAS PubMed.
- D. N. H. Nam, N. V. Dai, L. V. Hong, N. X. Phuc, S. C. Yu, M. Tachibana and E. Takayama Muromachi, J. Appl. Phys., 2008, 103, 043905 CrossRef.
- S. K. Barik, C. Krishnamoorthi and R. Mahendiran, J. Magn. Magn. Mater., 2011, 323, 1015e1021 CrossRef.
- A. Arrott, J. Appl. Phys., 2008, 103, 07C715 CrossRef.
- J. Amaral, N. Silva and V. Amaral, Appl. Phys. Lett., 2007, 91, 172503e172503 CrossRef.
- A. M. Tishin and Y. I. Spichkin, The Magnetocaloric Effect and its Applications, IOP Publishing, 2003, Bristol Search PubMed.
- J. Amaral, N. Silva and V. Amaral, Appl. Phys. Lett., 2007, 91, 172503e172503 CrossRef.
- M. Cyrot, et al., Magnétisme I-Fondement, Presses universitaires de Grenoble, Grenoble, 1999 Search PubMed.
- Ah. Dhahri, M. Jemmali, K. Taibi, E. Dhahri and E. K. Hlil, J. Alloys Compd., 2015, 618, 488–496 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |