DOI:
10.1039/C8RA09878F
(Paper)
RSC Adv., 2019,
9, 5417-5430
Molecule design and properties of bridged 2,2-bi(1,3,4-oxadiazole) energetic derivatives
Received
1st December 2018
, Accepted 29th January 2019
First published on 12th February 2019
Abstract
A series of bridged 2,2-bi(1,3,4-oxadiazole) energetic derivatives were designed and their geometrical structures, electronic structures, heats of formation, detonation properties, thermal stabilities and thermodynamic properties were fully investigated by density functional theory. The results showed that the –N3 group and the –N– bridge play an important role in improving heats of formation of these 2,2-bi(1,3,4-oxadiazole) derivatives. The calculated detonation properties indicated that the –NF2 group and the –N– bridge were very useful for enhancing the heats of detonation, detonation velocities and detonation pressures. Twenty-four compounds were found to possess equal or higher detonation properties than those of RDX, while 14 compounds had equal or higher detonation properties than those of HMX. The analysis of the bond-dissociation energies suggested that the –CN group was the effective structural unit for increasing the thermal stabilities while the –NHNH2 group decreased these values. Overall, taking both the detonation properties and thermal stabilities into consideration, 22 compounds (A4, A6, A8, A9, B4, B9, C2, C3, C4, C5, C7, C, C9 D4, D8, D9, E9, F4, F9, G9, H4 and H9) were selected as the potential candidates for high-energy-density materials.
1. Introduction
Nitrogen-rich energetic materials with high densities, high positive heats of formation, excellent detonation properties (detonation velocity and detonation pressure) and acceptable thermal stabilities have gained considerable attention in the area of high-energy-density materials.1–7 Five- or six-numbered heterocyclic compounds were found to be one of the most effective structural units for synthesizing high-energetic-density materials. Not surprisingly, 1,2,4-oxadiazole, 1,2,5-oxadiazole, 1,3,4-oxadiazole, and 1,2,3-oxadiazole, which are named as oxadiazoles, contain this type of structure with a nitrogen content of 40%. To the best of our knowledge, a large number of 1,2,4-oxadiazole and 1,2,5-oxadiazole (furazan)-based energetic materials are synthesized and their properties are fully investigated, while there has been fewer research on either 1,3,4-oxadiazole or 1,2,3-oxadiazole-based energetic materials.8–11 Additionally, 1,2,3-oxadiazole is also presented as an unstable structure, which reverts to the diazoketone tautomer.12 Consequently, 1,3,4-oxadiazole and their derivatives may offer good backbones for the development of new energetic compounds. Recently, a promising high-energy-density material based on 1,3,4-oxadiazole (Scheme 1, ICM-101) was synthesized with excellent detonation properties (ρ, 1.99 g cm−3; D, 9481 m s−1 and P, 41.9 GPa) and thermal stabilities (Td, 210 °C).13 Then, it led to the idea of what changes will happen if other energetic groups and bridges were introduced to the bi-1,3,4-oxadiazole structure.
 |
| | Scheme 1 Synthetic route of ICM-101. | |
In this study, a systematic research on the heats of formation, electronic structures, detonation properties, thermal stabilities and thermodynamic properties of 1,3,4-oxadiazole bridged compounds (such as –CH2–, –NH–, –O–, –CH2–CH2–, –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–, –NH–NH– and –N
CH–, –NH–NH– and –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–) with various energetic groups (such as –CN, –N3, –NO2, –NF2, –NH2, –NHNO2, –NHNH2, –CH(NO2)2 and –C(NO2)3) (Scheme 2, series A–H) were reported.
N–) with various energetic groups (such as –CN, –N3, –NO2, –NF2, –NH2, –NHNO2, –NHNH2, –CH(NO2)2 and –C(NO2)3) (Scheme 2, series A–H) were reported.
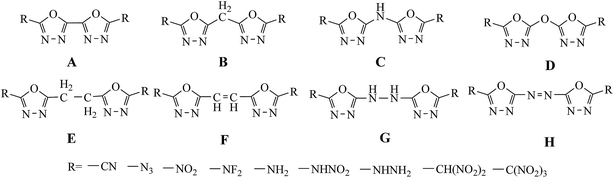 |
| | Scheme 2 The designed molecules based on bridged 2,2-bi(1,3,4-oxadiazole). | |
2. Computational methods
The density functional theory (DFT) method has been demonstrated as an economical and liable tool in predicting the physicochemical properties of energetic materials. Studies on the optimized molecular structures, accurate energies, frontier molecular orbitals, heats of formation, vibrational frequencies, energetic properties, bond dissociation energies and thermodynamic parameters of the designed compounds were carried out by using the hybrid DFT/B3LYP functional with the 6-311G(d,p) basis set.14,15 All the calculations were performed on the Gaussian 03 software16 and the optimized structures were characterized to be the local energy minimum on the potential energy surface without imaginary frequencies.
Heat of formation (HOF) was an important parameter in evaluating the energetic properties of an energetic material. Herein, isodesmic reactions were designed to predict the accurate gas-phase HOFs (ΔHf,gas) of the designed compounds. This is because, isodesmic reactions17–21 can decrease the calculation errors of HOF greatly since all kinds of bonds and electronic environments of atoms in the reactants and products are very similar. The isodesmic reactions and related equations were presented in the following form (Scheme 3):
| | |
ΔH298 K = ∑ΔHf,p − ∑ΔHf,R
| (1) |
| | |
ΔH298 K = ΔE298 K + Δ(PV) = ΔE0 + ΔZPE + ΔHT + ΔnRT
| (2) |
where Δ
H298 K is the HOF that needs to be calculated, Δ
Hf,p and Δ
Hf,R are the HOFs of products and reactants, respectively, Δ
E0 is the energy change between products and reactants, ΔZPE is the difference between the zero-point energy (ZPE) of the products and reactants, Δ
HT is the thermal correction from 0 to 298 K,
n is the number of energetic groups and Δ(
PV) equals to Δ
nRT.
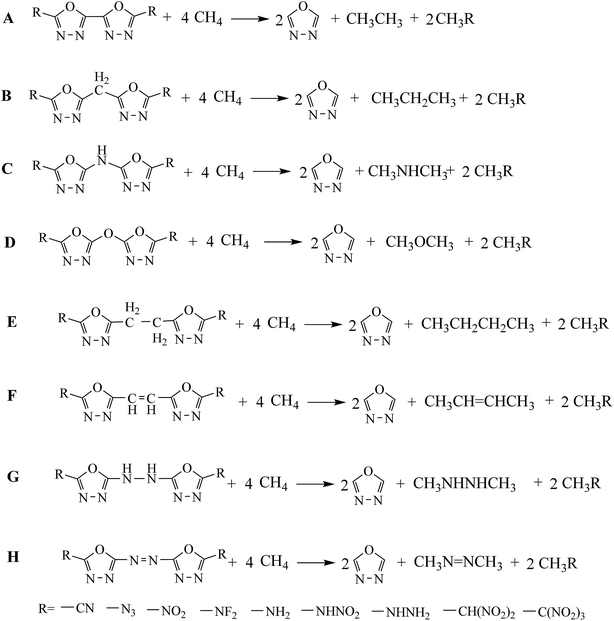 |
| | Scheme 3 The designed isodesmic reactions for each series of compounds. | |
Also, it should be noted that the HOFs of familiar species such as CH4, CH3NH2, CH3NHNH2, CH3NO2, CH3CN, CH3CH3, CH3CH2CH3, CH3NHCH3 and CH3CH2CH2CH3 were available while the HOFs of CH3NF2, CH3NHNO2, CH3N3, CH3NHNHCH3, CH3N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NCH3, CH3CH(NO2)2, CH3C(NO2)3, and
NCH3, CH3CH(NO2)2, CH3C(NO2)3, and  were unavailable. Therefore, the atomization reaction CaHbNc → aC(g) + bH(g) + cN(g) was employed to evaluate the HOFs of CH3NF2, CH3NHNO2, CH3N3, CH3NHNHCH3, CH3N
were unavailable. Therefore, the atomization reaction CaHbNc → aC(g) + bH(g) + cN(g) was employed to evaluate the HOFs of CH3NF2, CH3NHNO2, CH3N3, CH3NHNHCH3, CH3N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NCH3 and
NCH3 and  at CBS-Q level22 while the HOFs of the compounds CH3CH(NO2)2 and CH3C(NO2)3 were calculated via isodesmic reactions:
at CBS-Q level22 while the HOFs of the compounds CH3CH(NO2)2 and CH3C(NO2)3 were calculated via isodesmic reactions:
| CH3CH(NO2)2 + 2CH4 → CH3CH3 + 2CH3NO2 |
| CH3C(NO2)3 + 3CH4 → CH3CH3 + 3CH3NO2 |
Furthermore, HOFs of the energetic materials were always in the solid-phase, while HOFs that were obtained from the isodesmic reactions were in the gas-phase. According to Hess's law of constant heat summation, the values of ΔHf,gas and heat of sublimation (ΔHsub) can be used to evaluate the accurate data of solid-phase HOFs (ΔHf,solid) based on the following equation:23
| | |
ΔHf,solid = ΔHf,gas − ΔHsub
| (3) |
where, Δ
Hsub is the heat of sublimation. Politzer
et al. proposed that Δ
Hsub can also be correlated with the molecular surface area
A and the electrostatic interaction index
vσtot2 by the empirical expression:
24| | |
ΔHsub = aA2 + b(νσtot2)0.5 + c
| (4) |
where,
a,
b and
c are coefficients and represented as 2.670 × 10
−4 kcal mol
−1 Å
−4, 1.650 kcal mol
−1, and 2.966 kcal mol
−1, respectively;
25 A is the surface area of the 0.001 e bohr
−3 isosurface of electronic density of the molecule;
ν is the degree of balance between positive and negative potential on the isosurface;
σtot2 is the measure of variability of the electrostatic potential on the molecular surface.
Densities (ρ) that were used to calculate the detonation velocity and detonation pressure were obtained by an improved equation proposed by Politzer et al.:26
| |
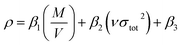 | (5) |
where
β1,
β2, and
β3 are coefficients and represented as 0.9183, 0.0028, and 0.0443, respectively,
M stands for the molecular mass (g mol
−1),
V stands for the volume of a molecule (m
3 mol
−1),
ν stands for the degree of balance between positive and negative potential on the isosurface and
σtot2 stands for measure of variability of the electrostatic potential on the molecular surface.
Energetic properties (detonation velocity and detonation pressures) were estimated by the Kamlet–Jacobs equations:27
| |
D = 1.01(N![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) 0.5Q0.5)0.5(1 + 1.3ρ) 0.5Q0.5)0.5(1 + 1.3ρ)
| (6) |
| |
P = 1.558ρ2N![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) 0.5Q0.5 0.5Q0.5
| (7) |
where
D is the detonation velocity (km s
−1);
P is the detonation pressure (GPa);
N,
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
and
Q are the moles of detonation gases per-gram explosive (mol g
−1), the average molecular weight of these gases (g mol
−1) and heat of detonation (cal g
−1), respectively.
Bond dissociation energy (BDE), which is regarded as the strength of bonding, was an important indicator in predicting the way of bond cleavage and the thermal decomposition mechanism of high-energy-density materials. The homolytic BDEs were calculated as follows:
| | |
BDE0(A − B) = E0(A˙) + E0(B˙) − E0(A − B)
| (8) |
The BDEs with zero-point energy (ZPE) corrections were finally calculated based on the following equation:
| | |
BDE(A − B)ZPE = BDE0(A − B) + ΔEZPE
| (9) |
where Δ
EZPE is the difference between the ZPEs of the products and the reactants.
3. Results and discussion
3.1 Electronic structures
The frontier molecular orbital which means the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), can provide useful information on optical polarizability, kinetic stability and chemical reactivity.28 The frontier molecular orbital energies and their energy gaps (ΔELUMO–HOMO) for the designed compounds are listed in Table 1. For each series, it is found that the HOMO energy levels increase evidently while the –NH2 and –NHNH2 groups are introduced to the rings. Oppositely, the HOMO energy levels decrease when attaching with other groups, especially the –NF2 and –C(NO2)3 groups. The same is true for the LUMO energy levels. The influence of energetic groups on the sequence of the HOMO and LUMO energy levels can be written as follows: –NH2 ≈ –NHNH2 > –N3 > –NHNO2 > –NF2 > –CN > –CH(NO2)2 > –NO2 ≈ –C(NO2)3. Furthermore, the HOMO and LUMO energy levels present no regularity when different bridges are incorporated. The case is that, the LUMO energy levels decrease when –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– and –N
CH– and –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bridges are added, whereas the attaching of –CH2– and –O– bridges decreases the HOMO energy levels. Also, it should be noticed that the HOMO energy levels of series E (–CH2–CH2– bridged ones) show no regularity compared with series A. Overall, incorporating different energetic groups and bridges into the rings shows different variation trends of HOMO and LUMO energy levels. It indicates that both the energetic groups and bridges interact with the frontier molecular orbitals.
N– bridges are added, whereas the attaching of –CH2– and –O– bridges decreases the HOMO energy levels. Also, it should be noticed that the HOMO energy levels of series E (–CH2–CH2– bridged ones) show no regularity compared with series A. Overall, incorporating different energetic groups and bridges into the rings shows different variation trends of HOMO and LUMO energy levels. It indicates that both the energetic groups and bridges interact with the frontier molecular orbitals.
Table 1 Calculated HOMO and LUMO energies (eV) and energy gaps (ΔELUMO–HOMO) of the designed compounds
| Compd |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
A9 |
| HOMO |
−8.76 |
−7.20 |
−9.25 |
−8.48 |
−6.26 |
−7.99 |
−6.24 |
−8.85 |
−9.18 |
| LUMO |
−3.85 |
−2.66 |
−4.41 |
−3.40 |
−1.52 |
−3.04 |
−1.65 |
−3.67 |
−4.24 |
| ΔEHOMO–LUMO |
4.91 |
4.54 |
4.84 |
5.08 |
4.74 |
4.95 |
4.59 |
5.18 |
4.94 |
| Compd |
B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
B7 |
B8 |
B9 |
| HOMO |
−8.82 |
−7.45 |
−9.26 |
−8.61 |
−6.62 |
−8.19 |
−6.52 |
−8.93 |
−9.23 |
| LUMO |
−2.83 |
−2.06 |
−3.80 |
−2.29 |
−0.38 |
−2.60 |
−0.36 |
−3.44 |
−4.03 |
| ΔEHOMO–LUMO |
5.99 |
5.39 |
5.45 |
6.32 |
6.24 |
5.59 |
6.16 |
5.49 |
5.20 |
| Compd |
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C8 |
C9 |
| HOMO |
−7.85 |
−6.63 |
−8.19 |
−7.68 |
−5.93 |
−7.32 |
−6.00 |
−7.93 |
−8.25 |
| LUMO |
−2.88 |
−2.03 |
−3.82 |
−2.42 |
−0.20 |
−2.57 |
−0.44 |
−3.41 |
−4.04 |
| ΔEHOMO–LUMO |
4.97 |
4.60 |
4.37 |
5.26 |
5.73 |
4.75 |
5.56 |
4.52 |
4.21 |
| Compd |
D1 |
D2 |
D3 |
D4 |
D5 |
D6 |
D7 |
D8 |
D9 |
| HOMO |
−8.87 |
−7.52 |
−9.15 |
−8.67 |
−6.77 |
−8.28 |
−6.71 |
−8.96 |
−9.21 |
| LUMO |
−2.99 |
−2.28 |
−4.03 |
−2.56 |
−0.32 |
−2.68 |
−0.40 |
−3.51 |
−4.10 |
| ΔEHOMO–LUMO |
5.88 |
5.24 |
5.12 |
6.11 |
6.45 |
5.60 |
6.31 |
5.45 |
5.11 |
| Compd |
E1 |
E2 |
E3 |
E4 |
E5 |
E6 |
E7 |
E8 |
E9 |
| HOMO |
−8.68 |
−7.32 |
−9.05 |
−8.25 |
−6.47 |
−7.87 |
−6.53 |
−8.82 |
−9.14 |
| LUMO |
−2.75 |
−2.05 |
−3.66 |
−2.09 |
−0.01 |
−2.37 |
−0.40 |
−3.34 |
−3.96 |
| ΔEHOMO–LUMO |
5.93 |
5.15 |
5.39 |
6.16 |
6.46 |
5.50 |
6.13 |
5.48 |
5.18 |
| Compd |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
| HOMO |
−7.93 |
−6.73 |
−8.31 |
−7.73 |
−5.90 |
−7.36 |
−6.02 |
−7.99 |
−8.39 |
| LUMO |
−3.86 |
−2.96 |
−4.31 |
−3.59 |
−2.15 |
−3.26 |
−2.26 |
−3.79 |
−4.25 |
| ΔEHOMO–LUMO |
4.07 |
3.77 |
4.00 |
4.14 |
3.75 |
4.10 |
3.76 |
4.20 |
4.14 |
| Compd |
G1 |
G2 |
G3 |
G4 |
G5 |
G6 |
G7 |
G8 |
G9 |
| HOMO |
−7.40 |
−6.79 |
−7.66 |
−7.82 |
−5.81 |
−7.37 |
−6.16 |
−7.62 |
−8.26 |
| LUMO |
−2.55 |
−1.98 |
−3.61 |
−2.05 |
0.25 |
−2.35 |
−0.62 |
−3.36 |
−3.95 |
| ΔEHOMO–LUMO |
4.85 |
4.81 |
4.05 |
5.77 |
5.56 |
5.02 |
5.54 |
4.26 |
4.31 |
| Compd |
H1 |
H2 |
H3 |
H4 |
H5 |
H6 |
H7 |
H8 |
H9 |
| HOMO |
−8.52 |
−7.03 |
−9.02 |
−8.39 |
−6.29 |
−7.86 |
−6.21 |
−8.79 |
−9.09 |
| LUMO |
−4.97 |
−3.93 |
−5.25 |
−4.71 |
−3.11 |
−4.32 |
−3.17 |
−4.93 |
−5.22 |
| ΔEHOMO–LUMO |
3.55 |
3.10 |
3.77 |
3.68 |
3.18 |
3.54 |
3.04 |
3.86 |
3.87 |
Fig. 1 displays the variation trends of ΔELUMO–HOMO of the designed compounds. It is found that the volatilities of ΔELUMO–HOMO of series B, C, D, E and G are more evident than those of series A, F and H. It reveals that the parent structures are the main influence factors on ΔELUMO–HOMO for series A, F and H while the energetic groups make more contribution to ΔELUMO–HOMO for series B, C, D, E and G. The ΔELUMO–HOMO of the –CH2–, –O– and –CH2–CH2– bridged compounds increases, whereas the addition of –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– and –N
CH– and –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bridges decreases the ΔELUMO–HOMO evidently. But for the –NH– and –N
N– bridges decreases the ΔELUMO–HOMO evidently. But for the –NH– and –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bridged compounds, there is less effect on ΔELUMO–HOMO compared with those of series A. Besides, the order of the average ΔELUMO–HOMO for each series can be written in the following form: –CH2– ≈ –O– ≈ –CH2–CH2– > directly linked ≈ –NH– ≈ –NH–NH– > –CH
N– bridged compounds, there is less effect on ΔELUMO–HOMO compared with those of series A. Besides, the order of the average ΔELUMO–HOMO for each series can be written in the following form: –CH2– ≈ –O– ≈ –CH2–CH2– > directly linked ≈ –NH– ≈ –NH–NH– > –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– > –N
CH– > –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–. In view of all the designed compounds, compound E5 (6.46 eV) has the highest ΔELUMO–HOMO while compound H7 (3.04 eV) has the smallest ΔELUMO–HOMO. In other words, it is to say that compound H7 was the most reactive under external stimulus while compound E5 showed inertia to these stimuli.
N–. In view of all the designed compounds, compound E5 (6.46 eV) has the highest ΔELUMO–HOMO while compound H7 (3.04 eV) has the smallest ΔELUMO–HOMO. In other words, it is to say that compound H7 was the most reactive under external stimulus while compound E5 showed inertia to these stimuli.
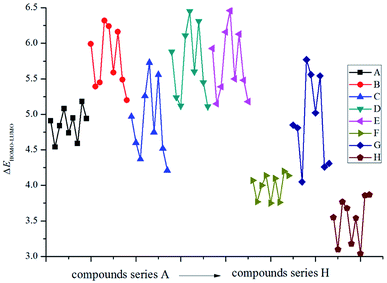 |
| | Fig. 1 The variation trends of ΔELUMO–HOMO of the designed compounds. | |
3.2 Heats of formation
Heat of formation (HOF), which is usually taken as the indicator of the “energy content”, is an important parameter in predicting the detonation properties (especially the heat of detonation) of an energetic material. Therefore, the accurate HOFs were predicted by either atomization reactions (mainly for small molecules) or isodesmic reactions (mainly for the title compounds). Table 2 lists the total energies, ZPEs, and thermal corrections for the reference compounds in the isodesmic reactions.
Table 2 Calculated total energies (E0), zero-point energies (ZPE), thermal corrections (HT) and heats of formation (HOFs) of the reference compounds
| Compound. |
E0a (a.u.) |
ZPEa (kJ mol−1) |
HTa (kJ mol−1) |
ΔHf,gas (kJ mol−1) |
| Calculated at B3LYP/6-311G(d,p) level. Obtained from http://webbook.nist.gov. Calculated values at the CBS-Q level. Obtained by isodesmic reaction. |
| CH4 |
−40.533748 |
117.0 |
10.0 |
−74.6b |
| CH3NHNH2 |
−151.217035 |
213.0 |
14.3 |
94.5b |
| CH3NF2 |
−294.298331 |
122.8 |
13.6 |
−98.4c |
| CH3NH2 |
−95.888444 |
167.6 |
11.4 |
−23.5b |
| CH3NHNO2 |
−300.434462 |
176.5 |
16.0 |
−8.5c |
| CH3NO2 |
−245.081687 |
130.6 |
13.9 |
−81.0b |
| CH3CN |
−132.793330 |
118.7 |
11.9 |
74.0b |
| CH3N3 |
−204.148401 |
131.7 |
14.2 |
289.9c |
| CH3CH3 |
−79.856261 |
195.3 |
11.6 |
84.0b |
| CH3CH2CH3 |
−119.180686 |
270.4 |
14.4 |
−104.7b |
| CH3NHCH3 |
−135.695161 |
254.5 |
14.9 |
−19.0b |
| CH3OCH3 |
−155.071921 |
208.2 |
13.8 |
−184.1b |
| CH3CH2CH2CH3 |
−158.504982 |
345.1 |
17.7 |
−125.6b |
CH3CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH3 CHCH3 |
−157.273161 |
282.0 |
16.9 |
−10.7b |
| CH3NHNHCH3 |
−190.535853 |
286.9 |
17.1 |
109.3c |
CH3N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NCH3 NCH3 |
−189.328011 |
220.6 |
16.0 |
160.5c |
| CH3CH(NO2)2 |
−488.950712 |
212.3 |
22.8 |
81.8d |
| CH3C(NO2)3 |
−693.479196 |
215.6 |
29.3 |
105.1d |
 |
−262.161719 |
121.4 |
11.5 |
65.4c |
Table 3 presents the total energies, ZPEs, thermal corrections, ΔHf,gas, A, ν, σtot2, ΔHsub and ΔHf,solid of the bridged 2,2-bi(1,3,4-oxadiazole) derivatives. It is seen that all the compounds (except for D5, −5.9 kJ mol−1) have positive ΔHf,gas in the range 28.6 (E5) to 2094.9 kJ mol−1 (C2). However, only 66 compounds (except for B5, −60.5 kJ mol−1; D4, −23.9 kJ mol−1; D5, −125.7 kJ mol−1; E4, −18.8 kJ mol−1; E5, −102.1 kJ mol−1; F5, −5.0 kJ mol−1) have positive ΔHf,solid in the range 15.4 (E3) to 1970.6 kJ mol−1 (C2). It reveals that the –N3 group plays an important role in improving the HOF of an energetic material while the –NH2 group makes contribution to these data. Overall, the variation trends of the ΔHf,gas and ΔHf,solid were similar to each other. Again for ΔHf,solid, 60 compounds have higher ΔHf,solid than that of RDX (79.0 kJ mol−1) while 57 compounds have higher ΔHf,solid than that of HMX (102.4 kJ mol−1).29 These high positive HOFs make a great contribution in increasing the detonation properties, such as heats of detonation, detonation velocities and detonation pressures.
Table 3 Calculated total energies, thermal corrections, zero point energies, molecular properties and heats of formation of the designed compounds
| Compd. |
E0 (au) |
ZPE (kJ mol−1) |
HT (kJ mol−1) |
ΔHf,gas (kJ mol−1) |
A (Å2) |
ν |
σtot2 (kcal mol−1)2 |
ΔHsub (kJ mol−1) |
ΔHf,solid (kJ mol−1) |
| A1 |
−707.621475 |
182.6 |
30.0 |
949.3 |
202.1 |
0.168 |
170.0 |
95.0 |
854.3 |
| A2 |
−850.377196 |
207.6 |
34.6 |
1260.4 |
222.2 |
0.246 |
166.5 |
111.8 |
1148.6 |
| A3 |
−932.180624 |
202.0 |
34.4 |
681.4 |
210.8 |
0.097 |
220.3 |
94.0 |
587.4 |
| A4 |
−1030.617350 |
185.4 |
36.2 |
1032.6 |
207.1 |
0.204 |
170.3 |
101.1 |
931.5 |
| A5 |
−633.893216 |
279.9 |
28.2 |
539.0 |
182.5 |
0.244 |
364.9 |
114.8 |
424.2 |
| A6 |
−1042.926774 |
292.2 |
40.4 |
720.0 |
242.2 |
0.142 |
223.0 |
116.8 |
603.2 |
| A7 |
−744.551016 |
370.9 |
35.3 |
774.8 |
214.3 |
0.250 |
254.4 |
118.8 |
656.0 |
| A8 |
−1419.932522 |
362.7 |
55.9 |
696.2 |
304.2 |
0.076 |
247.5 |
145.8 |
550.4 |
| A9 |
−1828.967187 |
366.7 |
70.1 |
800.0 |
344.7 |
0.076 |
145.0 |
168.1 |
631.9 |
| B1 |
−746.957827 |
257.6 |
33.5 |
454.6 |
222.8 |
0.182 |
210.9 |
110.7 |
343.9 |
| B2 |
−889.709693 |
282.9 |
38.1 |
776.0 |
244.1 |
0.240 |
175.7 |
123.9 |
652.1 |
| B3 |
−971.519095 |
277.4 |
37.8 |
181.3 |
232.4 |
0.136 |
205.8 |
109.3 |
72.0 |
| B4 |
−1069.953819 |
260.6 |
39.6 |
143.9 |
229.0 |
0.205 |
189.9 |
114.1 |
29.8 |
| B5 |
−673.223066 |
355.4 |
31.6 |
61.6 |
204.5 |
0.250 |
332.5 |
122.1 |
−60.5 |
| B6 |
−1082.261977 |
367.6 |
43.8 |
228.5 |
262.8 |
0.176 |
288.9 |
138.9 |
89.6 |
| B7 |
−783.879076 |
446.3 |
38.6 |
302.0 |
234.9 |
0.240 |
240.9 |
126.6 |
175.4 |
| B8 |
−1459.268527 |
437.9 |
59.3 |
477.8 |
324.4 |
0.108 |
250.4 |
166.0 |
311.8 |
| B9 |
−1868.305088 |
442.0 |
73.6 |
576.8 |
365.0 |
0.091 |
201.7 |
190.9 |
385.9 |
| C1 |
−763.000285 |
227.4 |
33.3 |
1764.4 |
216.3 |
0.149 |
278.6 |
109.2 |
1655.2 |
| C2 |
−905.748663 |
252.0 |
38.3 |
2094.9 |
236.6 |
0.250 |
203.7 |
124.3 |
1970.6 |
| C3 |
−987.561813 |
247.2 |
37.6 |
1490.6 |
225.0 |
0.109 |
277.3 |
107.0 |
1383.6 |
| C4 |
−1085.994461 |
229.8 |
39.7 |
1458.4 |
221.8 |
0.154 |
249.4 |
110.2 |
1348.2 |
| C5 |
−689.259280 |
324.7 |
31.8 |
1387.9 |
197.3 |
0.249 |
355.9 |
120.9 |
1267.0 |
| C6 |
−1098.302817 |
336.8 |
43.8 |
1542.3 |
256.7 |
0.155 |
255.0 |
129.5 |
1412.8 |
| C7 |
−799.916632 |
415.8 |
38.6 |
1624.7 |
229.0 |
0.250 |
266.0 |
127.4 |
1497.3 |
| C8 |
−1475.310251 |
407.4 |
59.2 |
1789.5 |
318.4 |
0.083 |
306.7 |
160.6 |
1628.9 |
| C9 |
−1884.348017 |
411.8 |
73.4 |
1885.6 |
358.5 |
0.062 |
259.1 |
183.7 |
1701.9 |
| D1 |
−782.845020 |
194.3 |
32.4 |
384.1 |
213.3 |
0.190 |
153.3 |
100.5 |
283.6 |
| D2 |
−925.594326 |
218.5 |
37.2 |
711.4 |
233.8 |
0.249 |
182.6 |
120.1 |
591.3 |
| D3 |
−1007.399335 |
212.5 |
34.8 |
125.7 |
221.7 |
0.092 |
249.5 |
100.4 |
25.3 |
| D4 |
−1105.836802 |
196.4 |
38.7 |
83.9 |
218.7 |
0.214 |
172.3 |
107.8 |
−23.9 |
| D5 |
−709.108853 |
291.0 |
30.8 |
−5.9 |
194.4 |
0.239 |
372.2 |
119.8 |
−125.7 |
| D6 |
−1118.150451 |
303.9 |
42.8 |
154.4 |
253.5 |
0.142 |
222.8 |
123.1 |
31.3 |
| D7 |
−819.769222 |
383.1 |
37.5 |
224.0 |
225.6 |
0.250 |
252.1 |
124.1 |
99.9 |
| D8 |
−1495.155645 |
374.4 |
58.3 |
407.5 |
315.1 |
0.089 |
235.1 |
155.0 |
252.5 |
| D9 |
−1904.190918 |
378.5 |
72.6 |
509.9 |
355.6 |
0.084 |
145.9 |
177.9 |
332.0 |
| E1 |
−786.288860 |
332.9 |
37.2 |
416.9 |
245.0 |
0.212 |
167.6 |
120.7 |
296.2 |
| E2 |
−929.038343 |
357.7 |
41.8 |
744.2 |
264.9 |
0.224 |
182.2 |
135.0 |
609.2 |
| E3 |
−1010.852874 |
351.7 |
41.8 |
135.8 |
250.7 |
0.177 |
169.0 |
120.4 |
15.4 |
| E4 |
−1109.283300 |
335.3 |
43.0 |
109.5 |
245.8 |
0.237 |
206.7 |
128.3 |
−18.8 |
| E5 |
−712.552050 |
429.5 |
35.7 |
28.6 |
223.0 |
0.249 |
331.5 |
130.7 |
−102.1 |
| E6 |
−1121.592652 |
443.2 |
47.0 |
191.7 |
280.4 |
0.210 |
187.9 |
143.7 |
48.0 |
| E7 |
−823.207464 |
521.2 |
42.2 |
270.8 |
257.4 |
0.238 |
243.9 |
139.1 |
131.7 |
| E8 |
−1498.598700 |
513.1 |
63.0 |
442.4 |
346.9 |
0.122 |
217.1 |
182.5 |
259.9 |
| E9 |
−1907.638388 |
517.0 |
77.3 |
533.0 |
385.7 |
0.108 |
167.6 |
208.1 |
324.9 |
| F1 |
−785.062414 |
270.8 |
35.7 |
518.0 |
237.2 |
0.227 |
133.6 |
113.3 |
404.7 |
| F2 |
−927.813680 |
295.5 |
40.4 |
840.6 |
257.4 |
0.228 |
155.9 |
127.6 |
713.0 |
| F3 |
−1009.623916 |
290.6 |
40.0 |
244.2 |
245.8 |
0.172 |
157.0 |
115.8 |
128.4 |
| F4 |
−1108.057319 |
273.1 |
42.1 |
209.9 |
242.3 |
0.237 |
133.4 |
116.9 |
93.0 |
| F5 |
−711.326903 |
368.0 |
34.0 |
126.7 |
218.0 |
0.248 |
370.2 |
131.7 |
−5.0 |
| F6 |
−1120.366353 |
380.8 |
46.0 |
292.6 |
277.3 |
0.188 |
180.2 |
138.6 |
154.0 |
| F7 |
−821.987326 |
459.1 |
40.8 |
355.5 |
249.7 |
0.249 |
279.0 |
139.7 |
215.8 |
| F8 |
−1497.372134 |
450.8 |
61.7 |
543.8 |
339.3 |
0.119 |
193.3 |
174.2 |
369.6 |
| F9 |
−1906.410426 |
455.4 |
75.7 |
638.4 |
379.6 |
0.109 |
150.0 |
201.4 |
437.0 |
| G1 |
−818.332921 |
270.6 |
34.4 |
610.8 |
232.2 |
0.171 |
229.6 |
116.0 |
494.8 |
| G2 |
−961.083454 |
297.4 |
40.9 |
939.3 |
253.1 |
0.250 |
268.8 |
140.6 |
798.7 |
| G3 |
−1042.894775 |
290.0 |
38.8 |
335.9 |
240.5 |
0.128 |
252.2 |
116.3 |
219.6 |
| G4 |
−1141.330500 |
274.0 |
42.8 |
298.9 |
236.3 |
0.176 |
295.6 |
124.6 |
174.3 |
| G5 |
−744.588899 |
368.9 |
32.5 |
242.8 |
213.1 |
0.250 |
323.7 |
125.3 |
117.5 |
| G6 |
−1153.639466 |
381.7 |
46.8 |
381.8 |
271.1 |
0.172 |
255.1 |
140.3 |
241.5 |
| G7 |
−855.244403 |
460.9 |
38.8 |
484.9 |
247.2 |
0.250 |
261.3 |
136.5 |
348.4 |
| G8 |
−1530.635854 |
451.5 |
60.0 |
655.0 |
335.8 |
0.086 |
292.8 |
173.1 |
481.9 |
| G9 |
−1939.685922 |
456.4 |
76.5 |
721.5 |
375.0 |
0.078 |
286.2 |
202.2 |
519.3 |
| H1 |
−817.087030 |
205.7 |
35.1 |
765.1 |
228.9 |
0.190 |
158.8 |
108.9 |
656.2 |
| H2 |
−959.828694 |
230.7 |
39.2 |
1112.7 |
244.6 |
0.250 |
148.6 |
121.4 |
991.3 |
| H3 |
−1041.650351 |
225.8 |
39.0 |
486.5 |
237.3 |
0.114 |
212.8 |
109.4 |
377.1 |
| H4 |
−1140.085203 |
130.6 |
13.9 |
343.5 |
233.6 |
0.230 |
178.8 |
117.7 |
225.8 |
| H5 |
−743.369994 |
303.6 |
32.8 |
325.5 |
208.5 |
0.235 |
386.2 |
126.8 |
198.7 |
| H6 |
−1152.393136 |
315.4 |
45.4 |
533.7 |
268.8 |
0.170 |
222.8 |
135.7 |
398.0 |
| H7 |
−854.028806 |
393.8 |
40.4 |
558.4 |
240.4 |
0.249 |
262.2 |
132.8 |
425.6 |
| H8 |
−1529.401790 |
386.8 |
60.2 |
777.9 |
330.5 |
0.088 |
246.4 |
166.7 |
611.2 |
| H9 |
−1938.436395 |
390.6 |
74.7 |
882.0 |
371.2 |
0.094 |
148.9 |
192.3 |
689.7 |
Fig. 2 illustrates the variation trends in the ΔHf,solid for the designed derivatives. It is found that the –NH– bridged compounds (series C) possess the highest ΔHf,solid while the –CH2–, –O–, –CH2–CH2–, –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–, –NH–NH– and –N
CH–, –NH–NH– and –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bridged ones have a lower ΔHf,solid. The influences of different bridge links on ΔHf,solid can be written in the following order: –NH– > directly linked > –N
N– bridged ones have a lower ΔHf,solid. The influences of different bridge links on ΔHf,solid can be written in the following order: –NH– > directly linked > –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– > –NH–NH– > –CH
N– > –NH–NH– > –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– > –CH2– > –CH2–CH2– > –O–. Obviously, the –NH– bridge is the most effective link in improving the ΔHf,solid for the 2, 2-bi(1,3,4-oxadiazole) derivatives while the –O– bridge link has the opposite effect. The substituted derivatives with the conjugated bridges (–CH
CH– > –CH2– > –CH2–CH2– > –O–. Obviously, the –NH– bridge is the most effective link in improving the ΔHf,solid for the 2, 2-bi(1,3,4-oxadiazole) derivatives while the –O– bridge link has the opposite effect. The substituted derivatives with the conjugated bridges (–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– or –N
CH– or –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–) have higher ΔHf,solid than those of the corresponding ones with the unconjugated bridges (–CH2–CH2– or –NH–NH–). This may be caused by the large conjugated system that is built by 2,2-bi(1,3,4-oxadiazole) and the conjugated bridge. For each of the series, ΔHf,solid increases evidently when the parent molecules are substituted by the –N3 group, whereas the opposite is true for the –NH2 substituent. The influences of the different energetic groups on ΔHf,solid can be written in the following order for series B–H: –N3 > –C(NO2)3 > –CN ≈ –CH(NO2)2 > –NHNH2 > –NHNO2 ≈ –NO2 > –NF2 > –NH2 while that for series A can be presented as follows: –N3 > –NF2 > –CN > –NHNH2 > –C(NO2)3 > –NHNO2 ≈ –NO2 > –CH(NO2)2 > –NH2. Overall, all the results reveal that the effects of the bridged links on the ΔHf,solid values of the designed compounds were coupled to those of the substituted energetic groups.
N–) have higher ΔHf,solid than those of the corresponding ones with the unconjugated bridges (–CH2–CH2– or –NH–NH–). This may be caused by the large conjugated system that is built by 2,2-bi(1,3,4-oxadiazole) and the conjugated bridge. For each of the series, ΔHf,solid increases evidently when the parent molecules are substituted by the –N3 group, whereas the opposite is true for the –NH2 substituent. The influences of the different energetic groups on ΔHf,solid can be written in the following order for series B–H: –N3 > –C(NO2)3 > –CN ≈ –CH(NO2)2 > –NHNH2 > –NHNO2 ≈ –NO2 > –NF2 > –NH2 while that for series A can be presented as follows: –N3 > –NF2 > –CN > –NHNH2 > –C(NO2)3 > –NHNO2 ≈ –NO2 > –CH(NO2)2 > –NH2. Overall, all the results reveal that the effects of the bridged links on the ΔHf,solid values of the designed compounds were coupled to those of the substituted energetic groups.
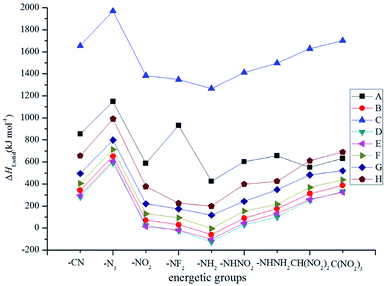 |
| | Fig. 2 The variation trends of ΔHf,solid of the designed compounds. | |
3.3 Detonation properties
The detonation properties that are related to oxygen balance (OB), density (ρ), heat of detonation (Q), detonation velocity (D) and detonation pressure (P) are summarized in Table 4. For a comparison, the detonation properties of the two well-known explosives 1,3,5-trinitro-1,3,5-triazinane (RDX) and 1,3,5, 7-tetranitro-1,3,5,7-tetrazocane (HMX) are also presented. It is seen that most of the designed compounds have a negative OB except for compounds A9, C9, D9, G9 and H9. Twenty-one compounds have higher OBs than those of RDX and HMX (−21.6%) while 51 compounds are on the opposite side. Generally speaking, it is better to keep the values of OB at around zero when designing energetic materials since too much oxygen will produce O2, which will remove a great deal of the energy produced during the explosion process. Obviously, compounds A9 (7.34%), B9 (−3.56%), C9 (5.32%), D3 (−6.56%), D8 (−8.84%), D9 (10.62%), E9 (−13.79%), F9 (−10.39%), G9 (3.43%) and H9 (6.90%) possess acceptable values of OB. It can be deduced that –C(NO2)3 is the best group in controlling the OB of all the designed compounds while the –NO2 and –CH(NO2)2 groups can only play an important role in controlling the OB of the –O– bridged compounds. The bridged 2,2-bi(1,3,4-oxadiazole) derivatives with different substituent groups are also found to have different ρ, Q, D and P values: values of ρ range from 1.54 (E5) to 2.16 g cm−3 (D4); values of Q range from 465.3 (E5) to 2586.9 cal g−1 (C4); values of D range from 5.46 (E5) to 10.6 km s−1 (A4) and values of P range from 12.0 (E5) to 54.5 GPa (A4). Interestingly, it is found that compound E5 has the smallest values of ρ, Q, D and P while compound A4 possesses the highest values of D and P. For a comparison, 28 compounds (A3, A4, A6, A9, B4, B9, C2, C3, C4, C6, C8, C9, D2, D3, D4, D6, D8, D9, E4, E9, F4, F9, G4, G6,G9, H4, H6 and H9) were found to have superior densities to that of RDX while 9 compounds (A4, A9, B4, C4, D4, D9, E4, F4, G4 and H4) were found to have superior densities to that of HMX; 24 compounds (A4, A6, A8, A9, B4, B9, C2, C3, C4, C5, C6, C7, C8, C9, D4, D8, D9, E9, F4, F9, G4, G9, H4 and H9) were found to possess equal or higher detonation velocities and detonation pressures than those of RDX while 14 (A4, A9, B9, C2, C3, C4, C6, C8, C9, D4, D8, D9, G4 and H4) compounds have equal or higher detonation velocities and detonation pressures than those of HMX.
Table 4 Predicted densities (ρ), heats of detonation (Q), detonation velocities (D) and detonation pressures (P) of the designed compounds
| Compound |
OB |
ρ (g cm−3) |
Q (cal g−1) |
D (km s−1) |
P (GPa) |
| A1 |
−85.11 |
1.64 |
1586.3 |
6.92 |
20.1 |
| A2 |
−43.64 |
1.80 |
1675.3 |
8.38 |
31.2 |
| A3 |
−38.10 |
1.83 |
1955.3 |
8.58 |
33.0 |
| A4 |
−40.00 |
2.12 |
2311.0 |
10.60 |
54.5 |
| A5 |
−76.19 |
1.68 |
1291.6 |
7.36 |
23.0 |
| A6 |
−18.60 |
1.83 |
1694.1 |
8.88 |
35.3 |
| A7 |
−72.73 |
1.69 |
1375.7 |
7.96 |
27.0 |
| A8 |
−13.87 |
1.80 |
1770.4 |
8.79 |
34.3 |
| A9 |
7.34 |
1.93 |
1640.7 |
9.19 |
39.0 |
| B1 |
−102.97 |
1.58 |
925.8 |
5.82 |
13.8 |
| B2 |
−61.54 |
1.72 |
1114.0 |
7.22 |
22.5 |
| B3 |
−33.06 |
1.77 |
1281.5 |
7.81 |
26.8 |
| B4 |
−56.69 |
2.00 |
1377.8 |
8.78 |
36.3 |
| B5 |
−96.70 |
1.67 |
555.7 |
6.00 |
15.2 |
| B6 |
−35.29 |
1.78 |
1195.3 |
7.86 |
27.3 |
| B7 |
−90.57 |
1.63 |
743.0 |
6.67 |
18.6 |
| B8 |
−26.67 |
1.78 |
1573.1 |
8.38 |
30.9 |
| B9 |
−3.56 |
1.90 |
1691.9 |
9.15 |
38.3 |
| C1 |
−82.76 |
1.64 |
2438.6 |
7.92 |
26.3 |
| C2 |
−44.26 |
1.83 |
2427.3 |
9.42 |
39.8 |
| C3 |
−16.46 |
1.84 |
2544.1 |
9.78 |
43.0 |
| C4 |
−40.78 |
2.03 |
2586.9 |
10.58 |
53.8 |
| C5 |
−74.32 |
1.71 |
2286.4 |
8.88 |
33.9 |
| C6 |
−20.51 |
1.83 |
2329.6 |
9.69 |
42.0 |
| C7 |
−71.36 |
1.73 |
2222.8 |
9.31 |
37.5 |
| C8 |
−15.51 |
1.81 |
2425.8 |
9.61 |
41.1 |
| C9 |
5.32 |
1.89 |
2217.2 |
9.83 |
44.1 |
| D1 |
−70.59 |
1.69 |
1023.8 |
6.52 |
18.1 |
| D2 |
−33.90 |
1.85 |
1196.6 |
7.97 |
28.6 |
| D3 |
−6.56 |
1.85 |
1373.9 |
8.41 |
31.9 |
| D4 |
−31.25 |
2.16 |
1458.5 |
9.67 |
45.8 |
| D5 |
−60.87 |
1.73 |
720.6 |
6.63 |
19.0 |
| D6 |
−11.68 |
1.85 |
1268.0 |
8.39 |
31.7 |
| D7 |
−59.81 |
1.71 |
921.9 |
7.16 |
22.0 |
| D8 |
−8.84 |
1.83 |
1885.2 |
9.17 |
37.7 |
| D9 |
10.62 |
1.93 |
1424.0 |
9.42 |
41.0 |
| E1 |
−118.52 |
1.55 |
862.9 |
5.56 |
12.3 |
| E2 |
−77.42 |
1.63 |
1053.2 |
6.75 |
19.0 |
| E3 |
−50.00 |
1.74 |
1200.7 |
7.49 |
24.4 |
| E4 |
−71.64 |
1.95 |
1302.6 |
8.37 |
32.6 |
| E5 |
−114.29 |
1.54 |
465.3 |
5.46 |
12.0 |
| E6 |
−50.35 |
1.75 |
1139.7 |
7.57 |
25.0 |
| E7 |
−106.19 |
1.55 |
650.8 |
6.24 |
15.7 |
| E8 |
−38.50 |
1.72 |
1509.9 |
8.02 |
27.8 |
| E9 |
−13.79 |
1.83 |
1632.7 |
8.76 |
34.2 |
| F1 |
−112.15 |
1.58 |
941.8 |
5.68 |
13.2 |
| F2 |
−71.54 |
1.66 |
1118.8 |
6.88 |
20.0 |
| F3 |
−44.09 |
1.73 |
1274.1 |
7.50 |
24.3 |
| F4 |
−66.17 |
2.03 |
1372.4 |
8.70 |
35.7 |
| F5 |
−107.22 |
1.57 |
589.7 |
5.65 |
13.0 |
| F6 |
−45.07 |
1.78 |
1199.0 |
7.70 |
26.2 |
| F7 |
−100.00 |
1.57 |
746.3 |
6.33 |
16.3 |
| F8 |
−34.41 |
1.74 |
1559.5 |
8.10 |
28.5 |
| F9 |
−10.39 |
1.87 |
1674.4 |
8.90 |
36.0 |
| G1 |
−80.73 |
1.67 |
1023.3 |
6.60 |
18.4 |
| G2 |
−44.80 |
1.79 |
1182.9 |
7.83 |
27.1 |
| G3 |
−18.60 |
1.84 |
1338.8 |
8.40 |
31.7 |
| G4 |
−41.48 |
2.00 |
1424.0 |
9.14 |
39.3 |
| G5 |
−72.73 |
1.69 |
725.7 |
6.78 |
19.6 |
| G6 |
−22.22 |
1.82 |
1254.9 |
8.32 |
30.9 |
| G7 |
−70.18 |
1.79 |
872.2 |
7.67 |
26.0 |
| G8 |
−17.02 |
1.80 |
1614.3 |
8.70 |
33.6 |
| G9 |
3.43 |
1.88 |
1601.3 |
9.08 |
37.5 |
| H1 |
−74.07 |
1.65 |
1161.5 |
6.68 |
18.7 |
| H2 |
−38.71 |
1.80 |
1334.6 |
8.04 |
28.6 |
| H3 |
−12.50 |
1.82 |
1454.2 |
8.44 |
31.8 |
| H4 |
−35.82 |
2.13 |
1440.4 |
9.52 |
44.2 |
| H5 |
−65.31 |
1.70 |
832.1 |
6.79 |
19.8 |
| H6 |
−16.78 |
1.85 |
1356.8 |
8.53 |
32.8 |
| H7 |
−63.72 |
1.70 |
961.6 |
7.38 |
23.3 |
| H8 |
−12.83 |
1.80 |
1676.7 |
8.73 |
33.8 |
| H9 |
6.90 |
1.86 |
1571.4 |
8.89 |
35.8 |
| RDX30 |
−21.6 |
1.82 |
1590.7 |
8.75 |
34.0 |
| HMX30 |
−21.6 |
1.91 |
1633.9 |
9.10 |
39.0 |
Fig. 3 displays the variation trends of ρ, Q, D and P of the designed compounds together with those for the popular explosives RDX and HMX. Obviously, the variation trends of ρ, Q, D and P were approximately the same throughout the series. That is to say, the energetic molecules with higher ρ and Q will also possess higher D and P. It can be predicted that ρ and Q (or HOFs) are always the important factors to be considered when an energetic molecule is designed. Fig. 3(a) shows the influence of different energetic groups on density. It can be seen that the compounds that are substituted by the –NF2 group have the highest ρ while the –CN, –NH2 or –NHNH2 substituted ones have a smaller ρ. When the bridge groups are –CH2–, –CH2–CH2– and –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–, the ρ values of the designed compounds are smaller than those of the directly linked ones (series A) with the same substituents. In addition, compounds with the conjugated bridge –CH
CH–, the ρ values of the designed compounds are smaller than those of the directly linked ones (series A) with the same substituents. In addition, compounds with the conjugated bridge –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– are found to have higher ρ than the corresponding ones with the unconjugated bridge –CH2–CH2–. Oppositely, compounds with the conjugated bridge –N
CH– are found to have higher ρ than the corresponding ones with the unconjugated bridge –CH2–CH2–. Oppositely, compounds with the conjugated bridge –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– show no regularity compared to the corresponding ones with the unconjugated bridge –NH–NH–. Overall, the effects of the bridges on the ρ values are coupled to those of the substituents. Fig. 3(b) shows the influence of different energetic groups on Q. It is clearly seen that different bridge groups have different effects on Q values: the –NH– bridged compounds possess higher Q values than those of the other series with the same substituents, but the –CH2–CH2– bridged ones have the smallest values of Q compared to those of the other series with the same substituents. It can be inferred that the –NH– bridge is the most effective group in improving Q of the 2,2-bi(1,3,4-oxadiazole) derivatives while the –CH2–CH2– bridge will decrease the Q values. For a comparison, all the –NH– bridged compounds have higher Q values than those of RDX and HMX while Q values of the –O–, –CH2–CH2–, –CH
N– show no regularity compared to the corresponding ones with the unconjugated bridge –NH–NH–. Overall, the effects of the bridges on the ρ values are coupled to those of the substituents. Fig. 3(b) shows the influence of different energetic groups on Q. It is clearly seen that different bridge groups have different effects on Q values: the –NH– bridged compounds possess higher Q values than those of the other series with the same substituents, but the –CH2–CH2– bridged ones have the smallest values of Q compared to those of the other series with the same substituents. It can be inferred that the –NH– bridge is the most effective group in improving Q of the 2,2-bi(1,3,4-oxadiazole) derivatives while the –CH2–CH2– bridge will decrease the Q values. For a comparison, all the –NH– bridged compounds have higher Q values than those of RDX and HMX while Q values of the –O–, –CH2–CH2–, –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–, –NH–NH– and –N
CH–, –NH–NH– and –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bridged ones are smaller (except for D8, F9 and H8) than those of HMX. However, the Q values of the directly linked compounds (series A) fluctuated around Q values of RDX and HMX. Additionally, the –NH2 substituted compounds were also found have the smallest values for all the designed compounds except for compound C7. It is predicted that the –NH2 and –NHH2 groups may make less contribution to the values of Q than other energetic groups. In view of Fig. 3(c) and (d), it is seen that the influence of the different energetic groups on the values of D and P is approximately the same throughout all the series. The general influence order of the different energetic groups on the values of D and P can be written as follows: –NF2 > –C(N2)3 > –NO2 ≈ –NHNO2 ≈ –CH(NO2)2 > –N3 ≈ –NHNH2 > –NH2 > –CN, while the influence of the different bridges on the values of D and P can be written in the order of –NH– > directly linked > –O– ≈ –NH–NH– ≈ –N
N– bridged ones are smaller (except for D8, F9 and H8) than those of HMX. However, the Q values of the directly linked compounds (series A) fluctuated around Q values of RDX and HMX. Additionally, the –NH2 substituted compounds were also found have the smallest values for all the designed compounds except for compound C7. It is predicted that the –NH2 and –NHH2 groups may make less contribution to the values of Q than other energetic groups. In view of Fig. 3(c) and (d), it is seen that the influence of the different energetic groups on the values of D and P is approximately the same throughout all the series. The general influence order of the different energetic groups on the values of D and P can be written as follows: –NF2 > –C(N2)3 > –NO2 ≈ –NHNO2 ≈ –CH(NO2)2 > –N3 ≈ –NHNH2 > –NH2 > –CN, while the influence of the different bridges on the values of D and P can be written in the order of –NH– > directly linked > –O– ≈ –NH–NH– ≈ –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– > –CH2– > –CH2–CH2– ≈ –CH
N– > –CH2– > –CH2–CH2– ≈ –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–. It can be concluded that the –NF2 and –NH– bridge are the most effective groups in improving the D and P values while it is on the opposite side for the –CN, –CH2–CH2– and –CH
CH–. It can be concluded that the –NF2 and –NH– bridge are the most effective groups in improving the D and P values while it is on the opposite side for the –CN, –CH2–CH2– and –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– bridged compounds. It is also found that the compounds with the conjugated bridge have similar D and P values compared to the corresponding unconjugated bridged compounds. For example, the –CH2–CH2– bridged compounds have similar D and P values to that of the –CH
CH– bridged compounds. It is also found that the compounds with the conjugated bridge have similar D and P values compared to the corresponding unconjugated bridged compounds. For example, the –CH2–CH2– bridged compounds have similar D and P values to that of the –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– bridged compounds, and the same is true of the –N
CH– bridged compounds, and the same is true of the –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– and –NH–NH– bridged ones. For a comparison, most of the –CN, –NH2 or –NHNH2 substituted compounds have smaller D and P values than that of RDX. It is also worth noting that the –NH2 or –NHNH2 substituted compounds with the –NH– bridge have equal D and P values to those of RDX, and, consequently, the –NH– bridge is the most important influence group in improving D and P values rather than the energetic groups.
N– and –NH–NH– bridged ones. For a comparison, most of the –CN, –NH2 or –NHNH2 substituted compounds have smaller D and P values than that of RDX. It is also worth noting that the –NH2 or –NHNH2 substituted compounds with the –NH– bridge have equal D and P values to those of RDX, and, consequently, the –NH– bridge is the most important influence group in improving D and P values rather than the energetic groups.
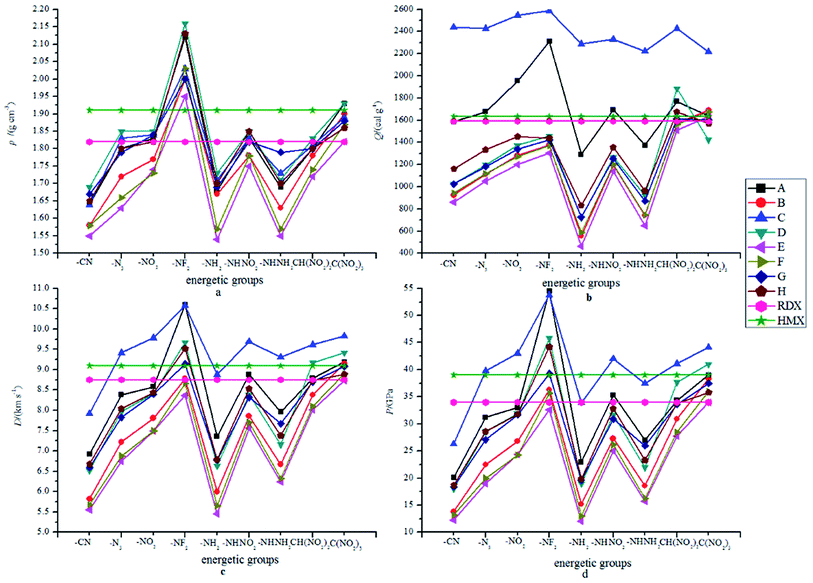 |
| | Fig. 3 The variation trends of ρ, Q, D and P of the designed compounds. | |
3.4 Thermal stabilities
The bond dissociation energy (BDE) for each of the possible trigger bonds was often investigated since it is an important factor in understanding the thermally stability, guaranteeing the safety and enhancing the controllability of kinetic energy release. Generally speaking, the smaller is the energy needed for breaking a bond, the weaker is the bond, and, consequently, this chemical bond may act as the trigger bond. Previous studies have also demonstrated that the bridge or energetic groups that are attached to the side chain of a ring usually act as the initial step during the decomposition process, and, thus, some possible trigger bonds were elucidated to predict the pyrolysis mechanism of the bridged 2,2-bi(1,3,4-oxadiazole) derivatives: (1) ring–R; (2) C–C (bridge); (3) C–N (bridge); (4) C–O (bridge); (5) N–N or N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N (bridge); (6) NH–NH2 or NH–NO2 or C–NO2. Note that the possible trigger bonds with the weakest BDEs were selected as the breaking bonds based on natural bond orbital (NBO) analyses. Take compound G6 for example, the possible trigger bonds were C(ring)–NHNO2, –C(ring)–N(bridge)–, –N–N–(bridge) and NH–NO2, and the corresponding BDEs of these possible trigger bonds were 453.4, 357.6, 120.7 and 69.9 kJ mol−1, respectively. Finally, the NH–NO2 bond was selected as the trigger bond since it had the smallest value of BDE (69.9 kJ mol−1). The bond order and BDEs of all the designed compounds are summarized and listed in Table 5.
N (bridge); (6) NH–NH2 or NH–NO2 or C–NO2. Note that the possible trigger bonds with the weakest BDEs were selected as the breaking bonds based on natural bond orbital (NBO) analyses. Take compound G6 for example, the possible trigger bonds were C(ring)–NHNO2, –C(ring)–N(bridge)–, –N–N–(bridge) and NH–NO2, and the corresponding BDEs of these possible trigger bonds were 453.4, 357.6, 120.7 and 69.9 kJ mol−1, respectively. Finally, the NH–NO2 bond was selected as the trigger bond since it had the smallest value of BDE (69.9 kJ mol−1). The bond order and BDEs of all the designed compounds are summarized and listed in Table 5.
Table 5 Bond dissociation energies (BDE, kJ mol−1) for the weakest bonds of the designed compounds
| Compd. |
Ring-R |
C–C (bridge) |
C–N (bridge) |
C–O (bridge) |
N–N/N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N (bridge) N (bridge) |
NH–NH2/NH–NO2/C–NO2 |
| BO |
BDE |
BO |
BDE |
BO |
BDE |
BO |
BDE |
BO |
BDE |
BO |
BDE |
| A1 |
1.082 |
551.0 |
1.063 |
522.8 |
— |
— |
— |
— |
— |
— |
— |
— |
| A2 |
1.113 |
379.7 |
1.074 |
538.0 |
— |
— |
— |
— |
— |
— |
— |
— |
| A3 |
0.893 |
245.8 |
1.062 |
489.1 |
— |
— |
— |
— |
— |
— |
— |
— |
| A4 |
1.022 |
274.2 |
1.063 |
527.0 |
— |
— |
— |
— |
— |
— |
— |
— |
| A5 |
1.169 |
476.8 |
1.078 |
534.4 |
— |
— |
— |
— |
— |
— |
— |
— |
| A6 |
1.062 |
428.2 |
1.064 |
523.3 |
— |
— |
— |
— |
— |
— |
0.925 |
84.2 |
| A7 |
1.116 |
380.0 |
1.082 |
535.9 |
— |
— |
— |
— |
— |
— |
1.037 |
191.9 |
| A8 |
1.009 |
450.0 |
1.062 |
528.7 |
— |
— |
— |
— |
— |
— |
0.828 |
112.2 |
| A9 |
1.009 |
454.4 |
1.060 |
525.0 |
— |
— |
— |
— |
— |
— |
0.807 |
93.4 |
| B1 |
1.080 |
553.0 |
1.014 |
383.5 |
— |
— |
— |
— |
— |
— |
— |
— |
| B2 |
1.101 |
375.7 |
1.013 |
381.8 |
— |
— |
— |
— |
— |
— |
— |
— |
| B3 |
0.895 |
249.2 |
1.016 |
383.4 |
— |
— |
— |
— |
— |
— |
— |
— |
| B4 |
1.016 |
274.6 |
1.014 |
387.2 |
— |
— |
— |
— |
— |
— |
— |
— |
| B5 |
1.153 |
470.7 |
1.012 |
377.9 |
— |
— |
— |
— |
— |
— |
— |
— |
| B6 |
1.048 |
428.7 |
1.014 |
384.5 |
— |
— |
— |
— |
— |
— |
0.935 |
87.3 |
| B7 |
1.133 |
375.4 |
1.013 |
373.5 |
— |
— |
— |
— |
— |
— |
1.032 |
199.1 |
| B8 |
1.008 |
452.4 |
1.015 |
388.5 |
— |
— |
— |
— |
— |
— |
0.827 |
115.0 |
| B9 |
1.009 |
457.9 |
1.015 |
386.4 |
— |
— |
— |
— |
— |
— |
0.806 |
93.5 |
| C1 |
1.088 |
555.4 |
— |
— |
1.087 |
385.8 |
— |
— |
— |
— |
— |
— |
| C2 |
1.099 |
375.2 |
— |
— |
1.088 |
355.1 |
— |
— |
— |
— |
— |
— |
| C3 |
0.908 |
252.1 |
— |
— |
1.101 |
383.9 |
— |
— |
— |
— |
— |
— |
| C4 |
1.021 |
276.2 |
— |
— |
1.094 |
376.6 |
— |
— |
— |
— |
— |
— |
| C5 |
1.147 |
467.8 |
— |
— |
1.055 |
341.2 |
— |
— |
— |
— |
— |
— |
| C6 |
1.050 |
429.3 |
— |
— |
1.080 |
373.8 |
— |
— |
— |
— |
0.931 |
72.7 |
| C7 |
1.119 |
367.0 |
— |
— |
1.055 |
339.5 |
— |
— |
— |
— |
1.029 |
168.6 |
| C8 |
1.014 |
451.3 |
— |
— |
1.083 |
390.0 |
— |
— |
— |
— |
0.889 |
106.9 |
| C9 |
1.015 |
462.0 |
— |
— |
1.090 |
393.4 |
— |
— |
— |
— |
0.802 |
85.6 |
| D1 |
1.082 |
548.9 |
— |
— |
— |
— |
0.951 |
282.7 |
— |
— |
— |
— |
| D2 |
1.106 |
375.2 |
— |
— |
— |
— |
0.970 |
248.4 |
— |
— |
— |
— |
| D3 |
0.897 |
172.4 |
— |
— |
— |
— |
0.983 |
270.4 |
— |
— |
— |
— |
| D4 |
1.018 |
271.5 |
— |
— |
— |
— |
0.976 |
267.2 |
— |
— |
— |
— |
| D5 |
1.152 |
470.9 |
— |
— |
— |
— |
0.960 |
226.7 |
— |
— |
— |
— |
| D6 |
1.056 |
428.4 |
— |
— |
— |
— |
0.951 |
264.2 |
— |
— |
0.924 |
78.8 |
| D7 |
1.131 |
374.0 |
— |
— |
— |
— |
0.942 |
228.7 |
— |
— |
1.031 |
185.7 |
| D8 |
1.009 |
447.8 |
— |
— |
— |
— |
0.952 |
287.7 |
— |
— |
0.826 |
110.9 |
| D9 |
1.010 |
452.1 |
— |
— |
— |
— |
0.959 |
289.1 |
— |
— |
0.804 |
92.9 |
| E1 |
1.081 |
552.9 |
0.985 |
230.0 |
— |
— |
— |
— |
— |
— |
— |
— |
| E2 |
1.104 |
365.9 |
0.985 |
216.0 |
— |
— |
— |
— |
— |
— |
— |
— |
| E3 |
0.898 |
252.2 |
1.005 |
236.3 |
— |
— |
— |
— |
— |
— |
— |
— |
| E4 |
1.015 |
276.9 |
1.005 |
229.6 |
— |
— |
— |
— |
— |
— |
— |
— |
| E5 |
1.147 |
468.1 |
1.005 |
220.5 |
— |
— |
— |
— |
— |
— |
— |
— |
| E6 |
1.048 |
426.6 |
1.004 |
233.6 |
— |
— |
— |
— |
— |
— |
0.937 |
85.8 |
| E7 |
1.134 |
370.7 |
0.984 |
212.5 |
— |
— |
— |
— |
— |
— |
1.035 |
193.4 |
| E8 |
1.009 |
450.1 |
0.985 |
233.0 |
— |
— |
— |
— |
— |
— |
0.827 |
114.8 |
| E9 |
1.010 |
4605 |
0.995 |
236.0 |
— |
— |
— |
— |
— |
— |
0.806 |
93.4 |
| F1 |
1.085 |
554.6 |
1.116 |
519.2 |
— |
— |
— |
— |
— |
— |
— |
— |
| F2 |
1.106 |
478.2 |
1.123 |
623.1 |
— |
— |
— |
— |
— |
— |
— |
— |
| F3 |
0.900 |
250.4 |
1.116 |
516.8 |
— |
— |
— |
— |
— |
— |
— |
— |
| F4 |
1.020 |
276.8 |
1.116 |
521.3 |
— |
— |
— |
— |
— |
— |
— |
— |
| F5 |
1.160 |
472.0 |
1.127 |
521.8 |
— |
— |
— |
— |
— |
— |
— |
— |
| F6 |
1.055 |
428.7 |
1.115 |
517.2 |
— |
— |
— |
— |
— |
— |
0.932 |
76.0 |
| F7 |
1.152 |
375.8 |
1.141 |
525.5 |
— |
— |
— |
— |
— |
— |
1.038 |
181.1 |
| F8 |
1.011 |
451.8 |
1.114 |
521.0 |
— |
— |
— |
— |
— |
— |
0.825 |
107.2 |
| F9 |
1.012 |
457.7 |
1.121 |
519.9 |
— |
— |
— |
— |
— |
— |
0.804 |
85.0 |
| G1 |
1.091 |
543.0 |
— |
— |
1.148 |
350.0 |
— |
— |
1.003 |
129.1 |
— |
— |
| G2 |
1.097 |
373.3 |
— |
— |
1.082 |
351.1 |
— |
— |
1.021 |
87.8 |
— |
— |
| G3 |
0.913 |
241.2 |
— |
— |
1.154 |
350.8 |
— |
— |
1.005 |
132.9 |
— |
— |
| G4 |
1.020 |
276.9 |
— |
— |
1.095 |
359.6 |
— |
— |
1.035 |
128.5 |
— |
— |
| G5 |
1.139 |
453.4 |
— |
— |
1.104 |
333.6 |
— |
— |
0.997 |
52.9 |
— |
— |
| G6 |
1.050 |
428.2 |
— |
— |
1.099 |
357.6 |
— |
— |
1.032 |
120.7 |
0.931 |
69.9 |
| G7 |
1.128 |
348.7 |
— |
— |
1.091 |
330.1 |
— |
— |
0.957 |
26.3 |
1.029 |
154.6 |
| G8 |
1.016 |
428.0 |
— |
— |
1.120 |
335.9 |
— |
— |
0.982 |
101.3 |
0.821 |
80.2 |
| G9 |
1.018 |
462.6 |
— |
— |
1.110 |
364.9 |
— |
— |
1.030 |
149.5 |
0.801 |
83.6 |
| H1 |
1.084 |
550.5 |
— |
— |
1.136 |
295.6 |
— |
— |
1.720 |
211.9 |
— |
— |
| H2 |
1.119 |
380.6 |
— |
— |
1.124 |
263.9 |
— |
— |
1.767 |
78.5 |
— |
— |
| H3 |
0.890 |
241.4 |
— |
— |
1.156 |
301.5 |
— |
— |
1.709 |
143.6 |
— |
— |
| H4 |
1.024 |
352.2 |
— |
— |
1.137 |
379.5 |
— |
— |
1.703 |
216.8 |
— |
— |
| H5 |
1.196 |
478.7 |
— |
— |
1.207 |
322.6 |
— |
— |
1.616 |
94.4 |
— |
— |
| H6 |
1.071 |
428.3 |
— |
— |
1.145 |
297.3 |
— |
— |
1.706 |
107.9 |
0.924 |
71.1 |
| H7 |
1.188 |
384.2 |
— |
— |
1.218 |
327.1 |
— |
— |
1.599 |
76.2 |
1.041 |
186.4 |
| H8 |
1.009 |
444.7 |
— |
— |
1.155 |
306.6 |
— |
— |
1.706 |
198.1 |
0.828 |
96.2 |
| H9 |
1.008 |
449.0 |
— |
— |
1.152 |
303.8 |
— |
— |
1.714 |
194.9 |
0.807 |
85.2 |
Fig. 4 displays the variation trends of BDEs of the designed compounds. It is seen that the variation trends of BDEs for each series are approximately the same with each other. Incorporating the bridge –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– (series F) makes less change to the values of BDEs compared to the directly linked ones (series A). For example, the BDEs of compounds A1 and F1 are 522.8 and 519.2 kJ mol−1, and the same is true for compounds A3–A6 and F3–F6. The volatilities of BDEs for each series can be written in the following order: directly linked ≈ –CH
CH– (series F) makes less change to the values of BDEs compared to the directly linked ones (series A). For example, the BDEs of compounds A1 and F1 are 522.8 and 519.2 kJ mol−1, and the same is true for compounds A3–A6 and F3–F6. The volatilities of BDEs for each series can be written in the following order: directly linked ≈ –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– > –C– ≈ –N– > –O– > –CH2–CH2– ≈ –N
CH– > –C– ≈ –N– > –O– > –CH2–CH2– ≈ –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– > –NH–NH–. It reveals that the energetic groups acted as the main influence factor on BDEs for the directly linked and –CH
N– > –NH–NH–. It reveals that the energetic groups acted as the main influence factor on BDEs for the directly linked and –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– bridged compounds while the parent structure was the most important influence factor for the –NH–NH– bridged ones. The average BDEs of the –NH–NH– bridged ones were found to be the lowest, and, hence, it can be inferred that the introduction of the –NH–NH– bridge might decrease the thermal stability of the 2,2-bi(1,3,4-oxadiazole) derivatives. Evident regularity was also found in each series: BDEs of the –CN, –N3, –NO2, –NF2, –NH2 substituted ones in series A, B, C, E and F were higher than those of the –NHNO2, –NHNH2, –CH(NO2)2 and –C(NO2)3 substituted ones. In view of the influence of energetic groups, –CN was the most effective group in improving the BDEs of an energetic material while the –NHNH2 group acted on the opposite side.
CH– bridged compounds while the parent structure was the most important influence factor for the –NH–NH– bridged ones. The average BDEs of the –NH–NH– bridged ones were found to be the lowest, and, hence, it can be inferred that the introduction of the –NH–NH– bridge might decrease the thermal stability of the 2,2-bi(1,3,4-oxadiazole) derivatives. Evident regularity was also found in each series: BDEs of the –CN, –N3, –NO2, –NF2, –NH2 substituted ones in series A, B, C, E and F were higher than those of the –NHNO2, –NHNH2, –CH(NO2)2 and –C(NO2)3 substituted ones. In view of the influence of energetic groups, –CN was the most effective group in improving the BDEs of an energetic material while the –NHNH2 group acted on the opposite side.
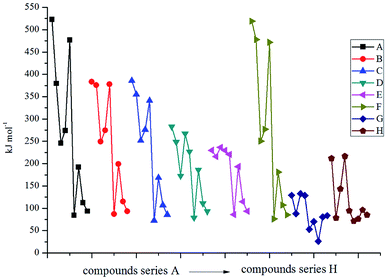 |
| | Fig. 4 The variation trends of BDE of the designed compounds. | |
It is well known that a promising high-energy-density material should not only have superior detonation properties to those of RDX or HMX, but should also possess acceptable thermal stability. Taking both detonation properties and thermal stabilities31 into consideration, 22 compounds (A4, A6, A8, A9, B4, B9, C2, C3, C4, C5, C7, C8, C9 D4, D8, D9, E9, F4, F9, G9, H4 and H9) were finally screened as candidates for high-energy explosives with acceptable thermal stabilities.
3.5 Thermodynamic properties
As the main thermodynamic parameters, standard molar heat capacity (Cθp,m) standard molar entropy (Sθm) and standard molar enthalpy (Hθm) can provide useful information on the state equation, macroscopic properties and chemical reactions of an energetic material.32 The variation trends of Cθp,m, Sθm and Hθm of the title compounds at different temperatures (from 200 to 600 K) were investigated. The related equation for these parameters at different temperatures can be written in the following form:
| X = a + bT + cT2 (X = Cθp,m, Sθm and Hθm) |
where a, b and c are constants and are summarized in Table 6. It is seen that Cθp,m, Sθm and Hθm of all the designed compounds improved as the temperature increased. However, there existed differences in the growth rates of these parameters. The case is that the growth rates Cθp,m and Sθm decreased evidently as the temperature increased while the growth rate Hθm increased. The reason is that the translations and rotations of chemical bonds were the main influencing factors at a low temperature while vibrational movement occurred and intensified at a high temperature. At certain temperatures, it was also found that the values of these thermodynamic parameters increases as the volume of energetic groups increased. This phenomenon may be caused by the strong space steric effects of the energetic groups. Take compounds A8 and A9 for example, Cθp,m, Sθm and Hθm of compound A8 and A9 were 228.2 kJ mol−1 K−1, 575.8 kJ mol−1 K−1, 30.1 kJ mol−1 and 294.0 kJ mol−1 K−1, 643.5 kJ mol−1 K−1, 37.1 kJ mol−1, respectively (200 K). Obviously, Cθp,m, Sθm and Hθm of compound A9 were higher than those of compound A8.
Table 6 Calculated Sθm, Cθp,m and Hθm of the designed compounds
| |
Sθm |
Cθp,m |
Hθm |
R2 |
| a |
b |
C × 10−4 |
a |
b |
C × 10−4 |
a |
b |
C × 10−4 |
| A1 |
250.8 |
0.70 |
−2.49 |
24.3 |
0.56 |
−3.22 |
−4.66 |
0.07 |
1.51 |
0.9999 |
| A2 |
265.5 |
0.80 |
−2.88 |
29.0 |
0.64 |
−3.65 |
−5.35 |
0.08 |
1.73 |
0.9999 |
| A3 |
277.4 |
0.78 |
−2.65 |
28.2 |
0.62 |
−3.32 |
−4.11 |
0.08 |
1.80 |
0.9999 |
| A4 |
274.9 |
0.84 |
−2.97 |
25.0 |
0.70 |
−4.16 |
−5.50 |
0.09 |
1.83 |
0.9999 |
| A5 |
230.3 |
0.67 |
−2.04 |
10.3 |
0.61 |
−3.34 |
−4.28 |
0.06 |
1.70 |
0.9999 |
| A6 |
287.4 |
0.92 |
−2.96 |
24.9 |
0.78 |
−4.21 |
−4.90 |
0.09 |
2.24 |
0.9999 |
| A7 |
252.4 |
0.81 |
−2.52 |
24.0 |
0.68 |
−3.30 |
−4.50 |
0.07 |
2.07 |
0.9999 |
| A8 |
340.6 |
1.27 |
−4.40 |
54.2 |
0.97 |
−4.99 |
−6.88 |
0.13 |
2.86 |
0.9999 |
| A9 |
338.7 |
1.65 |
−6.39 |
83.2 |
1.19 |
−6.74 |
−12.8 |
0.18 |
3.25 |
0.9999 |
| B1 |
267.2 |
0.77 |
−2.53 |
23.8 |
0.63 |
−3.37 |
−4.26 |
0.07 |
1.83 |
0.9999 |
| B2 |
283.3 |
0.87 |
−2.89 |
27.3 |
0.72 |
−3.85 |
−4.91 |
0.08 |
2.06 |
0.9999 |
| B3 |
293.5 |
0.85 |
−2.66 |
26.28 |
0.70 |
−3.53 |
−3.77 |
0.07 |
2.12 |
0.9999 |
| B4 |
290.1 |
0.90 |
−2.99 |
23.07 |
0.78 |
−4.38 |
−5.18 |
0.09 |
2.15 |
0.9999 |
| B5 |
247.6 |
0.73 |
−2.00 |
7.56 |
0.69 |
−3.53 |
−3.80 |
0.06 |
2.04 |
0.9999 |
| B6 |
302.5 |
0.99 |
−2.98 |
24.2 |
0.86 |
−4.35 |
−4.51 |
0.09 |
2.56 |
0.9999 |
| B7 |
269.8 |
0.87 |
−2.46 |
22.0 |
0.75 |
−3.47 |
−3.82 |
0.07 |
2.41 |
0.9999 |
| B8 |
352.7 |
1.34 |
−4.44 |
53.9 |
1.04 |
−5.14 |
−6.64 |
0.13 |
3.18 |
0.9999 |
| B9 |
355.7 |
1.73 |
−6.43 |
82.8 |
1.26 |
−6.90 |
−12.5 |
0.18 |
3.57 |
0.9999 |
| C1 |
260.4 |
0.78 |
−2.76 |
24.9 |
0.64 |
−3.70 |
−5.40 |
0.08 |
1.70 |
0.9999 |
| C2 |
285.4 |
0.89 |
−3.20 |
31.3 |
0.71 |
−4.10 |
−5.98 |
0.09 |
1.92 |
0.9999 |
| C3 |
285.3 |
0.86 |
−2.89 |
28.1 |
0.70 |
−3.79 |
−4.82 |
0.08 |
2.00 |
0.9999 |
| C4 |
294.5 |
0.92 |
−3.26 |
26.0 |
0.78 |
−4.65 |
−6.10 |
0.09 |
2.02 |
0.9999 |
| C5 |
245.5 |
0.74 |
−2.29 |
12.2 |
0.68 |
−3.72 |
−4.80 |
0.06 |
1.89 |
0.9999 |
| C6 |
296.0 |
1.00 |
−3.26 |
26.2 |
0.86 |
−4.69 |
−5.76 |
0.09 |
2.43 |
0.9999 |
| C7 |
267.7 |
0.89 |
−2.73 |
24.2 |
0.76 |
−3.78 |
−4.92 |
0.08 |
2.28 |
0.9999 |
| C8 |
348.5 |
1.35 |
−4.70 |
55.5 |
1.04 |
−5.46 |
−7.72 |
0.13 |
3.05 |
0.9999 |
| C9 |
345.5 |
1.74 |
−6.67 |
84.0 |
1.27 |
−7.22 |
−13.6 |
0.19 |
3.44 |
0.9999 |
| D1 |
264.3 |
0.75 |
−2.70 |
24.5 |
0.61 |
−3.60 |
−5.03 |
0.08 |
1.62 |
0.9999 |
| D2 |
283.6 |
0.86 |
−3.11 |
28.7 |
0.70 |
−4.12 |
−5.76 |
0.09 |
1.85 |
0.9999 |
| D3 |
276.9 |
0.80 |
−2.61 |
21.0 |
0.68 |
−3.74 |
−4.52 |
0.08 |
1.91 |
0.9999 |
| D4 |
286.8 |
0.90 |
−3.20 |
24.5 |
0.76 |
−4.63 |
−6.03 |
0.09 |
1.95 |
0.9999 |
| D5 |
249.5 |
0.72 |
−2.21 |
9.11 |
0.67 |
−3.77 |
−4.53 |
0.06 |
1.83 |
0.9999 |
| D6 |
298.8 |
0.98 |
−3.17 |
24.9 |
0.84 |
−4.61 |
−5.35 |
0.09 |
2.36 |
0.9999 |
| D7 |
267.2 |
0.86 |
−2.62 |
21.7 |
0.74 |
−3.75 |
−4.59 |
0.08 |
2.21 |
0.9999 |
| D8 |
352.1 |
1.32 |
−4.61 |
54.7 |
1.02 |
−5.38 |
−7.34 |
0.13 |
2.98 |
0.9999 |
| D9 |
355.4 |
1.71 |
−6.62 |
84.05 |
1.24 |
−7.12 |
−13.2 |
0.19 |
3.36 |
0.9999 |
| E1 |
282.1 |
0.84 |
−2.57 |
23.9 |
0.71 |
−3.50 |
−3.83 |
0.07 |
2.14 |
0.9999 |
| E2 |
295.8 |
0.94 |
−2.97 |
28.8 |
0.79 |
−3.94 |
−4.61 |
0.09 |
2.37 |
0.9999 |
| E3 |
307.1 |
0.92 |
−2.77 |
30.2 |
0.76 |
−3.53 |
−3.36 |
0.08 |
2.43 |
0.9999 |
| E4 |
300.7 |
0.98 |
−3.05 |
23.1 |
0.85 |
−4.55 |
−5.08 |
0.09 |
2.47 |
0.9999 |
| E5 |
263.0 |
0.80 |
−2.12 |
12.3 |
0.74 |
−3.49 |
−3.39 |
0.06 |
2.33 |
0.9999 |
| E6 |
311.6 |
1.05 |
−3.00 |
23.2 |
0.93 |
−4.51 |
−4.36 |
0.09 |
2.88 |
0.9999 |
| E7 |
282.6 |
0.94 |
−2.52 |
22.0 |
0.83 |
−3.64 |
−3.55 |
0.07 |
2.72 |
0.9999 |
| E8 |
371.3 |
1.41 |
−4.48 |
54.1 |
1.11 |
−5.27 |
−6.18 |
0.13 |
3.50 |
0.9999 |
| E9 |
369.1 |
1.80 |
−6.50 |
84.0 |
1.33 |
−7.00 |
−12.2 |
0.19 |
3.88 |
0.9999 |
| F1 |
265.8 |
0.82 |
−2.74 |
25.7 |
0.68 |
−3.67 |
−4.92 |
0.07 |
1.94 |
0.9999 |
| F2 |
281.5 |
0.93 |
−3.14 |
30.9 |
0.76 |
−4.10 |
−5.62 |
0.09 |
2.17 |
0.9999 |
| F3 |
289.5 |
0.90 |
−2.88 |
28.3 |
0.75 |
−3.83 |
−4.51 |
0.08 |
2.24 |
0.9999 |
| F4 |
291.4 |
0.97 |
−3.24 |
26.7 |
0.82 |
−4.63 |
−5.80 |
0.09 |
2.26 |
0.9999 |
| F5 |
246.4 |
0.79 |
−2.27 |
11.4 |
0.73 |
−3.79 |
−4.65 |
0.07 |
2.14 |
0.9999 |
| F6 |
301.6 |
1.04 |
−3.19 |
25.0 |
0.91 |
−4.71 |
−5.23 |
0.09 |
2.68 |
0.9999 |
| F7 |
265.8 |
0.93 |
−2.71 |
22.8 |
0.81 |
−3.90 |
−4.85 |
0.08 |
2.52 |
0.9999 |
| F8 |
356.6 |
1.39 |
−4.66 |
56.1 |
1.09 |
−5.44 |
−7.15 |
0.13 |
3.30 |
0.9999 |
| F9 |
355.6 |
1.78 |
−6.63 |
82.7 |
1.32 |
−7.29 |
−13.1 |
0.19 |
3.69 |
0.9999 |
| G1 |
249.6 |
0.82 |
−2.75 |
19.9 |
0.70 |
−4.05 |
−6.02 |
0.08 |
1.89 |
0.9999 |
| G2 |
285.2 |
0.95 |
−3.30 |
28.8 |
0.79 |
−4.50 |
−6.36 |
0.10 |
2.15 |
0.9999 |
| G3 |
270.6 |
0.90 |
−2.93 |
24.6 |
0.77 |
−4.13 |
−5.63 |
0.09 |
2.18 |
0.9999 |
| G4 |
288.2 |
1.00 |
−3.51 |
27.2 |
0.85 |
−5.07 |
−7.06 |
0.10 |
2.22 |
0.9999 |
| G5 |
236.0 |
0.77 |
−2.16 |
4.67 |
0.74 |
−4.03 |
−5.00 |
0.06 |
2.11 |
0.9999 |
| G6 |
293.5 |
1.08 |
−3.46 |
26.0 |
0.93 |
−5.10 |
−6.38 |
0.10 |
2.64 |
0.9999 |
| G7 |
257.5 |
0.89 |
−2.42 |
11.3 |
0.83 |
−4.15 |
−4.67 |
0.07 |
2.53 |
0.9999 |
| G8 |
339.0 |
1.37 |
−4.54 |
47.2 |
1.11 |
−5.79 |
−7.75 |
0.13 |
3.28 |
0.9999 |
| G9 |
356.1 |
1.81 |
−6.88 |
84.6 |
1.34 |
−7.61 |
−14.2 |
0.20 |
3.65 |
0.9999 |
| H1 |
270.7 |
0.81 |
−2.96 |
31.4 |
0.64 |
−3.64 |
−5.46 |
0.09 |
1.73 |
0.9999 |
| H2 |
280.6 |
0.91 |
−3.26 |
31.1 |
0.74 |
−4.27 |
−6.23 |
0.09 |
1.98 |
0.9999 |
| H3 |
291.0 |
0.89 |
−3.06 |
31.0 |
0.72 |
−3.92 |
−5.10 |
0.09 |
2.04 |
0.9999 |
| H4 |
289.1 |
0.95 |
−3.41 |
29.5 |
0.79 |
−4.71 |
−6.54 |
0.10 |
2.06 |
0.9999 |
| H5 |
238.8 |
0.78 |
−2.47 |
13.8 |
0.70 |
−3.94 |
−5.68 |
0.07 |
1.93 |
0.9999 |
| H6 |
303.1 |
1.04 |
−3.43 |
31.7 |
0.86 |
−4.65 |
−5.80 |
0.09 |
2.46 |
0.9999 |
| H7 |
267.8 |
0.93 |
−3.00 |
31.1 |
0.76 |
−3.82 |
−5.48 |
0.09 |
2.30 |
0.9999 |
| H8 |
345.5 |
1.38 |
−4.79 |
56.7 |
1.06 |
−5.60 |
−8.01 |
0.14 |
3.10 |
0.9999 |
| H9 |
350.4 |
1.77 |
−6.80 |
86.2 |
1.28 |
−7.34 |
−13.8 |
0.20 |
3.48 |
0.9999 |
4. Conclusions
In this study, a series of bridged 2,2-bi(1,3,4-oxadiazole) energetic derivatives were designed and investigated by the density functional theory method at B3LYP/6-311G(d,p) level. The substitution of –CH2–, –O– and –CH2–CH2– bridges improves the HOMO–LUMO gap while the –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bridge decreases the values. Most of the designed compounds (except for B5, D4, D5, E4, E5 and F5) possess high positive heats of formation (range from 15.4 to 1148.6 kJ mol−1). The –N3 and –NH– groups act as effective structural units for increasing the solid-phase heats of formation of these derivatives. The calculated detonation properties show that the –NF2 and –NH– groups can improve the heats of detonation, detonation velocities and detonation pressures evidently. The analysis of the bond dissociation energies suggests that most of the designed compounds have acceptable thermal stabilities with the values ranging from 26.3 to 522.8 kJ mol−1. Finally, 22 compounds (A4, A6, A8, A9, B4, B9, C2, C3, C4, C5, C7, C8, C9 D4, D8, D9, E9, F4, F9, G9, H4 and H9) were selected as potential candidates for promising high-energy-density materials.
N– bridge decreases the values. Most of the designed compounds (except for B5, D4, D5, E4, E5 and F5) possess high positive heats of formation (range from 15.4 to 1148.6 kJ mol−1). The –N3 and –NH– groups act as effective structural units for increasing the solid-phase heats of formation of these derivatives. The calculated detonation properties show that the –NF2 and –NH– groups can improve the heats of detonation, detonation velocities and detonation pressures evidently. The analysis of the bond dissociation energies suggests that most of the designed compounds have acceptable thermal stabilities with the values ranging from 26.3 to 522.8 kJ mol−1. Finally, 22 compounds (A4, A6, A8, A9, B4, B9, C2, C3, C4, C5, C7, C8, C9 D4, D8, D9, E9, F4, F9, G9, H4 and H9) were selected as potential candidates for promising high-energy-density materials.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This study was supported by the National Natural Science Foundation of China (Grant No. 11602121).
References
- C. Zhang, C. G. Sun, B. C. Hu, C. M. Yu and M. Lu, Science, 2017, 355, 374–376 CrossRef CAS PubMed.
- M. B. Talawar, R. Sivabalan, T. Mukundan, H. Muthurajan, A. K. Sikder, B. R. Gandhe and A. S. Rao, J. Hazard. Mater., 2009, 161, 589–607 CrossRef CAS PubMed.
- V. D. Ghule, D. Sonal, A. Devi and T. R. Kumar, Ind. Eng. Chem. Res., 2016, 55, 875–881 CrossRef CAS.
- A. K. Sikder and N. Sikder, J. Hazard. Mater., 2004, 112, 1–15 CrossRef CAS PubMed.
- X. H. Jin, J. H. Zhou, S. J. Wang and B. C. Hu, Quim. Nova, 2016, 39, 467–473 Search PubMed.
- W. Chi, RSC Adv., 2015, 5, 7766–7772 RSC.
- W. Chi, L. L. Li, B. T. Li and H. S. Wu, Struct. Chem., 2012, 23, 1837–1841 CrossRef CAS.
- Z. Fu, R. Su, Y. Wang, Y. F. Wang, W. Zeng, N. Xiao, Y. Wu, Z. Zhou, J. Chen and F. Chen, Chem.– Eur. J., 2012, 18, 1886–1889 CrossRef CAS PubMed.
- A. V. Sergievskii, T. V. Romanova, S. F. Melikova and I. V. Yselinskii, Russ. J. Org. Chem., 2005, 41, 261–267 CrossRef CAS.
- J. H. Zhang and J. M. Shreeve, J. Am. Chem. Soc., 2014, 136, 4437–4445 CrossRef CAS PubMed.
- H. Wei, C. L. He, J. H. Zhang and J. M. Shreeve, Angew. Chem., Int. Ed., 2015, 54, 9367–9371 CrossRef CAS PubMed.
- J. A. Joule, K. Mills and G. F. Smith, Heterocyclic Chemistry, Taylor & Francis, New York, 3rd edn, 1995 Search PubMed.
- W. Q. Zhang, J. H. Zhang, M. C. Deng, X. J. Qi, F. D. Nie and Q. H. Zhang, Nat. Commun., 2017, 8, 181–187 CrossRef PubMed.
- Q. Wu, W. H. Zhu and H. M. Xiao, J. Chem. Eng. Data, 2013, 58, 2748–2762 CrossRef CAS.
- F. Wang, G. X. Wang, H. C. Du, J. Y. Zhang and X. D. Gong, J. Phys. Chem. A, 2011, 115, 13858–13864 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Gaussian Inc, Pittsburgh, PA, 2003 Search PubMed.
- Y. H. Joo, B. Twamley, S. Garg and J. M. Shreeve, Angew. Chem., Int. Ed., 2008, 120, 6332–6335 CrossRef.
- Y. Y. Guo, W. J. Chi, Z. S. Li and Q. S. Li, RSC Adv., 2015, 5, 38048–38055 RSC.
- X. H. Jin, J. H. Zhou, B. C. Hu and C. M. Ma, J. Phys. Org. Chem., 2017, 30, e3704 CrossRef.
- G. H. Tao, B. Twamley and J. M. Shreeve, J. Mater. Chem., 2009, 19, 5850–5854 RSC.
- K. E. Gutowski, R. D. Rogers and D. A. Dixon, J. Phys. Chem. B, 2007, 111, 4788–4800 CrossRef CAS PubMed.
- B. S. Jursic, J. Mol. Struct.: THEOCHEM, 2000, 499, 137–140 CrossRef CAS.
- P. W. Atkins, Physical Chemistry. Oxford University Press, Oxford, 2nd edn, 1982 Search PubMed.
- P. Politzer, Y. Ma, P. Lane and M. C. Concha, Int. J. Quantum Chem., 2005, 105, 341–347 CrossRef CAS.
- E. F. C. Byrd and B. M. Rice, J. Phys. Chem. A, 2006, 110, 1005–1013 CrossRef CAS PubMed.
- P. Politzer, J. Martinez, J. S. Murray, M. C. Concha and A. Toro-Labbé, Mol. Phys., 2009, 107, 2095–2101 CrossRef CAS.
- M. J. Kamlet and S. J. Jacobs, J. Chem. Phys., 1968, 48, 23–25 CrossRef CAS.
- D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187–10198 CrossRef CAS PubMed.
- B. M. Rice, S. V. Pai and J. Hare, Combust. Flame, 1999, 118, 445–458 CrossRef CAS.
- Y. Pan, W. H. Zhu and H. M. Xiao, J. Mol. Model., 2012, 18, 3125–3138 CrossRef CAS PubMed.
- G. S. Chung, M. W. Schmidt and M. S. Gordon, J. Phys. Chem. A, 2000, 104, 5647–5650 CrossRef CAS.
- J. Zhang and H. M. Xiao, J. Chem. Phys., 2002, 116, 10674–10683 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Menghui Xiaoa,
Guowei Zhoua,
Jianhua Zhoua and
Bingcheng Hub
*a,
Menghui Xiaoa,
Guowei Zhoua,
Jianhua Zhoua and
Bingcheng Hub
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–, –NH–NH– and –N
CH–, –NH–NH– and –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–) with various energetic groups (such as –CN, –N3, –NO2, –NF2, –NH2, –NHNO2, –NHNH2, –CH(NO2)2 and –C(NO2)3) (Scheme 2, series A–H) were reported.
N–) with various energetic groups (such as –CN, –N3, –NO2, –NF2, –NH2, –NHNO2, –NHNH2, –CH(NO2)2 and –C(NO2)3) (Scheme 2, series A–H) were reported.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NCH3, CH3CH(NO2)2, CH3C(NO2)3, and
NCH3, CH3CH(NO2)2, CH3C(NO2)3, and  were unavailable. Therefore, the atomization reaction CaHbNc → aC(g) + bH(g) + cN(g) was employed to evaluate the HOFs of CH3NF2, CH3NHNO2, CH3N3, CH3NHNHCH3, CH3N
were unavailable. Therefore, the atomization reaction CaHbNc → aC(g) + bH(g) + cN(g) was employed to evaluate the HOFs of CH3NF2, CH3NHNO2, CH3N3, CH3NHNHCH3, CH3N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NCH3 and
NCH3 and  at CBS-Q level22 while the HOFs of the compounds CH3CH(NO2)2 and CH3C(NO2)3 were calculated via isodesmic reactions:
at CBS-Q level22 while the HOFs of the compounds CH3CH(NO2)2 and CH3C(NO2)3 were calculated via isodesmic reactions: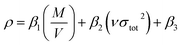
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) 0.5Q0.5)0.5(1 + 1.3ρ)
0.5Q0.5)0.5(1 + 1.3ρ)
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) 0.5Q0.5
0.5Q0.5
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) and Q are the moles of detonation gases per-gram explosive (mol g−1), the average molecular weight of these gases (g mol−1) and heat of detonation (cal g−1), respectively.
and Q are the moles of detonation gases per-gram explosive (mol g−1), the average molecular weight of these gases (g mol−1) and heat of detonation (cal g−1), respectively.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– and –N
CH– and –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bridges are added, whereas the attaching of –CH2– and –O– bridges decreases the HOMO energy levels. Also, it should be noticed that the HOMO energy levels of series E (–CH2–CH2– bridged ones) show no regularity compared with series A. Overall, incorporating different energetic groups and bridges into the rings shows different variation trends of HOMO and LUMO energy levels. It indicates that both the energetic groups and bridges interact with the frontier molecular orbitals.
N– bridges are added, whereas the attaching of –CH2– and –O– bridges decreases the HOMO energy levels. Also, it should be noticed that the HOMO energy levels of series E (–CH2–CH2– bridged ones) show no regularity compared with series A. Overall, incorporating different energetic groups and bridges into the rings shows different variation trends of HOMO and LUMO energy levels. It indicates that both the energetic groups and bridges interact with the frontier molecular orbitals.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– and –N
CH– and –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bridges decreases the ΔELUMO–HOMO evidently. But for the –NH– and –N
N– bridges decreases the ΔELUMO–HOMO evidently. But for the –NH– and –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bridged compounds, there is less effect on ΔELUMO–HOMO compared with those of series A. Besides, the order of the average ΔELUMO–HOMO for each series can be written in the following form: –CH2– ≈ –O– ≈ –CH2–CH2– > directly linked ≈ –NH– ≈ –NH–NH– > –CH
N– bridged compounds, there is less effect on ΔELUMO–HOMO compared with those of series A. Besides, the order of the average ΔELUMO–HOMO for each series can be written in the following form: –CH2– ≈ –O– ≈ –CH2–CH2– > directly linked ≈ –NH– ≈ –NH–NH– > –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– > –N
CH– > –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–. In view of all the designed compounds, compound E5 (6.46 eV) has the highest ΔELUMO–HOMO while compound H7 (3.04 eV) has the smallest ΔELUMO–HOMO. In other words, it is to say that compound H7 was the most reactive under external stimulus while compound E5 showed inertia to these stimuli.
N–. In view of all the designed compounds, compound E5 (6.46 eV) has the highest ΔELUMO–HOMO while compound H7 (3.04 eV) has the smallest ΔELUMO–HOMO. In other words, it is to say that compound H7 was the most reactive under external stimulus while compound E5 showed inertia to these stimuli.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH3
CHCH3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NCH3
NCH3
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–, –NH–NH– and –N
CH–, –NH–NH– and –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bridged ones have a lower ΔHf,solid. The influences of different bridge links on ΔHf,solid can be written in the following order: –NH– > directly linked > –N
N– bridged ones have a lower ΔHf,solid. The influences of different bridge links on ΔHf,solid can be written in the following order: –NH– > directly linked > –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– > –NH–NH– > –CH
N– > –NH–NH– > –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– > –CH2– > –CH2–CH2– > –O–. Obviously, the –NH– bridge is the most effective link in improving the ΔHf,solid for the 2, 2-bi(1,3,4-oxadiazole) derivatives while the –O– bridge link has the opposite effect. The substituted derivatives with the conjugated bridges (–CH
CH– > –CH2– > –CH2–CH2– > –O–. Obviously, the –NH– bridge is the most effective link in improving the ΔHf,solid for the 2, 2-bi(1,3,4-oxadiazole) derivatives while the –O– bridge link has the opposite effect. The substituted derivatives with the conjugated bridges (–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– or –N
CH– or –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–) have higher ΔHf,solid than those of the corresponding ones with the unconjugated bridges (–CH2–CH2– or –NH–NH–). This may be caused by the large conjugated system that is built by 2,2-bi(1,3,4-oxadiazole) and the conjugated bridge. For each of the series, ΔHf,solid increases evidently when the parent molecules are substituted by the –N3 group, whereas the opposite is true for the –NH2 substituent. The influences of the different energetic groups on ΔHf,solid can be written in the following order for series B–H: –N3 > –C(NO2)3 > –CN ≈ –CH(NO2)2 > –NHNH2 > –NHNO2 ≈ –NO2 > –NF2 > –NH2 while that for series A can be presented as follows: –N3 > –NF2 > –CN > –NHNH2 > –C(NO2)3 > –NHNO2 ≈ –NO2 > –CH(NO2)2 > –NH2. Overall, all the results reveal that the effects of the bridged links on the ΔHf,solid values of the designed compounds were coupled to those of the substituted energetic groups.
N–) have higher ΔHf,solid than those of the corresponding ones with the unconjugated bridges (–CH2–CH2– or –NH–NH–). This may be caused by the large conjugated system that is built by 2,2-bi(1,3,4-oxadiazole) and the conjugated bridge. For each of the series, ΔHf,solid increases evidently when the parent molecules are substituted by the –N3 group, whereas the opposite is true for the –NH2 substituent. The influences of the different energetic groups on ΔHf,solid can be written in the following order for series B–H: –N3 > –C(NO2)3 > –CN ≈ –CH(NO2)2 > –NHNH2 > –NHNO2 ≈ –NO2 > –NF2 > –NH2 while that for series A can be presented as follows: –N3 > –NF2 > –CN > –NHNH2 > –C(NO2)3 > –NHNO2 ≈ –NO2 > –CH(NO2)2 > –NH2. Overall, all the results reveal that the effects of the bridged links on the ΔHf,solid values of the designed compounds were coupled to those of the substituted energetic groups.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–, the ρ values of the designed compounds are smaller than those of the directly linked ones (series A) with the same substituents. In addition, compounds with the conjugated bridge –CH
CH–, the ρ values of the designed compounds are smaller than those of the directly linked ones (series A) with the same substituents. In addition, compounds with the conjugated bridge –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– are found to have higher ρ than the corresponding ones with the unconjugated bridge –CH2–CH2–. Oppositely, compounds with the conjugated bridge –N
CH– are found to have higher ρ than the corresponding ones with the unconjugated bridge –CH2–CH2–. Oppositely, compounds with the conjugated bridge –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– show no regularity compared to the corresponding ones with the unconjugated bridge –NH–NH–. Overall, the effects of the bridges on the ρ values are coupled to those of the substituents. Fig. 3(b) shows the influence of different energetic groups on Q. It is clearly seen that different bridge groups have different effects on Q values: the –NH– bridged compounds possess higher Q values than those of the other series with the same substituents, but the –CH2–CH2– bridged ones have the smallest values of Q compared to those of the other series with the same substituents. It can be inferred that the –NH– bridge is the most effective group in improving Q of the 2,2-bi(1,3,4-oxadiazole) derivatives while the –CH2–CH2– bridge will decrease the Q values. For a comparison, all the –NH– bridged compounds have higher Q values than those of RDX and HMX while Q values of the –O–, –CH2–CH2–, –CH
N– show no regularity compared to the corresponding ones with the unconjugated bridge –NH–NH–. Overall, the effects of the bridges on the ρ values are coupled to those of the substituents. Fig. 3(b) shows the influence of different energetic groups on Q. It is clearly seen that different bridge groups have different effects on Q values: the –NH– bridged compounds possess higher Q values than those of the other series with the same substituents, but the –CH2–CH2– bridged ones have the smallest values of Q compared to those of the other series with the same substituents. It can be inferred that the –NH– bridge is the most effective group in improving Q of the 2,2-bi(1,3,4-oxadiazole) derivatives while the –CH2–CH2– bridge will decrease the Q values. For a comparison, all the –NH– bridged compounds have higher Q values than those of RDX and HMX while Q values of the –O–, –CH2–CH2–, –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–, –NH–NH– and –N
CH–, –NH–NH– and –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bridged ones are smaller (except for D8, F9 and H8) than those of HMX. However, the Q values of the directly linked compounds (series A) fluctuated around Q values of RDX and HMX. Additionally, the –NH2 substituted compounds were also found have the smallest values for all the designed compounds except for compound C7. It is predicted that the –NH2 and –NHH2 groups may make less contribution to the values of Q than other energetic groups. In view of Fig. 3(c) and (d), it is seen that the influence of the different energetic groups on the values of D and P is approximately the same throughout all the series. The general influence order of the different energetic groups on the values of D and P can be written as follows: –NF2 > –C(N2)3 > –NO2 ≈ –NHNO2 ≈ –CH(NO2)2 > –N3 ≈ –NHNH2 > –NH2 > –CN, while the influence of the different bridges on the values of D and P can be written in the order of –NH– > directly linked > –O– ≈ –NH–NH– ≈ –N
N– bridged ones are smaller (except for D8, F9 and H8) than those of HMX. However, the Q values of the directly linked compounds (series A) fluctuated around Q values of RDX and HMX. Additionally, the –NH2 substituted compounds were also found have the smallest values for all the designed compounds except for compound C7. It is predicted that the –NH2 and –NHH2 groups may make less contribution to the values of Q than other energetic groups. In view of Fig. 3(c) and (d), it is seen that the influence of the different energetic groups on the values of D and P is approximately the same throughout all the series. The general influence order of the different energetic groups on the values of D and P can be written as follows: –NF2 > –C(N2)3 > –NO2 ≈ –NHNO2 ≈ –CH(NO2)2 > –N3 ≈ –NHNH2 > –NH2 > –CN, while the influence of the different bridges on the values of D and P can be written in the order of –NH– > directly linked > –O– ≈ –NH–NH– ≈ –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– > –CH2– > –CH2–CH2– ≈ –CH
N– > –CH2– > –CH2–CH2– ≈ –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–. It can be concluded that the –NF2 and –NH– bridge are the most effective groups in improving the D and P values while it is on the opposite side for the –CN, –CH2–CH2– and –CH
CH–. It can be concluded that the –NF2 and –NH– bridge are the most effective groups in improving the D and P values while it is on the opposite side for the –CN, –CH2–CH2– and –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– bridged compounds. It is also found that the compounds with the conjugated bridge have similar D and P values compared to the corresponding unconjugated bridged compounds. For example, the –CH2–CH2– bridged compounds have similar D and P values to that of the –CH
CH– bridged compounds. It is also found that the compounds with the conjugated bridge have similar D and P values compared to the corresponding unconjugated bridged compounds. For example, the –CH2–CH2– bridged compounds have similar D and P values to that of the –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– bridged compounds, and the same is true of the –N
CH– bridged compounds, and the same is true of the –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– and –NH–NH– bridged ones. For a comparison, most of the –CN, –NH2 or –NHNH2 substituted compounds have smaller D and P values than that of RDX. It is also worth noting that the –NH2 or –NHNH2 substituted compounds with the –NH– bridge have equal D and P values to those of RDX, and, consequently, the –NH– bridge is the most important influence group in improving D and P values rather than the energetic groups.
N– and –NH–NH– bridged ones. For a comparison, most of the –CN, –NH2 or –NHNH2 substituted compounds have smaller D and P values than that of RDX. It is also worth noting that the –NH2 or –NHNH2 substituted compounds with the –NH– bridge have equal D and P values to those of RDX, and, consequently, the –NH– bridge is the most important influence group in improving D and P values rather than the energetic groups.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N (bridge); (6) NH–NH2 or NH–NO2 or C–NO2. Note that the possible trigger bonds with the weakest BDEs were selected as the breaking bonds based on natural bond orbital (NBO) analyses. Take compound G6 for example, the possible trigger bonds were C(ring)–NHNO2, –C(ring)–N(bridge)–, –N–N–(bridge) and NH–NO2, and the corresponding BDEs of these possible trigger bonds were 453.4, 357.6, 120.7 and 69.9 kJ mol−1, respectively. Finally, the NH–NO2 bond was selected as the trigger bond since it had the smallest value of BDE (69.9 kJ mol−1). The bond order and BDEs of all the designed compounds are summarized and listed in Table 5.
N (bridge); (6) NH–NH2 or NH–NO2 or C–NO2. Note that the possible trigger bonds with the weakest BDEs were selected as the breaking bonds based on natural bond orbital (NBO) analyses. Take compound G6 for example, the possible trigger bonds were C(ring)–NHNO2, –C(ring)–N(bridge)–, –N–N–(bridge) and NH–NO2, and the corresponding BDEs of these possible trigger bonds were 453.4, 357.6, 120.7 and 69.9 kJ mol−1, respectively. Finally, the NH–NO2 bond was selected as the trigger bond since it had the smallest value of BDE (69.9 kJ mol−1). The bond order and BDEs of all the designed compounds are summarized and listed in Table 5.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N (bridge)
N (bridge)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– (series F) makes less change to the values of BDEs compared to the directly linked ones (series A). For example, the BDEs of compounds A1 and F1 are 522.8 and 519.2 kJ mol−1, and the same is true for compounds A3–A6 and F3–F6. The volatilities of BDEs for each series can be written in the following order: directly linked ≈ –CH
CH– (series F) makes less change to the values of BDEs compared to the directly linked ones (series A). For example, the BDEs of compounds A1 and F1 are 522.8 and 519.2 kJ mol−1, and the same is true for compounds A3–A6 and F3–F6. The volatilities of BDEs for each series can be written in the following order: directly linked ≈ –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– > –C– ≈ –N– > –O– > –CH2–CH2– ≈ –N
CH– > –C– ≈ –N– > –O– > –CH2–CH2– ≈ –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– > –NH–NH–. It reveals that the energetic groups acted as the main influence factor on BDEs for the directly linked and –CH
N– > –NH–NH–. It reveals that the energetic groups acted as the main influence factor on BDEs for the directly linked and –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– bridged compounds while the parent structure was the most important influence factor for the –NH–NH– bridged ones. The average BDEs of the –NH–NH– bridged ones were found to be the lowest, and, hence, it can be inferred that the introduction of the –NH–NH– bridge might decrease the thermal stability of the 2,2-bi(1,3,4-oxadiazole) derivatives. Evident regularity was also found in each series: BDEs of the –CN, –N3, –NO2, –NF2, –NH2 substituted ones in series A, B, C, E and F were higher than those of the –NHNO2, –NHNH2, –CH(NO2)2 and –C(NO2)3 substituted ones. In view of the influence of energetic groups, –CN was the most effective group in improving the BDEs of an energetic material while the –NHNH2 group acted on the opposite side.
CH– bridged compounds while the parent structure was the most important influence factor for the –NH–NH– bridged ones. The average BDEs of the –NH–NH– bridged ones were found to be the lowest, and, hence, it can be inferred that the introduction of the –NH–NH– bridge might decrease the thermal stability of the 2,2-bi(1,3,4-oxadiazole) derivatives. Evident regularity was also found in each series: BDEs of the –CN, –N3, –NO2, –NF2, –NH2 substituted ones in series A, B, C, E and F were higher than those of the –NHNO2, –NHNH2, –CH(NO2)2 and –C(NO2)3 substituted ones. In view of the influence of energetic groups, –CN was the most effective group in improving the BDEs of an energetic material while the –NHNH2 group acted on the opposite side.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bridge decreases the values. Most of the designed compounds (except for B5, D4, D5, E4, E5 and F5) possess high positive heats of formation (range from 15.4 to 1148.6 kJ mol−1). The –N3 and –NH– groups act as effective structural units for increasing the solid-phase heats of formation of these derivatives. The calculated detonation properties show that the –NF2 and –NH– groups can improve the heats of detonation, detonation velocities and detonation pressures evidently. The analysis of the bond dissociation energies suggests that most of the designed compounds have acceptable thermal stabilities with the values ranging from 26.3 to 522.8 kJ mol−1. Finally, 22 compounds (A4, A6, A8, A9, B4, B9, C2, C3, C4, C5, C7, C8, C9 D4, D8, D9, E9, F4, F9, G9, H4 and H9) were selected as potential candidates for promising high-energy-density materials.
N– bridge decreases the values. Most of the designed compounds (except for B5, D4, D5, E4, E5 and F5) possess high positive heats of formation (range from 15.4 to 1148.6 kJ mol−1). The –N3 and –NH– groups act as effective structural units for increasing the solid-phase heats of formation of these derivatives. The calculated detonation properties show that the –NF2 and –NH– groups can improve the heats of detonation, detonation velocities and detonation pressures evidently. The analysis of the bond dissociation energies suggests that most of the designed compounds have acceptable thermal stabilities with the values ranging from 26.3 to 522.8 kJ mol−1. Finally, 22 compounds (A4, A6, A8, A9, B4, B9, C2, C3, C4, C5, C7, C8, C9 D4, D8, D9, E9, F4, F9, G9, H4 and H9) were selected as potential candidates for promising high-energy-density materials.







