Open Access Article
Open Access ArticleEnhanced thermal conductance at the graphene–water interface based on functionalized alkane chains
Shuyu Chen†
 ab,
Ming Yang†a,
Bin Liua,
Min Xua,
Teng Zhang*c,
Bilin Zhuangd,
Ding Ding*e,
Xiulan Huaiab and
Hang Zhang
ab,
Ming Yang†a,
Bin Liua,
Min Xua,
Teng Zhang*c,
Bilin Zhuangd,
Ding Ding*e,
Xiulan Huaiab and
Hang Zhang *ab
*ab
aInstitute of Engineering Thermophysics, Chinese Academy of Sciences, Beijing 100190, China. E-mail: zhanghang@iet.cn
bUniversity of Chinese Academy of Sciences, Beijing 100049, China
cMaterials Science, Schrödinger, New York, NY 10035, USA. E-mail: zhteg4@gmail.com
dInstitute of High Performance Computing, A*STAR Research Entities, Singapore 138632
eInstitute of Materials Research and Engineering, A*STAR Research Entities, Singapore 138634. E-mail: ding_ding@imre.a-star.edu.sg
First published on 6th February 2019
Abstract
Highly efficient thermal transport between graphene and water is crucial in applications such as microscopic heat dissipation, solar steam generation, sea-water desalination, and thermally conductive composites. However, a practical approach for enhancing thermal transport across graphene–water interfaces is lacking. We propose an effective and universal method to improve thermal-transport properties at the interface between multilayer graphene and water by a factor of ∼4 by grafting functionalized groups onto graphene. The most improved interfacial thermal conductance was 121.0 ± 11.4 MW m−2 K−1. This design is compatible with industrial processes. We also undertook molecular-level analyses to unveil the underlying mechanism for heat-transport enhancement. This study could provide new approaches for engineering heat transport across two-dimensional materials and water interfaces.
I. Introduction
Graphene,1 as a material with excellent mechanical properties,2 ultrahigh electric and thermal conductivities,3–5 and special optical properties,6 has garnered attention worldwide. Among these features, its excellent thermal properties have great potential for thermal management in fields such as electronics and biochemistry.7–9 If the characteristic dimensions of objects reach nanometer scales, thermal resistances on the interfaces have increasingly important roles and even dominate thermal-transport properties.10–12Some studies have demonstrated that the thermal conductivity of graphene can reach approximately 5000 W m−1 K−1 at room temperature,3,13 but the interfaces between graphene and soft materials demonstrate only mediocre interfacial thermal conductance.14,15 Therefore, attention has focused on improving thermal-transport properties across graphene–soft-material interfaces. Ma et al.16 suggested that charge decoration on graphene can decrease the Kapitza resistance between graphene and water. Alexeev et al.17 found that the number of the layers in few-layer graphene determined the Kapitza resistance between graphene and water by molecular dynamics (MD) simulations. Cao et al.18 found that the interfacial thermal resistance between graphene and water could be reduced with interlayer functionalization by oxygen atoms. Wang et al.19 demonstrated that intercalated water can enhance thermal transport between the cell membrane–graphene interface.
Functionalization on graphene is considered an effective approach to improve thermal transport across interfaces between graphene and soft materials.20,21 Yang et al.22 improved the solar-to-vapor conversion efficiency by functionalizing graphene with hydrophilic groups through experiments. Teng et al.23 improved the thermal conductivity of GNS-filled epoxy composites through non-covalent functionalization to graphene in experiments. Wang et al.24 used MD simulation to study the interfacial thermal resistance in polymer composites reinforced by various covalently functionalized types of graphene. Wang et al.25 investigated thermal transport across graphene–polymer interfaces functionalized with end-grafted polymer chains using MD simulations. Tang et al.26 found thermal transport between graphene and polymers to be enhanced with alkane chains functionalized to graphene via MD simulations. Lin et al.27 found that alkyl-pyrene as a linker candidate could enhance out-of-plane thermal conductance of the graphene–organic compound interface through MD simulations. However, very few studies have utilized functionalized graphene (FG) to achieve highly efficient thermal transport across graphene–water interfaces.
We report a theoretical study on improving the thermal-transport properties of graphene–water interfaces by grafting alkane chains (CnH2n+1) on graphene. To provide a systematic study, a series of FG–water models were built with different alkane chain lengths and surface coverage for tunable interfacial thermal conductance. This work could provide new insights for applications such as self-assembled monolayers,28 nanoscale microchannels,29 microelectronics,30 nanofluids,31 solar thermal steam generation22 and biological cells.19
II. Methods
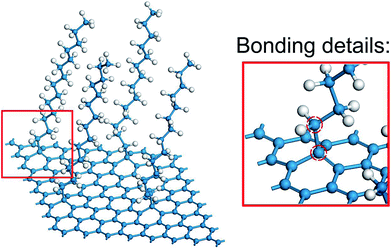
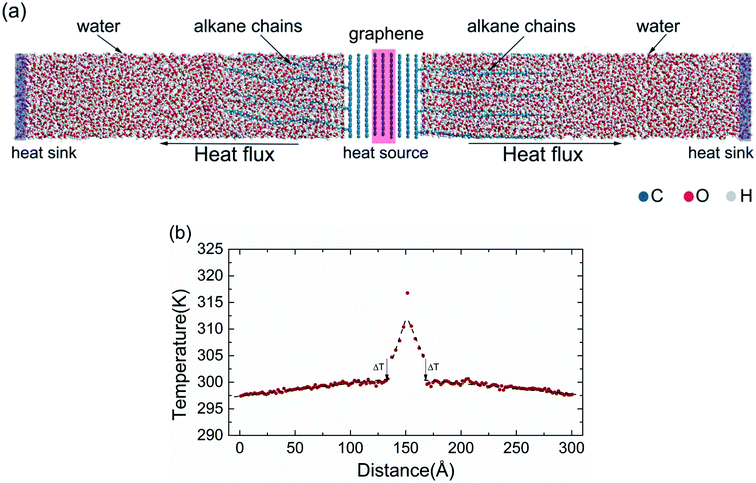
In the view of the practical applications and literature mentioned above,16–18 multilayer graphene (MLG) was constructed and simulated in the present study, and the outermost graphene was functionalized. In the FG models, the alkane chains (CnH2n+1) were grafted in an orderly manner to one side of the graphene surface by sp3-hybridized C–C bonds32 (Fig. 1). Then, the water molecules were fully filled into the remaining spaces of the simulation boxes with density of 1 g cm−3. All the models were designed in a box of 20 Å × 20 Å × 300 Å, with periodic boundary conditions applied in all directions. Thereafter, the structures were relaxed with the isothermal–isobaric (NPT) ensemble, and optimized by the conjugate gradient method.The interfacial thermal conductance was calculated through non-equilibrium molecular dynamics (NEMDs), which are based on the Muller–Plathe approach.33 In NEMDs, heat sink and heat source were applied. The heat flux and temperature field were created by exchanging the momentum between atoms in heat sink and heat source. Periodic boundary conditions were applied in all directions.34 Some details are shown in Fig. 2(a). All NEMD simulation processes were carried out in Forcite.35 DREIDING, a generic force field, was used to describe the interatomic interactions in the system. DREIDING has been used widely to simulate the structures and dynamics of organic and main-group inorganic molecules, and the van der Waals interactions are described by the Lennard-Jones potential.36 DREIDING is suitable for graphene–water systems.
A small time step of 0.5 fs was chosen for all simulations. Prior to the simulations, all models were relaxed using an isothermal–isobaric (NPT) ensemble at 300 K and 1 atm for 1 ns to release residual stresses. To further relax the structures, a constant volume in a canonical (NVT) ensemble at 300 K was used. Then, the systems were simulated using a micro-canonical (NVE) ensemble with two thermostated regions. The momentum exchange between the heat sink and heat source was done every 1000 time steps. After the simulations had reached a steady state, the temperature profiles were averaged over 4 ns to calculate the interfacial thermal conductance between graphene and water.
The interfacial thermal conductance (G) was calculated as
| G = q/ΔT | (1) |
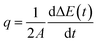 | (2) |
III. Results and discussions
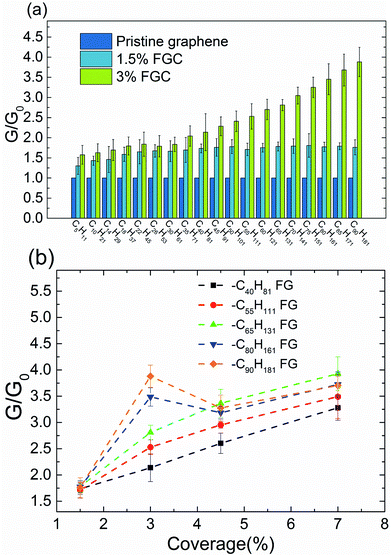
First, we simulated the interfacial thermal conduction between pristine graphene and water. The temperature profile was found to change linearly along the heat-flux direction in bulk water and had a sharp drop at the graphene–water interface (Fig. 2(b)). The interfacial thermal conductance (G) was calculated by heat flux over the temperature drop. Then, the interfacial thermal conductance of FG with different alkane chains (–CnH2n+1) was calculated. To have a direct insight of the effect of functionalization of the graphene surface on the interface, the relative interfacial thermal conductance G/G0 (where G0 is the interfacial thermal conductance between pristine graphene and water) was carried out to describe the enhancement. Here, the G0 between five-layer graphene and water was calculated to be 30.8 ± 2.2 MW m−2 K−1, which is in accordance with the reported thermal resistance of graphene–water: ∼4.0 × 10−8 K m2 W−1 (∼25.0 MW m−2 K−1) from Alexeev et al.,17 ∼3.2 × 10−8 K m2 W−1 (∼31.2 MW m−2 K−1) from Ma et al.16 and ∼2.9 × 10−8 K m2 W−1 (∼34.5 MW m−2 K−1) from Cao et al.18 The functional group coverage (FGC) was defined as the ratio of the number of alkane chains to the carbon atoms of the outermost layer of graphene.The interfacial thermal conductance was found to be improved significantly by surface functionalization. The best improved interfacial thermal conductance reached 121.0 ± 11.4 MW m−2 K−1 at –C65H131 FG in 7% FGC. The interfacial thermal conductance increased by a factor of 1.3–1.8 under a FGC of 1.5%. At 3% FGC, the improvement could be as much as fourfold. At 3% FGC, the interfacial thermal conductance was found to increase as the alkane chains became longer. Such a trend was found at 1.5% FGC for some short chains, but the increasing trend was not obvious if the increase was more than –C18H37. To carry out a systematic investigation, FGs were simulated further with various chain lengths (–C40H81, –C55H111, –C65H131, –C80H161 and –C90H181) and different FGCs (1.5%, 3%, 4.5% and 7%). In general, the relative interfacial thermal conductance increased with coverage (Fig. 3(b)), and showed a clear trend with respect to the alkane length at 3% FGC. However, the relative interfacial thermal conductance did not increase if the coverage was >3% in –C80H161 FG and –C90H181 FG.
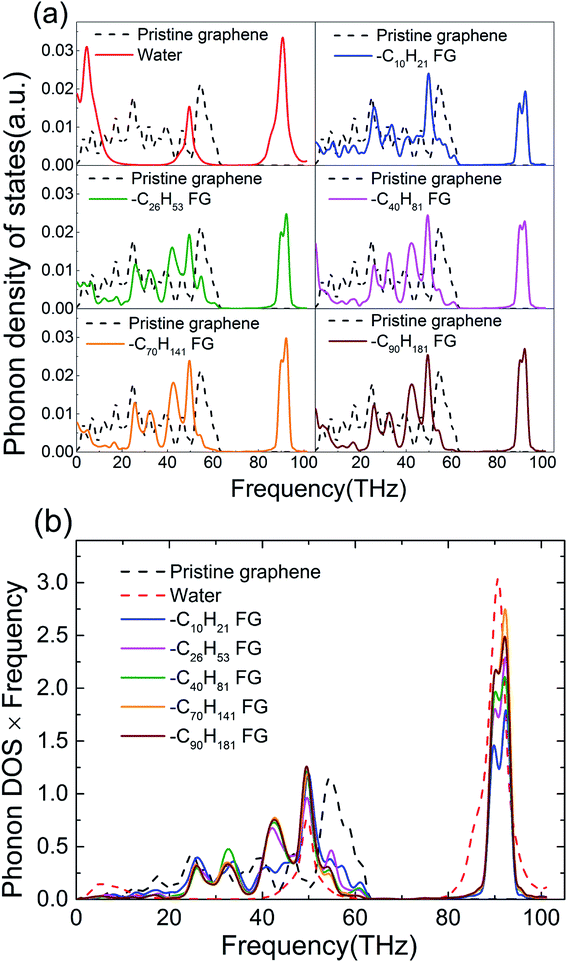
To reveal the underlying mechanism behind enhancement of the thermal conductance of the graphene–water interface, we investigated the atomic and corresponding phononic information of the system. Hydrogen atoms in the alkane chains had an important role in this enhancement because they provide extra energy-transfer paths between carbon atoms in graphene and the atoms in water. Studies have shown that hydrogen bonds can improve the efficiency of interfacial thermal transport significantly if stronger hydrogen bonds “pull” the organic molecules closer to the interface and establish better contact.14 Greater similarity in phonon vibration properties has been reported to facilitate interfacial heat exchange.11,37–43 Furthermore, the spectral information of phonons was calculated (Fig. 4). The phonon density of states (PDOS) were calculated by taking the fast Fourier transform of atomistic velocity autocorrelation functions (VAFs).27,44 Specifically, the density of states, ω, was given by
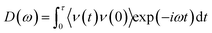 | (3) |
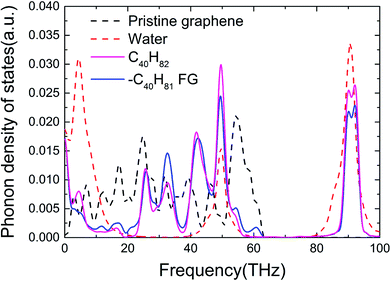
Fig. 4 shows the PDOS spectra of pristine graphene, water, a typical FG and its functional groups. It can be clearly observed that the functionalized alkane dramatically altered the graphene phonon vibration modes of graphene. Water molecules are rich in H–O bonds with a vibration frequency as high as ∼3000 cm−1 (∼90 THz),45 which is in accordance with the peaks at 90 THz in Fig. 4. Graphene is formed by in-plane carbon atoms combined by sp2-hybridized C–C bonds, which cannot provide ultra-high vibration frequencies. Functionalization of alkane chains is based on methyl and methylene groups, in which the sp3-hybridized C–C bonds and C–H bonds also exhibit high vibration frequencies at ∼3000 cm−1.45 Thus, we can infer that the two high-frequency peaks from FG corresponded mainly to C–H bonds in the functional groups (Fig. 4). In addition, the alkane-functionalization itself had vibration modes with frequency <5 THz, and distortion of the graphene plane due to functionalization also impacts low frequency phonons. These low-frequency phonons due to functionalization provided better overlap with those in amorphous water. In addition, a larger overlap area ∼50 THz and ∼90 THz between the PDOS spectra of water and FG due to the similar sp3-hybridized carbon served as another factor for enhancement of thermal conductance.
PDOSs and PDOSs multiplied by the vibration frequency were calculated for graphene functionalized with alkanes of various chain lengths to examine further the vibration overlap between water and FGs (Fig. 5). The energy distribution can be described by the product of phonon DOSs and frequency (Fig. 5(b)), so a large fraction of energy was carried by high-frequency heat carriers in FG. Though heat carriers of high frequency do not contribute as much to in-plane thermal transport as diffusion,37,39,46 they are important in thermal transport across interfaces.11 As demonstrated by the significant enhancements in interfacial thermal conductance between FG and water, heat carriers of high frequencies in FG served as critical energy carriers beyond the low-frequency propagon.
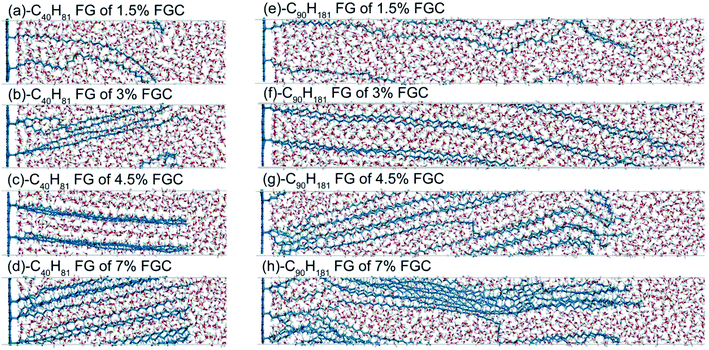
Because longer alkane chains and higher coverage provide more high-frequency heat carriers that could enhance interfacial thermal transport between water and graphene, the interfacial thermal conductance increases monotonically with chain length and coverage in general. This phenomenon is consistent with our results showing that the interfacial thermal conductance changed with chain length at 3% FGC. However, the growth of the alkane chains did not lead to further improvement at coverage of 1.5%, 4.5%, and 7% (Fig. 3). At low coverage (1.5%), thermal transport across the interface was dominated by water molecules interacting directly with carbon atoms in the graphene layer. The improvement in thermal conductance due to alkane functionalization was not significant. As a result, the effect of chain length was buried by noise (standard deviation). At a coverage of 3%, the interfacial thermal conductance increased with chain length due to additional energy paths between alkane chains and water, as expected. If the coverage is >3%, the interfacial thermal conductance did not increase with increasing chain length. We inferred that the increase of coverage at long alkane chains could lead to cluttered (or even entangled) chains and, thus, could not further improve the interfacial thermal conductance. As shown in Fig. 6, the alkane chains became straighter in general as the coverage increased for –C40H81 FGs, and this change corresponded to the conductance trend shown in Fig. 3(b). However, the morphology of the –C90H181 FGs alkane did not change monotonically with coverage. Though chains continued to become more extended from 1.5% FGC to 3% FGC, the spatial span decreased due to bending and knots as the converge increased from 3% to 7% FGC. The –C90H181 alkane chains were also more aggregated compared with –C40H81 FGs, thereby hampering the entry of water molecules. These effects hindered thermal transport to a large extent, and explained the sudden decrease of G/G0s from 3% to 4.5% FGC (Fig. 3(b)).
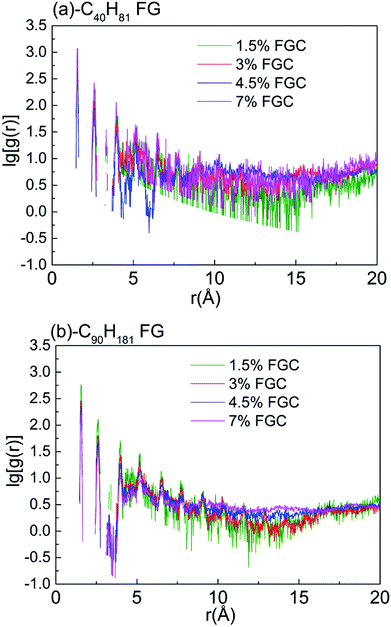
Thermal transport in polymers is affected strongly by chain morphology.47 To describe the structural changes, the radial distribution function (RDF)46,48–50 of carbon atoms in alkane chains was calculated to characterize the chain order. Sharper peaks in RDF calculations indicate a higher structure order. Fig. 7 shows that the RDF of carbon atoms of –C90H18 chains without bending and knots, and serves as a reference. As shown in Fig. 8, RDFs of –C90H181 FGs in 4.5% and 7% FGC had broader and smoother peaks compared with those of 1.5% FGC, indicating that the alkane chains become more chaotic when coverage increased. Compared with the RDFs of –C40H81 FGs, the overall peaks of –C90H181 FGs were gentler, indicating a higher level of disorder and lower thermal transport.
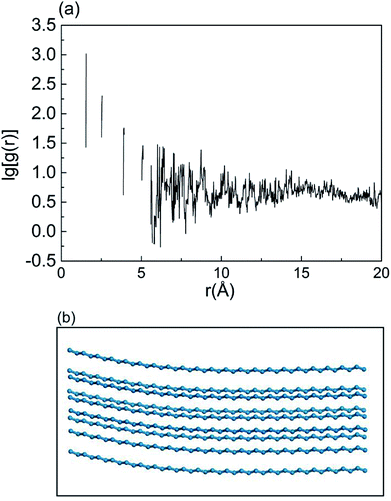 | ||
| Fig. 7 (a) A typical radial distribution function (RDF) and (b) schematic diagram of C-atom structure in undeformed –C90H181 chains of 7% FGC. | ||
IV. Conclusions
The interfacial thermal conductance between multilayer graphene and water was investigated via NEMD simulations. The alkane chains in FG could improve thermal transport across the graphene–water interface greatly. The most improved interfacial thermal conductance was up to 121.0 ± 11.4 MW m−2 K−1. The length and coverage of alkane chains were the major factors contributing to enhancements in interfacial thermal conductance. With analysis on phonon scattering and diffusion effect, we attributed the improvement to the addition of hydrogen, which facilitated phonon transport between graphene and water. The interfacial conductance increases with alkane coverage in general, and it also increases with the alkane chain length when the functionalized group coverage is about 3%. We provided a general method to promote the interfacial thermal conductance of graphene–water interfaces by “tuning” the morphology of graphene and alkane chains. By revealing the fundamental mechanism at the molecular level, our findings provide guidance for development of high-performance graphene–water interfacial thermal transport.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We thank Professor Ruining Wang for the kind help with computations. This work was supported by National Key Research and Development Program (2017YFB0601803), National Natural Science Foundation of China (51606192, 51606190), Natural Science Foundation of Hebei Province (A2017201219), and CAS Pioneer Hundred Talents Program. Calculations were supported by the National Supercomputer Center in Guangzhou and the Institute of Engineering Thermophysics, CAS.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Nano Lett., 2008, 8, 902 CrossRef CAS PubMed.
- Z. Lin, Y. Liu, Y. Yao, O. J. Hildreth, Z. Li, K. Moon and C. Wong, J. Phys. Chem. C, 2011, 115, 7120–7125 CrossRef CAS.
- A. A. Balandin, Nat. Mater., 2011, 10, 569 CrossRef CAS PubMed.
- R. Mas-Ballesté, C. Gómez-Navarro, J. Gómez-Herrero and F. Zamora, Nanoscale, 2011, 3, 20–30 RSC.
- J. Y. Kim and J. C. Grossman, Nano Lett., 2015, 15, 2830–2835 CrossRef CAS PubMed.
- N. Xiao, X. Dong, L. Song, D. Liu, Y. Tay, S. Wu, L. J. Li, Y. Zhao, T. Yu and H. Zhang, ACS Nano, 2011, 5, 2749–2755 CrossRef CAS PubMed.
- X. An, T. Simmons, R. Shah, C. Wolfe, K. M. Lewis, M. Washington, S. K. Nayak, S. Talapatra and S. Kar, Nano Lett., 2010, 10, 4295–4301 CrossRef CAS PubMed.
- D. G. Cahill, W. K. Ford, K. E. Goodson, G. D. Mahan, A. Majumdar, H. J. Maris, R. Merlin and S. R. Phillpot, J. Appl. Phys., 2003, 93, 793–818 CrossRef CAS.
- D. G. Cahill, P. V. Braun, G. Chen, D. R. Clarke, S. Fan, K. E. Goodson, P. Keblinski, W. P. King, G. D. Mahan and A. Majumdar, Appl. Phys. Rev., 2014, 1, 251–265 Search PubMed.
- Z. Y. Ong and E. Pop, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 9226–9231 Search PubMed.
- S. Ghosh, I. Calizo, D. Teweldebrhan and E. P. Pokatilov, Appl. Phys. Lett., 2008, 92, 151911–151913 CrossRef.
- T. Zhang, A. R. Gans-Forrest, E. Lee, X. Q. Zhang, C. Qu, Y. S. Pang, F. Sun and T. F. Luo, ACS Appl. Mater. Interfaces, 2016, 8, 33326–33334 CrossRef CAS PubMed.
- X. F. Wei, T. Zhang and T. F. Luo, ACS Energy Lett., 2017, 2, 2283–2292 CrossRef CAS.
- Y. Ma, Z. Zhang, J. Chen, K. Sääskilahti, S. Volz and C. Jie, Carbon, 2018, 135, 263–269 CrossRef CAS.
- D. Alexeev, J. Chen, J. H. Walther, K. P. Giapis, P. Angelikopoulos and P. Koumoutsakos, Nano Lett., 2015, 15, 5744–5749 CrossRef CAS PubMed.
- B. Y. Cao, J. H. Zou, G. J. Hu and G. X. Cao, Appl. Phys. Lett., 2018, 112, 041603 CrossRef.
- Y. Wang, Z. Qin, M. J. Buehler and Z. P. Xu, Nat. Commun., 2016, 7, 12854 CrossRef CAS PubMed.
- D. Cai and M. Song, J. Mater. Chem., 2010, 20, 7906–7915 RSC.
- H. Han, Y. Zhang, N. Wang, S. M. Kabiri, Y. Ni, Z. Y. Mijbil, E. Michael, S. Xiong, S. Kimmo and M. Murali, Nat. Commun., 2016, 7, 11281 CrossRef CAS PubMed.
- J. Yang, Y. Pang, W. Huang, S. K. Shaw, J. Schiffbauer, M. A. Pillers, X. Mu, S. Luo, T. Zhang and Y. Huang, ACS Nano, 2017, 11, 5510 CrossRef CAS PubMed.
- C. Teng, C. M. Ma, K. Chiou and T. Lee, presented in part at the 2010 5th International Microsystems Packaging Assembly and Circuits Technology Conference, 20–22 Oct. 2010, 2010 Search PubMed.
- Y. Wang, H. F. Zhan, Y. Xiang, C. Yang, C. M. Wang and Y. Y. Zhang, J. Phys. Chem. C, 2015, 119, 12731–12738 CrossRef CAS.
- M. Wang, N. Hu, L. Zhou and C. Yan, Carbon, 2015, 85, 414–421 CrossRef CAS.
- H. Tang, H. Ye, X. Chen, X. Fan and G. Zhang, presented in part at the 2017 18th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), 3–5 April 2017, 2017 Search PubMed.
- S. Lin and M. J. Buehler, Nanotechnology, 2013, 24, 165702 CrossRef PubMed.
- X. Wei, Z. Teng and T. Luo, ACS Appl. Mater. Interfaces, 2017, 9, 33740–33748 CrossRef CAS PubMed.
- B. Radha, A. Esfandiar, F. C. Wang, A. P. Rooney, K. Gopinadhan, A. Keerthi, A. Mishchenko, A. Janardanan, P. Blake and L. Fumagalli, Nature, 2016, 538, 222–225 CrossRef CAS PubMed.
- H. Han, S. Merabia and F. Müllerplathe, J. Phys. Chem. Lett., 2017, 8, 1946–1951 CrossRef CAS PubMed.
- E. Sadeghinezhad, M. Mehrali, R. Saidur, M. Mehrali, S. T. Latibari, A. R. Akhiani and H. S. C. Metselaar, Energy Convers. Manage., 2016, 111, 466–487 CrossRef CAS.
- P. A. Denis and F. Iribarne, Chem.–Eur. J., 2012, 18, 7568–7574 CrossRef CAS PubMed.
- F. Müllerplathe, J. Chem. Phys., 1997, 106, 6082–6085 CrossRef.
- P. C. Howell, J. Comput. Theor. Nanosci., 2011, 8, 2129–2143 CrossRef CAS.
- W. H. Press, B. P. Flannery, S. A. Teukolsky and W. T. Vetterling, Numerical recipes: the art of scientific computing, Cambridge University Press, Cambridge, 1986 Search PubMed.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- P. B. Allen, J. L. Feldman, J. Fabian and F. Wooten, Philos. Mag. B, 1999, 79, 1715–1731 CrossRef CAS.
- E. T. Swartz and R. O. Pohl, Rev. Mod. Phys., 1989, 61, 605–668 CrossRef.
- J. Moon, B. Latour and A. J. Minnich, Phys. Rev. B, 2018, 97, 024201 CrossRef CAS.
- Q. Liang, X. Yao, W. Wang, Y. Liu and C. P. Wong, ACS Nano, 2011, 5, 2392–2401 CrossRef CAS PubMed.
- Y. Zhou, Z. Fan, G. Qin, J. Y. Yang, T. Ouyang and M. Hu, ACS Omega, 2017, 3, 3278–3284 CrossRef.
- M. D. Losego, M. E. Grady, N. R. Sottos, D. G. Cahill and P. V. Braun, Nat. Mater., 2012, 11, 502–506 CrossRef CAS PubMed.
- P. E. Hopkins, M. Baraket, E. V. Barnat, T. E. Beechem, S. P. Kearney, J. C. Duda, J. T. Robinson and S. G. Walton, Nano Lett., 2012, 12, 590–595 CrossRef CAS PubMed.
- J. M. Dickey and A. Paskin, Phys. Rev., 1969, 188, 1407–1418 CrossRef CAS.
- M. R. Lee and D. Ben-Amotz, J. Chem. Phys., 1993, 99, 10074–10077 CrossRef CAS.
- J. M. Larkin and A. J. H. Mcgaughey, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 9, 620–637 Search PubMed.
- X. Wei, T. Zhang and T. Luo, Phys. Chem. Chem. Phys., 2016, 18, 32146 RSC.
- T. Zhang and T. Luo, J. Appl. Phys., 2012, 112, 1571 Search PubMed.
- E. Lorch, J. Phys. C: Solid State Phys., 2002, 2, 229 CrossRef.
- K. Laaziri, S. Kycia, S. Roorda, M. Chicoine, J. L. Robertson, J. Wang and S. C. Moss, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 13520–13533 CrossRef CAS.
Footnote |
| † Shuyu Chen and Ming Yang contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |