Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Highly diastereoselective construction of novel dispiropyrrolo[2,1-a]isoquinoline derivatives via multicomponent 1,3-dipolar cycloaddition of cyclic diketones-based tetrahydroisoquinolinium N-ylides†
Sarra Boudriga *a,
Saoussen Haddada,
Moheddine Askri
*a,
Saoussen Haddada,
Moheddine Askri *a,
Armand Solderab,
Michael Knorr
*a,
Armand Solderab,
Michael Knorr c,
Carsten Strohmannd and
Christopher Golzd
c,
Carsten Strohmannd and
Christopher Golzd
aLaboratory of Heterocyclic Chemistry Natural Product and Reactivity/CHPNR, Department of Chemistry, Faculty of Science of Monastir, 5000 Monastir, Tunisia. E-mail: sarra_boudriga@yahoo.fr
bDepartement of Chemistry, Quebec Center for Functional Materials University of Sherbrooke, Sherbrooke, Quebec, Canada J1K 2R1
cInstitut UTINAM - UMR CNRS 6213, Université Bourgogne Franche-Comté, 16 Route de Gray, 25030 Besançon, France
dTechnische Universität Dortmund, Anorganische Chemie, Otto-Hahn-Strasse 6, 44221 Dortmund, Germany
First published on 9th April 2019
Abstract
In the quest for new heterocyclic scaffolds exhibiting potentially biological activities for medicinal chemistry, a multicomponent 1,3-dipolar cycloaddition reaction of tetrahydroisoquinolinium N-ylides, generated in situ from cyclic diketones and isoquinoline, and (E)-3-arylidene-1-phenyl-pyrrolidine-2,5-diones has been developed. This route provides workable access to dispiropyrrolo[2,1-a]isoquinoline-fused pyrrolidine-2,5-diones bearing two adjacent spiro-carbons. An unprecedented regioselectivity was observed in this 1,3-dipolar cycloaddition, leading to the construction of a novel dispirooxindole skeleton. The structure and relative stereochemistry of the spiranic adducts have been confirmed by three X-ray diffraction studies. To reinforce the observed regio- and stereoselectivity of the [3+2] cycloaddition, calculations using the DFT approach at the B3LYP/6-31G(d,p) level were carried out. It was found that this reaction affords the kinetic products.
Introduction
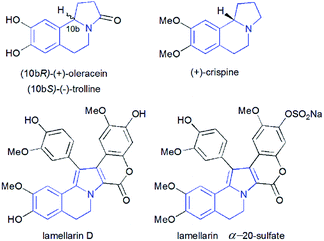
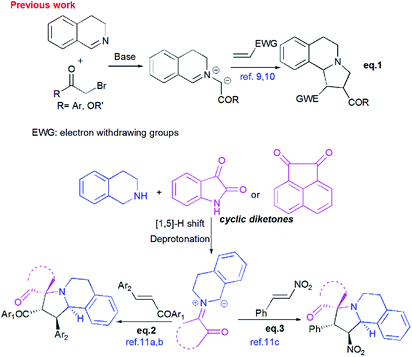
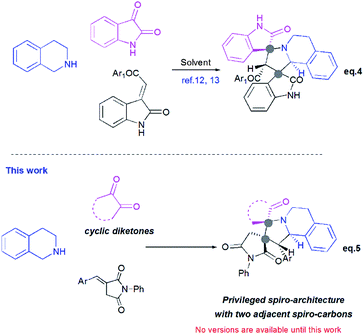
Pyrrolo[2,1-a]isoquinolines as structural motifs have drawn considerable interest in the area of synthetic organic chemistry and medicinal chemistry as they represent substructures often encountered in numerous bioactive natural isolates and pharmaceutically important compounds.1 Some illustrative examples are depicted in Fig. 1 including (+)-oleracein,1b (−)-trolline,1c (+)-crispine1d and lamellarin alkaloids such as lamellarin D and lamellarin α-20-sulfate.1f Most of the pyrrolo[2,1-a]isoquinoline alkaloids display remarkable antitumor,2 antibacterial and antiviral,3 anti-inflammatory,4 antidepressant5 and cardiovascular6 properties. Furthermore, lamellarin D, isolated from marine molluscs, has been reported to be an inhibitor of human topoisomerase,7 whereas lamellarin α-20-sulfate inhibits the enzyme HIV integrase.1e,8 Owing to the intriguing synthetic value and multiple biological activities of these heterocyclic systems, development of efficient and versatile synthetic methods allowing the construction of such scaffolds was strongly encouraged.In the past decade, 1,3-dipolar cycloaddition reactions of isoquinolinium N-ylides with activated alkynes or olefins9 have arguably emerged as a fascinating and powerful tool for the synthesis of pyrrolo[2,1-a]isoquinoline derivatives. However, a survey of the literature reveals that the reported 1,3-dipoles were generated in situ by basic deprotonation of their corresponding isoquinolinium bromides (Scheme 1, eqn (1)).9,10 These latter were prepared mainly by the condensation of isoquinoline with substituted phenacyl bromide or alkylbromoacetates.
However, tetrahydroisoquinolinium N-ylide stemming from cyclic diketones have rarely been considered as azomethine ylide precursors.
So far, Sarrafi et al.11 developed the first examples of multicomponent 1,3-dipolar cycloaddition reaction involving acenaphthenequinone and isatin as cyclic diketones-based tetrahydroisoquinolinium N-ylides with chalcone and nitrostyrene derivatives as dipolarophiles (Scheme 1, eqn 2 and 3).11 The azomethine ylides were produced in situ via [1,5]-H shift and subsequent deprotonation.
Recently, Huang12 and Kumar13 successfully developed a [3+2]-cycloaddition reaction of 2-oxoindolin-3-ylidene derivatives with azomethine ylides derived from isatin and 1,2,3,4-tetrahydroisoquinoline, and only one single regioisomer, namely dispiroindoline-3,1′-pyrrolo[2,1-a]isoquinoline-3′,3′-indoline-2,2′′-dione was obtained. Generally, it has been found that dispiropyrrolo[2,1-a]isoquinoline derivatives were selectively formed in this kind of 1,3-dipolar cycloadditions. However, the alternative regioisomer incorporating two adjacent spiro-carbons, has never been reported (Scheme 2, eqn (4)).12–14 In spite of this initial work, the systematic investigation on 1,3-dipolar cycloaddition involving exocyclic enones and tetrahydroisoquinolinium N-ylides derived from cyclic diketones is still rather limited and represents certainly interesting opportunities for further development.
 | ||
| Scheme 2 Profile of 1,3-dipolar cycloaddition for exocyclic enones with tetrahydroisoquinolinium N-ylides derived from cyclic diketones. | ||
New advances in this area could afford a convenient approach to structurally novel pyrrolo[2,1-a]isoquinoline derivatives bearing multiple neighboured stereogenic centres, which may provide some benefits to medicinal chemistry and drug discovery. Considering this challenge, we wondered whether α-alkylidenesuccinimides could be employed as exocyclic enones to undergo [3+2] cycloaddition using tetrahydroisoquinolinium N-ylides derived from cyclic diketones, thus yielding dispiropyrrolo[2,1-a]isoquinoline derivatives.
On the other hand, our targeted formal 1,3-dipolar cycloaddition products contain pyrrolidinone-2,5-dione scaffolds. These latter have the important advantage of being present in a great variety of natural products as well as in a vast library of synthetic compounds endowed with several bioactivities.15 Recently, we reported the synthesis of functionalized spirooxindolepyrrolidines and dispiropyrrolothiazoles containing the pyrrolidine-2,5-dione motif which exhibits antibacterial, antifungal, antimalarial, and antimycobacterial activities.16
Herein, and in continuation of our research in the area of [3+2] cycloaddition of azomethine ylides,16,17 we describe for the first time the formation of the hitherto unknown regioisomer, with two adjacent spiro-carbons, by 1,3-dipolar cycloaddition reactions of cyclic diketones-based tetrahydroisoquinolinium N-ylides and α-alkylidenesuccinimides. This route provides an attractive access to novel dispiropyrrolo[2,1-a]isoquinolines with a broad substrate scope in good to high yields. The stereochemistry of the spiroadducts has been confirmed by three X-ray diffraction studies. Moreover, to better rationalize mechanistically this kind of reaction, the regio- and stereochemistry of dispiropyrrolo[2,1-a]isoquinoline was investigated by means of Density Functional Theory (DFT) calculations.
Results and discussion
Three-component synthesis of the spiropyrrolo[2,1-a]isoquinolines
At the onset of our work, (E)-3-benzylidene-1-phenylpyrrolidine-2,5-dione 1a, isatin 2a and 1,2,3,4-tetrahydroisoquinoline (THIQ) 3 were employed as substrate models to optimize the reaction conditions (Scheme 3, Table 1). The reaction was investigated with different solvents of different polarities such as methanol, ethanol, acetonitrile and toluene.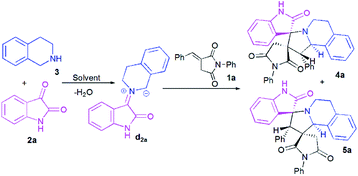 | ||
| Scheme 3 Reaction of (E)-3-benzylidene-1-phenylpyrrolidine-2,5-dione 1a with isatin 2a and 1,2,3,4-tetrahydroisoquinoline (THIQ) 3. | ||
| Entry | Solvent | T (°C) | Time (h) | rrc (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5) 5) |
Yieldd (%) |
|---|---|---|---|---|---|
a The reaction was carried out in 0.2 mmol scale in solvent (2 mL), and the ratio of 1a/2a/3 is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2.b No reaction due to insufficient solubility.c The regioisomeric ratio (rr) was determined by 1H NMR spectra of the crude reaction mixture.d Combined yield of isolated 4a and 5a. 1.2.b No reaction due to insufficient solubility.c The regioisomeric ratio (rr) was determined by 1H NMR spectra of the crude reaction mixture.d Combined yield of isolated 4a and 5a. |
|||||
| 1 | PhCH3 | 25 | 24 | — | NRb |
| 2 | MeOH | 25 | 24 | — | NRb |
| 3 | EtOH | 25 | 24 | — | NRb |
| 4 | CH3CN | 25 | 24 | — | NRb |
| 5 | PhCH3 | Reflux | 12 | — | Trace |
| 6 | CH3CN | Reflux | 6 | 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48 48 |
55 |
| 7 | EtOH | Reflux | 4 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
65 |
| 8 | MeOH | Reflux | 4 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
85 |
As shown in Table 1, the reaction does not proceed at room temperature (Table 1, entries 1–4) and does not occur in refluxing toluene (Table 1, entry 5). Surprisingly, in acetonitrile, the reaction proceeds smoothly affording the corresponding spiropyrrolo[2,1-a]isoquinolines as a mixture of two regioisomers 4a and 5a in a 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 ratio, albeit with a moderate yield (Table 1, entry 6). As can be seen from Table 1, the best results were obtained by refluxing the reaction mixture in methanol for 4 h, providing isomeric dispiropyrrolo[2,1-a]isoquinolineoxindoles 4a and 5a in high yield (85%), along with high diastereoselectivities (Table 1, entry 8).
40 ratio, albeit with a moderate yield (Table 1, entry 6). As can be seen from Table 1, the best results were obtained by refluxing the reaction mixture in methanol for 4 h, providing isomeric dispiropyrrolo[2,1-a]isoquinolineoxindoles 4a and 5a in high yield (85%), along with high diastereoselectivities (Table 1, entry 8).
Once the optimal conditions being established (Table 1, entry 8), we tried to extend the scope of this reaction with different p-aryl substituted dipolarophiles 1, as well as with various diketones 2a–d (Scheme 4, Table 2). The electronic properties exerted by the substituent at the p-position of the aryl group of imides 1 were shown to have little influence on the efficiency of this reaction (Table 2). For example, enones 1 bearing an electron-neutral (H), or electron-donating (e.g., 4-Me or 4-OMe) group or electron-withdrawing substituent (Cl) or group (2-pyridinyl) reacted smoothly to give isomeric spiropyrrolo[2,1-a]isoquinolineoxindoles products in excellent yields (Table 2, entries 1–5).
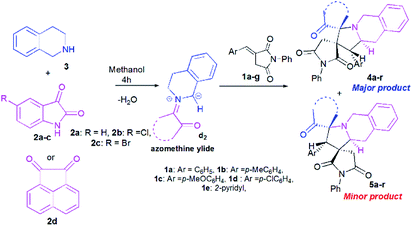 | ||
| Scheme 4 Reaction of (E)-3-arylidene-1-phenylpyrrolidine-2,5-dione 1a–g with cyclic diketones 2 and 1,2,3,4-tetrahydroisoquinoline (THIQ) 3. | ||
| Entry | Comp. | Diketone | Ar | rrb (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5) 5) |
Yieldd (%) |
|---|---|---|---|---|---|
a The reaction was carried out in 1 mmol scale in methanol (5 mL) at reflux for 4 h, and the ratio of 1/2/3 is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2.b Unless otherwise noted, the regioisomeric ratio (rr) was determined by the isolated yields of 4 and 5.c Determined by 1H NMR analysis of the crude product.d Combined yields of isolated 4 and 5.e Failed to separate compound 5.f Failed to separate compound 4. 1.2.b Unless otherwise noted, the regioisomeric ratio (rr) was determined by the isolated yields of 4 and 5.c Determined by 1H NMR analysis of the crude product.d Combined yields of isolated 4 and 5.e Failed to separate compound 5.f Failed to separate compound 4. |
|||||
| 1 | 4a + 5a | 2a | C6H5 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40c 40c |
85 |
| 2 | 4b + 5b | 2a | p-MeC6H4 | 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 35 |
88 |
| 3 | 4c + 5c | 2a | p-MeOC6H4 | 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32c 32c |
87 |
| 4 | 4d + 5d | 2a | p-ClC6H4 | 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32c 32c |
80 |
| 5 | 4e + 5e | 2a | 2-Pyridyl | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
82e |
| 6 | 4f + 5f | 2b | C6H5 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
85 |
| 7 | 4g + 5g | 2b | p-MeC6H4 | 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 17 |
83 |
| 8 | 4h + 5h | 2b | p-MeOC6H4 | >90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
87e |
| 9 | 4i + 5i | 2b | 2-Pyridyl | >90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
85e |
| 10 | 4j + 5j | 2c | C6H5 | >90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
80e |
| 11 | 4k + 5k | 2c | p-MeC6H4 | 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 15 |
88 |
| 12 | 4l + 5l | 2c | p-MeOC6H4 | 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 14 |
85 |
| 13 | 4m + 5m | 2c | 2-Pyridyl | >90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
83e |
| 14 | 4n + 5n | 2d | C6H5 | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 23 |
72 |
| 15 | 4o + 5o | 2d | p-MeC6H4 | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22c 22c |
75f |
| 16 | 4p + 5p | 2d | p-MeOC6H4 | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 22 |
67 |
| 17 | 4q + 5q | 2d | p-ClC6H4 | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
63 |
| 18 | 4r + 5r | 2d | 2-Pyridyl | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20c 20c |
65f |
However, the regioselectivity of these reactions was quite poor. Moreover, it seems that the electronic effects induced by (i) halogen substituents (Cl and Br) on the phenyl ring of isatin (Table 2, entries 6–13) or (ii) acenaphthenequinone 2d, as cyclic diketone (Table 2, entries 14–18), were beneficial for increasing the regioselectivities. All compounds were isolated as colourless solids.
Spectroscopic and crystallographic characterization of the isomeric cycloadducts
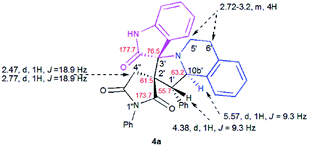
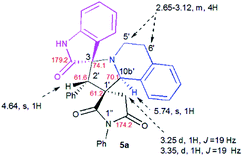
The structure and the relative configuration of the isomeric pyrrolo[2,1-a]isoquinolines resulting from the cycloaddition were deduced from NMR in solution and, in the solid state from X-ray structure determinations performed on cycloadducts 4a, 5a and 5r.Relevant 1H and 13C chemical shifts of pyrrolo[2,1-a]isoquinolines 4a and 5a are shown in Fig. 2 and 3, respectively. The 1H NMR spectrum of 4a shows two mutually coupled doublets at δ 2.47 and 2.77 ppm (J = 18.9 Hz) corresponding to the diastereotopic 4′-CH2, as well as two further doublets at δ 4.38 (J = 9.3 Hz) and 5.57 ppm (J = 9.3 Hz) assigned to the pyrrolidine H-1′ and H-10b′ protons (Fig. 2), respectively.
Their coupling constants of approximately 9 Hz indicate that these protons are trans-arranged. The occurrence and the multiplicity of these signals clearly prove the regiochemistry of the cycloaddition reaction. In contrast, in the 1H NMR spectrum of regioisomer 5a (Fig. 3), the pyrrolidinyl protons H-2′ and H-10b′ appear as two singlets resonating at δ 4.64 and 5.74 ppm, respectively. The 13C NMR spectra of all synthesized spirooxindoles exhibit two peaks atδ 74.1–76.5 and 177.7–179.2 ppm for the spiro-carbon and the oxindole carbonyl group, respectively.
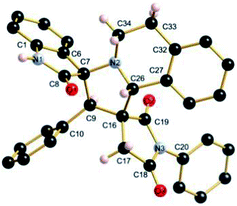
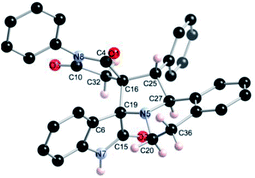
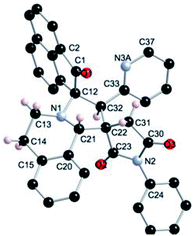
The regio- and the stereochemical outcome of the cycloadditions were unambiguously ascertained by X-ray analysis of the crystal structure of cycloadducts 4a, 5a and 5r, whose molecular structures are depicted in Fig. 4, 5 and 6, respectively. The crystal data collection and refinement data are summarized in Table 3.
| Compound/formula | 4a/C34H27N3O3 | 5a/C34H27N3O3 | 5r/C37H27N3O3 |
|---|---|---|---|
| Formula weight | 525.58 | 525.58 | 561.61 |
| Temperature/K | 150(2) | 150(2) | 150(2) |
| Wavelength/Å | 0.71073 | 0.71073 | 0.71069 |
| Crystal system | Triclinic | Orthorhombic | Monoclinic |
| Space group | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P212121 | P21/c |
| a/Å | 7.8139(9) | 9.5047(6) | 11.7916(5) |
| b/Å | 12.9798(6) | 11.4368(7) | 9.7185(4) |
| c/Å | 14.2280(7) | 23.899(2) | 24.5997(10) |
| α | 65.084(5)° | 90° | 90° |
| β | 80.892(11)° | 90° | 91.888(4)° |
| γ | 79.404(3)° | 90° | 90° |
| Volume/Å3 | 1281.12(11) | 2598.0(3) | 2817.5(2) |
| Z | 2 | 4 | 4 |
| Density (calculated) g cm−3 | 1.362 | 1.344 | 1.324 |
| Absorp. coefficient/mm−1 | 0.088 | 0.087 | 0.085 |
| F(000) | 552.0 | 1104.0 | 1176 |
| Crystal size/mm3 | 0.10 × 0.10 × 0.41 | 0.19 × 0.11 × 0.07 | 0.30 × 0.20 × 0.10 |
| Theta range for data collection/° | 5.32 to 54.00 | 4.61 to 51.99 | 4.50 to 54.00 |
| Index ranges | −9 ≤ h ≤ 9, | −10 ≤ h ≤ 11 | −15 ≤ h ≤ 15 |
| −16 ≤ k ≤ 16 | −12 ≤ k ≤ 14 | −13 ≤ k ≤ 13 | |
| −18 ≤ l ≤ 18 | −26 ≤ l ≤ 29 | −31 ≤ l ≤ 31 | |
| Reflections collected | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 514 514 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 626 626 |
39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 113 113 |
| Independent reflections | 5562 [R(int) = 0.0384] | 5098 [R(int) = 0.0419] | 6140 [R(int) = 0.0470] |
| Refinement method | Full-matrix least-squares on F2 | Full-matrix least-squares on F2 | Full-matrix least-squares on F2 |
| Data/restraints/parameters | 5562/1/365 | 5098/1/365 | 6140/0/407 |
| Goodness-of-fit on F2 | 1.041 | 1.032 | 1.016 |
| Final R indices [I > 2sigma(I)] | R1 = 0.0423 | R1 = 0.0451 | R1 = 0.0440 |
| wR2 = 0.0973 | wR2 = 0.0785 | wR2 = 0.0934 | |
| R indices (all data) | R1 = 0.0563, | R1 = 0.0679, | R1 = 0.0607, |
| wR2 = 0.1040 | wR2 = 0.0875 | wR2 = 0.1022 | |
| Largest diff. peak and hole/e Å−3 | 0.31 and −0.24 | 0.18 and −0.24 | 0.26 and −0.24 |
Elucidation of the three structures reveals that (i) the two carbonyl carbons of the enone part and isatin or acenaphthenequinone moieties are in trans-relationship, and (ii) a cis-relationship between the carbonyl of the oxindole or acenaphthenequinone ring and the proton attached at C-10b′. Thus, the cycloadducts are formed through an exo-approach between the syn-d2 and (E)-3-arylidene-1-phenyl-pyrrolidine-2,5-diones 1 (Scheme 4). The cycloaddition proceeds with high exo-diastereoselectivity affording in each case only one diastereomer. It is worth noting that our result is in contrast to the observed diastereoselectivity outcome from previously published studies.11 These works handled 1,3-dipolar cycloaddition reactions with tetrahydroisoquinolinium N-ylides derived from cyclic diketones. The authors revealed that the products were formed selectively through an endo-approach between syn-ylide and the dipolarophile.
DFT calculations
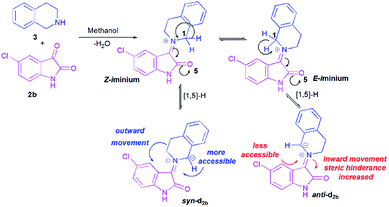
To better grasp the experimentally observed high diastereoselectivity in the multicomponent 1,3-dipolar cycloaddition, calculations using the density functional approach (DFT) were performed. The effect of solvent (methanol) was estimated using the polarizable continuum model (PCM) approach.The model case study was the reaction of the dipolarophile 1a with azomethine ylide d2b formed from the condensation of THIQ with chloroisatin 2b which should lead to the formation of the two types of iminium ions, Z and E (Scheme 5). For the generation of an azomethine ylide via a [1,5]-H shift, the oxygen of the carbonyl group of the E form is spatially too far from the benzylic hydrogen, while in the Z form they are close enough to permit a H-shift.18 So, one can expect that the syn-d2b N-ylide would be formed from the Z-iminium salt.
Moreover, and in accordance with our previous work,16b,17b the attack of the dipolarophile on syn-d2b would enforce the inward movement of THIQ ring to the cyclic diketones core, thus enhancing the steric hindrance between these later nuclei. In the case of anti-d2b, the 1,3-dipolar cycloaddition of the N-ylide would be favoured because no apparent steric hindrance would have evolved from the outward movement of the THIQ core.14,15b Therefore, only the syn-N-ylide forming azomethine ylide d2b are considered in the subsequent calculations.
This syn intermediate could in principle react with the dipolarophile 1a along four reactive channels related to two regioisomeric and two stereoisomeric approaches (Scheme 6). The cycloadducts were labelled 4f, 4′f, 5f, 5′f and their transition states (TS) exo-TS1, endo-TS1, exo-TS2 and endo-TS2 were energetically optimized and characterized under the same level of calculation by using the Berny analytical gradient method.19 These TS, which are characterized by a saddle point with a single imaginary frequency, are depicted in Fig. 7. The differences between reactants and transition states in the Gibbs free energy (ΔG), enthalpy (ΔH), entropy (ΔS) and internal energy (ΔU), for the different stationary points along the reactive pathways are compiled in Table 4.
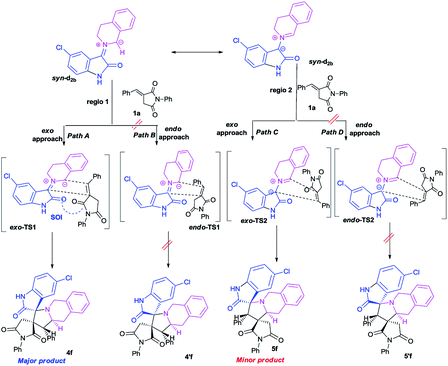 | ||
| Scheme 6 Plausible mechanism for the regio- and stereoisomeric 1,3-dipolar cycloaddition reaction of dipolarophile 1a with syn-d2b. | ||
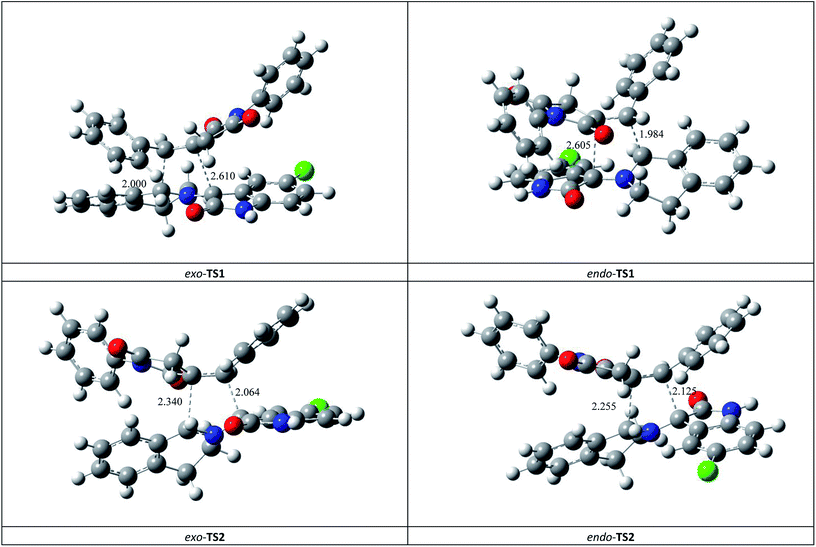 | ||
| Fig. 7 Four possible TS for the 1,3-dipolar cycloaddition of syn-d2b across 1a, optimized at the B3LYP/6-31G(d,p) level. The lengths of the bonds directly involved in the reaction are given in Å. Coordinates are given in the ESI.† | ||
| ΔG | ΔH | ΔS | ΔU | |
|---|---|---|---|---|
| 4f | 3.1 | −10.6 | −46.0 | −13.7 |
| 4′f | 6.6 | −6.7 | −44.8 | −9.4 |
| 5f | 6.7 | −8.7 | −51.6 | −11.1 |
| 5′f | 9.6 | −5.4 | −50.1 | −7.7 |
| exo-TS1 | 23.8 | 9.5 | −47.8 | 8.3 |
| endo-TS1 | 25.5 | 11.7 | −46.1 | 10.7 |
| exo-TS2 | 23.1 | 9.3 | −46.2 | 8.2 |
| endo-TS2 | 26.7 | 13.2 | −45.3 | 12.1 |
All the energy values have been corrected for the zero point energy. The kinetic parameters (activation energy ΔG#, activation enthalpies ΔH#, and activation entropies ΔS# between reactants and TS) are first discussed.
The corresponding activation parameters, ΔH#, ΔS# and ΔG#, are in fairly good agreement with the experiment results. However, the strong negative entropy values of exo-TS1 and exo-TS2 suggest a highly ordered rate-determining transition state, as expected for a polar concerted cycloaddition.20
The potential energy requested to reach the TS, i.e., the activation energy, was shown to increase in the following order: exo-TS2 < exo-TS1 < endo-TS1 < endo-TS2.
The favoured exo approaches compared with the endo attack agree well with experimental findings showing that mixtures of the two exo-regioisomers are observed only.
The thermodynamic parameters, ΔG, ΔH and ΔS, between reactants and products of the investigated reactions are reported in Table 4.
The lowest ΔG value is achieved for the exo approach on 4f (3.1 kcal mol−1). In addition, cycloadditions leading to 4f, 5f, 4′f and 5′f are exothermic processes, and the most negative values of ΔH correspond to 4f and 5f (−10.6 and −8.7 kcal mol−1, respectively). It is worth noting that calculations in methanol solution indicate positive free Gibbs energies (ΔG > 0) for these reactions. Moreover, the cycloadduct 4f resulting from the exo approach of syn-d2b with dipolarophile 1a is the most favourable thermodynamic product. TSs exo-TS1 and exo-TS2 of the two cycloadducts 4f and 5f respectively, exhibit comparable energies. They are thus the two outcomes, but due to a clear difference in energy, 4f is the major product.
All the TS are concerted asynchronous as expected for a typical normal-demand 1,3-dipolar cycloaddition. To support this accordance, the two new σ bonds lengths I1 and I2 are measured. At the TSs associated with the approach affording the cycloadducts 4f and 4′f (Fig. 7), the length of the C-1′–C-10b′ forming bonds are 1.991 Å at exo-TS1 and 1.974 Å at endo-TS1, while the distance between the C-2′ and the C-3′ atoms is 2.469 Å at exo-TS1 and 2.649 Å at endo-TS1. However, the opposite trend is found for fused transition structures (exo-TS2 and endo-TS2), with forming C-1′–C-3′ bond lengths of 1.996 Å and 2.001 Å, respectively. The computed distance between the C-2′ and the C-10b′ atoms is 2.490 Å at exo-TS2 and 2.417 Å at endo-TS2.
The extent of the asynchronicity of the bond-formation can thus be measured by the difference between the lengths of the two σ bonds being formed in the reaction, i.e., Δd = l1 − l2. The asynchronicity at the first trend leading 4f and 4′f is Δd = 0.478 Å at exo-TS1 and 0.675 Å at endo-TS1, while that at the second tend affording 5f and 5′f is Δd = 0.494 Å at exo-TS2 and 0.416 Å at endo-TS2. Therefore, the formation of the TSs associated with 4f and 5f is favoured. In addition, these geometrical parameters indicate that these cycloadditions correspond to asynchronous concerted processes.
Frontier molecular orbitals (FMO) have been determined in order to get global reactivity indices. These indices, namely, electronic chemical potential, μ, chemical hardness, η, and global electrophilicity, ω, are powerful tools for studying the feasibility of the reaction, as well as the reactivity of the reagents.21 They have been computed for the separated reagents involved in the [3+2] cycloaddition reaction of dipolarophile 1a with azomethineylide syn-d2b. The chemical hardness η reveals the stability and reactivity of a chemical system.22–24 The global electrophilicity ω measures the propensity or capacity of a species to accept electrons.24g,25 All the data are displayed in Table S1.†
Analysis of the reactive indices suggests that the electronic chemical potential μ of dipole syn-d2b (−3.921 eV) is higher than that of dipolarophile 1a (−4.343 eV) and the chemical hardness of syn-d2b (η = 3.624 eV) is lower than of 1a (η = 4.595 eV). This result indicates that the charge transfer will take place from the dipole toward dipolarophile. Over and above, the electrophilicity of dipolarophile 1a (ω = 2.052 eV) is greater than that of syn-d2b (ω = 2.237 eV), indicating that the 1,3-dipole will act as a nucleophile due to its low ω value and high global nucleophilicity values (N = 4.422 eV). However, the dipole syn-d2b is classified as strong nucleophiles due to its high nucleophilicity index, N > 3 eV.26 1a will thus act as an electrophile.
After evaluation of the global nucleophilic/electrophilic character, a local analysis was carried out with the calculation of condensed Fukui functions considering the cationic and anionic systems in their optimized geometries of the corresponding neutral systems. Fukui function parameters have been evaluated through the calculation of the electrostatic potential (ESP) derived atomic populations.27 The calculated local chemical reactivity parameters of syn-d2b and dipolarophile 1a are shown in Fig. S1 (in the ESI).† We can notice that C-10b′ of azomethine ylide syn-d2 has more nucleophilic character (f− = 0.162). On the other hand, the dipolarophile 1a has the highest electrophilic centre at C-1′ (f+ = 0.118). The electrophilicity at C-1′ can be attributed to the presence of a strong electron-withdrawing carbonyl group. Thereby, the most favourable nucleophilic/electrophilic interaction will occur between C-10b′ carbon atom of syn-d2 and C-1′ atom of enone 1a leading to preferred formation of major regioisomer 4f. These results perfectly agree with the experimental observations (Scheme 5).
Conclusion
We have thus developed an efficient method for the synthesis of a novel class of dispiropyrrolo[2,1-a]isoquinolines fused pyrrolidine-2,5-dione bearing two adjacent spiro-carbons in good to high yields with high diastereoselectivity. Our strategy to prepare these cycloadducts involves three-component 1,3-dipolar cycloaddition reaction between cyclic diketones as tetrahydroisoquinolinium N-ylides precursors and α-alkylidenesuccinimides as dipolarophiles. More importantly, these findings proved the versatile utility of this strategy for the synthesis of complex dispiroheteropolycyclic systems, which is of great importance for the development of medicinally active drugs.An analysis based on theoretical calculations using the DFT approach, B3LYP/6-31G(d,p) reveals that the isomeric spirocycloadducts 4 and 5 are obtained through a 1,3-dipolar cycloaddition reaction via a high asynchronous mechanism with very low activation energies, when compared to the other possible reaction paths. This outcome is in agreement with the experimental observations.
Experimental
Apparatus and general information
NMR spectra were recorded with a Bruker-Spectrospin AC 300 spectrometer operating at 300 MHz for 1H and 75 MHz for 13C using tetramethylsilane as the internal standard (0.00 ppm) in CDCl3 as solvent. The following abbreviations were used to explain the multiplicities: bs = broad singlet, s = singlet, d = doublet, m = multiplet.Elemental analyses were performed on a Perkin Elmer 2400 Series II Elemental CHNS analyzer. Materials: thin-layer chromatography (TLC): TLC plates (Merck, silica gel 60 F254 0.2 mm 200 × 200 nm); substances were detected using UV light at 254 nm.
Typical representative procedure for preparation of cycloadducts 4a–5a
A mixture of 1a (2 63 mg, 1.0 mmol), isatin 2a (147 mg, 1 mmol) and tetrahydroisoquinoline 3 (159.7 mg, 1.2 mmol) was refluxed in methanol (5 mL) for 4 h. After completion of the reaction (TLC), the solvent was removed under vacuum. The residue was chromatographed on silica gel employing ethyl acetate-cyclohexane (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 v/v) as eluent to obtain the pure products 4a (0.26 g, 51%) and 5a (0.17 g, 34%). Spectroscopic data and further experimental details for the all compound are presented in the ESI.†
7 v/v) as eluent to obtain the pure products 4a (0.26 g, 51%) and 5a (0.17 g, 34%). Spectroscopic data and further experimental details for the all compound are presented in the ESI.†
DFT calculations
The geometric optimizations of all reactants, TS, and products were performed using the B3LYP functional and the 6-31G(d,p) basis set in the Gaussian 09 (ref. 27) environment, by using the Berny analytical gradient method.28 The global electrophilicity index, ω, was calculated following the expression,24,25 ω = (μ2/2η), where μ is the electronic chemical potential, μ = (EHOMO + ELUMO)/2, and η is the chemical hardness, η = (ELUMO − EHOMO). The Fukui condensed functions have been calculated from local populations found from single point calculations carried out on reduced, neutral, and oxidized forms with geometries optimized for neutral species. The most favourable attack site can also be disclosed by theoretical calculations. The actual DFT-based local chemical reactivity Fukui function parameters for nucleophilic (fk+) and electrophilic (fk−) attacks were calculated through the electrostatic potential (ESP) derived atomic populations.26Characterizations have been performed under the same level of calculation. Vibrational analysis has been performed for all the stationary points. TS are characterized by a single negative imaginary frequency. For all TS structures, the intrinsic reaction coordinate27 calculation, using the Hessian-based predictor–corrector method,28 was performed to ascertain that each TS connected the expected reactants and products. Thermal corrections were computed from unscaled frequencies for a standard state of 298.15 K and 1 atm in methanol solution and within the harmonic approximation.
Crystal structure determinations
A suitable crystal of 4a, 5a and 5r was selected and mounted on an Xcalibur, Sapphire3 diffractometer. The crystals were kept at 150(2) K during data collection. Using Olex2,29 the structures were solved with the ShelXS30 structure solution program using Direct Methods and refined with the XL30 refinement package using Least Squares minimisation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The computational resources were provided by Calcul Quebec and Compute Canada, through the financial support of the Canadian Foundation for Innovation (CFI).References
-
(a) E. Marco, W. Laine, C. Tardy, A. Lansiaux, M. Iwao, F. Ishibashi, C. Bailly and F. Gago, J. Med. Chem., 2005, 48, 3796–3807 CrossRef CAS PubMed
; (b) L. Xiang, D. Xing, W. Wang, R. Wang, Y. Ding and L. Du, Phytochemistry, 2005, 66, 2595–2601 CrossRef CAS PubMed
; (c) R. F. Wang, X. W. Yang, C. M. Ma, S. Q. Cai, J. N. Li and S. Yukihiro, Heterocycles, 2004, 63, 1443–1448 CrossRef CAS
; (d) Q. Zhang, G. Tu, Y. Zhao and T. Cheng, Tetrahedron, 2002, 58, 6795–6798 CrossRef CAS
; (e) M. V. R. Reddy, M. R. Rao, D. Rhodes, M. S. T. Hansen, K. Rubins, F. D. Bushman, Y. Venkateswarlu and D. J. Faulkner, J. Med. Chem., 1999, 42, 1901–1907 CrossRef CAS PubMed
; (f) R. J. Andersen, D. J. Faulkner, H. C. Heng, G. D. V. Duyne and J. Clardy, J. Am. Chem. Soc., 1985, 107, 5492–5495 CrossRef CAS
.
-
(a) K. Tangdenpaisal, R. Worayuthakarn, S. Karnkla, P. Ploypradith, P. Intachote, S. Sengsai, B. Saimanee, S. uchirawat and M. Chittchang, Chem.–Asian J., 2015, 10, 925–937 CrossRef CAS PubMed
; (b) A. Theppawong, P. Ploypradith, P. Chuawong, S. Ruchirawat and M. Chittchang, Chem.–Asian J., 2015, 10, 2631–2650 CrossRef CAS PubMed
; (c) F. Plisson, X. C. Huang, H. Zhang, Z. Khalil and R. J. Capon, Chem.–Asian J., 2012, 7, 1616–1623 CrossRef CAS PubMed
.
-
(a) B. Su, C. Cai, M. Deng, D. Liang, L. Wang and Q. Wang, Bioorg. Med. Chem. Lett., 2014, 24, 2881–2884 CrossRef CAS PubMed
; (b) R. F. Wang, X. W. Yang, C. M. Ma, S. Q. Cai, J. N. Li and Y. Shoyama, Heterocycles, 2004, 63, 1443 CrossRef CAS
.
- C. J. Cavallito and A. P. Gray, Fr. Pat. 2135297, 1973Chem. Abstr. 1973, 79, 96989
.
- B. E. Maryanoff, J. L. Vaught, R. P. Shank, D. F. McComsey, M. J. Costanzo and S. O. Nortey, J. Med. Chem., 1990, 33, 2793–2797 CrossRef CAS
.
- B. E. Maryanoff, D. F. MeComsey, J. F. Gardocki, R. P. Shank, M. J. Constanzo, S. O. Nortey, C. R. Schneider and P. E. Setler, J. Med. Chem., 1987, 30, 1433–1454 CrossRef CAS
.
- E. Marco, W. Laine, C. Tardy, A. Lansiaux, M. Iwao, F. Ishibashi, C. Bailly and F. Gago, J. Med. Chem., 2005, 48, 3796–3807 CrossRef CAS PubMed
.
- A. Aubry, X.-S. Pan, L. M. Fisher, V. Jarlier and E. Cambau, Antimicrob. Agents Chemother., 2004, 48, 1281–1288 CrossRef CAS
.
-
(a) R.-G. Shi, J. Sun and C.-G. Yan, ACS Omega, 2017, 11, 7820–7830 CrossRef
; (b) J. Sun, G.-l. Shen, Y. Huang and C.-G. Yan, Sci. Rep., 2017, 7, 41024 CrossRef PubMed
; (c) R. Liu, R.-G. Shi, J. Sun and C.-G. Yan, Org. Chem. Front., 2017, 4, 354–357 RSC
; (d) X.-H. Wang and C.-G. Yan, Synthesis, 2014, 46, 1059–1066 CrossRef
; (e) J. An, Q.-Q. Yang, Q. Wang and W.-J. Xiao, Tetrahedron Lett., 2013, 54, 3834–3837 CrossRef CAS
; (f) F. Dumitrascu, E. Georgescu, F. Georgescu, M. M. Popa and D. Dumitrescu, Molecules, 2013, 18, 2635–2645 CrossRef CAS PubMed
; (g) L. Wu, J. Sun and C.-G. Yan, Org. Biomol. Chem., 2012, 10, 9452–9463 RSC
; (h) Y. Shang, L. Wang, X. He and M. Zhang, RSC Adv., 2012, 2, 7681–7688 RSC
; (i) J. L. G. Ruano, A. Fraile, M. R. Martín, G. González, C. Fajardo and A. M. M-Castro, J. Org. Chem., 2011, 76, 3296–3305 CrossRef PubMed
; (j) J. L. G. Ruano, A. Fraile, M. R. Martín, G. González, C. Fajardo and A. M. M. Castro, J. Org. Chem., 2011, 76, 3296–3305 CrossRef PubMed
; (k) F. Dumitrascu, M. R. Caira, E. Georgescu, F. Georgescu, C. Draghici and M. M. Popa, Heteroat. Chem., 2011, 22, 723–729 CrossRef CAS
; (l) K. M. Dawood, E. A. Ragab and N. A. Khedr, J. Chin. Chem. Soc., 2009, 56, 1180–1185 CrossRef CAS
; (m) Y. Liu, H.-Y. Hu, Q.-J. Liu, H.-W. Hu and J.-H. Xu, Tetrahedron, 2007, 63, 2024–2033 CrossRef CAS
; (n) W. Peng and S. Zhu, J. Chem. Soc., Perkin Trans. 1, 2001, 3204–3210 RSC
.
-
(a) S. Mondal, A. Maity, R. Paira, M. Banerjee, Y. P. Bharitkar, A. Hazra, S. Banerjee and N. B. Mondal, Tetrahedron Lett., 2012, 53, 6288–6291 CrossRef CAS
; (b) J. An, Q.-Q. Yang, Q. Wang and W. Xiao, Tetrahedron Lett., 2013, 54, 3834–3837 CrossRef CAS
; (c) Y. Liu, H.-Y. Hu, Q.-J. Liu, H.-W. Hu and J.-H. Xu, Tetrahedron, 2007, 63, 2024–2033 CrossRef CAS
; (d) F. Dumitrascu, E. Georgescu, F. Georgescu, M. M. Popa and D. Dumitrescu, Molecules, 2013, 18, 2635–2645 CrossRef CAS PubMed
; (e) A. Fujiya, M. Tanaka, E. Yamaguchi, N. Tada and A. Itoh, J. Org. Chem., 2016, 81, 7262–7270 CrossRef CAS PubMed
; (f) H.-M. Huang, Y.-J. Li, Q. Ye, W.-B. Yu, L. Han, J.-H. Jia and J.-R. Gao, J. Org. Chem., 2014, 79, 1084–1092 CrossRef CAS PubMed
.
-
(a) Y. Sarrafi, M. Hamzehlouian, K. Alimohammadi and H. R. Khavasi, Tetrahedron Lett., 2010, 51, 4734–4737 CrossRef CAS
; (b) Y. Sarrafi, A. Asghari, M. Hamzehloueian, K. Alimohammadic and M. Sadatshahabia, J. Braz. Chem. Soc., 2013, 24(12), 1957–1963 CAS
; (c) K. Alimohammadi, Y. Sarrafi and B. Rajab, C. R. Chim., 2013, 17, 156–163 CrossRef
.
- Y. Huang, Y. X. Huang, J. Sun and C. G. Yan, RSC Adv., 2018, 8, 23990–23995 RSC
.
- N. S. Kumar, M. S. Reddy, V. R. Bheeram, S. B. Mukkamala, L. R. Chowhan and L. C. Rao, Environ. Chem. Lett., 2018, 1–10 Search PubMed
.
- I. Fejes, M. Nyerges, A. Szollosy, G. Blasko and L. Toke, Tetrahedron, 2001, 57, 1129–1137 CrossRef CAS
.
-
(a) A. Fredenhagen, S. Y. Tamura, P. T. M. Kenny, H. Komura, Y. Naya, K. Nakanishi, K. Nishiyama, M. Sugiura and H. Kita, J. Am. Chem. Soc., 1987, 109, 4409–4411 CrossRef CAS
; (b) M. Isaka, N. Rugseree, P. Maithip, P. Kongsaeree, S. Prabpai and Y. Thebtaranonth, Tetrahedron, 2005, 61, 5577–5583 CrossRef CAS
; (c) T. Matviiuk, G. Morid, C. Lherbeta, F. Rodriguez, M. R. Pasca, M. Gorichko, B. Guidettia, Z. Voitenko and M. Baltasa, Eur. J. Med. Chem., 2014, 71, 46–52 CrossRef CAS PubMed
; (d) M. Z. Wróbel, A. Chodkowski, F. Herold, A. Gomółka, J. Kleps, A. P. Mazurek, F. Pluciński, A. Mazurek, G. Nowak, A. Siwek, K. Stachowicz, A. Slawinska, M. Wolak, B. Szewczyk, G. Satala, A. J. Bojarski and J. Turlo, Eur. J. Med. Chem., 2013, 63, 484–500 CrossRef PubMed
.
-
(a) S. Haddad, S. Boudriga, T. N. Akhaja, J. P. Raval, F. Porzio, A. Soldera, M. Askri, M. Knorr, Y. Rousselin, M. M. Kubicki and D. Rajani, New J. Chem., 2015, 39, 520–528 RSC
; (b) S. Haddad, S. Boudriga, F. Porzio, A. Soldera, M. Askri, D. Sriram, P. Yogeeswari, M. Knorr, Y. Rousselin and M. M. Kubicki, RSC Adv., 2014, 4, 59462–59471 RSC
.
-
(a) C. Mhiri, S. Boudriga, M. Askri, M. Knorr, D. Sriram, P. Yogeeswari, F. Nana, K. Golz and C. Strohmanni, Bioorg. Med. Chem. Lett., 2015, 25, 4308–4313 CrossRef CAS PubMed
; (b) S. Haddad, S. Boudriga, F. Parzo, A. Soldera, M. Askri, M. Knorr, Y. Rousselin, M. M. Kubicki, K. Golz and C. Strohmann, J. Org. Chem., 2015, 80, 9064–9075 CrossRef CAS PubMed
; (c) C. Mhiri, F. Rouatbi, S. Boudriga, M. Askri, K. Ciamala, M. Knorr, K. Monnier-Jobé, A. Khatyr, Y. Rousselin and M. M. Kubicki, Mediterr. J. Chem., 2015, 4, 30–50 CrossRef CAS
; (d) F. Rouatbi, M. Askri, F. Nana, G. Kirsch, S. Sriram and P. Yogeeswari, Tetrahedron Lett., 2015, 57, 163–167 CrossRef
.
-
(a) K. Alimohammadi, Y. Sarrafi, M. Tajbakhsh, S. Yeganegi and M. Hamzehloueian, Tetrahedron, 2011, 67, 1589–1597 CrossRef CAS
; (b) P. J. Xia, Y. H. Sun, J. A. Xiao, Z. F. Zhou, S. S. Wen, Y. Xiong, G. C. Ou, X. Q. Chen and H. Yang, J. Org. Chem., 2015, 80, 11573–11579 CrossRef CAS PubMed
.
-
(a) M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327–335 CrossRef CAS
; (b) E. Cances, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef CAS
; (c) V. Barone, M. Cossi and J. Tomasi, J. Comput. Chem., 1998, 19, 404–417 CrossRef CAS
.
-
(a) R. Huisgen, 1,3-Dipolar Cycloadditions−Introduction, Survey, Mechanism, in 1,3-Dipolar Cycloaddition Chemistry, ed. A. Padwa, John Wiley & Sons, Inc., New York, 1984, vol. 1, pp. 1–176 Search PubMed
; (b) K. N. Houk and K. Yamaguchi, Theory of 1,3-Dipolar Cycloadditions, in 1,3-Dipolar Cycloaddition Chemistry, ed. A. Padwa, John Wiley & Sons, New York, 1984, vol. 2, pp. 407–447 Search PubMed
.
- L. R. Domingo and J. A. Saez, Org. Biomol. Chem., 2009, 7, 3576–3583 RSC
.
-
(a) A. V. Londhe, B. Gupta, S. Kohli, P. Pardasani and R. T. Z. Pardasani, Z. Naturforsch., B: J. Chem. Sci., 2006, 61, 213–220 CAS
; (b) R. T. Pardasani, P. Pardasani, A. Jain and K. Arora, Indian J. Chem., 2006, 45B, 1204–1209 CAS
; (c) K. Arora, D. Jose, D. Singh, R. S. Gupta, P. Pardasaniand and R. T. Pardasani, Heteroat. Chem., 2009, 20, 379–392 CAS
.
-
(a) K. N. Houk, Acc. Chem. Res., 1975, 8, 361–369 CrossRef CAS
; (b) K. N. Houk, J. Sims, R. E. Duke, R. W. Strozier and J. K. George, J. Am. Chem. Soc., 1973, 95, 7287–7301 CrossRef CAS
; (c) K. N. Houk, J. Sims, C. R. Watts and L. J. Luskus, J. Am. Chem. Soc., 1973, 95, 7301–7315 CrossRef CAS
.
-
(a) R. G. Pearson, Hard and soft acids and bases, Dowden, Hutchinson, and Ross, Stroudsburg, PA, 1973 Search PubMed
; (b) R. G. Pearson, Acc. Chem. Res., 1993, 26, 250–255 CrossRef CAS
; (c) R. G. Pearson, Chemical hardness: application from molecules to solid, Wiley-VCH, Weinheim, 1997 CrossRef
; (d) K. D. Sen and D. M. P. Mingos, Chemical hardness: structure and bonding, Springer, Berlin, 1993 CrossRef
; (e) R. G. Parr and W. Yang, Density functional theory of atoms and molecules, Oxford University Press, New York, 1989 Search PubMed
; (f) P. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef
; (g) A. Vektariene, G. Vektaris and J. Svoboda, ARKIVOC, 2009, 7, 311–329 Search PubMed
.
- R. G. Parr, L. Szentpaly and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS
.
-
(a) W. Yang and R. G. Parr, Hardness, softness, and the Fukui function in the electronic theory of metals and catalysis, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 6723 CrossRef CAS PubMed
; (b) S. Arulmozhiraja and P. Kolandaivel, Mol. Phys., 1997, 90, 55–62 CrossRef CAS
; (c) P. W. Ayers, W. Yang and L. Bartolotti, Chemical Reactivity Theory: A Density Functional, ed. P. K. Chattaraj, CRC Press, Boca Raton, FL, 2009, ch. 18 Search PubMed
.
-
(a) W. J. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Ab initio Molecular Orbital Theory, Wiley, New York, 1986 Search PubMed
; (b) K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163 CrossRef CAS
.
-
(a) H. P. Hratchian and H. B Schlegel, J. Chem. Theory Comput., 2005, 1, 61–69 CrossRef CAS PubMed
; (b) V. Barone, M. Cossi and J. J. Tomasi, Comput. Chem., 1998, 19, 404–417 CrossRef CAS
.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS
.
-
(a) G. M. Sheldrick, Acta Crystallogr., 2008, A64, 112–122 CrossRef PubMed
; (b) G. M. Sheldrick, Acta Crystallogr., 2015, A71, 3–8 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1585506, 1585512 and 1585515. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8ra09884k |
| This journal is © The Royal Society of Chemistry 2019 |