Open Access Article
Open Access ArticleEffect of the surface curvature on amyloid-β peptide adsorption for graphene†
Xiuhua Yina,
Baoyu Lia,
Shengtang Liua,
Zonglin Gua,
Bo Zhoub and
Zaixing Yang *a
*a
aInstitute of Quantitative Biology and Medicine, State Key Laboratory of Radiation Medicine and Protection, School of Radiation Medicine and Protection, Collaborative Innovation Center of Radiological Medicine of Jiangsu Higher Education Institutions, Soochow University, Jiangsu 215123, China. E-mail: zxyang@suda.edu.cn
bSchool of Electronic Engineering, Chengdu Technological University, Chengdu 611730, China
First published on 1st April 2019
Abstract
The adsorption of amyloid-β peptide (Aβ) onto graphene nanosheets with curvature at a neutral pH has been studied by using molecular dynamics simulations in combination with umbrella sampling. We found that Aβ adsorbed onto graphene with distinct characteristics, causing the breakage of hydrogen bonds which leads to its conformational change. Interestingly, the adsorption capacity of graphene's surface varies significantly depending on its curvature, namely, the surface with negative curvature has a higher probability to adsorb the Aβ than the one with positive curvature. This phenomenon is further evidenced by the binding energy between the complex of graphene and Aβ derived from the potential of mean force (PMF). The hydrophobic interactions and the direct dispersion interactions between the graphene nanosheet and the Aβ play a dominant role in the adsorption process. These findings indicate that not only is the chemical composition an important factor but also the shape of the nanoparticle is important in determining its interaction with proteins: the contacting surface curvature can lead to different adsorption capability.
Introduction
Since the discovery of fullerene C60 in 1985,1 carbon nanotubes (CNTs) in 1991,2 and graphene in 2004,3 carbon-based materials have been intensively investigated due to their excellent mechanical, optical, and electrical properties, which make them ideal building blocks for future applications in areas as diverse as environmental applications, electronics, energy, and medicine among others.4–13The interaction between nanomaterials and biomolecules is essential to nanoparticle-based biotechnology and biomedical applications, such as gene delivery, cellular imaging, nanotoxicology, and biological experimental technology,14–19 since this may bring some biosafety concerns. Recently, a great deal of research attention has been paid to the adsorption of proteins onto nanomaterials, particularly graphitic nanomaterials such as carbon nanotubes and fullerenes, both experimentally and theoretically. It has been shown that these adsorptions can affect both protein structures and functions. For example, HP35 loses most of its native secondary and tertiary structures after the adsorption onto graphene.20 Single-wall carbon nanotubes (SWCNT) can plug into the hydrophobic core of protein WW domains and occupy the proline-rich binding motifs (PRM) active sites, preventing the regular binding of the PRM ligand and thus disrupting the biological function of the WW domain.21 The conformational and active site changes of proteins after adsorbing onto the SWCNT surfaces have been investigated using atomic force microscope and Fourier transform infrared spectroscopy.22 Also, it has been found that proteins interacting with C60 generally have good shape matching with C60 through their docking studies.23 Besides, the effects of graphene-based nanomaterials on the structural and conformations of amyloid fibrils have been extensively studied using both experimental and theoretical methods.24–28
All the aforementioned studies have improved our understanding of the interaction between nanomaterial particularly graphitic nanomaterials and biomolecules. Decade ago, experimental results have demonstrated that SWCNTs with suitable sizes and shapes are effective in blocking some biological membrane ion channel.29 Very recent studies have showed that protein adsorption onto the surface of carbon-based nanomaterials (CBNs) becomes more notable as the local curvature of the CBNs decreases.30 However, it is unclear that how negative curvature of graphene's surface could affect the process of protein adsorption. Thus, it is of interest to simulate the interaction between protein and graphene with curvature and indicate how the shape of the nanoparticle affects the process of protein adsorbing onto graphene.
In this study, we take the complex of amyloid-β peptide (Aβ) and graphene nanosheet as the model to investigate the adsorption of Aβ onto graphene using large scale molecular dynamics (MD) simulations. Our simulations show that Aβ adsorbed onto both graphene's surfaces with positive and negative curvatures. Interestingly, we observed that there is a big difference on the adsorption quantity based on the curvature. We also conduct pulling simulations to calculate the potential of mean force (PMF) along specific coordinates for systems that contain the single β-sheet and graphene with positive (negative) curvature to profile the binding energy. The results of binding energy suggest that the surface of negative curvature has a stronger adsorption capacity than the one of positive curvature.
Models and methods
Molecular dynamics (MD) simulations in combination with umbrella sampling (US)31 are widely used in computational biophysics for the calculation of PMF along specific coordinates.32–34 In this study, we constructed three systems, one for performing molecular dynamics simulation and the other two for running umbrella sampling.Our first system includes a Aβ peptide and a graphene nanosheet (chirality (25, 25), 19.54 Å in length) with curvature. The β-amyloid peptide contains 40 β-sheets and its initial crystal structure was prepared from the Protein Data Bank (PDB code: 3OW9) and modeled by the OPLS-AA force field.35 The model of graphene nanosheet consists of 1216 carbon atoms, which was built using the VMD36 (version 1.9.1) software. The carbon atoms of the graphene were modeled as uncharged Lennard-Jones particles with a cross-section of σc–c = 3.4 Å and a potential well depth of εc–c = 0.36 kJ mol−1.37,38 In our simulation system, the graphene nanosheet was initially placed on top of the Aβ peptide, with its long edges set vertically to the plane of the Aβ peptide (see Fig. 1). The graphene nanosheet was restrained in all simulations and periodic boundary conditions were applied in all three directions. The TIP3P water model was used for the salvation, and 40 Cl− were added into solution to neutralize the system. The final complex system size is 82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231 atoms. Then the solvated systems were simulated using the GROMACS39,40 package software (4.6.4). In the simulation, the covalent bonds involving the H atoms were constrained by the LINCS algorithm, which allowed a time step of 2 fs. The structural configurations were saved every 1 ps for subsequent analysis. The van der Waals (vdW) interactions were handled with the usual smooth cutoff with the cutoff distance set at 10 Å, while the long-range electrostatic interactions were treated with the particle-mesh Ewald method41 (PME) with a grid spacing of 1.2 Å. After energy minimization, the complex systems were equilibrated for 200 ps at a constant temperature of 310 K using V-rescale thermostat.42 Three independent systems were performed to simulate the adsorption process with each lasted up to 900 ns. Visualizations and analysis were performed using the VMD software packages.
231 atoms. Then the solvated systems were simulated using the GROMACS39,40 package software (4.6.4). In the simulation, the covalent bonds involving the H atoms were constrained by the LINCS algorithm, which allowed a time step of 2 fs. The structural configurations were saved every 1 ps for subsequent analysis. The van der Waals (vdW) interactions were handled with the usual smooth cutoff with the cutoff distance set at 10 Å, while the long-range electrostatic interactions were treated with the particle-mesh Ewald method41 (PME) with a grid spacing of 1.2 Å. After energy minimization, the complex systems were equilibrated for 200 ps at a constant temperature of 310 K using V-rescale thermostat.42 Three independent systems were performed to simulate the adsorption process with each lasted up to 900 ns. Visualizations and analysis were performed using the VMD software packages.
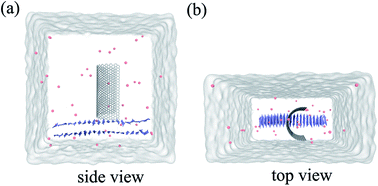 | ||
| Fig. 1 Side view (a) and top view (b) of the system in our simulation. Here the graphene is shown in white stick and the Aβ is shown in ice-blue, Cl− ions are shown in pink spheres. | ||
As for the two systems set up for umbrella sampling, they both consist of one β-sheet and a graphene nanosheet. The graphene nanosheet was derived from the structure used in the above system but with shorter length in order to reduce the computational cost. The β-sheet was placed at the position close to the negative and positive curvature surfaces. After a short MD simulation, the structure and atom coordinates corresponding to the time when the energy was equalized and lowest were taken and used as the model for the pulling simulations. After conducting umbrella sampling simulations by generating a series of configurations along a reaction coordinate, biasing simulations were carried out and used to extract the PMF. The potential of mean force (PMF) of a single peptide being dissociated from protofibril was calculated by umbrella sampling. The reaction coordinate of the PMF was defined as the distance between centroid of a peptide to the curved graphene along the y-axis (ranges from 10 Å to 50 Å). A constant harmonic force of 2000 kJ mol−1 nm−2 was applied on the peptide. The reaction path was divided into 30 windows with each simulating for 3 ns. The Weighted Histogram Analysis Method43,44 (WHAM) was adopted to calculate the PMF. All PMF profiles were offset by its value at the distance of 50 Å, where the PMF value reaches a plateau.
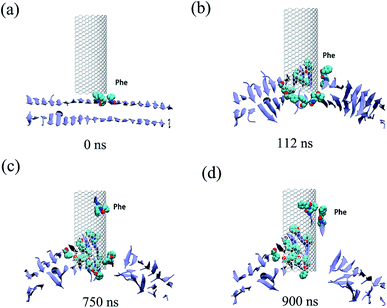
All three trajectories obtained from the simulations demonstrate that the Aβ peptide adsorbed onto both the internal and external surfaces of the graphene nanosheet during the given simulation time. Fig. 2 shows some representative snapshots of one typical example (run 1) at different simulation times illustrating the adsorption process. Interestingly, there is a conspicuous adsorption difference between the internal and external surfaces of graphene, namely, the Aβ peptide adsorbed onto the internal surface with negative curvature much more than the external one with positive curvature. On the other hand, the phenylalanine (Phe) residues of Aβ peptides are firstly attached to the graphene, indicating π–π stacking interaction between the two Phe residues and graphene surface seems to play a driving role in the initial peptide extracting process. Once extracted, besides the π–π stacking interaction, the hydrophobic interactions between other nonpolar residues (Leu/Val) of the peptide and the direct vdW dispersion interactions between peptide with graphene surface also contribute to the adsorption.
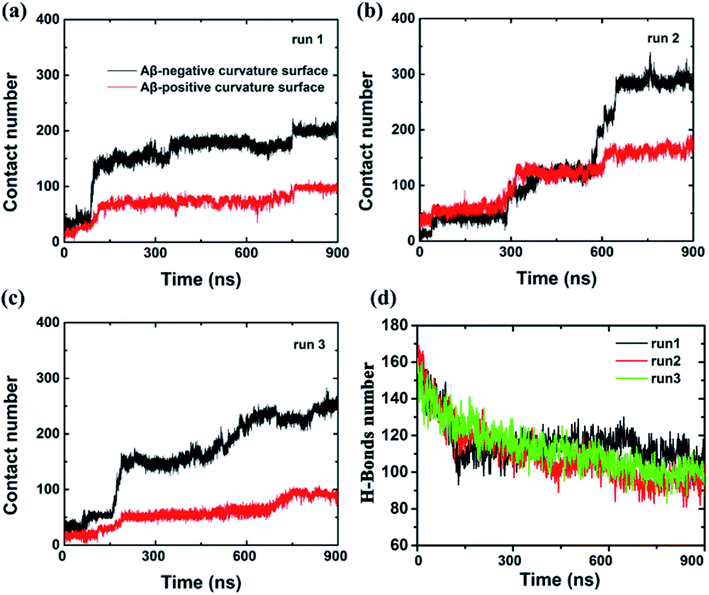
To further characterize this phenomenal difference of adsorption caused by different surface curvatures, we computed the contact numbers between the Aβ peptide and the internal and external surfaces of graphene (see Fig. 3) in run 1. Here, a contact is counted if the distance between a carbon atom in the graphene and a non-hydrogen atom in the Aβ peptide is less than 6 Å. During the first 80 ns, both contact numbers between the Aβ peptide and the internal and external surfaces of graphene increase only slightly. Then the contact number between the peptide and the external surface of graphene gradually increases to ∼80 from the period of ∼80 ns to ∼750 ns. After that, it grows a little more, to about 100 and stays there until the end of the simulation. However, the contact number between the Aβ peptide and the internal surface of graphene behaves much different, it spikes up at ∼80 ns and gradually increases to 180 at ∼750 ns. From then on, it fluctuates at that level for the remaining time. It is also noteworthy that at the early graphene penetration stage (<80 ns), the backbone hydrogen bonds at the graphene inserting position are considerably broken in all three independent simulations, indicating a severe damage of the Aβ fibril in this phase (Fig. 3d). Then, the decrease in the backbone hydrogen bond number becomes mild, suggesting the destructive effect of the graphene to the β-sheet structure of the Aβ fibril is somewhat slowing down.
In addition, we also computed the van der Waals interaction energy between the Aβ peptide and the internal and external surfaces of graphene as shown in Fig. 4. Clearly, the van der Waals interaction between the Aβ peptide and the internal surface of graphene is much stronger than the one between the peptide and the external surface of graphene. So far, we consider that the internal and external surface of graphene nanosheet has different adsorption capacity is due to they have diverse curvature (internal surface has negative curvature and external surface has positive curvature).
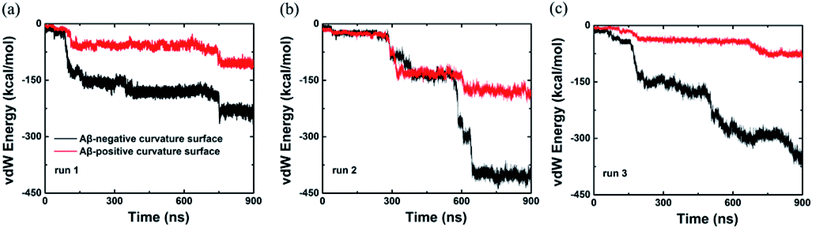 | ||
| Fig. 4 van der Waals energy between the Aβ and graphene surface with positive and negative curvature as a function of simulation time from three independent trajectories. | ||
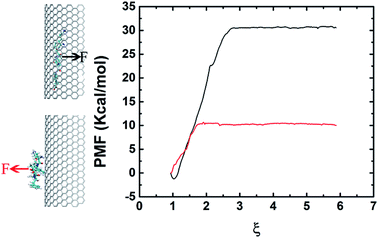
In order to elucidate the difference on adsorption capacity between the negative and positive curvature surfaces of the graphene nanosheet, we conducted pulling simulations to calculate the binding energy. The binding energy is derived from the PMF, extracted from a series of umbrella sampling simulations.45 Fig. 5 shows the free energy profile which indicates clearly the binding between the negative curvature surface and β-sheet (with binding energy at about 30 kcal mol−1) is stronger than the one between the positive curvature surface and β-sheet (with binding energy at about 10 kcal mol−1). The results corresponds to the surface with negative curvature has a higher probability than the surface with positive curvature to adsorb Aβ. In addition to the positive/negative curvature, the surface curvature size also significantly affects the peptide adsorption (Fig. S1†). More specifically, with the decreasing of the curvature size the curved graphene behaves more and more similar to its flat graphene nano-sheet counterpart in the peptide-adsorption behavior, which is in good consistent with some previous literatures on the effect of nanomaterials curvature on the adsorption of globular proteins.46,47
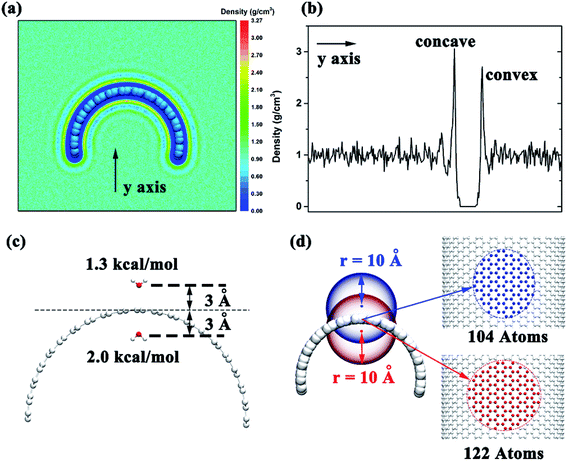
To investigate the detailed conformation of the contacting surface curvature can lead to different adsorption mechanisms, we put the graphene in the box filled with water and calculated the water distribution after the system reach a stable state. We selected a 10 ns time period and calculated the water distribution around the graphene. The results show that the water density around the negative curvature surface was a little higher than the positive curvature surface (3.1 g cm−3 vs. 2.7 g cm−3, Fig. 6a and b). This shows that in comparison to the positive curvature surface of graphene, water molecule around the negative curvature surface has a stronger vdW dispersion interaction with graphene. On the other hand, we placed two water molecules inside and outside the graphene to calculate theirs vdW interaction energy with graphene. The results indicated that water molecule around the concave surface has a stronger dispersion interaction energy (2.0 kcal mol−1) than that around the convex surface of the graphene (1.3 kcal mol−1) (Fig. 6c). This is reasonable. The curved geometry of graphene can makes water molecule around the concave surface interacting more carbon atoms than that around convex surface at the same cutoff. For instance (Fig. 6d), when an atom is placed 3 Å away from the concave surface of graphene, it can contacts 122 carbon atoms at 10 Å cutoff. However, at the same cutoff, when an atom is placed 3 Å away from the convex surface of graphene, it can only contacts 104 carbon atoms. Based on these data, we can make clear that why the surface with negative curvature has a higher probability to adsorb the Aβ than the one with positive curvature: in addition to the graphene's hydrophobicity, the strong direct dispersion interaction can remarkably affects the peptide adsorption process.
Conclusion
In conclusion, molecular dynamics simulations have been applied to study the process of Aβ adsorbed onto graphene with curvature. We found that the surface with negative curvature has a stronger adsorption capacity than the one with positive curvature. The binding energy between the complex of graphene and Aβ derived from the potential of mean force provides strong evidences to explain this phenomenon. These findings indicate that not only the chemical composition but also the shape of the nanoparticle is an important factor in determining its interaction with proteins: the contacting surface curvature can lead to different adsorption capability.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
We thank Ruhong Zhou, Bruce Berne, Hongsuk Kang, and Xuanyu Meng for helpful discussions. This work was partially supported by the National Natural Science Foundation of China (Grants No. 11404233, 11574224, and 11504032) and the Natural Science Foundation of Jiangsu Province (Grants No BK20161213). ZY acknowledges the support from A Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD), and Jiangsu Provincial Key Laboratory of Radiation Medicine and Protection.References
- H. W. Kroto, J. R. Heath, S. C. Obrien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163 CrossRef CAS.
- S. Iijima, Nature, 1991, 354, 56–58 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451–10453 CrossRef CAS PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200 CrossRef CAS PubMed.
- A. Krishnan, E. Dujardin, T. W. Ebbesen, P. N. Yianilos and M. M. J. Treacy, Phys. Rev. B, 1998, 58, 14013–14019 CrossRef CAS.
- T. W. Ebbesen, H. J. Lezec, H. Hiura, J. W. Bennett, H. F. Ghaemi and T. Thio, Nature, 1996, 382, 54–56 CrossRef CAS.
- N. L. Rangel, J. C. Sotelo and J. M. Seminario, J. Chem. Phys., 2009, 131, 031105 CrossRef PubMed.
- J. W. Che, T. Cagin and W. A. Goddard, Nanotechnology, 2000, 11, 65–69 CrossRef CAS.
- O. C. Compton and S. T. Nguyen, Small, 2010, 6, 711–723 CrossRef CAS PubMed.
- L. L. Zhang and X. S. Zhao, Chem. Soc. Rev., 2009, 38, 2520–2531 RSC.
- M. Liu, X. B. Yin, E. Ulin-Avila, B. S. Geng, T. Zentgraf, L. Ju, F. Wang and X. Zhang, Nature, 2011, 474, 64–67 CrossRef CAS PubMed.
- M. S. Mauter and M. Elimelech, Environ. Sci. Technol., 2008, 42, 5843–5859 CrossRef CAS PubMed.
- H. Q. Bao, Y. Z. Pan, Y. Ping, N. G. Sahoo, T. F. Wu, L. Li, J. Li and L. H. Gan, Small, 2011, 7, 1569–1578 CrossRef CAS PubMed.
- X. Michalet, F. F. Pinaud, L. A. Bentolila, J. M. Tsay, S. Doose, J. J. Li, G. Sundaresan, A. M. Wu, S. S. Gambhir and S. Weiss, Science, 2005, 307, 538–544 CrossRef CAS PubMed.
- X. Wang, L. L. Yang, Z. Chen and D. M. Shin, Ca-Cancer J. Clin., 2008, 58, 97–110 CrossRef PubMed.
- H. Li, J. Huang, J. Lv, H. An, X. Zhang, Z. Zhang, C. Fan and J. Hu, Angew. Chem., 2005, 44, 5100–5103 CrossRef CAS PubMed.
- Y. Chong, C. Ge, Z. Y. Yang, J. A. Garate, Z. Gu, J. K. Weber, J. J. Liu and R. H. Zhou, ACS Nano, 2015, 9, 5713–5724 CrossRef CAS PubMed.
- X. Tian, Z. X. Yang, G. X. Duan, A. Q. Wu, Z. L. Gu, L. L. Zhang, C. Y. Chen, Z. F. Chai, C. C. Ge and R. H. Zhou, Small, 2017, 13, 1602133 CrossRef PubMed.
- G. H. Zuo, X. Zhou, Q. Huang, H. P. Fang and R. H. Zhou, J. Phys. Chem. C, 2011, 115, 23323–23328 CrossRef CAS.
- G. H. Zuo, Q. Huang, G. H. Wei, R. H. Zhou and H. P. Fang, ACS Nano, 2010, 4, 7508–7514 CrossRef CAS PubMed.
- S. S. Karajanagi, A. A. Vertegel, R. S. Kane and J. S. Dordick, Langmuir, 2004, 20, 11594–11599 CrossRef CAS PubMed.
- M. Calvaresi and F. Zerbetto, ACS Nano, 2010, 4, 2283–2299 CrossRef CAS PubMed.
- M. Li, X. J. Yang, J. S. Ren, K. G. Qu and X. G. Qu, Adv. Mater., 2012, 24, 1722–1728 CrossRef CAS PubMed.
- C. X. Li, J. Adamcik and R. Mezzenga, Nat. Nanotechnol., 2012, 7, 421–427 CrossRef CAS PubMed.
- M. Mahmoudi, O. Akhavan, M. Ghavami, F. Rezaee and S. M. A. Ghiasi, Nanoscale, 2012, 4, 7322–7325 RSC.
- D. M. Bozinovski, P. V. Petrovic, M. R. Belic and S. D. Zaric, Chemphyschem, 2018, 19, 1226–1233 CrossRef CAS PubMed.
- Z. X. Yang, C. C. Ge, J. J. Liu, Y. Chong, Z. L. Gu, C. A. Jimenez-Cruz, Z. F. Chai and R. H. Zhou, Nanoscale, 2015, 7, 18725–18737 RSC.
- K. H. Park, M. Chhowalla, Z. Iqbal and F. Sesti, J. Biol. Chem., 2003, 278, 50212–50216 CrossRef CAS PubMed.
- Z. L. Gu, Z. X. Yang, Y. Chong, C. C. Ge, J. K. Weber, D. R. Bell and R. H. Zhou, Sci. Rep., 2015, 5, 10886 CrossRef CAS PubMed.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- W. L. Jorgensen, J. Am. Chem. Soc., 1989, 111, 3770–3771 CrossRef CAS.
- H. J. Woo and B. Roux, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6825–6830 CrossRef CAS PubMed.
- F. Zeller and M. Zacharias, J. Chem. Theory Comput., 2014, 10, 703–710 CrossRef CAS PubMed.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38 CrossRef CAS.
- B. Shi, G. H. Zuo, P. Xiu and R. H. Zhou, J. Phys. Chem. B, 2013, 117, 3541–3547 CrossRef CAS PubMed.
- R. Sitko, B. Zawisza and E. Malicka, TrAC, Trends Anal. Chem., 2012, 37, 22–31 CrossRef CAS.
- E. Lindahl, B. Hess and D. van der Spoel, J. Mol. Model., 2001, 7, 306–317 CrossRef CAS.
- D. Van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- J. S. Hub, B. L. de Groot and D. van der Spoel, J. Chem. Theory Comput., 2010, 6, 3713–3720 CrossRef CAS.
- B. Roux, Comput. Phys. Commun., 1995, 91, 275–282 CrossRef CAS.
- Z. L. Gu, Z. Y. Yang, Y. Chong, C. C. Ge, J. K. Weber, D. R. Bell and R. H. Zhou, Sci. Rep., 2015, 5, 10886 CrossRef CAS PubMed.
- G. B. Yu and J. Zhou, Phys. Chem. Chem. Phys., 2016, 18, 23500–23507 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra10015b |
| This journal is © The Royal Society of Chemistry 2019 |