DOI:
10.1039/C8RA10153A
(Paper)
RSC Adv., 2019,
9, 11281-11288
Solvation effect and binding of rhaponticin with iron: a spectroscopic and DFT/TDDFT study†
Received
11th December 2018
, Accepted 12th March 2019
First published on 11th April 2019
Abstract
In this article, both experimental and computational methods are employed to investigate the photophysics of rhaponticin (RH). The bathochromic shift was observed in absorption and fluorescence spectra with increasing solvent polarity, which implied that the charge transition of RH involved was π → π*. The results showed that RH possess strong intramolecular charge transfer (ICT), and the most important parameter to characterize the photophysical behavior of RH is the intermolecular hydrogen bonding ability of the solvent. The hydrogen bonding effect occurred at the localized electron-acceptor oxygen at the glycoside bond. Density functional theory (DFT) and time dependent density functional theory (TDDFT) were used to obtain the most stable structure, electronic excitation energy, dipole moments and charge distribution. The result was found to be 2.23 and 3.67 D in ground state and excited state respectively. Fluorescence quenching of RH owing to the photoinduced electron transfer (PET) is facilitated in alkaline media. The pKa value of RH was 6.39, which defined RH as a highly efficient “off–on” switcher. The effect of different metal ions on the fluorescence spectra of RH was also investigated, and the fluorescence quenching of RH depended on the nature of ions. The best performance was accomplished for binding with the Fe3+ ion. The interactions of RH with the Fe3+ ion were studied by FT-IR and HPLC, and the binding parameter was calculated by the Stern–Volmer equation. The results obtained reveal the binding activity of RH can make this a candidate as a good source of new agents for thalassemic patients.
Introduction
The most serious complication of β-thalassemia is iron overload, and it is vital to control it within a reasonable range. Recently, a comprehensive overview on iron overload in β-thalassemia has been presented in a paper by Crisponia and Remelli.1 Design and development of iron selective fluorescent chemosensors has caused great concern, due to their importance in many biological and environmental processes.
As a major representative of the stilbene glucoside compounds, rhaponticin (RH, Fig. 1) exists widely in medicinal plant of Rheum L., such as Rheum officinale, Rheum undulatum, Rheum hotaoense and Rheum palmatum.2 Previous works of our working-team showed that RH possessed various biological effects including potent antitumor, antitumor-promoting, antithrombotic, antioxidant and vasorelaxant activities.3–5 Moreover, the atoms of the stilbene moiety are nearly coplanar in the molecule of RH, and the dihedral angle between ring (C2–C7) and ring (C10–C15) is 9.0°. The hydrogen bonds exist among the hydroxyl group (–OH), methoxy group (–OCH3) and O atom, and link the molecules into a complicated 3D framework.3 Moreover, the hydroxyl groups at C-11 and methoxy group at C-12 of act electron donor and the glycoside fragment functions as a receptor unit, and there exists electronic transition as π → π*, belong to polyphenol derivatives. Therefore, RH would show optical property which is highly sensitive to its surroundings, it is reasonable to use it as a polarity probe and it also can be applied in medicine and chemistry.6 The multiple pharmacological activities make it be worth carrying out a further study on the photophysical property of RH.
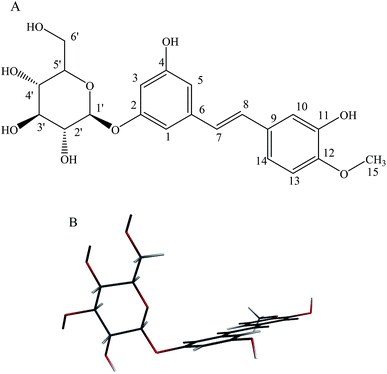 |
| | Fig. 1 (A): Chemical structure of rhaponticin (RH), (B): minimum-energy B3LYP/DZP structure of RH. | |
Solvent effect is closely related to the nature and extent of solute–solvent interactions developed locally in the immediate vicinity of solute. One key approach to understand solvent effects is the solvent-induced changes in the electronic transition of solutes generally referred to as solvatochromism. The application of computational methods to studies in photophysics chemistry is instrumental in understanding phosphorescent mechanisms.7 In recent years, approaches using density functional theory (DFT) and time dependent density functional theory (TDDFT) have received large acceptance for describing the ground state and excited state properties of photoluminescence molecules, such as geometrical parameters, energy gap, dipole moments and excited energy.8
Until now, there is no report available in the literature on the luminescent mechanism of RH. Therefore, we focus on the photophysical properties of RH, and we present a comparative study of the experimental absorption and fluorescence spectra with DFT/TDDFT calculations in this work. The binding of RH with iron was also studied by spectroscopic, chromatographic methods, which would have a great significance in pharmacology and clinical medicine as well as methodology.
Materials and methods
RH was isolated by authors from R. hotaoense,3 and its purity was evaluated to be above 99% (HPLC and spectral analysis). The stock solutions of RH (1.5 × 10−5 M) were prepared by dissolving appropriate amount of RH in 10 mL different solvents, and the solvents applied were analytical grade and used without further purification.
All fluorescence spectra were carried out on an F-7000 fluorescence spectrometer (Hitachi, Japan) equipped with a 150 W xenon lamp, and the slit width was 5 nm. All absorption spectra were recorded by UV-2501PC spectrophotometer (Shimadzu, Japan) in the range of 200–400 nm. Fourier Transform Infrared Spectroscopy (FT-IR) spectra were obtained using an EQUINOX55 fourier transformed infrared spectrometry (Bruker Company, Germany) in the range of 4000–600 cm−1. HPLC analyses were performed on an Agilent 1200 series system (Agilent, Santa Clara, CA), which consisted of an auto sampler, a Zorbax carbohydrate column (0.46 × 15.0 cm), a solvent system of acetonitrile/methanol (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70), at a flow rate of 1.0 mL min−1 with the UV detector wavelength set at 324 nm, and the injection volume was 20 μL. Data were acquired and processed with an Agilent ChemStation software external calibration.
70), at a flow rate of 1.0 mL min−1 with the UV detector wavelength set at 324 nm, and the injection volume was 20 μL. Data were acquired and processed with an Agilent ChemStation software external calibration.
The solvatochromic method was used to calculate the dipole moment in ground and excited state. All calculations in the present study were performed by using the Amsterdam Density Functional package (ADF) 2010.01 program.9 Geometry optimization in the ground state was carried out using B3LYP density functional calculations, with the DZP basis sets.10 The lowest singlet excited-states of both the isolated RH and the hydrogen-bonded RH were calculated using time-dependent density functional theory (TD-DFT) with B3LYP hybrid functional and the TZVP basis set.11
Results and discussions
Solvent effects on the absorption and fluorescence spectra of RH
Theoretical density functional theory (DFT) calculations were performed to gain more insight into the electronic properties of these systems that appear as promising molecules for light-harvesting applications.12 Fig. 1B displays the minimum-energy molecular geometry computed for RH at the B3LYP-DZP level. As expected, RH exhibits the typical boat conformation, and the atoms of the stilbene moiety are coplanar, suggesting that an efficient π-conjugation can operate between the donor and acceptor units in RH molecule. The absorption and fluorescence spectra of RH in different solvents were presented in Fig. 2. The values of the absorption and fluorescence spectral maxima were listed in Table 1. As we know, the shift can be described as hypsocromic or bathochromic depending on whether the absorption maximum occurs at a shorter or longer wavelength respectively. As seen from Fig. 2A, the absorption maximum is obtained around 311 nm in dioxane and it is about 327 nm in water. In the present study, the absorption spectra shift to longer wavelength with increasing solvent polarity, indicating RH exhibits a positive solvatochromism and π → π* transition. According to Jayabharathi, the bathochromic shift happens when the dipole moment of the compound increases during the electronic transition i.e., the dipole moment of excited state is higher compared to that in the ground state (μe > μg) and the excited state is formed in solvent cage of already partly oriented solvent molecules.13 In such cases, the relaxed excited state S1 will be energetically stabilized relative to the ground state S0 and a significant red shift of the absorption will be observed.
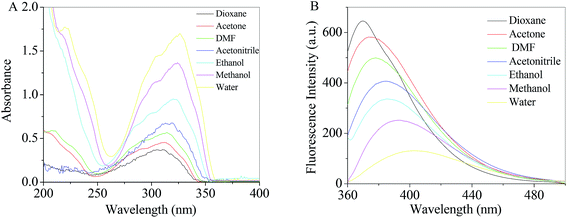 |
| | Fig. 2 Absorption (A) and fluorescence (B) spectra of RH in different solvents. | |
Table 1 The physical or spectral parameters of solvents and spectral data of RHa
| Solvents |
λa (nm) |
λF (nm) |
Δλ (nm) |
IF (a.u.) |
ε |
n |
F1 |
F2 |
| F1 = f(ε, n), F2 = f(ε, n) + 2g(n). |
| 2,4-Dioxane |
311 |
370 |
59 |
656 |
2.21 |
1.422 |
0.044 |
0.671 |
| Toluene |
312 |
371 |
59 |
642 |
2.38 |
1.497 |
0.029 |
0.700 |
| Diethylether |
312 |
372 |
60 |
637 |
4.27 |
1.353 |
0.371 |
0.851 |
| Ethyl acetate |
312 |
372 |
60 |
628 |
6.02 |
1.370 |
0.493 |
1.001 |
| Chloroform |
312 |
373 |
61 |
615 |
4.81 |
1.443 |
0.371 |
0.985 |
| THF |
314 |
375 |
61 |
610 |
7.52 |
1.407 |
0.550 |
1.103 |
| Acetone |
314 |
376 |
62 |
595 |
21.01 |
1.359 |
0.795 |
1.282 |
| DMF |
314 |
378 |
64 |
501 |
36.70 |
1.431 |
0.844 |
1.424 |
| DMSO |
316 |
381 |
65 |
456 |
47.20 |
1.479 |
0.843 |
1.496 |
| Acetonitrile |
321 |
387 |
66 |
402 |
38.80 |
1.344 |
0.861 |
1.332 |
| Butanol |
319 |
385 |
64 |
385 |
17.40 |
1.399 |
0.749 |
1.296 |
| Propanol |
320 |
386 |
66 |
363 |
1.385 |
20.60 |
0.781 |
1.303 |
| Ethanol |
323 |
390 |
67 |
343 |
24.55 |
1.361 |
0.812 |
0.651 |
| Methanol |
325 |
394 |
69 |
252 |
33.70 |
1.329 |
0.860 |
0.648 |
| Water |
327 |
403 |
76 |
109 |
78.50 |
1.333 |
0.914 |
0.683 |
At the same time, the fluorescence spectral studies of RH with excitation wavelength of 355 nm were carried out in different solvents (Fig. 2B), the peak maximum shifted from 370 to 403 nm (bathochromic shift) as the solvent polarity increased (dioxane to water). Meantime, the Stokes shift of RH in dioxane is 56 nm, whereas the Stokes shifts in water increases to 76 nm, respectively. The increasing Stokes shift in polar protic solvents suggests that the fluorescent state of RH is the intramolecular charge transfer (ICT) feature.
Table 1 and Fig. 2B show fluorescence quenching and red-shift behavior of RH in protic solvents compared with that in aprotic solvent. On the one hand, in a polar protic solvent with a relatively high hydrophilicity (e.g., methanol or water), RH takes a stretched conformation with the plane of stilbene moiety. In a non-polar solvent with a high hydrophobicity (e.g., dioxane), the conformation of the RH molecule is twisted and the twisted intramolecular charge transfer (TICT) state and self-association fluorescence emission emerge.14 On the other hand, ICT state is more likely to relax by non-radiative processes than by radiative processes, which results in quenching of RH in protic solvents. Moreover, quenching and red-shift are mainly therefore clearly associated with hydrogen bonding, and the excitated-state hydrogen bond strengthening effect of RH with protic solvents.15 When the acceptor (oxygen atom at glycoside band) is hydrogen-bonded, a more charge-separated chromophore is more stabilized and the hydrogen bond in the corresponding electronic excited state is strengthened. Therefore, the quenching and red-shift in proic solvent is caused by the TICT process and excited-state hydrogen bond strengthening effect. In addition, as shown in Table 1, the effect of solvents on the emission spectra of RH is more remarkable than that on absorption spectra (absorption and emission wavelength shifts 16 and 33 nm from dioxane to water, respectively), which implies that the less polar nature of RH in the ground state than in excited state and the ground state energy distribution is not affected by the solvents.
Determination of dipole moments of RH
The dipole moment of the ground and excited state is related to the electron distribution, which will be affected by various solvents. Thus, it is important to study the dipole moments of ground and exited state of RH for it offers information about the change in the electronic distribution on excitation. According to Valeur et al.,16 quantum mechanical second-order perturbation theory of absorption (νa) and fluorescence (νf) band shifts in different solvents of varying permittivity (ε) and refractive index (n) relative to the band position of a solute molecule is obtained. In order to avoid the hydrogen bonding between RH and protic solvents, we choose the aprotic solvents in Table 1, from 2,4-dioxane to acetonitrile, and the related equations are as followed:| | |
νa − νf = m1f(ε, n) + const
| (1) |
| | |
νa + νf = −m2[f(ε, n) + 2g(n)] + const
| (2) |
where| |
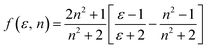 | (3) |
with| |
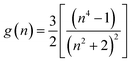 | (4) |
where, ε is the dielectric constant and n is the refractive index.| |
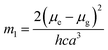 | (5) |
and| |
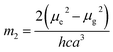 | (6) |
where, h is the Planck's constant and c is the velocity of light in vacuum, and m1 and m2 were calculated from the eqn (1) and (2) denoting the absorption and fluorescence band shifts. The values of ground state and excited state dipole moment, μg and μe, were obtained from eqn (5) and (6):17,18| |
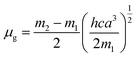 | (7) |
| |
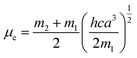 | (8) |
and| |
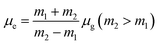 | (9) |
The value of the solute cavity radius a was calculated from the molecular volume by Suppan's equation:19
| |
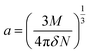 | (10) |
Here N is the Avogadro's number, M is the solute's weight and δ is the solid-state density of solute molecule. Here m is the slope of the linear plot of permittivity (ε) and refractive index (n) versus Stokes shift (Fig. S1A and B, ESI†). Then the dipole moment can be calculated by above parameters. One can see that μg = 2.23 D and μe = 3.67 D. The dipole moment of the RH in excited state is higher than that in ground state owing to the change in electronic distribution. This result means a more polar and stable structure in excited state than that of in ground state, which is consistent with the result of absorption spectra.
Theoretical calculation using DFT and TDDFT
Fig. 3 shows the orbital energy levels of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) and their energy gap for RH in dioxane, acetone, ethanol and water. And the calculated energy gaps, wavelengths of the lowest electronic transitions, oscillator strengths, and main orbital transition contribution and corresponding CI coefficients of the low-lying electronically excited states of RH in four solvents were listed in Table 2. The observed positive solvatochromism is reproduced by DFT/TDDFT calculations, and the maximum oscillator strengths are corresponding to the HOMO → LUMO+2 orbital transition. The occupied orbital was mainly localized on the stilbene unit whereas the LUMO+2 is centered on the glycoside part, suggesting a strong propensity for intramolecular charge transfer from the electron-donor hydroxyl groups at C-11 and methoxy group at C-12 to the glycoside acceptor, and therefore correspond to π → π* transitions. As seen from Fig. 3 that the energy level of the HOMO increases from −5.23 eV in dioxane to −5.18 eV in water, suggesting the intermolecular hydrogen bonding raises the energy level of the HOMO. Meantime, the energy level of the LUMO decreases slightly from −2.57 to −2.58 eV from dioxane to water, indicating that intermolecular hydrogen bonding shows less effect to the electronically excited state of RH than ground state.20 The energy gap (Eg) between the HOMO and LUMO reduces from 2.66 to 2.60 eV from dioxane to water. The reducing energy gap between the HOMOs and LUMOs is consistent with the absorption and fluorescence spectral red-shift of RH in polar solvents. On the other hand, from dioxane to water, there is a quasi parallel energy stabilization of the HOMO−2 and HOMO and a concomitant small destabilization of the LUMO. These evolutions result in the decrease of the HOMO → LUMO and HOMO → (LUMO+2) gap and thus in a bathochromic shift of the corresponding spectral behavior.21
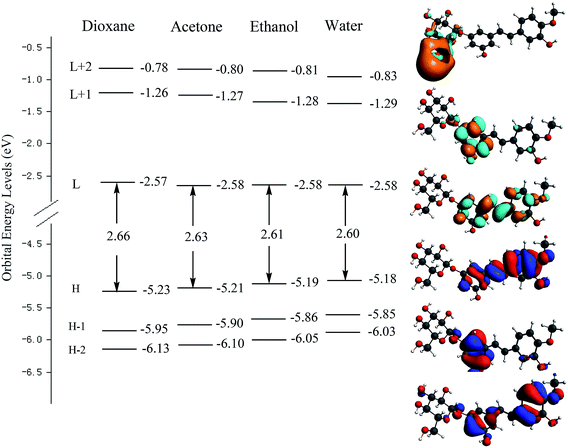 |
| | Fig. 3 Electron density contours and orbital energies calculated for the HOMOs and LUMOs of RH at the B3LYP/DZP level. H and L denote HOMO and LUMO, respectively. | |
Table 2 Calculated energy gap (Eg), oscillator strength (f) and main orbital transition contribution (Contrib.) and absorption wavelength for RH in different solvents
| Solvent |
Contrib. |
CI componenta |
Theory (nm) |
Experiment (nm) |
Eg (eV) |
f |
| The transition was shown by an arrow from one orbital to another, followed by its percentage CI (configuration interaction) component. |
| Dioxane |
HOMO → LUMO+2 |
0.951 |
315 |
311 |
2.66 |
0.243 |
| Toluene |
HOMO → LUMO+2 |
0.904 |
320 |
314 |
2.63 |
0.246 |
| Ethanol |
HOMO → LUMO+2 |
0.939 |
331 |
323 |
2.61 |
0.248 |
| Water |
HOMO → LUMO+2 |
0.943 |
339 |
327 |
2.60 |
0.252 |
The electronic excitation energies and corresponding oscillator strengths of RH and the hydrogen-bonded RH are calculated using the TDDFT method and presented in Table 3. For both the isolated RH and the hydrogen-bonded RH, the S1 state has the largest oscillator strength, which means that both of them can be initially photoexcited to the S1 state. The excitation energy of the S1 state is calculated to be at 4.11 and 3.92 eV for RH and the hydrogen bonded RH, suggesting that the hydrogen bonding induces a decrease for the excitation energy of the S1 state, and the hydrogen bond is strengthened in this excited state.22,23
Table 3 Calculated TD-DFT excitation energy (E) and corresponding oscillator strengths (in the parentheses) of RH and the hydrogen-bonded RH complex at the TD-DFT/B3LYP/TZVP level. The orbital transitions (S0 → S1) and contributions are also listed. HOMO: H, LUMO: L
| |
RH |
Hydrogen-bonded RH complex |
| S1 |
4.11 (0.241) |
3.92 (0.261) |
| H → L (93.2%) |
H → L (94.3%) |
| S2 |
4.30 (0.034) |
4.25 (0.123) |
| S3 |
4.52 (0.202) |
4.48 (0.082) |
| S4 |
4.68 (0.023) |
4.62 (0.023) |
| S5 |
4.85 (0.253) |
4.78 (0.232) |
| S6 |
4.92 (0.021) |
4.86 (0.051) |
The orbital transition contributions for the lowest single states S1 state of the isolated RH and the hydrogen-bonded RH are also presented in Table 3. It can be seen that only the HOMO and LUMO are involved in the S1 state. To depict the nature of the lowest singlet excited state S1, the HOMO and LUMO of both the RH and the hydrogen-bonded RH have been calculated and are shown in Fig. 4. As shown in Fig. 4, the electron density on the hydroxyl oxygen atom at C-11 in hydrogen-bonded RH is also remarkably decreased after the HOMO–LUMO transition. However, due to the formation of the intermolecular hydrogen bonds, the intramolecular hydrogen bond between the hydroxyl groups at C-11 and methoxy group at C-12 is not strengthened. On the contrary, the intermolecular hydrogen bond is significantly strengthened due to the remarkable decrease of the electron density on the hydroxyl oxygen atom at C-11.24 Moreover, compared to RH, the calculated absorption of hydrogen-bonded RH shift to longer wavelengths (ca. 5 nm, Fig. S2†). Compared with RH, the formation of the intermolecular hydrogen bonds will stabilize both the HOMO and the LUMO of the hydrogen-bonded form. The HOMO–LUMO energy decreases from 2.55 eV in the RH form to 2.36 eV in the hydrogen-bonded form respectively, which should be responsible for the 5 nm red shift of the S1 absorption for the hydrogen bonded RH. In addition, it can be found that the HOMO and LUMO are the π and π* character for both the RH and hydrogen bonded RH, suggesting that the S1 state is of the π–π* feature.
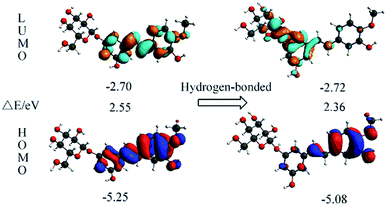 |
| | Fig. 4 Calculated for the HOMOs and LUMOs of RH (left) and the hydrogen-bonded RH with the oxygen atom at glycosidic bond (right). The orbital energies and energy gaps are also shown. | |
Moreover, the value of the dipole moments (Dm) in the excited states is 3.87 D (Table 4), and the difference between the dipole moments of the excited and ground states is 1.31 D, indicating that the value of dipole moment in the excited state of RH is lager, which explains well the experimental observations that RH shows a bathochromic shift of spectra and the large Stokes shift with increasing solvent polarity. The results of theoretical calculations have previously been shown to be in good agreement with experimental data.
Table 4 Calculated dipole moment (debye) for the ground (μg) and the excited (μe) states of RH and hydrogen bonded RH in vacuuma
| Compound |
Experimental |
Theoretical |
Calculation |
| μg |
μe |
Δμ |
μg |
μe |
Δμ |
λa (nm) |
| Oscillator strength. |
| RH |
2.23 |
3.67 |
1.44 |
2.56 |
3.87 |
1.31 |
324 |
| RH⋯H |
— |
— |
— |
6.82 |
10.58 |
3.76 |
329 |
Effect of pH on the fluorescence spectra of RH
The pH effects on the emission and excitation spectra of RH were investigate in methanol. As seen from Fig. 5A, when the excitation wavelength is set at 340 nm, RH exhibits a maximum around 390 nm. The intensity decreases gradually with increasing pH along with a red shift (from 390 to 402 nm). Fluorescence excitation spectra of RH are the similar response to the change of pH (Fig. 5B). After careful titration from pH 3 to 11, the emission intensity decreases practically eleven times (fluorescence quenching, FQ = 11.43) (Fig. 5B insert). The pKa value of RH is calculated to be 6.39 by the eqn (11).25| | |
log[(IF max − IF/IF − IF min)] = pH − pKa
| (11) |
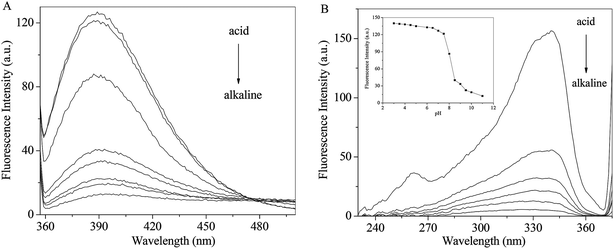 |
| | Fig. 5 Effect of pH on the emission (A) and excitation (B) spectra of RH; insert: pH dependence of the fluorescence intensity of RH in methanol. The excitation and emission wavelengths were set at 340 and 390 nm, respectively, c(RH) = 50.0 μM. | |
The pKa result suggests that RH is highly efficient “off–on” switchers for pH, and also it is a potential useful sensor for higher pH measurement. Moreover, from these changes the emission is switched “off–on” between ca. pH 6.8 and 8.0. This switching process is also found to be reversible. These changes are of such magnitude that they can be considered as representing two different “states”, where the fluorescence emission is “switched off” in alkaline solution and “switched on” in acidic solution. These changes are due to the deprotonation of the hydroxyl groups of RH at 4-C and 11-C, which engages in photoinduced electron transfer (PET) quenching of RH excited state and upon protonation of the hydroxyl groups, and the quenching process is substantially removed.26
Effect of metal ions on the fluorescence spectra of RH
The effects of different metal ions on the fluorescence spectra of RH are investigated. The presence of metal ions in RH solution as guests is signaled by fluorescence quenching (FQ). The FQ value is determined from the ratio of the maximum fluorescence intensity (solution free of metal ions) to the one after metal ions addition. Fig. 6 presents the FQ values for RH in the presence of different metal ions at the same concentration of 10.0 μM. As seen these values depends on the nature of the added ions and their ability to coordinate with the RH ligands. The highest FQ value is observed in the presence of Fe3+ ion. The binding ability of RH with different concentrations of Fe3+ ion is investigated by the spectroscopic and chromatographic methods.
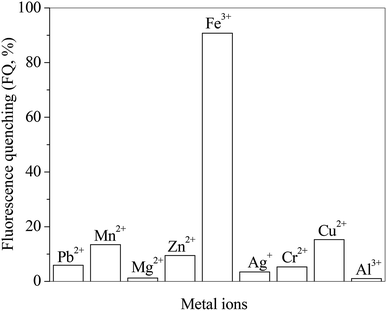 |
| | Fig. 6 Effect of different metal ions on the ratio of fluorescence quenching of RH in methanol. c(metal ions) = 10.0 μM, c(RH) = 50.0 μM. T = 298 K. | |
As shown in Fig. 7A, the fluorescence intensity of RH drops sharply with increasing concentrations of Fe3+ ion along with the maxima bathochromic shift 9 nm. The absorbance of RH increases and maxima shifts towards shorter wavelength region with the addition of Fe3+ ion. The spectral results indicate that Fe3+ ion binds with RH and a non-luminance RH–Fe3+ complex forms.
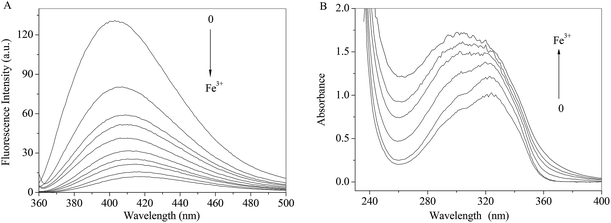 |
| | Fig. 7 Effect of Fe3+ ion on the fluorescence (A) and absorption (B) spectra of RH in methanol. c(Fe3+) = 0–13.0 μM, c(RH) = 50.0 μM. T = 298 K. | |
In order to eliminate the influence of water and complex of RH–Fe3+, FT-IR measurements were performed in the absence and presence of Fe3+ ion. The major differences in FT-IR spectra are observed in the regions of 1500, 1660 and 3300–3340 cm−1. A sharp peak near 1660 cm−1 appears after addition of Fe3+ ion, which causes by H2O. The peak at 3309 cm−1 (Fig. 8A) related to the large amount of –OH in the RH molecule, and in the presence of Fe3+ ion, the hydroxyl peak shifts to 3336 cm−1. According to the result of FT-IR spectra, we can confirm that the formation of RH–Fe3+ complex. The addition of Fe3+ ion results in noticeable decrease of transmittance of hydroxyl peak due to H-bonded hydroxyls and the increasing intensity of the bridged OH groups. Double bond C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretches at 1500 cm−1 and the decreasing intensity could be attributed to the contraction of the aromatic ring after the addition of Fe3+ ion. On the other hand, as seen from Fig. 8B that the intensity and peak area decrease with the addition of Fe3+ ion, and the peak time changes slightly from 1.57 to 1.65 min. The HPLC result indicates that Fe3+ ion binds with RH non-covalently and a RH–Fe3+ complex forms.
C stretches at 1500 cm−1 and the decreasing intensity could be attributed to the contraction of the aromatic ring after the addition of Fe3+ ion. On the other hand, as seen from Fig. 8B that the intensity and peak area decrease with the addition of Fe3+ ion, and the peak time changes slightly from 1.57 to 1.65 min. The HPLC result indicates that Fe3+ ion binds with RH non-covalently and a RH–Fe3+ complex forms.
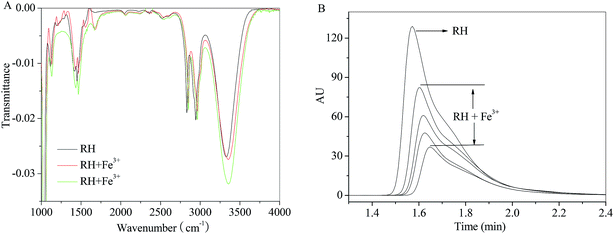 |
| | Fig. 8 Effect of Fe3+ ion on the FT-IR spectra and HPLC of RH in methanol. c(Fe3+) = 0–13.0 μM, c(RH) = 50.0 μM. T = 298 K. | |
Combining with the results of spectra and chromatography, we deduce that the binding of Fe3+ ion with RH occurs at the C-11 hydroxyl groups and the O atom of the methoxy group through hydrogen bond, and the decreasing electron donor ability facilitates the quenching (Fig. S3†). And the double bond C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C linking aromatic ring of RH molecule distorts more strictly by binding with Fe3+ ion.
C linking aromatic ring of RH molecule distorts more strictly by binding with Fe3+ ion.
Binding parameters of interaction of RH with Fe3+
Fluorescence quenching can occur by different mechanisms, usually classified as dynamic quenching and static quenching. In order to clarify the quenching mechanism, the Stern–Volmer equation was used to analyze the quenching data:27| | |
F0/F = 1 + KSV[iron]
| (12) |
where F0 and F are the fluorescence intensities in the absence and presence of quencher (Fe3+ ion), respectively, KSV is the Stern–Volmer quenching constant and [iron] is the concentration of Fe3+ ion. The values of KSV could be measured from the slope by plotting F0/F against [iron] (Fig. S4A†), and the corresponding results were listed in Table S1.† The binding constants and numbers of binding sites of interaction of RH with Fe3+ could be determined by the modified Stern–Volmer equation:21| |
lg[(F0 − F)/F] = lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K + n K + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lg[iron] lg[iron]
| (13) |
where K is the binding constant, n is the number of binding sites per RH for Fe3+ ion, and F0, F and [iron] have the same meanings as in eqn (12). The values of K and n are measured from the intercept and slope by plotting lg[(F0 − F)/F] against lg[iron] (intercept = lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, slope = n) (Fig. S4B†), and the corresponding results are listed in Table S1.† As shown in Table S1,† the value of KSV and K is almost 106 M, indicating that the quenching and binding effect is considerable, and RH can be candidate as a good source of new iron binding agents. The value of n approximately is equaled to 1, indicating that there is one class binding site in RH for Fe3+. Because of the formation of the RH–Fe3+ complex, the quenching of RH is initiated by static quenching.
K, slope = n) (Fig. S4B†), and the corresponding results are listed in Table S1.† As shown in Table S1,† the value of KSV and K is almost 106 M, indicating that the quenching and binding effect is considerable, and RH can be candidate as a good source of new iron binding agents. The value of n approximately is equaled to 1, indicating that there is one class binding site in RH for Fe3+. Because of the formation of the RH–Fe3+ complex, the quenching of RH is initiated by static quenching.
Conclusion
In this work, solvent effect on the photophysical behavior of RH has been studied by absorption, fluorescence spectra and DFT/TDDFT calculations. The observed solvatochromic shift of spectra was used to calculate the ground and excited state pole moment of 2.23 and 3.67 D by Lippert–Suppan equation, respectively. Moreover, the increased Stokes shift in polar solvents suggests that RH is TICT feature, and correspond to π → π* transitions. The photoluminescence behavior of RH is strongly modulated by the formation of intermolecular hydrogen bonds between RH and protic solvents. The excitation energy of the S1 state is calculated to be at 4.11 and 3.92 eV for RH and the hydrogen bonded RH, suggesting that the hydrogen bonding induces a decrease for the excitation energy of the S1 state, and the hydrogen bond is strengthened in this excited state. Quantitative estimation of the relative contribution of several solvatochromic parameters indicates that the hydrogen-bond donor ability of the solvent is one of the factors governing the excited-state properties of RH, which were verified by DFT/TDDFT calculations. The intermolecular hydrogen bonding occurred at the localized electron-acceptor oxygen at the glycoside bond. The effect of pH indicates that the fluorescence quenching of RH owing to the deprotonation of donor group and PET is facilitated in alkaline media. The pKa is 6.39, which defines RH as a highly efficient “off–on” switcher. The interactions of RH with Fe3+ ion are studied by FT-IR and HPLC, and the binding parameter is calculated by the Stern–Volmer equation, and there is one class binding site of RH for Fe3+ ion. These experimental data would be available for clinical and analytical application of RH as an active drug and chromogenic reagent.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Training Programs of Innovation and Entrepreneurship for Undergraduates (No. 201511080589).
References
- G. Crisponia and M. Remelli, Coord. Chem. Rev., 2008, 252, 1225–1240 CrossRef.
- N. Rupprich and H. Hildebrand, Arch. Biochem. Biophys., 1980, 200, 72–78 CrossRef CAS PubMed.
- Y. Y. Zhao, X. Y. Qin, S. P. Chen, Y. M. Zhang, R. C. Lin and W. J. Sun, J. Chem. Crystallogr., 2010, 10, 275–293 Search PubMed.
- Y. Y. Zhao, Q. Su, X. L. Cheng, X. J Tan, X. Bai and R. C. Lin, Bioanalysis, 2012, 6, 713–723 CrossRef PubMed.
- Y. Y. Zhao, L. L. Wang, H. Miao, C. C. Ho, J. Li, X. L. Cheng, Y. M. Zhang, R. C. Lin and W. J. Sun, Chromatographia, 2011, 73, 599–603 CrossRef CAS.
- Y. Sun, Z. Ji, X. H. Liang, G. B. Li, S. Y. Yang, S. Wei, Y. Y. Zhao, X. Y. Hu and J. Fan, Spectrochim. Acta, Part A, 2012, 87, 171–178 CrossRef CAS PubMed.
- G. J. Zhao and K. L. Han, Acc. Chem. Res., 2012, 45, 404–413 CrossRef CAS PubMed.
- J. Jayabharathi, V. Thanikachalam, M. V. Perumal and N. Srinivasan, Spectrochim. Acta, Part A, 2011, 79, 236–244 CrossRef CAS PubMed.
- ADF 2010.01, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed.
- K. H. Birjkumar, N. D. Bryan and N. Kaltsoyannis, Dalton Trans., 2011, 40, 11248–11257 RSC.
- G. J. Zhao and K. L. Han, ChemPhysChem, 2008, 9, 1842–1846 CrossRef CAS PubMed.
- P. A. Bouit, C. Villegas, J. L. Delgado, P. M. Viruela, R. P. Amérigo, E. Ortí and N. Martín, Org. Lett., 2011, 13, 604–607 CrossRef CAS PubMed.
- K. Saravanan, N. Srinivasan, V. Thanikachalam, J. Jayabharathi and J. Fluoresc, Chem. Phys. Lett., 2011, 21, 65–80 CAS.
- A. Perrier, S. Aloïse, Z. Pawlowska, M. Sliwa, F. Maurel and J. Abe, Photoinduced intramolecular charge transfer process of betaine pyridinium: a theoretical spectroscopic study, Chem. Phys. Lett., 2011, 515, 42–48 CrossRef CAS.
- G. J. Zhao, J. Y. Liu, L. C. Zhou and K. L. Han, J. Phys. Chem. B, 2007, 111, 8940–8945 CrossRef CAS PubMed.
- B. Valeur, M. Nuno and B. Santos, Analytical Methods in Supramolecular Chemistry, Wiley-VCH, Weinheim, 2012 Search PubMed.
- A. Maciejewski1, E. Krystkowiak, J. Koput and K. Dobek, ChemPhysChem, 2011, 12, 1322–1332 Search PubMed.
- L. Cisse, A. Djande, M. C. Chichi, F. Delatre, A. Saba, A. Tine and J. J. Aaron, Spectrochim. Acta, Part A, 2011, 79, 428–436 CrossRef CAS PubMed.
- Z. Pawlowska, A. Lietard, S. Aloïse, M. Sliwa, A. Idrissi, O. Poizat, G. Buntinx, S. Delbaere, A. Perrier, F. Maurel, P. Jacques and J. Abe, Phys. Chem. Chem. Phys., 2011, 13, 13185–13195 RSC.
- A. Perrier, S. Aloïse, Z. Pawlowska, M. Sliwa, F. Maurel and J. Abe, Chem. Phys. Lett., 2011, 515, 42–48 CrossRef CAS.
- K. M. Al-Ahmary, M. M. Habeeb and E. A. Al-Solmy, J. Mol. Liq., 2011, 162, 129–134 CrossRef CAS.
- G. J. Zhao and K. L. Han, J. Chem. Phys., 2007, 127, 024306 CrossRef PubMed.
- G. J. Zhao and K. L. Han, Biophys. J., 2008, 94, 38–46 CrossRef CAS PubMed.
- D. P. Yang, Y. G. Yang and Y. F. Liu, Comput. Theor. Chem., 2012, 997, 42–48 CrossRef CAS.
- N. I. Georgiev, V. B. Bojinov and P. S. Nikolov, Dyes Pigm., 2011, 88, 350–357 CrossRef CAS.
- J. M. Chovelon and I. Grabchev, Spectrochim. Acta, Part A, 2007, 67, 87–91 CrossRef PubMed.
- Y. J. Hu, Y. Liu, R. M. Zhao, J. X. Dong and S. S. Qu, J. Photochem. Photobiol., A, 2006, 179, 324–329 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra10153a |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *,
Ling Xue,
Yuan Jia,
Boyu Lou and
Juxiang Yang
*,
Ling Xue,
Yuan Jia,
Boyu Lou and
Juxiang Yang
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70), at a flow rate of 1.0 mL min−1 with the UV detector wavelength set at 324 nm, and the injection volume was 20 μL. Data were acquired and processed with an Agilent ChemStation software external calibration.
70), at a flow rate of 1.0 mL min−1 with the UV detector wavelength set at 324 nm, and the injection volume was 20 μL. Data were acquired and processed with an Agilent ChemStation software external calibration.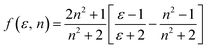
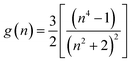
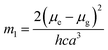
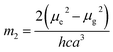
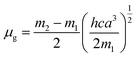
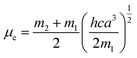
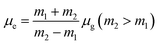
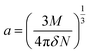




![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretches at 1500 cm−1 and the decreasing intensity could be attributed to the contraction of the aromatic ring after the addition of Fe3+ ion. On the other hand, as seen from Fig. 8B that the intensity and peak area decrease with the addition of Fe3+ ion, and the peak time changes slightly from 1.57 to 1.65 min. The HPLC result indicates that Fe3+ ion binds with RH non-covalently and a RH–Fe3+ complex forms.
C stretches at 1500 cm−1 and the decreasing intensity could be attributed to the contraction of the aromatic ring after the addition of Fe3+ ion. On the other hand, as seen from Fig. 8B that the intensity and peak area decrease with the addition of Fe3+ ion, and the peak time changes slightly from 1.57 to 1.65 min. The HPLC result indicates that Fe3+ ion binds with RH non-covalently and a RH–Fe3+ complex forms.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C linking aromatic ring of RH molecule distorts more strictly by binding with Fe3+ ion.
C linking aromatic ring of RH molecule distorts more strictly by binding with Fe3+ ion.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K + n
K + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lg[iron]
lg[iron]
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, slope = n) (Fig. S4B†), and the corresponding results are listed in Table S1.† As shown in Table S1,† the value of KSV and K is almost 106 M, indicating that the quenching and binding effect is considerable, and RH can be candidate as a good source of new iron binding agents. The value of n approximately is equaled to 1, indicating that there is one class binding site in RH for Fe3+. Because of the formation of the RH–Fe3+ complex, the quenching of RH is initiated by static quenching.
K, slope = n) (Fig. S4B†), and the corresponding results are listed in Table S1.† As shown in Table S1,† the value of KSV and K is almost 106 M, indicating that the quenching and binding effect is considerable, and RH can be candidate as a good source of new iron binding agents. The value of n approximately is equaled to 1, indicating that there is one class binding site in RH for Fe3+. Because of the formation of the RH–Fe3+ complex, the quenching of RH is initiated by static quenching.



