Open Access Article
Open Access ArticleRedistribution of native defects and photoconductivity in ZnO under pressure†
Partha Pratim Das a,
Sudeshna Samantabc,
Lin Wangb,
Jaeyong Kimc,
Thomas Vogtd,
P. Sujatha Devi
a,
Sudeshna Samantabc,
Lin Wangb,
Jaeyong Kimc,
Thomas Vogtd,
P. Sujatha Devi e and
Yongjae Lee*ab
e and
Yongjae Lee*ab
aDepartment of Earth System Sciences, Yonsei University, Seoul 120749, Korea. E-mail: yongjaelee@yonsei.ac.kr
bCenter for High Pressure Science and Technology Advanced Research, Shanghai, China
cDepartment of Physics, Hanyang University, Seoul 133791, Korea
dNano Center & Department of Chemistry and Biochemistry, University of South Carolina, Columbia, SC 29208, USA
eSensor and Actuator Division, CSIR-Central Glass and Ceramic Research Institute, Kolkata 700032, India
First published on 1st February 2019
Abstract
Control and design of native defects in semiconductors are extremely important for industrial applications. Here, we investigated the effect of external hydrostatic pressure on the redistribution of native defects and their impact on structural phase transitions and photoconductivity in ZnO. We investigated morphologically distinct rod- (ZnO-R) and flower-like (ZnO-F) ZnO microstructures where the latter contains several native defects namely, oxygen vacancies, zinc interstitials and oxygen interstitials. Synchrotron X-ray diffraction reveals pressure-induced irreversible phase transformation of ZnO-F with the emergence of a hexagonal metallic Zn phase due to enhanced diffusion of interstitial Zn during decompression. In contrast, ZnO-R undergoes a reversible structural phase transition displaying a large hysteresis during decompression. We evidenced that the pressure-induced strain and inhomogeneous distribution of defects play crucial roles at structural phase transition. Raman spectroscopy and emission studies further confirm that the recovered ZnO-R appears less defective than ZnO-F. It resulted in lower photocurrent gain and slower photoresponse during time-dependent transient photoresponse with the synergistic application of pressure and illumination (ultra-violet). While successive pressure treatments improved the photoconductivity in ZnO-R, ZnO-F failed to recover even its ambient photoresponse. Pressure-induced redistribution of native defects and the optoelectronic response in ZnO might provide new opportunities in promising semiconductors.
1. Introduction
Native intrinsic defects such as vacancies, self-interstitials, and anti-sites are unavoidable in crystal lattices and have enormous impact on the functionality of semiconducting materials.1,2 The defects renovate chemically inert, covalently bonded silicon and gallium arsenide into the efficient carriers of electronic charge for the entire electronic industry. A remarkable superconductivity emerges in high-temperature cuprate by the introduction of atomic point defects where the parent compound remains insulator. A nominal change in defect concentration can demonstrate profound changes in functionality, such as transition from nonmagnetic to magnetic or metallic to insulating states.3 Defect profiles in semiconductors are tuned by introducing foreign atoms, several physical–mechanical treatments and also by their chemical synthesis routes.1–4 In nanoscale systems, ion and vacancy migration length scales are comparable to the system dimensions.5 Therefore, the significant consequences on the formation energies, donor–acceptor levels, optical transition energies, defect clustering and electronic structures of native defects control the physical and chemical properties of semiconductors.6,7 Zinc oxide (ZnO) is an important wide band-gap oxide semiconductor whose opto-electrical and magnetic properties are highly dependent on the presence of non-stoichiometric intrinsic native defects.8–14 Oxygen vacancies (VO), Zn interstitial (Zni) and its anti-sites, Zn vacancies (VZn) are regarded as the most common defects in ZnO. Oxygen interstitials (Oi) and anti-sites and their respective formation energies have been reviewed earlier.15,16 First-principle calculations provided electronic band-structures, defect energy levels as well as their impact on the physicochemical properties of ZnO.15,16 In recent years, ab initio calculations explored the role of hydrostatic pressure on the native defects to engineer desired structural, electrical, and optical properties of it.17,18 Theoretically, the formation enthalpies and transition energy levels of various native defects in the NaCl-type structure up to 20 GPa was investigated. In addition, Hu et al.18 explored its band-gap and optical properties up to 12 GPa incorporating such defects. Controversies still exist as none of these approaches consider the pressure-induced first-order structural phase transition from the ambient hexagonal wurtzite (WZ) (B4) → cubic rock-salt (RS) (B1) structure near 10 GPa.19,20 On the contrary, pressure-dependent photoluminescence studies21,22 established the correlation between B4 → B1 transition to direct band-gap transition in ZnO, thereby hinting that electronic properties are highly-tunable with applied pressure. To the best of our knowledge, important thermodynamic aspects, i.e., the status of the native defects under pressure and their concomitant influence on pressure-induced phase transformation in ZnO have not been explored, and thus, is the main focus of our present study.In this study we investigated the pressure responses of ZnO with considerable disagreements to previous reports.19,23–25 Despite B4 → B1 phase transition,20,26–28 only a few reports on nanotubes, nanowires, and nanobelts explored the effect of morphology on the compressibility and structural transitions.20,29,30 Here, we pay attention to this particular aspect by studying two morphologically distinct samples of ZnO;9,10,12,13 (i) a rod-like (ZnO-R) and (ii) a flower-like microstructure (ZnO-F). Diverse synthesis routes and different morphologies created different amounts of native defects in as prepared samples.10,31–34 Ongoing theoretical developments pursued to understand the kinetics of formation, diffusion, and migration of native defects only in bulk ZnO.15 Unfortunately, no experimental evidence of pressure-induced response in morphologically distinct samples is available. Along with pressure, effect of illumination mediated by the dynamic oxygen vacancy is extremely strong in ZnO. Simultaneous application of both gate-voltage and ultra-violet illumination showed the control of the charge carrier density, a substantial enhancement of the photocurrent in ZnO single crystals.35,36 We explored the synergistic application of light and pressure in order to understand the defect dynamics encompassing its pressure-induced structural phase transition, for the first time in ZnO microstructures. We demonstrate the stability, routes of structural phase transitions, and the related kinetics of ZnO-R and ZnO-F using a combination of synchrotron XRD, micro-Raman spectroscopy, and photoconductivity under hydrostatic compression.
2. Experimental
ZnO rod-like microstructures were prepared by the solution-processed sonochemical method using zinc acetate as the precursor and ammonium hydroxide as the precipitating agent, keeping the pH of the solution at approximately 9.10 In contrast, ammonium hydroxide was added to zinc acetate in order to maintain a higher pH of above 10 while preparing water lily-type ZnO flowers, as reported elsewhere in detail.31 The microstructures of the ZnO samples in this study were probed using a scanning electron microscope (SEM, LEO 430i, Carl Zeiss). High-pressure experiments were performed by loading the respective samples along with a few small ruby chips as a pressure gauge in a symmetric diamond anvil cell (DAC) with a pair of type-I diamonds with a culet size of 400 μm. A pre-indented stainless-steel gasket with a hole diameter of 120 μm upon drilling was used as the sample chamber. A mixture of methanol and ethanol at the ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in volume was used as a pressure transmitting medium.37,38 The pressure was determined by measuring the shift in the R1 of the ruby fluorescence. Synchrotron and laboratory micro X-rays were used for the high-pressure monochromatic XRD measurements at the 6D beamline at Pohang Accelerator Laboratory (PAL) and Yonsei University, respectively. At PAL, 18.785 keV X-ray of 100 μm in diameter was used in combination with CCD detector while at Yonsei; micro-focusing X-ray from a rotating-anode Mo target was used with an imaging plate detector. Micro-Raman measurements were performed using the offline Raman system at the Advanced Photon Source (APS) where an Ar ion multiline laser source (working wavelength 532 nm), ISA HR460 spectrometer with 300 and 1800 g mm−1 gratings, Peltier cooled Andor 1024 × 128 pixel CCD detector and 20X (32 mm WD) Mitutoyo objective lens were used. The room temperature photoluminescence spectra (PL) were measured on a steady-state spectrofluorometer (QM-40, Photon Technology International, PTI) using a xenon lamp (150 W) as an excitation source at an excitation wavelength of 345 nm and a bandpass of 5 nm.
1 in volume was used as a pressure transmitting medium.37,38 The pressure was determined by measuring the shift in the R1 of the ruby fluorescence. Synchrotron and laboratory micro X-rays were used for the high-pressure monochromatic XRD measurements at the 6D beamline at Pohang Accelerator Laboratory (PAL) and Yonsei University, respectively. At PAL, 18.785 keV X-ray of 100 μm in diameter was used in combination with CCD detector while at Yonsei; micro-focusing X-ray from a rotating-anode Mo target was used with an imaging plate detector. Micro-Raman measurements were performed using the offline Raman system at the Advanced Photon Source (APS) where an Ar ion multiline laser source (working wavelength 532 nm), ISA HR460 spectrometer with 300 and 1800 g mm−1 gratings, Peltier cooled Andor 1024 × 128 pixel CCD detector and 20X (32 mm WD) Mitutoyo objective lens were used. The room temperature photoluminescence spectra (PL) were measured on a steady-state spectrofluorometer (QM-40, Photon Technology International, PTI) using a xenon lamp (150 W) as an excitation source at an excitation wavelength of 345 nm and a bandpass of 5 nm.
Here, we studied pressure-induced photoconductivity of ZnO considering its interactions with native defects under ultraviolet (UV) irradiation (325 nm E325 nm > Eg ∼3.3 eV). In situ 4-probe photoconductivity and resistivity of the samples were measured using a Keithley Source-meter 2410 in the voltage range of 0–0.2 V at room temperature. A symmetrical DAC was used to generate high pressure up to ∼14 GPa. Nonmagnetic stainless steel gaskets were pre-indented to 40 μm in thickness and laser drilled to secure a central hole as sample chamber. Fine cubic boron nitride powder was pressed to prepare the insulating gaskets avoiding any contact between sample and gasket. In situ high pressure resistance measurements were performed in a DAC with four-probe direct current (d.c) method with platinum electrodes. No pressure transmitting medium was used during the electrical transport and photoconductivity measurements. For the current–voltage (I–V) characteristics, we restricted the current to 1.0 mA to avoid combustion and heating of the sample. This experiment was performed using an UV laser source of wavelength 325 nm (IK3301R-G He-Cd Laser, K KIMMON). We used a fixed laser exposure time of 20 s throughout the experiments.
3. Results and discussion
3.1. ZnO at ambient conditions
The FESEM images of as synthesized ZnO microstructures are shown in Fig. 1. The corresponding SAED patterns are in the insets of Fig. 1(a) and (b) corresponding to (100), (103), (102) and (110) planes of the hexagonal wurtzite structure of ZnO. Fig. 1(a) reveals one-dimensional rod like microstructures having six open facets. The average length and diameter of the rods are ∼1.5 μm and ∼350 nm, respectively, leading to an aspect ratio ∼4. An anisotropic growth along the c-axis forming this particular ZnO microstructure involves considerably high surface energy.39 The other ZnO sample has a flower-like morphology with a larger size (∼4 μm) and several multi-directional petals (Fig. 1(b)). It has a combination of 10–14 rod-like sub-units with wide bases and tapered tips attached at a common center. This microstructure is expected to have a higher surface area with lower surface energy.31,40 Published literatures found that the surface energy associated with different morphologies plays a crucial role in structural phase transformation.29,41 Additionally, the sample with higher surface area is capable to accommodate a larger amount of adsorbed oxygen which is highly allied to its photoconductivity.42 | ||
| Fig. 1 FESEM images of ZnO (a) and (b) rods and flowers like microstructures, respectively. Inset shows the corresponding SAED patterns. | ||
At ambient conditions, the XRD patterns of ZnO microstructures were measured and confirmed the hexagonal wurtzite structure with high crystallinity (Fig. S1(a)†). The obtained lattice parameters after a full profile fit were compared with the standard zincite structure reported by Kihara et al. as listed in Table 1.43,44 The enhanced c/a ratio 1.608(3) suggests the c-axis orientation of ZnO-R with higher surface energy compared to ZnO-F.39,40 A significant enhancement in unit cell volume V = 55.21(5) Å3 for ZnO-F suggests the existence of higher number of intrinsic structural defects in it.10
| ZnO sample | a (Å) | c (Å) | c/a | V (Å)3 | IE2-high/IE1-LO |
|---|---|---|---|---|---|
| Rods | 3.246(1) | 5.220(2) | 1.608(3) | 55.01(1) | 6.29(6) |
| Flowers | 3.256(1) | 5.215(3) | 1.601(7) | 55.21(5) | 2.73(2) |
| K. Kihara, et al., Anharmonic thermal vibrations in ZnO, Canadian Mineralogist, 1985, 23, 647–654 | 3.249(4) | 5.203(8) | 1.601(4) | 54.94(5) | — |
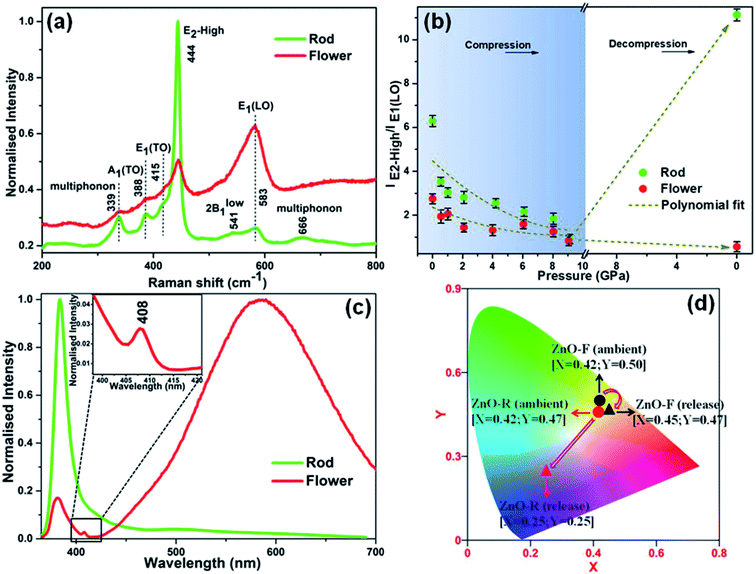
A qualitative estimation of the amount and type of native defects present in ZnO-R and ZnO-F were done by Raman spectroscopy at ambient conditions (Fig. S1(b)†). The data set corresponding to the intensity of the Raman spectrum of each sample has been normalized by the respective maximum value and plotted thereafter as ‘normalised intensity’. The intense E2 mode at ∼444 cm−1 is the characteristics of the hexagonal wurtzite phase of ZnO.45 Moreover, the Raman active bands at 389, 415 and 541 cm−1 attributed to A1(TO), E1(TO) and 2Blow1 modes, respectively, are similar for both ZnO microstructures.45 Likewise, the bands for the multi-phonon scattering process appeared at approximately 338 and 666 cm−1.45 Additionally, a band at 583 cm−1 assigned to E1(LO) originating from impurities and the defects (i.e., oxygen vacancies, zinc interstitial, free carriers etc.) has a considerably lower intensity for ZnO-R.10,45–47 Moreover, a higher intensity ratio of E2-high/E1(LO) ≈ 6.29(6) was found for ZnO-R in contrast to 2.73(2) for ZnO-F as listed in Table 1. It supports the conjecture that ZnO-R exhibits a better crystal quality with fewer defects than the ZnO-F at ambient conditions.
Fig. 2(a) shows the emission spectra recorded under 345 nm light excitation at room temperature. A strong band-edge UV emission related to the recombination of free excitons was observed near 381 nm for ZnO-R. On the other side, the deep-level emissions of the samples in the green to orange region arise mainly from double ionized oxygen vacancies (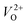 ) in the ZnO structure and oxygen interstitials related to the chemisorbed oxygen at the grain boundaries.10,47 A broader visible emission band for ZnO-F reflects the presence of higher amount of structural defects compared to ZnO-R.31,33 The presence of intrinsic structural defects, such as Zni, especially in ZnO-F, cannot be ignored, and reveals weak emission bands in the blue region at approximately 405 and 430 nm, as displayed in the inset of Fig. 2(a).48
) in the ZnO structure and oxygen interstitials related to the chemisorbed oxygen at the grain boundaries.10,47 A broader visible emission band for ZnO-F reflects the presence of higher amount of structural defects compared to ZnO-R.31,33 The presence of intrinsic structural defects, such as Zni, especially in ZnO-F, cannot be ignored, and reveals weak emission bands in the blue region at approximately 405 and 430 nm, as displayed in the inset of Fig. 2(a).48
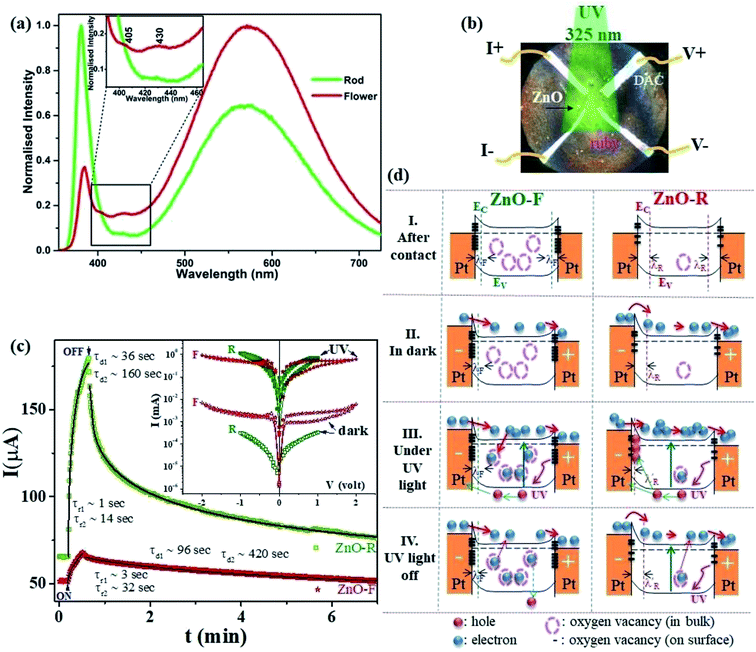 | ||
| Fig. 2 (a) Room temperature emission spectra of the ZnO samples in ethanol. (b) The optical microscopic image of a DAC containing ZnO and furnished with four platinum electrodes for d.c electrical transport measurements. (c) Time-dependent transient photocurrent gain at very low pressure (∼0.2 GPa) for ZnO-F and ZnO-R. The rise and decay time constants are marked when illumination is turned on and off. The solid lines show fits with a bi-exponential relaxation (ref. 49). Inset shows the corresponding I-V characteristics in the dark and under illumination. (d) The schematic band diagrams for ZnO-F and ZnO-R in dark and under illumination. Filled (red and blue) and empty circles represent intrinsic carriers and native oxygen vacancies inside ZnO, respectively. Thick dashes represent the surface oxygen vacancies. ZnO-F comprises with more bulk and surface oxygen vacancies (more dash circles and lines) than ZnO-R (see text). | ||
3.2. Photoconductivity at low pressures (∼0.2 GPa)
Fig. 2(b) indicates the optical microscopic image of a diamond-anvil-cell containing the ZnO sample and is furnished with four platinum electrical contact probes. The details of the electrical transport and photoconductivity measurements techniques are mentioned in the experimental section. The interaction of any semiconductor with a photon is a complex phenomenon and depends on the electron–hole pair generation, trapping, and recombination. The dark-current (Idark) was recorded as 50(3) μA and 62(2) μA for ZnO-F and ZnO-R, respectively. We recorded the time-dependent transient photo-response (Iph–t) (0.2 V) along with their I–V characteristics, as shown in Fig. 2(c).Photocurrent increased sharply in both cases when the illumination turned on. The current gain ΔIph = (I − Idark)/Idark was calculated as 0.33(2) and 1.75(5) for ZnO-F and ZnO-R, respectively, showing a superior photocurrent/dark current ratio in rods. When the illumination turned off, current started to decrease and approached to Idark after a specific decay time. We fitted (solid lines in Fig. 2(c)) the rise and decay edges with two time components for the quantitative analysis of the response time scales.49 The fast responses were attributed to the rapid change in carrier concentration when the light turned on or off. The slow responses were due to carrier- trapping and de-trapping at native defects. The calculated relaxation time-constants τr (rise) and τd (decay) are tabulated in Table 2. The difference in recovery time-constants in ZnO-R clearly indicate the presence of fewer native defects compared to ZnO-F.
| ZnO Sample | ΔIph = (Iph − Idark)/Idark | τr (sec) | τd (sec) | τd1/τd2 |
|---|---|---|---|---|
| ZnO-F | 0.33(2) | τr1 = 3(1) | τd1 = 96(8) | 0.228(6) (slower) |
| τr2 = 32(2) | τd2 = 420(20) | |||
| ZnO-R | 1.75(5) | τr1 = 1(1) | τd1 = 36(2) | 0.225(1) (faster) |
| τr2 = 14(1) | τd2 = 160(8) |
We introduced a simple schematic energy band diagrams in Fig. 2(d)(I–IV) to understand the photoresponse mechanism in rods and flowers outlining the semiconductor–metal (M–S) interface. The carrier conduction mechanism at M–S interface can be significantly tuned by oxygen vacancies available in the semiconductor. With high concentration oxygen vacancy, the Fermi level of ZnO-F is expected to be pinned to the defect levels VO [+2.0] resulting a narrower (a few atomic layers thick) depletion width λF (positively ionized oxygen vacancies) in contrast to λR (created by shallow ionized donors) for ZnO-R (Fig. 2(d)-I). It might result carrier transport by tunneling in the case of ZnO-F (Fig. 2(d)-II) and by thermionic emission through a barrier in ZnO-R (Fig. 2(d)-II). Under illumination, due to a higher abundance of oxygen vacancies in ZnO-F, the photo-generated carriers were captured more easily and a lower ΔIph (Fig. 2(d)-III and (c)) with delayed response time (τr/d) was observed. In ZnO-R, the photo-generated holes were trapped in the depletion region λR and finally narrowed down to a width 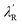 (Fig. 2(d)-III). Due to fewer oxygen vacancies in ZnO-R, photo-generated electrons and holes underwent a rapid separation and migrated to the respective electrodes. Thus we observed a larger and faster photoresponse ZnO-R compared to ZnO-F. When illumination turned off (Fig. 2(d)-IV), the electrons in the conduction band (CB) are captured at recombination centers, annihilated by band-to-band transition (fast decay components), or captured by oxygen vacancies are released and recombine with holes slowly (slower recovery components). Inside a closed DAC, samples remained isolated from atmospheric oxygen. The initial oxygen on sample surfaces, repetitive adsorption and desorption of those oxygen might rule the equilibrium. Although, theoretically, the atomic and electronic structures of native defects in ZnO were explored under high pressure;16–18,50 no experimental evidence is available on the impact of defects on synergistic application of light and pressure.
(Fig. 2(d)-III). Due to fewer oxygen vacancies in ZnO-R, photo-generated electrons and holes underwent a rapid separation and migrated to the respective electrodes. Thus we observed a larger and faster photoresponse ZnO-R compared to ZnO-F. When illumination turned off (Fig. 2(d)-IV), the electrons in the conduction band (CB) are captured at recombination centers, annihilated by band-to-band transition (fast decay components), or captured by oxygen vacancies are released and recombine with holes slowly (slower recovery components). Inside a closed DAC, samples remained isolated from atmospheric oxygen. The initial oxygen on sample surfaces, repetitive adsorption and desorption of those oxygen might rule the equilibrium. Although, theoretically, the atomic and electronic structures of native defects in ZnO were explored under high pressure;16–18,50 no experimental evidence is available on the impact of defects on synergistic application of light and pressure.
3.3. Structural changes at high-pressures (∼10 GPa)
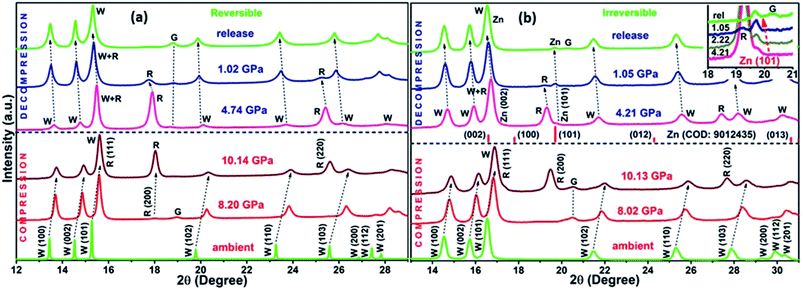
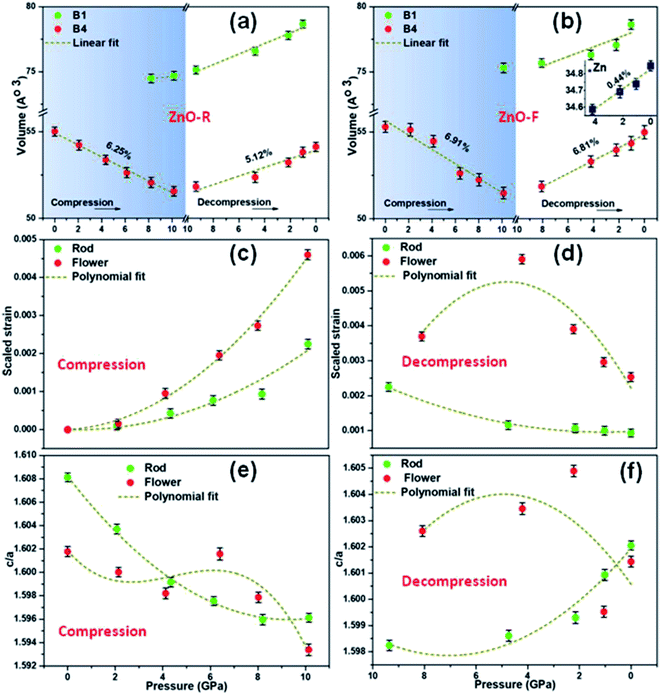
The XRD patterns for compression and decompression cycles of ZnO-R and ZnO-F are shown in ESI (Fig. S2 (a–d)†). The selective XRD patterns at few representative pressures are depicted in Fig. 3(a) and (b). A mixture of B4 and B1 phases coexisted above 10 GPa in both samples, as corroborated by previous studies.19,20 For ZnO-R, the appearance of the (200) peak of the B1 phase was observed as early as 8.20(10) GPa during compression (Fig. 3(a), S2(a)†). Interestingly, the (200) and (220) peaks of the B1 phase of ZnO-R persisted significantly down to ∼1 GPa during decompression (Fig. 3(a), S2(c)†). Hence, with the pressure cycling, a larger hysteresis in the pressure induced phase transformation was observed for ZnO-R. Detailed XRD profile fitting results are in ESI (Fig. S3 and S4†).The flower-shaped morphology with a much lower surface energy experienced a larger volume reduction (∼6.91(2)% in B4), as shown in Fig. 4(b). It has a structural phase transformation at a relatively higher pressure compared to the rod-like morphology with a volume collapse of ∼6.25(1)% at ~10 GPa (Fig. 3(b), S2(b)† and 4(a)). We evidenced an anomalous behaviour in the phase transformation kinetics between two different microstructures as described earlier by Dong et al.29 There exists a pressure range of constant volume around 5 GPa, especially for ZnO-F during compression.
During decompression to B4 phase, ZnO-R followed a reversible path but led to a 5.12(1)% smaller unit cell volume at release as shown in Fig. 3(a), S2(c)† and 4(a). Such volume reduction in recovered ZnO-R points more defect-free, ordered structure. In contrast, during the decompression of ZnO-F, a phase of hexagonal Zn indicated by two of its most intense Bragg diffraction peaks, (002) and (101) were found to emerge (Fig. 3(b) and S2(d)†).51 The diffraction pattern of the standard Zn (sample name: 9012435; Crystallography Open Database) is plotted together in Fig. 3(b) for comparison. This phase started to appear at 4.21(10) GPa and survived in the recovered sample as well, along with the B4 phase, as shown in Fig. 3(b). The evolution of the (101) plane of the Zn during decompression has also been highlighted in the inset of Fig. 3(b). The intensity ratio of the diffraction peaks corresponding to Zn 〈101〉 and ZnO 〈100〉 increased to 0.48(3), 0.54(1), 0.56(3), at 4.21(10), 2.22(10), 1.05(10) GPa, respectively, and finally to 0.57(1) at release. The XRD profile fitting of the recovered ZnO-F is shown in Fig. S5.† The unit cell volume of the pressure-released ZnO-F was 6.81(2)% smaller for the B4 phase and was 0.44(1)% smaller for the hexagonal Zn phase (Fig. 4(b)). We predict that the aforementioned structural defects in the rod and flower-like morphologies might tune the phase transformation kinetics.
A gradual rise of microscopic strain with pressure was found during compression in both samples as estimated by Williamson–Hall equation52,53 and are shown in Fig. 4(c) and (d). The strain enhancement was much profound for ZnO-F and its distribution became highly inhomogeneous during decompression (Fig. 4(d)). Interestingly, the strain was highest at 4.21(10) GPa, where the emergence of the hexagonal Zn phase was experimentally found, and all the three phases namely, B1, B4 and hexagonal Zn, coexisted. The fitted polynomial curves (dotted lines) are guide to eyes. It appears that a relatively defect-free structure of ZnO-R allows it to sustain a larger hysteresis and reversible phase transformation under pressure.
To further understand the mechanism of the phase transformation, the pressure-dependent variations of ‘c/a’ of both samples have been investigated (Fig. 4(e) and (f)). We observed a continuous decrease (increase) in the ‘c/a’ ratio for ZnO-R at compression (decompression) during the evolution of the B1 (B4) phase. Both observations point to B4 → B1 phase transition along a hexagonal path, as proposed by Limpijumnong et al.54 Few anomalies in maintaining this particular trend for ZnO-F illustrate that the defects highly influence the strain generated during the structural phase transformation.
Variation in the ratios of d100/d002 of B4 and d200/d220 of B1 with pressure can provide further information about the transition pathways (Fig. S6†). The competition between the growth of B4 and B1 phases at different pressures imposes a certain amount of stress on each. The crystallographic relationship requires an increase of the d100 spacing of B4 when B4 → B1 transition occurs. It could be reversed when d110 or d220 of B1 gets contracted to the smaller dimension of (100) plane of B4.54,55 We found a successive increase of d100 in B4 (compression) followed by the reduction of both d100 in B4 and d220 in B1 (decompression) in ZnO-R. In contrast, a rapid increase of d220 of B1 after ~4 GPa was noted for ZnO-F during decompression. It strongly correlates an impact of the hexagonal Zn phase on the phase transition of ZnO-F which has never been addressed so far.
3.4. In situ pressure-dependent Raman studies; comparison of emission properties
Despite of the above-discussed features, Fig. S7† depicts the room temperature Raman spectra of the two ZnO microstructures as a function of pressure and are in well agreement with the XRD results. Both samples exhibited a red shift in the Raman modes upon compression along with the appearance of the B1 phase near ∼10 GPa. A significant pressure-induced broadening of the short-range structure sensitive Raman profile was observed; and ZnO-F was revealing more broadened features compared to ZnO-R. It resulted from the increase in structural disorder due to a considerable number of defects and vacancies as mentioned before.56 Furthermore, all the Raman active bands for ZnO-F, even at release, remained broadened, indicates the irreversibility of the structural transition.41,56The Raman spectra of the released phases of two morphologies are compared in Fig. 5(a). A qualitative estimation of the structural defects was done from the ratio of the E2-high/E1-LO modes in the B4 phase and plotted in Fig. 5(b) against pressure. In both cases, the ratios decreased upon compression as indicated by the polynomial fitted curves (dashed lines). Interestingly, an enhancement about ∼77% in E2-high/E1-LO occurred in recovered ZnO-R upon decompression. On the other hand, the E1-LO became the most predominant mode and eventually a lower E2-high/E1-LO was observed for the recovered ZnO-F. It apparently can be explained that the oxygen vacancies and interstitials in these structures underwent the pressure-induced reordering resulting a more defect-free, ordered ZnO-R and a severely disordered ZnO-F upon release.
It is worth noting that visible emission peaks associated with the “structural defects” of the recovered ZnO-R almost disappeared, those in ZnO-F became stronger (Fig. 5(c)). In addition, the band-edge emission in the UV region associated with the “crystallinity” became weaker in ZnO-F at release. The complete disappearance of 405 and 430 nm peaks in the photo-emission spectra for the recovered ZnO-F thereby indicating to the excision of the interstitial zinc (Zni) from the ZnO lattice during decompression. Moreover, a new emission peak near 408 nm associated with the inter-band electronic transition in metallic Zn independently confirms the formation of metallic Zn from ZnO-F.57 The results are highly consistent with our decompression XRD data shown in Fig. 3(b) and S2(d)† to support the emergence of a Zn metal phase in ZnO-F. The released energy during the transformation back to a more stable B4 phase from the mixture of B1 and B4 phase near ~10 GPa is likely to be sufficient for the interstitial zinc in the ZnO-F to overcome a low migration barrier and diffuse out and form a hexagonal Zn phase.15 The Commission Internationale de l’Éclairage (CIE) chromaticity color coordinates for the samples were also calculated (Fig. 5(d)). The CIE coordinates observed at the green-yellow region (0.42, 0.50) for ambient ZnO-F were found to get shifted to (0.45, 0.47) which correspond to the yellow-orange emission associated with the more disordered structure of the ZnO-F after pressure treatment. On the contrary, a considerable shift in the CIE coordinates from yellow (0.42, 0.47) to blue-violet region (0.25, 0.25) indicates an almost defect free structure of the recovered ZnO-R.
3.5. Photoconductivity at high-pressures (∼14 GPa)
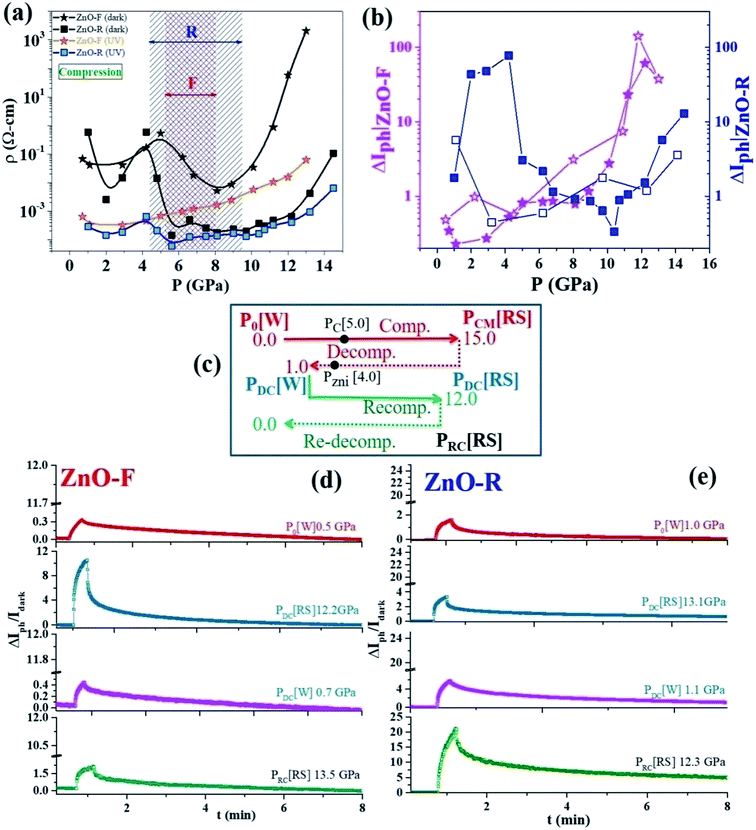
To examine a pressure impact on the electronic band structures in ZnO, we measured photoconductivity up to ~14 GPa. Pressure-induced four-probe I–V characteristics of ZnO-F and ZnO-R in the dark and under UV excitation are shown in ESI (Fig. S8(a) and (b)†). Large current hysteresis was observed in the I–V curves for both samples. The resistivity (ρ) for the high-resistive state (HRS) in dark and low-resistive state (LRS) under UV illumination for ZnO-F and ZnO-R is shown in Fig. 6(a) for compression. In the dark, below 5 GPa (B4 phase), resistivity increased in ZnO-F sharply compared to ZnO-R. Above 5 GPa, resistivity lowered moderately in ZnO-F and rapidly for ZnO-R. It rises steeply in ZnO-F near B4 → B1 phase transition and had a resistivity value four-order higher than its ambient phase. In contrast, ZnO-R had a broad minimum near the B4 → B1 phase transition and regained its resistivity value in the B1 phase comparable to its ambient phase.A pressure-induced decrease of resistivity at B4 → B1 transition was observed earlier in dumbbell-like ZnO at 11.1(1) GPa due to a reduction of band-gap in B1 phase, in contrast with our data.58 First-principles ab initio studies58 predicted that 5 GPa is a critical pressure (PC) for the creation of native oxygen vacancies with a minimum valence-band width.18 The band-gap increases sharply with pressure up to 5 GPa and slowly later with oxygen vacancies. The calculations also pointed the dramatic effect of Zni, where the band-gap increases linearly with pressure. The shortening of the Zn-O bonds and the increased hybridization of O and Zn states explain the increase of the band-gap during compression.58 The increase of the coupling strength for oxygen vacancies was lower compared to Zni results in a metallic character and tune its optoelectronic responses. Such system containing Zni had a very strong UV (323 nm) absorption with increasing pressure.58 In agreement with the theoretical predictions, we experimentally verified the similar trends in ZnO-F having a higher concentration of oxygen vacancies and interstitial Zni.
The resistivity peak broadening for ZnO-F near PC is consistent with an anomaly in ‘c/a’ ratio near 5 GPa which was absent in ZnO-R. The ideal value for the ‘c/a’ ratio is 1.633 in a perfect ZnO wurtzite crystal, and any deviation suggests a structural distortion and displacement of oxygen with the positions (1/3, 2/3, u) (u(c/a)1/2) in the B4 phase which in turn influences the structural phase transition.28,59
The metallic filamentary conduction (Zn2+ → Zn(2−n)+)60,61 process might be helpful to explain the decrease in resistivity just above 5 GPa. A critical concentration of neutral oxygen vacancies promotes the formation of highly conductive Zn(2−n)+ filaments and a newly ordered crystalline phase might occur. Here, we propose that PC is the critical pressure at which the conducting filaments begin to grow and the excess O(ad)2− in ZnO-F easily recombines with oxygen vacancies, thus impeding the filament formation compared to ZnO-R in dark. The presence of excess Zni might lead to a deterioration of the electrical conductivity by forming different branches of conducting filaments in ZnO-F. The pressure dependent resistivity is highly hysteretic and reversible under non-hydrostatic conditions, as previously reported.62
ZnO with its high concentration of Zni is a good candidate for UV absorption, and strengthens under compression.18 An increase in photocurrent due to Zni in ZnO nanowires was observed by Bera et al., at ambient conditions.63 The interactions of photo-generated free excitons with Zni produced ionized Zni and contributed extra free electrons to CB. A large photocurrent gain ΔIph with pressure and its sharp rise above 9 GPa is shown in Fig. 6(b). ZnO-R had the highest ΔIph in both B4 and B1 phases in contrast to ZnO-F. Upon decompression (B4 phase), where recovered ZnO-R exhibited an enhanced photoconductivity by one order, recovered ZnO-F completely failed to regain its initial value. These results thereby indicate the nearly defect-free and highly defective natures of the recovered B4 ZnO-R and ZnO-F, respectively, in consistent with earlier observations.
We present an experimental scheme in Fig. 6(c) to compare the performances of the samples subjected to the repeated pressure cycles (i.e., compression → decompression → recompression). We plotted ΔIph–t data in Fig. 6(d) and (e) for a few representative pressure points for both samples. With re-compression to ~12 GPa, ZnO-R surprisingly exhibited a high ΔIph even in the B1 phase. ZnO-F could not recover its photoactivity anymore as lost after decompression. The resistivities of all the three pressure cycles were compared to study the impact of the structural phase transition in both samples (Fig. S9†). The observations are in line with our XRD data demonstrating the appearance of a new peak due to a phase of metallic Zn upon decompression to around 4 GPa, accounting for lost photoconductivity in ZnO-F after decompression. It ruled out the presence of excessive Zni in ZnO-R and proved that Zni was one of the main native defects in ZnO-F led to strong modifications in photoconductivity across phase transition. If Zni significantly reduced due to the phase separation and form metallic Zn, the system might be nearly “photo-inactive” even under UV illumination (last panel of Fig. 6(d)).
4. Conclusions
In summary, we investigated structural, vibrational responses of two different samples of ZnO with rod- and flower-like morphologies under pressure at ambient temperature. We have established that the optoelectronic responses of these materials are dramatically tuned by pressure, and eventually, highly correlated to defect redistribution associated with the structural phase transformations. It demonstrated that ZnO-F have many intrinsic structural defects, such as doubly ionized oxygen vacancies, zinc interstitials and oxygen interstitials. The irreversible B4 ↔ B1 transition in ZnO-F was associated with the formation of a hexagonal Zn phase by diffusion and aggregation of interstitial Zn during decompression. The findings suggest that ZnO-R recovered with a higher crystallinity, a more defect-free structure, and a better photoconductivity after being subjected to various pressure cycles. Our results are in agreement with ab initio calculations and provide an experimental evidence of a band-gap modification of ZnO at high pressure in the presence of native defects. The redistribution of native defects and pressure-induced photoconductivity may be very relevant for applications in various optoelectronic micro-devices with stress-controlled elements.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Leader Researcher program (NRF-2018R1A3B1052042) of the Korean Ministry of Science and ICT. We also thank the support of the NRF grant 2016K1A4A3914691. PSD acknowledges Ministry of New and Renewable Energy (MNRE), India for financial support under the CSIR-TAPSUN program.References
- H. J. Queisser and E. E. Haller, Science, 1998, 281, 945–950 CrossRef CAS PubMed.
- E. G. Seebauer and M. C. Kratzer, Mater. Sci. Eng., 2006, 55, 57–149 CrossRef.
- S. V. Kalinin and N. A. Spaldin, Science, 2013, 341, 857–859 CrossRef PubMed.
- B. Liu, J. Li, W. Yang, X. Zhang, X. Jiang and Y. Bando, Small, 2017, 13, 1701998 CrossRef PubMed.
- Y. Matsukawa and S. J. Zinkle, Science, 2007, 318, 959–962 CrossRef CAS PubMed.
- D. B. Laks, C. G. Van de Walle, G. F. Neumark and S. T. Pantelides, Phys. Rev. Lett., 1991, 66, 648–651 CrossRef CAS PubMed.
- E. R. Weber, Phys. B, 2003, 340–342, 1–14 CrossRef CAS.
- Z. L. Wang and J. Song, Science, 2006, 312, 242–246 CrossRef CAS PubMed.
- M. Ahmad and J. Zhu, J. Mater. Chem., 2011, 21, 599–614 RSC.
- P. P. Das, S. A. Agarkar, S. Mukhopadhyay, U. Manju, S. B. Ogale and P. S. Devi, Inorg. Chem., 2014, 53, 3961–3972 CrossRef CAS PubMed.
- P. Zhu, Z. Weng, X. Li, X. Liu, S. Wu, K. W. K. Yeung, X. Wang, Z. Cui, X. Yang and P. K. Chu, Adv. Funct. Mater., 2016, 3, 1500494 Search PubMed.
- L. S. Mende and J. L. M. Driscoll, Mater. Today, 2007, 10, 40–48 CrossRef.
- A. B. Djurisic, X. Chen, H. L. Yu and A. M. C. Ng, J. Mater. Chem., 2012, 22, 6526–6535 RSC.
- D. Q. Fang, A. L. Rosa, R. Q. Zhang and Th. Frauenheim, J. Phys. Chem. C, 2010, 114(13), 5760–5766 CrossRef CAS.
- A. Janotti and C. G. Van de Walle, Phys. Rev. B, 2007, 76, 165202 CrossRef.
- F. Oba, M. Choi, A. Togo and I. Tanaka, Sci. Technol. Adv. Mater., 2011, 12, 034302 CrossRef PubMed.
- X. Sha, F. Tian, D. Li, D. Duan, B. Chu, Y. Liu, B. Liu and T. Cui, Solid State Commun., 2015, 201, 130–134 CrossRef CAS.
- Y. Hu, C. Mao, S. Zhang and B. Cai, Mod. Phys. Lett. B, 2016, 30, 1650275 CrossRef CAS.
- C. H. Bates, W. B. White and R. Roy, Science, 1962, 137, 993–994 CrossRef CAS.
- H. Dongbin, Y. Ma, C. Gao, J. Chaudhuri, R. G. Lee and H. Yang, J. Appl. Phys., 2009, 105, 104317-4 Search PubMed.
- W. Shan, W. Walukiewicz, J. W. Ager, K. M. Yu, Y. Zhang, S. S. Mao, R. Kling, C. Kirchuer and A. Waag, Appl. Phys. Lett., 2005, 86, 153117 CrossRef.
- M. J. Bushiri, R. Vinod, A. Segura and J. A. Sans, J. Phys. Condens. Matter, 2015, 27, 385401 CrossRef PubMed.
- H. Karzel, W. Potzel, M. Kofferlein, W. Schiessi, M. Steiner, U. Hiller, G. M. Kalvius, D. W. Mitchell, T. P. Das, P. Blaha, K. Schwarz and M. P. Pasternak, Phys. Rev. B, 1996, 53, 11425–11438 CrossRef CAS.
- K. K. Zhuravlev, W. M. Hlaing Oo, M. D. McCluskey, J. Huso, J. L. Morrison and L. Bergman, J. Appl. Phys., 2009, 106, 4 CrossRef.
- A. N. Baranov, P. S. Sokolov, V. A. Tafeenko, C. Lathe, Y. V. Zubavichus, A. A. Veligzhanin, M. V. Chukichev and V. L. Solozhenko, Chem. Mater., 2013, 25, 1775–1782 CrossRef CAS.
- J. E. Jaffe and A. C. Hess, Phys. Rev. B, 1993, 48, 7903–7909 CrossRef CAS.
- J. Serrano, A. H. Romero, F. J. Manjon, R. Lauck, M. Cardona and A. Rubio, Phys. Rev. B, 2004, 69, 094306–094314 CrossRef.
- J. Sun, H. T. Wang, J. He and Y. Tian, Phys. Rev. B, 2005, 71, 125132–125135 CrossRef.
- Z. Dong, K. K. Zhuravlev, S. A. Morin, L. Li, S. Jin and Y. Song, J. Phys. Chem. C, 2012, 116, 2102–2107 CrossRef CAS.
- L. Wang, H. Liu, J. Qian, W. Yang and Y. Zhao, J. Phys. Chem. C, 2012, 116, 2074–2079 CrossRef CAS.
- A. Jana, N. R. Bandyopadhyay and P. S. Devi, Solid State Sci., 2011, 13, 1633–1637 CrossRef CAS.
- S. Mukhopadhyay, P. P. Das, S. Maity, P. Ghosh and P. S. Devi, Appl. Catal., B, 2015, 165, 128–138 CrossRef CAS.
- P. P. Das, S. Mukhopadhyay, S. A. Agarkar, A. Jana and P. S. Devi, Solid State Sci., 2015, 48, 237–243 CrossRef CAS.
- A. Jana, P. P. Das, S. A. Agarkar and P. S. Devi, Sol. Energy, 2014, 102, 143–151 CrossRef CAS.
- S. Mondal and A. K. Raychaudhuri, Appl. Phys. Lett., 2011, 98, 023501 CrossRef.
- S. Mondal, R. R. Ghimire and A. K. Raychaudhuri, Appl. Phys. Lett., 2013, 103, 231105 CrossRef.
- R. J. Angel, M. Bujak, J. Zhao, G. D. Gatta and S. D. Jacobsen, J. Appl. Crystallogr., 2007, 40, 26–32 CrossRef CAS.
- S. Klotz, J. C. Chervin, P. Munsch and G. L. Marchand, J. Phys. D: Appl. Phys., 2009, 42, 075413 CrossRef.
- B. Ludi and M. Niederberger, Dalton Trans., 2013, 42, 12554–12568 RSC.
- Y. Lai, M. Meng, Y. Yu, X. Wang and T. Ding, Appl. Catal., B, 2011, 105, 335–345 CrossRef CAS.
- Z. Dong and Y. Song, Chem. Phys. Lett., 2009, 480, 90–95 CrossRef CAS.
- J. Bao, I. Shalish, Z. Su, R. Gurwitz, F. Capasso, X. Wang and Z. Ren, Nanoscale Res. Lett., 2011, 6, 404 CrossRef PubMed.
- B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213 CrossRef CAS.
- K. Kihara and G. Donnay, Can. Mineral., 1985, 23, 647–654 CAS.
- R. Cusco, E. A. Llado, J. Ibanez, L. Artus, J. Jimenez, B. Wang and M. J. Callahan, Phys. Rev. B, 2007, 75, 165202–165212 CrossRef.
- M. J. Calleja and M. Cardona, Phys. Rev. B, 1977, 16, 3753–3761 CrossRef.
- R. Podila, W. Queen, A. Nath, J. T. Arantes, A. L. Schoenhalz, A. Fazzio, G. M. Dalpain, J. He, S. J. Hwu, M. J. Skove and A. M. Rao, Nano Lett., 2010, 10, 1383–1386 CrossRef CAS PubMed.
- H. Zeng, G. Duan, Y. Li, S. Yang, X. Xu and W. Cai, Adv. Funct. Mater., 2010, 20, 561–572 CrossRef CAS.
- S. R. Moulik, S. Samanta and B. Ghosh, Appl. Phys. Lett., 2014, 104, 232107 CrossRef.
- S. Lany and A. Zunger, Phys. Rev. Lett., 2004, 98, 045501 CrossRef PubMed.
- E. R. Jette and F. Foote, J. Chem. Phys., 1935, 3, 605–616 CrossRef CAS.
- G. K. Williamson and W. H. Hall, Acta Metall., 1953, 1, 22–31 CrossRef CAS.
- S. W. Park, J. Jang, J. Cheon, H. H. Lee, D. R. Lee and Y. Lee, J. Phys. Chem. C, 2008, 112, 9627–9631 CrossRef CAS.
- S. Limpijumnong and W. R. L. Lambrecht, Phys. Rev. Lett., 2001, 86, 91 CrossRef CAS PubMed.
- X. Yan, H. Dong, Y. Li, C. Lin, C. Park, D. He and W. Yang, Sci. Rep., 2016, 6, 24958 CrossRef CAS PubMed.
- G. Gouadee and P. Colomban, Prog. Cryst. Growth Charact. Mater., 2007, 53, 1–56 CrossRef.
- J. H. Lin, R. A. Patil, R. S. Devan, Z.-A. Liu, Y. P. Wang, C. H. Ho, Y. Liou and Y. R. Ma, Sci. Rep., 2014, 4, 6967 CrossRef CAS PubMed.
- C. Yu, Q. Yu, C. Gao, H. Yang, B. Liu, G. Peng, Y. Han, D. Zhang, X. Cui, C. Liu, Y. Wang, B. Wu, C. He, X. Huang and G. Zou, J. Appl. Phys., 2008, 103, 114901 CrossRef.
- S. Desgreniers, Phys. Rev. B, 1998, 58(21), 14102–14105 CrossRef CAS.
- F. C. Chiu, P. W. Li and W. Y. Chang, Nanoscale Res. Lett., 2012, 7, 178 CrossRef PubMed.
- F. M. Simanjuntak, D. Panda, K. H. Wei and T. Y. Tseng, Nanoscale Res. Lett., 2016, 11, 368 CrossRef PubMed.
- K. Kusuba, Y. Syono and T. Kikegawa, Proc. Jpn. Acad., Ser. B, 1999, 75, 1–6 CrossRef.
- A. Bera, T. Ghosh and D. Basak, ACS Appl. Mater. Interfaces, 2010, 2(10), 2898–2903 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Pressure-dependent X-ray diffraction patterns, pressure-dependent Raman spectra of ZnO-R and ZnO-F, whole profile fitting of the X-ray diffraction patterns of both ZnO micro-structures, pressure-dependent ratio of the d-spacing of (100) and (002) planes of wurtzite, (200) and (220) planes of rocksalt phase of both the ZnO micro-structures; pressure-dependent I–V characteristics and resistivity of ZnO-R and ZnO-F. See DOI: 10.1039/c8ra10219h |
| This journal is © The Royal Society of Chemistry 2019 |