Open Access Article
Open Access ArticleA contact lens promising for non-invasive continuous intraocular pressure monitoring
Yu Pang ab,
Yuxing Liab,
Xuefeng Wangab,
Chenjie Qic,
Yi Yangab and
Tian-Ling Ren
ab,
Yuxing Liab,
Xuefeng Wangab,
Chenjie Qic,
Yi Yangab and
Tian-Ling Ren *ab
*ab
aInstitute of Microelectronics, Tsinghua University, 100084, Beijing, China. E-mail: rentl@tsinghua.edu.cn
bBeijing National Research Center for Information Science and Technology (BNRist), Tsinghua University, 100084, Beijing, China
cSchool of Applied Science, Beijing Information Science & Technology University, 100192, Beijing, China
First published on 11th February 2019
Abstract
Intraocular pressure (IOP) is the key indicator to assess the risk for and status of glaucoma patients, and medication at high IOP values slows down exacerbation of glaucoma. However, the IOP value is subject to circadian variation and cannot be measured continuously in clinical practice. Herein, we have fabricated a contact lens with a Wheatstone bridge circuit for non-invasive monitoring of IOP. A metal electrode has been used as a strain gauge to measure the weak deformation of the eyeball caused by IOP variation. Tests on a model eye indicate that the contact lens exhibits a high sensitivity of 20 μV mmHg−1 and excellent dynamic cycling performance at different speeds of IOP variation. These results demonstrate that the contact lens sensor is promising for continuous IOP monitoring of glaucoma disease, regardless of the posture and activities of the patient.
Introduction
At present, more than 65 million people around the world suffer from glaucoma, and this figure is expected to increase to 80 million by 2020, making glaucoma the second most common cause of visual field loss and even blindness among human eye diseases.1–3 Although there is no cure for glaucoma yet, but medication at an early stage to reduce IOP can effectively slow down the deterioration of vision or partially recover sight in severe cases. The fluctuation of IOP value is the most important indicator to assess the risk for patients with glaucoma.4,5 In general, normal IOP ranges from 10 to 21 mmHg with an average of 15.3 mmHg.6 High IOP and wide diurnal IOP variation are the primary risk factors for glaucoma pejoration. Uninterrupted measurement demonstrates that IOP is subject to time-dependent circadian variation. Healthy eyes show around a 6 mmHg fluctuation in IOP over a period of 24 hours, while this fluctuation is much higher for glaucoma eyes.7 Hughes et al. have reported that 24 hour IOP monitoring is useful in facilitating early detection of glaucoma in almost 80% of clinic patients.8 To prevent glaucoma pejoration, therefore, it is necessary to continuously monitor IOP variation.Currently, in the hospital setting the normative IOP measuring instrument is the Goldmann applanation tonometer, which needs local anesthesia for the pressing of the tip onto the cornea surface. However, it cannot achieve continuous IOP monitoring owing to the requirements for precise measurements and expert operation. Therefore, it is urgent to develop simple, low-cost and continuous IOP monitoring techniques, especially wearable sensors. So far, several methods based on the working principles of hydrodynamics,9 capacitive and inductive reactance,10–13 and piezo-resistive effect14–17 have been investigated to meet those new requirements. Araci et al. have developed an implantable contact lens with an airtight microfluidic channel, but it is difficult to read the pressure through a hazy cornea.9 Via a change in the distance between capacitive electrodes or the length in inductance coils, the IOP pressure can be detected and received by an external oscillator circuit. Capacitive IOP sensors with a sensitivity of 160 kHz mmHg−1 and a sensitivity of 15 kHz mmHg−1 were reported in 2009 and 2013, respectively.10,11 However, both sensors need surgery to implant them inside the eyes. In addition, piezo-resistive sensors provide promising non-invasive techniques to detect the curvature variation of the cornea. By using a conducting polymer bi-layer film, Laukhin et al. have fabricated a strain sensor over the whole area of a contact lens with good linearity and reproducibility but a low sensitivity of 1.5 Ω mmHg−1.14 Renaud and co-workers have fabricated an IOP contact lens with a sensitivity of 8.37 μV mmHg−1.16 However, the use of nontransparent materials (polycarbonate and polyimide) in these contact lenses would greatly influence the visual field during long-term IOP monitoring. Moreover, the sensitivity and dynamic response of the output in response to the IOP variation need to be improved for potential practical application.
In this work our effort was to develop a non-invasive contact lens with high sensitivity, transmittance and linearity for 24 hour IOP monitoring. A Wheatstone circuit was designed to improve the precision and eliminate the temperature drift. Using transparent polyethylene terephthalate (PET) as substrate, two counterpart active strain gauges and two counterpart passive strain gauges were embedded in the contact lens. The sensor shows a sensitivity of 20 μV mmHg−1 within the large range of 9–30 mmHg on a polymer eyeball model. Besides this, it exhibits outstanding response to different speeds of IOP change and a high linearity of 0.996. The contact lens sensor could allow continuous IOP monitoring regardless of the position and activities of a patient, and displays promise for point-of-care management in glaucoma patients.
Design and fabrication
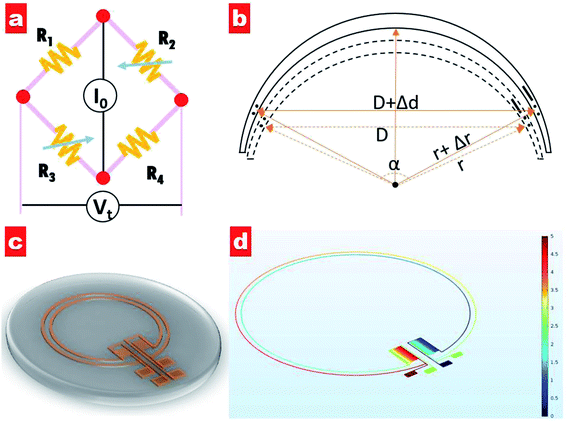
Generally, an IOP change of 1 mmHg would cause a change of central corneal curvature of about 3 μm (for a corneal curvature of 7.8 mm),18 which can induce a small expansion or constriction of the corneal perimeter. A piezo-resistive strain gauge was designed to detect the weak deformation which leads to a resistance increase or decrease. A Wheatstone bridge is adopted to measure the weak signal variation, having the advantage of high sensitivity and precision; see Fig. 1a. The bridge contains a counter pair of measuring resistances (R2, R3) and a counter pair of fixed resistances (R1, R4). If a constant voltage is supplied to the bridge, the output voltage Vt can be expressed by the following equation:19
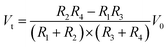 | (1) |
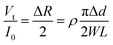 | (2) |
The change in diameter, Δd, is determined by the pressure variation in the eyes, which relates to the physical parameter of the eyeball.13 Note that the arc length of the contact lens remains the same for the pressure increasing and decreasing. Thus, Δd can be expressed by the equation:
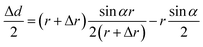 | (3) |
| Δd ≈ AΔr | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(α/2)-α
sin(α/2)-α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(α/2). Moreover, the IOP change generates a certain variation of corneal curvature, and thus Δr can be expressed by the following equation:
cos(α/2). Moreover, the IOP change generates a certain variation of corneal curvature, and thus Δr can be expressed by the following equation:| Δr = BΔp | (5) |
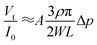 | (6) |
It can be seen that the output voltage displays a linear relationship with the IOP variation. Notably, micro-sized piezo-resistive electrodes (W, L) and large radius (α) could contribute to high sensitivity of the IOP sensor. The designed parameters of the as-prepared sensor are shown in Table 1.
| Diameter of the inside strain gauge | 10 mm |
| Diameter of the outside strain gauge | 10.04 mm |
| Width of the strain gauge | 10 μm |
| Diameter of the contact lens | 14 mm |
| Radius of curvature of the contact lens | 10 mm |
| Central thickness of the contact lens | 100 μm |
Fig. 1c shows a schematic of the designed IOP contact lens sensor. It can be seen that two electrode coils as strain gauges are set at the lens edge and two zigzag electrode elements as fixed resistances are positioned along the radius orientation. Four electrode pads extend out for the power supply and output voltage detection. Moreover, the potential distribution of our designed circuit has been simulated, as shown in Fig. 1d. Under a voltage supply of 5 V for one counterpart pair of electrode pads, the voltage in each electrode of the other counterpart pair exhibits the same value of 2.5 V, indicating that four electrodes with the same length have zero contribution to the output voltage.
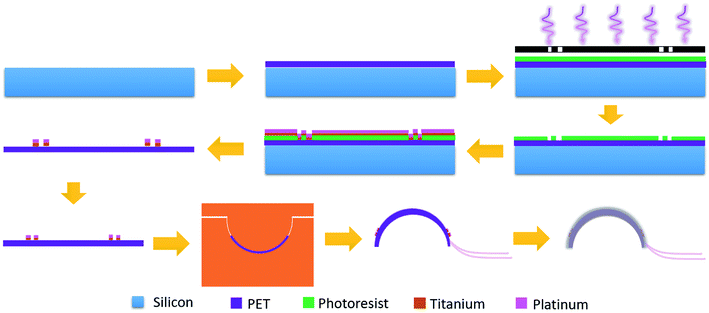
Fig. 2 shows the fabrication process of the contact lens for IOP monitoring. Firstly, a two-inch silicon wafer (Institute of Tianjin Semiconductor) was cleaned with acetone and deionized water. Flexible and transparent PET film (XFNANO, Materials Tech Co. Ltd) with a thickness of 50 μm was fixed on the wafer. At a rotation speed of 3000 rpm, the positive photoresist (AZ 5350) was spin-coated onto the film and prebaked at 100 °C for 2 min. Then the sample was exposed under a mercury lamp (H94-17 G, Sichuan Nanguang Vacuum Technology Co., Ltd) for 90 s and developed to form the designed pattern. After drying using the nitrogen, an oxygen plasma system (Branson IPC 3000) was used to remove the residual photoresist for 5 min, which is beneficial to the adhesion of a deposited metal layer to the PET substrate. A titanium layer with a thickness of 10 nm and a platinum layer with a thickness of 50 nm were deposited in sequence (KJCL Lab 18, Kurt Lesker). Acetone was used to lift off the deposited samples and peel off the PET film from the silicon substrate.
Fig. 3a shows the microscopy image after lifting off. Two passive zigzag electrodes with width of 10 μm are observed. The as-prepared resistance of each bridge is about 12.3 kΩ. After cutting the as-prepared sensor into a circle, it was thermally molded using an aluminum model with a diameter of 10 mm at a temperature of 200 °C, as shown in Fig. 3b. To get a desirable curvature, a weight of 100 g was put on the upper surface of the aluminum model. Aluminum foils attached by silver paste were used to lead out from the four contact pads. Finally, the sensor was encapsulated by a polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning) layer using the prepolymer ingredient with base silicone and curing agent in a weight ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. PDMS has the advantages of high biocompatibility, flexibility and transparency,20,21 and has found various applications in pressure sensors,22 microfluidics23 and artificial skin.24 As shown in Fig. 3c, the as-prepared contact lens is smooth and transparent, which would be beneficial for human optesthesia. The measured thickness of the eyeball sensor is about 120 μm at the edge and about 100 μm at the centre.
1. PDMS has the advantages of high biocompatibility, flexibility and transparency,20,21 and has found various applications in pressure sensors,22 microfluidics23 and artificial skin.24 As shown in Fig. 3c, the as-prepared contact lens is smooth and transparent, which would be beneficial for human optesthesia. The measured thickness of the eyeball sensor is about 120 μm at the edge and about 100 μm at the centre.
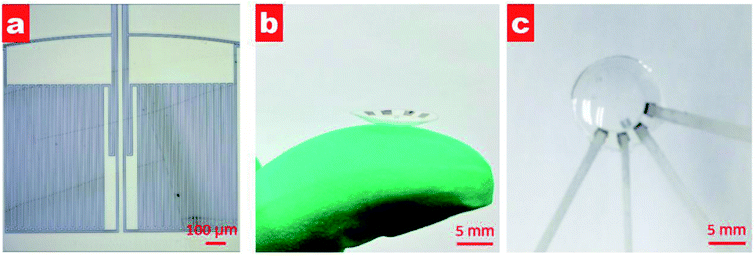 | ||
| Fig. 3 (a) Microscopy image of fabricated sensor after lifting off; (b) photograph of the contact lens on a finger after thermal molding; and (c) photograph of the contact lens after PDMS packing. | ||
Results and discussion
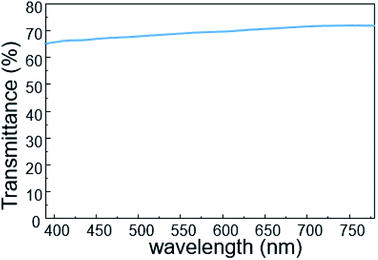
To investigate its visual properties, we measured the transmittance of the as-prepared contact lens in the visible spectrum, as shown in Fig. 4. The contact lens has a transmittance of about 70% in the wavelength range of 390–780 nm, indicating adequate visual performance for potential long-term usage. Furthermore, higher transmittance can be obtained with thinner PET substrate and PDMS packing.The real-time performance of the contact lens sensor was measured on a silicone model eye with a thickness of about 150 μm and diameter of 10 mm, which has been widely used to investigate pressure variation in electronic eyes.25 Fig. 5 shows the home-made test system used to monitor IOP variation in the eyeball model. A syringe pump was used to inject water into the silicone eye for pressure increase and to extract water for pressure decrease. To calibrate the relationship between the output voltage and pressure variation, a standard pressure sensor (MIK-P300, Hanzhou Meacon Automation Technology, China) was used to record the pressure while water was pumped in or out. A semiconductor analyzer (Keithley 4200) was used to supply a constant current of 100 μA and to detect the output voltage signal.
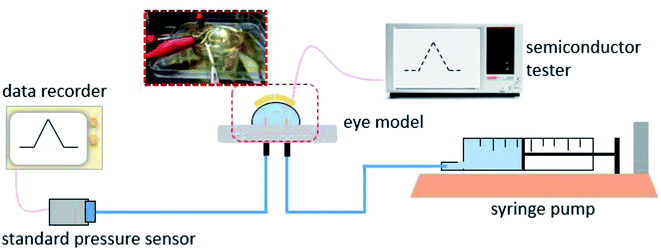 | ||
| Fig. 5 The test platform for measuring performance of the contact lens sensor on the silicone eye model. | ||
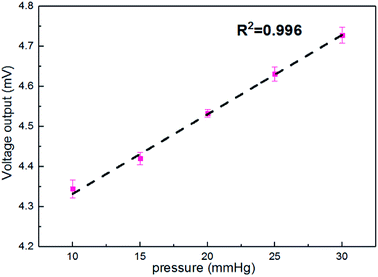
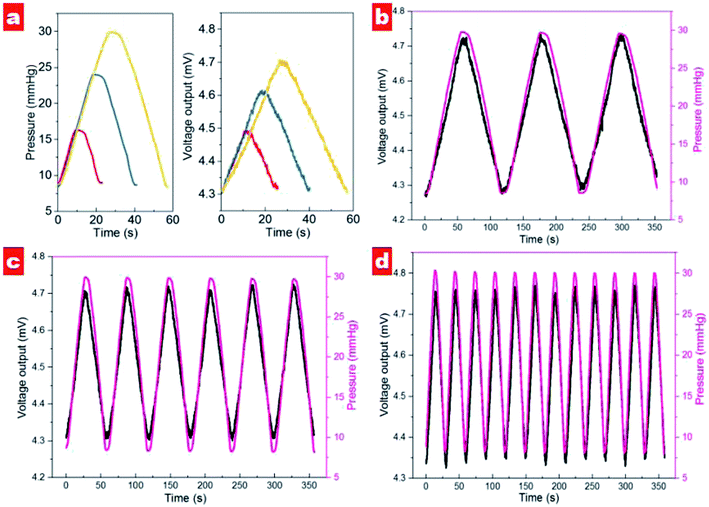
Fig. 6 shows the output voltages at different pressures in the silicon eyeball model. It can be seen that the output voltage is 4.34 mV for the initial pressure of 10 mmHg and shows enhancement with increasing IOP. Moreover, the output signal exhibits an excellent linear relationship (R2 = 0.996) in the IOP range of 10–30 mmHg. The sensitivity is defined as (V–V0)/(V0P), where V0 and V are initial output voltage and response output voltage under the changed pressure, respectively. The calculated sensitivity of the contact lens for IOP measurement is 20 μV mmHg−1. A performance comparison with previous reports is shown in Table 2.
| Working principle | Invasive or non-invasive | Sensitivity | Ref. |
|---|---|---|---|
| Microfluidic | Invasive | 137 μm mmHg−1 | 9 |
| Capacitive | Invasive | 15 kHz mmHg−1 | 10 |
| Capacitive | Invasive | 160 kHz mmHg−1 | 11 |
| Capacitive | Non-invasive | 32 kHz mmHg−1 | 12 |
| Inductive | Non-invasive | 8 kHz mmHg−1 | 13 |
| Piezo-resistive | Non-invasive | 1.5 Ω mmHg−1 | 14 |
| Piezo-resistive | Non-invasive | ∼0.025 Ω mmHg−1 | 15 |
| Piezo-resistive | Non-invasive | 8.37 μV mmHg−1 | 16 |
| Piezo-resistive | Non-invasive | 20 μV mmHg−1 | This work |
The dynamical cycling performance of contact lens in different pressure ranges was tested, as shown in Fig. 7a. It should be noted that output voltage exhibits an excellent linear response in different pressure ranges. In the range 8.7–16.3 mmHg, the voltage signal displays a variation of about 155 μV. For the measuring ranges of 8.4–24.0 and 8.7–29.9 mmHg the output voltages show variations of 307 and 402 μV, respectively. It is noted that the output voltage of the contact lens shows the same slope for pressure increase and decrease, indicating excellent recoverability. Moreover, the contact lens exhibits excellent response to different rates of pressure changes; see Fig. 7b–d. In the range 9–30 mmHg, the contact lens shows output voltage variation that follows IOP changes well. Interestingly, with increased speed of pressure change the variation of output voltage shows the decreased values of 440, 414, and 408 μV for slow, medium and fast speeds, respectively. We suppose that high speed of injection and extraction would reduce the effective response time for each cycle and contribute to the small fluctuation of output signals.
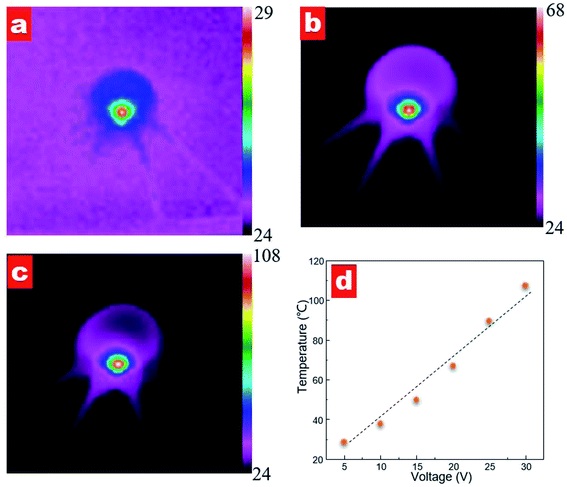
To investigate the heating effect of different power supplies, we measured the temperature distribution of the contact lens, as shown in Fig. 8. When a voltage supplied to the contact lens, the sensor shows an instant heating response. Fig. 8a–c shows the temperature distribution images at a supplied voltage of 10, 20 and 30 V, respectively. It can be seen that a highlight heating area is observed in the zigzag resistance region for all supplied voltages while no obvious heating area is observed along the active strain gauges. The measured maximum temperature values are 37.8, 67.1 and 107.3 °C with voltage supplies of 10, 20 and 30 V, respectively. Furthermore, the maximum temperature varies linearly as a function of the supplied voltage; see Fig. 8d. The calculated ratio of temperature versus voltage is 3.0 °C V−1.
Conclusions
In conclusion, we have developed a non-invasive contact lens for IOP monitoring based on the transparent substrate PET. A Wheatstone bridge was designed to improve the detection of weak deformation of the eyeball, which is beneficial for high sensitivity and precision. Via lithography and deposition processes, two active strain gauges and two passive strain gauges were fabricated. A thermal model was used to form a contact lens shape, which was then encapsulated in a bio-compatible PDMS layer. In the visible spectrum the contact lens exhibits a transmittance of 70%. The calculated sensitivity of the contact lens is 20 μV mmHg−1 in the IOP range of 10–30 mmHg. Moreover, it exhibits excellent dynamic response to different speeds of IOP pressure variation. The contact lens shows promising application in continuous IOP monitoring, which would be beneficial in the diagnosis and therapy of glaucoma patients.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key R&D Program (2016YFA0200400), National Natural Science Foundation (61434001, 61574083, 61874065, 51861145202), and National Basic Research Program (2015CB352101) of China. The authors are also thankful for the support of the Research Fund from the Beijing Innovation Center for Future Chip (KYJJ2018005), Beijing Natural Science Foundation (4184091), and Shenzhen Science and Technology Program (JCYJ20150831192224146).Notes and references
- H. A. Quigley and A. T. Broman, Br. J. Ophthalmol., 2006, 90, 262–267 CrossRef CAS PubMed.
- D. Pascolini and S. P. Mariotti, Br. J. Ophthalmol., 2010, 96, 614–618 CrossRef PubMed.
- H. K. J. Liu, K. Mansouri and R. N. Weinreb, PLoS One, 2015, 10, e0129529 CrossRef PubMed.
- K. Mansouri, R. N. Weinreb and F. A. Medeiros, Semin. Ophthalmol., 2013, 28, 157–164 CrossRef PubMed.
- J. Choi, K. H. Kim, J. Jeong, H. S. Cho and M. S. Lee, Invest. Ophthalmol. Visual Sci., 2007, 48, 104–111 CrossRef PubMed.
- B. E. Klein, R. Klein and K. L. Linton, Invest. Ophthalmol. Visual Sci., 1992, 33, 2224–2228 CAS.
- N. A. Loewen, J. H. K. Liu and R. N. Weinreb, Invest. Ophthalmol. Visual Sci., 2010, 51, 933–937 CrossRef PubMed.
- E. Hughes, P. Spry and J. Diamond, J. Glaucoma, 2003, 12, 232–236 CrossRef PubMed.
- I. E. Araci, B. Su, S. R. Quake and Y. Mandel, Nat. Med., 2014, 20, 1074–1078 CrossRef CAS PubMed.
- G. Chitnis, T. Maleki, B. Samuels, L. B. Cantor and B. Ziaie, IEEE Trans. Biomed. Eng., 2013, 60, 250–256 Search PubMed.
- P. J. Chen, S. Saati, R. Varma, M. S. Humayun and Y. C. Tai, MEMS IEEE 22nd International Conference on Micro Electro Mechanical Systems, 2009, pp. 244–247 Search PubMed.
- G. Z. Chen, I. S. Chan and D. C. C. Lam, Sens. Actuators, A, 2013, 203, 112–118 CrossRef CAS.
- G. Z. Chen, I. S. Chan and D. C. C. Lam, Med. Eng. Phys., 2014, 36, 1134–1139 CrossRef PubMed.
- V. Laukhin, I. Sánchez, A. Moya, E. Laukhina, R. Martin, F. Ussa, C. Rovira, A. Guimera, R. Villa and J. Aguiló, Sens. Actuators, A, 2011, 170, 36–43 CrossRef CAS.
- M. Leonardi, P. Leuenberger, D. Bertrand, A. Bertsch and Ph. Renaud, TRANSDUCERS, 12th International Conference on Solid-State Sensors, Actuators and Microsystems, 2003, vol. 2, pp. 1043–1046 Search PubMed.
- M. Leonardi, P. Leuenberger, D. Bertrand, A. Bertsch and Ph. Renaud, Invest. Ophthalmol. Visual Sci., 2004, 45, 3113–3117 CrossRef PubMed.
- M. D. Twa, C. J. Roberts, H. J. Karol, A. M. Mahmoud, P. A. Weber and R. H. Small, J. Glaucoma, 2010, 19, 382–390 CrossRef PubMed.
- A. K. C. Lam and W. A. Douthwaite, Ophthal. Phys. Opt., 1997, 17, 18–24 CrossRef CAS.
- A. Thanachayanont and S. Sangtong, ETRI J., 2007, 29, 70–78 CrossRef.
- X. Liu, Y. Zhu, M. Nomani, X. Wen, T. Y. Hsia and G. Koley, J. Micromech. Microeng., 2013, 23, 025022 CrossRef.
- D. Baker, X. Liu, H. Wang, C. Luo and L. Tang, Biomacromolecules, 2011, 12, 997–1005 CrossRef CAS PubMed.
- Y. Pang, K. Zhang, Z. Yang, S. Jiang, Z. Ju, Y. Li, X. Wang, D. Wang, M. Jian, Y. Zhang, R. Liang, H. Tian, Y. Yang and T. L. Ren, ACS Nano, 2018, 12, 2346–2354 CrossRef CAS PubMed.
- A. R. Abate, D. Lee, T. Do, C. Holtze and D. A. Weitz, Lab Chip, 2008, 8, 516–518 RSC.
- H. K. Lee, S. I. Chang and E. Yoon, J. Microelectromech. Syst., 2006, 15, 1681–1686 CAS.
- I. Jung, J. Xiao, V. Malyarchuk, C. Lu, M. Li, Z. Liu, J. Yoon, Y. Huang and J. A. Rogers, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1789–1793 Search PubMed.
| This journal is © The Royal Society of Chemistry 2019 |