Open Access Article
Open Access ArticleNon-scrambling of hydrogen in NH4+(H2O)3 clusters
K. Hansen *ab,
A. E. K. Sundén†
c,
K. Støchkeld,
S. Brøndsted Nielsen
*ab,
A. E. K. Sundén†
c,
K. Støchkeld,
S. Brøndsted Nielsen d and
B. Dyneforse
d and
B. Dyneforse
aCenter for Joint Quantum Studies, Department of Physics, Tianjin University, Tianjin 300072, China. E-mail: KlavsHansen@tju.edu.cn
bDepartment of Physics, University of Gothenburg, 41296 Gothenburg, Sweden. E-mail: klavs.hansen@physics.gu.se; Web: http://physics.gu.se/˜klavs/
cDepartment of Physics, University of Gothenburg, 41296 Gothenburg, Sweden
dDepartment of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
eChalmers University of Technology, 41296 Gothenburg, Sweden
First published on 26th February 2019
Abstract
We have measured the metastable decay of protonated, ammonia-doped, deuterated water clusters produced in an electrospray source, dn-NH4+(H2O)3, n = 0–6. The mass spectra show a very strong odd–even effect, consistent with a low degree of scrambling of the hydrogen bound to water and to the ammonia. The relative evaporation rate constant for light water was almost twice the one for heavy water, with the rate for mixed protium–deuterium water molecule intermediate between these two values.
1. Introduction
The structure of water is intimately linked to the hydrogen bond, both determining the properties of bulk water and those of finite size droplets. Several effects related to the hydrogen bonds are of fundamental interest, such as hydrogen quantum mechanical tunneling1,2 and hydrogen mobility in general. The use of clusters in molecular beams to study the phenomenon of hydrogen scrambling can provide detailed insight into the phenomenon because this type of experiments can be performed with exactly known numbers of constituents. This allows a mapping of the development of quantities with particle size. The possibility to add deuterium in controlled doses allows further details to be revealed because of the ease with which a replacement of a protium with a deuteron is detected mass spectrometrically.Several studies have indicated that the hydrogen exchange in protonated water clusters occurs on the time scales of molecular beam experiments or faster. From the experiments reported in ref. 3 it was concluded that collisions at thermal energies between deuterium labelled water and hydronium ions lead to an exchange with an efficiency corresponding to the collision cross section. The exchange between hydronium ions and ammonia, on the other hand, was limited to transfer of the charge to the ammonia, with no replacement of the other three hydrogen taking place. Theoretical simulations, which usually cover rather short time scales, also give indications of very rapid hydrogen scrambling in water.3–7 The tendency is not universal, however, as indicated by the mixed results on exchange in ref. 8–10 where ligand water molecules are exchanged intactly, without any evidence for scrambling. Experimentally, isotope distributions in decay products following low and medium energy collisions between ammoniated water clusters with water molecules have shown a low tendency to H/D exchange for the smallest clusters, with an increasing trend with cluster size.11,12 For pure water clusters, in contrast, isotope-resolved fragmentation yields following low energy collisions of light water clusters with heavy water molecules were interpreted in ref. 13 as very rapid H/D exchange rates for small clusters, with rates decreasing with increasing cluster size, although the measured branching ratios in fact showed the opposite size dependence. The somewhat counter-intuitive interpretation emphasizes the need for experiments with more transparent interpretations.
The small amount of H/D exchange in the small ammonia–water cluster could be assigned to the different proton affinity of water and ammonia, although this in itself does not prevent hydrogen exchange between the two types of molecules. The difference in proton affinity between the free ammonia and the water molecules, 1.7 eV,14 is not representative of the difference in binding energies of protonated ammonia and water molecules in a cluster. Studies of evaporative branching ratios show that protonated water clusters doped with even a single ammonia molecule have an observable branching ratio to loss of ammonia, and consequently for the transfer of a proton to the water molecules.15 Given the low equivalent temperature of these clusters (significantly below room temperature), this fact implies a strong reduction in the effective difference in proton affinity in the cluster. The values of the evaporative free energy differences extracted from the experiments are around 0.05 eV for a range of small mixed water ammonia clusters.15 The question of hydrogen scrambling between the ammonia and water molecules is therefore not as trivial as the values of the vacuum proton affinities suggest. The small free energy differences alone suggest a facile exchange of protons, but obviously does not address the question of the value of the energy barrier for the proton exchange in the cluster which, for the scrambling, is then the only relevant parameter.
The spontaneous decay of preformed species allows these phenomena to be studied without the complications due to attachment and the re-evaporation processes that occur in collision experiments, and hence neither collisional energy transfer nor unimolecular reactions need to be modelled to interpret the data. This article reports experiments on the scrambling of the smallest protium and deuterium containing protonated ammonia–water clusters.
2. Experimental procedure
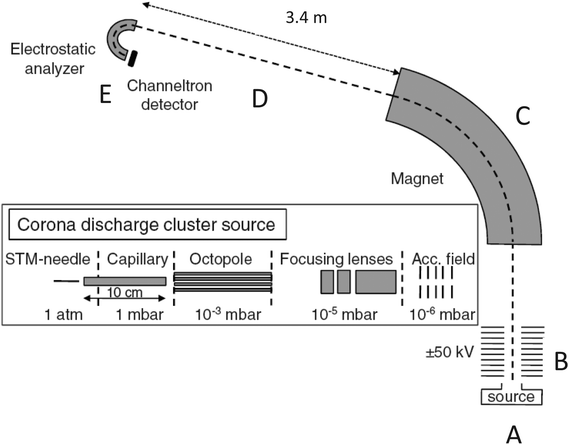
The experimental apparatus used is shown in Fig. 1. It has been used previously in ref. 15–18 and is well tested. The positively charged clusters were produced in a corona discharge source (position (A) in Fig. 1) and entered vacuum through a 10 cm long capillary held at room temperature. The voltage on the STM-needle that was used to create the discharge was kept at a potential at 4 kV. After entry into vacuum, the cluster ion beam was guided through an octopole which was flooded to ca. 3 × 10−2 mbar of heavy water vapor pressure with a needle valve, and where low energy cluster-water molecule collisions and the subsequent incorporation of deuterium took place. The kinetic energy of the clusters did not exceed 5 eV in the octopole.For cluster sizes up to a total of five molecules, the source predominantly produced species containing a single ammonia molecule and a varying number of water molecules. The clusters were not mass selected at this point. After passage through the octopole and a set of electrostatic lenses, the clusters were accelerated to 50 keV (position indicated by a (B)), mass selected in a magnet (at position (C)) and then flew freely for 3.37 m (position (D)). They were then energy-analyzed in a hemispherical electrostatic analyzer17 (at (E)), which effectively performed a mass analysis of the cluster distribution created by the decay of the mass selected species during the free flight after acceleration. The processes measured were of the nature
| NH3(H2O)3H+ → NH3(H2O)2H+ + H2O, | (1) |
The mass distribution produced in the source was measured with a scan of the magnetic field. The compositions of the clusters were tested for several masses by collision with an inert gas in a gas cell located at the mid-point of the free flight path and the fragments identified analogously to the procedure used without the inert gas present.
In a second procedure, the deuterium in the form of heavy water was introduced into the nascent clusters in the corona discharge region. The mass spectrum was recorded but the intensity of the beam only allowed measurements of spontaneous decay of the clusters containing one or two deuterium. These data will mainly be used for comparison with the main series, generated by collisions in the octopole.
3. Results and analysis
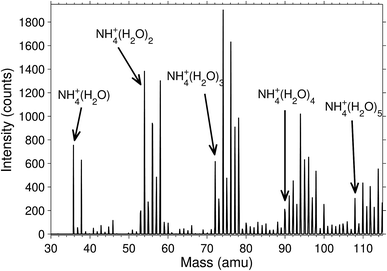
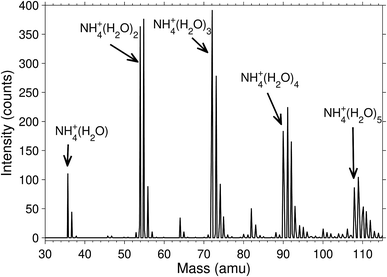
The degree of deuteration was, unsurprisingly, found to be related to the heavy water pressure in the octopole where the molecular attachment and exchange takes place. A magnet scan mass spectrum is shown in Fig. 2 for the pressure P = 3.5 × 10−3 mbar. Independent of pressure, the cluster abundances were significantly higher for the even than for the odd deuterium numbers. We observed that there was always only a very small signal for clusters where the last four hydrogen had been replaced by deuterium, even at high heavy water pressure in the octopole. This is either due to a strong preference for equilibrium distributions where the ammonia contains only protium, or that the rate of exchange is strongly reduced on the experimental time scales due to high energy barriers.A mass spectrum of the clusters that are deuterated already in the corona discharge region is shown in Fig. 3. The isotopologue intensity distributions are smooth with little sign of odd–even effects. The average number of deuterium per water hydrogen atom is, for clusters with 1 through 4 water molecules, equal to 0.17, 0.17, 0.11, 0.17, suggesting a formation mechanism considerable different from the one in the octopole trap. The distributions of the number of deuterons and protons in these clusters are neither Poisson nor binomial distributions, from which we can rule out formation mechanisms described by the kinetics associated with these two theoretical distributions. The absence of odd–even effects in this spectrum is ascribed to the high energy processes involved in the formation of the ammonia molecules. We expect that the details of such mass spectra are determined by a number of factors, including details of the electronically excited states, plasma parameters, and the kinetics. A complete modelling of the situation is not only likely to be rather complicated but also to depend on specifics of the source used. We will therefore not enter a discussion of this problem.
In the following we will analyse the measurements of the metastable decay of the NH4+(H2O)3 clusters by the reaction in eqn (1) for all observed degrees of deuteration. The metastable branching ratio of all seven different isotope compositions represented in the beam were measured, both for the clusters produced by heavy water attachment in the octopole and for those few measurable species produced by flooding the STM needle with heavy water vapor.
Single water molecules were observed to be the major loss during free flight. Ammonia loss by the reaction
| NH3(H2O)3H+ → NH3 + (H2O)3H+, | (2) |
The loss of NH3 alone, without the accompanying deuterated channel present, is consistent with the non-scrambling of the ammonia hydrogen observed in the absence of the four highest possible deuterated species in the mass spectra, mentioned above.
The loss of H2O from an undeuterated cluster should be unity but is experimentally observed to be 0.97. The small deviation from unity is ascribed to contamination and is indicative of the overall systematic uncertainty on the data.
The total evaporation rates, i.e. the rates summed over all the three channels, corresponding to loss of H2O, HDO, and D2O, in the free flight region between the exit of the magnet and the entry into the mass analyser were identical for the different isotopologues within the statistical uncertainties and consistent with the values found previously for pure light water species.16 The metastable decay fraction depends on the dissociation energy and, for a not too narrow excitation energy distribution, also on the heat capacity of the decaying cluster,16 in addition to the normalizing pre-acceleration abundance. For the broad excitation energy distributions expected under the experimental settings used here, the dependence is linear in both the heat capacity and the dissociation energy. These dependences are consequences of broad internal excitation energy distributions. A detailed explanation of the origin of these dependences is given in ref. 16 and 20. The simplest explanation for the observations is that both of these quantities are independent of the isotopic distribution.
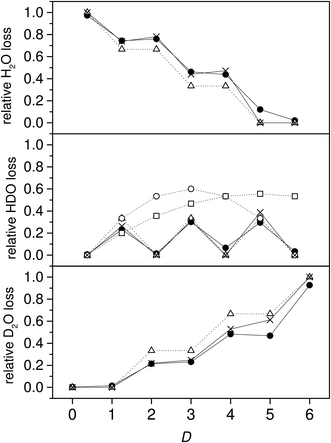
The water molecules evaporated were almost all pure light or heavy water species for the even deuterium number clusters, and both mixed and pure for the odd deuterium number clusters. This is illustrated by plotting the branching ratios of the HDO channel vs. the total deuterium content in the clusters. The values are shown in Fig. 4, together with the branching ratios for the two other channels. There is a very pronounced odd–even effect, with the even deuterium number clusters evaporating virtually no HDO, and the odd number clusters evaporating between 23 and 30%. When deuterium numbers, D, are even, the almost vanishing branching to the HDO evaporation channel indicates that either no scrambling occurs or that the evaporation is selectively of the isotopically pure species.
The trend for the branching ratio of HDO and the step-like behavior for D2O are qualitatively well reproduced if we assume that there is no scrambling and that the evaporation rate constants for H2O, HDO, and D2O are proportional to their mole fraction in the clusters. The middle frame in Fig. 4 includes the calculated branching ratios under the three different degrees of hydrogen scrambling, assuming identical evaporation rate constants for all three evaporated molecular species. The situation that describes the data best at this level is the one with no scrambling in the clusters, and where any HDO present in the cluster is produced in the chamber before attachment intact to the cluster. For this situation, the probability of a HDO loss is 1/3 for the odd values of D and 0 for the even, corresponding to the relative HDO abundances in the cluster. In the second scenario protium and deuterium are scrambled completely among the water molecules only, and in the third freely between all possible sites in both the water and the ammonia. For the last two situations the isotope distributions of the emitted water molecules are given by
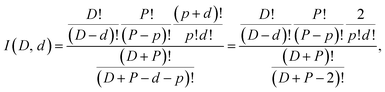 | (3) |
From the middle frame in Fig. 4 it is clear that the non-scrambling hypothesis fares significant better than the two other possibilities. However, there are minor but significant deviations from the predictions of branching ratios for the non-scrambling and equal rate constant model. We can relax the assumption of equal evaporation rate constants for the three different water species if we make the less far-reaching assumption that evaporation rates of the three isotopologues are not identical and instead proportional to the content of the molecular species in the cluster, but still otherwise independent of the composition of the cluster. This describes interactions between the water molecules in the cluster that are independent of the isotopic composition. We will also relax the assumption of no scrambling between the six water molecule hydrogen atoms.
We then consider the branching ratios I(D, d) for evaporating a water molecule containing d deuterium from a protonated cluster with D deuterium. This branching ratio is proportional to the rate constant for loss of a H2−dDdO molecule, kD,d, and the mole fraction f(D, d) of the H2−dDdO molecules in the parent cluster:
| I(D, d) ∝ kD,df(D, d). | (4) |
This generalizes eqn (3) by introducing specific D, d-dependent rate constants, and relaxing the assumption about the isotopologue populations. We can use normalized populations without loss of generality:
| f(D, 0) + f(D, 1) + f(D, 2) = 1. | (5) |
As a working hypothesis we will make the assumption that the amount of scrambling is symmetric, such that
| f(D, d) = f(6 − D, 2 − d). | (6) |
This only has numerical consequences when D = 2 and D = 4 clusters are compared. The symmetry is fulfilled trivially for the exchanges D = 0 ↔ 6 and D = 1 ↔ 5. For those compositions, the populations are f(0, 0) = 1, f(0, 1) = 0, f(1, 1) = f(5, 1) = 1/3 etc. Also the D = 3 populations are constrained; f(3, 0) = f(3, 2). This case gives a good example of the physical meaning of the symmetry assumption. The possible configurations are restricted to be either all HDO water molecules or one each of H2O, D2O, and HDO, i.e. either one or zero each of H2O and D2O. The ansatz makes no assumption about the relative weight of these two possibilities.
With these populations we can establish several predictions of the water-only scrambling hypothesis. They are as follows:
| I(0, 1) = I(0, 2) = I(6, 0) = I(6, 1) = I(1, 2) = I(5, 0) = 0 | (7) |
| I(0, 0) = I(6, 2) = 1, | (8) |
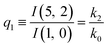 | (9) |
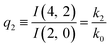 | (10) |
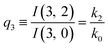 | (11) |
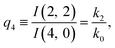 | (12) |
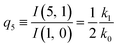 | (13) |
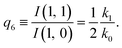 | (14) |
The predictions from this set of equations are highly non-trivial because they give 14 relations for only two ratios of rate constants.
The relations in eqn (7) compare well with the five experimentally observed values between 0.004 and 0.02, and a single value, for I(5, 0), of 0.12. Eqn (8) gives experimentally 0.96 (for D = 0) and 0.93 (for D = 6), which is also a fairly good agreement. Both comparisons corroborate the preliminary conclusion of only a small degree of scrambling with the hydrogen in the ammonia core, and the overall agreement with the non-scrambling hypothesis must then be considered fairly good. The relations for the rate constants expressed by the qn's, n = 1–4, give values for k2/k0 ranging from 0.49 to 0.64, with a average of 0.56 ± 0.05 (standard deviation of the mean). The last two ratios give k1/k0 = 0.71 ± 0.12 (all uncertainties quoted are one standard deviation). Not all ratios used are statistically independent and the uncertainties are likely to be slightly overestimated. In conclusion we find that the evaporation of light water proceeds with almost twice the rate constant of the heavy water evaporation, and for the mixed molecule with a factor which is close to the geometric average of the light and heavy water rate constants.
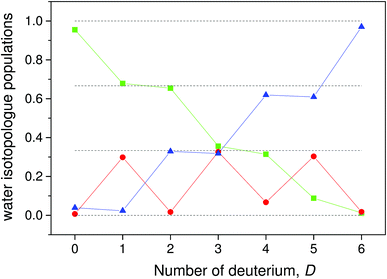
We can use the results to find the relative abundances of the different water species for all the different cluster compositions. Rewrite eqn (4) as
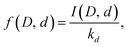 | (15) |
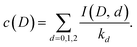 | (16) |
This gives the relative populations
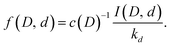 | (17) |
The populations calculated from the data with this equation are shown in Fig. 5. With a few exceptions the data fall very close to the ratios 0, 1/3, 2/3 and 1 that are expected in the absence of scrambling between the water molecules.
4. Discussion
The hydrogen scrambling was found here to be marginal between the water molecules and almost absent for the ammonia core of the protonated clusters in this study. A reduced inter-ammonia scrambling was also observed in the flowing afterglow experiments of ref. 4, whereas water scrambling was found to be extensive. Other results, both experimental and theoretical, also suggest a facile scrambling of the hydrogen in the water molecules, see e.g. ref. 6 and 7, in addition to the cases already mentioned in the introduction. The virtually absence of H–D exchange in ammonia is similar to the transition metal in ref. 10. We assign the resilience toward the exchange to high barriers and less to binding energy differences.Evaporation rates measured on bulk surfaces in similar temperature ranges as ours have given similar results. In ref. 21, it was found that the evaporation rate for D2O relative to H2O is a factor of approximately two lower. This is in striking agreement with the results here, in spite of the different nature of the systems studied. The collision induced dissociation (CID) of small protonated water clusters in ref. 4 produce the opposite conclusion, viz. that deuterium containing species are evaporated slightly easier. These data are measured on pure, protonated water clusters, but we suspect that also effects of non-equilibrium processes in the CID may be responsible for part of the discrepancy to the present data and the bulk water measurements.
An enrichment of deuterated species was likewise found in ref. 22 by preferential evaporation of light water molecules in a molecular beam. It is also of interest to note that the factor of two in the light-to-heavy water evaporation rates in the present experiments are also seen for the analogous processes in pure, protonated water clusters.23 These data were recorded in a molecular beam in vacuum, i.e. under conditions very similar to those used to record the data reported here. Furthermore, experimentally measured nucleation rates of heavy and light water differ by a large factor (at identical P and T), with heavy water having the highest nucleation rate.24 Given that nucleation involves a large number of absorption and evaporation events for each net molecule gained, this is consistent with the observed light water evaporation bias. These results are not directly transferable to the present experiments because of the different thermal conditions, but points to the same difference in evaporation rates.
Finally, the presence of the ammonia evaporation channel in the five-fold deuterated species indicates a difference between isotopologues. It is interesting to note that spectroscopic studies show differences in structure for the similar systems of HD8O4+ and H9O4+,25 with the presence of two isotopomers for the former and one for the latter. The existence of more than one isotopomer goes beyond the spectroscopic changes induced by simple deuterium substitution, as for example described in ref. 26. Such difference have been discussed previously,27 and corroborate isotopologue-specific structures and hence cluster energies for the clusters studied here.
5. Conclusions
We have determined the relative evaporation rate constant for H2O, HDO and D2O from a protonated ammonia-containing water cluster with three water molecules with 0 to 6 deuterium. The populations were consistent with no scrambling, with only a couple of uncertain points. The rate constant for light water evaporation was twice the value for heavy water evaporation, with the mixed isotope composition between these two values. The methods used to analyze the data in this work are generally applicable for the study of similar quantities for deuterated water-containing clusters, for example in the study of the size dependence of scrambling efficiencies. Studies of pure clusters, either pure ammonia or water, will be of particular interest in this connection.Conflicts of interest
There are no conflicts of interest to declare.References
- M. Y. Ovchinnikova, Chem. Phys., 1979, 36, 85 CrossRef CAS.
- R. A. M. O'Ferrall, J. Phys. Org. Chem., 2010, 23, 572 CrossRef.
- D. Smith, N. G. Adams and M. J. Henchman, J. Chem. Phys., 1980, 72, 4951 CrossRef CAS.
- S. T. Graul, M. D. Brickhouse and R. R. Squires, J. Am. Chem. Soc., 1990, 112, 631 CrossRef CAS.
- N. G. Adams, D. Smith and M. J. Henchman, Int. J. Mass Spectrom. Ion Processes, 1982, 42, 11 CrossRef CAS.
- Z. Sun, C. K. Siu, O. P. Balaj, M. Gruber, V. E. Bondybey and M. K. Beyer, Angew. Chem., Int. Ed., 2006, 45, 4027–4030 CrossRef CAS PubMed.
- M. Mella and A. Ponti, ChemPhysChem, 2006, 7, 894903 CrossRef PubMed.
- S. W. Lee, H. N. Lee, S. Kim and J. L. Beauchamp, J. Am. Chem. Soc., 1998, 120, 5800–5805 CrossRef CAS.
- P. J. Marinelli and R. R. Squires, J. Am. Chem. Soc., 1989, 111, 4101–4103 CrossRef CAS.
- S. B. Nielsen and G. Bojesen, Chem. Commun., 1998, 5, 613–614 RSC.
- K. Honma and P. B. Armentrout, J. Chem. Phys., 2004, 121, 8307–8320 CrossRef CAS PubMed.
- P. U. Andersson, M. J. Ryding, O. Sekiguchi and E. Uggerud, Phys. Chem. Chem. Phys., 2008, 10, 6127–6134 RSC.
- S. Yamaguchi, S. Kudoh, Y. Okada, T. Orii, K. Takeuchi, T. Ichikawa and H. Nakai, Chem. Phys. Lett., 2002, 359, 480 CrossRef CAS.
- E. P. L. Hunter and S. G. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413–656 CrossRef CAS.
- A. E. K. Sundén, K. Støchkel, P. Hvelplund, S. B. Nielsen, B. Dynefors and K. Hansen, J. Chem. Phys., 2018, 148, 184306 CrossRef PubMed.
- A. E. K. Sundén, K. Støchkel, S. Panja, U. Kadhane, P. Hvelplund, S. B. Nielsen, H. Zettergren, B. Dynefors and K. Hansen, J. Chem. Phys., 2009, 130, 224308 CrossRef PubMed.
- H. Shen, P. Hvelplund, D. Mathur, A. Bárány, H. Cederquist, N. Selberg and D. C. Lorents, Phys. Rev. A, 1995, 52, 3847–3851 CrossRef CAS.
- P. Hvelplund, L. H. Andersen, C. Brink, D. H. Yu, D. C. Lorents and R. Ruoff, Z. Phys., 1994, 30, 323–326 CAS.
- K. Honma, L. S. Sunderlin and P. B. Armentrout, Int. J. Mass Spectrom. Ion Processes, 1992, 117, 237–259 CrossRef CAS.
- K. Hansen, Statistical Physics of Nanoparticles in the Gas Phase, Springer, 2018 Search PubMed.
- J. A. Smith, F. E. Livingston and S. M. George, J. Phys. Chem. B, 2003, 107, 3871–3877 CrossRef CAS.
- B. D. Kay and J. A. W. Castleman, J. Chem. Phys., 1983, 78, 4297–4302 CrossRef CAS.
- K. Hansen, et al., to be published.
- J. Wölk and R. Strey, J. Phys. Chem. B, 2005, 105, 11683 CrossRef.
- C. H. Duong, N. Yang, P. J. Kelleher, M. A. Johnson, R. J. DiRisio, A. B. McCoy, Q. Yu, J. M. Bowman, B. V. Henderson and K. D. Jordan, J. Phys. Chem. A, 2018, 122, 9275–9284 CrossRef CAS PubMed.
- O. Vendrell, F. Gatti and H.-D. Meyer, Angew. Chem., Int. Ed., 2009, 48, 352–355 CrossRef CAS PubMed.
- M. Tachikawa and M. Shiga, J. Am. Chem. Soc., 2005, 127, 11908–11909 CrossRef CAS PubMed.
Footnote |
| † Present address: Stralsakerhetsmyndigheten, Stockholm, Sweden. |
| This journal is © The Royal Society of Chemistry 2019 |