Effects of solvents on the DACBO-catalyzed vinylogous Henry reaction of isatin with 3,5-dimethyl-4-nitroisoxazole “on-water” and in solution from QM/MM MC simulations

Abstract

The mechanism of the DABCO-catalyzed vinylogous Henry reaction of isatin with 3,5-dimethyl-4-nitroisoxazole and solvent effects on it have been investigated using density functional theory (DFT) methods and QM/MM Monte Carlo (MC) simulation under “on-water” conditions as well as in methanol and THF solutions. The DFT calculations concluded that Path A, in which DABCO directly catalyzes the reaction of isatin 1a with 3,5-dimethyl-4-nitroisoxazole 2 in water, is the most favorable and the first step, the proton transfer process, is the rate-determining step for the reaction. For the roles of solvents in the reaction, QM/MM MC simulations using free energy perturbation theory and PDDG/PM3 as the QM method have been utilized to predict the free energy profiles. The results indicated that the QM/MM method reproduced well the large rate increases on-water. Solute–solvent energy pair distribution and radial distribution functions were also analyzed and illustrated that hydrogen bonding plays a significant role in stabilizing the transition structures. This work reveals the feasible reaction mechanisms and provides new insight into solvent effects for the DACBO-catalyzed vinylogous Henry reaction.

---

1. Introduction

Water, as a green solvent, is nonflammable, nontoxic, and abundant. It is cheaper and milder than most organic solvents.^1–8 In the past two decades, great progress has been made in the study of organic synthesis in water or water-containing organic solvents as the reaction medium,^9,10 because water has many unique properties compared to organic solvents, for example, hydrogen bonding, and hydrophilic and hydrophobic interactions with the reactants. The rate enhancing of Diels–Alder reactions in pure water was first exposed by Breslow et al. in the early 1980s.¹¹ They found that the reaction rate in water was more than 700-fold faster than in isooctane, with higher internal (endo) selectivity. This work set a precedent for modern aqueous phase organic reactions. In 2005, Sharpless and co-workers reported some reactions “in water”, which means that the reactants are dissolved homogeneously in water with large rate and yield increases compared to organic solvents.¹² Subsequently, they introduced the concept “on-water”, which was defined as a reaction environment where the reaction occurs in an aqueous organic emulsion prepared by vigorously stirring insoluble reactants with water.^13,14 Since then, water as a reaction medium has received more attention for the synthesis of simple and complex molecules.^15–19

In 1895, Henry proposed nitroaldol (Henry) reactions between nitroalkanes and carbonyl compounds, which became an important and classic synthetic method for C–C bond formation in organic chemistry.²⁰ Nevertheless, the reactions encountered low selectivity and side products. Recently, many organocatalytic or metallic-catalyzed Henry reactions have been successfully carried out with enhancement of reactivities and selectivities.^21–23 However, few vinylogous-type Henry reactions in the aqueous phase had been studied.^24–26 Nitrogen-containing heterocyclic products are typical natural complex and biologically active molecules.^27,28 It is essential to find a facile synthetic approach for direct vinylogous Henry reactions with high yield and selectivity in pharmacochemistry and green chemistry. Therefore, effective methods for direct vinylogous Henry reactions have been discovered and explored in recent years.^29,30

In 2015, Zhang et al. first reported the vinylogous Henry reaction between isatin and 3,5-dialkyl-4-nitroisoxazole, leading to isoxazole-substituted 3-hydroxy-2-oxindole derivatives, medicinally important compounds, using water as the solvent for optimizing the reaction conditions at room temperature.²⁹ They found that organic base catalysts are more effective than inorganic bases and 1,4-diazabicyclo[2.2.2]octane (DABCO) is the optimal catalyst with a near quantitative yield (>99%) in 1.5 hours for the synthesis of the desired vinylogous product. Furthermore, the effects of different solvents on the rate and yield of the reaction were observed. In typical cases, when the organic solvent THF was used, a moderate product yield of 53% was obtained in 12 hours. Using a protic organic solvent such as CH₃OH, the reaction efficiency showed a significant improvement so that the yield was about 92% after 6 hours. It was also found that water was the most suitable solvent with high yield (>99%) and the shortest reaction time (1.5 hours) compared to other organic solvents under “on-water” conditions.²⁹ However, the active catalysis mechanism and the internal causes of the remarkable rate enhancement for the reaction in water are still unclear. These require a detailed understanding at the molecular level.

To gain further insights into the effects of the solvents on the rate and geometries of transition states at the theoretical level, in this work, isatin 1a and 3,5-dimethyl-4-nitroisoxazole 2 are selected as the reactants and DABCO as the catalyst to investigate this vinylogous Henry reaction “on-water” and in the organic solvents THF and CH₃OH (Scheme 1) by using a combination of multiscale computational levels. The computational results will be contrasted with the experimental study by Zhang et al.²⁹ First, we adopt density functional theory (DFT) M06-2X/SMD/6-311+G(d,p)//B3LYP/SMD/6-31+G(d,p) methods to investigate the reaction mechanism and obtain the structures of the transition states and ground states in water. Three possible reaction pathways are considered. Then, the effects of three solvents, water, CH₃OH, and THF, on the rate-limiting step of the reaction are studied and compared. Meanwhile, microsolvent models with one, three, and six water molecules are employed for the reaction in water. Finally, to describe the solvent effect correctly, quantum mechanics and molecular mechanics (QM/MM) calculation in conjunction with Monte Carlo (MC) simulation and free energy perturbation (FEP) theory at 298.15 K and 101.325 kPa are performed for the rate-determining step of the vinylogous Henry reaction “on-water” and in CH₃OH and THF. The reaction system has been treated using the semiempirical PDDG/PM3 method with complete sampling of the geometry of the reacting systems and explicit representation of the solvent components. The QM/MM/MC method has reproduced very well the experimentally observed solvent effects in various reactions, such as S_N2 reactions,³¹ nucleophilic aromatic substitution reactions,³² Cope eliminations,³³ decomposition of amino acids,³⁴ 1,3-dipolar cycloadditions,^35,36 and aldol reactions.^37,38 This method can calculate the absolute free energy of activation, ΔG^≠, and characterize the nature of the Henry reaction at atomic-level structural details. The energy pair distribution functions and radial distribution functions (rdfs) are evaluated to further explain the effects of solvent molecules on the reaction.

Scheme 1 The vinylogous Henry reaction of isatin 1a and 3,5-dimethyl-4-nitroisoxazole 2 “on-water”.

2. Computational methods

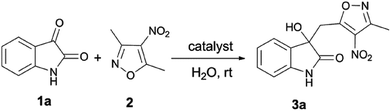
The mixed quantum mechanics and molecular mechanics (QM/MM) calculations were performed using the BOSS 4.9 program³⁹ for the reacting systems. The QM method is the semi-empirical PDDG/PM3.^40,41 Calculations of the energy and atomic charges in the QM method were carried out for every attempted solute move, occurring every 100 configurations in QM/MM simulations. The free energy changes were computed using FEP theory in conjunction with double-wide sampling in Metropolis MC simulations at 25 °C and 1 atm. To consider the electrostatic contributions to the solute–solvent interaction energy, CM3 charges⁴² were obtained for the solute using PDDG/PM3 calculations with a scaling factor of 1.14. All QM/MM calculations were completed from the stored solvent boxes of the BOSS program. The solvent molecules were represented with the united-atom OPLS^43,44 force field for the organic solvents and with the TIP4P model for water.⁴⁵ The systems were composed of reactants plus 494 solvent molecules for the water environment, 396 solvent molecules for the THF environment or 391 solvent molecules for the methanol environment. The boxes were periodic and tetragonal systems with c/a = 1.5 where a was about 25, 27, and 33 Å for water, methanol, and THF, respectively. FEP calculations were carried out in combination with NVT and NPT Metropolis MC simulations for on-water and in organic solvent environments.

As shown in Fig. 1, calculations for the reaction on-water were performed in a similar manner to those for the homogeneous solution-phase (in CH₃OH and THF, Fig. S1 and S2 in ESI†), expect that the periodicity was removed from the z axis of a box with the explicit 494 water molecules and the two solutes, i.e., DABCO and 3,5-dimethyl-4-nitroisoxazole 2. In addition, the catalyst DABCO was on the top of the z axis. Hence, an essential orientation analysis of multiple snapshots of reactants relative to the surface of the slab (perpendicular to the z axis) found that the DABCO was inclined to lie almost flat on the surface of the water slab and reactant 2 was placed in the water. The structure demonstrates that the on-water reaction of DABCO and 2 takes place in the interface between the gas phase and the liquid phase.

Fig. 1 Illustration of the on-water transition structure for the proton migration process of the DACBO-catalyzed vinylogous Henry reaction of isatin with 3,5-dimethyl-4-nitroisoxazole on-water from QM/MM calculations.

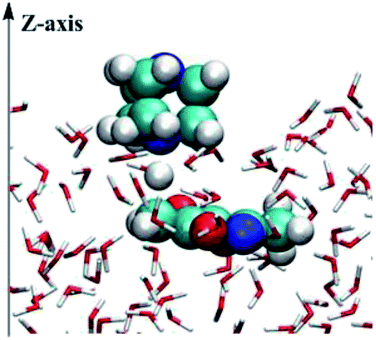
One-dimensional free energy profiles were established by utilizing the distance of one transforming bond, RC1, as the reaction coordinate shown in Fig. 2. The reactant state was defined by R_8C–4N = 3.50 Å and RC1 = 1.2 Å. The free energy profiles were flat in the vicinity of the reactant state. For the reacting system, each window of a FEP calculation entailed 60 million configurations of equilibration followed by 80 million configurations of averaging by using increments of 0.01 Å for the RC1. Solute–solvent and solvent–solvent intermolecular cutoff distances of 12 Å were employed for the reacting system on-water, in methanol, and in THF. The entire solute–solvent or solvent–solvent interaction was computed if any distance was within the cutoff. Adjustments to the allowed ranges for rotations, translations, and dihedral angle movements led to overall acceptance rates of 30–50% and solute move acceptance rates of 3–30% for new configurations. The ranges for bond stretching and angle bending were set automatically by the BOSS program on the basis of force constants and temperature. All QM/MM/MC simulations were run on a Linux cluster.

Fig. 2 Reaction coordinate RC1 for the proton transfer of the reaction.

All the optimized geometrical structures were obtained by performing the DFT calculations using the B3LYP^46,47 method with the 6-31+G(d,p) basis set and the polarizable continuum solvation model SMD⁴⁸ in the Gaussian 09 program.⁴⁹ The harmonic frequency calculations at the same level were carried out to ensure that all stationary points were either as ground states with all-positive frequencies or transition structures (TSs) with only one imaginary frequency. The intrinsic reaction coordinate (IRC)⁵⁰ calculations were conducted to check the energy profiles connecting each TS to the two associated minima. The Gibbs free energy corrections at 298.15 K and 101.325 kPa were obtained from frequency calculations. The solvent effects in the three solvents were taken into account with the B3LYP/SMD/6-31+G(d,p) level. Moreover, the single-point energy calculations were also performed at the M06-2X/SMD/6-311+G(d,p) levels by using the B3LYP/SMD/6-31+G(d,p) optimized structures. All the optimization structures of the reactants, transition states, intermediates, and products are shown in the ESI.†

3. Results and discussion

We investigated the three feasible reaction pathways for the vinylogous Henry reaction of isatin 1a with 3,5-dialkyl-4-nitroisoxazole 2 in water for exploring the functions of water and the catalyst DABCO. Subsequently, we considered the solvent effects in three solvents: water, THF and methanol. Then, microsolvent models were employed for the rate-limiting step. Finally, QM/MM/MC simulations were carried out for the rate-determining step and the roles of the solvents were analyzed in detail.

3.1 Reaction mechanism in water studied by DFT calculations

For this vinylogous Henry reaction, we proposed three reasonable pathways: Paths A–C, as shown in Scheme 2. In Path A, DABCO directly catalyzes the reaction of 1a with 2. The reaction begins with hydrogen transfer, where the hydrogen atom at the 8C atom of the CH₃ group in reactant 2 transfers to the 4N atom of DABCO, followed by formation of a new C–C bond between C of 1a and 8C of 2. The last step is the transferring of the hydrogen atom of 4N in DABCO to the 5O atom of 1a and hydroxyl formation. In Path B, it initiates when one water molecule is activated by DABCO through transferring its one H atom to the N atom of DABCO and then accepting the proton from –CH₃ in 2. The following step is the C–C bond formation, which is the same as Path A. The last step is hydroxyl forming by means of an auxiliary water molecule. For Path C, three auxiliary water molecules are involved in the deprotonation of –CH₃ in 2 without the catalyst DABCO. There are two steps in the reaction. In the first step, the hydrogen atom at 8C of 2 transfers to one water molecule of a three-water-molecule chain. The second step is the simultaneous formation of a C–C bond and a hydrogen atom combining with the 5O atom to form hydroxyl.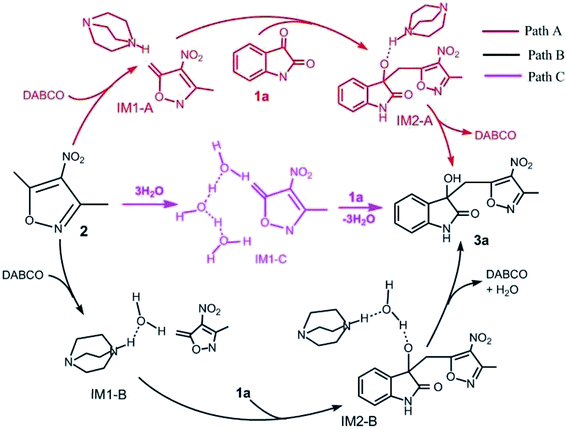

Scheme 2 Three possible reaction pathways of vinylogous Henry reactions between 3,5-dialkyl-4-nitroisoxazole and isatin in water.

The free energy profiles of the three pathways mentioned above are depicted in Fig. S3 in the ESI.† The results of the free energy barriers of activation for each elementary step obtained using the B3LYP/SMD/6-31+G(d,p) and M06-2X/SMD/6-311++G(d,p)//B3LYP/SMD/6-31+G(d,p) methods are listed in Table 1. The two levels give similar results and the same trend. The following discussion is performed based on the DFT methods M06-2X/SMD/6-311++G (d,p)//B3LYP/SMD/6-31+G(d,p) used. As one can see from Table 1, it is relatively difficult for Path C to take place with the high free energy barriers of 34.0 kcal mol⁻¹ for step 1 and 6.1 kcal mol⁻¹ for step 2 compared with the other two pathways. For Path B, the free energy of activation of step 1 is 27.6 kcal mol⁻¹. The subsequent two steps are easy to occur with low or even no free energy barriers. Path A is also a three-step process with free energies of activation of 21.2, 5.0, and −2.4 kcal mol⁻¹, respectively. Meanwhile, the rate-determining step of all Paths A, B, and C is the first step (the deprotonation of the –CH₃ group in 2). Obviously, by comparison, the most preponderant route is Path A with the lowest free energy barrier of 21.2 kcal mol⁻¹ in its rate-determining step. Thus, the presence of catalyst DABCO significantly reduces the free energy barrier.

Table 1 Free energy of activation, ΔG^≠ (kcal mol⁻¹), calculated at 25 °C and 1 atm, for three mechanisms of vinylogous Henry reactions between 3,5-dialkyl-4-nitroisoxazole and isatin in water

Pathway	Step	B3LYP/SMD/6-31+G(d,p)	M06-2X/SMD/6-311++G(d,p)//B3LYP/SMD/6-31+G(d,p)
Path A	1	22.4	21.2
	2	7.6	5.0
	3	−1.0	−2.4
Path B	1	26.9	27.6
	2	7.0	4.9
	3	−0.2	−0.6
Path C	1	35.0	34.0
	2	7.6	6.1

---

3.2 Effects of solvents studied by DFT calculations with the SMD model

Next, we focus on the solvent effects on the dynamic property in the rate-determining step (the first step, the deprotonation of the –CH₃ group in 2) of the favored Path A under different solvents containing water, methanol, and THF. The free energy values of the related reactants and transition states in THF and methanol were also calculated at the M06-2X/SMD/6-311++G(d,p)//B3LYP/SMD/6-31+G(d,p) level, which was the same as used in water. The final free energies of activation in water, CH₃OH, and THF obtained using the B3LYP/SMD/6-31+G(d,p) and M06-2X/SMD/6-311+G(d,p)//B3LYP/SMD/6-31+G(d,p) methods are listed in Table 2. One can see from Table 2 that the free energy barriers of activation ΔG^≠ are 22.4, 20.3, and 21.7 kcal mol⁻¹ using B3LYP/SMD/6-31+G(d,p) as well as 21.2, 19.4, and 21.2 kcal mol⁻¹ using M06-2X/SMD/6-311++G(d,p)//B3LYP/SMD/6-31+G(d,p) in water, CH₃OH, and THF, respectively. All the computed ΔG^≠ values in organic solvents are lower than those in water, indicating that the DACBO-catalyzed vinylogous Henry reaction takes place more easily in organic solvents than in water. However, the results are inconsistent with the experimental research, in which the reaction rate in water is faster than those in THF and methanol.²⁹

Table 2 Free energies of activation, ΔG^≠ (kcal mol⁻¹), calculated at 25 °C and 1 atm for the rate-determining step of vinylogous Henry reactions between 3,5-dialkyl-4-nitroisoxazole and isatin in different solvents

Solvent		B3LYP/SMD/6-31+G(d,p)	M06-2X/SMD/6-311++G(d,p)//B3LYP/6-31+G(d,p)
Water	0-H2O	22.4	21.2
	1-H2O	22.4	21.0
	3-H2O	22.1	21.2
	6-H2O	22.0	20.6
CH3OH		20.3	19.4
THF		21.7	21.2

---

Whereafter, for the rate-determining step of Path A in water, microsolvent models with the introduction of one-, three-, and up to six-water clusters to the reaction centers were employed to simulate the local microhydration surrounding (the corresponding geometry structures of the reactants, transition states, and intermediates are given in Fig. S4 of the ESI†). The free energy of activation values ΔG^≠ are also given in Table 2. It can be seen that the ΔG^≠ values for the microsolvent models are slightly decreased compared with the one in water without the assistance of the water cluster and still higher than those in THF and methanol. This indicates that the calculations using the implicit SMD solvent model without or with the involvement of auxiliary water molecules are unfit to reproduce the experimentally observed changes of the rate of this vinylogous Henry reaction in water and organic solvents. It is noteworthy that some investigations using the DFT methods and the polarizable continuum solvation models also failed to represent the accurate sequence of reaction rates for the 1,3-dipolar cycloadditions,^35,36 the allyl p-tolyl ether rearrangement,³⁷ and the uncatalyzed aldol reaction³⁸ in solution. Thus, it should be realized that the specific changes of hydrogen bond interactions between reaction molecules and solvents along the reaction path are important to the reaction under an “on-water” environment, but they are not reflected in the continuum treatment. Therefore, the QM/MM/MC calculations for the rate-limiting step of Path A in the title reaction were performed (under the solution conditions: on-water, in CH₃OH, and in THF, for comparison) to gain an explicit representation of solvent molecules in the following work.

3.3 Role of solvents in the rate-limiting step studied by QM/MM MC simulations

3.3.1 Structures. Geometries for the proton transfer in the first step of the DACBO-catalyzed vinylogous Henry reaction between 1a and 2 in solution were located with the QM/MM/MC simulations. Configurationally averaged free energy profiles, ΔG (kcal mol⁻¹), were calculated by perturbing the distance of the broken bond 8C–3H via potential of mean force (PMF) calculations in increments of 0.01 Å. All internal degrees of freedom, except for reaction coordinate RC1, were fully sampled during the simulations. The free energy profiles for the reactions on-water, in THF and in methanol are shown in Fig. 3. The initial ranges were from 1.12 to 2.50 Å for RC1. From the free energy profiles, the rate-determining step in the three different solvents was a one-step reaction with only one transition structure. The feasibility of false data was eliminated firstly, then we concluded all potential factors and inferred that the deviation between reaction rates may be attributed to the solvent effect, which plays a large role in organic reactions.

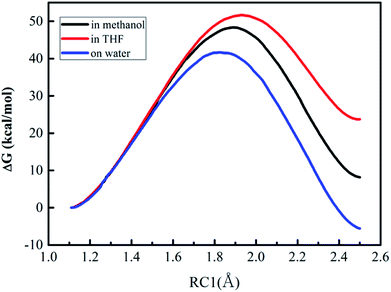Fig. 3 Free energy profiles for the proton transfer (the first step of Path A) in three different solvents.

The values of RC1 in the transition state of the proton migration process in the three solvent conditions were computed from DFT method and QM/MM/MC simulations, respectively, and are listed in Table 3. It is explicit that the geometrical structures of the transition states in the three different solvents did not have large variations with RC1 lengths of 1.89 ± 0.05 Å from the QM/MM/MC/PDDG/PM3 method and 1.37 ± 0.07 Å from the B3LYP/SMD/6-31+G(d,p) method. It can be also seen that the change tendency of RC1 length along the solvent polarity computed by the QM/MM/MC simulations with PDDG/PM3 as the QM method was similar to the one by using DFT at the B3LYP/SMD/6-31+G(d,p) level of theory although the absolute values of RC1 distance at the TSs from the former simulation were much longer than those obtained from the latter method. The QM/MM/MC simulations predicted the transition states to be more product-like.

Table 3 Calculated bond lengths (Å) of reaction coordinate RC1 in transition state for the proton transfer of DACBO-catalyzed vinylogous Henry reaction between isatin and 3,5-dimethyl-4-nitroisoxazole from two methods

System	B3LYP/SMD/6-31+G(d,p)	QM/MM/MC/PDDG/PM3
On-water	1.36	1.83
In CH3OH	1.37	1.89
In THF	1.44	1.93

---

3.3.2 Energetics. The free energies in the three solvents at 25 °C and 1 atm were calculated for the rate-determining step (the first step) of Path A of the DACBO-catalyzed vinylogous Henry reaction of isatin with 3,5-dimethyl-4-nitroisoxazole from the QM/MM/MC simulations beginning from a 3.5 Å separation distance between DABCO and 2. The resultant free energy changes relative to the reactants are summarized in Table 4 and Fig. 3. The error ranges in the computed free energy values have been evaluated from fluctuations in the ΔG values for each FEP window by using the batch means procedure with batch sizes of 0.5 million configurations; the overall uncertainties in the computed free energies ΔG were below 0.7 kcal mol⁻¹. From Tables 4 and 2, all the absolute ΔG^≠ values from the QM/MM/MC simulations are higher than the corresponding ones from DFT/SMD computation by about 20–30 kcal mol⁻¹. It is important to realize that the overestimation of the absolute ΔG^≠ in the semiempirical PDDG/PM3 method is a systematic error and is not limited to this vinylogous Henry reaction. Similar discoveries have been reported for Diels–Alder reactions,⁵¹ ene reactions,⁵² methyl-transfer reactions,⁵³ Claisen rearrangements,³⁷ 1,3-dipolar cycloadditions,³⁵ and aldol reactions.³⁸

Table 4 Free energy changes relative to reactants, ΔG (kcal mol⁻¹), calculated at 25 °C and 1 atm, for the proton migration process (the first step of Path A) of DACBO-catalyzed vinylogous Henry reaction of isatin with 3,5-dimethyl-4-nitroisoxazole obtained from the QM/MM/MC simulations with PDDG/PM3 as the QM method

System	On-water	In CH3OH	In THF
Reactant	0.0	0.0	0.0
TS	41.6	48.4	51.7
Product	−5.6	8.1	23.7

---

As described in Fig. 3, the free energy profiles reveal that the proton transfer process for the DACBO-catalyzed vinylogous Henry reaction undergoes a one-step mechanism under the three different solvent conditions. From Table 4, the free energies of activation from QM/MM/MC simulations were 41.6, 48.4, and 51.7 kcal mol⁻¹ for on-water, in methanol and in THF, respectively. We found that the ΔG^≠ value on the surface of water is approximately 7–10 kcal mol⁻¹ lower than those in methanol and in THF and the ΔG values of the product are also much lower. Therefore, it could be concluded that the rate-determining step of Path A of the DACBO-catalyzed vinylogous Henry reaction on-water takes place more easily than in methanol and in THF and that the rate change in three different solvent conditions follows the order of “on-water” > “in methanol” > “in THF”, which is in great accordance with the experiment research.²⁹

3.3.3 Solute–solvent energy pair distributions. As is well known, water, as a polar molecule, is a great hydrogen bond acceptor and donor.⁵⁴ In previous theoretical studies of the Henry reaction,^55,56 the solvent effect was a remarkable factor for the reaction rate through hydrogen bonding stabilizing the transition structures. For the DACBO-catalyzed vinylogous Henry reaction here, there are strong hydrogen-bonding reception sites at 2O and 3O atoms in reactant 2. Additionally, water can form more and stronger hydrogen bond than methanol and THF because water is a strongly polar solvent. The present results are fully consistent with these ideas. Subsequently, the detailed insights into the changes in the hydrogen-bonding interactions in different solvents along the rate-limiting step are discussed below.

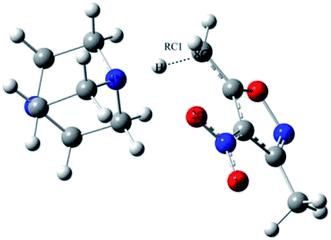
The computed tendency of the rate change reflected by the free energy of activation for the title reaction, as mentioned above, which is in agreement with the experimental results, indicates that the QM/MM/MC calculations obtained the origin of the solvent effect at the molecular level. In particular, the hydrogen bond interactions between the reaction system and solvent molecules can be described by the solute–solvent energy pair distributions that record average number of solvent molecules interacting with the solute and the associated interaction energy. Through analyzing the QM/MM/MC results near the reactant state and at the transition structure FEP windows, the interaction energies were obtained. The solute–solvent energy pair distributions for the proton transfer process between reactant 2 and DABCO on-water, in methanol, and in THF are shown in Fig. 4. The hydrogen bonds on-water and in methanol are found in the left-most region with solute–solvent interaction energies more attractive than −4 kcal mol⁻¹. The most favorable dipole–dipole electrostatic interactions in THF cover the region from −10 to −5 kcal mol⁻¹. The large bands near 0 kcal mol⁻¹ result from the weak interactions with the outer shells of many distant solvent molecules.

Fig. 4 Solute–solvent energy pair distributions for the proton transfer of the DACBO-catalyzed vinylogous Henry reaction for structures near the reactants (solid red) and transition states (dash red). The ordinate records the number of solvent molecules that interact with the solutes and their interaction energy is on the abscissa. Units for the ordinate are number of molecules per kcal per mol.

According to Fig. 4, with comparison of bands in solid red lines and dashed red lines, we can see that the transition structures have a stronger band than those of the reactant structures for on-water, in methanol, and in THF, respectively. Furthermore, there are remarkable differences between on-water and in non-aqueous solvent. The low-energy bands for the aprotic solvent are less favorable interactions than those for on-water. In “on-water”, strong solute–solvent interactions were obvious for the reactants and transition structure, with the interaction energies in the range from −10 to −4 kcal mol⁻¹. The results of the solute–solvent energy pair distributions under three solvent conditions integrated to −4 kcal mol⁻¹ are listed in Table 5.

Table 5 Solute–solvent energy pair distributions for the proton transfer of the DACBO-catalyzed vinylogous Henry reaction for the reactants (GS) and transition structure (TS) under three solvent conditions integrated to −4 kcal mol⁻¹ from the results in Fig. 4

	On-water	In CH3OH	In THF
GS	2.6	2.6	2.9
TS	5.4	5.2	4.7
Δ(TS–GS)	2.8	2.6	1.8

---

In Table 5, it is clear that the variations of solute–solvent interactions for proton transfer from reactants to the TSs have the same tendency under the three different solvent environments. Integration of the transition structure band from −12 to −4 kcal mol⁻¹ yields about 5.4 water molecules interacting strongly with the solute for the on-water condition, 5.2 methanol molecules in methanol, and 4.7 tetrahydrofuran molecules in THF. Therefore, the interaction intensity of the reaction system with solvent molecules is changed in the order of tetrahydrofuran < methanol < water. In all solvent conditions, the number of hydrogen bonds between solvent and solute for the TS is greater than that for the reactants, indicating that the reduction in the free energy of activation can be attributed to the heightened hydrogen bond interactions in the transition structure. Furthermore, the numbers of solvent molecules strongly interacting with the solute increase by 2.8, 2.6, and 1.8 “on-water”, in CH₃OH, and in THF, respectively, on going from reactants to transition state. These results show that the stabilization of the transition structure relative to its reactant is different in different solvents. In “on-water” and methanol, the better solvation of the TS is owing to the larger increase in the extent of the solute–solvent hydrogen bond interaction, while in THF the change for the interactions with the solvent along the reaction path is smaller.

3.3.4 Radial distribution functions (rdfs). The radial distribution function (rdf), g(R), can be used to further characterize the solute–solvent structures for the first step (proton transfer) of the DACBO-catalyzed vinylogous Henry reaction on-water, in methanol and in THF. The g(R) value is calculated by the following equation:

g_xy(R) = dN/(4πρR²dR) = <N(R,R + dR)>/(4πρR²dR) (1)

The g_xy(R) value gives the probability of the occurrence of an atom of type y at a distance R from an atom of type x, normalized to account for the bulk density ρ of the atoms and for the volume element 4πR²dR.

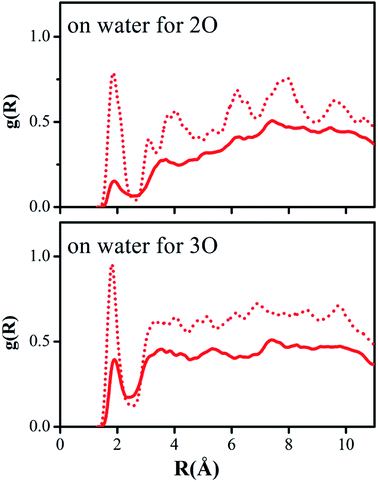
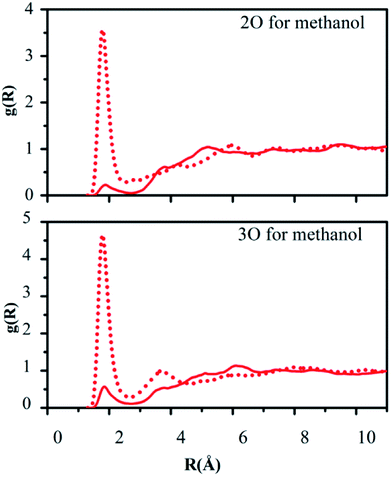
Hydrogen bonding between the oxygen atoms 2O and 3O in the NO₂ group of reactant 2 and the hydrogen atoms of water or methanol, O(solute)–H(solvent), should yield contacts shorter than 2.7 Å. Fig. 5 and 6 depict the computed g(R) values of the O(solute)–H(solvent) radial distribution functions for the reactant and transition structures in the rate-limiting step of the DACBO-catalyzed vinylogous Henry reaction “on-water” and in CH₃OH, which reflect the probability of finding the hydrogen atom of the solvent molecules at a distance R from the oxygen atom of the reaction system.

Fig. 5 Computed O(solute)–H(water) radial distribution functions for the rate-limiting step of DACBO-catalyzed vinylogous Henry reaction on-water: transition structure (dash red), reactant (solid red) at 25 °C and 1 atm.

Fig. 6 Computed O(solute)–H(methanol) radial distribution functions for the rate-limiting step of DACBO-catalyzed vinylogous Henry reaction in methanol: transition structure (dash red), reactant (solid red) at 25 °C and 1 atm.

As illustrated in Fig. 5 and 6, both for 2O and 3O, we can see that the hydrogen bonds are obviously greater for the transition state (TS) compared to those of the reactant structures, with a well-defined first peak centered at 1.9 Å and a minimum near 2.4–2.7 Å. The second peak in the O(solute)–H(solvent) rdf at 3.2–3.8 Å is owing to the more remote hydrogen of the linearly hydrogen-bonding solvent molecules. However, from the 2O atom, the integration of peaks from 0.0 to the minima at 2.4–2.7 Å reveals an increased number of site-specific 2O(solute)–H(solvent) hydrogen bonds for the TS relative to the reactants on-water and in methanol, namely, from GS to TS it is 0.2 to 0.7 for on-water and 0.1 to 0.5 for in methanol (Table 6). Analogously, there are hydrogen bonds for 3O in the TS, reaching 1.0 for on-water and 0.7 for in methanol. It changes from 0.6 to 1.7 for on-water, and from 0.3 to 1.2 for in methanol. The increase of hydrogen bond interactions between the O(solute) and H(solvent) from the reactants to TS for on-water is more than that in methanol. This could be the major reason leading to the greater reaction acceleration on-water than in CH₃OH.

Table 6 Number of solvent molecules interacting with oxygen atoms of solute for reactant (GS) and transition state (TS) in the proton transfer process on-water and in methanol from radial distribution functions^a

	On-water		In methanol
	GS	TS	GS	TS
a Integration of the first peak to 2.4–2.7 Å from the results shown in Fig. 5 and 6.
2O	0.2	0.7	0.1	0.5
3O	0.4	1.0	0.2	0.7
Total	0.6	1.7	0.3	1.2

---

As depicted in Fig. S5 of the ESI,† the interactions between the oxygen of the reactant and the united-atom CH₂ group on THF, O(solute)⋯CH₂(solvent), were also detected by radial distribution functions for the reactant and transition state. We found that the probability of finding the CH₂ group on THF molecule from the oxygen atom of the solute requires a larger distance R compared to those “on-water” or in methanol. The O⋯CH₂ interactions are reflected in the first peak centered at around 3.6 Å, which is extended to its minimum with a distance of about 4.5 Å. The second peak in the O⋯CH₂ rdf at around 5.5 Å arises from the more remote united-atom –CH₂ group of the THF molecules. Consistent with the results in Fig. S5,† the difference between the reactant and transition state is much diminished in comparison to the results for on-water and in methanol.

4. Conclusion

In conclusion, three feasible pathways for the DACBO-catalyzed vinylogous Henry reaction between 3,5-dialkyl-4-nitroisoxazole and isatin have been explored theoretically under water as the solvent by DFT calculations: (A) direct catalyzation of DACBO; (B) attacking of one water molecule activated by the catalyst; and (C) catalyzation of three auxiliary water molecules without catalyst. We found that Path A is the most favorable mechanism and the first step, the proton migration process, is the rate-limiting step. Additionally, the solvent effects of three different solvents, namely, water, methanol, and tetrahydrofuran, have been considered by DFT methods with SMD model. The microsolvent models with one-, three-, or six-water-molecule clusters have also been adopted for the rate-determining step in water. However, the results of solvent effects obtained from DFT calculations are contrary to the experimental research of Zhang et al.²⁹

QM/MM/MC simulations have been carried out for the rate-limiting step of Path A in the title reaction on the water surface, in methanol and in tetrahydrofuran. The calculated ΔG^≠ values of 41.6, 48.4 and 51.7 kcal mol⁻¹ under on-water, in methanol and in THF, respectively, indicate that the reaction rate order is “on-water” > “in methanol” > “in THF”. This qualitatively agrees with the experimental observation. Furthermore, the hydrogen-bonding effects are better in the reaction on-water than in the other two solvents. The reaction rate acceleration for the proton transfer step is connected with the on-water environment because of the ability of the interfacial water molecules to stabilize the transition structure. Solute–solvent energy pair distribution and radial distribution functions further expound the increase of site-specific (2O and 3O atoms in reactant 2) hydrogen bond interactions in the transition structure in the rate-determining step. Therefore, our studies will broaden the understanding of the reaction mechanism and the role of water for the vinylogous Henry reaction theoretically.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project has been supported by the National Natural Science Foundation of China (Grant No. 21573153).

References

1. F. Q. Shi, X. Li, Y. Z. Xia, L. M. Zhang and Z.-X. Yu, J. Am. Chem. Soc., 2007, 129, 15503–15512.
2. S. Minakata and M. Komatsu, Chem. Rev., 2009, 109, 711–724.
3. Y. Liang, H. L. Zhou and Z.-X. Yu, J. Am. Chem. Soc., 2009, 131, 17783–17785.
4. R. N. Butler and A. G. Coyne, Chem. Rev., 2010, 110, 6302–6337.
5. Y. Y. Zheng and J. P. Zhang, J. Phys. Chem. A, 2010, 114, 4325–4333.
6. M. B. Gawande, V. D. B. Bonifacio, R. Luque, P. S. Branco and R. S. Varma, Chem. Soc. Rev., 2013, 42, 5522–5551.
7. M. Sengoden and T. Punniyamurthy, Angew. Chem., Int. Ed., 2013, 125, 600–603.
8. H. Y. Yuan, Y. Y. Zheng, Z. X. Fang, X. H. Bi and J. P. Zhang, Green Chem., 2014, 16, 2653–2663.
9. J. B. F. N. Engberts and M. J. Blandamer, Chem. Commun., 2001, 1701–1708.
10. G. W. V. Cave, C. L. Raston and J. L. Scott, Chem. Commun., 2001, 2159–2169.
11. D. C. Riadeout and R. Breslow, J. Am. Chem. Soc., 1980, 102, 7816–7817.
12. S. Narayan, J. Muldoon, M. G. Finn, V. V. Fokin, H. C. Kolb and K. B. Sharpless, Angew. Chem., Int. Ed., 2005, 44, 3275–3279.
13. Y. Hayashi, Angew. Chem., Int. Ed., 2006, 45, 8103–8104.
14. J. E. Klijin and J. B. F. N. Engberts, Nature, 2005, 435, 746–747.
15. C. J. Li, Chem. Rev., 2005, 105, 3095–3166.
16. C. J. Li and L. Chen, Chem. Soc. Rev., 2006, 35, 68–82.
17. A. Chanda and V. V. Fokin, Chem. Rev., 2009, 109, 725–748.
18. R. N. Butler and A. G. Coyne, Chem. Rev., 2010, 110, 6302–6337.
19. M. O. Simon and C. J. Li, Chem. Soc. Rev., 2012, 41, 1415–1427.
20. L. Henry and C. R. Hebd, C. R. Seances Acad. Sci. Roum., 1895, 120, 1265–1270.
21. A. Noole, K. Lippur, A. Metsala, M. Lopp and T. Kanger, J. Org. Chem., 2010, 75, 1313–1316.
22. Y. Zhang, Z. J. Li, H. S. Xu, Y. Zhang and W. Wang, RSC Adv., 2011, 1, 389–392.
23. M. Holmquist, G. Blay and J. R. Pedro, Chem. Commun., 2014, 50, 9309–9312.
24. G. Casiraghi, F. Zanardi, G. Appendino and G. Rassu, Chem. Rev., 2000, 100, 1929–1972.
25. G. Casiraghi, L. Battistini, C. Curti, G. Rassu and F. Zanardi, Chem. Rev., 2011, 111, 3076–3154.
26. C. Schneider and F. Abels, Org. Biomol. Chem., 2014, 12, 3531–3543.
27. A. R. Katritzky, C. W. Rees and E. F. V. Scriven, Comprehensive Heterocyclic Chemistry II, Oxford, 1996.
28. A. R. Katritzky, C. A. Ramsden, E. F. V. Scriven and R. J. K. Taylor, Comprehensive Heterocyclic Chemistry III, Oxford, 2008.
29. Y. Zhang, B. W. Wei, H. Lin, L. Zhang, J. X. Lin, H. Q. Luo and X. L. Fan, Green Chem., 2015, 17, 3266–3270.
30. Y. Zhang, B. W. Wei, L. N. Zou, M. L. Kang, H. Q. Luo and X. L. Fan, Tetrahedron, 2016, 72, 2472–2475.
31. G. Vayner, K. N. Houk, W. L. Jorgensen and J. I. Brauman, J. Am. Chem. Soc., 2004, 126, 9054–9058.
32. O. Acevedo and W. L. Jorgensen, Org. Lett., 2004, 6, 2881–2884.
33. O. Acevedo and W. L. Jorgensen, J. Am. Chem. Soc., 2005, 127, 8829–8834.
34. A. N. Alexandrova and W. L. Jorgensen, J. Phys. Chem. B, 2011, 115, 13624–13632.
35. X. Yang and Y. Xue, Phys. Chem. Chem. Phys., 2013, 15, 11846–11855.
36. X. Yang and Y. Xue, J. Org. Chem., 2014, 79, 4863–4870.
37. O. Acevedo and K. Armacost, J. Am. Chem. Soc., 2010, 132, 1966–1975.
38. J. M. Zhao, F. He, F. Zhang, X. Yang, Z. Y. Tian and Y. Xue, ChemPhysChem, 2017, 18, 2123–2131.
39. W. L. Jorgensen and J. Tirado-Rives, J. Comput. Chem., 2005, 26, 1689–1700.
40. M. P. Repasku, J. Chandrasekhar and W. L. Jorgensen, J. Comput. Chem., 2002, 23, 1601–1622.
41. I. Tuber-Brohman, C. R. W. Guimarăes, M. P. Repasky and W. L. Jorgensen, J. Comput. Chem., 2003, 25, 138–150.
42. J. D. Thompson, C. J. Cramer and D. G. Truhlar, J. Comput. Chem., 2003, 24, 1291–1304.
43. G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487.
44. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
45. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
46. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
47. C. Lee, W. Yang and R. G. Parr, Phys. Rev., 1988, 37, 785–789.
48. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
49. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Wallingford CT, 2010.
50. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
51. O. Acevedo and W. L. Jorgensen, J. Chem. Theory Comput., 2007, 3, 1412–1419.
52. A. N. Sheppard and O. Acevedo, J. Am. Chem. Soc., 2009, 131, 2530–2540.
53. H. Gunaydin, O. Acevedo, W. L. Jorgensen and K. N. Houk, J. Chem. Theory Comput., 2007, 3, 1028–1035.
54. V. Polo, L. R. Domingo and J. Andrés, J. Phys. Chem. A, 2005, 109, 10438–10444.
55. J. Kostal, A. M. Voutchkova and W. L. Jorgensen, Org. Lett., 2012, 14, 260–263.
56. D. Zorn, V. S.-Y. Lin, M. Pruski and M. S. Gordon, J. Phys. Chem. A, 2008, 112, 10635–10649.

---

Footnote

† Electronic supplementary information (ESI) available: Illustrations of the transition structures of the proton migration process in solvents methanol and tetrahydrofuran; DFT-calculated free energy profiles of three pathways for the vinylogous Henry reaction in water; the geometry structures of stationary states for the rate-limiting step by employing microsolvent models with one-, three- and six-water clusters; additional radial distribution functions; coordinates of all structures optimized using DFT methods. See DOI: 10.1039/c9ra00082h

---