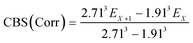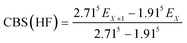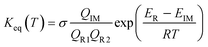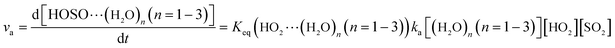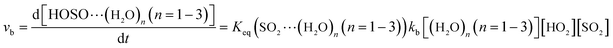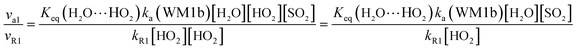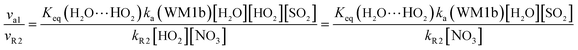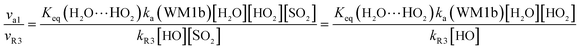DOI:
10.1039/C9RA00169G
(Paper)
RSC Adv., 2019,
9, 16195-16207
Catalytic effect of (H2O)n (n = 1–3) clusters on the HO2 + SO2 → HOSO + 3O2 reaction under tropospheric conditions†
Received
8th January 2019
, Accepted 2nd May 2019
First published on 23rd May 2019
Abstract
The HO2 + SO2 → HOSO + 3O2 reaction, both without a catalyst and with (H2O)n (n = 1–3) as a catalyst, has been investigated using CCSD(T)/CBS//M06-2X/aug-cc-pVTZ methods, and canonical variational transition state theory with small curvature tunneling (CVT/SCT). The calculated results show that H2O exerts the strongest catalytic role in the hydrogen atom transfer processes of HO2 + SO2 → HOSO + 3O2 as compared with (H2O)2 and (H2O)3. In the atmosphere at 0 km altitude within the temperature range of 280.0–320.0 K, the reaction with H2O is dominant, compared with the reaction without a catalyst, with an effective rate constant 2–3 orders of magnitude larger. In addition, at 0 km, it is worth mentioning that the relevance of the HO2 + SO2 → HOSO + 3O2 reaction with H2O depends heavily on its ability to compete with the primary loss mechanism of HO2 radicals (such as the HO2 + HO2 and HO2 + NO3 reactions) and SO2 (such as the SO2 + HO reaction). The calculated results show that the HO2 + SO2 → HOSO + 3O2 reaction with H2O cannot be neglected in the primary loss mechanism of the HO2 radical and SO2. The calculated results also show that for the formation of HOSO and 3O2, the contribution of H2O decreases from 99.98% to 27.27% with an increase in altitude from 0 km to 15 km, due to the lower relative concentration of water. With the altitude increase, the HO2 + SO2 → HOSO + 3O2 reaction with H2O cannot compete with the primary loss mechanism of HO2 radicals. The present results provide new insight into (H2O)n (n = 1–3) catalysts, showing that they not only affect energy barriers, but also have an influence on loss mechanisms. The present findings should have broad implications in computational chemistry and atmospheric chemistry.
1. Introduction
As a significant gaseous pollutant from both industrial and natural sources,1 sulfur dioxide (SO2)2,3 can cause a wide range of issues for human health, agriculture and the global climate.4 It leads to acid rain that damages forest and crops, and plays a role in the formation of atmospheric aerosols.5,6 Furthermore, short-term exposure to high levels of SO2 in the air can be life-threatening, as it can cause breathing difficulties and obstruct airways, while long-term exposure to persistent levels of SO2 can cause chronic bronchitis, emphysema and respiratory illness.7 Similar to SO2, the hydroperoxyl radical (HO2) is also an important atmospheric species, which plays important roles in both the troposphere and the stratosphere.8 In the troposphere, the HO2 radical is central to the production of ozone and the generation of hydroxyl radicals, whereas in the stratosphere, it is involved in catalytic cycles. HO2 also acts as a significant transient intermediate in the combustion of hydrocarbon fuels, atmospheric photolysis cycles, and biochemical processes.9,10 The reaction between HO2 and SO2 has aroused great interest from many research groups due to its great importance to supply a reverse path between SO2 and HOSO (or SO3) in the sulfur cycle. This reaction may take place via a number of pathways including the three main product paths shown in eqn (1)–(3), namely, O2 + HOSO formation, O2 + HSO2 formation, and OH + SO3 formation.3,11 It is noteworthy that, as one of the most important products of the HO2 + SO2 reaction, HOSO has been found to be relatively stable12 and its subsequent reactions13 are important for atmospheric chemistry. Therefore, its structure,14,15 harmonic vibrational frequencies,16 thermochemistry12,17 and subsequent reactions13,18 have been widely investigated.| | |
HO2 + SO2 → HOSO + O2
| (1) |
| | |
HO2 + SO2 → HSO2 + O2
| (3) |
The kinetics and mechanism of the HO2 + SO2 reaction have been studied experimentally and theoretically for a range of temperatures and pressures. In an experimental study, Payne et al.19 found that the rate constant of the HO2 + SO2 reaction was (8.7 ± 1.8) × 10−16 cm3 per molecule per s at 300 K and a pressure of 30 Torr. Meanwhile, the rate constant of the HO2 + SO2 reaction at 298 K was found to be 2.01 × 10−17 cm3 per molecule per s, as measured by Burrows et al.20 at low pressure. The kinetics and mechanism for the reaction of HO2 with SO2 were investigated by Wang et al.11 with ab initio molecular orbital and transition state theory calculations. Their results showed that the reaction firstly proceeds to form a five-member-ring complex SO2⋯HO2, and then the complex undergoes barrierless decomposition to produce O2 + HOSO. These investigations provide meaningful information about the mechanisms and kinetics for the HO2 + SO2 reaction under atmospheric conditions. However, this effort has only focused on the non-catalytic process of the HO2 + SO2 reaction.
Water has long been considered as a subject of chemical interest due to its abundance and unique properties in atmospheric chemistry.21 It not only forms hydrogen-bonded complexes with HO2,22,23 OH,24–26 formic acid21 and nitric acid,8 but also can actively participate in atmospheric reactions as a catalyst,27,28 of which HO2⋯H2O is a well-studied example.29–31 An interesting result29 concerning this complex is that the HO2 self-reaction can be up to three times faster in the presence of water, since 30% of HO2 radicals may exist in the form of HO2⋯H2O.32 Moreover, many experimental and theoretical studies have been reported on the electronic structure of the clusters SO2⋯H2O33–37 and the gaseous hydrolysis reaction of SO2 + H2O.3,11 These situations stimulated our interest in modeling the gas-phase reaction of the H2O⋯HO2⋯SO2 ternary system, in which a single water molecule serves as a catalyst.
Recently, Chen et al.3 employed the CCSD(T)/aug-cc-pVTZ//B3LYP/aug-cc-pVTZ method to investigate the reactions of HO2 + SO2 and HO2⋯H2O + SO2. Their calculations showed that H2O slightly accelerates the SO2 + HO2 reaction to form a HSO4⋯H2O radical complex. Although Chen et al.3 provided meaningful information on the mechanism and kinetics of HO2⋯H2O + SO2 and HO2 + SO2 reactions under tropospheric conditions, the most favorable, water-assisted channel (HO2 + SO2 → HOSO + O2) has not yet been investigated in this way. Thus, it is still difficult to judge whether water molecules have an obvious positive catalytic effect on the HO2 + SO2 reaction or not. Furthermore, many experimental and theoretical studies have appeared in the literature on the electronic structure of the clusters HO2⋯(H2O)n (n = 2–3)38,39 and SO2⋯(H2O)n (n = 2–3).40,41 On the other hand, some studies have shown that water dimers38,42–49 and trimers39,49–52 can also have a significant catalytic effect in hydrogen abstraction reactions and hydrolysis of sulfur dioxide.53,54 Thus, the investigation of the effect of (H2O)n (n = 1–3) on the HO2 + SO2 → HOSO + 3O2 reaction is a logical path to pursue.
In the present study, the detailed effects of (H2O)n (n = 1–3) on the hydrogen atom transfer processes of the HO2 + SO2 → HOSO + 3O2 reaction have been investigated at the CCSD(T)/CBS//M06-2X/aug-cc-pVTZ level of theory, which is organized as follows. Firstly, incorporation of (H2O)n (n = 1–3) into the HO2 + SO2 → HOSO + O2 reaction produced two different types reactions: HO2⋯(H2O)n (n = 1–3) + SO2 and SO2⋯(H2O)n (n = 1–3) + HO2. Then, these (H2O)n (n = 1–3)-catalyzed channels were evaluated by investigating the direct hydrogen abstraction process and the double hydrogen transfer mechanism. Secondly, the rate constants and effective rate constant of the hydrogen abstraction reaction of HO2 + SO2 → HOSO + O2 without and with (H2O)n (n = 1–3) were calculated to identify the favorable routes. Finally, the atmospheric relevance of the effect of (H2O)n (n = 1–3) was investigated by their competition with the primary loss mechanism of HO2 radicals (such as the HO2 + HO2 and HO2 + NO3 reactions) and SO2 (such as the SO2 + HO reaction). Overall, this work may lead to a better understanding of the effects of (H2O)n (n = 1–3) on gas-phase reactions under tropospheric conditions.
2. Computational details
The geometries of all the reactants, pre-reactive intermediates, post-reactive intermediates, transition states and products were optimized at the M06-2X/aug-cc-pVTZ level of theory,55 and frequency analysis at the same level was performed to study the stationary point as well as the transition states. Moreover, the minimum energy path (MEP) was achieved by the intrinsic reaction coordinate (IRC)56 theory with a gradient step size of 0.01–0.05 (amu)1/2 Bohr, to confirm that the TS connects to minima along the reaction path. To obtain more reliable energy information, single-point energy calculations for the stationary points were obtained using the CCSD(T)57/CBS method at the M06-2X/aug-cc-pVTZ optimized geometries. It is worth pointing out that single point energy calculations of CCSD(T)/CBS were carried out for all species at the CCSD(T) level of theory using the aug-cc-pVDZ and aug-cc-pVTZ basis sets. The energy values obtained at the DZ and TZ levels were used to extrapolate the results to a complete basis set (CBS) limit. The method used here for CBS extrapolation was proposed and developed by Varandas and Pansini.58 In this method, the energy at the CBS limit is obtained by extrapolating the correlation (Corr) energy and Hartree–Fock (HF) energy separately using two different equations. To extrapolate the Corr energy and HF energy, the following equations were used:| |
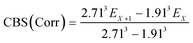 | (4) |
| |
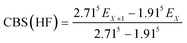 | (5) |
To estimate the effect of (H2O)n (n = 1–3), the theoretical rate constants of canonical variational transition (CVT)59–61 state theory with small curvature tunneling (SCT)62,63 correction for every reaction channel were calculated using the VKLab64 program coupled with the steady state approximation.
As described in eqn (6), the HO2 + SO2 → HOSO + O2 reaction without and with (H2O)n (n = 1–3) all began with the formation of pre-reactive intermediates before occurring through the transition state.
| |
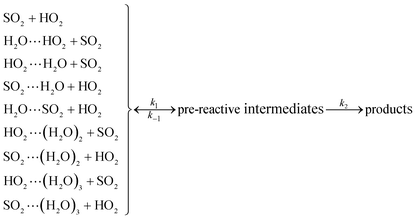 | (6) |
Similar to the water-catalyzed OH + HOCl reaction,26 the free energy results displayed in Table S4† suggest that the intermediates are, in part, shifted to the reactants. Assuming that the pre-reactive intermediates of the HO2 + SO2 → HOSO + O2 reaction without and with (H2O)n (n = 1–3) are in equilibrium with the corresponding reactants and are at steady state, the overall rate constant of the SO2 + HO2 reaction is expressed as:
| |
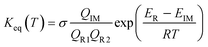 | (8) |
Here, the various
Q values denote the partition functions of the intermediates, reactants R1 and R2.
ER and
EIM stand for the total energies of the reactants and intermediate, respectively, while
σ is the symmetry factor. The rate constant
k2 of the second step of
eqn (7) was evaluated by the VKLab
64 program in the framework of the CVT. To include tunneling effects for motion along the reaction coordinate of the title reaction at the CCSD(T)/CBS//M06-2X/aug-cc-pVTZ level, the SCT tunneling approximation was adopted. The electronic structure calculations were performed using Gaussian09 (
ref. 65) software.
3. Results and discussion
The transition state in each reaction channel was denoted by “TS” followed by a number, and each pre-reactive intermediate was denoted by “IM” followed by a number. The letter “a” was used to distinguish the transition states and pre-reactive intermediates which are conformers of each other and therefore have the same features; species in the presence of H2O, (H2O)2, and (H2O)3 were respectively denoted by a “WM”, “WD”, and “WT” suffix.
3.1 Potential energy surfaces for the SO2 + HO2 → HOSO + O2 reaction
Consistent with previous studies on the HO2 + SO2 reaction,3,11 three kinds of product pairs, HOSO + O2, HSO2 + O2, and SO3 + HO could be found. Two H-abstraction channels and one O-abstraction route were modeled for the HO2 + SO2 reaction without water, as shown in Fig. S1.† From an energetic point of view, the channel for HOSO + O2 formation was determined to be the major channel, and this is in good agreement with previous results reported by Wang et al.11 Herein, as seen in Fig. 1, the SO2 + HO2 → HOSO + O2 reaction was mainly discussed, in order to focus on the catalytic role of (H2O)n (n = 1–3) in the SO2 + HO2 → HOSO + O2 reaction under atmospheric conditions. As shown in Fig. 1, for the formation of HOSO and O2, the reaction begins with the formation of the pre-reactive intermediate IM1. IM1 exhibits a five-membered ring structure. The relative energy of IM1 to the reactants (HO2 + SO2) is −5.6 kcal mol−1, which is in reasonable agreement with the previous value (−6.2 kcal mol−1) of CR1b reported by Wang et al.11 The pre-reactive intermediate IM1 goes through an H-abstraction transition state TS1 to form the post-reactive intermediate IMF1. From an energetic standpoint, the transition state TS1 has been predicted to be 0.3 kcal mol−1 below the reactants, which is slightly different from the corresponding values (−0.5 kcal mol−1) obtained by Wang et al.11 Intermediate IMF1 retains a five-membered ring structure with a binding energy of 1.4 kcal mol−1, and it dissociates to produce HOSO + O2, which lies 3.6 kcal mol−1 above the energy of the HO2 + SO2 reactants.
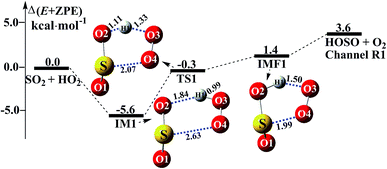 |
| | Fig. 1 Schematic energy diagrams of the SO2 + HO2 → HOSO + O2 reaction without water at the CCSD(T)/CBS//M06-2X/aug-cc-pVTZ level. | |
3.2 Geometrical analysis of the HO2⋯(H2O)n (n = 1–3) and SO2⋯(H2O)n (n = 1–3) complexes
It is noteworthy that the rates of pure termolecular interactions are insignificant as compared to the rates of sequential bimolecular interactions.67 In this sense, in the presence of (H2O)n (n = 1–3), both HO2 and SO2 mainly interact with (H2O)n (n = 1–3) via hydrogen bonding to form two-body complexes of HO2⋯(H2O)n (n = 1–3) and SO2⋯(H2O)n (n = 1–3), respectively, in the entrance channels, before interacting with the third body, SO2 or HO2. Therefore, it is highly necessary to first find stable configurations of the complexes HO2⋯(H2O)n (n = 1–3) and SO2⋯(H2O)n (n = 1–3). In order to find all possible stable configurations of the complexes HO2⋯(H2O)n (n = 1–3) and SO2⋯(H2O)n (n = 1–3), global minimum searching of geometric structures was carried out using Tsinghua Global Minimum (TGMin).68,69 Then, the initial structures for HO2⋯(H2O)n (n = 1–3) and SO2⋯(H2O)n (n = 1–3) were selected for geometry optimization using the M06-2X/6-31G(d) method. The isomer structures within 6.0 kcal mol−1 of the global minimum were re-optimized using the M06-2X/aug-cc-pVTZ method. Fig. 2 and S2† show the possible stable geometrical structures of HO2⋯(H2O)n (n = 1–3) and SO2⋯(H2O)n (n = 1–3), which are in good agreement with the available experimental results70 and the previously calculated values.33,42,43,47 Interestingly, each type of equilibrium structure of the HO2⋯(H2O)n (n = 1–3) and SO2⋯(H2O)n (n = 1–3) complexes mainly differs in the relative orientations of the dangling hydrogen atoms of (H2O)n (n = 1–3). Thus, for each type of equilibrium structure of HO2⋯(H2O)n (n = 1–3) and SO2⋯(H2O)n (n = 1–3), as shown in Fig. 2, we focus our attention on only one configuration, which has a larger stabilization energy than its isomers.
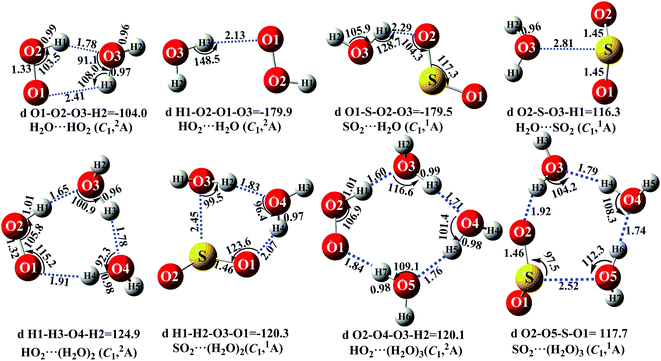 |
| | Fig. 2 The optimized geometrical reactants for the SO2 + HO2 reaction without and with catalyst X (X = H2O, (H2O)2 and (H2O)3) at the M06-2X/aug-cc-PVTZ level of theory. | |
As shown in Fig. 2, consistent with previous reports,70,71 the stable complex between HO2 and H2O is H2O⋯HO2, which involves a five-membered ring structure. Its bonding energy, listed in Table S3,† is 6.9 kcal mol−1, which is much more stable than hydrogen bonded (van der Waals interaction) complexes of HO2⋯H2O, SO2⋯H2O and H2O⋯SO2. Stable termolecular complexes of HO2⋯(H2O)2 and SO2⋯(H2O)2 are made up of HO2 or SO2 and a water dimer (H2O⋯H2O). Similar to a binary complex of H2O⋯HO2, both HO2 (SO2) and the water dimer in these two complexes act simultaneously as a hydrogen bond acceptor and a hydrogen bond donor. From an energetic standpoint, due to ring tension, the stabilization energy of the seven-membered-ring HO2⋯(H2O)2 complex is 12.6 kcal mol−1, whereas the bonding energy of the six-membered ring SO2⋯(H2O)2 complex is 6.9 kcal mol−1. With HO2 or SO2 inserted into (H2O)3, two stable geometries, HO2⋯(H2O)3 and SO2⋯(H2O)3, are obtained. Complex HO2⋯(H2O)3 exhibits a nine-membered-ring structure with a bonding energy of 12.3 kcal mol−1, which is less stable than that of complex HO2⋯(H2O)2. Similarly, the binding energy of the eight-membered-ring SO2⋯(H2O)3 complex is 6.5 kcal mol−1, which is 0.4 kcal mol−1 lower than that of SO2⋯(H2O)2 due to the effect of ring strain. The present study mainly focuses on the catalytic roles of (H2O)n (n = 1–3) in the SO2 + HO2 → HOSO + O2 reaction. Only the favorable reaction channels will be discussed according to their energy barriers and thermodynamic properties. Details on the remaining reaction channels are presented in the ESI.†
3.3 Mechanism for H2O-assisted SO2 + HO2 → HOSO + O2 reaction
The significance of the water-catalyzed SO2 + HO2 → HOSO + O2 reaction depends on the extent to which the respective bimolecular complexes, H2O⋯HO2, HO2⋯H2O, SO2⋯H2O and H2O⋯SO2 exist, which can be determined by computing their stability, as above (Fig. 2), and their corresponding equilibrium constants, as shown in Table S2.† The equilibrium constants of these complexes at 298 K are 8.59 × 10−19, 6.56 × 10−23, 3.08 × 10−24 and 4.88 × 10−24 cm3 per molecule, respectively (Table S2†). Taking into account typical tropospheric concentrations of 7.73 × 1017 molecules per cm3 of H2O, 3 × 108 molecules per cm3 of HO2,72 and 1.0 × 1012 molecules per cm3 of SO2,33 it is estimated that the atmospheric concentration of the H2O⋯HO2 complex is 1.99 × 108 molecules per cm3. Meanwhile, the concentrations of the HO2⋯H2O, SO2⋯H2O and H2O⋯SO2 complexes are estimated to be 1.52 × 104, 2.38 × 106, and 3.77 × 106 molecules per cm3. Thus, as shown in Fig. 3 and 4, when one water molecule is introduced into the SO2 + HO2 → HOSO + O2 reaction, there are four possible types of bimolecular reactions, labeled as Channels WM1, WM2, WM3, and WM4.| | |
H2O⋯HO2 + SO2 → H2O⋯HOSO + O2
| (9) |
| | |
HO2⋯H2O + SO2 → H2O + HOSO + O2
| (10) |
| | |
SO2⋯H2O + HO2 → HOSO⋯H2O + O2
| (11) |
| | |
H2O⋯SO2 + HO2 → HOSO⋯H2O + O2
| (12) |
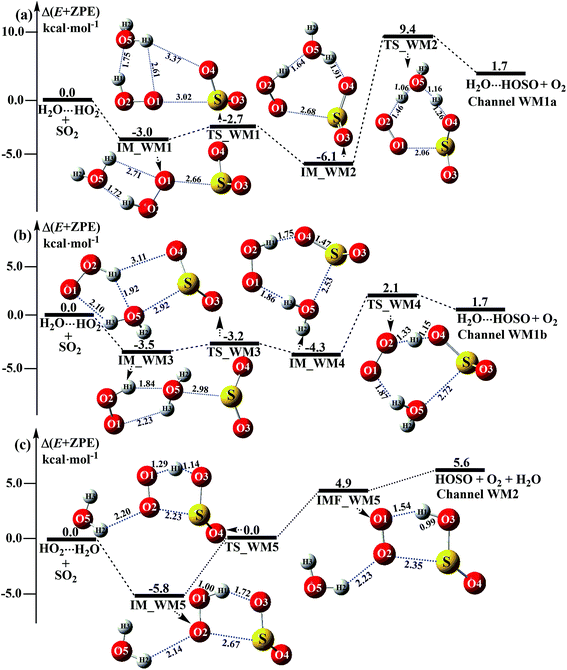 |
| | Fig. 3 Schematic energy diagrams of the water-assisted channel of HOSO + O2 formation, occurring through H2O⋯HO2 + SO2 and HO2⋯H2O + SO2 at the CCSD(T)/CBS//M06-2X/aug-cc-pVTZ level. | |
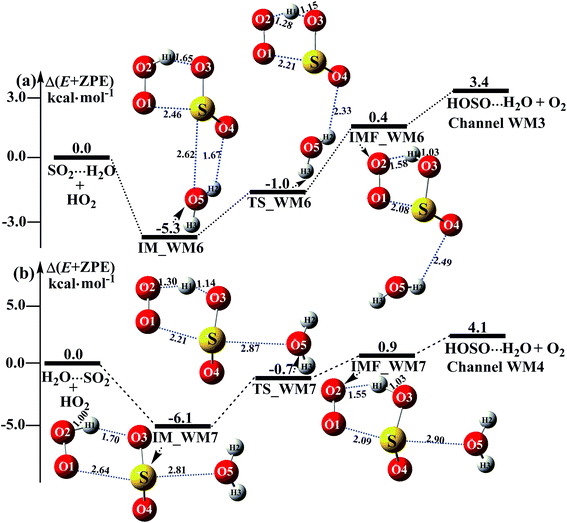 |
| | Fig. 4 Schematic energy diagrams of the water-assisted channel of HOSO + O2 formation, occurring through SO2⋯H2O + HO2 and H2O⋯SO2 + HO2 at the CCSD(T)/CBS//M06-2X/aug-cc-pVTZ level. | |
3.3.1 Mechanism of H2O⋯HO2 + SO2 and HO2⋯H2O + SO2 reactions. For the formation of HOSO⋯H2O + O2 occurring through the H2O⋯HO2 + SO2 reaction, Fig. 3 displays two Channels, namely Channel WM1a and Channel WM1b. Similar to other water-catalyzed reactions reported before,26,33,73 the influence of the water monomer in the H2O⋯HO2 + SO2 reaction was investigated by a stepwise mechanism, where the reaction occurs via a ring enlargement at first, and then proceeds through a hydrogen abstraction mechanism. However, the stepwise mechanism of Channel WM1a is different from Channel WM1b in three aspects. First, for the ring enlargement, the form of the S⋯O in complex IM_WM3 is different from that in complex IM_WM1. In complex IM_WM3, the S⋯O bond is formed by the S atom of SO2 and the O atom of the H2O moiety in the HO2⋯H2O complex, whereas the S⋯O bond in the IM_WM1 complex is formed by the S atom of SO2 and the terminal O atom of the HO2 moiety in the HO2⋯H2O complex. However, the stabilization energies of complexes IM_WM3 and IM_WM1 are close to each other, but with a difference of 0.5 kcal mol−1. Secondly, the complex IM_WM4 has similar seven-membered cyclic structures as IM_WM2, except that SO2 and H2O have exchanged their positions. This is possibly the reason that the stabilization energy of complex IM_WM4 is 1.8 kcal mol−1 lower than that of complex IM_WM2. The third one is that, for the rate-determining step of hydrogen abstraction, the barrier height of Channel WM1b is 2.1 kcal mol−1, which is 7.3 kcal mol−1 lower than the process of IM_WM2 → TS_WM2 → H2O⋯HOSO + O2 in Channel WM1a. This indicates that the double hydrogen transfer mechanism in Channel WM1a is less favorable than the direct hydrogen abstraction involved in Channel WM1b. This conclusion is consistent with our previous reports.71,73,74 As a result, in the following section, the reaction type of the multiple hydrogen transfer mechanism, where water molecules serve as a “bridge”, will be neglected in the stepwise reaction between SO2 and HO2⋯(H2O)2 (or HO2⋯(H2O)3).As for Channel WM2, it can be seen in Fig. 3c that a hydrogen bond complex, IM_WM5, has been identified, with a stabilization energy of 5.8 kcal mol−1. From a geometrical point of view, complex IM_WM5 exhibits a five-membered ring structure, which is similar to the five-membered ring structure of complex IM1 in the reaction without a catalyst, as shown in Fig. 1. Compared with complex IM1, an additional O⋯H bond (O2⋯H2, 2.14 Å) is involved in IM_WM5. This leads to the stabilization energy of complex IM_WM5 being enhanced by 0.2 kcal mol−1. Starting from complex IM_WM5 seen in Fig. 3c, the products HOSO + H2O + O2 can be obtained via transition state TS_WM5. From a geometrical point of view, similar to the naked transition state TS1, TS_WM5 follows direct hydrogen abstraction. Compared with TS1, the additional water molecule in the transition state TS_WM5 is bonded to the terminal O atom of the HO2 radical. Such a weak hydrogen bonding (O2⋯H2, 2.23 Å) interaction may lead to the energy of the TS_WM5 to HO2⋯H2O + SO2 reactants being 0.3 kcal mol−1 higher than that of the TS1 to the HO2 + SO2 reactants.
3.3.2 Potential energy surfaces for SO2⋯H2O + HO2 and H2O⋯SO2 + HO2 reactions. Beyond the water-assisted reaction channels described above, two additional water-assisted channels for HOSO + O2 formation were found by taking into account the bimolecular reactions of SO2⋯H2O + HO2 (Channel WM3) and H2O⋯SO2 + HO2 (Channel WM4).As for Channel WM3, the reaction of the SO2⋯H2O + HO2 entry channel proceeds through the formation of complex IM_WM6 before the transition state TS_WM6 and complex IMF_WM6. From a geometric point of view, complex IM_WM6 has one five-membered ring, H(1)–O(2)–O(1)⋯S–O(3), and one four-membered ring, O(4)⋯H(2)–O(5)⋯S, with a computed relative energy of 5.3 kcal mol−1 below the reactants of SO2⋯H2O + HO2, as shown in Table S4† and Fig. 4. Starting from complex IM_WM6, with the H atom of HO2 migrating to one O atom of the SO2 moiety in the SO2⋯H2O complex, the reaction can proceed via the transition state TS_WM6 to form complex IMF_WM6. As shown in Fig. 4, only the five-membered ring was retained in both the transition state TS_WM6 and complex IMF_WM6 with the elongation of the S⋯O5 bond. Compared with the transition state TS1 in Fig. 1, the additional water molecule in TS_WM6 did not change the active features of the five-membered ring. Furthermore, with the water molecule added, the relative energy of TS_WM6 to SO2⋯H2O + HO2 is 0.7 kcal mol−1 less than the corresponding value of TS1 (−0.3 kcal mol−1) to SO2 + HO2.
The fourth channel of the water-assisted SO2 + HO2 → HOSO + O2 reaction (Channel WM4, Fig. 4b) begins with complex IM_WM7 via the interaction between the O atom of H2O and the S atom of the SO2 moiety in H2O⋯SO2. The relative energy of complex IM_WM7 to the H2O⋯SO2 + HO2 reactants is 6.1 kcal mol−1. Complex IM_WM7 then decomposes via transition state TS_WM7 to form complex IMF_WM7. As shown in Fig. 4, similar to the structure of TS_WM6 and complex IMF_WM6, a five-membered ring is still involved in both TS_WM7 and complex IMF_WM7. Compared with TS1 in Fig. 1, the additional water molecule in TS_WM7 leads to the relative energy of TS_WM7 to H2O⋯SO2 + HO2 being 0.7 kcal mol−1, which is 0.4 kcal mol−1 less than the corresponding value of TS1 (−0.3 kcal mol−1) to SO2 + HO2.
3.4 Mechanism for (H2O)2-catalyzed the SO2 + HO2 → HOSO + O2 reaction
As shown in Fig. 5, (H2O)2 catalyzed channels were determined, starting from HO2⋯(H2O)2 + SO2 and SO2⋯(H2O)2 + HO2 reactants, which are labeled as Channel WD1 and Channel WD2.
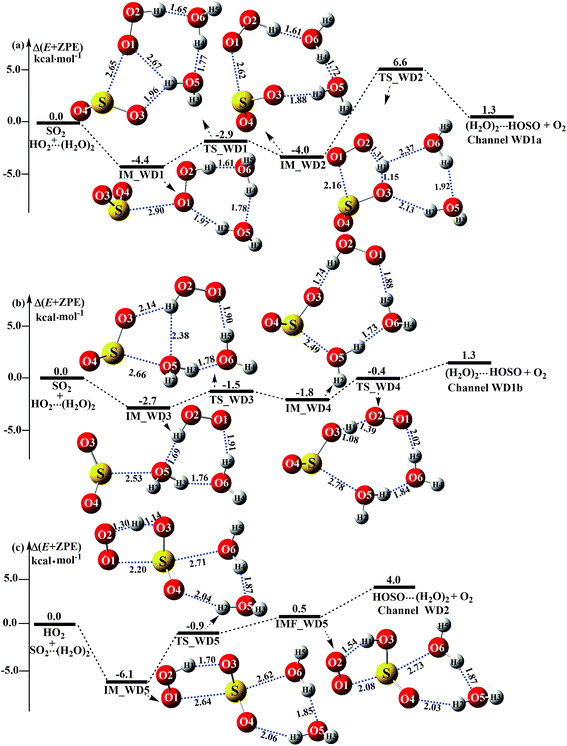 |
| | Fig. 5 Schematic energy diagrams of the dimer water-assisted channel of HOSO + O2 formation, occurring through HO2⋯(H2O)2 + SO2 and SO2⋯(H2O)2 + HO2 at the CCSD(T)/CBS//M06-2X/aug-cc-pVTZ level. | |
For the HO2⋯(H2O)2 + SO2 reaction (Channel WD1), two reaction types, namely Channel WD1a and Channel WD1b were found, depending on how the S atom of SO2 approaches the complex of HO2⋯(H2O)2. In the same way as the H2O⋯HO2 + SO2 reaction above (Fig. 3), both Channels WD1a and WD1b occur via a stepwise mechanism, which involves a direct hydrogen abstraction with one O atom of SO2 abstracting the H atom of a HO2 moiety in the HO2⋯(H2O)2 complex. However, as shown in Fig. 5, unlike the hydrogen abstraction in Channel WD1a, where the number of rings increases with decreasing ring size, in Channel WD1b the hydrogen abstraction does not change the ring size or the ring number. This discrepancy of hydrogen abstraction between Channels WD1a and WD1b may mean that, in Channel WD1a, the barrier height of the rate determining step (IM_WD2 → TS_WD2 → (H2O)2⋯HOSO + O2) is 8.4 kcal mol−1 higher than the corresponding barrier height of the rate determining step (IM_WD4 → TS_WD4 → (H2O)2⋯HOSO + O2) in Channel WD1b. As a result, for the HO2⋯(H2O)2 + SO2 reaction, Channel WD1b is mainly taken into account here.
For Channel WD1b, with the interaction between the S atom of SO2 and O(5) of the H2O moiety in the HO2⋯(H2O)2 complex, the reaction begins with the seven-membered cyclic complex IM_WD3, whose stability has been computed to be 2.7 kcal mol−1. Then, the reaction proceeds through the ring enlargement from IM_WD3 to IM_WD4 via the transition state TS_WD3, with an energy barrier of 1.5 kcal mol−1. Complex IM_WD4 has a similar structure to IM_WM4 (Fig. 3), but with a water monomer substituted by a water dimer. The binding energy of IM_WD4 is 1.8 kcal mol−1, which is 0.9 kcal mol−1 less stable than the complex IM_WD3. Starting from the complex IM_WD4, the reaction can proceed via the transition state TS_WD4 to form the products of (H2O)2⋯HOSO + O2. Similar to complex IM_WD4, TS_WD4 also shows a nine-membered ring structure with three components of (H2O)2, the SO moiety of SO2 and the HO2 radical. The relative energy of TS_WD4 to HO2⋯(H2O)2 + SO2 is 0.4 kcal mol−1, which is 2.5 kcal mol−1 lower than that of the H2O-assisted transition state TS_WM4 to H2O⋯HO2 + SO2 reactants. Meanwhile, from the viewpoint of ring sizes, for TSW2 and TSWD, with the ring size increase, the rate constant of the rate-determining step increases when one water molecule has been replaced by a water dimer. This is possibly because when the seven-membered ring has been replaced by a nine-membered ring, the number of hydrogen bonds increases, leading to the stabilization of the ring increasing. These facts indicate that the second water molecule plays a positive catalytic role by significantly reducing the barrier height of the SO2 + HO2 → HOSO + O2 reaction.
As for Channel WD2, starting from SO2⋯(H2O)2 + HO2 reactants, the reaction begins with the formation of complex IM_WD5. As shown in Fig. 5c, complex IM_WD5 exhibits a double-ring structure with a five-membered ring, O2⋯H1–O3–S⋯O1, and a six-membered ring, O4⋯H2–O5⋯H4–O6⋯S. Aside from these characteristics, complex IM_WD5 has a similar structure to that of IM_WM5, but with an additional water molecule inserted at the site between H2O and SO2. This leads to the stabilization energy of complex IM_WD5 (Table S4† and Fig. 5) being enhanced by 0.3 kcal mol−1 compared with complex IM_WM5. After complex IM_WD5, with the H atom of HO2 migrating to one O atom of the SO2 moiety in the SO2⋯(H2O)2 complex, the products of HOSO⋯(H2O)2 + O2 can be obtained via transition state TS_WD5 and complex IMF_WD5. As shown in Fig. 5, the double-ring structure is retained in transition state TS_WD5 and complex IMF_WD5. Compared with TS_WM5 in Fig. 4, with the introduction of the second water molecule, the active features of the five-membered ring in TS_WD5 exhibit no change. The relative energy of TS_WD5 to SO2⋯(H2O)2 + HO2 is 0.9 kcal mol−1, which is only changed by 0.6–0.9 kcal mol−1 compared with the corresponding values of TS_WM5 with H2O and TS1 without a catalyst. This implies that Channel WD2 proceeds easily.
3.5 Mechanism for (H2O)3-catalyzed the SO2 + HO2 → HOSO + O2 reaction
Similar to the instance of the (H2O)2-assisted reaction that occurs through the HO2⋯(H2O)2 + SO2 and SO2⋯(H2O)2 + HO2 reactions discussed above, the (H2O)3-assisted SO2 + HO2 → HOSO + O2 reaction can be obtained both by the insertion of SO2 into the HO2⋯(H2O)3 complex, and by the collision of the HO2 radical with the SO2⋯(H2O)3 complex. Through the SO2⋯(H2O)3 + HO2 reaction (which proceeds easily, as shown in Table S6,† with an energy barrier of 1.3 kcal mol−1, as shown in Table S2†), the concentration of SO2⋯(H2O)3 at 298 K is 4 orders of magnitude smaller than that of HO2⋯(H2O)3. Therefore, the SO2⋯(H2O)3 + HO2 reaction can be neglected under tropospheric conditions, and herein, we only focus our attention on the HO2⋯(H2O)3 + SO2 reaction. For comparison, a schematic energy diagram of HO2 + SO2⋯(H2O)3 reaction is displayed in Fig. S6.†
Similar to H2O⋯HO2 + SO2 and HO2⋯(H2O)2 + SO2 reactions above, HO2⋯(H2O)2 + SO2 reaction (Channel WT1) shown in Fig. 6
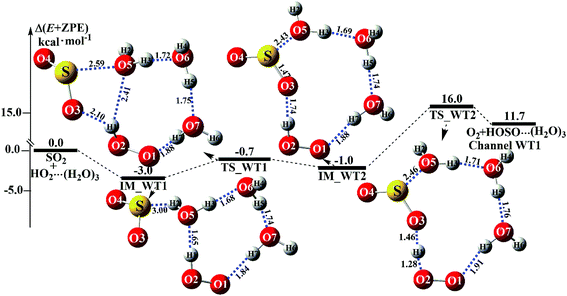 |
| | Fig. 6 Schematic energy diagrams of the trimer water-assisted channel of HOSO + O2 formation, occurring through HO2⋯(H2O)3 + SO2 at the CCSD(T)/CBS//M06-2X/aug-cc-pVTZ level. | |
also proceeds through a stepwise mechanism to form HOSO⋯(H
2O)
3 + O
2. In the first step, the reaction starts with complex IM_WT1, which has a binding energy of 3.0 kcal mol
−1. From a geometrical point of view, complex IM_WT1 has one nine-membered ring-like structure. After complex IM_WT1, the ring enlargement from complex IM_WT1 to the eleven-membered ring complex IM_WT2 occurs
via the double-ring transition state TS_WT1 (nine-membered ring, right; four-membered ring, left) with a barrier height of 0.7 kcal mol
−1. Complex IM_WT2 has similar quasi-planar structures to IM_WD4, with an additional water molecule inserted between SO
2 and HO
2. Complex IM_WT2 is 1.0 kcal mol
−1 less stable than IM_WT1, and is also 0.8 kcal mol
−1 less stable than IM_WD4. In the second step, following complex IM_WT2, Channel WT1 proceeds through transition state TS_WT2 to produce the product of HOSO⋯(H
2O)
3 + O
2. At transition state TS_WT2, the eleven-membered ring structure is still conserved, and the structure is similar to TS_WD4, but with an additional water molecule inserted between SO
2 and HO
2. From the viewpoint of ring sizes, for TS_WT2 and TS_WD4, although the hydrogen bonds increase in the ring when the nine-membered ring becomes an eleven-membered ring, the eleven-membered ring is unstable, and the tension is large, so TS_WT2 lies 16.0 kcal mol
−1 above the HO
2⋯(H
2O)
3 + SO
2 reactants, which is 16.4 kcal mol
−1 higher in energy than the relative energy of TS_WD4 to HO
2⋯(H
2O)
2 + SO
2 reactants. Meanwhile, the rate constant of the rate-determining step decreases when the water dimer has been replaced by the water trimer (
Fig. 6).
3.6 Reaction kinetics
With regard to the reactions involving (H2O)n (n = 1–3), we consider HO2⋯(H2O)n (n = 1–3) and SO2 or SO2⋯(H2O)n (n = 1–3) and HO2. When HO2⋯(H2O)n (n = 1–3) and SO2 act as reactants, the reactions occur via the following reaction mechanism:| | |
HO2 + (H2O)n (n = 1–3) ↔ HO2⋯(H2O)n (n = 1–3)
| (13) |
| | |
HO2⋯(H2O)n (n = 1–3) + SO2 → HOSO⋯(H2O)n (n = 1–3) + O2
| (14) |
Meanwhile when SO2⋯(H2O)n (n = 1–3) and HO2 are considered to be the reactants, the reaction mechanism is as follows:
| | |
SO2 + (H2O)n (n = 1–3) ↔ SO2⋯(H2O)n (n = 1–3)
| (15) |
| | |
SO2⋯(H2O)n (n = 1–3) + HO2 → HOSO⋯(H2O)n (n = 1–3) + O2
| (16) |
The rate via the reaction processes (13) and (14) is expressed in eqn (17).
| |
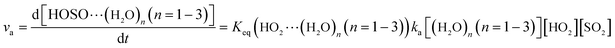 | (17) |
Here,
Keq(HO
2⋯(H
2O)
n (
n = 1–3)) is the equilibrium constant for the formation of the HO
2⋯(H
2O)
n (
n = 1–3) complex from isolated HO
2 and (H
2O)
n (
n = 1–3) and
ka represents the rate constant of
eqn (14). The rate
via the reaction processes
(15) and
(16) is expressed in
eqn (18).
| |
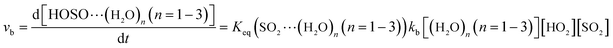 | (18) |
Here,
Keq(SO
2⋯(H
2O)
n (
n = 1–3)) is the equilibrium constant for the formation of the SO
2⋯(H
2O)
n (
n = 1–3) complex from isolated SO
2 and (H
2O)
n (
n = 1–3) and
kb represents the rate constant of
eqn (16). It is worth noting that, herein, we do not consider how pressure effects influence the formation of these complexes, because there are no experimental results showing that the equilibrium constants of these complexes depend on pressure.
The computed rate constants are provided in Table 1. For the reaction without a catalyst, the computed rate constant (k(R1)) is 9.09 × 10−18 to 5.22 × 10−17 cm3 per molecule per s in the temperature range of 218.6–320.0 K. At 298 K, the calculated value of k(R1) is 3.87 × 10−17 cm3 per molecule per s, which is close to the experimental value (1.0 × 10−18 cm3 per molecule per s).66 For the reaction with (H2O)n (n = 1–3), the rate ratio va/vb of the HO2 + SO2 + (H2O)n (n = 1–3) reaction shows that the entrance of HO2⋯(H2O)n (n = 1–3) and SO2 is more important than that of SO2⋯(H2O)n (n = 1–3) and HO2 because the rate ratios va1/vb1, va2/vb2, and va3/vb3 are 2.15 × 109 to 1.27 × 107, 5.00 × 108 to 4.95 × 106, 4.03 × 1013 to 4.12 × 109, respectively, between 275.0 and 320.0 K (Table 1).
Table 1 Ratio of reaction rate and effective rate constants (cm3 per molecules per s) for HOSO + O2 formation from the SO2 + HO2 reaction without and with (H2O)n (n = 1–3) within the temperature range of 275.0–320.0 Ka
| T (K) |
kR |
va1/vb1 |
va2/vb2 |
va3/vb3 |
k′a(WM1) |
k′a(WD1) |
k′a(WT1) |
| The letters “a” and “b” are used to distinguish the complexes: “a” is the complex of HO2⋯(H2O)n (n = 1–3), while “b” is the complex of SO2⋯(H2O)n (n = 1–3). va1, va2 and va3 are the reaction rates of HO2⋯(H2O)n (n = 1–3), vb1, vb2 and vb3 are the equilibrium constants of SO2⋯(H2O)n (n = 1–3). Species in the presence of a water molecule, water dimer and water trimer are respectively denoted by “1”, “2”, and “3”. k′a(WM1) is the effective rate constant for the process of HO2⋯H2O + SO2 → HOSO⋯H2O + O2. k′a(WD1) is the rate constant for the process of HO2⋯(H2O)2 + SO2 → HOSO⋯(H2O)2 + O2. k′a(WT1) is the rate constant for the process of HO2⋯(H2O)3 + SO2 → HOSO⋯(H2O)3 + O2. |
| 218.6 |
9.09 × 10−18 |
2.15 × 109 |
5.00 × 108 |
4.03 × 1013 |
5.84 × 10−13 |
2.99 × 10−23 |
— |
| 223.7 |
1.02 × 10−17 |
1.48 × 109 |
3.69 × 108 |
1.73 × 1014 |
5.38 × 10−13 |
3.57 × 10−22 |
— |
| 229.7 |
1.08 × 10−17 |
9.78 × 107 |
3.96 × 108 |
1.78 × 1012 |
4.93 × 10−13 |
5.07 × 10−18 |
1.68 × 10−21 |
| 235.1 |
1.31 × 10−17 |
6.82 × 108 |
1.97 × 108 |
9.96 × 1011 |
4.57 × 10−13 |
1.81 × 10−18 |
— |
| 249.9 |
1.75 × 10−17 |
2.78 × 109 |
9.59 × 107 |
1.58 × 1012 |
3.83 × 10−13 |
5.73 × 10−18 |
— |
| 259.3 |
1.76 × 10−17 |
1.66 × 108 |
4.07 × 105 |
3.24 × 1011 |
3.47 × 10−13 |
3.09 × 10−18 |
5.95 × 10−21 |
| 275.0 |
2.72 × 10−17 |
7.64 × 107 |
3.47 × 107 |
8.65 × 1010 |
3.02 × 10−13 |
3.90 × 10−17 |
1.63 × 10−19 |
| 280.0 |
2.95 × 10−17 |
6.07 × 107 |
2.92 × 107 |
3.10 × 1010 |
2.90 × 10−13 |
4.57 × 10−17 |
1.55 × 10−18 |
| 290.0 |
3.44 × 10−17 |
3.92 × 107 |
2.09 × 107 |
4.12 × 109 |
2.71 × 10−13 |
6.58 × 10−17 |
1.54 × 10−19 |
| 298.2 |
3.87 × 10−17 |
2.82 × 108 |
1.63 × 108 |
7.88 × 1013 |
2.57 × 10−13 |
8.95 × 10−17 |
1.59 × 10−18 |
| 300.0 |
3.98 × 10−17 |
2.62 × 108 |
1.54 × 107 |
3.19 × 1013 |
2.54 × 10−13 |
9.50 × 10−17 |
1.58 × 10−18 |
| 310.0 |
4.57 × 10−17 |
1.80 × 108 |
1.16 × 107 |
4.87 × 1010 |
2.41 × 10−13 |
1.32 × 10−16 |
1.57 × 10−19 |
| 320.0 |
5.22 × 10−17 |
1.27 × 107 |
4.95 × 106 |
2.72 × 1011 |
2.30 × 10−13 |
1.72 × 10−16 |
1.48 × 10−18 |
In the HO2⋯(H2O)n (n = 1–3) + SO2 reaction, it is necessary to calculate its effective rate constant k′, which can be considered as a measure of the efficiencies of the different catalysts of (H2O)n (n = 1–3) under atmospheric conditions, as it includes the concentration of (H2O)n (n = 1–3), equilibrium constants of HO2⋯(H2O)n (n = 1–3), and the rate constant from eqn (14). Based on this, the rates for the channels of the H2O⋯HO2 + SO2 reaction (ka(WM1b)), the HO2⋯(H2O)2 + SO2 reaction (ka(WD1b)) and the HO2⋯(H2O)3 + SO2 reaction (ka(WT1)) are respectively written as follows.
| | |
va(WM1b) = ka(WM1b)[H2O⋯HO2][SO2] = k′a(WM1b)[SO2][HO2]
| (19) |
| | |
va(WD1b) = ka(WD1b)[HO2⋯(H2O)2][SO2] = k′a(WD1b)[HO2][SO2]
| (20) |
| | |
va(WT1) = ka(WT1)[HO2⋯(H2O)3][SO2] = k′a(WT1)[HO2][SO2]
| (21) |
In these equations,
k′
a(WM1b) =
ka(WM1b)
Keq(H
2O⋯HO
2)[H
2O];
k′
a(WD1b) =
ka(WD1b)
Keq(HO
2⋯(H
2O)
2)[(H
2O)
2]; and
k′
a(WT1) =
ka(WT1)
Keq(HO
2⋯(H
2O)
3)[(H
2O)
3].
Keq(H
2O⋯HO
2),
Keq(HO
2⋯(H
2O)
2) and
Keq(HO
2⋯(H
2O)
3) are the equilibrium constants for the formation of the H
2O⋯HO
2, HO
2⋯(H
2O)
2 and HO
2⋯(H
2O)
3 complexes, respectively. [H
2O], [(H
2O)
2] and [(H
2O)
3] are the concentrations of H
2O, (H
2O)
2, and (H
2O)
3, respectively. As shown in
Table 1, within the temperature range of 275.0–320.0 K, the effective rate constant of
k′
a(WM1b) is 1.32 × 10
−14 to 2.01 × 10
−14 cm
3 per molecule per s, which is 2–3 and 3–6 orders of magnitude larger than the corresponding values of
k′
a(WD1b) and
k′
a(WT1), respectively, indicating that the catalytic effect of H
2O is the largest among the (H
2O)
n (
n = 1–3) catalysts, and the catalytic effect of (H
2O)
2, and (H
2O)
3 is negligible. Compared with the rate constant of the naked reaction of SO
2 + HO
2 → HOSO + O
2, the value of
k′
a(WM1b) is 2–3 orders of magnitude larger within the temperature range of 275.0–320.0 K, indicating that at 0 km altitude within this temperature range, the positive effect of water is significant under atmospheric conditions.
The average concentrations of water at 5, 10 and 15 km altitudes are known to be 2.41 × 1016, 4.92 × 1015 and 1.96 × 1013 molecules per cm3, respectively.75 Considering the average concentrations of water at 5, 10 and 15 km altitudes in the troposphere, the calculated effective rate constants of the H2O-assisted Channel WM1, the (H2O)2-assisted Channel WD1 and the (H2O)3-assisted Channel WT1 are listed in Table 2. Compared with an altitude of 0 km, the dominant channel does not change in the three different cases, which is similar to the dominant channel in Table 1. Meanwhile, the values of k′(WM1) are 7.49 × 10−17, 2.68 × 10−17 and 2.95 × 10−18 at altitudes of 5, 10 and 15 km, respectively. Compared with the value of k′(WM1) at 0 km, we found that the values of k′(WM1) show a declining trend, decreasing by about 4–5 orders of magnitude, as we move towards higher altitude. Furthermore, as shown in Table 2, it has been estimated that the enhancement factors of water vapor are 99.98%, 78.23%, 69.63% and 27.27% at altitudes of 0, 5, 10 and 15 km, respectively. This implies that, as we move towards higher altitudes, the contribution of water on increasing the reaction rate becomes gradually lessened.
Table 2 Effective rate constants (cm3 per molecules per s) for HOSO + O2 formation from the SO2 + HO2 reaction without and with (H2O)n (n = 1–3) within the altitude range of 0–15 kma
| Alt. (km) |
T (K) |
k′a(WM1) |
k′a(WD1) |
k′b(WD2) |
k′a(WT1) |
k′a(WM)/ktot |
| k′a(WM1) is the effective rate constant occurring through Channel WM1. k′a(WD1) and k′b(WD2) are the effective rate constants of Channel WD1 and WD2, respectively; k′a(WT1) is the effective rate constant of Channel WT1. ktot = kR1 + k′a(WM)(100% RH). |
| 0 |
298.2 |
1.67 × 10−13 |
1.15 × 10−21 |
4.03 × 10−17 |
1.59 × 10−18 |
99.98% |
| 5 |
259.3 |
7.49 × 10−17 |
3.09 × 10−18 |
1.10 × 10−18 |
3.53 × 10−20 |
78.23% |
| 10 |
229.7 |
2.68 × 10−17 |
5.07 × 10−18 |
1.40 × 10−18 |
1.68 × 10−21 |
69.63% |
| 15 |
212.6 |
2.95 × 10−18 |
8.95 × 10−17 |
2.63 × 10−22 |
2.42 × 10−26 |
27.27% |
3.7 Atmospheric implications
In gas-phase reactions of the atmosphere, previous investigations have shown that the dominant sink of HO2 is its reaction with HO2 (ref. 71) and NO3.76 Therefore, it is of great importance to discuss the effective rate constant of the H2O⋯HO2 + SO2 reaction (k′a(WM1b)) with the rate constant of these dominant sink processes of HO2. To meet this goal, the reaction mechanisms of HO2 + HO2 and HO2 + NO3 at the CCSD(T)/CBS//M06-2X/aug-cc-pVTZ level are shown in Fig. S7,† while their rate constants within the temperature range of 218.6–320.0 K are listed in Table 3, with rate ratios between H2O⋯HO2 + SO2 and HO2 + HO2 (HO2 + NO3) as shown in eqn (22). The calculated rate constants are in good agreement with the available experimental values.77–79| |
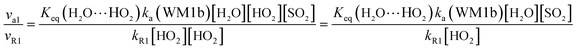 | (22) |
| |
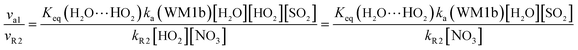 | (23) |
Here, kR1 and kR2 are the rate constants of the HO2 + HO2 reaction and the HO2 + NO3 reaction, respectively, obtained from Table 3. The rate ratios va1/vR1 and va1/vR2 depend on the H2O, SO2, NO3 and HO2 concentrations in the atmosphere. At 298 K, when the concentration of water is at a relative humidity of 100%, SO2 and NO3 are 7.73 × 1017, 1 × 1012 and 2.46 × 107 molecules per cm3, respectively, and the gas-phase concentration of HO2 is 3 × 108 molecules per cm3, the H2O⋯HO2 + SO2 reaction can compete with the HO2 + HO2 reaction, because the rate ratio va1/vR1 is about 4.35 × 102 at 298 K. Meanwhile, the H2O⋯HO2 + SO2 reaction can compete well with the HO2 + NO3 reaction because the rate ratio va1/vR2 is about 6.83 × 103 at 298 K. Thus, compared with the primary loss mechanism of HO2 radicals, the HO2 + SO2 → HOSO + 3O2 reaction with H2O cannot be neglected. Meanwhile, with increasing altitude, the values of va1/vR1 and va1/vR2 obviously decrease. At 218.6 K, the values of va1/vR1 and va1/vR2 are 5.22 × 10−4 and 1.73 × 10−3, showing that the HO2 + SO2 → HOSO + 3O2 reaction with H2O cannot compete with the primary loss mechanism of HO2 radicals.
Table 3 Rate constants (cm3 per molecules per s) for H2O2 + O2 formation from the HO2 + HO2 reaction (R1), HNO3 + O2 formation from the NO3 + HO2 reaction (R2) and HSO3 formation from the SO2 + OH reaction (R3) within the temperature range of 218.6–320.0 K
| T (K) |
kR1 |
va1/vR1 |
kR2 |
va1/vR2 |
kR3 |
va1/vR3 |
va1/vR3(night) |
| 218.6 |
1.38 × 10−10 |
5.22 × 10−4 |
5.06 × 10−10 |
1.74 × 10−3 |
2.06 × 10−12 |
3.15 × 10−3 |
3.15 × 10−1 |
| 223.7 |
8.29 × 10−11 |
8.24 × 10−4 |
2.55 × 10−10 |
1.09 × 10−3 |
2.09 × 10−12 |
3.27 × 10−4 |
3.27 × 10−2 |
| 229.7 |
4.69 × 10−11 |
1.63 × 10−1 |
1.22 × 10−10 |
2.55 × 10−1 |
2.14 × 10−12 |
3.58 × 10−2 |
3.58 × 100 |
| 235.1 |
2.88 × 10−11 |
4.54 × 10−4 |
6.72 × 10−11 |
7.92 × 10−4 |
2.20 × 10−12 |
5.95 × 10−5 |
5.95 × 10−3 |
| 249.9 |
8.50 × 10−11 |
2.53 × 10−3 |
1.68 × 10−11 |
5.20 × 10−2 |
2.32 × 10−12 |
9.26 × 10−4 |
9.26 × 10−2 |
| 259.3 |
4.22 × 10−11 |
1.02 × 100 |
8.20 × 10−12 |
2.13 × 101 |
2.37 × 10−12 |
1.82 × 10−1 |
1.82 × 101 |
| 280.0 |
1.08 × 10−11 |
1.27 × 101 |
2.32 × 10−12 |
2.41 × 102 |
2.53 × 10−12 |
5.43 × 10−1 |
5.43 × 101 |
| 290.0 |
6.01 × 10−12 |
2.53 × 101 |
1.42 × 10−12 |
4.35 × 102 |
2.64 × 10−12 |
5.76 × 10−1 |
5.76 × 101 |
| 298.2 |
3.85 × 10−12 |
4.35 × 102 |
9.96 × 10−13 |
6.83 × 103 |
2.70 × 10−12 |
6.20 × 100 |
6.20 × 102 |
| 300.0 |
3.49 × 10−12 |
4.88 × 102 |
9.23 × 10−13 |
7.51 × 103 |
2.71 × 10−12 |
6.29 × 100 |
6.29 × 102 |
| 310.0 |
2.11 × 10−12 |
8.88 × 102 |
6.29 × 10−13 |
1.21 × 104 |
2.79 × 10−12 |
6.72 × 100 |
6.72 × 102 |
| 320.0 |
1.32 × 10−12 |
1.53 × 102 |
4.46 × 10−13 |
1.84 × 103 |
2.90 × 10−12 |
6.95 × 10−1 |
6.95 × 101 |
In order to test the competition of the H2O⋯HO2 + SO2 reaction with the primary loss mechanism of SO2 (such as the SO2 + HO reaction), it is of great importance to discuss the rate ratio between H2O⋯HO2 + SO2 and SO2 + OH, as shown in eqn (24).
| |
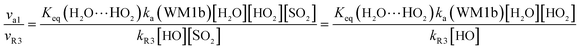 | (24) |
Here,
kR3 is the rate constant of the SO
2 + OH reaction, which is obtained from
Table 3. The rate ratio
va1/
vR3 depends on the H
2O, OH, and HO
2 concentrations in the atmosphere, At 298 K, when the concentration of water is at a relative humidity of 100%, OH is 7.73 × 10
17 and 1 × 10
6 molecules per cm
3, respectively, and the gas-phase concentration of HO
2 is 3 × 10
8 molecules per cm
3, the H
2O⋯HO
2 + SO
2 reaction can compete with the SO
2 + HO reaction, because the rate ratio v
a1/v
R3 is about 6.20 at 298 K. Consequently, the hydrogen atom transfer processes of the H
2O⋯HO
2 + SO
2 reaction are more obvious in the atmosphere during the day than those of the SO
2 + HO reaction. Meanwhile, when the OH concentration decreases to 1 × 10
4 molecules per cm
3 during the night,
80 the H
2O⋯HO
2 + SO
2 reaction can compete well with the SO
2 + HO reaction because the rate ratio
va1/
vR3 is about 6.20 × 10
2 at 298 K. Thus, the H
2O⋯HO
2 + SO
2 reaction can also make a contribution to the sink of SO
2 during the night under the conditions of OH (10
4 molecules per cm
3), HO
2 (molecules per cm
3), and H
2O (molecules per cm
3).
4. Summary and conclusions
In this article, the hydrogen atom transfer processes of the HO2 + SO2 → HOSO + 3O2 reaction without and with (H2O)n (n = 1–3) have been investigated using the CCSD(T)/CBS//M06-2X/aug-cc-pVTZ method and canonical variational transition state theory with small curvature tunneling (CVT/SCT). The calculated results show that, for the (H2O)n (n = 1–3) + HO2 + SO2 reaction, the main entrance channel is the reaction of the HO2⋯(H2O)n (n = 1–3) complex with SO2. Additionally, H2O exerts the strongest catalytic influence in the hydrogen atom transfer processes of the HO2 + SO2 → HOSO + 3O2 reaction compared with (H2O)2 and (H2O)3, which is due to the fact that the effective rate constant of the HO2⋯H2O + SO2 reaction is 2–3 and 4–6 orders of magnitude larger than the corresponding rate constants of the HO2⋯(H2O)2 + SO2 and HO2⋯(H2O)3 + SO2 reactions, respectively.
In the gas-phase reactions of the atmosphere, the importance of the HO2⋯H2O + SO2 reaction depends on its competition with the HO2 + SO2 → HOSO + 3O2 reaction. We show that, at 0 km altitude within the temperature range of 275–320 K, the effective rate constant of the HO2⋯H2O + SO2 reaction was 2–3 orders of magnitude larger than that of the HO2 + SO2 → HOSO + 3O2 reaction without a catalyst, indicating that the water monomer plays an obvious positive role in increasing the rate of the HO2 + SO2 → HOSO + 3O2 reaction. Compared with the primary loss mechanism of HO2 radicals and SO2, the HO2 + SO2 → HOSO + 3O2 reaction with H2O cannot be neglected with its rate constant close to the rate constant of those reactions of HO2 + HO2, HO2 + NO3 and SO2 + HO. In addition, with the altitude increase, for the formation of HOSO + 3O2, the contribution of H2O decreases from 99.98% to 27.27% at the lower relative concentration of water, which indicates that the HO2⋯H2O + SO2 reaction cannot compete with the primary loss processes of HO2 radicals and SO2 at higher altitudes.
The findings of the present work not only show a specific (H2O)n (n = 1–3) catalyzed reaction for its reaction mechanism and kinetics, but also show that H2O can obviously promote the hydrogen atom transfer processes of the HO2 + SO2 → HOSO + 3O2 reaction. Thus, the present investigation has wide applications in the hydrogen atom transfer processes of atmospheric processes, such as HO2 + HO2 and HO2 + NO3 reactions.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 21603132, 41805107), the Project of Education Department in Shaanxi (18JK0147) and the Funds of Research Programs of Shaanxi University of Technology (No. SLGQD13(2)-3, SLGQD13(2)-4).
References
- C. N. Hewitt, Atmos. Environ., 2011, 35, 1155–1170 CrossRef.
- B. Long, J. L. Bao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2017, 19, 8091–8100 RSC.
- X. Chen, C. Tao, L. Zhong, Y. Gao, W. Yao and S. Li, Chem. Phys. Lett., 2014, 608, 272–276 CrossRef CAS.
- J. Liu, S. Fang, Z. Wang, W. Yi, F. M. Tao and J. Liu, Environ. Sci. Technol., 2015, 49, 13112–13120 CrossRef CAS PubMed.
- M. R. Rd, T. Berndt, M. Sipilä, P. Paasonen, T. Petäjä, S. Kim, T. Kurtén, F. Stratmann, V. M. Kerminen and M. Kulmala, Nature, 2012, 488, 193 CrossRef PubMed.
- R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Chem. Rev., 2011, 112, 1957–2011 CrossRef PubMed.
- N. Sang, Y. Yun and G. Y. Yao, et al., Toxicol. Sci., 2011, 124, 400–413 CrossRef CAS PubMed.
- Y. Tang, G. S. Tyndall and J. J. Orlando, J. Phys. Chem. A, 2010, 114, 369–378 CrossRef CAS.
- P. D. Lightfoot, R. A. Cox, J. N. Crowley, M. Destriau, G. D. Hayman, M. E. Jenkin, G. K. Moortgat and F. Zabel, Atmos. Environ., 1992, 26, 1805–1961 CrossRef.
- D. Stone, L. K. Whalley and D. E. Heard, Chem. Soc. Rev., 2012, 41, 6348–6404 RSC.
- B. Wang and H. Hou, Phys. Lett., 2005, 410, 235–241 CAS.
- S. E. Wheeler, J. Phys. Chem. A, 2009, 113, 6779–6788 CrossRef CAS PubMed.
- A. Lesar and A. Tavčar, J. Phys. Chem. A, 2011, 115, 11008–11015 CrossRef CAS PubMed.
- A. J. Frank, M. Sadílek, J. G. Ferrier and F. E. Tureček, J. Am. Chem. Soc., 1996, 118, 11321–11322 CrossRef CAS.
- E. Isoniemi, L. Khriachtchev, J. Lundell and M. Räsänen, J. Mol. Struct., 2001, 563, 261–265 CrossRef.
- R. J. Boyd, A. Gupta, R. F. Langler, S. P. Lownie and J. A. Pincock, Can. J. Chem., 1980, 58, 331–338 CrossRef CAS.
- M. C. Mccarthy, V. Lattanzi, J. Oscar Martinez and F. E. Tureček, J. Phys. Chem. Lett., 2013, 4, 4074–4079 CrossRef CAS.
- Y. Q. Sun, X. Wang, F. Y. Bai and X. M. Pan, Environ. Chem., 2017, 14, 19–30 CrossRef CAS.
- W. A. Payne, L. J. Stief and D. D. Davis, J. Am. Chem. Soc., 1973, 95, 7614–7619 CrossRef CAS.
- J. P. Burrows, D. I. Cliff, G. W. Harris, B. A. Thrush and J. P. T. Wilkinson, Proc. R. Soc. London, Ser. A, 1979, 368, 463–481 CrossRef CAS.
- R. J. Buszek, J. S. Francisco and J. M. Anglada, Int. Rev. Phys. Chem., 2011, 30, 335–369 Search PubMed.
- T. Zhang, W. Wang, P. Zhang, J. Lü and Y. Zhang, Phys. Chem. Chem. Phys., 2011, 13, 20794–20805 RSC.
- R. J. Buszek, M. Torrentsucarrat, J. M. Anglada and J. S. Francisco, J. Phys. Chem. A, 2012, 116, 5821–5829 CrossRef CAS PubMed.
- J. M. Anglada and J. Gonzalez, ChemPhysChem, 2009, 10, 3034–3045 CrossRef CAS.
- J. Gonzalez and J. M. Anglada, J. Phys. Chem. A, 2010, 114, 9151–9162 CrossRef CAS PubMed.
- J. Gonzalez, J. M. Anglada, R. J. Buszek and J. S. Francisco, J. Am. Chem. Soc., 2011, 133, 3345–3353 CrossRef CAS PubMed.
- J. C. Hansen and J. S. Francisco, ChemPhysChem, 2002, 3, 833–840 CrossRef CAS PubMed.
- V. Vaida, H. G. Kjaergaard, P. E. Hintze and D. J. Donaldson, Science, 2003, 299, 1566–1568 CrossRef CAS PubMed.
- N. Kanno, K. Tonokura, A. Tezaki and M. Koshi, J. Phys. Chem. A, 2005, 109, 3153–3158 CrossRef CAS PubMed.
- K. Suma, Y. Sumiyoshi and Y. Endo, Science, 2006, 311, 1278–1281 CrossRef CAS PubMed.
- N. Butkovskaya, M. T. Rayez, J. C. Rayez, A. Kukui and G. L. Bras, J. Phys. Chem. A, 2009, 113, 11327–11342 CrossRef CAS PubMed.
- S. Aloisio, J. S. Francisco and R. R. Friedl, J. Phys. Chem. A, 2000, 104, 6597–6601 CrossRef CAS.
- J. Liu, S. Fang, W. Liu, A. Kukui and G. L. Bras, J. Phys. Chem. A, 2015, 119, 102–111 CrossRef CAS PubMed.
- T. L. Tarbuck and G. L. Richmond, J. Am. Chem. Soc., 2005, 127, 16806–16807 CrossRef CAS PubMed.
- T. L. Tarbuck and G. L. Richmond, J. Am. Chem. Soc., 2006, 128, 3256–3267 CrossRef CAS.
- S. T. Ota and G. L. Richmond, J. Am. Chem. Soc., 2011, 133, 7497–7508 CrossRef CAS.
- K. Matsumura, F. J. Lovas and R. D. Suenram, J. Chem. Phys., 1989, 91, 5887–5894 CrossRef CAS.
- T. Zhang, C. Yang, X. Feng, J. Kang, L. Song, Y. Lu, Z. Wang, Q. Xu, W. Wang and Z. Wang, Phys. Chem. Chem. Phys., 2016, 18, 17414–17427 RSC.
- L. P. Viegas and A. J. C. Varandas, Eur. Phys. J. D, 2016, 70, 48 CrossRef.
- Y. P. Zhao and Y. P. Zeng, Chin. J. Struct. Chem., 2010, 29, 499–508 CrossRef CAS.
- R. Steudel and Y. Steudel, Eur. J. Inorg. Chem., 2009, 2009, 1393–1405 CrossRef.
- B. Du and W. Zhang, Comput. Theor. Chem., 2014, 1049, 90–96 CrossRef CAS.
- E. Vöhringermartinez, B. Hansmann and H. Hernandezsoto, Science, 2007, 315, 497–501 CrossRef PubMed.
- R. Wang, J. Kang and S. Zhang, Comput. Theor. Chem., 2017, 1110, 25–34 CrossRef CAS.
- P. Kumar, P. Biswas and B. Bandyopadhyay, Phys. Chem. Chem. Phys., 2016, 18, 27728–27732 RSC.
- B. Du and W. Zhang, Comput. Theor. Chem., 2015, 1069, 77–85 CrossRef CAS.
- L. P. Viegas and A. J. Varandas, J. Phys. Chem. B, 2016, 120, 1560–1568 CrossRef CAS PubMed.
- J. M. Anglada, G. J. Hoffman, L. V. Slipchenko, M. M. Costa, M. F. Ruizlópez and J. S. Francisco, J. Phys. Chem. A, 2013, 117, 10381–10396 CrossRef CAS PubMed.
- P. Miró and C. J. Cramer, Phys. Chem. Chem. Phys., 2013, 15, 1837–1843 RSC.
- J. Hernández-Rojas and D. J. Wales, Chem. Phys., 2014, 444, 23–29 CrossRef.
- E. A. Cobar, P. R. Horn, R. G. Bergman and M. Headgordon, Phys. Chem. Chem. Phys., 2012, 14, 15328–15339 RSC.
- J. A. Anderson, K. Crager, L. Fedoroff and G. S. Tschumper, J. Chem. Phys., 2004, 121, 11023–11029 CrossRef CAS PubMed.
- M. E. Dunn, E. K. Pokon and G. C. Shields, J. Am. Chem. Soc., 2004, 126, 2647–2653 CrossRef CAS PubMed.
- N. Goldman, R. S. Fellers and C. Leforestier, J. Phys. Chem. A, 2001, 105, 515–519 CrossRef CAS.
- Y. S. Lee, S. A. Kucharski and R. J. Bartlett, J. Chem. Phys., 1985, 82, 5761 CrossRef.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS.
- Y. S. Lee, S. A. Kucharski and R. J. Bartlett, J. Chem. Phys., 1984, 81, 5906–5912 CrossRef.
- A. J. C. Varandas and F. N. N. Pansini, J. Chem. Phys., 2014, 141, 224113 CrossRef CAS PubMed.
- B. C. Garrett and D. G. Truhlar, J. Chem. Phys., 1979, 70, 1593–1598 CrossRef CAS.
- B. C. Garrett and D. G. Truhlar, Chem. Informationsdienst, 1979, 10, 4534–4548 Search PubMed.
- B. C. Garrett, D. G. Truhlar, R. S. Grev and A. W. Magnuson, J. Chem. Phys., 1980, 84, 1730–1748 CrossRef CAS.
- D. H. Lu, T. N. Truong, S. G. Melissas, C. Lynch, Y. P. Liu and B. C. Garrett, Comput. Phys. Commun., 1992, 71, 235–262 CrossRef CAS.
- Y. P. Liu, G. C. Lynch, T. N. Truong, D. H. Lu, D. G. Truhlar and B. C. Garrettet, J. Am. Chem. Soc., 1993, 6, 2408–2415 CrossRef.
- S. W. Zhang and N. T. Truong, VKLab, version 1.0, University of Utah, Salt Lake City, 2001 Search PubMed.
- M. J. Frisch, G. W. Trucks and J. A. Pople, Gaussian 09, Revision A.01, Gaussian Inc., Pittsburgh, PA, 2009 Search PubMed.
- R. Atkinson, D. L. Baulch and R. A. Cox, Atmos. Chem. Phys., 2004, 3, 1461–1738 CrossRef.
- R. J. Buszek, J. R. Barker and J. S. Francisco, J. Phys. Chem. A, 2012, 116, 4712–4719 CrossRef CAS PubMed.
- X. Chen, Y. F. Zhao, L. S. Wang and J. Li, Comput. Theor. Chem., 2017, 1107, 57–65 CrossRef CAS.
- Y. Zhao, X. Chen and J. Li, Nano Res., 2017, 10, 3407–3420 CrossRef CAS.
- B. Long, X. F. Tan, Z. W. Long, Y. B. Wang, D. S. Ren and W. J. Zhang, J. Phys. Chem. A, 2011, 115, 6559–6567 CrossRef CAS PubMed.
- T. Zhang, R. Wang, W. Wang, S. Min, Q. Xu, Z. Wang, C. Zhao and Z. Wang, Comput. Theor. Chem., 2014, 1045, 135–144 CrossRef CAS.
- J. Gonzalez, M. Torrent-Sucarrat and J. M. Anglada, Phys. Chem. Chem. Phys., 2010, 12, 2116–2125 RSC.
- T. Zhang, W. Wang, C. Li and Y. Du, RSC Adv., 2013, 3, 7381–7391 RSC.
- T. Zhang, R. Wang, H. Chen, S. Min, Z. Wang, C. Zhao, Q. Xu, L. Jin, W. Wang and Z. Wang, Phys. Chem. Chem. Phys., 2015, 17, 15046–15055 RSC.
- S. Mallick, S. Sarkar, P. Kumar and B. Bandyopadhyay, J. Phys. Chem. A, 2018, 122, 350–363 CrossRef CAS.
- A. Mellouki, R. K. Talukdar and A. M. R. P. Bopegedera, Int. J. Chem. Kinet., 1993, 25, 25–39 CrossRef CAS.
- D. Stone and D. M. Rowley, Phys. Chem. Chem. Phys., 2005, 7, 2156–2163 RSC.
- E. Becker, M. M. Rahman and R. N. Schindler, Ber. Bunsenges. Phys. Chem., 1992, 96, 776–783 CrossRef CAS.
- D. Fulle, H. F. Hamann and H. Hippler, Phys. Chem. Chem. Phys., 1999, 1, 2695–2702 RSC.
- M. A. H. Khan, M. J. Ashfold, G. Nickless, D. Martin, L. A. Watson, P. D. Hamer, R. P. Wayne, C. E. Canosa-Mas and D. E. Shallcross, Atmos. Sci. Lett., 2008, 9, 140–146 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra00169g |
| ‡ Qiuyue Yao, Mingjie Wen, Shaobo Tian, and Yan Wang contributed equally to this work. |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Qiuyue Yao‡
b,
Mingjie Wen‡a,
Shaobo Tian‡a,
Yan Wang‡a,
Zhiyin Wanga,
Xiaohu Yu
*a,
Qiuyue Yao‡
b,
Mingjie Wen‡a,
Shaobo Tian‡a,
Yan Wang‡a,
Zhiyin Wanga,
Xiaohu Yu a,
Xianzhao Shaoa and
Long Chencd
a,
Xianzhao Shaoa and
Long Chencd