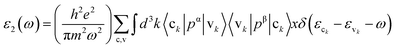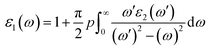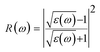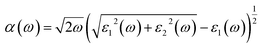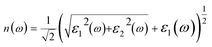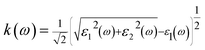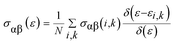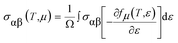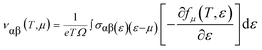Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Investigation on the electronic structure, optical, elastic, mechanical, thermodynamic and thermoelectric properties of wide band gap semiconductor double perovskite Ba2InTaO6
Sajad Ahmad Dar *a,
Ramesh Sharmab,
Vipul Srivastavac and
Umesh Kumar Sakalled
*a,
Ramesh Sharmab,
Vipul Srivastavac and
Umesh Kumar Sakalled
aDepartment of Physics, Govt. Motilal Vigyan Mahavidyalaya College, Bhopal-462008, Madhya Pradesh State, India. E-mail: sajad54453@gmail.com
bDepartment of Applied Science, Feroze Gandhi Institute of Engineering and Technology, Raebareli-229001, Uttar Pradesh State, India
cDepartment of Physics, School of Chemical Engineering & Physical Sciences, Lovely Professional University, Phagwara-144411, Punjab State, India
dDepartment of Physics, Govt. PG College, BHEL, Bhopal-462022, Madhya Pradesh State, India
First published on 26th March 2019
Abstract
In the present paper, double perovskite Ba2InTaO6 was investigated in terms of its structural, electronic, optical, elastic, mechanical, thermodynamic and thermoelectric properties using density-functional theory (DFT). The generalized gradient approximation (GGA) in the scheme of Perdew, Burke and Ernzerhof (PBE) and the modified Becke–Johnson (mBJ) potential were employed for the exchange–correlation potential. The computed lattice constant was found to be in agreement with the available experimental and theoretical results. The electronic profile shows a semiconducting nature. Further analysis of the complex dielectric constant ε(ω), refractive index n(ω), reflectivity R(ω), absorption coefficient α(ω), optical conductivity (ω) and energy loss function were also reported with the incident photon energy. The elastic constants were also calculated and used to determine mechanical properties like Young's modulus (Y), the shear modulus (G), Poisson's ratio (ν) and the anisotropic factor (A). The electrical conductivity (σ/τ) and Seebeck coefficient (S) also demonstrated the semiconducting nature of the compound with electrons as the majority carriers. The value of the power factor was calculated to be 1.20 × 1012 W K−2 m−1 s−1 at 1000 K. From thermodynamic investigations, the heat capacity and Grüneisen parameter were also predicted.
1. Introduction
Perovskites are a class of materials with rich diversity and have hence attracted researchers from all over the globe in the last decade. These materials are employed for novel applications like solid oxide fuel cells, perovskite fuel cells, spintronics applications, etc. Among these innovative materials, double perovskites have developed an important role. Double perovskite oxides have been widely utilized in the fields of thermoelectricity, solar energy conversion, transparent conductors, heterogeneous catalysts, pigments and photocatalysts. Double perovskite compounds were discovered in the early 1950s1 and they have remarkable properties and industrial applications.2–9 Advancements in computing power along with improvements in quantum modeling allow one to perform effective and precise quantum mechanical calculations and have thus overextended the calculating power to such an extent that those properties of materials which once looked impossible to determine can now be easily calculated with great precision.10–13 The present scenario with escalation in the industries and the increasing demand for natural resources to overcome the energy demands forces us to not only search for alternative energy sources but also reduce our energy consumption levels. Thermoelectric materials have received worldwide attention in their ability to convert waste heat into useful energy and hence are seen as forthcoming sources of green energy.14–17 At present, the world is in need of thermoelectric materials to decrease the dependence on vanishing fossil fuels. Perovskite materials with quite pleasing thermoelectric performance are represented as promising aspirants for thermoelectric devices.18–24 In recent years, double perovskites have received great attention as far as high-temperature thermoelectric investigations are concerned.25–27 Wide band gap materials have also been given attention for their high-temperature thermoelectric properties,28 and further, double perovskites have also been investigated for their electronic, thermoelectric, optical and magnetic properties using DFT.29–31Ba2InTaO6, an important member of the vast perovskite family, has not yet been investigated for its structural, elastic, mechanical, thermodynamic and thermoelectric properties. Lufaso et al.32 have investigated Ba2InTaO6 and found it to crystallize in an ordered cubic double perovskite structure with a lattice parameter of 8.2814 Å. Dutta et al.33 have theoretically investigated Ba2InTaO6 with respect to its electronic and optical properties. Hammink et al.34 have investigated Ba2InTaO6 under a different range of temperatures. They observed that the material has cubic symmetry, space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (225), a lattice constant of 8.282 Å with Ba atoms at 8c (1/4, 1/4, 1/4), In atoms at 4b (0.5, 0.5, 0.5), Ta cited at 4a (0, 0, 0) and O atoms at position 24e (x, 0, 0) of the unit cell where x = 0.2565. Zhou et al.35 have reported structural phase transition in Sr-doped Ba2InTaO6, using synchrotron X-ray and neutron powder diffraction techniques, where Ba2−xSrxInTaO6 underwent a series of phase transitions from cubic to monoclinic. Song et al.36 have also reported the ordered cubic structure in Ba2InTaO6. They further observed it as a wide band gap semiconductor with photocatalytic activity for overall water splitting under UV irradiation. Hence, as far as the literature is concerned, a systematic study on this compound within the most successful density functional theory (DFT)37,38 is absent.
m (225), a lattice constant of 8.282 Å with Ba atoms at 8c (1/4, 1/4, 1/4), In atoms at 4b (0.5, 0.5, 0.5), Ta cited at 4a (0, 0, 0) and O atoms at position 24e (x, 0, 0) of the unit cell where x = 0.2565. Zhou et al.35 have reported structural phase transition in Sr-doped Ba2InTaO6, using synchrotron X-ray and neutron powder diffraction techniques, where Ba2−xSrxInTaO6 underwent a series of phase transitions from cubic to monoclinic. Song et al.36 have also reported the ordered cubic structure in Ba2InTaO6. They further observed it as a wide band gap semiconductor with photocatalytic activity for overall water splitting under UV irradiation. Hence, as far as the literature is concerned, a systematic study on this compound within the most successful density functional theory (DFT)37,38 is absent.
Therefore, in the present work, an attempt has been made to investigate its electronic, elastic, mechanical, optical, thermoelectronic and thermodynamic properties within GGA39 and mBJ.40 The Quasi-harmonic Debye model41–43 was used for the investigation of pressure- and temperature-dependent thermodynamic behavior including specific heat, bulks modulus, volume, Grüneisen parameter, etc. Post-DFT Boltztrap code44 was employed for thermoelectric investigation. Therefore, the present investigation may provide important data for future experimental and theoretical investigations.
2. Computational methodology
To investigate the double perovskite Ba2InTaO6 with respect to its electronic, mechanical, thermal and thermoelectric properties, the full-potential linearized augmented plane-wave method (FP-LAPW)45 based upon density functional theory (DFT) as implemented in WIEN2K code37,38 was used. It has been found that Ba2InTaO6 crystallizes in the simple B1-phase (NaCl-type structure).32,34,36 In the unit cell, the position of 8c (0.25, 0.25, 0.25) is occupied by Ba atoms, Ta at 4b (0.5, 0.5, 0.5), In at 4a (0, 0, 0) and 24e (x, 0, 0) by O atoms where x = 0.2565.34 Optimization of the structure was achieved using generalized gradient approximation (GGA) scheme of Perdew, Burke and Ernzerhof (PBE),39 considering the ferromagnetic and paramagnetic phases. Furthermore, the electronic properties were also investigated within the modified Becke–Johnson (mBJ).40 For the convergence of energy, the multiplication of the atomic radius, RMT and k, vector was set to 7 (RMTKmax = 7), the angular moment Lmax was set to 10, and Gmax = 12 (a.u.)−1. To avoid any leakage of charge from the core, we used the RMT (muffin-tin radii) values of 2.60, 2.12, 2.10 and 1.63 for Ba, In, Ta and O, respectively. The convergence was considered when the total energy was stable within 0.001 Ry and the charge difference was less than 0.001e per a.u.3 per unit cell. The tetrahedron method46 was used to calculate the density of states with a mesh of 1000 K points in Brillouin-zone integration. Further, the Charpin method47 as integrated into the Wien2k package was used for elastic constant calculations. Furthermore, various thermodynamic parameters were generated using the Quasi-harmonic Debye model41–43 while tuning temperature and pressure.3. Results and discussion
3.1 Structural properties and electronic investigation
As stated above, the structure of Ba2InTaO6 is NaCl-type with an experimental lattice parameter value of 8.282 Å.34 The structural optimization based on Murnaghan's equation of state48 was performed to obtain a relaxed structure with minimum energy in the paramagnetic (PM) and ferromagnetic (FM) states. The obtained ground structure results including lattice parameters are summarized in Table 1. Our calculated values of the lattice parameters are slightly higher than the available experimental data. This is usually expected for GGA as it tends to overestimate the lattice parameters. The crystal structure and the optimization of Ba2InTaO6 were presented in Fig. 1(a and b), respectively. It has been found, as depicted in Fig. 1(b), that the E–V curves show a minimum energy in the paramagnetic (PM) state, and hence Ba2InTaO6 is stable in the PM state. The optimized ground state properties like the lattice constant (a0), bulk modulus (B0), and the pressure derivative of the bulk modulus (B′) were found to be very close to the available experimental and other theoretical data, which are summarized in Table 1. We have also calculated the bond lengths between Ba–O, In–O and Ta–O and when compared with the available experimental results34 as presented in Table 1, a good agreement is found.| Ba2InTaO6 | Present | Other |
|---|---|---|
| Lattice constant | 8.362 | 8.28 (ref. 32) |
| 8.70 (ref. 33) | ||
| 8.28 (ref. 34) | ||
| 8.29 (ref. 36) | ||
| Volume | 986.67 | — |
| B | 155 | 142 (ref. 33) |
| B′ | 4.58 | 4.64(ref. 33) |
| Ba–O | 2.93 | 2.92 (ref. 34) |
| ΔEH(kJ mol−1) | −2626.72 | |
| In–O | 2.13 | 2.11 (ref. 34) |
| Ta–O | 2.03 | 2.02 (ref. 34) |
| Bandgap | ||
| GGA (eV) | 4.0 | 4.17 (ref. 36) |
| 3.82 (ref. 49) | ||
| mBJ (eV) | 5.0 |
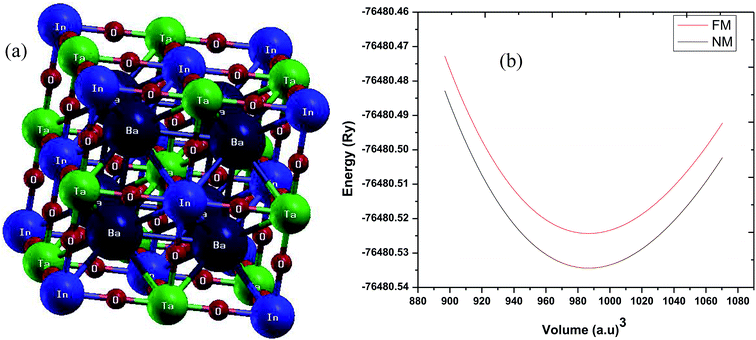 | ||
| Fig. 1 (a) Crystal structure of Ba2InTaO6; (b) calculated total energy as a function of volume for ferromagnetic (FM) and non-magnetic (NM) phases for Ba2InTaO6. | ||
To further verify the thermodynamic stability, we computed the enthalpy of formation (ΔH) by taking the energy difference between the compound and its individual atoms from the following equation:
| ΔH = Etotal(Ba2InTaO6) − aEBa − bEIn − cETa − dEO |
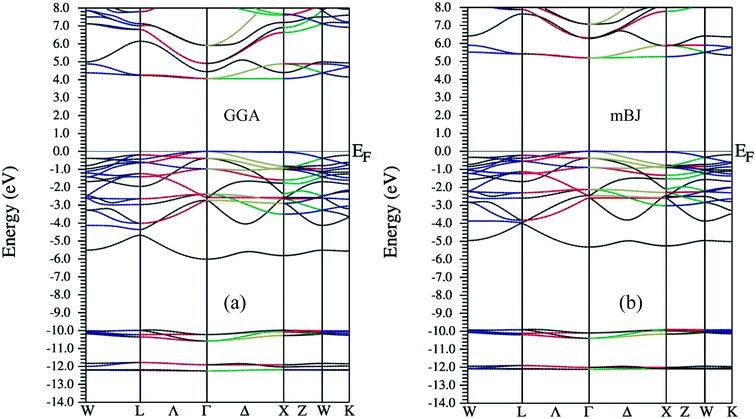
As far as electronic structure calculation of Ba2InTaO6 is concerned, it has been calculated along the high symmetry directions using GGA and mBJ in Fig. 2. Fig. 2(a and b) present the diagram of the band structures within GGA and mBJ exchange–correlation potentials, respectively. It is clear from the figures that the material presents semiconducting nature in both approximations. In GGA, the calculated value of the band gap is high and estimated to be 4.0 eV, while in mBJ it is somewhat higher (i.e., 5.15 eV). Lv et al.49 have reported Ba2InTaO6 as an important candidate for photocatalytic properties with a direct band gap observed at around 3.82 eV. So utilizing the mBJ potential, the band gap is overestimated. From the examination of band structure utilizing the PBE exchange–correlation potential, we see that it is a direct band gap semiconductor with a band gap of 4.0 eV, which is closer to the experimental value.49 The valance band maxima (VBM) and the conduction band minima (CBM) were found to lie on same symmetry point ‘Γ’ in both approximations, hence presenting the nature of the direct band gap. The direct band gap of both approximations with other theoretical and experimental results are listed in Table 1.
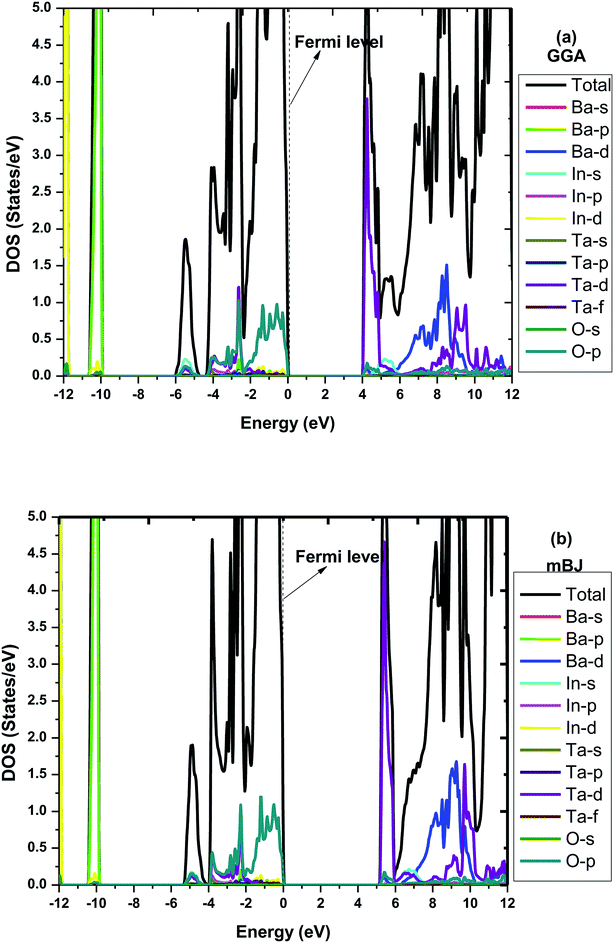
To make it more clear, we have plotted the combined total density of states (TDOS) and partial density of states (PDOS) within GGA and mBJ in the range of −12 to 12 eV as shown in Fig. 3(a and b), respectively. Both figures represent a wide band gap semiconducting nature. Here in these plots, we can also understand the elemental contribution to TDOS. The density of states contour indicates that the upper region of the valence band extending from 0 to −5 eV is predominantly occupied due to O p states with a small aggregate of Ta ‘d’ states, while the bands in the energy range of −10.3 eV to −10.0 eV are due to the Ba ‘p’ states. In the conduction band, the Ta ‘d’ states are responsible for the bands in the region of 2.5 eV to 4.8 eV. The bands occurring inside the higher energy level of the conduction band are due to the hybridization between the In ‘d’ states with a small aggregate of Ba and Ta ‘d’ states. The main contribution to the valance band in both GGA and mBJ is found from the Ba-p, In-d and O-p states, while for the conduction band, Ba-d and Ta-d are dominant and traces of In-s were also noticed. One can observe from the DOS plots that hybridization between the In-d and O-p states is present in the valance band close to the Fermi-level. These bands close to the Fermi-level were observed for both GGA and mBJ. The bands due to the Ba-d, Ta-d and O-p states present in the conduction band were observed to change with the application of mBJ. In case of GGA, these bands are present from 3.9 eV, hybridized with one another; however, in case of mBJ, these bands were found to shift towards a higher energy conduction band and were found at 4.5 eV, hence increasing the band gap. Therefore, both band structure and DOS show the wide band gap nature of the material.
3.2 Elastic and mechanical properties
Elastic and mechanical properties of materials, particularly manufacturing materials become important, where materials are subjected to forces both during fabrication and processing. In this context, it becomes necessary to know how atom-to-atom bonding and further mechanical stability can also be defined. We have, therefore, investigated elastic constants (C11, C12, C44) under ambient conditions for Ba2InTaO6. The elastic constants were calculated by the Thomas Charpin method.47 The existence of the crystal isn't possible in the stable or meta-stable state unless its elastic constants obey the generalized mechanical stability criteria.50 Our calculated values of the elastic constants and Bulk moduli properly follow the cubic stability criteria. From the values of the elastic constants, mechanical properties like Young's modulus (Y), which presents the strength of the material; the bulk modulus (B), which describes the stiffness of a material, higher the value of B, the higher its stiffness resistance is; and the shear modulus (G), which describes the calculated plastic twist of a material. The value of the shear modulus (G) has been obtained from the Voigt–Reuss–Hill approximation51,52 using GV and GR and is presented in Table 2. One can find the physical formula to calculate GV and GR in ref. 42. The obtained value of the shear modulus is 88.24 GPa, which is small, meaning that the compound shows less plastic twist.| GGA | Ba2InTaO6 |
|---|---|
| C11 | 282.67 |
| C12 | 91.39 |
| C44 | 85.22 |
| B | 155 |
| GV | 89.38 |
| GR | 89.10 |
| G | 89.24 |
| Y | 224.64 |
| ν | 0.2587 |
| B/G | 1.73 |
| C12–C44 | 6.13 |
| A | 0.891 |
| Tm | 2223 ± 300 |
The value of Young's modulus (Y) was obtained from the bulk modulus (B) and the shear modulus (G).42 As Y deals with the strength of the material, the higher the value of Y, the higher its strength is. The obtained value of Y was calculated to be 224.64 GPa, which is large enough, and hence, Ba2InTaO6 behaves as a hard material. Another parameter anisotropic factor A42,53 was also calculated and found to be 0.891 (less than 1), signifying that the material has elastic anisotropic nature.
In order to define the ductile or brittle behavior of Ba2InTaO6, we obtained the B/G ratio, which was calculated to be 1.73, and according to Pugh,54 the B/G ratio is near to 1.75 in value and shows a ductile nature. An estimation of ductility and brittleness can also be obtained from the Cauchy pressure value (C12–C44); positive values characterize a material as ductile and negative values as brittle. From the information in Table 2, it is clear that the Cauchy's pressure is positive for Ba2InTaO6, which emphasize its ductile nature. Poisson's ratio ‘ν’ is another rule utilized for determining the ductility and brittleness of a compound. If its value is greater than 0.26, the material possesses ductile nature; otherwise, the material is considered to be brittle. Table 2 shows that Poisson's ratio for Ba2InTaO6 is close to 0.26, which confirms its ductile nature. Poisson's ratio ‘ν’ also gives knowledge about the bonding forces available in solid materials. For central force solids, Poisson's ratio has a range of 0.25 to 0.5.55 From the data in Table 2, it is clear that our computed Poisson's ratio lies in this range, implying that the bonding forces are of central types. As per our insight, no theoretical or experimental data exist in the literature on this compound for elastic properties to which we can compare our work. We believe that our work can stimulate further research in this direction in the future.
We have also obtained the melting temperature of the compound56 equal to 2223 ± 300 K under ambient conditions from the elastic constant values by using the following equation:
| Tm (K) =[553 (K) + (5.911)C12] GPa ± 300 K |
The computed values of the elastic constants, mechanical properties and melting temperature are grouped in Table 2.
3.3 Optical properties
Motivated by the prospect of using its interesting electronic structure for optoelectronic semiconductor applications, the optical and electronic transport properties of the double perovskite oxide Ba2InTaO6 were studied. The frequency-dependent optical properties were studied and calculated through the dielectric functions.57,58 It was realized that the optical properties of a solid can be portrayed by the complex dielectric work ε(ω), which has two sections, real and imaginary, and can be communicated as:| ε = ε1(ω) + iε2(ω) |
The imaginary part ε2(ω), which arises from interband and intraband transitions, shows the possible transitions from the occupied to unoccupied states with fixed (k-vectors) over the Brillouin zone (BZ), which are dependent on density of states (DOS) and the momentum matrix P; it can be mathematically defined as:
where p implies the principal value of the integral.
The reflectance can be calculated using the relation:
The absorption coefficient (α) can be deduced from the dielectric function as given below:
The real and imaginary parts of the dielectric function allow us to obtain some important optical parameter like the refractive index n(ω) and the extinction coefficient k(ω).
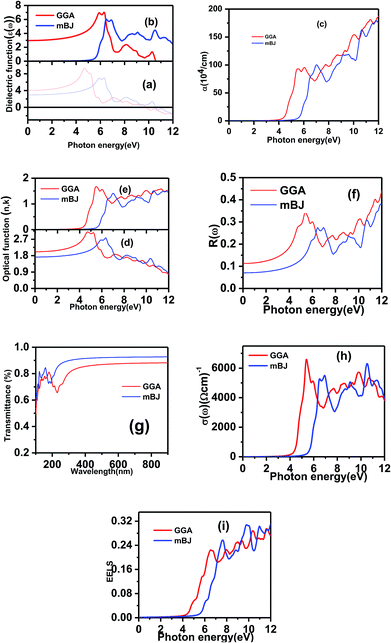
In this work, we focused on the optical parameters such as dielectric function, absorption coefficient α(ω), energy loss spectrum L(ω), reflectivity R(ω) and refractive coefficient, which can be obtained from ε1(ω) and ε2(ω). The optical calculations of Ba2InTaO6 were presented in Fig. 4(a–i) as follows: Fig. 4(a) and (b) for the dielectric function, Fig. 4(c) for the absorption spectra, Fig. 4(d and e) for the refractive coefficient, Fig. 4(f) for reflectivity, Fig. 4(g) for the transmittance spectra, Fig. 4(h) for optical conductivity and Fig. 4(i) for the energy loss function.
The compound under investigation Ba2InTaO6 has cubic symmetry. We have the principal tensor component εxx = εyy = εzz for cubic symmetry; therefore, we have calculated only one component of the complex dielectric function. As shown in Fig. 4(a), static dielectric constants ε1(0) of Ba2InTaO6 are 4.07 (GGA), 2.97 (mBJ). After reaching maximum values, it starts to decrease and flattens with few variations. In the energy range of 0–9.8 eV (GGA), 0–10.57 eV (mBJ), ε1(ω) is shown to be positive due to the semiconductor nature, while in the energy range of 9.8 to 12 eV (GGA), 10.57 to 12 (mBJ), the ε1(ω) value is negative, which shows the characteristics of the metal due to the transition of the Ta-5d electrons.
The imaginary part ε2(ω) of the dielectric function in Fig. 4(b) shows the principal peak of the optical critical point at 7.06 (GGA), 6.09 (mBJ), with the corresponding energy range 6.30 eV (GGA), 6.47 eV (mBJ) arising due to the transition between some noticeable peaks located at 5.90 eV, 8.15 eV, and 10.26 eV (GGA); for mBJ, these peaks are located at 6.90 eV, 9.07 eV, and 10.50 eV. The threshold point of optical direct transition corresponding to the Xv − Xc splitting (among the lowest conduction band and the highest valence band) is recognized as the absorption edge. Above this threshold point, with the increase in energy, we have seen that the curve increases instantaneously due to the real part ε2(ω) of the dielectric function. The transition between the occupied states of the valence region to the unoccupied states of the conduction region arise due to rapid peak in the optical spectrum. The density of states defined by the origin of these peaks lies in the interband transition. For mBJ as compared to GGA, the principal peak of the real and imaginary parts shifts due to the increase in energy.
In Fig. 4(c), we have shown the absorption coefficient, which is represented as the attenuation percentage of light intensity that propagates per unit distance in a material. The shape of the absorption spectrum is quite similar to the peak of the imaginary part ε2(ω) of the complex dielectric function, showing that through the linear absorption spectra originating from the imaginary parts of the electronic dielectric function, we found peaks at the energies of 4.5 eV (GGA), 5.7 eV (mBJ); 5.1 eV (GGA), 7.02 eV (mBJ); 6.8 eV (GGA), 7.9 eV (mBJ) and 7.8 eV (GGA), 8.6 eV (mBJ). At the lower energy range from 0 to 4 eV, there is no absorption, meaning that the material is transparent from the partially ultra-violet to the visible light area due to the phonon energy within the forbidden band. The absorption region is more stretched towards high energy for mBJ as compared to GGA. As we can see from the absorption spectra, as the energy decreases, the absorption coefficient decreases rapidly, which shows the behavior of common semiconductors. In general, the differences among the propagation of an electromagnetic wave via vacuum and some different material may be described as N(ω) = n(ω) + ik(ω). The computed refractive index profile and the extinction coefficient of Ba2InTaO6 are displayed in Fig. 4(d). As can be seen, the refractive index increases with increasing energy and reaches a maximum. The same can be observed for the dielectric characteristic function, and these are associated with the relation n(0) = √ε(0); the static refractive index n(0) was found to have the value 2.01 (0.05 eV) (GGA), 1.72 (0.043 eV) (mBJ) as can be seen from Fig. 4(d). The same value was calculated via n(0) = √ε(0) = 2.0 (GGA), 1.72 (mBJ). The principal peak of the refractive index occurs at 3.12 (4.70 eV) for GGA, 2.76 (6.35 eV) for mBJ. The nature of the refractive index and dielectric function are both the same. The variation of the extinction coefficient k(ω) as a function of photon energy is shown in Fig. 4(e). From the extinction coefficient k(ω) spectrum, we determined that the k(ω) of Ba2InTaO6 increases with energy in the transparent region and reaches a maximum value. The k(ω) was found to have the highest value at 5.48 eV (GGA), 1.52 eV (mBJ), which indicated that absorption is also notable at about 5.48 eV (GGA), 1.52 eV (mBJ).
The computed reflectivity spectrum R(ω) as shown in Fig. 4(f) shows that the zero frequency limit of reflectivity R(ω) was found to be 0.11 for (GGA) and 0.07 for (mBJ). The most illustrated reflection peaks at energies for GGA are 5.39 eV, 7.73 eV, 8.70 eV, 10.08 eV, 11.48 eV and for mBJ are 6.45 eV, 6.95 eV, 9.11 eV, 10.70 eV corresponding to the negative values of ε1(ω), which shows that there is a highest value of reflectivity due to the interband transition. The plot of the transmittance versus wavelength is presented in Fig. 4(g); as can be seen from the figure, Ba2InTaO6 has high transparency in the visible and IR region due to the wide band gap, while the transmittance has a lower value. Considerable variation arises from the enlarged optical band gap and reflectivity in the UV region. The transmittance of GGA becomes larger than the mBJ in the UV region; however, for IR and the visible light region, mBJ shows a larger transmittance than GGA. The average optical transmittance of Ba2InTaO6 is 86% (GGA) and 91% (mBJ), respectively. Thus, this double perovskite Ba2InTaO6 in its structure acts transparently in the visible light region and absorbent in the ultraviolet region.
The calculated real part of the optical conductivity profile is depicted in Fig. 4(h). As shown in the figure, it can be seen that the first transition located at the energies of 6617.26 (5.34 eV), 5300.68 (6.48 eV) for GGA and mBJ, respectively, arises in the Γ direction of the Brillouin zone. The second transition occurs from an sp transition. The electron energy-loss function (ELF) defines interactions such as interband, intraband and plasmon. The energy which is lost by a fast-moving electron while travelling through the material is ELF. The ELF is computed and depicted in Fig. 4(i). It can be seen that the maximum energy loss function L(ω) with GGA occurs at 0.29 (11.66), whereas for mBJ, the maximum energy loss function occurs at 0.31 (9.75 eV); the abrupt reduction of reflectivity spectrum arises due to the sharp peak of the energy loss spectrum. There is no loss in the region from 0 to 4 eV (GGA) and 0 to 5 eV (mBJ). The computed results for the optical properties of Ba2InTaO6 are in accordance with the results of the optical properties measured by Zurmuhlen et al.59
The computed value of the real part of the dielectric function ε(0), the refractive index n(0), the extinction coefficient k(ω), reflectivity R(0), the optical absorption coefficient α(ω), the real part of optical conductivity σ(ω) and the energy-loss function L(ω) for the double perovskite Ba2InTaO6 are tabulated in Table 3.
| Optical properties | Ba2InTaO6 | |
|---|---|---|
| GGA | ε1(0) | 4.05 |
| α(ω) | 4.35 | |
| n(0) | 2.01 | |
| k(ω) | 1.67 | |
| R(0) | 0.11 | |
| σ(ω) (Ω cm)−1 | 6630.15 | |
| mBJ | ε1(0) | 2.94 |
| α(ω) (eV) | 5.56 | |
| n(0) | 1.71 | |
| k(ω) | 1.51 | |
| R(0) | 0.07 | |
| σ(ω) (Ω cm)−1 | 6378.86 | |
3.4 Thermoelectric properties
To investigate the transport of the belongings of the double perovskite oxide Ba2InTaO6, we have employed semi-classical Boltzmann theory and the rigid band approach as implemented in the BoltzTraP code44 interface with the Wien2K program. It peruses from these approaches that the dependence of the conductivity on transport distribution is:The k-dependent transport tensor is given as:
| σα,β(i, k) = e2τi,kνα(i, k)νβ(i, k) |
In the above equation, i, k and τ, να(i, k) and e express the band index, wave vector, relaxation time, the group velocities and the electron charge, respectively.
By integrating the transport distribution over energy, the electrical conductivity can be expressed as a function of temperature, T, and also the chemical potential, μ, via the subsequent equations:
The complexity of the carrier scattering mechanisms in the solid arises from the relaxation time considered as the energy-independent constant. For evaluating the electrical transport properties, the above approach has been already tested on distinct compounds shown to be a reasonable approximation.
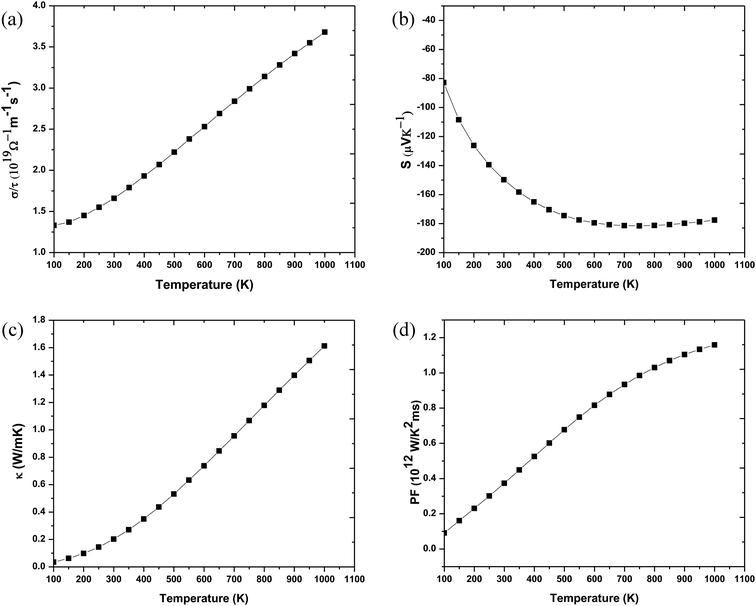
For a material to have efficient thermoelectric properties, it is mandatory to have high electrical conductivity, a large Seebeck coefficient and low thermal conductivity. Perovskites have received great attention as thermoelectric materials in the recent past. The thermoelectric properties like electrical conductivity (σ/τ), where τ is the relaxation time, the Seebeck coefficient (S), electronic thermal conductivity (κe/τ) and the power factor (PF) were calculated. Fig. 5(a) presents the temperature variation of electrical conductivity (σ/τ) for Ba2InTaO6. The value of σ/τ does not vary much up to room temperature; it later increases with increasing temperature above room temperature. The increasing character of σ/τ suggests that the material should behave as a semiconductor. The value of σ/τ was found to increase from a small value of 1.33 × 1019 (Ω−1 m−1 s−1) at 50 K to 3.75 × 1019 (Ω−1 m−1 s−1) at 1000 K. The Seebeck coefficient (S) for the compound as a function of temperature is depicted in Fig. 5(b). It was seen from the plot that the calculated values of the (S) is negative in the complete temperature range; therefore, it suggests the presence of electrons as charge carriers. The value of S decreases from −76 μV K−1 at 50 K to −180 μV K−1 at 700 K and then again starts to increase smoothly upon a further increase in temperature. Fig. 5(c) depicts the response of thermal conductivity within 100 K and 1000 K for Ba2InTaO6. The figure clearly presents the increasing nature of thermal conductivity with respect to a temperature similar to the variation of the electrical conductivity plot. With the increase of temperature the value of (Ke/τ) increases progressively from a very low value of 0.03 × 1015Ω−1 m−1 s−1 at 100 K to 1.61 × 1015 Ω−1 m−1 s−1 at 1000 K. The power factor (PF) is one of the significant parameters for evaluating the efficiency of a material for thermoelectric applications; it is actually the product of the Seebeck coefficient and electrical conductivity. Fig. 5(d) shows the variation of the calculated power factor with the temperature, showing that the power factor increases from 0.09 × 1012 W K−2 m−1 s−1 at 100 K to 1.20 × 1012 W K−2 m−1 s−1 at 1000 K. The pleasant value of the power factor implied that the Ba2InTaO6 material could possibly be a convenient material for high-temperature thermoelectric applications.
3.5 Thermodynamic properties
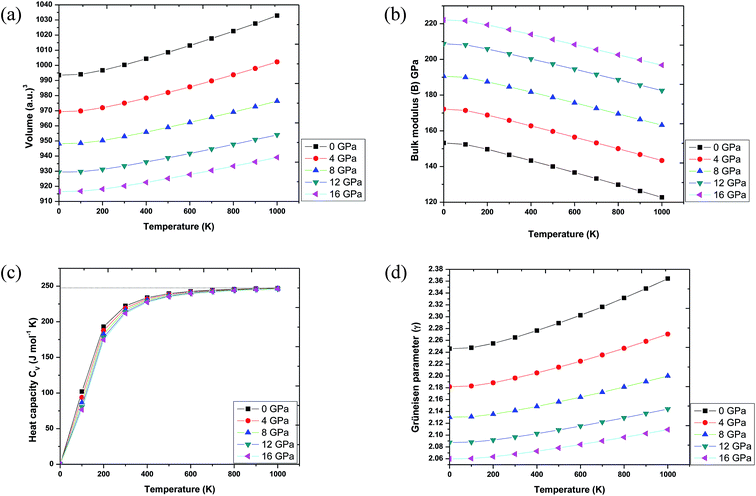
In order to make Ba2InTaO6 a suitable material for device fabrications and other industrial applications, we have calculated various thermodynamic variables under temperature (0 K to 1000 K) and pressure (0 GPa to 16 GPa) using the quasi-harmonic Debye model.41–43 These thermodynamic variables like volume (V), bulk moduli (B), specific heat at constant volume (Cv) and Grüneisen parameter (γ) were computed for Ba2InTaO6. Fig. 6(a) presents the variation in unit cell volume as a function of temperature and pressure. It can be clearly seen from the figure that cell volume increases with increasing temperature for a particular pressure value; on the other hand, it decreases with increasing pressure for a particular temperature value. Such behavior is quite general in solids, and one can understand that pressure compresses a solid, while temperature provides expansion. Fig. 6(b) shows the variation of bulk modulus under temperature and pressure. It is quite clear from the figure that the variation of the bulk modulus under temperature and pressure has the opposite effect, as noticed in the case of variation of volume under temperature and pressure. According to Fig. 6(b), the bulk modulus increases with increasing pressure and decreases with increasing temperature. One can understand the reason for such an increase or decrease in the B value with pressure and temperature that temperature reduces the hardness, while pressure increases it. Secondly, with increasing temperature, the unit cell volume increases and the interatomic distance also increases, while pressure has the reverse effect.Further, the specific heat at a constant volume (CV), which provides information about the lattice vibration, phase transition and measures the motion of molecules, was calculated, and its variation with temperature and pressure is depicted in Fig. 6(c). From Fig. 6(c), one can see that the CV increases rapidly under lower temperature values of 0 to 400 K. Above 400 K, a lethargic increase in CV can be observed, which further becomes constant at a temperature of 700 K and reaches the famous Dulong–Petit limit.60 The value of CV for Ba2InTaO6 at 300 K and 0 GPa was found to be 222.29 J mol−1 K−1. The calculated value of CV under ambient conditions may serve as valuable data for experimental studies. The Grüneisen parameter (γ) expresses the anharmonicity in the crystal and was used to deduce the thermodynamic properties of the material under a high temperature and pressure. It also describes the temperature and pressure dependence of phonon frequencies or vibrational frequencies.61 We have, therefore, calculated the pressure and temperature dependence of γ for Ba2InTaO6 for the first time and is shown in Fig. 6(d). The value of γ increases slowly with increasing temperature and decreases with increasing pressure. The calculated value of γ under ambient conditions was found to be 2.26, which is in the order of the reported value of Ba2MgReO6.62
4. Conclusion
We summarized the present work by combining ab initio density functional theory, quasi-harmonic Debye model and the Post-DFT Boltztrap code used for the investigation of electronic structure as well as the elastic, mechanical, optical, thermoelectric and thermodynamic properties of the double perovskite Ba2InTaO6. The calculated electronic properties showed Ba2InTaO6 to be a semiconductor, and a direct band due to the lowest energy in the conduction region and the highest band within the valence region present on the same X−X symmetry point. There is a strong hybridization between the d states of Ba and Ta and the 2p states of oxygen, which mainly contribute to the electrical properties. By considering the elastic constant and mechanical calculations, the material was found to be mechanically stable and showed ductile and anisotropic nature. The large value of Young's modulus indicated that the material could serve as an important candidate for the manufacture of ultra-hard materials. Furthermore, by using the quasi-harmonic Debye model, the pressure and temperature dependence of thermodynamic parameters such as the volume, bulk moduli, heat capacity (Cv) at constant volume and the Grüneisen parameter (γ) in the range 0–16 GPa and 0–1000 K are also projected and provide a possible future scope for suitable applications. The optical properties conjointly advocate the prominent utilization of Ba2InTaO6 in optical devices. It was found from the electronic band profile that the material had a wide band gap and was hence an important candidate for thermoelectric properties. Finally, thermoelectric properties like electrical conductivity (σ/τ), the Seebeck coefficient (S) and the power factor (PF) for Ba2InTaO6 were also reported for the first time. The pleasant value of the power factor implied that the material could also be used in thermoelectric devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful to Prof. P. Blaha for the Wien2k code.References
- M. T. Anderson, K. B. Greenwood, G. A. Taylor and K. R. Poeppelmeier, Prog. Solid State Chem., 1993, 22, 197 CrossRef CAS.
- T. Nakagawa, J. Phys. Soc. Jpn., 1968, 24, 806 CrossRef CAS.
- M. Fiebig, T. Lottermoser, D. Frohlich, A. V. Goltsev and R. V. Pisarev, Nature, 2002, 419, 818 CrossRef CAS PubMed.
- K. I. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Nature, 1998, 395, 677 CrossRef CAS.
- H. Das, M. De Raychaudhury and T. Saha-Dasgupta, Appl. Phys. Lett., 2008, 92, 201912 CrossRef.
- T. Aharen, J. E. Greedan, C. A. Bridges, A. A. Aczel, J. Rodriguez, G. MacDougall, G. M. Luke, T. Imai, V. K. Michaelis, S. Kroeker, H. Zhou, C. R. Wiebe and L. M. D. Cranswick, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 224409 CrossRef.
- C. R. Wiebe, J. E. Greedan, G. M. Luke and J. S. Gardner, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 144413 CrossRef.
- M. A. de Vries, A. C. Mclaughlin and J.-W. G. Bos, Phys. Rev. Lett., 2010, 104, 177202 CrossRef CAS PubMed.
- J. P. Carlo, J. P. Clancy, T. Aharen, Z. Yamani, J. P. C. Ruff, J. J. Wagman, G. J. Van Gastel, H. M. L. Noad, G. E. Granroth, J. E. Greedan, H. A. Dabkowska and B. D. Gaulin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 100404 CrossRef.
- D. R. Bowler, J. Phys.: Condens. Matter, 2016, 28, 421001 CrossRef CAS PubMed.
- J. C. Smith, F. Sagredo and K. Burke, 2017, arxiv:1701.00873.
- N. Crouseilles, P.-A. Hervieux and G. Manfredi, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 155412 CrossRef.
- A. Becker, W. Lorenzen, J. J. Fortney, N. Nettel-mann, M. Schttler and R. Redmer, Astrophys. J., Suppl. Ser., 2014, 215, 21 CrossRef.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105 CrossRef CAS PubMed.
- B. G. Levi, Phys. Today, 2014, 67, 14 Search PubMed.
- X. Zhang and L.-D. Zhao, Journal of Materiomics, 2015, 1, 92 CrossRef.
- A. D. LaLonde, Y. Pei, H. Wang and G. J. Snyder, Materials Today, 2011, 14, 526 CrossRef CAS.
- P. V. Arribi, P. Garcıa-Fernandez, J. Junquera and V. Pardo, Phys. Rev. B, 2016, 94, 035124 CrossRef.
- M. Saxena and T. Maiti, Scr. Mater., 2018, 155, 85 CrossRef CAS.
- A. I. Hochbaum, Nature, 2008, 451, 163 CrossRef CAS PubMed.
- P. Roy, I. Bose and T. Maiti, Integr. Ferroelectr., 2016, 174, 34 CrossRef CAS.
- L. E. Bell, Science, 2008, 321, 1457 CrossRef CAS PubMed.
- M. Akasaka, T. Iida, A. Matsumoto, K. Yamanaka, Y. Takanashi, T. Imai and N. Hamada, J. Appl. Phys., 2008, 104, 013703 CrossRef.
- S. Chen and Z. Ren, Materials Today, 2013, 16, 10 CrossRef.
- M. H. Aguirre, D. Logvinovich, L. Bocher, R. Robert, S. G. Ebbinghaus and A. Weidenkaff, Acta Mater., 2009, 57, 108 CrossRef CAS.
- P. Roy, I. Bose and T. Maiti, Integr. Ferroelectr., 2016, 174, 34 CrossRef CAS.
- M. Saxena and T. Maiti, Ceram. Int., 2018, 44, 2732 CrossRef CAS.
- B. Kucukgok, Q. He, A. Carlson, A. G. Melton, I. T. Ferguson and N. Lu, Symposium B – Thermoelectric Materials Research and Device Development for Power Conversion and Refrigeration, 2013, vol. 1490, p. 161 Search PubMed.
- B. Rameshe, M. Rajagopalan and B. Palanivel, Computational Condensed Matter, 2015, 4, 13 CrossRef.
- D. P. Rai, A. Shankar, M. P. Ghimire, Sandeep and R. K. Thapa, Comput. Mater. Sci., 2015, 101, 313 CrossRef CAS.
- M. H.-E. Musa Saad and A. Elhag, Results Phys., 2018, 9, 793 CrossRef.
- M. W. Lufaso, P. W. Barnes and P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 397 CrossRef PubMed.
- A. Dutta and T. P. Sinha, Solid State Commun., 2010, 150, 1173 CrossRef CAS.
- T. S. Hammink, W. T. Fu and D. J. W. IJdo, J. Solid State Chem., 2011, 184, 848 CrossRef CAS.
- Q. Zhou, T.-Y. Tan, B. Kennedy and J. R. Hester, J. Solid State Chem., 2013, 206, 122 CrossRef CAS.
- K. Song, J. Yang, P. Jiang, W. Gao, R. Cong and T. Yang, Eur. J. Inorg. Chem., 2015, 5786 CrossRef CAS.
- K. Schwarz, P. Blaha and G. K. H. Madsen, Comput. Phys. Commun., 2002, 147, 71 CrossRef.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kuasnicke and J. Luitz, Introduction to WIEN2K, An Augmented plane wave plus local orbitals program for calculating crystal properties, Vienna university of technology, Vienna, Austria, 2001 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- M. A. Blanco, A. M. Pendas and E. J. Francisco, J. Mol. Struct.: THEOCHEM, 1996, 268, 245 CrossRef.
- S. A. Dar, V. Srivastava and U. K. Sakalle, J. Electron. Mater., 2017, 46, 6870 CrossRef CAS.
- A. Otero-de-la-Roza and V. Luaea, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 184103 CrossRef.
- G. K. Madsen and D. J. Sing, Comput. Phys. Commun., 2006, 175, 67 CrossRef CAS.
- Z. Wu and R. E. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235116 CrossRef.
- P. E. Blochl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49 23, 16223 CrossRef.
- T. Charpin, A Package for Calculating elastic tensors of cubic phases using WIEN, Laboratory of Geometrix F-75252, Paris, France, 2001 Search PubMed.
- F. Birch, Phys. Rev., 1947, 71, 809 CrossRef CAS.
- M. Lv, Y. Wang, L. Lu, R. Wang, S. Ni, G. Liuc and X. Xu, Phys. Chem. Chem. Phys., 2016, 18, 21491 RSC.
- G. V. Sinko and N. A Smirnov, J. Phys.: Condens. Matter, 2002, 14, 6989 CrossRef CAS.
- R. Hill, Proc. Phys. Soc., London, 1952, 65, 349 CrossRef.
- A. Reuss, Z. Angew. Math. Mech., 1929, 9, 49 CrossRef CAS.
- T. Vergaard and J. W. Hutchinson, J. Am. Ceram. Soc., 1988, 71, 157 CrossRef.
- S. F. Pugh, Philos. Mag., 1954, 45, 823 CAS.
- G. N. Greaves, A. L. Greer, R. S. Lakes and T. Rouxel, Nat. Mater., 2011, 10, 823 CrossRef CAS PubMed.
- S. A. Dar, V. Srivastava, U. K. Sakalle and V. Parey, Eur. Phys. J. Plus, 2018, 131, 64 CrossRef.
- C. Ambrosh-Draxl and J. O. Sofo, Comput. Phys. Commun., 2006, 175, 1 CrossRef.
- P. E. Blochl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223 CrossRef CAS.
- R. Zurmuhlen, J. Petzelt, S. Kamba, V. V. Voitsekhovskii, E. Colla and N. Setter, J. Appl. Phys., 1995, 77, 5341 CrossRef.
- A. T. Petit and P. L. Dulong, Ann. Chim. Phys., 1819, 10, 395 Search PubMed.
- L. Quiang, H. Duo-Hui, C. Qi-Long and W. Fan-Hou, Chin. Phys. B, 2013, 22, 037101 CrossRef.
- S. A. Dar, V. Srivastava, U. K. Sakalle and G. Pagare, Computational Condensed Matter, 2018, 14, 137–143 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |