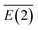Open Access Article
Open Access ArticleStructural evolution of LiNn+ (n = 2, 4, 6, 8, and 10) clusters: mass spectrometry and theoretical calculations†
Zhongxue Ge*ab,
Kewei Ding ab,
Yisu Lic,
Hongguang Xud,
Zhaoqiang Chenc,
Yiding Ma
ab,
Yisu Lic,
Hongguang Xud,
Zhaoqiang Chenc,
Yiding Ma b,
Taoqi Lib,
Weiliang Zhu*c and
Weijun Zheng
b,
Taoqi Lib,
Weiliang Zhu*c and
Weijun Zheng *d
*d
aState Key Laboratory of Fluorine & Nitrogen Chemicals, Xi'an 710065, China
bXi'an Modern Chemistry Research Institute, Xi'an 710065, China. E-mail: gzx204@sina.com.cn
cDrug Discovery and Design Center, Shanghai Institute of Materia Medica, Chinese Academy of Sciences, Shanghai 201203, China. E-mail: wlzhu@mail.shcnc.ac.cn
dBeijing National Laboratory for Molecular Sciences (BNLMS), State Key Laboratory of Molecular Reaction Dynamics, Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, China. E-mail: zhengwj@iccas.ac.cn
First published on 26th February 2019
Abstract
Mixed nitrogen-lithium cluster cations LiNn+ were generated by laser vaporization and analyzed by time-of-flight mass spectrometry. It is found that LiN8+ has the highest ion abundance among the LiNn+ ions in the mass spectrum. Density functional calculations were conducted to search for the stable structures of the Li–N clusters. The theoretical results show that the most stable isomers of LiNn+ clusters are in the form of Li+(N2)n/2, and the order of their calculated binding energies is consistent with that of Li–N2 bond lengths. The most stable structures of LiNn+ evolve from one-dimensional linear type (C∞v, n = 2; D∞h, n = 4), to two-dimensional branch type (D3h, n = 6), then to three-dimensional tetrahedral (Td, n = 8) and square pyramid (C4v, n = 10) types. Further natural bond orbital analyses show that electrons are transferred from the lone pair on Nα of every N2 unit to the empty orbitals of lithium atom in LiN2–8+, while in LiN10+, electrons are transferred from the bonding orbital of the Li–Nα bonds to the antibonding orbital of the other Li–Nα bonds. In both cases, the N2 units become dipoles and strongly interact with Li+. The average second-order perturbation stabilization energy for LiN8+ is the highest among the observed LiNn+ clusters. For neutral LiN2–8 clusters, the most stable isomers were also formed by a Li atom and n/2 number of N2 units, while that of LiN10 is in the form of Li+(N2)3(η1-N4).
1 Introduction
Nitrogen clusters have been predicted to be potential high energy density materials (HEDM)1,2 by numerous theoretical3,4 studies. Since the identification of N5+, N4, and N5−,5–7 the search for new polynitrogen species by a variety of experimental techniques has received intense attention. However, only a few efforts have been successful due to the low stability of these clusters. Metal doped nitrogen clusters MNn have advantages in designing new polynitrogen structural groups because the metal–nitrogen interactions may be able to stabilize polynitrogen groups in MNn with respect to the corresponding isolated Nn species.8 Many novel polynitrogen structural groups such as cyclic N4,9–12 N5,13 N6,14 and N7 (ref. 15) have been predicted to exist in this form. Thus, it is interesting to generate metal-doped nitrogen clusters, gradually increase their nitrogen content and study their structural characteristics.To date, extensive experimental works have been undertaken to investigate mixed nitrogen–metal clusters. Numerous homoleptic azides of the type M(N3)n (M = Ti, Nb, Ta, Mo, W, etc.)16–27 and their derived salts have been prepared and characterized to understand the properties of highly energetic materials. Nb+(N2)n and V+(N2)n complexes were investigated using photodissociation spectroscopy.28,29 Rh(N2)4+ complexes were studied by infrared laser photodissociation spectroscopy and theoretical calculations.30 TiN12+ was generated by laser ablation, and the most stable structure was found to be Ti(N2)6+ with Oh symmetry.31 The VNn+ (n = 8, 9, and 10) clusters were generated and their most stable isomers were found to be in the form of V(N2)4+, (η2-N4)V+N(N2)2 and (η4-N4)V+(N2)3, respectively.32
Lithium is the lightest metal. It is highly reactive and can react with nitrogen gas to form lithium nitride.33 In addition, lithium atoms have been successfully used as dopants in many clusters, such as silicon,34 germanium,35 boron36 and aluminum37 clusters, to tailor their structural and electronic properties. Although the experimental studies on lithium-doped nitrogen clusters were very scarce, these clusters have been investigated in preliminary studies by many theoretical calculations. Cheng and Li predicted that lithium and N42− ring could form bipyramidal Li2N4 structures38 with significant barriers for isomerization and dissociation. Glukhovtsev and Schleyer studied the structure and stability of N5Li and found that N5Li favours a planar C2v structure.39 Investigation of lithium–nitrogen clusters may provide useful information for understanding the lithium–nitrogen interactions and for the design of high nitrogen content species.
In this work, we investigated lithium–nitrogen binary clusters by laser ablation experiments coupled with theoretical calculations to gain insights into the geometric structures and electronic properties of LiNn+ and their neutral counterparts.
2 Experimental and theoretical methods
2.1 Experimental method
The experiments were conducted using a home-built apparatus equipped with a laser vaporization supersonic cluster source and a reflectron time-of-flight mass spectrometer (RTOF-MS) that has been described elsewhere.40 The laser vaporization source was cooled by liquid nitrogen. The disk targets made of LiCl, LiF, LiF/ZrN (mole ratio 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), LiF/AlN (mole ratio 2
1), LiF/AlN (mole ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) or LiF/BN (mole ratio 2
1) or LiF/BN (mole ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) were used in the experiments to provide Li+ ions. The LiNn+ (n = 2, 4, 6, 8, and 10) cluster cations were generated in the laser vaporization source by laser ablation the rotating and translating disk targets in N2 gas with the second harmonic of a nanosecond Nd:YAG laser (Continuum Surelite II-10). Nitrogen carrier gas with ∼4 atm backing pressure was allowed to expand through a pulsed valve (General Valve Series 9) into the source to provide nitrogen and to cool the formed clusters. The typical laser power used in this work was approximately 10 mJ per pulse. The generated cluster cations were mass-analysed by the RTOF-MS.
1) were used in the experiments to provide Li+ ions. The LiNn+ (n = 2, 4, 6, 8, and 10) cluster cations were generated in the laser vaporization source by laser ablation the rotating and translating disk targets in N2 gas with the second harmonic of a nanosecond Nd:YAG laser (Continuum Surelite II-10). Nitrogen carrier gas with ∼4 atm backing pressure was allowed to expand through a pulsed valve (General Valve Series 9) into the source to provide nitrogen and to cool the formed clusters. The typical laser power used in this work was approximately 10 mJ per pulse. The generated cluster cations were mass-analysed by the RTOF-MS.
2.2 Theoretical methods
The geometry optimization and frequency calculations were performed with Gaussian 09 program package using density functional theory (DFT) at the M06-2X/6-311+G(d,p) level.41–43 Every stationary point on the potential energy surface (PES) was confirmed to be local minimum-energy structure by all positive harmonic frequencies. The bond length of the N2 molecule was calculated to verify the accuracy of the theoretical method. The calculated N–N bond length is about 1.090 Å, which is consistent with an experimental value of 1.097 Å.44 The binding energies of nitrogen to Li+/0 were calculated for each LiNn+/0 species. The binding energy is defined as:| Eb1 = 2[E(Li) + n/2E(N2) − E(LiNn)]/n (for the neutrals) | (I) |
| Eb2 = 2[E(Li+) + n/2E(N2) − E(LiNn+)]/n (for the cations) |
To get further insight into the interactions between N2 molecule and Li+/0, we performed natural bond orbital (NBO) analysis45 where the electronic wave function is interpreted in terms of a set of occupied Lewis orbitals and a set of unoccupied non-Lewis delocalized orbitals. For each donor NBO (i) and acceptor NBO (j), the stabilization energy E2 associated with charge transfer i → j is given by
| E(2) = ΔEij = qiF(i, j)2/(εi − εj) | (II) |
The average E(2) of LiNn+ is defined as:
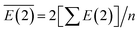 | (III) |
3 Experimental results
Fig. 1 shows a typical mass spectrum of the clusters generated in the experiment with LiCl as the substrate and N2 as the carrier gas. It is observed that the main series of lithium–nitrogen clusters are LiN2+, LiN4+, LiN6+, LiN8+ and LiN10+. The mass intensity of LiN8+ is predominant compared to those of the other LiNn+ species. No mass peak of LiNn+ with odd numbers of nitrogen atoms has been detected. In addition to the mass peaks of lithium–nitrogen clusters, the mass peaks of LiN2(H2O)+, LiN4(H2O)+, LiN6(H2O)+ and LiN8(H2O)+ are also observed. The formation of LiNn(H2O)+ more likely is due to the presence of trace amounts of water in the carrier gas. In laser ablation experiments with LiF, LiF/ZrN, LiF/AlN and LiF/BN as substrates, similar lithium–nitrogen clusters were obtained (ESI, Fig. S1–S4†).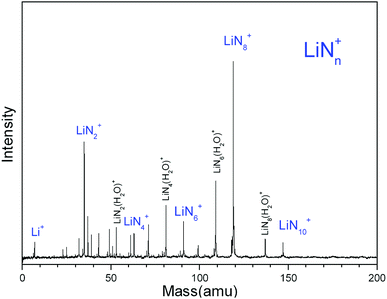 | ||
| Fig. 1 Typical mass spectrum of Li–N clusters generated by laser ablation of a LiCl target with N2 as the carrier gas. | ||
4 Theoretical results
To search for the stable structures of LiNn+ and LiNn (n = 2, 4, 6, 8, and 10), we have conducted calculations for nine different categories of structures, from LiN2 to LiN10. Starting from the simplest one containing only two nitrogen atoms and a lithium atom, by adding one nitrogen atom at a time to the system, we obtained an increasing number of geometrical configurations as the system became larger. By placing the nitrogen atoms at different locations, we constructed the initial geometrical structures with a series of units such as N2 molecules, N3 chain and ring, N4 chain and ring, and N5, N6, and N7 rings and so on containing lithium atoms. To ensure that the geometry optimizations located the true minima on the potential surfaces, frequency calculations were conducted for all optimized structures. For each initial geometrical configuration, we also considered many spin multiplicities (2, 4, and 6 for neutral species and 1, 3, and 5 for positive ions). After full relaxation, a rather large number of low-lying isomers of LiNn+ and LiNn (n = 2, 4, 6, 8, and 10) were found. Here, we show the typical isomers of LiNn+ (n = 2, 4, 6, 8, and 10) in Fig. 2 with the most stable structures on the left and those of LiNn (n = 2, 4, 6, 8, and 10) in Fig. 3.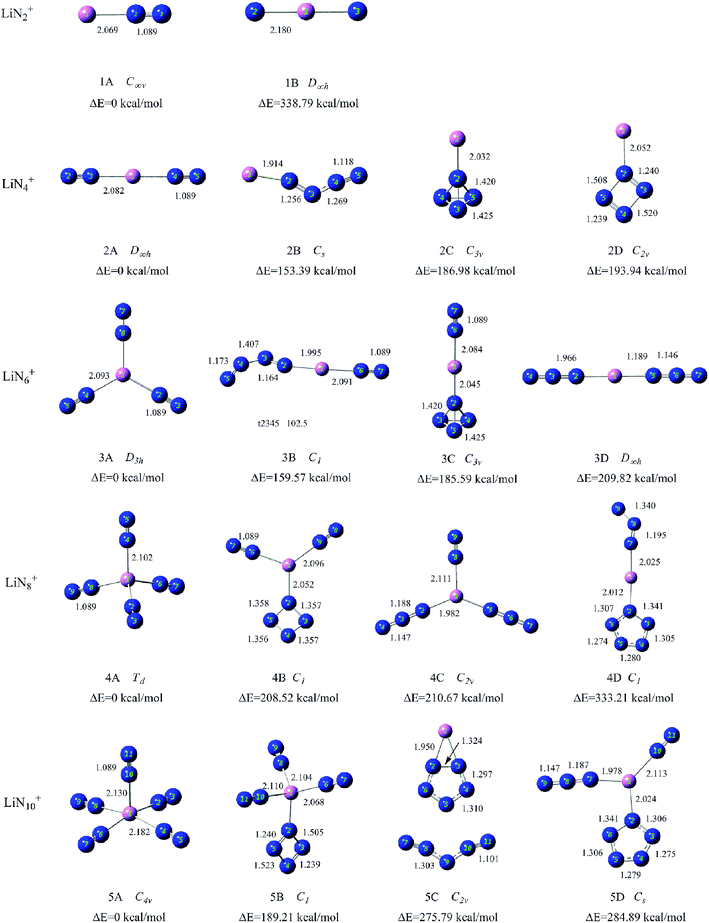 | ||
| Fig. 2 Typical low-lying isomers of LiNn+ (n = 2, 4, 6, 8, and 10) clusters. The bond lengths are given in angstroms. | ||
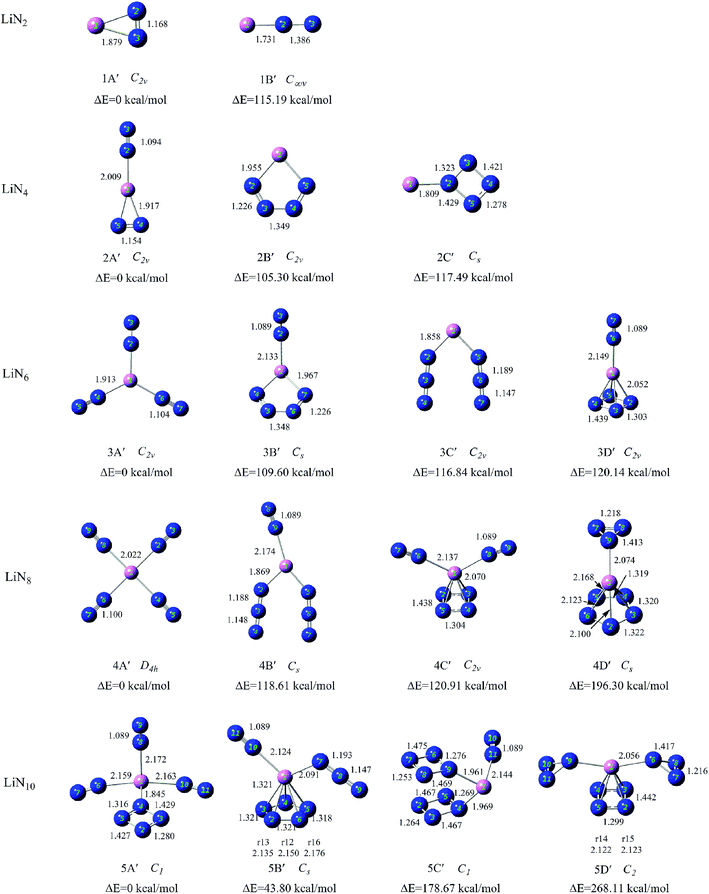 | ||
| Fig. 3 Structures and relative energies of the low-lying isomers of neutral LiNn (n = 2, 4, 6, 8, and 10) clusters. The bond lengths are given in angstroms. | ||
4.1 Structures of LiN2+ and LiN2
The ground state structure of LiN2+ (1A) is a C∞v symmetry linear structure formed by attaching an end-on N2 molecule to a Li atom. The N–N bond lengths in the N2 unit are 1.089 Å. The second isomer (1B) is a D∞h symmetry linear structure formed by inserting a Li atom between two N atoms. It is much higher in energy than 1A.For neutral LiN2, the most stable isomer 1A′ has a C2v symmetry triangular structure consisting of a side-on N2 molecule and an Li atom. The N–N bond length in the side-on N2 unit is 1.168 Å, which is longer than that of isolated N2 molecule. The second stable structure 1B′ has one end-on N2 unit and one Li atom, similar to 1A of LiN2+. However, the N–N bond length in the end-on N2 unit increases to 1.386 Å.
4.2 Structures of LiN4+ and LiN4
The ground state structure of LiN4+ (2A) is a D∞h symmetry linear structure, in which two N2 molecules are attached directly to the central Li atom. The N–N bond lengths in the N2 units are 1.089 Å. In the other low-lying isomers of LiN4+ (2B–2D), N4 units were found and they interact with Li atoms as a whole. For example, in isomers 2B, 2C and 2D, the N4 units exhibit chain, tetrahedral, and cyclic configurations, respectively, and connect to Li atom via one nitrogen atom. These N4 units have been reported in many previous studies and the interaction between Li+ and N4 ring was also predicted by Li et al.38,46–48For neutral LiN4, isomer 2A′ with one end-on and one side-on distances of the end-on and side-on N2 units are 1.094 and 1.154 Å, respectively. A N4 chain is found in isomer 2B′ and is connected to the Li atom through two terminal nitrogen atoms. Isomer 2C′ has a Li atom interacting with a η1-N4 ring similar to isomer 2D LiN4+. We could not find any isomer with a tetrahedral N4(Td) unit in neutral LiN4.
4.3 Structures of LiN6+ and LiN6
For LiN6+, the lowest energy isomer (3A) has a planar structure with D3h symmetry, in which three N2 molecules interact equally with the central Li atom via their terminal nitrogen atoms. The N–N bond lengths in the N2 units are 1.089 Å. The low-lying isomers containing other all-nitrogen units are also found and their energies are much higher than that of 3A. Isomer 3B has one end-on bound N2 molecule and one N4 chain coordinating to the Li atom via their terminal nitrogen atoms. The N4 chain can be regarded as a complex of two N2 sub-units because the bond linking the two N2 sub-units is relatively weak. Isomer 3C contains one end-on bound N2 molecule and one tetrahedral N4 unit that coordinates to the Li atom through one vertex nitrogen atom. Isomer 3D is a D∞h symmetry linear structure formed by attaching two N3 ligands to the Li atom.The ground state structure of LiN6 (3A′) is similar to that of LiN6+ (3A). It was also formed by attaching three N2 molecules to the central Li atom, but its symmetry changes to C2v. In the other low-lying isomers, N3, N4 and N6 units are the main building blocks. Isomer 3B′ contains one end-on bound N2 molecule and one N4 chain that connects to the Li atom through its two terminal nitrogen atoms. Isomer 3C′ has two end-on N3 units. Isomer 3D′ has one end-on N2 molecule and one η4-N4 ring.
4.4 Structures of LiN8+ and LiN8
The most stable structure of LiN8+ (4A) is a Td symmetry structure formed by attaching four end-on N2 molecules to a Li atom. The N–N bond lengths in the N2 units are 1.089 Å. The other low-lying isomers are much higher in energy than 4A. Isomer 4B has one η1-N4 ring and two end-on bound N2 molecules. Isomer 4C contains two N3 units and one end-on bound N2 molecule. 4D has one η1-N5 ring and one N3 unit. The planar structure Li-η1-N5 in 4D was also studied by Glukhovtsev and considered as a possible isomer of LiN5.39For LiN8, the lowest energy isomer (4A′) has a planar structure with D4h symmetry in which four N2 molecules interact equally with the central Li atom via their terminal nitrogen atoms. The N–N bond lengths in the N2 units are 1.089 Å. Isomer 4B′ was formed by attaching two N3 units and one end-on bound N2 molecule to a Li atom. Isomer 4C′ has one η4-N4 ring and two end-on bound N2 molecules. Isomers 4B′ and 4C′ could be considered to evolve from isomers 3C′ and 3D′ by the addition of one end-on bound N2 molecule. Isomer 4D′ has one η5-N5 ring and one η1-N3 units. This pyramidal structure formed by N5 ring and metal ions has been proposed in many theoretical studies.39,49,50 [N3MN5]q structure was also calculated by Jin et al., and their results suggested that the [N3MN5]q in heterodecked form are thermodynamically more stable than the sandwich-like isomers [N4MN4]q(D4d) with even-membered N42− ring [(M, q) = (Ni, 0), (Co, −1), (Fe, −2)].51
4.5 Structures of LiN10+ and LiN10
The most stable isomer of LiN10+ (5A) consists of five N2 molecules placed around the Li atom and exhibits C4v symmetry. 5B is the second stable structure and has three N2 molecules and one η1-N4 ring and its energy is much higher than that of 5A. The third isomer 5C has one N10 unit consisting of an N5 ring and an N5 chain. This N10 unit was similar to the N5+N5− ionic compound.52 Isomer 5D is the fourth stable structure and has one η1-N5 ring, one N2 and one N3 unit.The low-lying isomers of neutral LiN10 are different from those of its positive charged counterpart. As shown in Fig. 3, 5A′ has three N2 molecules and one η1-N4 ring. 5B′ consists of one N2 molecule, one N3 unit and one η5-N5 ring. It is higher in energy than 5A′ by 43.80 kcal mol−1. Isomer 5C′ consists of two face-to-face η1-N4 rings and one N2 unit. The adjacent N4 rings anchored on the Li atom in 5C′ are a precursor for the formation of other all-nitrogen structures. The most stable isomer with the N3 ring is 5D′ that has two η1-N3 rings and one η4-N4 ring. The nitrogen rings in 5D′ make it a highly energetic cluster.
5 Discussion
5.1 Structure of Li–N clusters
In our experiments, it is found that LiNn+ clusters (n = 2, 4, 6, 8, and 10) can be generated by laser ablation of LiCl without any solid nitrogen source, indicating that the carrier gas (N2) used in the experiments participated in the formation of Li–N clusters. The LiNn+ clusters generated in our experiment all have even numbers of nitrogen atoms, suggesting that the generated LiNn+ clusters may be formed by N2 sub-units.As shown in Fig. 3, the most stable isomers of LiNn+ (1A–5A) obtained by theoretical calculations are formed by a lithium cation and a number of end-on bound N2 units, that is in the form of Li+(N2)n/2. This is consistent with the facts that the generated LiNn+ cluster cations all have even number of nitrogen atoms and their numbers of nitrogen atoms differ by multiples of 2. An examination of the most stable isomers 1A–5A shows that the structures of these observed LiNn+ (n = 2, 4, 6, 8, and 10) cluster cations evolve from one-dimensional linear type (C∞v, D∞h) to two-dimensional branch type (D3h) to three-dimensional tetrahedral (Td) and square pyramid (C4v) types with increasing number of N2 units. LiN8+ has a highly symmetrical structure with Td symmetry. It also has high nitrogen content (94.1%) and may be used as a potential precursor for production of poly-nitrogen species.
Among the low-lying isomers of LiNn+/0 (n = 2, 4, 6, 8, and 10) presented in Fig. 2 and 3, the end-on bound N2 units are the most common with the N–N bond lengths of approximately 1.09 Å, which are nearly the same as those in isolated nitrogen molecules. The side-on bound N2 units are found in isomers 1A′ and 2A′, and the N–N bonds in these clusters are clearly weakened by coordination and the N–N bond lengths increase to approximately 1.16 Å. In addition, the isomers with a high number of N2 units commonly have relatively lower energies than those with the other all-nitrogen units. This is very similar to the results obtained in our previous studies.31,32
Other all-nitrogen groups, such as linear N3, circular N3, chain-shaped N4, circular N4, tetrahedral N4, circular N5, circular N6 and so on, were also found in the low-lying isomers of LiNn+/0 (n = 2, 4, 6, 8, and 10) clusters. This suggests that the doping of lithium atom could promote the stability of the above all-nitrogen groups, and these energetic LiNn+/0 (n = 2, 4, 6, 8, and 10) isomers may exist in principle. Many N5 units found in LiNn+/0 isomers were in the form of the η1-N5 ring, which is consistent with the coordination mode of compounds synthesized to date such as [M(H2O)4(N5)2]·4H2O (M = Mn, Fe and Co).53,54
5.2 Binding energies of the most stable isomers
To estimate the strength of the interactions between the Li atom and nitrogen ligands, we calculated the binding energies of the most stable isomers of LiNn+/0 (n = 2, 4, 6, 8, and 10). The calculation results are shown in Table 1 and Fig. 4. The Li–N2 distances in LiNn+/0 (n = 2, 4, 6, 8, and 10) are also listed in Table 1 for comparison.| Positive cluster | Symmetry | Multiplicity | Li–N2 distance | Eb (eV) | Neutral cluster | Symmetry | Multiplicity | Li–N2 distance | Eb (eV) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a The average Li–N2 distance. | |||||||||||
| Li–N2+ | 1A | C∞v | 1 | 2.069 | 0.57 | Li–N2 | 1A′ | C2v | 2 | 1.879 | −0.12 |
| Li–N4+ | 2A | D∞h | 1 | 2.082 | 0.54 | Li–N4 | 2A′ | C2v | 2 | 2.009, 1.917 | 0.12 |
| Li–N6+ | 3A | D3h | 1 | 2.093 | 0.51 | Li–N6 | 3A′ | C2v | 2 | 1.913 | 0.23 |
| Li–N8+ | 4A | Td | 1 | 2.102 | 0.49 | Li–N8 | 4A′ | D4h | 2 | 2.022 | 0.26 |
| Li–N10+ | 5A | C4v | 1 | 2.172a | 0.45 | Li–N10 | 5A′ | C1 | 2 | 2.165a | −0.79 |
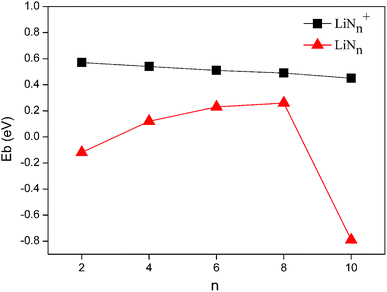
An examination of the results presented in Table 1 and Fig. 4 shows that binding energies of the ground states of LiNn+ (n = 2, 4, 6, 8, and 10) are positive, suggesting a substantial energy stabilization of the LiNn+ (n = 2, 4, 6, 8, and 10) species compared to the bare Li cation and N2 molecules. The stabilizing effects decrease slowly as the numbers of end-on bound N2 units increase. Considering that the N–N distances in the N2 units of LiNn+ (n = 2, 4, 6, 8, and 10) are all equal to that of the N2 molecules calculated in this work, we wish to stress that the calculated binding energies reflect the Li–N2 bond strengths in the clusters. Moreover, as shown in Table 1, the Li–N2 distances were found to be in the order of LiN2+ < LiN4+ < LiN6+ < LiN8+ < LiN10+, which is consistent with the order of the binding energies.
For neutral LiNn (n = 2, 4, 6, 8, and 10) clusters, with the exception of the 1A′ and 5A′ clusters, the binding energies of the ground states are also positive, indicating the presence of similar stabilizing effects. However, for 1A′ with only one side-on bound N2 unit, the binding energy is negative, possibly because the side-on bound N2 unit has a higher energy than the N2 molecule due to the weakening of the N–N bond (1.168 Å). The binding energy of 5A′ with N4 rings is also negative and is much lower than those of the other stable Li–N isomers. This is because the energetic N4 ring drastically increases the relative energy of isomer 5A′.
5.3 NBO analyses for the most stable isomers of LiNn+
To further understand the binding and electronic structures of the Li–N clusters observed in the mass spectra, we performed NBO analyses for the most stable isomers of LiNn+ (n = 2, 4, 6, 8, and 10), and the calculated results are presented in Tables S1–S5.† In the NBO model, the strength of the interaction of the electron donor and electron acceptor NBOs is defined by the stabilization energy E(2). To evaluate the general contribution of all of the interactions between the electron donors and electron acceptors to the stabilization energy of the LiNn+ clusters, the sum of all of the stabilization energies, ∑E(2), was divided by the number of N2 units, as shown in eqn (III), to obtain the average stabilization energy,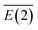 . Table 2 shows the NPA charge distributions and average second-order perturbation stabilization energies of the most stable isomers of the LiNn+ clusters.
. Table 2 shows the NPA charge distributions and average second-order perturbation stabilization energies of the most stable isomers of the LiNn+ clusters.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Nβ)n/2 clusters
Nβ)n/2 clusters
| Cluster | q (Li) | q (Nα) | q (Nβ) | Charge transfer | (kcal mol−1) | |
|---|---|---|---|---|---|---|
| Li–N2+ | 1A | 0.97607 | −0.19289 | 0.21682 | LP(1)Nα → LP*Li | 8.93 |
| Li–N4+ | 2A | 0.89635 | −0.15482 | 0.20665 | LP(1)Nα → LP*Li | 22.65 |
| Li–N6+ | 3A | 0.76153 | −0.11126 | 0.19075 | LP(1)Nα → LP*Li | 37.36 |
| Li–N8+ | 4A | 0.59306 | −0.07581 | 0.17754 | LP(1)Nα → LP*Li | 50.48 |
| Li–N10+ | 5A | 0.47380 | −0.05275 | 0.15651 | BD(1)Li–Nα → BD*(1)Li–Nα | 31.32 |
| −0.05449 | 0.16567 | |||||
Based on the NBO data, it was concluded that for LiNn+ (n = 2, 4, 6, 8), electrons are transferred from the lone pair (LP) on Nα of every N2 unit to the empty orbital LP* of the lithium atom, LP(1)Nα → LP*Li, leading to a lowering in the average stabilization energy by 8.93, 22.65, 37.36 and 50.48 kcal mol−1, respectively. Meanwhile, for LiN10+, the interaction is occurs mainly between the Li1–N2, Li1–N4, Li1–N6 and Li1–N8 bonds, and the electrons are transferred from the bonding orbital (BD) of the Li–Nα bonds to the antibonding orbital (BD*) of the other Li–Nα bonds, giving rise to the 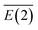 values of approximately 31.32 kcal mol−1. In both cases, the Nα and Nβ in N2 units carry negative and positive charges, respectively, forming a dipole that strongly interacts with Li+. The average stabilization energy,
values of approximately 31.32 kcal mol−1. In both cases, the Nα and Nβ in N2 units carry negative and positive charges, respectively, forming a dipole that strongly interacts with Li+. The average stabilization energy, 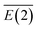 , of LiN8+ is the highest among the LiNn+ (n = 2, 4, 6, 8, and 10) clusters, providing a partial explanation for the highest abundance of LiN8+ in the mass spectra.
, of LiN8+ is the highest among the LiNn+ (n = 2, 4, 6, 8, and 10) clusters, providing a partial explanation for the highest abundance of LiN8+ in the mass spectra.
6 Conclusions
LiNn+ (n = 2, 4, 6, 8, and 10) clusters were generated by laser ablation. LiN8+ is found to be the most abundant. Density functional calculations were conducted to search for the stable structures of LiNn+/0. The theoretical results show that the most stable isomers of LiNn+ (n = 2, 4, 6, 8, and 10) are in the form of Li+(N2)n/2, and their structures evolve from one-dimensional linear type (C∞v, n = 2; D∞h, n = 4), to two-dimensional branch type (D3h, n = 6) to three-dimensional tetrahedral (Td, n = 8) and square pyramid (C4v, n = 10) types. The calculated binding energies suggest a substantial energy stabilization of the LiNn+ (n = 2, 4, 6, 8, and 10) species compared to the bare Li cation and N2 molecules. Further NBO analyses show that the N2 units in LiNn+ are actually dipoles that could interact with Li+ effectively, and LiN8+ has the highest average stabilization energy. For neutral LiNn (n = 2, 4, 6, and 8) clusters, the most stable isomers were also formed by a Li atom and the corresponding number of N2 units, while the most stable isomer of LiN10 is in the form of Li+(N2)3(η1-N4).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 21103202 and 21273246).Notes and references
- W. J. Lauderdale, J. F. Stanton and R. J. Bartlett, J. Phys. Chem., 1992, 96, 1173–1178 CrossRef CAS.
- H. Östmark, New Trends in Research of Energetic Materials Czech Republic, 2006, pp. 231–250 Search PubMed.
- P. C. Samartzis and A. M. Wodtke, Int. Rev. Phys. Chem., 2006, 25, 527–552 Search PubMed.
- M. N. Glukhovtsev, H. Jiao and P. v. R. Schleyer, Inorg. Chem., 1996, 35, 7124–7133 CrossRef CAS PubMed.
- K. O. Christe, W. W. Wilson, J. A. Sheehy and J. A. Boatz, Angew. Chem., Int. Ed., 1999, 38, 2004–2009 CrossRef CAS.
- F. Cacace, G. de Petris and A. Troiani, Science, 2002, 295, 480–481 CrossRef CAS PubMed.
- A. Vij, J. G. Pavlovich, W. W. Wilson, V. Vij and K. O. Christe, Angew. Chem., Int. Ed., 2002, 41, 3051–3054 CrossRef CAS PubMed.
- L. Gagliardi and P. Pyykkö, J. Phys. Chem. A, 2002, 106, 4690–4694 CrossRef CAS.
- G. von Zandwijk, R. A. J. Janssen and H. M. Buck, J. Am. Chem. Soc., 1990, 112, 4155–4164 CrossRef.
- Q. S. Li and L. P. Cheng, J. Phys. Chem. A, 2003, 107, 2882–2889 CrossRef CAS.
- L. P. Cheng and Q. S. Li, J. Phys. Chem. A, 2005, 109, 3182–3186 CrossRef CAS PubMed.
- J. M. Mercero, J. M. Matxain and J. M. Ugalde, Angew. Chem., Int. Ed., 2004, 43, 5485–5488 CrossRef CAS PubMed.
- L. Jin and Y.-h. Ding, J. Phys. Chem. A, 2009, 113, 13645–13650 CrossRef CAS PubMed.
- A. C. Tsipis and A. T. Chaviara, Inorg. Chem., 2004, 43, 1273–1286 CrossRef CAS PubMed.
- M. Lein, Chem.–Eur. J., 2001, 7, 4155–4163 CrossRef CAS.
- R. Haiges, J. A. Boatz, S. Schneider, T. Schroer, M. Yousufuddin and K. O. Christe, Angew. Chem., Int. Ed., 2004, 43, 3148–3152 CrossRef CAS PubMed.
- R. Haiges, J. A. Boatz, T. Schroer, M. Yousufuddin and K. O. Christe, Angew. Chem., Int. Ed., 2006, 45, 4830–4835 CrossRef CAS PubMed.
- R. Haiges, J. A. Boatz, M. Yousufuddin and K. O. Christe, Angew. Chem., Int. Ed., 2007, 46, 2869–2874 CrossRef CAS PubMed.
- R. Haiges, J. A. Boatz and K. O. Christe, Angew. Chem., Int. Ed., 2010, 49, 8008–8012 CrossRef CAS PubMed.
- R. Haiges, J. A. Boatz, R. Bau, S. Schneider, T. Schroer, M. Yousufuddin and K. O. Christe, Angew. Chem., Int. Ed., 2005, 44, 1860–1865 CrossRef CAS PubMed.
- A. C. Filippou, P. Portius, D. U. Neumann and K.-D. Wehrstedt, Angew. Chem., Int. Ed., 2000, 39, 4333–4336 CrossRef CAS PubMed.
- P. Portius, A. C. Filippou, G. Schnakenburg, M. Davis and K.-D. Wehrstedt, Angew. Chem., Int. Ed., 2010, 49, 8013–8016 CrossRef CAS PubMed.
- A. C. Filippou, P. Portius and G. Schnakenburg, J. Am. Chem. Soc., 2002, 124, 12396–12397 CrossRef CAS PubMed.
- A. Villinger and A. Schulz, Angew. Chem., Int. Ed., 2010, 49, 8017–8020 CrossRef CAS PubMed.
- C. Knapp and J. Passmore, Angew. Chem., Int. Ed., 2004, 43, 4834–4836 CrossRef CAS PubMed.
- T. M. Klapötke, B. Krumm, M. Scherr, R. Haiges and K. O. Christe, Angew. Chem., Int. Ed., 2007, 46, 8686–8690 CrossRef PubMed.
- T. M. Klapötke, B. Krumm, P. Mayer and I. Schwab, Angew. Chem., Int. Ed., 2003, 42, 5843–5846 CrossRef PubMed.
- E. D. Pillai, T. D. Jaeger and M. A. Duncan, J. Am. Chem. Soc., 2007, 129, 2297–2307 CrossRef CAS PubMed.
- E. D. Pillai, T. D. Jaeger and M. A. Duncan, J. Phys. Chem. A, 2005, 109, 3521–3526 CrossRef CAS PubMed.
- A. D. Brathwaite, H. L. Abbott-Lyon and M. A. Duncan, J. Phys. Chem. A, 2016, 120, 7659–7670 CrossRef CAS PubMed.
- K. W. Ding, X. W. Li, H. G. Xu, T. Q. Li, Z. X. Ge, Q. Wang and W. J. Zheng, Chem. Sci., 2015, 6, 4723–4729 RSC.
- K. W. Ding, H. G. Xu, Y. Yang, T. Q. Li, Z. Q. Chen, Z. X. Ge, W. L. Zhu and W. J. Zheng, J. Phys. Chem. A, 2018, 122, 4687–4695 CrossRef CAS PubMed.
- A. M. Sapse and P. V. R. Schleyer, Lithium Chemistry: Theoretical and Experimental Overview, Wiley Interscience, New York, USA, 1995 Search PubMed.
- D. Hao, J. Liu and J. Yang, J. Phys. Chem. A, 2008, 112, 10113–10119 CrossRef CAS PubMed.
- T. B. Tai and M. T. Nguyen, Chem. Phys. Lett., 2010, 492, 290–296 CrossRef CAS.
- L. F. Gong, W. L. Guo, X. M. Wu and Q. S. Li, Chem. Phys. Lett., 2006, 429, 326–331 CrossRef CAS.
- X. An, H. Zhuo, W. Tian, Q. Li, W. Li and J. Cheng, Mol. Phys., 2014, 112, 2954–2962 CrossRef CAS.
- Q. S. Li and L. P. Cheng, J. Phys. Chem. A, 2003, 107, 2882–2889 CrossRef CAS.
- M. N. Glukhovtsev, P. v. R. Schleyer and C. Maerker, J. Phys. Chem., 1993, 97, 8200–8206 CrossRef CAS.
- Y. C. Zhao, Z. G. Zhang, J. Y. Yuan, H. G. Xu and W. J. Zheng, Chin. J. Chem. Phys., 2009, 22, 655–662 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. M. N. Rega, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- R. Huenerbein, B. Schirmer, J. Moellmann and S. Grimme, Phys. Chem. Chem. Phys., 2010, 12, 6940–6948 RSC.
- CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, 95th edn, 2014–2015 Search PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- M. N. Glukhovtsev, H. Jiao and P. v. R. Schleyer, Inorg. Chem., 1996, 35, 7124–7133 CrossRef CAS PubMed.
- M. T. Nguyen, Coord. Chem. Rev., 2003, 244, 93–113 CrossRef CAS.
- A. Korkin, A. Balkova, R. J. Bartlett, R. J. Boyd and P. R. Schleyer, J. Phys. Chem., 1996, 100, 5702 CrossRef CAS.
- L. Gagliardi and P. Pyykko, J. Phys. Chem. A, 2002, 106, 4690–4694 CrossRef CAS.
- M. Lein, J. Frunzke, A. Timoshkin and G. Frenking, Chem.–Eur. J., 2001, 7, 4155–4163 CrossRef CAS.
- L. Jin and Y. Ding, J. Phys. Chem. A, 2009, 113, 13645–13650 CrossRef CAS PubMed.
- S. Fau, K. J. Wilson and R. J. Bartlett, J. Phys. Chem. A, 2002, 106, 4639–4644 CrossRef CAS.
- Y. Xu, Q. Wang, C. Shen, Q. Lin, P. Wang and M. Lu, Nature, 2017, 549, 78–81 CrossRef CAS PubMed.
- C. Zhang, C. Yang, B. Hu, C. Yu, Z. Zheng and C. Sun, Angew. Chem., Int. Ed., 2017, 56, 1–4 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Similar mass spectra and NBO data of the Li–N clusters. See DOI: 10.1039/c9ra00439d |
| This journal is © The Royal Society of Chemistry 2019 |