Open Access Article
Open Access ArticleTowards sensor applications of a polymer/Ag nanoparticle nanocomposite film
O. A. Yeshchenko *a,
S. Z. Malynych
*a,
S. Z. Malynych *bcd,
S. O. Polomareva,
Yu. Galaburad,
G. Chumanove and
I. Luzinov
*bcd,
S. O. Polomareva,
Yu. Galaburad,
G. Chumanove and
I. Luzinov *d
*d
aDepartment of Physics, Taras Shevchenko National University of Kyiv, 64/13 Volodymyrs'ka Str., 01601 Kyiv, Ukraine. E-mail: yes@univ.kiev.ua
bDepartment of Photonics, National University “Lviv Polytechnic”, 12 S. Bandery St, 79013 Lviv, Ukraine. E-mail: s.malynych@gmail.com
cDepartment of Electromechanics and Electronics, Hetman Petro Sahaidachnyi National Army Academy, 32 Heroes of Maidan, 79012 Lviv, Ukraine
dDepartment of Materials Science and Engineering, Clemson University, Clemson, South Carolina 29634, USA. E-mail: luzinov@clemson.edu
eDepartment of Chemistry, Clemson University, Clemson, South Carolina 29634, USA
First published on 13th March 2019
Abstract
We have demonstrated the capability of a nanocomposite film made of a 2D array of Ag nanoparticles embedded into a poly(glycidyl methacrylate), PGMA, matrix to monitor the presence of organic vapors in the atmosphere. Specifically, changes in the extinction spectra of the submicron nanocomposite film are used to sense the vapors. The transformations of the spectra are fully reversible and reproducible upon multiple exposures. We associate this reversibility and reproducibility with the construction of the nanocomposite film where the cross-linked PGMA network is able to spatially restore its structure upon deswelling. The structure of the extinction spectrum of the film is governed by a collective surface plasmon mode excited in the Ag NPs array. It was found that spectral bands associated with normal and tangential components of the plasmon mode change their width and position when the nanocomposite is exposed to organic vapors. This is due to increasing the spacing between neighboring NPs and a decrease of the refractive index of the polymer caused by swelling of the PGMA matrix. Therefore, the level of spectral transformation is directly related to the level of polymer–solvent thermodynamic affinity where the higher affinity corresponds to the higher level of the swelling. Therefore, we expect that the nanocomposite films (when designed for a particular solvent) can be effectively used as a sensing element in a low-cost volatile organic compounds (VOC) sensor device operating in visual light.
1. Introduction
Chemical monitoring of the environment is a vital problem for mankind since extensive industrial growth and human activity have resulted in the production of an enormous amount of substances that are not present in nature. Those substances contaminate natural habitats of all living species affecting the whole biosphere and obviously can cause a serious hazard to human health. Air pollution is a part of this global problem. Besides traditional air pollutants such as smokes, aerosols, and inorganic gases, volatile organic compounds (VOC) demonstrate a trend to increase their abundance in the atmosphere. Food decay,1 soil microorganisms' activity,2 and animal farms3 are among the major sources of VOC. Wide use of different organic solvents in laboratories and industry also requires the detection and control of VOC at places of work. Thus, there is a strong need for low cost and effective VOC sensors with rapid response.4–8To date a number of VOC sensors employing different techniques have been developed. Although well-known gas chromatography-mass spectrometry method allows detecting of trace gas contaminants and their identification it requires sophisticated and expensive equipment.9,10 Quartz crystal microbalance (QCM) is a resonant sensor whose resonant frequency shifts while the target molecules are absorbed onto the crystal's surface. Different coatings such as conventional polymers,11 molecularly imprinted polymers,12 and metalloporphyrins13 are used to increase sensitivity of the QCM based devices. For instance, an extremely low detection limit of acrylamide (about 10 ppb) was reported for QCM coated with certain Hunter/Vögtle-type macrocycles.14 Another approach to create a sensitive layer that is capable to absorb organic molecules relies on Langmuir–Blodgett (LB) nanoscale films.15 Those films can be exploited in surface acoustic wave devices.16 Changes of the LB films properties caused by absorption of the target molecules can be monitored by QCM and UV-vis spectroscopy as well, especially when they are accompanied by swelling of the polymer LB film.17 Surface plasmon resonance (SPR) technique has also been used to monitor changes in LB films.17,18 Moreover, surface plasmons related phenomena can be employed for sensing purposes by themselves.
It is well established that surface plasmons are collective oscillations of free electrons at the interface between conducting (usually metal) and dielectric media.19 The frequency of those oscillations is in resonance with the impinged electromagnetic wave that opens wide perspective for the practical application of SPR. In the extreme case, when the metal/dielectric interface is significantly warped and its curvature achieves high value the electron oscillations become trapped within the small volume limited by the surface of a metal. That situation is realized in metal nanoparticles (NPs), where electron oscillations are confined to the nanoparticle's volume and thus termed localized surface plasmon resonance (LSPR).20,21 Remarkably, that LSPR can be excited by visible light, while the resonant frequency depends on the nature of the metal, particle size, shape of a nanoparticle and dielectric environment.22 Localization and resonant character of free electron oscillations results in the enhancement of both electric and magnetic fields around the nanoparticle. The enhancement gives rise to various surface-enhanced techniques including SERS (Surface Enhanced Raman Scattering),23 SEPL (Surface Enhanced Photo Luminescence),24 SEIRA (Surface Enhanced IR Absorption),25 and can be also employed in the effective sensors for VOC detection26,27 or for monitoring of the refractive index of surrounding medium.28
In many practical analytical applications it is more rational to use ensembles of the NPs rather than individual NPs. Indeed, it is established that arranging of metal nanoparticles into closely spaced planar array on a surface of dielectric substrate leads to the strong electrodynamic coupling between LSPR in neighboring nanoparticles.19,28,29 As a result a collective plasmon mode emerges in the single layer of NPs upon visual light excitation. This mode appears as a sharp and intense peak in the extinction spectra of the array and is an eigenmode of the entire NP ensemble.19 The control over the optical response of 2D metal NP array can be achieved through the variation of the size of nanoparticles and distance between them.19,29 Two types of the collective modes are excited within the NPs ensemble depending on the orientation of the light induced electric dipoles, which can be parallel or perpendicular to the array plane.30,31 The extinction spectra of the array strongly depend on the polarization and the angle of incidence of the light beam.19,30,31 The 2D array of (Ag) NPs can be embedded into polymer film forming a nanocomposite material.30–32 We have found that reversible morphological changes have occurred in such composite films upon their swelling in organic vapors.32 As the polymer film absorbs solvent significant change in the distance between NP and refractive index of the film occurs. The level of swelling is dependent on the solvent–polymer affinity. Therefore, such submicron nanocomposite film can serve as a sensing element in a low-cost optical sensor operating in visual light. In fact, the sensing nanocomposite polymer films: (a) have thickness on the level of several hundred nm, (b) have <1 × 1 cm lateral dimensions, (c) can be made by simple dip-coating/annealing and (d) contain just minute amounts of Ag NPs and polymer. With these characteristics and industrial production the price of the film (including its fabrication) will be less than $1.
To this end, in the present work we studied in detail changes in the extinction spectra of planar array of closely spaced silver NPs embedded into poly(glycidyl methacrylate), PGMA host matrix upon its exposure to vapor of different organic solvents. The solvents were specially selected to have different thermodynamical affinity to the PGMA matrix. In general, we found that due to specific interactions between the macromolecules constituting the film and the molecules of solvent vapors, the observed spectroscopic response of the film to environment is highly chemically specific. Therefore, the observed effects can be used in a straightforward submicron-sized optical scheme for the detection of volatile organic molecules using nanoscale composite films.
In our work PGMA, a polymer possessing epoxy group in every monomeric unit, was selected to serve as a nanocomposite matrix for its ability to react with glass/silicon oxide/silver NPs surface and be cross-linked upon heating.33–36 In essence, the PGMA film is fabricated as a thin internally cross-linked film, covalently bound to the glass/native silicon oxide (covering the silicon surface) and silver nanoparticles using its epoxy group functionalities. This robust structure ensures structural stability and reversibility of the film upon multiple exposure to solvent vapors. In fact, in our preceding works we have demonstrated that the PGMA based polymer films are swelling reversibly upon absorption of solvent vapors.37–43 The level of swelling is related to thermodynamic affinity between the polymer and solvent vapors. In addition, the epoxy groups of PGMA, not involved in the reaction with the surface and cross-linking, can be used for the grafting of other polymer chains.33,35,38 In this work this grafting was used to modify the PGMA with poly(2-vinyl pyridine), P2VP macromolecules attracting silver nanoparticles via metal-complex formation.36,44 In the future design of the sensing nanocomposite films the grafting can be used to modify film/solvent affinity as reported elsewhere.37–39
2. Experimental details
2.1 Materials and sample preparation
Sample preparation was conducted in several steps and included Ag NPs synthesis, chemical modification of the surface of a substrate, preparation of 2D array of silver nanoparticles, and embedding of the array into polymer matrix. Silver nanoparticles were synthesized via reduction of supersaturated silver(I) oxide (99.99%, Alfa Aesar) aqueous solution by hydrogen gas (99.9999%, National Welders).45 The size of the NPs depends on the duration of the chemical reaction. The size and interparticle distance distribution of the silver nanoparticles were determined from SEM images (Fig. 1) by the analysis of about 250 nanoparticles yielding the mean nanoparticle size to be 〈d〉 = 115 nm with the standard deviation σd = 30 nm, and the mean interparticle distance within the layer to be 〈D〉 = 160 nm with σd = 70 nm.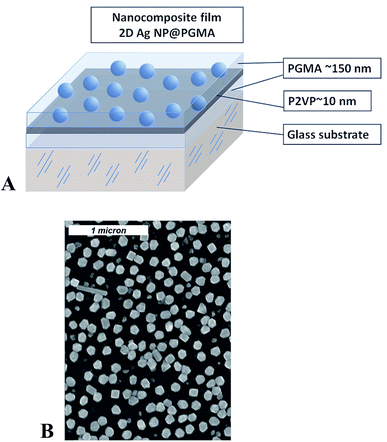 | ||
| Fig. 1 Schematics for the nanocomposite polymer film containing Ag nanoparticles (A); SEM image of 2D array of silver nanoparticles (B). | ||
Poly(glycidyl methacrylate) with number average molecular weight of 176![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 was prepared by radical polymerization of glycidyl methacrylate (Aldrich).33–35,37–39 Carboxyl-group-terminated poly(2-vinyl pyridine), P2VP–COOH (Mn = 40
000 g mol−1 was prepared by radical polymerization of glycidyl methacrylate (Aldrich).33–35,37–39 Carboxyl-group-terminated poly(2-vinyl pyridine), P2VP–COOH (Mn = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 g mol−1), was obtained from Polymer Source, Inc. Chloroform (Aldrich) was used as a solvent for preparing 2% PGMA and 2% P2VP–COOH solutions used during the fabrication of nanocomposite film.
600 g mol−1), was obtained from Polymer Source, Inc. Chloroform (Aldrich) was used as a solvent for preparing 2% PGMA and 2% P2VP–COOH solutions used during the fabrication of nanocomposite film.
In order to obtain the polymer film incorporating 2D array of Ag NPs conventional microscope glass slides (Fisher Scientific) and silicon wafers (University Wafer) were used as a substrate. Silicon wafers were employed only to determine the thickness of the polymer layers using ellipsometry and atomic force microscopy (AFM) by the “scratch” method. Glass substrates were used for optical measurements. The slides/wafers were cut into ∼8 × 25 mm pieces, cleaned for 30 minutes in freshly prepared 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture of 30% H2O2 and H2SO4 (“piranha” solution), rinsed with DI water, and dried under a stream of nitrogen gas.
3 mixture of 30% H2O2 and H2SO4 (“piranha” solution), rinsed with DI water, and dried under a stream of nitrogen gas.
PGMA film was deposited onto the surface of the slides/wafers by dip-coating technique using dip-coater Mayer Feintechnik D-3400. The slides were then annealed at 140 °C for 10 hours in a vacuum oven for anchoring the film to the surface and cross-linking.38,46 To remove any unanchored PGMA molecules from the sample's surface the slides/wafers were rinsed in chloroform at least three times and dried at ambient conditions. After that 2% P2VP solution was drop-wise cast on horizontally positioned substrate, so its surface becomes covered with the polymer–solution. Next, the sample was dried in ambient conditions for several hours and annealed. Annealing of the samples at 150 °C for 1 hour resulted in the formation of a P2VP layer grafted to the PGMA as described in details elsewhere.33,35 The procedure was completed by rinsing of the slides/wafers in chloroform for three times and drying at ambient conditions. With this procedure we fabricated PGMA film of the thickness ∼150 nm with a thin P2VP grafted layer on its surface. The thickness of the grafted layer was on the order of 10–15 nm. The P2VP layer was used for bounding of the NPs.47 For this purpose the modified slides/wafers were exposed overnight to an aqueous suspension of Ag NPs. As a result, a self-assembled 2D single layer of closely spaced nanoparticles was formed (Fig. 1). The detailed procedure of 2D Ag NPs array preparation can be found elsewhere.44 Analysis of the radial distribution function for Ag NPs in 2D array retrieved from the electron microscopy images reveals no periodicity or regular arrangement of the particles within the array. The average distance between nanoparticles in the array is about 210 nm.
Finally, the slides/wafers with self-assembled Ag NPs were again dipped into PGMA solution, dried and annealed at 140 °C for 10 hours in a vacuum oven. In this procedure, an additional 150–160 nm layer of surface anchored and cross-linked PGMA was formed and the entire 2D nanoparticle array became completely encapsulated into PGMA–P2VP–PGMA film. The topmost PGMA layer protects the nanoparticle array from external mechanical influence and preserves arrangement of the NPs. Therefore, we get a polymer (PGMA) nanocomposite film containing Ag NPs arranged in 2D system.30 Initial (lower) PGMA layer ensures homogeneity of the refractive index around the nanoparticles and also mitigates the influence of a substrate, which may significantly vary optical response of Ag NPs array.48
The thickness of the polymer films was measured using an automatic ellipsometer COMPEL (InOm Tech, Inc.) and an atomic force microscope (Dimension 3100, Digital Instruments, Inc.). The angle of incidence for ellipsometric measurements was set at 70°. It was assumed that the refractive index of the polymer layer was 1.525.34 Scanning electron microscope Hitachi S4800 was used for imaging of the samples.
Optical measurements
The extinction spectra of the PGMA/Ag NPs composite were recorded using Agilent Cary 60 UV-vis spectrophotometer equipped with double beam Czerny–Turner monochromator. Full spectrum xenon pulse lamp with 190–1100 nm wavelength range was used as a light source. Unpolarized light was used to probe the sample. The angle of incidence was set at θ = 45°. The sample was kept in the quartz cell 10 × 10 × 45 mm in dimensions during recording the spectra.3. Results and discussion
Spectroscopic measurements
As it was reported in our preceding works two types of collective SPR modes can be excited by visual incident light in 2D array of closely spaced Ag NPs.19,30,31 Those modes can be clearly distinguished when using linearly polarized light at oblique angles of incidence. Indeed, the electric vector of the incident light beam with s-polarization (TE) excites electron oscillations only in plane of the nanoparticle array. We denote this SPR mode as T.30,31 The electric vector of a p-polarized (TM) beam has both parallel and perpendicular components leading to the excitation of two modes, in-plane and orthogonal to the plane. This orthogonal component of free electrons oscillations can be denoted as P mode. Obviously, at normal incidence there is no difference between TM and TE polarizations with regard to the sample's plane and only one band is observed in the extinction spectrum of 2D Ag NPs array.19 Spectral bands corresponding to P or T mode are to a certain degree pronounced in the extinction spectra of 2D array depending on the angle of incidence. Increasing the angle results in the rise of the normal (P) component intensity. At the same time, the conditions of excitation of T mode with s-polarized light do not depend on the angle of incidence. Thus, varying the angle of incidence one can control the efficacy of excitation of P and T modes. In present work we used unpolarized light at the angle of incidence θ = 45°, so both P and T SPR modes were excited in 2D array of Ag NPs simultaneously. We expect that this optical configuration can be used in envisioned low-cost sensors.Emerging of two SPR modes in the array of Ag NPs results in overlapping of corresponding spectral bands that may complicate the analysis of possible transformations of the extinction spectra of the samples caused by external influence (e.g. exposing to VOC). It is, therefore, convenient to present the extinction spectrum of PGMA/Ag NPs nanocomposite film as the sum of two Gaussian functions that correspond to P and T SPR modes (Fig. 2). Now such parameters as the bandwidth and spectral position can be analyzed separately for each band.
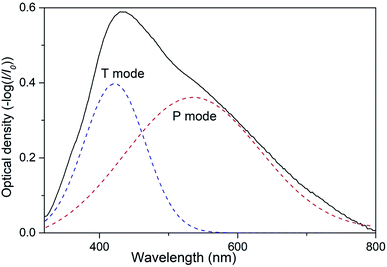 | ||
| Fig. 2 Extinction spectrum of nanocomposite taken at the angle of incidence θ = 45° and Gaussian fit for P and T plasmon modes. | ||
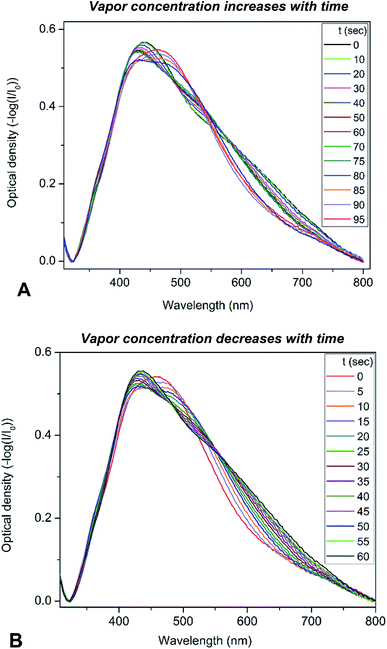
To determine the optical sensitivity of PGMA/Ag NPs submicron films towards the presence of organic vapors the experiments were performed using the following scenario. The sample was installed inside quartz cell with the dimensions 10 × 10 × 45 mm at the angle of 45° with respect to the incident light beam. A 20 μL droplet of organic solvent was injected into the cell using syringe, then the cell was tightly closed with a stopper. The extinction spectra were recorded every 5 s while the solvent was evaporating until no notable changes in the spectra were observed. It is worth noting that the droplet of solvent evaporated completely in the cell. Changes in the extinction spectra of PGMA/Ag NPs composite triggered by injection of chloroform vapor are shown in Fig. 3a. Since the maximum scan rate of the spectrophotometer is about 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 nm min−1, one can neglect spectral changes during the single scan. The extinction spectrum experience notable transformation with the increase of chloroform vapor concentration. Once the spectra stopped changing the stopper was removed and the extinction spectra were recorded again every 5 s until vapor escaped from the cell into the atmosphere, Fig. 3b. The same procedure was conducted for other organic solvents such as acetonitrile, ethanol, and toluene. Here we present the evolution of the extinction spectrum for chloroform only, since the transformation in extinction spectrum is most pronounced for this solvent comparing to other solvents studied. The transformations of the spectra are fully reversible and reproducible upon multiple exposures. We associate this reversibility and reproducibility with the construction of the nanocomposite film where cross-linked PGMA network demonstrate shape-memory properties.38 Therefore, the film is capable to spatially restore its structure upon deswelling, where every Ag NP is placed back by the contracting polymer network to its initial pre-swelling position.
000 nm min−1, one can neglect spectral changes during the single scan. The extinction spectrum experience notable transformation with the increase of chloroform vapor concentration. Once the spectra stopped changing the stopper was removed and the extinction spectra were recorded again every 5 s until vapor escaped from the cell into the atmosphere, Fig. 3b. The same procedure was conducted for other organic solvents such as acetonitrile, ethanol, and toluene. Here we present the evolution of the extinction spectrum for chloroform only, since the transformation in extinction spectrum is most pronounced for this solvent comparing to other solvents studied. The transformations of the spectra are fully reversible and reproducible upon multiple exposures. We associate this reversibility and reproducibility with the construction of the nanocomposite film where cross-linked PGMA network demonstrate shape-memory properties.38 Therefore, the film is capable to spatially restore its structure upon deswelling, where every Ag NP is placed back by the contracting polymer network to its initial pre-swelling position.
Polymer–solvent interaction
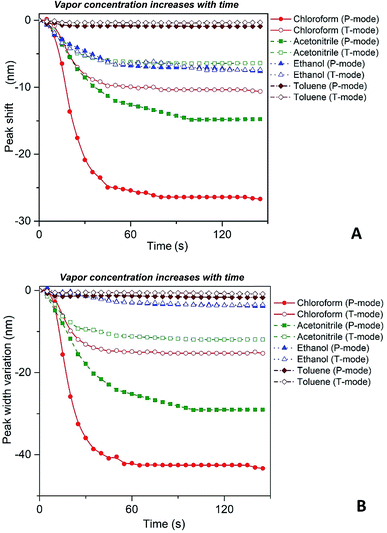
Fig. 4 depicts shift of the maximum peak position and the width of the spectral bands associated with P and T SPR modes caused by the various VOCs. Note that time dependences of those parameters saturate after 25 s, so that interval can be considered as a response time of the sensing film. The observed solvent-selective response can be approached from consideration of the thermodynamic affinity between the composite film and solvents, which can be estimated using Hansen solubility parameters and their components.49,50 The Hansen solubility parameter is defined as:51
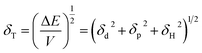 | (1) |
| Δδ = [(δd,pol − δd,solv)2 + (δp,pol − δp,solv)2 + (δH,pol − δH,solv)2]1/2 | (2) |
| Substance | δd [MPa1/2] | δp [MPa1/2] | δH [MPa1/2] | δtotal [MPa1/2] | Δδ [MPa1/2] | Refractive index, n | Δn |
|---|---|---|---|---|---|---|---|
| PGMA | 16.5 | 7.6 | 9.2 | 19.6 | — | 1.525 | — |
| Chloroform | 17.8 | 3.1 | 5.7 | 19 | 5.9 | 1.4459 | 0.0791 |
| Acetonitrile | 15.3 | 12.8 | 6.1 | 24.4 | 6.2 | 1.3442 | 0.1808 |
| Ethanol | 15.8 | 8.8 | 19.4 | 26.5 | 10.3 | 1.3611 | 0.1639 |
| Toluene | 18 | 1.4 | 2 | 18.2 | 9.6 | 1.4941 | 0.0309 |
Our spectroscopic results show that the larger peak shift and peak width variation are observed for the vapors with the higher affinity between the polymer and vapor molecules (Fig. 4). It is clearly seen that the nanocomposite possesses the highest sensitivity to chloroform vapor while the sensitivity to toluene vapor is quite low. The behavior of P and T plasmon modes is similar however, spectral transformations for P band are more prominent in comparison with those for T band. This indicates the higher sensitivity of the former plasmon mode to the organic vapor. Both P and T modes shift to the shorter wavelengths (blue shift) and their bandwidth decreases while the concentration of organic vapor increases. It is naturally to assume that the observed dependences are due to swelling of the PGMA matrix under the influence of organic vapor. Swelling of the polymer results in two processes, namely the increase of the distance between nanoparticles and changing the refractive index of the PGMA layer. The refractive index (real part of the dielectric function) of the surrounding affects mainly LSPR frequency, while any variations of the distance between nanoparticles in the array change coupling conditions for the plasmons. As a result, transformations of the extinction spectra of PGMA/Ag NPs composite are observed.
Proceeding from the Maxwell-Garnett effective medium model54 the effective dielectric permittivity of the nanocomposite medium is expressed as:
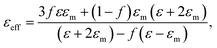 | (3) |
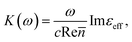 where c is the speed of light and
where c is the speed of light and ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) is the average refractive index of the composite. Thus the resonance absorption of light resulting from the localized plasmons excitation occurs at maximum of Imεeff that (in low damping approximation ε2 ≪ |ε1|) takes place at minimum of denominator of eqn (3). This condition can be written as:
is the average refractive index of the composite. Thus the resonance absorption of light resulting from the localized plasmons excitation occurs at maximum of Imεeff that (in low damping approximation ε2 ≪ |ε1|) takes place at minimum of denominator of eqn (3). This condition can be written as:
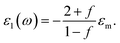 | (4) |
Taking the frequency dependent real part of the metal permittivity as:
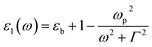 | (5) |
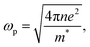 where ωp is the frequency of bulk plasmon, n is the free electrons concentration, e is the electron charge, m* is the effective mass of free electron, Γ is the damping constant of plasma oscillations, εb is the bound electrons contribution into the metal permittivity. Thus, substituting ε1(ω) from eqn (5) to eqn (4), we obtain the resonance frequency of localized surface plasmons for metal NPs embedded into dielectric matrix as:
where ωp is the frequency of bulk plasmon, n is the free electrons concentration, e is the electron charge, m* is the effective mass of free electron, Γ is the damping constant of plasma oscillations, εb is the bound electrons contribution into the metal permittivity. Thus, substituting ε1(ω) from eqn (5) to eqn (4), we obtain the resonance frequency of localized surface plasmons for metal NPs embedded into dielectric matrix as:
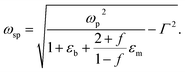 | (6) |
Filling factor f in the eqn (6) directly relates to the distance between NPs in the array. The lower the filling factor, the larger is the spacing between nanoparticles and LSPR frequency increases that proves our experimental finding. A shift of SPR spectral band towards shorter wavelengths with the increase of the distance between Ag NPs arranged in 2D array was previously reported elsewhere.55 The above discussion can be considered for both P and T plasmon modes. Enlarging of the distance between NPs in planar array due to swelling of PGMA film weakens the strength of the electrodynamic coupling of LSPR in neighboring silver NPs.
Let us discuss now the influence of the refractive index of the host matrix on the collective plasmon mode frequency. According to eqn (6) augmentation to the refractive index of dielectric surrounding results in the shift of spectral bands position towards longer wavelength. Those theoretical predictions are in good agreement with experimental results presented earlier.28,29 The published values for the refractive indexes for PGMA34 and solvents56 used in this work are presented in Table 1. We also show in Table 1 the difference (Δn) between the refractive index of PGMA and that of the solvents. All solvents possess the index which is lower than the one for PGMA matrix. Therefore, as the nanocomposite film swells the refractive index (n) of the film will decrease for all solvents. The difference is increasing in the following manner: toluene (the lowest value of Δn), chloroform, ethanol, and acetonitrile (the highest value of Δn). At the same degree of swelling the largest decrease in the refractive index of the film will be observed for acetonitrile, while the smallest will be observed for toluene. Based on this data one can expect the decrease of the permittivity of PGMA as the polymer swells. Such decrease of the permittivity of host medium εm, as follows from eqn (6), leads to the increase of the resonance frequency. Simultaneous action of those factors, namely increasing of the spacing between Ag NPs and lowering of the refractive index (permittivity εm) of PGMA film caused by swelling results in the observed blue shift of the spectral bands associated with P and T plasmon modes in 2D array of Ag NPs.
Origin of the spectroscopic transformations
To elaborate on our assumption for the origin of the observed transformations of the spectra, namely the increase of the distance between NPs and the decrease of the host polymer matrix refractive index due to polymer swelling, we calculated the dependence of the SPR peak shift on the polymer matrix swelling factor (η) using eqn (6). The factor is the quantitative measure of the degree of the polymer matrix swelling that can be defined as the ratio of the volume of swelled Ag NPs/polymer composite to its initial volume (volume without the solvent vapor), η = V/V0 = (r/r0)3. Here, r and r0 is the distance between NPs in swelled and initial polymer matrix respectively. Thus, the filling factor for Ag NPs can be expressed as:
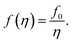 | (7) |
Considering that variation of the filling factor from f0 to 0 leads to variation of the refractive index of host matrix from npol to nsolv, the dependence of the polymer host matrix can be calculated as:
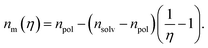 | (8) |
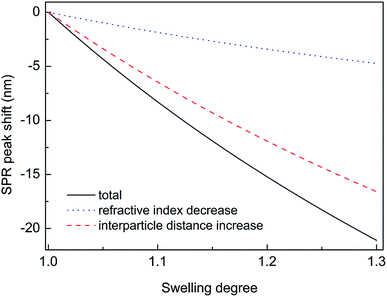
Thus, substituting the expressions (7) and (8) into the eqn (6), one can model the dependence of the shift of SPR peak on the swelling degree ΔλSPR(η). The results of these model calculations for Ag NPs/PGMA film, swollen to a different degree in the chloroform vapor, are shown in Fig. 5 as solid black line. One can see that quite moderate PGMA matrix swelling of about 1.3 times results in the SPR blue shift of more than 20 nm. Fig. 4a shows our experimental data where spectral shift of SPR P-mode for the nanocomposite film exposed to solvent vapors is followed as a function of time. During the experiment the concentration of the solvent vapor is increasing as more solvent is evaporating into the closed cell. It is obvious that there is a very good general agreement between the calculated and experimental shift of SPR P-mode observed for Ag NPs/PGMA composite exposed to chloroform vapor. Therefore, the above assumption of the role of interparticle distance increase and the host matrix refractive index decrease due to polymer swelling in the solvent vapor in the extinction spectra transformation can be accepted. This conclusion is also corroborated by the spectral data presented in Fig. 6a. In fact, spectral shift of SPR P-mode is decreasing as the concentration of the solvent vapor in the cell is decreasing. The decrease in concentration causes deswelling of Ag NPs/PGMA nanocomposite film and corresponding change in the interparticle distance and refractive index.
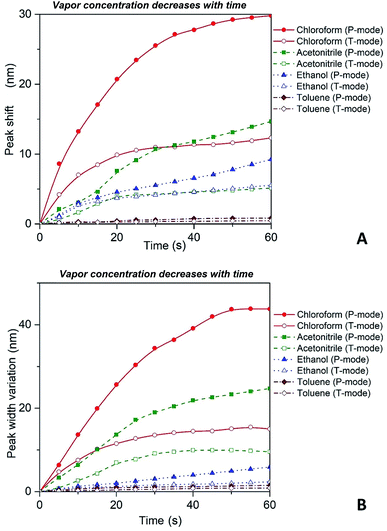 | ||
| Fig. 6 Red shift (A) and broadening (B) of P and T plasmon modes as the concentration of the solvent vapor in the cell is decreasing with time as more solvent is leaving the open to atmosphere cell. | ||
Another important question concerns the level of contribution of interparticle distance and the refractive index of PGMA matrix to the observed transformations of the spectra. We calculated contribution of the interparticle distance increase and the refractive index decrease separately. The results of calculations are also shown in Fig. 5. It is clearly seen that the increase of the interparticle distance is dominating factor while the decrease of the refractive index of host matrix affects the SPR peak spectral position to a lesser degree. The calculation of SPR shift depending on the swelling degree (Fig. 5) can be used for estimation of the maximal swelling factors reached in our experiments for different solvents. Using the values of P-mode shift (Fig. 4a) at highest concentrations of solvents −27 nm for chloroform, −15 nm for acetonitrile, −8 nm for ethanol and −1 nm for toluene, we estimated the swelling degree η for the solvents as 1.40 for chloroform (40% swelling of the PGMA matrix), 1.19 for acetonitrile (19%), 1.09 for ethanol (9%) and 1.01 for toluene (1%). The obtained difference in values of the swelling degree are caused by different values of affinity of the solvents to the polymer that is discussed above. Therefore, it is obvious that when the optical sensor is designed to detect a particular solvent the PGMA matrix can be modified accordingly to fine-tune its swelling. It can be done straightforwardly either via polymer grafting38 or via copolymerization of GMA with other monomers46 having higher affinity to targeted VOC.
It is important to reiterate that observed transformations of the extinction spectra of the PGMA/Ag NPs nanocomposite are fully reversible, i.e. it is possible to make a reusable VOC sensing device using the nanocomposite film. For instance, in one of our experiments the cell containing VOC was opened and the extinction spectra of the nanocomposite were recorded every 5 s. The organic vapor escaped out of the cell that cause shrinking of the PGMA matrix. As a result, the distance between Ag NPs in the array decreases while the refractive index of PGMA polymer increases. Fig. 6 depicts shift of the maximum peak position and the bandwidth variations for P and T modes. As it is expected both bands exhibit blue shift and broadening, which is in agreement with the eqn (6). The nanocomposite can withstand many cycles of exposure to organic vapors without losing its performance. The recovery (deswelling) time of the PGMA/Ag NPs sensing film in our experimental conditions can be determined from the SPR spectral shift and bandwidth dependences on vapor concentration for decreasing concentration (cell is open, Fig. 6). It is found that the recovery time is about 1 min.
Estimation of sensitivity
The detection sensitivity of PGMA/Ag NPs sensing film can be approximated as follows. We consider P mode since it exhibits higher sensitivity. The concentration of organic vapor in the cell when the solvent was completely evaporated can be calculated as follows:11
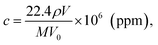 | (9) |
4. Conclusions
In general, we have demonstrated the capability of 2D array of closely spaced Ag nanoparticles embedded into PGMA host matrix to monitor presence of organic vapors in atmosphere. Namely, changes in the extinction spectra of the submicron nanocomposite film can be used to detect the vapors. The transformations of the spectra are fully reversible and reproducible upon multiple exposures. We associate this reversibility and reproducibility with the construction of the nanocomposite film where cross-linked PGMA network is capable to spatially restore its structure upon deswelling. The structure of the extinction spectrum of such nanocomposite is governed by collective surface plasmon mode excited in the Ag NPs array. Plasmon modes of two types are excited at oblique angle of incidence. They correspond to different orientation of charge oscillations in the nanoparticles with respect to the array's plane. It was found experimentally that spectral bands associated with normal and tangential components of the plasmon mode change their spectral width and position when the nanocomposite is exposed to organic vapors. The bands exhibit blue shift and spectral narrowing with the increase of vapor concentration. This is due to enlarging the spacing between neighboring NPs in the array caused by swelling of the PGMA polymer matrix. At the same time, the refractive index of the polymer film decreases with the swelling. Those two processes weaken electrodynamic coupling between LSPR in neighboring Ag NPs that explains the observed spectral changes. The level of spectral transformation is directly related to the level of polymer–solvent thermodynamic affinity, where the higher affinity corresponds to the higher level of the swelling. It was found that spectroscopic sensitivity of the nanocomposite film to chloroform (the best solvent for PGMA matrix) vapor is ∼0.02 nm ppm−1. The response time of the sensing film was found to be on the level of 25 s. The recovery time of the sensing film for next cycle of the VOC concentration measurement is about 1 min. For other organic compounds tested here (ethanol, acetonitrile, and toluene) the sensitivity is lower. However, it can be improved with chemical modification of the polymer matrix hosting nanoparticles. Therefore, we expect that the nanocomposite films (when fabricated for a certain analyte) can be effectively used as sensing element in a low-cost VOC sensor device operating in visual light.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by the NATO Science for Peace and Security Program (grant NUKR.SFPP 984617) and Ministry of Education and Science of Ukraine (grants DB/MEV No. 0118U000267, 19BF037-02, 19BF051-04). The work was also partially supported by the National Science Foundation via EPSCoR OIA 1655740 award.References
- N. T. Phan, K. H. Kim, E. C. Jeon, U. H. Kim, J. R. Sohn and S. K. Pandey, Environ. Monit. Assess., 2012, 184, 1683–1692 CrossRef CAS PubMed.
- H. Insam and M. S. A. Seewald, Biol. Fertil. Soils, 2010, 46, 199–213 CrossRef CAS.
- M. Ciganek and J. Neca, Vet. Med., 2008, 53, 641–651 CrossRef CAS.
- B. Li, G. Sauve, M. C. Iovu, M. Jeffries-El, R. Zhang, J. Cooper, S. Santhanam, L. Schultz, J. C. Revelli, A. G. Kusne, T. Kowalewski, J. L. Snyder, L. E. Weiss, G. K. Fedder, R. D. McCullough and D. N. Lambeth, Nano Lett., 2006, 6, 1598–1602 CrossRef CAS PubMed.
- V. Dua, S. P. Surwade, S. Ammu, S. R. Agnihotra, S. Jain, K. E. Roberts, S. Park, R. S. Ruoff and S. K. Manohar, Angew. Chem., Int. Ed., 2010, 49, 2154–2157 CrossRef CAS PubMed.
- X. Chen, S. G. Parker, G. Zou, W. Su and Q. J. Zhang, ACS Nano, 2010, 4, 6387–6394 CrossRef CAS PubMed.
- M. Schlupp, T. Weil, A. J. Berresheim, U. M. Wiesler, J. Bargon and K. Mullen, Angew. Chem., Int. Ed., 2001, 40, 4011–4015 CrossRef CAS.
- M. Avila, M. Zougagh, A. Escarpa and A. Rios, TrAC, Trends Anal. Chem., 2008, 27, 54–65 CrossRef CAS.
- E. D. Pellizzari, J. E. Bunch, R. E. Berkley and J. McRae, Anal. Chem., 1976, 48, 803–807 CrossRef CAS.
- L. Mondello, P. Q. Tranchida, P. Dugo and G. Dugo, Mass Spectrom. Rev., 2008, 27, 101–124 CrossRef CAS PubMed.
- X. Fan and B. Y. Du, Sens. Actuators, B, 2012, 166, 753–760 CrossRef.
- Y. Fu and H. O. Finklea, Anal. Chem., 2003, 75, 5387–5393 CrossRef CAS PubMed.
- J. A. J. Brunink, C. DiNatale, F. Bungaro, F. A. M. Davide, A. Damico, R. Paolesse, T. Boschi, M. Faccio and G. Ferri, Anal. Chim. Acta, 1996, 325, 53–64 CrossRef CAS.
- G. Kleefisch, C. Kreutz, J. Bargon, G. Silva and C. A. Schalley, Sensors, 2004, 4, 136–146 CrossRef CAS.
- T. Moriizumi, Thin Solid Films, 1988, 160, 413–429 CrossRef.
- B. Holcroft and G. G. Roberts, Thin Solid Films, 1988, 160, 445–452 CrossRef CAS.
- R. Capan, H. Goktas, Z. Ozbek, S. Sen, M. E. Ozel and F. Davis, Appl. Surf. Sci., 2015, 350, 129–134 CrossRef CAS.
- Y. Acikbas, R. Capan, M. Erdogan, L. Bulut and C. Soykan, Sens. Actuators, B, 2017, 241, 1111–1120 CrossRef CAS.
- S. Malynych and G. Chumanov, J. Am. Chem. Soc., 2003, 125, 2896–2898 CrossRef CAS PubMed.
- E. Ozbay, Science, 2006, 311, 189–193 CrossRef CAS PubMed.
- M. I. Stockman, Opt. Express, 2011, 19, 22029–22106 CrossRef PubMed.
- K. L. Kelly, E. Coronado, L. L. Zhao and G. C. Schatz, J. Phys. Chem. B, 2003, 107, 668–677 CrossRef CAS.
- G. McNay, D. Eustace, W. E. Smith, K. Faulds and D. Graham, Appl. Spectrosc., 2011, 65, 825–837 CrossRef CAS PubMed.
- O. A. Yeshchenko, I. S. Bondarchuk and M. Y. Losytskyy, J. Appl. Phys., 2014, 116 Search PubMed.
- F. Le, D. W. Brandl, Y. A. Urzhumov, H. Wang, J. Kundu, N. J. Halas, J. Aizpurua and P. Nordlander, ACS Nano, 2008, 2, 707–718 CrossRef CAS PubMed.
- K. Ode, M. Honjo, Y. Takashima, T. Tsuruoka and K. Akamatsu, ACS Appl. Mater. Interfaces, 2016, 8, 20522–20526 CrossRef CAS PubMed.
- B. Heli, E. Morales-Narvaez, H. Golmohammadi, A. Ajji and A. Merkoci, Nanoscale, 2016, 8, 7984–7991 RSC.
- S. Malynych and G. Chumanov, J. Opt. A: Pure Appl. Opt., 2006, 8, S144–S147 CrossRef CAS.
- L. L. Zhao, K. L. Kelly and G. C. Schatz, J. Phys. Chem. B, 2003, 107, 7343–7350 CrossRef CAS.
- O. Yeshchenko, I. Bondarchuk, S. Malynych, Y. Galabura, G. Chumanov and I. Luzinov, Plasmonics, 2015, 10, 655–665 CrossRef CAS.
- O. A. Yeshchenko, I. S. Bondarchuk, S. Z. Malynych, Y. Galabura, G. Chumanov, I. Luzinov and A. O. Pinchuk, Plasmonics, 2017, 12, 1571–1580 CrossRef CAS.
- K. S. Iyer, B. Zdyrko, S. Malynych, G. Chumanov and I. Luzinov, Soft Matter, 2011, 7, 2538–2542 RSC.
- B. Zdyrko and I. Luzinov, Macromol. Rapid Commun., 2011, 32, 859–869 CrossRef CAS PubMed.
- K. S. Iyer, B. Zdyrko, H. Malz, J. Pionteck and I. Luzinov, Macromolecules, 2003, 36, 6519–6526 CrossRef CAS.
- B. Zdyrko, V. Klep, X. W. Li, Q. Kang, S. Minko, X. J. Wen and I. Luzinov, Mater. Sci. Eng., C: Biomimetic Supramol. Syst., 2009, 29, 680–684 CrossRef CAS.
- K. Ramaratnam, S. K. Iyer, M. K. Kinnan, G. Chumanov, P. J. Brown and I. Luzinov, J. Eng. Fibers Fabr., 2008, 3, 1–14 CAS.
- V. Bliznyuk, Y. Galabura, R. Burtovyy, P. Karagani, N. Lavrik and I. Luzinov, Phys. Chem. Chem. Phys., 2014, 16, 1977–1986 RSC.
- N. Borodinov, A. P. Soliani, Y. Galabura, B. Zdyrko, C. Tysinger, S. Novak, Q. Du, Y. Huang, V. Singh, Z. Han, J. Hu, L. Kimerling, A. M. Agarwal, K. Richardson and I. Luzinov, ACS Nano, 2016, 10, 10716–10725 CrossRef CAS.
- M. Chyasnavichyus, V. Tsyalkovsky, B. Zdyrko and I. Luzinov, Macromol. Rapid Commun., 2012, 33, 237–241 CrossRef CAS.
- J. Giammarco, B. Zdyrko, L. Petit, J. D. Musgraves, J. Hu, A. Agarwal, L. Kimerling, K. Richardson and I. Luzinov, Chem. Commun., 2011, 47, 9104–9106 RSC.
- Y. Galabura, A. P. Soliani, J. Giammarco, B. Zdyrko and I. Luzinov, Soft Matter, 2014, 10, 2567–2573 RSC.
- V. Singh, P. T. Lin, N. Patel, H. Lin, L. Li, Y. Zou, F. Deng, C. Ni, J. Hu, J. Giammarco, A. P. Soliani, B. Zdyrko, I. Luzinov, S. Novak, J. Novak, P. Wachtel, S. Danto, J. D. Musgraves, K. Richardson, L. C. Kimerling and A. M. Agarwal, Sci. Technol. Adv. Mater., 2014, 15, 014603 CrossRef PubMed.
- H. Li, Z. Chen, N. Borodinov, Y. Z. Shao, I. Luzinov, G. F. Yu and P. S. Wang, IEEE Sens. J., 2017, 17, 3323–3331 CAS.
- S. Malynych, I. Luzinov and G. Chumanov, J. Phys. Chem. B, 2002, 106, 1280–1285 CrossRef CAS.
- D. D. Evanoff and G. Chumanov, J. Phys. Chem. B, 2004, 108, 13948–13956 CrossRef CAS.
- N. Borodinov, D. Gil, M. Savchak, C. E. Gross, N. S. Yadavalli, R. L. Ma, V. V. Tsukruk, S. Minko, A. Vertegel and I. Luzinov, ACS Appl. Mater. Interfaces, 2018, 10, 13941–13952 CrossRef CAS PubMed.
- B. Zdyrko, M. K. Kinnan, G. Chumanov and I. Luzinov, Chem. Commun., 2008, 1284–1286, 10.1039/b717222b.
- S. Malynych, N. L. Dmitruk and I. E. Moroz, Eur. Phys. J.: Appl. Phys., 2013, 64, 20402 CrossRef.
- L. H. Sperling, Introduction to Physical Polymer Science, Wiley-Interscience Hoboken, New Jersey, 4th edn, 2006 Search PubMed.
- D. W. Van Krevelen, Properties of polymers : their correlation with chemical structure, their numerical estimation and prediction from additive group contributions, Elsevier, Amsterdam; New York, 2000 Search PubMed.
- C. M. Hansen, Hansen solubility parameters: A User's Handbook, CRC Press, Boca Raton, 2nd edn, 2007 Search PubMed.
- C. M. Hansen, in Paint and Coating Testing Manual: Fifteenth Edition of the Gardner-Sward Handbook, ed. J. V. Koleske, ASTM International, West Conshohocken, 2012, ch. 38, pp. 470–494 Search PubMed.
- C. M. Hansen, S. Abbott, H. Yamamoto and R. S. Valpey III, HSPiP: Hansen Solubility Parameters in Practice, 2009 Search PubMed.
- U. Kreibig and M. Vollmer, Optical properties of metal clusters, Springer, Berlin; New York, 1995 Search PubMed.
- M. K. Kinnan and G. Chumanov, J. Phys. Chem. C, 2010, 114, 7496–7501 CrossRef CAS.
- J. R. Rumble, CRC handbook of chemistry and physics, Boca Raton, CRC Press, 99 edn, 2018 Search PubMed.
| This journal is © The Royal Society of Chemistry 2019 |