Open Access Article
Open Access ArticleTailoring of the electronic property of Zn-BTC metal–organic framework via ligand functionalization: an ab initio investigation†
Gemechis D. Degaga *a,
Ravindra Pandey
*a,
Ravindra Pandey *a,
Chansi Guptab and
Lalit Bharadwajb
*a,
Chansi Guptab and
Lalit Bharadwajb
aDepartment of Physics, Michigan Technological University, 1400 Townsend Drive, Houghton, MI 49931, USA. E-mail: gdegaga@mtu.edu; pandey@mtu.edu
bAmity Institute of Nanotechnology, Amity University, Noida, UP-201303, India
First published on 7th May 2019
Abstract
Metal–organic frameworks (MOFs) are porous materials of recent interest due to their promising properties for technological applications. In this paper, the structure–property relationships of pristine and functionalized Zn-BTC (Zn3(BTC)2) MOFs are investigated. The results based on density functional theory (DFT) find that MOFs with coordinatively saturated secondary building units (SBU) are metallic, and MOFs with coordinatively unsaturated SBU are semi-conducting. The ligand functionalization with electron acceptor (cyano-) and electron donor (amino-) groups appears to tailor the electronic properties of Zn-BTC MOFs; amino-functionalization led to a significant upward shift of the band-edges whereas cyano-functionalization yields shifting of band-edges in the opposite direction, which led to a narrowing of the band gap. Modifying the electronic properties through such ligand functionalization design principles can be useful in engineering MOFs for gas sensing and device applications.
1 Introduction
Metal–organic frameworks (MOFs), or porous coordination networks, are a class of advanced crystalline materials assembled from inorganic nodes connected by organic ligands.1–3 In the past two decades, MOFs’ unique structural properties and enormous possibility for chemical functionality have brought them to the attention of researchers in both academia and industry.4–6 From a crystal engineering point of view, MOFs’ structures allow the presence of a wide variety of microporous and mesoporous void cavities, thereby providing unique opportunities for the functionalization of both the organic linkers and the void, which enables great tunability of the MOFs’ properties.7–10While preserving or improving the porosity and surfaces areas of MOF structures, ligand functionalization has been demonstrated to enhance the gas adsorption phenomena,11–13 provide high selectivity in gas separation technologies,14,15 improve gas sensing,16,17 and catalytic properties.18,19 The functionalization of the ligand can be done either by substituting the ligand by its corresponding longer polymer or by adding a functional group to the parent ligand.15,20,21 An elongated ligand results in the formation of isoreticular families of the original MOF. Such a functionalization largely influences the porosity (surface area and pore volume) and pore structure (pore size and pore shape) which allows for the insertion of relatively large biological molecules such DNA, RNA, and proteins as well as the accommodation of more molecules per unit cell.22–26 We also note that ligand functionalization by functional groups is highly effective in fine-tuning electronic properties of the parent MOF structures. Additionally, this method of functionalization is key to improving the efficiency of MOFs in certain applications. For instance, as a host matrix for gas adsorption and storage, energy efficient gas mixture separation, gas sensing, catalysis, semiconductor, magnetic, and optical materials.15,26–30
Experimental exploration of the properties of the plethora of MOF structures increasingly reported in the literature is difficult to conduct at an accelerated pace, considering the time required to synthesize and characterize even a single MOF structure. Moreover, atomic level fundamental understanding, generally, cannot be obtained readily from experimental stand point to address various macroscopic properties. In this direction, theoretical modeling is not only a necessary complement to experimental investigations but is also used as an accelerated investigation and predictive tool by itself. Computational studies also provide the opportunity to study and characterize MOF materials based on atomistic-level information. Several reviews and published works show the increasing accuracy of predictive results due to the increasingly accurate construction of molecular dynamics (MD) force fields (FF) and DFT approximations for various MOFs’ property studies.31–37 The enormous possible combination of the inorganic and organic building blocks of thousands of MOF structures has also attracted the use of machine learning approaches for large-scale screening and prediction of hypothetical MOF structures for specific applications.38–40
One of the well-studied MOF structures is the HKUST-1 (or MOF-199), for which the isostructural families are represented by the formula M3(BTC)2, where M = Cu, Zn, Fe, or other metal atoms. Here, the organic ligand is benzene-1,3,5-tricarboxylate (BTC). The Cu3(BTC)2 MOF has shown promising use in various technologies. Recent studies show that functionalization of the BTC ligand of these MOF structures can further improve device efficiencies.41,42 For instance, amino and alkyl substitutions in Cu-BTC MOFs have been demonstrated to enhance the adsorption properties and gas-uptake of the pristine MOF crystal.43,44
It is well established that a fundamental understanding of the structure, stability and electronic properties of BTC MOFs is essential for their applications in sensing and semiconductor device engineering.45 To date, a few experimental and theoretical studies have considered the M3(BTC)2 MOF family.46 More importantly, ligand-functionalized BTC MOFs have not been theoretically investigated, despite synthesis of the stable crystalline structures of this MOF family.43,44 In this paper, we investigate the electronic properties of the pristine and ligand-functionalized Zn-BTC MOFs by employing density functional theory (DFT). Two functional groups were chosen, amino (–NH2) as a strong electron donating group and cyano (–CN) as a strong electron withdrawing group. This choice was inspired by the relative electron affinity of these functional groups as they are from the extreme opposite ends of the electron donating/accepting spectrum. In addition, recent results show not only the synthetic possibility of such functionalization of MOF structures but also the promising property improvements such as thermal stability, chemical decomposition, and proton conductivity of the original unaltered pristine MOF through such ligand functionalizations.43,47,48 The influence of amino substitution and cyanation on electronic properties, however, has never been reported. In this regard, our calculated results show that ligand functionalization of Zn-BTC MOFs with the electron donor (–NH2) and electron acceptor (–CN) groups leads to significant modification in the electronic properties of the pristine BTC MOF.
2 Method
Electronic structure calculations based on density functional theory (DFT) were performed using the Quantum Espresso Plane-Wave package.49 For each atom of Zn-BTC MOFs, the core-electrons were treated using the ultra-soft pseudo-potentials while the Perdew–Burke–Ernzerhof (PBE)50 functional form was used for the exchange and correlation approximation to DFT. For more accurate band gap predictions, we also used the HSE06![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51 functional with the inclusion of 25% of exact Hartree–Fock exchange. The wave function and density cutoffs were set to be 60 and 460 Ry, respectively. Atomic positions in the periodic unit cell were allowed to relax until the total forces on each atom were less than 2.6 × 10−4 eV Å−1 with structural symmetry kept preserved during geometry optimization calculations while self-consistency tolerance was set to 10−6 Ry. Note that calculations considering only Γ-point were sufficient to yield convergence of total energies within the numerical accuracy of 1 meV per atom. For density of states (DOS) calculations, integration of the Brillouin zone were made on a more dense 8 × 8 × 8 Monkhorst–Pack k-point mesh.52 XCrySDen crystalline- and molecular-structure visualization package was used for structural visualization and post-processing charge density plots.53
51 functional with the inclusion of 25% of exact Hartree–Fock exchange. The wave function and density cutoffs were set to be 60 and 460 Ry, respectively. Atomic positions in the periodic unit cell were allowed to relax until the total forces on each atom were less than 2.6 × 10−4 eV Å−1 with structural symmetry kept preserved during geometry optimization calculations while self-consistency tolerance was set to 10−6 Ry. Note that calculations considering only Γ-point were sufficient to yield convergence of total energies within the numerical accuracy of 1 meV per atom. For density of states (DOS) calculations, integration of the Brillouin zone were made on a more dense 8 × 8 × 8 Monkhorst–Pack k-point mesh.52 XCrySDen crystalline- and molecular-structure visualization package was used for structural visualization and post-processing charge density plots.53
3 Results and discussion
3.1 Structural properties
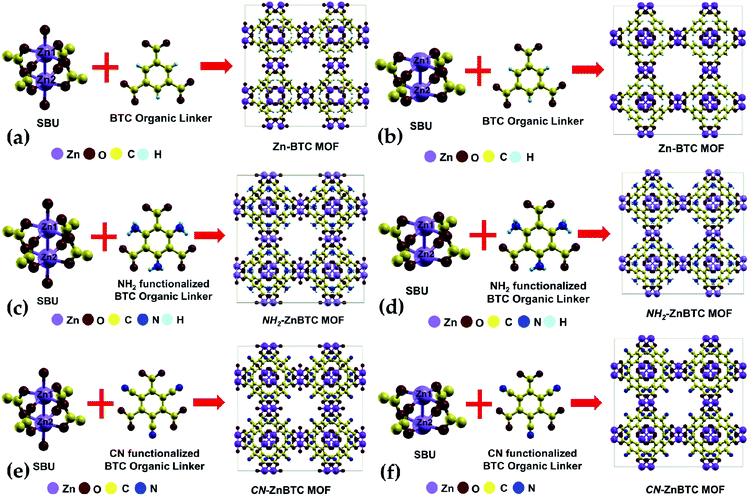
The crystallographic data suggests Zn-BTC MOF to be a cubic structure belonging to the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group with lattice parameters of a = b = c = 26.536 Å.54 Structurally, a BTC MOF can be characterized by a secondary building unit (SBU), six per unit cell, having a paddle-wheel-like configuration consisting of two bonded metal atoms along the wheel axis. Each paddle-wheel is connected to neighboring SBUs through four organic BTC linkers. Upon direct synthesis, the SBUs can be coordinatively saturated (Fig. 1a, c and e) where each metal center is bonded to five neighboring oxygen atoms, four of which are from the BTC linkers and the fifth one from the terminal oxygen atom. By using a post-synthesis modification (PSM) technique, the terminal oxygen atoms can be removed. This leaves the SBUs coordinatively unsaturated (Fig. 1b, d and f).54 These coordinatively unsaturated open metal sites provide two adsorption sites per SBU, a total of 12 primary open adsorption metal sites per unit cell.
m space group with lattice parameters of a = b = c = 26.536 Å.54 Structurally, a BTC MOF can be characterized by a secondary building unit (SBU), six per unit cell, having a paddle-wheel-like configuration consisting of two bonded metal atoms along the wheel axis. Each paddle-wheel is connected to neighboring SBUs through four organic BTC linkers. Upon direct synthesis, the SBUs can be coordinatively saturated (Fig. 1a, c and e) where each metal center is bonded to five neighboring oxygen atoms, four of which are from the BTC linkers and the fifth one from the terminal oxygen atom. By using a post-synthesis modification (PSM) technique, the terminal oxygen atoms can be removed. This leaves the SBUs coordinatively unsaturated (Fig. 1b, d and f).54 These coordinatively unsaturated open metal sites provide two adsorption sites per SBU, a total of 12 primary open adsorption metal sites per unit cell.
Functionalization of the BTC ligand was done in such a way that (–NH2) or (–CN) groups substitute H atoms, as shown in Fig. 1c, d, e and f. The calculated ground state structure of Zn-BTC is in good agreement with the experimentally measured structure.54 The difference between the computed and measured cell-parameters is about 1.8% (see ESI Table 1†). Note that the measured cell-parameter is obtained from Zn-BTC MOFs contaminated with dimethylformamide molecules, left as a residue from the synthesis process. For the ligand-functionalized Zn-BTC MOFs, the computed cell-parameters are slightly increased relative to their corresponding pristine structures, which, in turn, is reflected in the increased unit cell volumes as shown in Table 1. Between saturated and unsaturated SBU Zn-BTC MOFs, a noticeable structural change is predicted for the metal–metal (Zn1–Zn2) bond lengths within a secondary building unit; the Zn1–Zn2 bond lengths are substantially shortened in the unsaturated SBU MOFs. This trend is in agreement with experiment which finds shortening of the metal–metal bond length after the removal of terminal oxygen ligands due to the post-synthesis gas evacuation.54
| MOF system | SBU | Cell parameters (Å) | Cell volume (Å3) | Bond lengths (Å) | Cohesive energy (eV per atom) | |
|---|---|---|---|---|---|---|
| a = b = c | Zn1–Zn2 | 〈Zn–O〉 | ||||
| (bare)-Zn-BTC | Saturated | 27.02 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 726.77 726.77 |
3.38 | 2.03 | −6.93 |
| (bare)-Zn-BTC | Unsaturated | 27.08 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 858.48 858.48 |
2.57 | 2.03 | −6.55 |
| NH2-Zn-BTC | Saturated | 27.72 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300.00 300.00 |
3.26 | 2.06 | −6.74 |
| NH2-Zn-BTC | Unsaturated | 27.46 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 706.26 706.26 |
2.46 | 2.01 | −6.51 |
| CN-Zn-BTC | Saturated | 27.30 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 346.42 346.42 |
3.54 | 2.06 | −8.15 |
| CN-Zn-BTC | Unsaturated | 27.18 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 079.29 079.29 |
2.68 | 2.03 | −7.72 |
The calculated cohesive energy values listed in Table 1 suggest that the saturated SBU MOFs are slightly energetically more stable than their corresponding unsaturated SBU MOFs. Also, the cyano-functionalized MOFs are relatively energetically more stable than the amino-functionalized MOFs. The crystallinity of the amino- and cyano- functionalized Zn-BTC MOFs was preserved and confirmed by the computed powder X-ray diffraction (XRD) pattern analysis, as shown in Fig. 2. The XRD patterns of the functionalized MOFs coincide with that of the pristine Zn-BTC MOFs, except for minor nuances in peak intensities due to the presence of additional atoms through functionalization or removal of the terminal oxygen atoms. We can then say that the topology is retained and these functionalized members of the Zn-BTC family are isostructural.
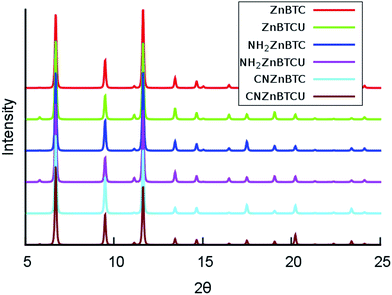 | ||
| Fig. 2 Simulated powder X-ray diffraction patterns for pristine and functionalized Zn-BTC MOF systems for both the saturated and unsaturated cases (θ is in degrees). | ||
3.2 Electronic properties
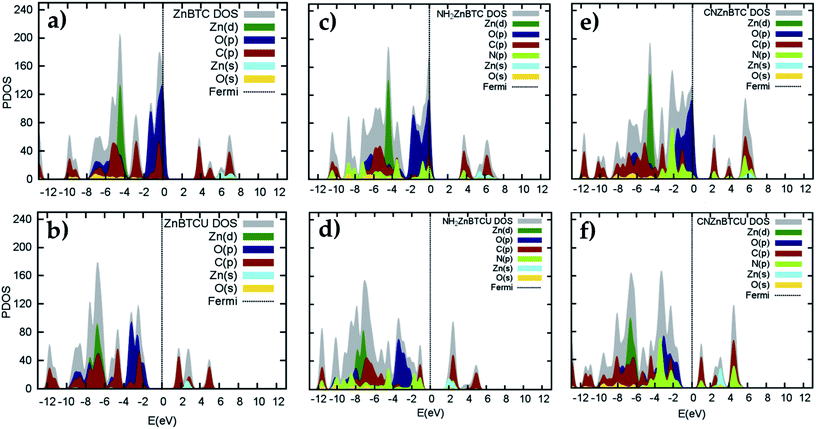
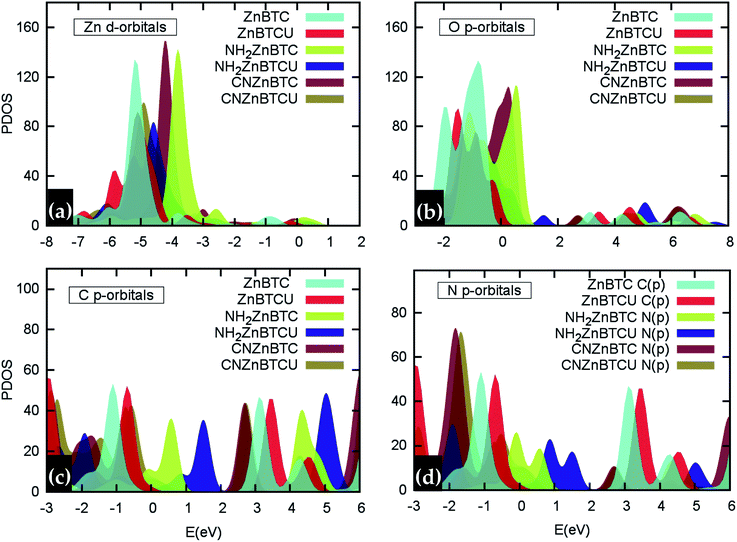
Density of states (DOS) calculations show that the pristine and ligand functionalized Zn-BTC MOFs with coordinatively saturated SBUs have metallic character. On the other hand, the coordinatively unsaturated Zn-BTC MOFs are semi-conducting with the Fermi energy lying between the valence band maximum (VBM) and the conduction band minimum (CBM) energy bands (see Fig. 3). In the amino-substituted unsaturated SBU MOFs, the Fermi energy lies close to the top of the valence band while in the cyano-substituted unsaturated SBU MOFs, the Fermi energy lies close to the bottom of the conduction band. This is due to the non-uniform distribution of N 2p and C 2p states at the band-edges introduced through functionalizations. Fig. 5 displays the relative positions of the VBM and CBM for the pristine and ligand-functionalized Zn-BTC MOFs.The calculated band gap is 2.4 eV for the unsaturated SBU pristine MOFs. This is larger than what is reported for pristine Cu-BTC MOFs (Eg ≈ 2.0 eV) at the same level of theory.55 Large band-edge shifts are predicted for the amino-substituted unsaturated SBU MOF relative to the VBM/CBM of the pristine counterpart; VBM is shifted up by 1.7 eV while CBM is shifted up by 1.2 eV, yielding a band gap of 1.9 eV. On the other hand, in the cyano-substituted unsaturated SBU MOF, VBM is shifted up only by 0.4 eV, while CBM is shifted down by 0.6 eV relative to the pristine unsaturated SBU MOF. Cyano-substitution of the BTC ligand resulted in a band gap of 1.4 eV, substantially narrowing the gap with respect to the pristine unsaturated SBU MOF. Fig. 3a and b show the calculated projected density of states (PDOS) for the atomic orbitals of both saturated and unsaturated SBU pristine MOFs. In both cases, it is found that the top of the valence band is dominated by O 2p orbitals while the bottom of the conduction band is dominated by C 2p orbitals. Thus, from an electronic principle stand point, the modifications in the valence and conduction band-edges of Zn-BTC MOFs require the introduction of atoms having different 2p orbital energies as dopants or through functionalization. This is the case for the amino- and cyano-substitution considered in this work. In the amino-functionalized saturated SBU MOF, VBM is dominated by O 2p states with minimal contribution from C 2p and N 2p states while CBM is dominated by C 2p states with small contribution from N 2p states, as shown in Fig. 3c.
In the amino-functionalized unsaturated SBU MOF, however, the top of the valence band is dominated by C 2p and N 2p while the bottom of the conduction band is characterized by C 2p and Zn 1s with a small contribution from O 2s states as shown in Fig. 3d. In the cyano-functionalized saturated SBU MOF, the top of the valence band is dominated by only O 2p states (Fig. 3e) while the bottom of the conduction band is dominated by C 2p with small contributions from N 2p states. In the cyano-functionalized unsaturated Zn-BTC MOF, the top of the valence band is dominated by O 2p and N 2p states while the bottom of the conduction band is dominated by C 2p, with small contributions from N 2p states, as shown in Fig. 3f.
As shown in Fig. 4, in saturated SBU MOFs, significant shifting of Zn 3d orbital centers is observed for amino- and cyano-functionalized MOFs with respect to the pristine Zn-BTC MOF. While the O 2p orbital center shift is also noticeable for functionalized saturated frameworks, the C 2p and N 2p orbital shifts are stronger for the unsaturated amino-substituted MOF.
 | ||
| Fig. 4 Relative shifting of (a) Zn 3d, (b) O 2p, (c) C 2p and (d) N 2p orbital centers in functionalized MOFs with respect to the pristine Zn-BTC MOFs. | ||
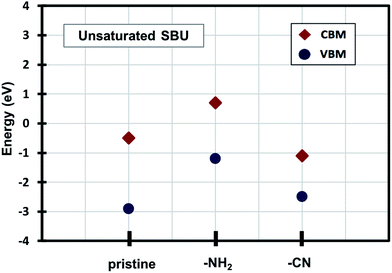 | ||
| Fig. 5 Relative positions of the valence band maximum and conduction band minimum of pristine and functionalized Zn-BTC MOFs. | ||
To investigate atomic charge transfer and redistribution at the SBU upon gas evacuation and ligand functionalization, we computed atomic charges for Zn, bridging O (Ob), and terminal O (Ot) atoms using Lowdin partial charge analysis.56 In the unsaturated SBU MOFs, removal of terminal oxygen atoms leads to a transfer of charges to the metal centers and Ob atoms. In the saturated SBU MOFs, on the other hand, charge accumulation is seen on Ot atoms with the amino-functionalization while the cyano-functionalization resulted in a charge depletion on Ot atoms (see Table 2).
| MOF systems | SBU | Atomic charges (e) | ||
|---|---|---|---|---|
| Zn | Ob | Ot | ||
| (bare)-Zn-BTC | Saturated | 10.43 | 6.46 | 6.52 |
| (bare)-Zn-BTC | Unsaturated | 10.57 | 6.55 | — |
| NH2-Zn-BTC | Saturated | 10.49 | 6.52 | 6.80 |
| NH2-Zn-BTC | Unsaturated | 10.58 | 6.58 | — |
| CN-Zn-BTC | Saturated | 10.45 | 6.46 | 6.46 |
| CN-Zn-BTC | Unsaturated | 10.54 | 6.52 | — |
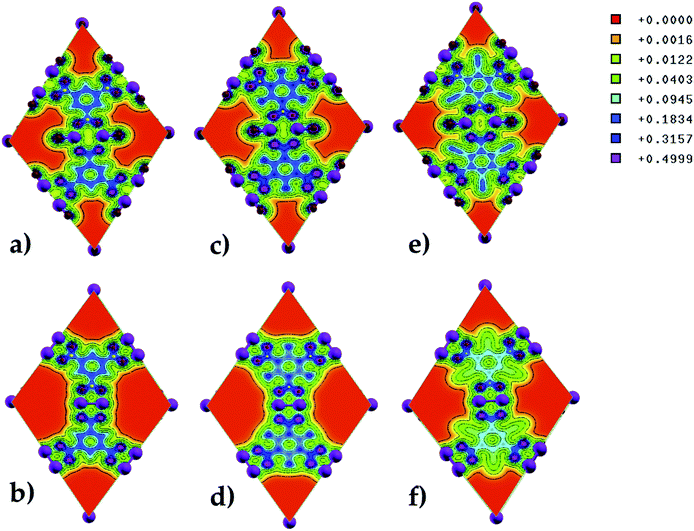
The electron charge density along the (100) direction was computed to determine the charge distribution in pristine and functionalized Zn-BTC MOFs (see Fig. 6). A strong charge localization is seen at the terminal and bridging oxygen atoms in the MOF lattice. In saturated SBU MOFs, there exists a larger orbital overlap between the metal atoms and oxygen terminal atoms than the metal atoms and bridging oxygen atoms. In unsaturated SBU MOFs, as the Zn–Zn distance shortened, the orbital overlap becomes more pronounced between the metal atoms and the bridging oxygen atoms. We may therefore say that the building units are strongly bonded for the case of unsaturated SBU MOFs. Due to the electron withdrawing nature of the cyano-groups, significant charge depletion is observed on the benzene rings of the BTCs in the unsaturated SBU MOF. In the amino-functionalized unsaturated SBU MOF, charge withdrawal is observed on C atoms bonded to the amino-groups; i.e. all the C atoms in BTCs do not share the same charge distribution as in the case of the pristine unsaturated SBU MOF.
A widely recognized fact regarding semi-local functionals approximation to DFT is the underestimation of band gaps. Such limitations can be overcome by using hybrid functionals.57 Even though the trends of the effects of ligand functionalization are thoroughly presented with PBE semi-local functionals, more accurate prediction of the band gaps was computed using hybrid HSE06 functionals.51 However, it should be noted that, since it is generally computationally expensive to perform geometry optimization with HSE06 for unit-cells containing a large number of atoms and for the cases where the majority of the space in the unit-cell is void with no atom occupation, especially in the case of MOF structures, a single point energy calculation was performed on geometries optimized at the PBE level. For all the saturated Zn-BTC MOFs, HSE06 predicts metallic character with no band gap. The HSE06 calculated band gap for the unsaturated pristine Zn-BTC MOF was recorded to be 3.4 eV. No experimental band gap has been reported for this structure, however, the calculated band gap is as large as what is experimentally and theoretically reported for Cu-BTC MOF (HKUST-1),55 see Table 3. The gaps opened up for HSE06 by ≈1 eV for the unsaturated pristine and amino-functionalized Zn-BTC as generally expected for materials exhibiting semiconducting behavior. The HSE06 results show that amino-functionalization has reduced the gap of the Zn-BTC MOF by ≈0.5 eV. Such reduction magnitude and trend has also been observed experimentally for UIO-66-Zr and UIO-67-Zn MOFs after amino-functionalization.37,48 HSE06 predicts the unsaturated cyano-functionalization to be metallic with no band gap supporting the substantial gap reduction trend seen in PBE-DFT calculations.
4 Summary
The structural and electronic properties of pristine and ligand functionalized Zn-BTC MOFs were determined using density functional theory. Amino (–NH2) and cyano (–CN) groups were used as strong electron donating and electron withdrawing groups respectively. Pristine and ligand functionalized Zn-BTC MOFs with coordinatively saturated SBUs are found to have metallic character while coordinatively unsaturated SBU MOFs are predicted to be semi-conducting with a finite band gap. Amino-functionalization of the BTC ligand resulted in a noticeable upward shifting of band-edges. On the other hand, cyano-functionalization caused the valence and conduction band-edges to shift in opposite directions yielding a smaller band gap and could farther lead to a metallic state. Electronic property manipulation through ligand functionalization presented in this work seems promising in tailoring novel and efficient MOF materials for various technological applications.Conflicts of interest
No conflict of interest is declared.Acknowledgements
Results reported in this work were obtained through the use of Superior, a high-performance computing (HPC) facility at Michigan Technological University.References
- H. Li, M. Eddaoudi, M. O’Keeffe and O. M. Yaghi, Nature, 1999, 402, 276 CrossRef CAS.
- O. M. Yaghi, M. O’Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705 CrossRef CAS PubMed.
- G. Férey, Chem. Soc. Rev., 2008, 37, 191–214 RSC.
- O. M. Yaghi, Nat. Mater., 2007, 6, 92 CrossRef CAS PubMed.
- O. M. Yaghi, Reticular Chemistry Construction, Properties, and Precision Reactions of Frameworks, 2016 Search PubMed.
- G. D. Degaga and L. Valenzano, Theor. Chem. Acc., 2018, 137, 42 Search PubMed.
- E. Klontzas, A. Mavrandonakis, E. Tylianakis and G. E. Froudakis, Nano Lett., 2008, 8, 1572–1576 CrossRef PubMed.
- Z. Wang and S. M. Cohen, Chem. Soc. Rev., 2009, 38, 1315–1329 RSC.
- K. K. Gangu, S. Maddila, S. B. Mukkamala and S. B. Jonnalagadda, Inorg. Chim. Acta, 2016, 446, 61–74 CrossRef CAS.
- P. Silva, S. M. Vilela, J. P. Tomé and F. A. A. Paz, Chem. Soc. Rev., 2015, 44, 6774–6803 RSC.
- R. Luebke, J. F. Eubank, A. J. Cairns, Y. Belmabkhout, L. Wojtas and M. Eddaoudi, Chem. Commun., 2012, 48, 1455–1457 RSC.
- F. Ke, L.-G. Qiu, Y.-P. Yuan, F.-M. Peng, X. Jiang, A.-J. Xie, Y.-H. Shen and J.-F. Zhu, J. Hazard. Mater., 2011, 196, 36–43 CrossRef CAS PubMed.
- G. D. Degaga and L. Valenzano, Chem. Phys. Lett., 2016, 660, 313–319 CrossRef CAS.
- B. Zornoza, A. Martinez-Joaristi, P. Serra-Crespo, C. Tellez, J. Coronas, J. Gascon and F. Kapteijn, Chem. Commun., 2011, 47, 9522–9524 RSC.
- Y. Zhao, H. Wu, T. J. Emge, Q. Gong, N. Nijem, Y. J. Chabal, L. Kong, D. C. Langreth, H. Liu and H. Zeng, et al., Chem.–Eur. J., 2011, 17, 5101–5109 CrossRef CAS PubMed.
- G. Nickerl, I. Senkovska and S. Kaskel, Chem. Commun., 2015, 51, 2280–2282 RSC.
- F.-Y. Yi, D. Chen, M.-K. Wu, L. Han and H.-L. Jiang, ChemPlusChem, 2016, 81, 675–690 CrossRef CAS.
- A. Herbst, A. Khutia and C. Janiak, Inorg. Chem., 2014, 53, 7319–7333 CrossRef CAS PubMed.
- Y. Fu, D. Sun, Y. Chen, R. Huang, Z. Ding, X. Fu and Z. Li, Angew. Chem., Int. Ed., 2012, 51, 3364–3367 CrossRef CAS PubMed.
- C. H. Hendon, D. Tiana, M. Fontecave, C. Sanchez, L. D’arras, C. Sassoye, L. Rozes, C. Mellot-Draznieks and A. Walsh, J. Am. Chem. Soc., 2013, 135, 10942–10945 CrossRef CAS PubMed.
- X. Lin, I. Telepeni, A. J. Blake, A. Dailly, C. M. Brown, J. M. Simmons, M. Zoppi, G. S. Walker, K. M. Thomas and T. J. Mays, et al., J. Am. Chem. Soc., 2009, 131, 2159–2171 CrossRef CAS PubMed.
- J. L. Rowsell, A. R. Millward, K. S. Park and O. M. Yaghi, J. Am. Chem. Soc., 2004, 126, 5666–5667 CrossRef CAS PubMed.
- M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O’Keeffe and O. M. Yaghi, Science, 2002, 295, 469–472 CrossRef CAS PubMed.
- Y. Jia, B. Wei, R. Duan, Y. Zhang, B. Wang, A. Hakeem, N. Liu, X. Ou, S. Xu and Z. Chen, et al., Sci. Rep., 2014, 4, 5929 CrossRef CAS PubMed.
- H. Furukawa, K. E. Cordova, M. O’Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- G. D. Degaga and L. Valenzano, Chem. Phys. Lett., 2017, 682, 168–174 CrossRef CAS.
- G. E. Cmarik, M. Kim, S. M. Cohen and K. S. Walton, Langmuir, 2012, 28, 15606–15613 CrossRef CAS PubMed.
- D. G. Park, H. J. Cho and K. Y. Lim, Method of forming a metal gate in a semiconductor device using atomic layer deposition process, 2007, US Pat., 7,157,359.
- J. Park, H. Kim and Y. Jung, J. Phys. Chem. Lett., 2013, 4, 2530–2534 CrossRef CAS.
- J. Heine and K. Müller-Buschbaum, Chem. Soc. Rev., 2013, 42, 9232–9242 RSC.
- M. Tafipolsky, S. Amirjalayer and R. Schmid, J. Comput. Chem., 2007, 28, 1169–1176 CrossRef CAS PubMed.
- S. Bureekaew, S. Amirjalayer, M. Tafipolsky, C. Spickermann, T. K. Roy and R. Schmid, Phys. Status Solidi B, 2013, 250, 1128–1141 CrossRef CAS.
- S. S. Han, S.-H. Choi and A. C. Van Duin, Chem. Commun., 2010, 46, 5713–5715 RSC.
- Q. Yang, D. Liu, C. Zhong and J.-R. Li, Chem. Rev., 2013, 113, 8261–8323 CrossRef CAS PubMed.
- S. O. Odoh, C. J. Cramer, D. G. Truhlar and L. Gagliardi, Chem. Rev., 2015, 115, 6051–6111 CrossRef CAS PubMed.
- L. Grajciar, A. D. Wiersum, P. L. Llewellyn, J.-S. Chang and P. Nachtigall, J. Phys. Chem. C, 2011, 115, 17925–17933 CrossRef CAS.
- S. Chavan, J. G. Vitillo, D. Gianolio, O. Zavorotynska, B. Civalleri, S. Jakobsen, M. H. Nilsen, L. Valenzano, C. Lamberti and K. P. Lillerud, et al., Phys. Chem. Chem. Phys., 2012, 14, 1614–1626 RSC.
- G. Borboudakis, T. Stergiannakos, M. Frysali, E. Klontzas, I. Tsamardinos and G. E. Froudakis, npj Comput. Mater., 2017, 3, 40 CrossRef.
- C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Nat. Chem., 2012, 4, 83 CrossRef CAS PubMed.
- M. Witman, S. Ling, S. Anderson, L. Tong, K. C. Stylianou, B. Slater, B. Smit and M. Haranczyk, Chem. Sci., 2016, 7, 6263–6272 RSC.
- S. Bordiga, L. Regli, F. Bonino, E. Groppo, C. Lamberti, B. Xiao, P. Wheatley, R. Morris and A. Zecchina, Phys. Chem. Chem. Phys., 2007, 9, 2676–2685 RSC.
- A. Asfaram, M. Ghaedi and K. Dashtian, Ultrason. Sonochem., 2017, 34, 561–570 CrossRef CAS PubMed.
- K. Peikert, F. Hoffmann and M. Fröba, Chem. Commun., 2012, 48, 11196–11198 RSC.
- Y. Cai, Y. Zhang, Y. Huang, S. R. Marder and K. S. Walton, Cryst. Growth Des., 2012, 12, 3709–3713 CrossRef CAS.
- H. C. Streit, M. Adlung, O. Shekhah, X. Stammer, H. K. Arslan, O. Zybaylo, T. Ladnorg, H. Gliemann, M. Franzreb and C. Wöll, et al., ChemPhysChem, 2012, 13, 2699–2702 CrossRef CAS PubMed.
- C. H. Hendon and A. Walsh, Chem. Sci., 2015, 6, 3674–3683 RSC.
- M. Kim, S. J. Garibay and S. M. Cohen, Inorg. Chem., 2011, 50, 729–731 CrossRef CAS PubMed.
- J. Li, T. Musho, J. Bright and N. Wu, J. Electrochem. Soc., 2019, 166, H3029–H3034 CrossRef CAS.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, et al., J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. D. Pack and H. J. Monkhorst, Phys. Rev. B, 1977, 16, 1748 CrossRef.
- A. Kokalj, J. Mol. Graphics Modell., 1999, 17, 176–179 CrossRef CAS.
- M. K. Bhunia, J. T. Hughes, J. C. Fettinger and A. Navrotsky, Langmuir, 2013, 29, 8140–8145 CrossRef CAS PubMed.
- Z.-G. Gu, L. Heinke, C. Wöll, T. Neumann, W. Wenzel, Q. Li, K. Fink, O. D. Gordan and D. R. Zahn, Appl. Phys. Lett., 2015, 107, 102_1 Search PubMed.
- I. Mayer, J. Comput. Chem., 2007, 28, 204–221 CrossRef CAS PubMed.
- J. Muscat, A. Wander and N. Harrison, Chem. Phys. Lett., 2001, 342, 397–401 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra00687g |
| This journal is © The Royal Society of Chemistry 2019 |