Open Access Article
Open Access ArticleDoubly spin-labeled nanodiscs to improve structural determination of membrane proteins by ESR†
Chieh-Chin Li ,
Chien-Lun Hung
,
Chien-Lun Hung ,
Pei-Shan Yeh,
Chi-En Li and
Yun-Wei Chiang
,
Pei-Shan Yeh,
Chi-En Li and
Yun-Wei Chiang *
*
Department of Chemistry, Frontier Research Center on Fundamental and Applied Sciences of Matters, National Tsing Hua University, Hsinchu 30013, Taiwan. E-mail: ywchiang@gapp.nthu.edu.tw
First published on 19th March 2019
Abstract
Pulsed dipolar spectroscopy (PDS) is a powerful tool to explore conformational changes of membrane proteins (MPs). However, the MPs suffer from relatively weak dipolar signals due to their complex nature in membrane environments, which consequently reduces the interspin distance resolution obtainable by PDS. Here we report the use of nanodiscs (NDs) to improve the distance resolution. Two genetically engineered membrane scaffold protein mutants are introduced, each of which is shown to form double-labeled ND efficiently and with high homogeneity. The resultant interspin distance distribution is featured by a small distribution width, suggesting high resolution. When PDS is performed on a binary mixture of the double-labeled ND devoid of MPs and the un-labeled ND with incorporated double-labeled MPs, the overall amplitude of dipolar signals is increased, leading to a critical enhancement of the distance resolution. A theoretical foundation is provided to validate the analysis. With this approach, the determination of MP structures can be studied at high resolution in NDs.
Introduction
More than 25% of the proteins encoded by the human genome are membrane proteins (MPs)—proteins that span across, interact with, or are part of, cell membranes.1 They are targets of over 50% of modern medical drugs as they perform a variety of functions essential to the survival of organisms, such as transporting solutes between aqueous compartments, serving as enzymes that catalyze vital biological processes, and transmitting stimuli received outside the cell to functional proteins inside.2 Nowadays, a major challenge in MP studies is to obtain detailed models of conformational transitions that are associated with the MP functions. A full understanding of the structure–function relationship of MPs requires the ability of capturing MP structural changes between multiple conformations in the functional cycle. Thus, studying MPs in an environment more closely resembling the native membranes is a necessary step for bridging structure and mechanism.Site-directed spin labeling (SDSL) in combination with pulsed dipolar ESR spectroscopy (PDS) techniques, such as double electron electron resonance (PELDOR/DEER), is a powerful tool for structural biology enabling the nanometer-range distance measurements in proteins and thus the determination of structural conformations between functional states in equilibrium.3–8 In combination with nanodiscs (ND), SDSL-PDS is proven to be a valuable tool for revealing conformational changes of MP between different functional states in a native-like lipid environment.9–11 However, the application of PDS to MP is often hindered by the fact that due to complex nature of membrane environment, dipolar signals in MP are relatively weak than in soluble proteins, hence leading to a weak modulation depth in the PDS data of MP. Without having a sufficiently adequate signal-to-noise ratio (SNR), distance distributions recovered from the PDS data using Tikhonov regularization (TIKR)12–16 would tend to exhibit large broadening and high inhomogeneity.17,18 When a broadly heterogeneous distribution is obtained for a MP study, it is a great challenge for the existing PDS methods to identify the genuine structural changes associated with the varying conditions (e.g., pH, concentration of ions, lipid compositions, and presence/absence of binding ligands). An approach to increase the distance resolution is urgently needed. As the determination of interspin distance distributions is associated with an ill-posed inverse problem, the solution (i.e., the distance distribution) to the inverse problem depends critically on the SNR of PDS data.19–21 Increasing the intensity of the modulation depth, which directly leads to an enhancement in the SNR of PDS data, is the key to improving the distance resolution.
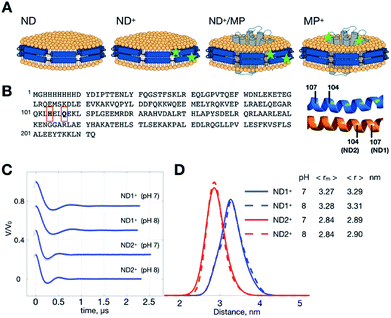
In this work, we report an advance in the application of PDS for MP using spin-labeled nanodiscs. Various nanodisc samples (Fig. 1A) were prepared, including empty nanodiscs consisting only of lipids and the membrane scaffold protein (MSP) (hereafter denoted by ND), nanodiscs encircled by the doubly spin-labeled MSP (denoted by ND+, where the superscript “+” denotes the formation of two spin-labeled R1 residues in MSP), ND+ with incorporated MP (ND+/MP), un-labeled ND with incorporated double-labeled MP (MP+), and a binary mixture of ND+ and MP+ with a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (i.e., a mixture of two types of nanodiscs, ND+ and MP+; cf. Fig. 1A). MP samples used in this study are wild-type or cysteine variants of YetJ membrane protein. YetJ is a bacterial TMBIM6 homolog protein found to be important for uptake of calcium into bacteria and mediating a pH-dependent Ca2+ flux in proteoliposomes.22 YetJ is a 7-helix transmembrane protein composed of 214 residues (ca. 24 kDa). Its crystal structures at various pH were previously reported exhibiting differences in the conformation.22 YetJ is, therefore, used as a model MP in this study to demonstrate potential applications of spin-labeled nanodiscs for improving MP study by PDS.
2 (i.e., a mixture of two types of nanodiscs, ND+ and MP+; cf. Fig. 1A). MP samples used in this study are wild-type or cysteine variants of YetJ membrane protein. YetJ is a bacterial TMBIM6 homolog protein found to be important for uptake of calcium into bacteria and mediating a pH-dependent Ca2+ flux in proteoliposomes.22 YetJ is a 7-helix transmembrane protein composed of 214 residues (ca. 24 kDa). Its crystal structures at various pH were previously reported exhibiting differences in the conformation.22 YetJ is, therefore, used as a model MP in this study to demonstrate potential applications of spin-labeled nanodiscs for improving MP study by PDS.
Results and discussion
Doubly spin-labeled MSP mutants form stable nanodiscs
MSP is a cysteine-free protein (Fig. 1B).23–26 To obtain spin-labeled MSP nanodiscs (i.e., ND+), we construct two different cysteine-variants of MSP mutant, Q107C and H104C (see also Experimental). As each ND is encircled by two identical MSP proteins in an antiparallel fashion, the MSP constructs allow us to have two different double-labeled ND, designated by ND1+ and ND2+, in which the former and the latter is assembled with MSP-Q107R1 and MSP-H104R1, respectively. We performed DEER measurements on ND1+ and ND2+ at pH 7 and 8 (Fig. 1C). Because of the great features of ND (which include high homogeneity in size, soluble nature, and monodispersity in solution)11,26 the time trace of the DEER data is characterized by strong intensity in the modulation depth (which leads to high SNR), and distinct dipolar evolutions, as good as what is commonly obtained for soluble monodisperse proteins. As a result, a highly homogeneous distance distribution, which reflects the local uniformity of MSP in ND+, is obtained for all of the measurements. The most probable distances are 3.27 nm (ND1+) and 2.84 nm (ND2+) (Fig. 1D), with a small full-width-at-half-maximum (FWHM) value (ca. 0.5 nm). The distance distributions exhibit little change with pH, indicating that the spin-labeled nanodiscs (ND1+ and ND2+) are stable within the pH range studied. The observed homogeneity in distance distributions also support that our spin-labeled ND prepared from the MSP mutants retain the monodispersity and homogeneity features of an unmodified (un-labeled) ND in solution.Changes in ND geometry associated with MP incorporation can be detected
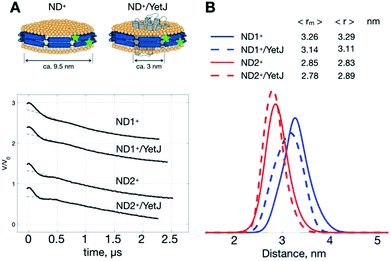
As such a relatively narrow and homogeneous distribution is obtainable with the use of ND+, we can utilize the ND+ to investigate how the geometry of ND is changed after the incorporation of wild-type YetJ. We compare the results of ND+ versus ND+/YetJ (Fig. 2). Both the studies of ND1+ and ND2+ show a small but distinct change in the average distances after the incorporation of YetJ. Given that the DEER data of ND+ are reproducible (Fig. S1†) in replicate experiments and nearly invariant with pH (Fig. 1), the differences observed here (Fig. 2) are considered significant and meaningful. Even though the incorporated YetJ is relatively smaller than the ND in diameter (Fig. 2A),22,26 its incorporation into ND causes changes to the geometry of ND, consistent with literature finding about the sensitivity of ND to a MP incorporation.27 Further comparisons of the DEER time-domain traces are given (Fig. S2†), which leads to the same conclusion about the high sensitivity of the ND+ samples. Clearly, the sensitivity of the DEER-derived results is improved, hence making it possible to discern the small changes in the ND geometry associated with the incorporation of YetJ. Potentially, the improved ability of PDS with ND+, when combined with small-angle X-ray scattering data,7,28 can provide even more valuable information about molecular details of ND environment.ND+ enhances the overall spin signals, hence improving the distance resolution
The improved-quality of the DEER data with ND+ can also be used to increase the distance resolution in a conventional MP study (i.e., a pure MP+ solution). We propose to perform DEER measurements on a mixture of two types of nanodiscs, MP+ and ND+. We expect that as signal amplitude of ND+ is more distinct than that of MP+, the overall SNR of DEER data for the mixture can be enhanced as compared to the data for the pure MP+ solution. This enhancement can directly lead to an increase in SNR and, consequently, an improved resolution in the TIKR distance distributions. As demonstrated elsewhere,20,21 increasing SNR of DEER data is of vital importance for improving the distance resolution in the TIKR result. Besides, as the monodisperse nature of ND+ in a pure ND+ solution is not different from that of ND+ in a binary mixture of ND+ and MP+, the distance distribution obtained from the binary mixture can be reasonably considered to be a superposition of two individual contributions from the respective ND+ and MP+ components. (See Experimental for the validity of the superposition principle and the separation procedure in the distance domain.) Thus, by subtracting the ND+ contribution, which has been obtained in the pure ND+ studies (Fig. 1), from the TIKR distance distribution of the binary mixture, we can obtain the distance distribution corresponding to MP+. One great advantage of measuring the mixture rather than a pure MP+ solution is that the SNR of PDS data is better in the former and so is the resultant distance resolution.Two conformations of YetJ in ND are clearly revealed
To demonstrate the idea of improving SNR of DEER signal with ND+, we performed DEER measurements on (YetJ-44/152)+ (hereafter, (44/152)+ for short), and a binary 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture of ND1+ and (44/152)+, in which (44/152)+ represents a doubly spin-labeled YetJ mutant 44R1/152R1 reconstituted into a ND (Fig. 3A). Data shown were obtained under the same experimental conditions (e.g., spin concentration, acquisition time, temperature, etc.; see Experimental). Crystal structures of YetJ were previously determined, showing that at pH 7 YetJ exists in two distinct conformations in equilibrium (Fig. 3A). Thus, two average distances between sites 152 and either of 44 (blue or green, Fig. 3A) are expected from the measurements.
2 mixture of ND1+ and (44/152)+, in which (44/152)+ represents a doubly spin-labeled YetJ mutant 44R1/152R1 reconstituted into a ND (Fig. 3A). Data shown were obtained under the same experimental conditions (e.g., spin concentration, acquisition time, temperature, etc.; see Experimental). Crystal structures of YetJ were previously determined, showing that at pH 7 YetJ exists in two distinct conformations in equilibrium (Fig. 3A). Thus, two average distances between sites 152 and either of 44 (blue or green, Fig. 3A) are expected from the measurements.
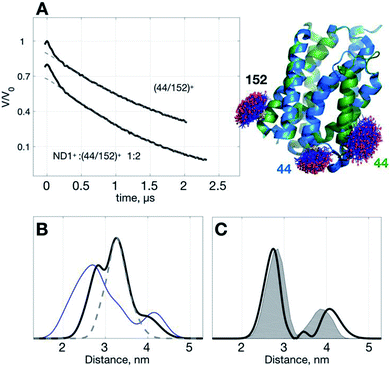 | ||
Fig. 3 Use of ND1+ to improve TIKR distance resolution for YetJ-44/152. (A) DEER time-domain traces (black) measured at pH 7 are shown on the left. Cartoon models displaying the two crystal structures of YetJ (PDB: 4PGS and 4PGR, colored in green and blue, respectively) found to be in equilibrium at pH 7. (B) Normalized TIKR distance distributions of (44/152)+ (blue) and ND1+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (44/152)+ 1 (44/152)+ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (black), in which the latter exhibits a clear reduction in the distribution width compared to the former. The result of ND1+ (gray dashed; taken from Fig. 1) is shown to indicate that the contribution of ND1+ can be conveniently removed from the TIKR result shown in black. (C) Distance distribution (black) after the subtraction of ND1+ component from the distance distribution of the ND1+ 2 (black), in which the latter exhibits a clear reduction in the distribution width compared to the former. The result of ND1+ (gray dashed; taken from Fig. 1) is shown to indicate that the contribution of ND1+ can be conveniently removed from the TIKR result shown in black. (C) Distance distribution (black) after the subtraction of ND1+ component from the distance distribution of the ND1+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (44/152)+ 1 (44/152)+ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 sample. It reveals two major peaks at 2.74 nm and 4.07 nm, in a reasonable agreement with the MtsslWizard predictions, 2.79 nm and 3.87 nm (gray shaded areas). 2 sample. It reveals two major peaks at 2.74 nm and 4.07 nm, in a reasonable agreement with the MtsslWizard predictions, 2.79 nm and 3.87 nm (gray shaded areas). | ||
Using the standard TIKR procedure (see Experimental), we obtained the TIKR distance distributions (Fig. 3B) for (44/152)+ (blue line) and ND1+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (44/152)+ 1
(44/152)+ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (black line), in which the former is clearly more broadened in the distribution width than the later (a binary 1
2 (black line), in which the former is clearly more broadened in the distribution width than the later (a binary 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture of ND1+ and (44/152)+). The dominant component (centered at 3.26 nm) in the distance distribution of the mixture corresponds to the interspin distance of ND1+ as it overlaps nicely with the result of the pure ND1+ measurement (gray dashed line; taken from the results in Fig. 1). After subtracting the ND1+ component from the TIKR result of the mixture, we obtain a bimodal-like distribution (black line in Fig. 3C) displaying two major peaks centered at 2.74 and 4.07 nm. In a comparison with the prediction of distance distributions of the crystal structures using MtsslWizard29 (gray-shaded area, with the most probable distances at 2.79 and 3.87 nm; Fig. 3C), the resultant TIKR appears to agree reasonably well with the model predictions (particularly in the distribution widths and the peak position of the dominant component at 2.74 nm). Nevertheless, a relatively greater discrepancy is observed for the minor component in the longer distance (ca. 4 nm). There are two possible reasons for the cause of the discrepancy: (i) there are some overlaps between the ND1+ and the minor component of the (44/152)+ around the distance of 4 nm; (ii) the structure of YetJ in ND is somewhat different from the reported X-ray structure determined in a detergent environment. The first reason is less likely to occur for the case studied here as the ND1+ component fits nicely to the dominant component in the TIKR result of the mixture. This result suggests a further investigation on the structural difference of YetJ between a detergent and a ND environment. Collectively, using ND1+ for improving the SNR of DEER data, we are able to obtain the TIKR distance distribution featured by a distinct reduction in the distribution width as compared with the (44/152)+ result (the blue line in Fig. 3B). As a result, the distances and structural dynamics of a MP, which is reflected by the distribution width, can be determined with an improved accuracy.
2 mixture of ND1+ and (44/152)+). The dominant component (centered at 3.26 nm) in the distance distribution of the mixture corresponds to the interspin distance of ND1+ as it overlaps nicely with the result of the pure ND1+ measurement (gray dashed line; taken from the results in Fig. 1). After subtracting the ND1+ component from the TIKR result of the mixture, we obtain a bimodal-like distribution (black line in Fig. 3C) displaying two major peaks centered at 2.74 and 4.07 nm. In a comparison with the prediction of distance distributions of the crystal structures using MtsslWizard29 (gray-shaded area, with the most probable distances at 2.79 and 3.87 nm; Fig. 3C), the resultant TIKR appears to agree reasonably well with the model predictions (particularly in the distribution widths and the peak position of the dominant component at 2.74 nm). Nevertheless, a relatively greater discrepancy is observed for the minor component in the longer distance (ca. 4 nm). There are two possible reasons for the cause of the discrepancy: (i) there are some overlaps between the ND1+ and the minor component of the (44/152)+ around the distance of 4 nm; (ii) the structure of YetJ in ND is somewhat different from the reported X-ray structure determined in a detergent environment. The first reason is less likely to occur for the case studied here as the ND1+ component fits nicely to the dominant component in the TIKR result of the mixture. This result suggests a further investigation on the structural difference of YetJ between a detergent and a ND environment. Collectively, using ND1+ for improving the SNR of DEER data, we are able to obtain the TIKR distance distribution featured by a distinct reduction in the distribution width as compared with the (44/152)+ result (the blue line in Fig. 3B). As a result, the distances and structural dynamics of a MP, which is reflected by the distribution width, can be determined with an improved accuracy.
Structure of YetJ in ND is studied at an improved resolution
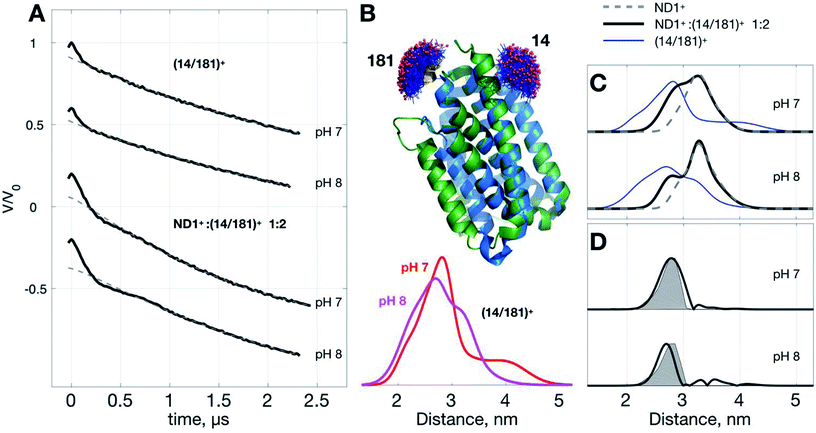
Below we demonstrate another improvement in the MP study by DEER that can be achieved with ND+ (Fig. 4). We performed DEER measurements on (Yet-14/181)+, i.e., ND with incorporated doubly spin-labeled YetJ mutant 14R1/181R1 (hereafter, (14/181)+ for short), at pH 7 and 8. The previous crystal study indicated that the distances between sites 14 and 181 is not changed with the pH variation (Fig. 4B) even though the relative population of the two conformations is changed.22 Our DEER results, however, show (Fig. 4B) that although there are some differences in the TIKR distance distributions between pH 7 and 8, they are minor, inhomogeneous, and not sufficiently substantial to derive a conclusive picture of the conformations between the pH conditions. This is a frequently-encountered problem in the MP study by PDS; that is, although the resultant distance distributions are somewhat different among the varied conditions, they appear broadly inhomogeneous such that the significance of the differences is easily compromised by the inhomogeneity. When this is a case, it is a challenging task to identify and confirm a meaningful difference in the DEER results. With the use of ND+, we now have a better way to increase the SNR of DEER data, which subsequently render the TIKR distance resolution improved.Fig. 4C shows the TIKR distance distributions of (14/181)+ (blue), ND1+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (14/181)+ 1
(14/181)+ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture (black), and ND1+, for pH 7 and 8. In the binary 1
2 mixture (black), and ND1+, for pH 7 and 8. In the binary 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture of ND1+ and (14/181)+, the intensity of modulation depth is clearly enhanced as compared to the (14/181)+ measurements (see also Fig. S3† for a detailed comparison). Because of the improved SNR, the distance distributions for the binary mixture are obtained by TIKR with a distinct reduction in the distribution width, namely, the distance resolution is improved. The distance component (centered ca. 3.26 nm) corresponding to the contribution of ND1+ can be directly subtracted from the TIKR results (for pH 7 and 8) as the ND1+ results (gray dashed lines) overlap nicely with the component centered around 3.26 nm in the TIKR result of the binary mixture. After the subtraction, we obtained a homogeneous-like distance distribution for each of the pH conditions (black lines in Fig. 4D). They are centered approximately at 2.87 nm (pH 7) and 2.74 nm (pH 8), reasonably close to the prediction of the distance distribution fo crystal structures using MtsslWizard (shaded areas in Fig. 4D). Importantly, the distribution widths are in a good agreement between the TIKR and the MtsslWizard results, which is considered as the landmark advance made possible by the use of ND1+. In this YetJ study, the addition of ND1+ into the (14/181)+ solution is useful to improve the overall SNR of DEER signals and thus increase the resolution in the TIKR distance distribution.
2 mixture of ND1+ and (14/181)+, the intensity of modulation depth is clearly enhanced as compared to the (14/181)+ measurements (see also Fig. S3† for a detailed comparison). Because of the improved SNR, the distance distributions for the binary mixture are obtained by TIKR with a distinct reduction in the distribution width, namely, the distance resolution is improved. The distance component (centered ca. 3.26 nm) corresponding to the contribution of ND1+ can be directly subtracted from the TIKR results (for pH 7 and 8) as the ND1+ results (gray dashed lines) overlap nicely with the component centered around 3.26 nm in the TIKR result of the binary mixture. After the subtraction, we obtained a homogeneous-like distance distribution for each of the pH conditions (black lines in Fig. 4D). They are centered approximately at 2.87 nm (pH 7) and 2.74 nm (pH 8), reasonably close to the prediction of the distance distribution fo crystal structures using MtsslWizard (shaded areas in Fig. 4D). Importantly, the distribution widths are in a good agreement between the TIKR and the MtsslWizard results, which is considered as the landmark advance made possible by the use of ND1+. In this YetJ study, the addition of ND1+ into the (14/181)+ solution is useful to improve the overall SNR of DEER signals and thus increase the resolution in the TIKR distance distribution.
Conclusions
In summary, this study has demonstrated a proof-of-concept approach for improving the MP study by PDS. Doubly spin-labeled ND samples, reported herein, are verified to retain several great features of conventional ND, which include monodispersity in solution and uniformity in ND shape, and thus are used to probe the changes in the geometry of ND associated with the MP incorporation. Making use of the distinct dipolar signals of ND+, we doped ND+ into a MP+ solution to increase the overall SNR of DEER time-domain traces. We show that the SNR of DEER data for the binary mixture is clearly increased as compared to that for a pure MP+ solution, and this increase is critical to the improvement in distance resolution obtainable by TIKR. The separation of the two contributions from ND+ and MP+ can be conveniently performed in the distance domain using the superposition principle introduced in the present study. Furthermore, as the two MSP mutants are proven suitable for spin-labeling studies, they can be massively produced and applied to different MP-embedded ND studies without extra modifications. With the two available choices of ND+, one can effectively avoid an overlap with distances of MP+. Unless dominant distances from ND+ and MP+ overlap largely, a single PDS measurement on the binary mixture is sufficient for studying structural conformations of MP.Experimental
Expression, purification, and spin-labeling of YetJ
YetJ was expressed and purified as previously described with minor modifications.22 Briefly, a pET-24 derived pNYCOMPS vector containing the deca-histidine affinity tag at C-terminus of YetJ was transformed into E. Coli pLysS BL21(DE3) (Agilent) for growth and expression. The DNA plasmid was a kind gift from Dr Qun Liu (New York Structural Biology Center). For protein expression, 10 mL of start-culture in Terrific Broth (TB) media supplemented with 30 μg mL−1 of kanamycin and 25 μg mL−1 of chloramphenicol was grown at 37 °C with shaking. A dense overnight culture was used to inoculate 5 L of TB culture supplemented with 30 μg mL−1 of kanamycin and 25 μg mL−1 of chloramphenicol. Cultures were grown at 37 °C with shaking to an OD600 approximately 0.6–0.8, and then induced with 0.4 mM isopropyl β-D-1-thiogalactopyranoside (IPTG) at 37 °C. After 4 h induction, cells were harvested by centrifugation at 9000g for 5 min at 4 °C and stored at −80 °C until purification.The cell pellets were resuspended in lysis buffer (50 mM HEPES, 0.3 M NaCl, 20 mM imidazole, 5% glycerol and 1 mM MgCl2, pH 7.8) and sonicated. The cell lysate was cleared by centrifugation at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800g for 40 min. Membrane pellets were collected by centrifugation at 44
800g for 40 min. Membrane pellets were collected by centrifugation at 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300g for 1 h and then resuspended in the lysis buffer with additional 1.5% (w/v) β-DDM for solubilization with vigorous agitation. After 1 h, supernatant was collected via centrifugation at 44
300g for 1 h and then resuspended in the lysis buffer with additional 1.5% (w/v) β-DDM for solubilization with vigorous agitation. After 1 h, supernatant was collected via centrifugation at 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300g for 30 min to remove insoluble components. The cleared lysate was passed through a 5 mL HisTrap HP column pre-equilibrated with the lysis buffer with additional 0.05% (w/v) β-DDM. The column was washed by 100 mL wash buffer (50 mM HEPES, 0.5 M NaCl, 75 mM imidazole, 5% glycerol and 0.05% (w/v) β-DDM, pH 7.8) and then was eluted by 30 mL elution buffer (50 mM HEPES, 0.3 M NaCl, 0.5 M imidazole, 5% glycerol and 0.05% (w/v) β-DDM, pH 7.8). Purified YetJ was then run on a Superdex 200 10/300 GL gel filtration column (GE Healthcare) in storage buffer (50 mM HEPES, 0.3 M NaCl and 0.05% (w/v) β-DDM, pH 7.8). Protein purity was checked by SDS-PAGE. As wild-type YetJ is a cysteine-free protein, its construct was directly used to prepare the two YetJ mutants (Q14C/T181C and P44C/A152C) in this study. For the spin-labeling reaction of YetJ mutants, it was performed by addition of 40-fold molar excess of MTSSL/MTSL (Enzo Life Sciences) from a 0.1 M stock solution in acetonitrile. The reaction was kept in dark overnight at room temperature and then concentrated to ∼10 mg mL−1 using Amicon Ultra-50K centrifugal filter units. The concentration of YetJ was determined by absorption at 280 nm (extinction coefficient 24
300g for 30 min to remove insoluble components. The cleared lysate was passed through a 5 mL HisTrap HP column pre-equilibrated with the lysis buffer with additional 0.05% (w/v) β-DDM. The column was washed by 100 mL wash buffer (50 mM HEPES, 0.5 M NaCl, 75 mM imidazole, 5% glycerol and 0.05% (w/v) β-DDM, pH 7.8) and then was eluted by 30 mL elution buffer (50 mM HEPES, 0.3 M NaCl, 0.5 M imidazole, 5% glycerol and 0.05% (w/v) β-DDM, pH 7.8). Purified YetJ was then run on a Superdex 200 10/300 GL gel filtration column (GE Healthcare) in storage buffer (50 mM HEPES, 0.3 M NaCl and 0.05% (w/v) β-DDM, pH 7.8). Protein purity was checked by SDS-PAGE. As wild-type YetJ is a cysteine-free protein, its construct was directly used to prepare the two YetJ mutants (Q14C/T181C and P44C/A152C) in this study. For the spin-labeling reaction of YetJ mutants, it was performed by addition of 40-fold molar excess of MTSSL/MTSL (Enzo Life Sciences) from a 0.1 M stock solution in acetonitrile. The reaction was kept in dark overnight at room temperature and then concentrated to ∼10 mg mL−1 using Amicon Ultra-50K centrifugal filter units. The concentration of YetJ was determined by absorption at 280 nm (extinction coefficient 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410 M−1 cm−1). Excess free spin labels were removed completely during the process of nanodisc samples preparation described below.
410 M−1 cm−1). Excess free spin labels were removed completely during the process of nanodisc samples preparation described below.
Expression, purification, and spin-labeling of MSP
Membrane scaffold protein (MSP1D1, herein denoted by MSP for simplification) was expressed and purified as previously described with minor modifications.24 The two single-cysteine variants of MSP H104C and Q107C (cf. Fig. 1) were selected and used for preparing spin-labeled ND in the present study because they were found to react with MTSSL labels efficiently to produce high-purity double-labeled ND. Briefly, E. coli BL21(DE3) cells (Agilent) containing the MSP1D1 gene in pET-28a (Addgene) were grown overnight in 10 mL of TB supplemented with 30 μg mL−1 kanamycin then inoculated in 1 L TB supplemented with 30 μg mL−1 kanamycin. Cultures were grown at 37 °C with shaking to an OD600 approximately 2–2.5, and then MSP was induced by addition of 1 mM IPTG. Cultures were grown for 4 h at 37 °C, and cells were harvested by centrifugation and stored at −80 °C until further purification. The cell pellets were resuspended in 30 mL of 20 mM sodium phosphate, 0.1 M NaCl, 1% Triton X-100, 10 mM MgSO4, pH 7.4, with additional 10 μg mL−1 DNase I and 300 μL 0.1 M solution of phenylmethylsulfonyl fluoride (PMSF) in ethanol, and then sonicated. The lysate was clarified by centrifugation at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800g for 50 min. The cleared lysate was passed through a 5 mL HisTrap HP column pre-equilibrated with 20 mM sodium phosphate, 0.1 M NaCl and 1% Triton X-100, pH 7.4. The column was washed with the following order of buffers: (i) 25 mL of 40 mM Tris–HCl, 0.3 M NaCl and 1% Triton X-100, pH 8.0 (ii) 25 mL of 40 mM Tris–HCl, 0.3 M NaCl and 50 mM sodium cholate (SC), pH 8.0 (iii) 25 mL of 40 mM Tris–HCl, 0.3 M NaCl and 40 mM imidazole, pH 8.0. MSP was eluted with 40 mM Tris–HCl, 0.3 M NaCl and 0.4 M imidazole, pH 8.0. Eluted MSP was buffer-exchanged into MSP buffer (20 mM Tris–HCl and 0.1 M NaCl, pH 7.4) and concentrated to ∼1 mg mL−1 using a 10K MWCO concentrator (Amicon). The N-terminal His-tag of MSP was cleaved by overnight incubation at 4 °C with sufficient amounts of tobacco etch virus (TEV) protease. For cysteine-variants of MSP mutant, spin-labeling was performed, followed by His-tag cleavage by direct addition of a 15-fold molar excess of MTSSL (Enzo Life Sciences) from a 0.1 M stock solution in acetonitrile. The reaction was kept in dark overnight at 4 °C. The enzyme and uncleaved MSP were then removed by a second passage through the nickel column. The flow through and wash fractions were collected and concentrated to ∼10 mg mL−1. The concentration of MSP was determined by absorption at 280 nm (extinction coefficients of 21
800g for 50 min. The cleared lysate was passed through a 5 mL HisTrap HP column pre-equilibrated with 20 mM sodium phosphate, 0.1 M NaCl and 1% Triton X-100, pH 7.4. The column was washed with the following order of buffers: (i) 25 mL of 40 mM Tris–HCl, 0.3 M NaCl and 1% Triton X-100, pH 8.0 (ii) 25 mL of 40 mM Tris–HCl, 0.3 M NaCl and 50 mM sodium cholate (SC), pH 8.0 (iii) 25 mL of 40 mM Tris–HCl, 0.3 M NaCl and 40 mM imidazole, pH 8.0. MSP was eluted with 40 mM Tris–HCl, 0.3 M NaCl and 0.4 M imidazole, pH 8.0. Eluted MSP was buffer-exchanged into MSP buffer (20 mM Tris–HCl and 0.1 M NaCl, pH 7.4) and concentrated to ∼1 mg mL−1 using a 10K MWCO concentrator (Amicon). The N-terminal His-tag of MSP was cleaved by overnight incubation at 4 °C with sufficient amounts of tobacco etch virus (TEV) protease. For cysteine-variants of MSP mutant, spin-labeling was performed, followed by His-tag cleavage by direct addition of a 15-fold molar excess of MTSSL (Enzo Life Sciences) from a 0.1 M stock solution in acetonitrile. The reaction was kept in dark overnight at 4 °C. The enzyme and uncleaved MSP were then removed by a second passage through the nickel column. The flow through and wash fractions were collected and concentrated to ∼10 mg mL−1. The concentration of MSP was determined by absorption at 280 nm (extinction coefficients of 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 430 and 18
430 and 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 M−1 cm−1 for uncleaved and cleaved MSP, respectively). Protein purity was checked by SDS-PAGE.
450 M−1 cm−1 for uncleaved and cleaved MSP, respectively). Protein purity was checked by SDS-PAGE.
Preparation of nanodisc samples
Nanodisc (ND) samples were prepared using a modified Sligar's protocol.23,25 For reconstitution of YetJ into ND (or ND+), spin-labeled YetJ mutants (or wild-type YetJ) in β-DDM micelles were mixed with appropriate lipid, MSP (or spin-labeled MSP) and sodium cholate (SC) in the following molar ratios: lipid/MSP, 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; MSP/YetJ, 4
1; MSP/YetJ, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; and SC/lipid, 2
1; and SC/lipid, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The reconstitution ratios for empty ND are: lipid/MSP, 65
1. The reconstitution ratios for empty ND are: lipid/MSP, 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; SC/lipid, 2
1; SC/lipid, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Mixtures were incubated on ice for 15 min. Biobeads SM-2 (1 g mL−1) (Bio-Rad) were added to the mixture and incubated for 4 h at 4 °C. Biobeads were removed by a short spin-down and the ND suspension were then purified by a second passage through the nickel column. The eluted fractions were collected and then run on a Superdex 200 10/300 GL gel filtration column (GE Healthcare) equilibrated with nanodisc buffer (50 mM HEPES and 0.3 M NaCl, pH 7.0). Purified ND/YetJ+ (or ND+/YetJ) samples were concentrated with Amicon Ultra-50K centrifugal filter units and the concentrations were determined by absorption at 280 nm (extinction coefficient of ND/YetJ 61
1. Mixtures were incubated on ice for 15 min. Biobeads SM-2 (1 g mL−1) (Bio-Rad) were added to the mixture and incubated for 4 h at 4 °C. Biobeads were removed by a short spin-down and the ND suspension were then purified by a second passage through the nickel column. The eluted fractions were collected and then run on a Superdex 200 10/300 GL gel filtration column (GE Healthcare) equilibrated with nanodisc buffer (50 mM HEPES and 0.3 M NaCl, pH 7.0). Purified ND/YetJ+ (or ND+/YetJ) samples were concentrated with Amicon Ultra-50K centrifugal filter units and the concentrations were determined by absorption at 280 nm (extinction coefficient of ND/YetJ 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 M−1 cm−1). The same procedure was applied for preparation of empty ND except the second passage through the nickel column was skipped.
310 M−1 cm−1). The same procedure was applied for preparation of empty ND except the second passage through the nickel column was skipped.
Sample preparation for DEER measurements
Nanodisc samples were buffer-exchanged into nanodisc buffer and concentrated to final ND concentration ca. 0.5 mM; the final spin-pair concentration is ca. 0.5 mM in all measurements studied. Approximately, 30 μL solution volume, containing 10% (v/v) d8-glycerol as cryoprotectant, was added into quartz ESR tube (i.d. 3 mm). All buffers in the DEER experiments were deuterated. A Bruker ELEXSYS E580-400 CW/Pulsed spectrometer, with a split-ring resonator (EN4118X-MS3) and a helium gas flow system (4118CF and 4112HV), was used. The ESR probe head was precooled to 80 K prior to the transfer of the ESR sample tube into the cavity. DEER experiments were performed using the typical four-pulse constant-time DEER sequence as previously described.3,7 The detection pulses were set to 32 and 16 ns for π and π/2 pulses, respectively, and the pump frequency was set to approximately 65 MHz lower than the detection pulse frequency. The pulse amplitudes were chosen to optimize the refocused echo. The π/2-pulse was employed with +x/−x phase cycles to eliminate receiver offsets. The duration of the pumping pulse was about 32 ns, and its frequency was coupled into the microwave bridge by a commercially available setup (E580-400U) from Bruker. All pulses were amplified via a pulsed traveling wave tube (TWT) amplifier (E580-1030). The field was adjusted such that the pump pulse is applied to the maximum of the nitroxide spectrum, where it selects the central mI = 0 transition of Azz together with the mI = ±1 transitions. The accumulation time for each set of data was about 10 h at a temperature of 80 K. A common cooling approach was used.6,7 The sample tube was plunge-cooled in liquid nitrogen and then transferred into the ESR probehead, which was precooled to 80 K using a helium flow system. The determination of interspin distance distribution of the DEER spectroscopy was performed using time-domain analysis by Tikhonov regularization based on the L-curve method,12,16 followed by a data refinement process using the maximum entropy method (MEM)13 to obtain the non-negative distance distributions.Separation of the DEER signal contributions from ND+ and MP+ samples
A complete expression for the experimental time-domain DEER traces VDEER(t) is an integral equation, which includes the time-domain background function B(t) describing the homogeneous distribution of intermolecular isolated spin pairs, and the intra-molecular dipolar-evolution function Vintra(t) for an ensemble of isolated interacting spin pairs with random orientation to the magnetic-field axis, as reported elsewhere.12–14 The integral equation can be expressed as a product,19,20| VDEER(t) = B(t) × [(1 − λ) + λVintra(t)] | (1) |
In the present study, we carried out DEER measurements on a mixture solution of two types of ND samples, ND+ and MP+, in which the former is ND (devoid of MP) with lipids and double-labeled MSP and the latter is un-labeled ND with reconstituted double-labeled MP. As both the types of ND are monodispersed in solution, in the same way as an un-labeled (regular) ND, they retain (almost) the same monodispersity nature and, therefore, the inter-molecular interactions among whichever individual ND samples can be reasonably removed from the collected VDEER(t) using the standard background-correction procedure in the DeerAnalysis. In other words, the B(t) for a solution containing either of the two types of ND is not different from that for a binary mixture of the two, provided that the total spin concentration, which determines the decay of the background B(t), is fixed.
After the background-correction procedure, Vintra(t), which accounts for intra-molecular dipolar interaction, is obtained. As individual ND samples are basically independent from each other after the removal of the background contribution, the Vintra(t) can therefore be considered as a superposition of the contributions from the two types of ND samples: Vintra(t) = VND+(t) + VMP+(t). This assumption of the superposition is supported by the following considerations. In a system containing two species of double-labeled samples, the collected experimental DEER data VDEER(t) is a product of the two contributions:
| VDEER(t) = B(t) × [(1 − λ1) + λ1V1(t)] × [(1 − λ2) + λ2V2(t)] = B(t) × [(1 − λ1)(1 − λ2) + λ1(1 − λ2)V1(t) + (1 − λ1)λ2V2(t) + λ1λ2V1(t)V2(t)] | (2) |
| VDEER(t) = B(t) × (1 − λ)[(1 − λ) + λ [V1(t) + V2(t)]] | (3) |
| VDEER(t) = B′(t) × [(1 − λ) + λ[V1(t) + V2(t)]] = B′(t) × [(1 − λ) + λVintra(t)] | (4) |
The equation connecting the background-corrected function Vintra(t) and the distance distribution function P(r) is in the form of Fredholm integral equation of the first kind, which is a prime example of ill-posed inverse programs.12–15 Experimentally, DEER signal is measured at discrete time points. The inverse problem can be expressed as a linear equation S = KP, where the matrix K corresponds to the kernel of the PDS integral equation, S is the data vector of Vintra(t), and P is the interspin distance distribution function P(r). A unique solution vector P to the equation can be obtained using the TIKR based on the L-curve method,12,16 followed by the separation of the two contributions in the distance domain, as summarized below.
| S = SND+ + SMP+ = KP = K(PND+ + PMP+) | (5) |
The distance distributions of the ND+ samples (cf. Fig. 1) are characterized by high homogeneity with a relatively narrow distribution width. Therefore, the presence of PND+ can be easily identified in the TIKR result P. The separation of the PND+ and PMP+ contributions is then performed by directly subtracting the PND+ from the P, yielding the desired PMP+. Given that the SNR of DEER data for the binary mixture is better than that for a pure solution of MP+, this study has demonstrated that the PMP+, obtained after the subtraction, is always featured with an improved distance resolution (Fig. 3 and 4).
Finally, we would like to add some notes of caution. First, it is important to observe the quality of fits between the PND+ and the P. When the quality becomes worse than what is presented in the present study, it indicates a need for using other ND+ samples (e.g., ND1+, ND2+, or other newly prepared MSP mutants) to avoid a distance overlap. Second, the optimal ratio of ND+ to MP+ depends critically on the signal intensity of MP+. Although increasing the population of ND+ in the binary mixture would surely lead to an increase in the overall SNR, it concurrently increases the chance that the MP+ is present insignificantly in the experimental DEER time-domain trace. The binary 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture of ND1+ and YetJ+ is an optimal choice for the YetJ studies.
2 mixture of ND1+ and YetJ+ is an optimal choice for the YetJ studies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by grants from the Ministry of Science and Technology of Taiwan (105-2628-M-007-005 and 106-2627-M-007-009). All of the CW/pulse ESR measurements were conducted in the Research Instrument Center of Taiwan located at NTHU.Notes and references
- M. S. Almén, K. J. V. Nordström, R. Fredriksson and H. B. Schiöth, Mapping the human membrane proteome: a majority of the human membrane proteins can be classified according to function and evolutionary origin, BMC Biol., 2009, 7, 50 CrossRef PubMed.
- J. P. Overington, B. Al-Lazikani and A. L. Hopkins, How many drug targets are there?, Nat. Rev. Drug Discovery, 2006, 5, 993–996 CrossRef CAS PubMed.
- G. Jeschke, DEER Distance Measurements on Proteins, Annu. Rev. Phys. Chem., 2012, 63, 419–446 CrossRef CAS PubMed.
- P. P. Borbat and J. H. Freed, Measuring distances by pulsed dipolar ESR spectroscopy: Spin-labeled histidine kinases, Methods Enzymol., 2007, 423, 52–116 CAS.
- B. Joseph, A. Sikora and D. S. Cafiso, Ligand Induced Conformational Changes of a Membrane Transporter in E. coli Cells Observed with DEER/PELDOR, J. Am. Chem. Soc., 2016, 138, 1844–1847 CrossRef CAS PubMed.
- C.-J. Tsai, S. Liu, C.-L. Hung, S.-R. Jhong, T.-C. Sung and Y.-W. Chiang, BAX-Induced Apoptosis Can Be Initiated through a Conformational Selection Mechanism, Structure, 2015, 23, 139–148 CrossRef CAS PubMed.
- T.-C. Sung, C.-Y. Li, Y.-C. Lai, C.-L. Hung, O. Shih, Y.-Q. Yeh, U.-S. Jeng and Y.-W. Chiang, Solution Structure of Apoptotic BAX Oligomer: Oligomerization Likely Precedes Membrane Insertion, Structure, 2015, 23, 1878–1888 CrossRef CAS PubMed.
- N. A. Eschmann, E. R. Georgieva, P. Ganguly, P. P. Borbat, M. D. Rappaport, Y. Akdogan, J. H. Freed, J.-E. Shea and S. Han, Signature of an aggregation-prone conformation of tau, Sci. Rep., 2017, 7, 44739 CrossRef PubMed.
- N. Van Eps, L. N. Caro, T. Morizumi, A. K. Kusnetzow, M. Szczepek, K. P. Hofmann, T. H. Bayburt, S. G. Sligar, O. P. Ernst and W. L. Hubbell, Conformational equilibria of light-activated rhodopsin in nanodiscs, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E3268–E3275 CrossRef CAS PubMed.
- R. Dastvan, A. W. Fischer, S. Mishra, J. Meiler and H. S. Mchaourab, Protonation-dependent conformational dynamics of the multidrug transporter EmrE, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 1220–1225 CrossRef CAS PubMed.
- S. Bibow, Y. Polyhach, C. Eichmann, C. N. Chi, J. Kowal, S. Albiez, R. A. McLeod, H. Stahlberg, G. Jeschke, P. Güntert and R. Riek, Solution structure of discoidal high-density lipoprotein particles with a shortened apolipoprotein A-I, Nat. Struct. Mol. Biol., 2017, 24, 187–193 CrossRef CAS PubMed.
- Y.-W. W. Chiang, P. P. Borbat and J. H. Freed, The Determination of Pair Distance Distributions by Pulsed ESR Using Tikhonov Regularization, J. Magn. Reson., 2005, 172, 279–295 CrossRef CAS PubMed.
- Y.-W. Chiang, P. P. Borbat and J. H. Freed, Maximum entropy: A complement to Tikhonov regularization for determination of pair distance distributions by pulsed ESR, J. Magn. Reson., 2005, 177, 184–196 CrossRef CAS PubMed.
- G. Jeschke, G. Panek, A. Godt, A. Bender and H. Paulsen, Data analysis procedures for pulse ELDOR measurements of broad distance distributions, Appl. Magn. Reson., 2004, 26, 223–244 CrossRef CAS.
- M. K. Bowman, A. G. Maryasov, N. Kim and V. J. DeRose, Visualization of distance distribution from pulsed double electron-electron resonance data, Appl. Magn. Reson., 2004, 26, 23–39 CrossRef CAS.
- G. Jeschke, V. Chechik, P. Ionita, A. Godt, H. Zimmermann, J. Banham, C. R. Timmel, D. Hilger and H. Jung, DeerAnalysis2006—a comprehensive software package for analyzing pulsed ELDOR data, Appl. Magn. Reson., 2006, 30, 473–498 CrossRef CAS.
- R. S. Cooper, E. R. Georgieva, P. P. Borbat, J. H. Freed and E. E. Heldwein, Structural basis for membrane anchoring and fusion regulation of the herpes simplex virus fusogen gB, Nat. Struct. Mol. Biol., 2018, 25, 416–424 CrossRef CAS.
- L. A. Bergdoll, M. T. Lerch, J. W. Patrick, K. Belardo, C. Altenbach, P. Bisignano, A. Laganowsky, M. Grabe, W. L. Hubbell and J. Abramson, Protonation state of glutamate 73 regulates the formation of a specific dimeric association of mVDAC1, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E172–E179 CrossRef CAS PubMed.
- T. H. Edwards and S. Stoll, A Bayesian approach to quantifying uncertainty from experimental noise in DEER spectroscopy, J. Magn. Reson., 2016, 270, 87–97 CrossRef CAS PubMed.
- S. Rein, P. Lewe, S. L. Andrade, S. Kacprzak and S. Weber, Global analysis of complex PELDOR time traces, J. Magn. Reson., 2018, 295, 17–26 CrossRef CAS PubMed.
- M. Srivastava, E. R. Georgieva and J. H. Freed, A New Wavelet Denoising Method for Experimental Time-Domain Signals: Pulsed Dipolar Electron Spin Resonance, J. Phys. Chem. A, 2017, 121, 2452–2465 CrossRef CAS PubMed.
- Y. Chang, R. Bruni, B. Kloss, Z. Assur, E. Kloppmann, B. Rost, W. A. Hendrickson and Q. Liu, Structural basis for a pH-sensitive calcium leak across membranes, Science, 2014, 344, 1131–1135 CrossRef CAS PubMed.
- I. G. Denisov, Y. V. Grinkova, A. A. Lazarides and S. G. Sligar, Directed Self-Assembly of Monodisperse Phospholipid Bilayer Nanodiscs with Controlled Size, J. Am. Chem. Soc., 2004, 126, 3477–3487 CrossRef CAS PubMed.
- C. Martens, R. A. Stein, M. Masureel, A. Roth, S. Mishra, R. Dawaliby, A. Konijnenberg, F. Sobott, C. Govaerts and H. S. Mchaourab, Lipids modulate the conformational dynamics of a secondary multidrug transporter, Nat. Struct. Mol. Biol., 2016, 23, 744–751 CrossRef CAS PubMed.
- T. H. Bayburt, Y. V. Grinkova and S. G. Sligar, Self-Assembly of Discoidal Phospholipid Bilayer Nanoparticles with Membrane Scaffold Proteins, Nano Lett., 2002, 2, 853–856 CrossRef CAS.
- I. G. Denisov and S. G. Sligar, Nanodiscs in Membrane Biochemistry and Biophysics, Chem. Rev., 2017, 117, 4669–4713 CrossRef CAS PubMed.
- S. A. R. Kynde, N. Skar-Gislinge, M. C. Pedersen, S. R. Midtgaard, J. B. Simonsen, R. Schweins, K. Mortensen and L. Arleth, Small-angle scattering gives direct structural information about a membrane protein inside a lipid environment, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2014, 70, 371–383 CrossRef CAS PubMed.
- O. Shih, Y.-Q. Yeh, K.-F. Liao, T.-C. Sung, Y.-W. Chiang and U.-S. Jeng, Oligomerization process of Bcl-2 associated X protein revealed from intermediate structures in solution, Phys. Chem. Chem. Phys., 2017, 19, 7947–7954 RSC.
- G. Hagelueken, D. Abdullin, R. Ward and O. Schiemann, mtsslSuite: In silico spin labelling, trilateration and distance-constrained rigid body docking in PyMOL, Mol. Phys., 2013, 111, 2757–2766 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra00896a |
| This journal is © The Royal Society of Chemistry 2019 |