Open Access Article
Open Access ArticlePhotophysical properties and singlet oxygen generation of meso-iodinated free-base corroles†
Fang Zhao a,
Xuan Zhanb,
Shu-Hui Laib,
Lei Zhang
a,
Xuan Zhanb,
Shu-Hui Laib,
Lei Zhang *a and
Hai-Yang Liu
*a and
Hai-Yang Liu *b
*b
aState Key Laboratory of Optoelectronic Materials and Technologies, School of Physics, Sun Yat-Sen University, Guangzhou 510275, China. E-mail: zhlei28@mail.sysu.edu.cn
bDepartment of Chemistry, The Key Laboratory of Fuel Cell Technology of Guangdong Province, South China University of Technology, Guangzhou 510641, China. E-mail: chhyliu@scut.edu.cn
First published on 24th April 2019
Abstract
In order to study the effect of meso-iodination of free-base corroles on their photophysical character, we designed and synthesized a series of free-base corrole derivatives F10–OH (iodine-free), F10–OH–I (mono-iodo) and F10–OH–2I (di-iodo), with different substitution patterns at the meso-position as candidates for photodynamic therapy (PDT). We employed several optical spectroscopic techniques, including time-resolved spectroscopy from a femtosecond to microsecond and singlet oxygen luminescence to study the properties of excited singlet and triplet states, as well as the singlet oxygen quantum yields. The sub-picosecond internal conversion, ∼1 ps intramolecular vibrational energy redistribution, tens of ps vibrational cooling, are similar across the three corroles. The addition of one (F10–OH–I) and two iodine (F10–OH–2I) atoms to the remote aryl ring of triarylcorroles induces a 4.6-fold and 6.2-fold decrease in fluorescence quantum yields Φfl and a 2.2-fold and 4.9-fold increase in the time constant of intersystem crossing kISC. In addition, a slight increase in intersystem crossing quantum yields ΦT was also observed from F10–OH to F10–OH–2I. It means the intersystem crossing is improved by the iodination, from F10–OH to F10–OH–2I, because of the heavy atom effect. However, the sample F10–OH–I, instead of F10–OH–2I, shows the highest singlet oxygen quantum yield ΦΔ.
1. Introduction
A corrole macrocycle is a contracted analog of porphyrin, and its symmetry decreases from D2h of free-base porphyrin to Cs due to the elimination of a meso methine unit. Recently, corrole derivatives have been used in photodynamic therapy (PDT), photodynamic diagnosis (PDD),1,2 dye-sensitized solar cells,3–5 catalysis,6,7 and corrole-based electron and energy transfer systems.8–10 Different central metals,3 axial ligands,11,12 and peripheral substituents13–16 drastically change the photophysical properties of corroles.Within these methods, halogenated pyrrole rings at the β-position have a remarkable effect on the photophysical properties of corroles via increasing the intersystem crossing (ISC) with heavy atom effects. Recently, the reduction potentials and catalytic activity of a series of β-pyrrole halogenated Co corroles (Co–X8, X = H, Cl, Br, F) had been investigated. It was found that the redox potentials of all halogenated complexes were positively shifted as compared to that of Co–H8.6,17 Also, both the iridium(III) corrole and its β-pyrrole brominated complex display near-IR phosphorescence at ambient temperature and the brominated corrole exhibits a longer triplet lifetime than the nonbrominated one.18 Moreover, the β-bromination decreases the fluorescence quantum yield and lifetime by promoting enhanced ISC for free-base corroles.19
As for iodination, the selective β-pyrrole iodinated aluminum, gallium and gold corroles were synthesized and displayed long-lived triplet excited states,13 prompt fluorescence, near-IR phosphorescence, delayed thermal fluorescence at room temperature,20 and reasonable singlet oxygen formation yields.21 Also, the excited-state dynamics and electronic structures of Al and Ga corrole complexes were found as a function of the number of β-pyrrole iodine substituents. Iodination could accelerate all of the involved processes, including the internal conversion from the Soret to the Q states (IC), vibrational cooling (VC) and ISC.22
Although much work has focused on corroles substituted with halogens at the beta-pyrrole positions, the study of heavy halide atoms effect at meso-phenyl rings is limited. Our group synthesized a series of halogenated free-base corroles, including two C6F5 and one 2-hydroxy-5-halogen-phenyl meso substituents (F10–OH–F, F10–OH–Cl, F10–OH–I). We found that the ISC rate constant kisc increased in the order F < Cl < I.23,24 We also compared free-base corroles with a different number of –C6F5 (F0, F5, F10, F15) at meso-positions. The order of kISC is F0C < F5C < F10C > F15C. It indicates that the electron-withdrawing effect of fluorophenyl substitutions, together with the heavy atom effect, influences the photophysical properties of excited states of corroles.25
Within the free-base corroles we studied, the F10–OH–I with a single I atom on the meso-ring shows the highest kISC, triplet quantum yield (ΦT) and singlet oxygen quantum yield (ΦΔ).23 Spurred by these results, we were interested in studying the effect of meso-iodination on the electronic structure and excited state properties of corroles. If kISC, ΦT and ΦΔ increase with increasing extent of meso-iodinations? How does the meso-iodination influence the relaxation progress from higher excited electronic states to the S1 state? What is the difference effect on the photophysical characters of corroles between the β- and meso-iodination? The answers to these questions are still unclear.
In this article, we designed and synthesized two free-base monohydroxyl iodinated corroles F10–OH–I (mono-iodo) and F10–OH–2I (di-iodo) and compared their photophysical properties to the noniodinated complex F10–OH (Scheme 1). The femtosecond to microsecond dynamics of Soret-band excitation was measured. From the analyses of time constants at different time windows, we obtained the time constants of all of the involved processes, including IC from the Soret to the Q states, intramolecular vibrational energy redistribution (IVR) and VC in Q states, and ISC. The singlet oxygen luminescence was performed to obtain ΦΔ.
For clarity, the three free-base corroles, F10–OH, F10–OH–I, and F10–OH–2I, are shortened as 1, 2 and 3, respectively in the following paragraphs.
2. Experimental
2.1 Samples preparation
The detailed experimental procedure for the synthesis of A2B free-base corroles were discussed elsewhere.24,26 We have adopted the same method for the synthesis of our targeted compounds. Corroles 1, 2 and 3 were well characterized by MS, 1H-NMR and 19F-NMR (see ESI 1†).2.2 Optical measurements
The steady-state absorption and emission spectra were measured using a PerkinElmer Lambda 850 UV-Vis spectrometer and a PerkinElmer LS55 luminescence spectrometer (PE Company, USA), respectively.The femtosecond transient absorption (TA) experiment was described earlier.25 Briefly, the femtosecond transient absorption set-up employed was equipped with a regenerative Ti:sapphire amplifier laser with 500 Hz repetition (Legend Elite USP HE+, Coherent, 35 fs, 800 nm) as the primary laser source. The output beam was split into two. One with a power of 6 μJ per pulse was focused on the water to generate a white light continuum as a probe beam. Before sample, a long-cut filter from 750 nm was used in the probe beam to remove the fundamental 800 nm laser beam. Therefore, we cannot record the TA signal above 750 nm. The other beam was frequency doubled using a 150 μm BBO crystal to generate a 400 nm pump beam (pulse width: 90–100 fs), and then passed to the translation stage. Two translation stages were used to cover the TA experiment from fs – 1 ns (M-ILS200HA, Newport) or from fs – 7.2 ns (M-IMS600CCHA, Newport, double-pass). A mechanical chopper was employed to modulate the pump repetition frequency to 1/2 the probe repetition rate. The pump and probe pulses were focused to a diameter of 500 and 200 μm, respectively, at the sample cell interface using two plano-concave mirrors. The probe pulse was recorded using a fiber spectrometer (Avantes, AvaSpec_ULS2048L-USB2) in external trigger mode. The polarization between the pump and the probe beam was set to the magic angle (54.7°) concerning the probe beam.
The optical path in samples was 5 mm. The pump energy was μJ per pulse. The sample was stirred to avoid the photodamage. UV-visible absorption spectra of the samples before and after the experiments showed almost no change.
The triplet TA experiment was measured by a laser flash photolysis apparatus described earlier.23 The relatively low concentration of the free-base corroles with the small absorbance of about 0.2 at the excitation wavelength 532 nm can avoid the formation of molecule aggregation. The pulse energy of the excitation is 2.0 mJ per pulse. Samples were put in a 1 cm path length quartz optical cell and degassed using the freeze–pump–thaw technique.
The lifetime of S1 fluorescence was detected using a photomultiplier tube (Hamamatsu, R3809U-50) and measured using a TCSPC (Becker & Hickl GmbH simple Tau152). Mai Tai (Spectra-Physics) was used as the laser source.
The steady-state luminescence of singlet oxygen was measured by using an FLS920 spectrofluorimeter (Edinburgh Instruments) with the wavelength range from 600 to 1700 nm. The FLS920 spectrofluorimeter was equipped with a TM300 excitation monochromator and a TM300 emission monochromator equipped with a NIR grating, and a Hamamatsu R5509-72 supercooled photomultiplier tube at 193 K. The excitation wavelength was 550 nm.
The relative errors are estimated as 10% for the lifetime of TA measurement, 15% on fluorescence quantum yield, 5% for fluorescence lifetime, 20% for triplet lifetime, 20% on singlet oxygen quantum yield. In the present study, all corrole samples were dissolved in benzene at room temperature, and the concentration was 25 μM. H2TPP (tetraphenylporphyrin) was performed as the standard sample and dissolved in toluene when calculating Φfl and ΦΔ.
3. Results
3.1 Steady-state spectra
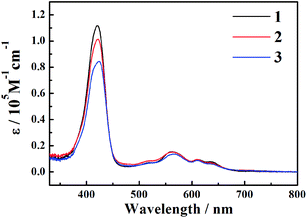
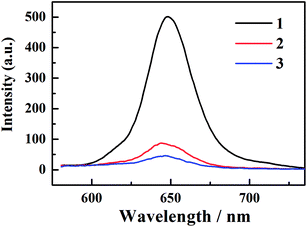
The steady-state absorption spectra of the three corroles are exhibited in Fig. 1. There is a typical Soret band (S2 excited state) around 420 nm and Q bands (S1 excited state) ranging from 500–700 nm. The different substitution at the meso – position does not change too much the shape of the UV-Visible spectra. No red-shift of Soret or Q bands was observed from 1 to 3, which is different from the β-iodination20 and β-bromination.19 The molar absorption coefficient (ε) of the Soret bands decreases with the number of iodine. The mole absorption coefficients at the absorption maxima of the Soret and Q bands are also exhibited in Table S1 of ESI.†The fluorescence spectra are shown in Fig. 2. The emission peaks are almost at the same position of ∼646 nm. With the adding of iodine atoms, the fluorescence quantum yield decreases drastically from 1 to 3, as summarized in Table 1.
| Compd | Emission, λmaxa (nm) | Φflb | τflc (ns) | krd (107 S−1) | knre (107 S−1) |
|---|---|---|---|---|---|
| a λmax stands for the wavelength of emission band at the maximum intensity.b Fluorescence quantum yields in aerated benzene were calculated based on the fluorescence spectra using H2TPP (tetraphenylporphyrin) as a standard (Φfl = 0.11). λex = 560 nm.c Fluorescence lifetime in aerated benzene. λex = 400 nm.d Radiative decay rate constants were determined by using the expression kr = Φfl/τfl.e Nonradiative decay rate constants were obtained from the expression knr = (1 − Φfl)/τfl. | |||||
| 1 | 648 | 0.143 | 3.59 | 3.98 | 23 |
| 2 | 644 | 0.031 | 1.87 | 1.67 | 51 |
| 3 | 646 | 0.023 | 0.83 | 2.78 | 117 |
3.2 Time-resolved fluorescence
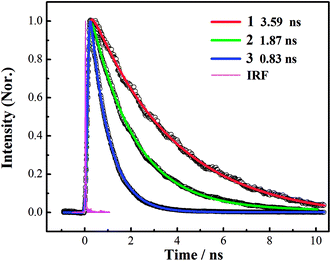
The fluorescence decay curve of all corroles at 648 nm is recorded by TCSPC system, as shown in Fig. 3. The goodness of fit is shown in Fig. S11 of ESI.† The lifetime of fluorescence (τfl) was obtained by fitting the time profiles with mono-exponential functions, as shown in Table 1. The fluorescence lifetime from 1 to 3 gradually turns shorter.3.3 Femtosecond to nanosecond transient absorption spectroscopy
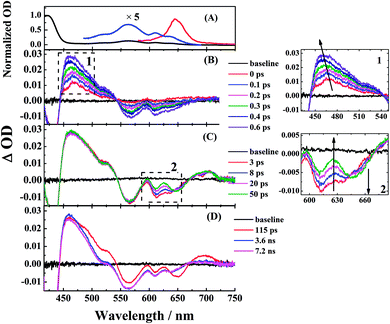
To study the photophysical properties in detail, we performed the transient absorption (TA) of three free corroles excited at 400 nm with the time domain from fs to 7 ns. For clarity, we select 2 as an example. The TA spectra of 2 in benzene at selected time delays are shown in Fig. 4. We chose two spectral windows and enlarged them at the right panel to show the evolution of the TA spectra. From Fig. 4, the main band of excited state absorption (ESA) at around 462 nm increases gradually from 0–0.6 ps, accompanied by a band maximum shifting to the blue for about 9 nm, as shown in region 1. Concomitantly, the GSB from Soret band (433 nm) and Q bands (564 nm, 610 nm, and 636 nm) increase. It may indicate that the TA at this time window belongs to two transient species. From 3 ps to 50 ps, the TA at 462 nm does not change appreciably, while, the negative bands from 600–700 nm exhibits some changes. As shown in region 2, the GSB of 610 nm and 636 nm decreases, while a new negative signal 650 nm, corresponding to the peak of the static S1 emission spectrum, appears concomitantly. Therefore, we assign it to sti-mulated emission (SE) from the lowest energy level of Q bands. From 115 ps to 7.2 ns, the TA of 462 nm turns narrow, accompanied by the decay of SE. As mentioned above, the fluorescence lifetime of 2 is 1.87 ns, which strongly suggests that the TA at 7.2 ns mainly comes from the first excited triplet state (T1) of corrole. The TA of 1 and 3 are shown in Fig. S1 and S2 of ESI.† Since the Soret band is located at ∼421 nm, the pump beam at 400 nm excites the corroles to its S2 state. Therefore, the positive signals come from the ESA of S2,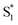 and T1, as well as negative ones from the ground-state bleaching (GSB) of Soret band and Q bands, and stimulated emission (SE) from the lowest energy level of Q bands.
and T1, as well as negative ones from the ground-state bleaching (GSB) of Soret band and Q bands, and stimulated emission (SE) from the lowest energy level of Q bands.
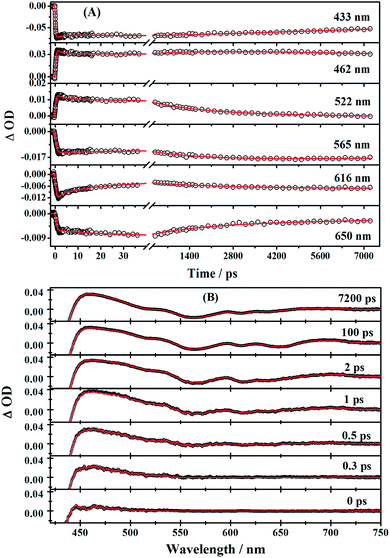
The time profiles at several selected wavelengths of 2 in benzene after 400 nm pump are shown in Fig. 5, along with the best fit obtained using the global fit analysis described in the latter part of this section (for 1 and 3, see Fig. S3–S6 in the ESI†). Apparently, the spectra overlap leads to the difficulty of analyzing by single-wavelength kinetic profile fitting. Therefore, we performed the global and target analysis. It will be introduced in detail in Section 3.6.
3.4 Triplet-state transient absorption spectra
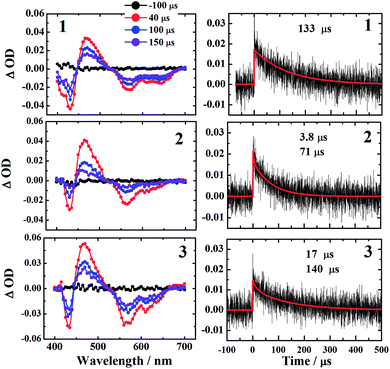
The microsecond time domain TA spectra in deaerated benzene are shown in Fig. 6. The TA of corroles in Fig. 6 is very similar to that at 7.2 ns in Fig. 4. It is also consistent with the previous study, which shows the TA of T1 →Tn is usually centered at 460 nm.23 Therefore, we fitted the kinetic trace at 460 nm by monoexponential or biexponential decay. The fast decay comes from the scattering of the laser pulse. The lifetimes of three corroles τT were shown in Table 3.| τ0T a (μs) | τT b (μs) | kTq (109 M−1 S−1) | c | φT | φΔ | |
|---|---|---|---|---|---|---|
| a The triplet lifetimes in deaerated benzene.b The triplet lifetimes in aerated benzene.c The proportion of triplet states quenched by O2. The relative errors are estimated as 20%. | ||||||
| 1 | 130 | 5.3 | 0.10 | 0.96 | 0.85 | 0.6 |
| 2 | 70 | 3.2 | 0.16 | 0.95 | 0.97 | 0.9 |
| 3 | 140 | 2.4 | 0.22 | 0.98 | 0.97 | 0.4 |
| Sequential model | Target model | Lifetimes and decay parameters | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | |||
| a k4 was fixed to the values obtained by TSCPC method.b kr was obtained from Table 1.c kISC was calculated by substituting kr from k4.d The value kEN was assumed as the rate constant for the formation of the encounter complexes. It was the same with k5 in the sequential model.e kT was obtained by the microsecond time domain TA experiments, and the values are shown in Table 3. | ||||||||
| k1 | (470 fs)−1 | (520 fs)−1 | (490 fs)−1 | kIC (kIC = k1) | S2, τIC | 470 fs | 520 fs | 490 fs |
| k2 | (0.99 ps)−1 | (0.98 ps)−1 | (0.98 ps)−1 | kIVR (kIVR = k2) | τIVR | 0.99 ps | 0.99 ps | 0.98 ps |
| k3 | (22 ps)−1 | (27 ps)−1 | (19 ps)−1 | kVC (kVC = k3) | τVC | 22 ps | 27 ps | 19 ps |
| ak4 | (3.59 ns)−1 | (1.87 ns)−1 | (0.83 ns)−1 | bkr | kr | (25 ns)−1 | (60 ns)−1 | (36 ns)−1 |
| ckISC (k4 = kr + kISC) | kISC | (4.19 ns)−1 | (1.93 ns)−1 | (0.86 ns)−1 | ||||
| k5 | (38 ns)−1 | (27 ns)−1 | (25 ns)−1 | dkEN (kEN = k5) | kEN | (38 ns)−1 | (27 ns)−1 | (25 ns)−1 |
| ekT | τT | 5.3 μs | 3.2 μs | 2.4 μs | ||||
The kinetic traces at the maximum of TA of T1 → Tn for corroles 1–3 in the aerated benzene were measured. As for other wavelengths, the signal-to-noise ratio of the kinetics was so low that it is difficult to derive the TA spectrum from them. Fitting the kinetic traces at 460 nm, and the lifetimes of T1 states in the aerated benzene were obtained, as shown in Fig. S10 of the ESI.† The fitted lifetime is listed in Table 3. According to eqn (1) and (2) (the Stern–Volmer equation), kTq and 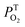 can be calculated,32,33 which are the oxygen quenching rate constant and the proportion of triplet states quenched by O2, respectively.
can be calculated,32,33 which are the oxygen quenching rate constant and the proportion of triplet states quenched by O2, respectively.
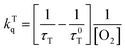 | (1) |
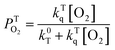 | (2) |
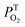 of the three samples are about unity, it indicates that the T1 states are almost entirely quenched by O2.
of the three samples are about unity, it indicates that the T1 states are almost entirely quenched by O2.
3.5 Singlet oxygen generation from the three corroles
All of the three samples exhibit the emission bands centered at 1275 nm, as shown in Fig. 7, which was known as the steady-state emission spectra of singlet oxygen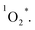 One can calculate the singlet oxygen quantum yields φΔ by using comparative actinometry method, as shown in Table 2 (shown in ESI† for the details). Although 3 shows the largest kTq, it does not exhibit the best φΔ. As is well studied, the T1 state of the sensitizer and the triplet ground-state
One can calculate the singlet oxygen quantum yields φΔ by using comparative actinometry method, as shown in Table 2 (shown in ESI† for the details). Although 3 shows the largest kTq, it does not exhibit the best φΔ. As is well studied, the T1 state of the sensitizer and the triplet ground-state 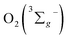 leads to the formation of excited
leads to the formation of excited 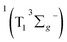 complexes. Then, the energy transfer (ET) occurs in the encounter complexes to get
complexes. Then, the energy transfer (ET) occurs in the encounter complexes to get 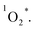 In competition with energy transfer, charge transfer (CT) may also occur within the complexes leading to superoxide (O2˙−).28 This competitive deactivation of T1 state by O2 may limit the φΔ, especially for corrole 3.
In competition with energy transfer, charge transfer (CT) may also occur within the complexes leading to superoxide (O2˙−).28 This competitive deactivation of T1 state by O2 may limit the φΔ, especially for corrole 3.
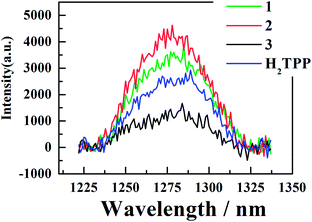 | ||
| Fig. 7 Singlet oxygen luminescence of corroles 1–3 in aerated benzene, H2TPP in aerated toluene, detected after excitation at 550 nm (Q band) for solutions of the three corroles. | ||
3.6 Global fitting of the TA spectra
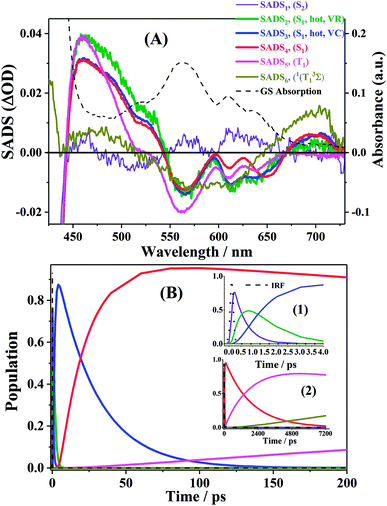
First, global fitting was performed in the sequential kinetic model to obtain gross spectral evolution of the data. From this step, we obtained five time constants. They are ∼ (500 fs)−1 (k1), ∼ (1 ps)−1 (k2), ∼ (20 ps)−1 (k3), (0.83 ps)−1 – (3.59 ps−1) (k4) and (25.1 ns)−1 – (38.1 ps−1) (k5), respectively, as shown in Table 3. However, the sequential model cannot provide us the real individual transient spectral and their time constants. Therefore, a target analysis was also performed to get the species-associated spectra (SADS). We received six SADS with seven time constants from this step, as shown in Fig. 9 (for 1 and 3, see Fig. S5 and S6 in ESI†). The goodness of the fits is shown in Fig. 5A and B. The schematic diagram of the relaxation dynamics for corroles 1–3 are shown in Fig. 8.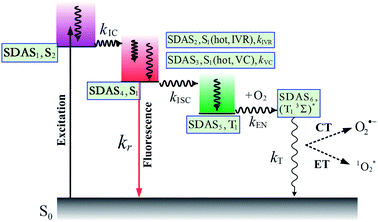 | ||
| Fig. 8 Schematic kinetic model used for target analysis of TA data of corroles 1–3 in benzene upon 400 nm excitation. | ||
Considering the Soret-band excitation, we assign SDAS1 as S2 state. As for SDAS1, the two positive band at 570 and 616 nm indicate a rise of Q bands bleaching. The negative signal at around 510 nm implies the growth of the Q band ESA. These observations are similar to that of Sb-corroles.29 The S2 state decays to a vibrationally “hot” S1 with the time constant of kIC. The value of kIC in the target model is the same with the k1 in the sequential model. Therefore, the lifetime of S2, τIC is fitted to be 470, 520 and 490 fs for 1, 2 and 3, respectively.
SDAS2 represents the vibrationally “hot” S1 state. The timescale of this hot S1 state τIVR is fitted to be 0.99 ps, 0.99 ps, and 0.98 ps for 1, 2 and 3, respectively, which are similar within these three corroles. We assigned the decay of SADS2 to the intramolecular vibrational energy redistribution (IVR). The value of τIVR is the same with 1/k2 obtained from the sequential model.
The timescale of SDAS3 τVC is 22.4 ps 27.1 18.6 ps, for 1, 2 and 3, respectively, and it decays to the thermally relaxed S1 state, via the solute–solvent intermolecular vibrational cooling (VC). τVC in the target fitting is obtained from 1/k3 in the sequential model.
There is no apparent 650 nm SE from SDAS2 and SDAS3, while it reaches to its maximum at SDAS4. Therefore, SDAS4 was assigned to the S1 state after the VC process. The S1 state decays to the ground states S0 by radiative (kr) and nonradiative (k0nr) pathway. It also decays via the ISC from S1 → T1 (kISC). Therefore, the fourth kinetic component k4 in the sequential model corresponds to the decay of S1 state: k4 = kr + k0nr + kISC. The significant fluorescence quenching and lifetime shortening caused by the iodinated corroles indicates that fluorescence and ISC are the main decay processes of the S1 state for the three corroles. Therefore, we ignored k0nr and assumed k4 ≈ kr + kISC in the target model. Because the TA spectra of S1 and T1 state overlap to each other, it was difficult to estimate the lifetime of S1 state precisely. Thus, the value of k4 was kept constant as obtained from TCSPC method in global fitting.30 kr was obtained from Table 1 and kISC can be calculated by substituting kr from k4, shown in Table 3.
SDAS5 is very similar to the TA at 7200 ps. This long-lived species should be attributed to T1 state. The lifetime of the T1 state τT has been measured to be several microseconds in aerated benzene. However, in the sequential model, k5 was fitted to several tens of nanoseconds, instead of microseconds. This ns decay can also be observed in the time profile of 460 nm, which indicates the correctness of the global fitting. Perhaps, the ns time resolution of our laser flash photolysis setup makes it difficult to observe this ns decay. Temporarily, we assigned this ns decay to the formation of the encounter complexes 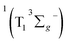 in the target model, named as kEN. Therefore, the last component SDAS6 is attributed to
in the target model, named as kEN. Therefore, the last component SDAS6 is attributed to 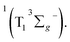 It decays to the ground state with the lifetime of τT. The relationship and the values of the rate constants are summarized in Table 3.
It decays to the ground state with the lifetime of τT. The relationship and the values of the rate constants are summarized in Table 3.
4. Discussion
4.1 Intersystem crossing
One can determine the quantum yield of ISC φT from eqn (3) as shown in Table 2. Both of the kISC and φT exhibits an increasing value from 1 to 3. The kISC increased from (4.19 ns)−1 for 1 (no iodine) to (0.86 ns)−1 for 3 (2 iodines), only 4.9-fold enlarged.
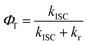 | (3) |
Lemen et al. studied the effect of the β-bromination on free-base corroles.19 They found that the β-bromination cause a splitting of Soret band absorption and a red-shift of the emission maximum of Q band. The knr (knr = k0nr + kISC) was drastically increased from 2 × 108 s−1 for no Br to 1 × 1010 s−1 for Br4, which should be ascribed to bromine heavy atom effect. Similarly, Pomarico et al. studied the impact of β-iodination on the excited-state dynamics and electronic structures of Al and Ga corrole complexes.22 They regarded τfl as 1/kISC, and found kISC drastically increased from 2.3 × 108 s−1 for 0-Ga (no iodine) to 6.7 × 1010 s−1 for 4-Ga (4 iodines). Both of these two studies show a two-fold order of magnitude increase of kISC by β-halogenation. The β-iodination was found to introduce a manifold of low-lying singlet and triplet iodine → corrole charge-transfer (CT) states by using TDDFT. Such a CT state accelerates ISC from nanosecond to picosecond.22 From our study, the lack of red-shift of the emission maximum of Q band may indicate that the change of the energy of electronic states should be negligible. Therefore, this CT state may not exist in the present meso-iodination corroles, because of the very tiny conjugation between the corrole and the meso-phenyl π systems.
Another problem arises that although kISC increases with the meso-iodination, the value of φΔ does not show a corresponding increase from 1 to 3. Sample 2 exhibits the highest φΔ, instead of 3. As mentioned above, in competition with ET between the T1 of sensitizer and 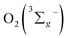 to form 1O2, the formation of ions (CT) may also occur to lead to the formation O2˙−, instead of
to form 1O2, the formation of ions (CT) may also occur to lead to the formation O2˙−, instead of 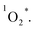 28 From eqn (4) (ref. 31 and 32)
28 From eqn (4) (ref. 31 and 32)
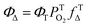 | (4) |
4.2 Internal conversion
The kIC (1/0.5 ps) from the Soret to the Q states are similar upon meso-iodination. We did not observe an increase of the IC time constant from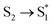 in this study. This observation is different from our previous research that the timescale of IC was shortened from 550 fs of F0C to 140 fs of F15C upon meso-fluorination.25 We explained that the fluorophenyl substitutions might result in withdrawal of the electron density from the macrocycle framework and increase non-planar structures. On the other hand, the timescale of the Soret → Q conversion accelerates upon β-iodination from 320 fs (0-Ga) to 180 fs (3-Ga) and 70 fs (4-Ga).22 It should be attributed to the manifold of CT excited states between Soret and Q states present in the iodinated complexes. In the present system, the meso-iodine atoms may exhibit neither enough withdrawal effect nor CT state to accelerate the IC timescale.
in this study. This observation is different from our previous research that the timescale of IC was shortened from 550 fs of F0C to 140 fs of F15C upon meso-fluorination.25 We explained that the fluorophenyl substitutions might result in withdrawal of the electron density from the macrocycle framework and increase non-planar structures. On the other hand, the timescale of the Soret → Q conversion accelerates upon β-iodination from 320 fs (0-Ga) to 180 fs (3-Ga) and 70 fs (4-Ga).22 It should be attributed to the manifold of CT excited states between Soret and Q states present in the iodinated complexes. In the present system, the meso-iodine atoms may exhibit neither enough withdrawal effect nor CT state to accelerate the IC timescale.
4.3 Vibrational relaxation
There are two vibrational energy relaxation (VR) processes for large molecules in solvents. One is intramolecular vibrational energy redistribution (IVR) between different modes of the excited solute that typically occurs on the timescale 10–100 fs. The other is the subsequent vibrational cooling (VC) that usually occurs on timescale from one to some tens of ps.33 These two processes sometimes entangle too close to be distinguished.34 In the present system, we observed the two VR processes. First, the short decay shows a timescale ∼1 ps. It is similar to the reported 1.4 ps IVR timescale for H2TPP.35 Moreover, a series of isomeric meso-(pyridyl) porphyrins (TpyPs) also shows 1–1.5 ps IVR timescale.30 Therefore, this short timescale should be attributed to IVR process. Second, VC usually presents a dependence at various probe wavelength, band shifting and narrowing.36,37 We observed an apparent rearrangement at the Q bands bleaching at about 611 to 650 nm, from 5 to ∼100 ps. The Q band bleachings at 610 nm and 636 nm decrease and the 650 nm SE rises gradually. Therefore, this several tens ps timescale is attributed to the VC process. The values τVC obtained from the target analysis are 22, 27 and 19 ps, respectively. It indicates that the substitute iodination does not influence the vibrational cooling process. Compared with our previous study, the fluorophenyl substitutions slow down the τVC from 9 ps for F0C to 24 ps for F15C.25 The possible mechanism we proposed was that the fluorophenyl substitutions change the position of Q bands, as well as the energy gap between the Franck – Condon active mode and the instantaneous normal modes of the solvent. The different energy gap results in a longer VC timescale for the fluorophenyl corroles. In the present system, neither the Q bands nor the τVC is influenced by the iodination. These two studies together may indicate that the τVC is related to the Q bands position. The typical VC lifetime is around 10–20 ps for these types of tetrapyrrole systems.35,38 Similar vibrational cooling timescale were reported about 10 ps to 20 ps for Sb-tpfc-F2 (ref. 29) and 6 ps for protoporphyrin IX (PPIX).37 Bangal's group found a 105 ps relaxation for 5,10,15,20-meso-tetrakis pentafluorophenyl porphyrin (H2F20TPP).39 They attributed it not only a VC lifetime but also an excited state conformational relaxation. In the present system, the conformation effect should be ignored.5. Conclusion
In sum, we have investigated the photophysical properties of a series of free-base corrole derivatives with different meso-iodination. With femtosecond transient absorption spectroscopy, the dynamics of F10–OH, F10–OH–I, and F10–OH–2I in benzene were examined upon excitation at 400 nm in the femtosecond and microsecond domain. All the three corroles show the sub-picosecond IC from Soret to Q bands, the ∼1 ps IVR, and the several tens of ps VC process within Q bands. The time constants of IC, IVR, and VC do not change upon meso-iodination, while the kISC and φT are increased by the iodination. This observation is quite different from that of β-iodination, which can accelerate all of the involved processes. Although F10–OH–2I shows the largest kISC and φT, it does not show the highest quantum yields of 1O2 (φΔ). Instead, F10–OH–I exhibits the highest φΔ. This may be caused by the competition between ET and CT in the encounter complexes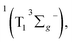 which generates 1O2 and O2˙−, respectively. This result may provide help to chemists when they synthesize iodinated free-base corroles as photosensitizers for PDT.
which generates 1O2 and O2˙−, respectively. This result may provide help to chemists when they synthesize iodinated free-base corroles as photosensitizers for PDT.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 61475196, 21671068), the National Basic Research Program (973 program) of China under grant 2013CB922403.Notes and references
- J. F. B. Barata, A. Zamarrón, M. G. P. M. S. Neves, M. A. F. Faustino, A. C. Tomé, J. A. S. Cavaleiro, B. Röder, Á. Juarranz and F. Sanz-Rodríguez, Eur. J. Med. Chem., 2015, 92, 135–144 CrossRef CAS PubMed.
- J. Y. Hwang, D. J. Lubow, D. Chu, J. Sims, F. Alonso-Valenteen, H. B. Gray, Z. Gross, D. L. Farkas and L. K. Medina-Kauwe, J. Controlled Release, 2012, 163, 368–373 CrossRef CAS PubMed.
- B. J. Brennan, Y. C. Lam, P. M. Kim, X. Zhang and G. W. Brudvig, ACS Appl. Mater. Interfaces, 2015, 7, 16124–16130 CrossRef CAS.
- D. Walker, S. Chappel, A. Mahammed, B. S. Brunschwig, J. R. Winkler, H. B. Gray, A. Zaban and Z. Gross, J. Porphyrins Phthalocyanines, 2006, 10, 1259–1262 CrossRef CAS.
- A. B. Alemayehu, N. U. Day, T. Mani, A. B. Rudine, K. E. Thomas, O. A. Gederaas, S. A. Vinogradov, C. C. Wamser and A. Ghosh, ACS Appl. Mater. Interfaces, 2016, 8, 18935–18942 CrossRef CAS.
- A. Mahammed, B. Mondal, A. Rana, A. Dey and Z. Gross, Chem. Commun., 2014, 50, 2725–2727 RSC.
- N. Levy, J. S. Shpilman, H. C. Honig, D. T. Major and L. Elbaz, Chem. Commun., 2017, 53, 12942–12945 RSC.
- L. Giribabu, K. Jain, K. Sudhakar, N. Duvva and R. Chitta, J. Lumin., 2016, 177, 209–218 CrossRef CAS.
- Y. Wang, Z. Wang, X. Guo, R. Cui, X. Gao, S. Yang, F. Chang, J. Dong and B. Sun, J. Nanosci. Nanotechnol., 2014, 14, 5370–5374 CrossRef CAS.
- L. Flamigni, D. Wyrostek, R. Voloshchuk and D. T. Gryko, Phys. Chem. Chem. Phys., 2010, 12, 474–483 RSC.
- I. Aviv-Hare and Z. Gross, Coord. Chem. Rev., 2011, 255, 717–736 CrossRef.
- A. Ghosh, Chem. Rev., 2017, 117, 3798–3881 CrossRef CAS PubMed.
- J. Vestfrid, M. Botoshansky, J. H. Palmer, A. C. Durrell, H. B. Gray and Z. Gross, J. Am. Chem. Soc., 2011, 133, 12899–12901 CrossRef CAS PubMed.
- L. Wagnert, A. Berg, E. Stavitski, T. Berthold, G. Kothe, I. Goldberg, A. Mahammed, L. Simkhovich, Z. Gross and H. Levanon, Appl. Magn. Reson., 2006, 30, 591 CrossRef CAS.
- L. Wagnert, R. Rubin, A. Berg, A. Mahammed, Z. Gross and H. Levanon, J. Phys. Chem. B, 2010, 114, 14303–14308 CrossRef CAS PubMed.
- C. M. Lemon, R. L. Halbach, M. Huynh and D. G. Nocera, Inorg. Chem., 2015, 54, 2713–2725 CrossRef CAS PubMed.
- A. Mahammed, M. Botoshansky and Z. Gross, Dalton Trans., 2012, 41, 10938–10940 RSC.
- J. H. Palmer, A. C. Durrell, Z. Gross, J. R. Winkler and H. B. Gray, J. Am. Chem. Soc., 2010, 132, 9230–9231 CrossRef CAS.
- C. M. Lemon, R. L. Halbach, M. Huynh and D. G. Nocera, Inorg. Chem., 2015, 54, 2713–2725 CrossRef CAS.
- J. Vestfrid, I. Goldberg and Z. Gross, Inorg. Chem., 2014, 53, 10536–10542 CrossRef CAS.
- M. Soll, K. Sudhakar, N. Fridman, A. Muller, B. Roder and Z. Gross, Org. Lett., 2016, 18, 5840–5843 CrossRef CAS.
- E. Pomarico, P. Pospíšil, M. E. F. Bouduban, J. Vestfrid, Z. Gross, S. Záliš, M. Chergui and A. Vlček, J. Phys. Chem. A, 2018, 122, 7256–7266 CrossRef CAS PubMed.
- W. Shao, H. Wang, S. He, L. Shi, K. Peng, Y. Lin, L. Zhang, L. Ji and H. Liu, J. Phys. Chem. B, 2012, 116, 14228–14234 CrossRef CAS PubMed.
- L. Shi, H.-Y. Liu, H. Shen, J. Hu, G.-L. Zhang, H. Wang, L.-N. Ji, C.-K. Chang and H.-F. Jiang, J. Porphyrins Phthalocyanines, 2009, 13, 1221–1226 CrossRef CAS.
- L. Zhang, Z. Y. Liu, X. Zhan, L. L. Wang, H. Wang and H. Y. Liu, Photochem. Photobiol. Sci., 2015, 14, 953–962 RSC.
- L. Shi, H. Y. Liu, L. P. Si, K. M. Peng, L. L. You, H. Wang, L. Zhang, L. N. Ji, C. K. Chang and H. F. Jiang, Chin. Chem. Lett., 2010, 21, 373–375 CrossRef CAS.
- M. Montalti and A. Credi, Handbook of Photochemistry CRC/Taylor & Francis, Boca Raton, 3rd edn, 2006, Chp. 9, p. 542 Search PubMed.
- C. Schweitzer and R. Schmidt, Chem. Rev., 2003, 103, 1685–1757 CrossRef CAS.
- C. Zahn, T. Stensitzki, M. Gerecke, A. Berg, A. Mahammed, Z. Gross and K. Heyne, Molecules, 2017, 22, 1174 CrossRef.
- Y. Venkatesh, M. Venkatesan, B. Ramakrishna and P. R. Bangal, J. Phys. Chem. B, 2016, 120, 9410–9421 CrossRef CAS.
- F. Wilkinson, W. P. Helman and A. B. Ross, J. Phys. Chem. Ref. Data, 1993, 22, 113–262 CrossRef CAS.
- J. H. Ha, G. Y. Jun, M. S. Kim, Y. H. Lee, K. Shin and Y. R. Kim, Bull. Korean Chem. Soc., 2001, 22, 63–67 CAS.
- J. Petersson, M. Eklund, J. Davidsson and L. Hammarstrom, J. Phys. Chem. B, 2010, 114, 14329–14338 CrossRef CAS.
- A. Pigliucci, G. Duvanel, L. M. L. Daku and E. Vauthey, J. Phys. Chem. A, 2007, 111, 6135–6145 CrossRef CAS.
- J. S. Baskin, H.-Z. Yu and A. H. Zewail, J. Phys. Chem. A, 2002, 106, 9837–9844 CrossRef CAS.
- C. T. Middleton, B. Cohen and B. Kohler, J. Phys. Chem. A, 2007, 111, 10460–10467 CrossRef CAS PubMed.
- A. Marcelli, I. J. Badovinac, N. Orlic, P. R. Salvi and C. Gellini, Photochem. Photobiol. Sci., 2013, 12, 348–355 RSC.
- H.-Z. Yu, J. S. Baskin and A. H. Zewail, J. Phys. Chem. A, 2002, 106, 9845–9854 CrossRef CAS.
- P. H. Kumar, Y. Venkatesh, D. Siva, B. Ramakrishna and P. R. Bangal, J. Phys. Chem. A, 2015, 119, 1267–1278 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra00928k |
| This journal is © The Royal Society of Chemistry 2019 |