Open Access Article
Open Access ArticleCapillary flow in microchannel circuitry of scleral lenses
Ali K. Yetisen *a,
Bugra Soylemezoglu
*a,
Bugra Soylemezoglu a,
Jie Donga,
Yunuen Montelongob,
Haider Butt
a,
Jie Donga,
Yunuen Montelongob,
Haider Butt c,
Martin Jakobi
c,
Martin Jakobi a and
Alexander W. Kocha
a and
Alexander W. Kocha
aInstitute for Measurement Systems and Sensor Technology, Technical University of Munich, 80333, Munich, Germany. E-mail: a.k.yetisen@tum.de
bSchool of Civil, Mechanical and Industrial Engineering, Universidad De La Salle Bajío, León, 37150, Mexico
cDepartment of Mechanical Engineering, Khalifa University, Abu Dhabi 127788, United Arab Emirates
First published on 9th April 2019
Abstract
Continuous monitoring of biomarkers in a quantitative manner at point-of-care settings can advance early diagnosis in medicine. Contact lenses offer a minimally-invasive platform to continuously detect biomarkers in tear fluid. Microfluidic components as lab-on-a-chip technology have the potential to transform contact lenses into fully-integrated multiplexed sensing devices. Here, simple and complex microchannels are created in scleral lenses that perform microfluidic operations via capillary action. The engraving of microchannels in scleral lenses were performed by laser micromilling, where a predictive computational model was developed to simulate the effect of laser power and exposure time on polymer behavior. Experimentally varying the CO2 laser power (1.2–3.6 W) and speed (38–100 mm s−1) allowed the micromilling of concave microchannels with groove depths of 10–240 μm and widths of 35–245 μm on polymetric substrates. The demonstrated laser micromilled circuitry in scleral lenses included linear channels, T/Y junctions, multiplexed arrays, mixers, and spiral channels, as well as serially organized multicomponent channels. Capillary forces acting in the microchannels allowed flowing rhodamine dye within the microfluidic components, which was visualized by optical microscopy in reflection and transmission modes simultaneously. The developed microfluidic components in scleral lenses may enable tear sampling, storage, analysis, and multiplexed detection capabilities for continuous monitoring applications.
Introduction
Contact lenses have emerged as a minimally-invasive sensing platform for point-of-care diagnostics.1 Contact lens sensors have been developed for analyzing the composition of tears as a surrogate medium for blood biomarker monitoring for potential application in the diagnosis of ocular or metabolic disorders. For minimally-invasive continuous monitoring applications, electrochemical sensors have been incorporated into the hydrogel film of contact lenses.2 In the contact lens matrix, glucose oxidase (GOx) allowed for creating an electrical charge due to the formation of an enzyme–glucose complex.3 The magnitude of the charge created was proportional to the concentration of glucose oxidase. In another study, graphene with silver nanowires was used to create an electronic contact lens to measure glucose concentration.4,5 This contact lens featured resistance, inductance and capacitance circuits operating at radio frequency to enable real-time glucose detection. A sensing probe consisting of glucose oxidase was incorporated in parylene as a substrate. The device detected glucose concentration of as low as 1 μM. Amperometric glucose sensors were also integrated in polyethylene terephthalate (PET) contact lenses by forming microstructures on a polymer substrate using photolithography.6 This enzyme-based electrochemical sensor was coated by a Nafion layer and allowed detecting glucose concentration as low as 0.1 mM.6 Hydrophilic poly(2-hydroxyethyl methacrylate) (p(HEMA)) contact lenses have been also utilized to create glucose oxidase based quantitative sensors.7Optical components have been also embedded in a contact lens.8 A light-emitting diode (LED) pixel, a rectifier circuit and a stretchable antenna were integrated onto a substrate with high optical transparency and low haze. This substrate was then molded to fit the shape of a contact lens. Transparent nanomaterials were used to prevent obstruction of the wearer's view. The detection of high glucose concentrations turned the LED pixel off to enable qualitative readouts. In another study, an optical contact lens sensor was created by incorporating a boronic acid derivative in the hydrogel film of the contact lens.9 The contact lens had a photonic microstructure printed with a specific periodicity constant, which acted as a wavelength filter and diffracted specific wavelengths according to Bragg's law. Thereby, volumetric changes due to variation in glucose concentration (<50 mM) were detected by Bragg peak shifts within 20 min. In another study, holographic diffusing microstructures as an optical transducer were imprinted on glucose-responsive hydrogel contact lenses through lithography.10 In this contact lens, the scattering efficiency of the phenylboronic acid functionalized sensor was modulated by volumetric changes to determine glucose concentrations quantitatively.
Laser micromilling has emerged as a robust fabrication method for micropatterning plastics.11 In laser micromilling, photoablation has been utilized for fabricating polymeric microfluidic channels.12 Laser emission wavelength affects the machining efficiency in ablation depending on the absorption spectra of the substrates.13 Micromachining via laser ablation can be achieved without a mask in a direct-write process, where the substrate material is selectively patterned by a focused laser beam controlled by a scanning head. The micromilled regions are usually square or rectangular shaped with straight walls, although, depending on the depth of the channel, the walls can become slanted because of successive pass and laser defocusing. A wide variety of patterns have been fabricated via laser ablation offering low-cost and high speed as compared to conventional photolithography.14 We have proposed direct laser micromilling as a viable fabrication method for patterning linear channels and microconcavities in hydrogels.15 By utilizing direct laser micromilling, microfluidic components can be created in contact lenses to expand the capabilities in sampling, mixing, processing, and multiplexing.
Here, we create simple and complex microfluidic components in p(HEMA) scleral lenses via direct CO2 laser micromilling. We have developed a computational model to predict the power and exposure time of the laser beam to form concave microchannels in scleral lenses. We experimentally demonstrate the fabrication of a wide range of microfluidic components including Y/T junctions, spiral channels, mixers, and multiplexed channels, as well as serially-organized multifunctional components in scleral lenses. Rhodamine B solution was utilized to optically visualize the capillary flow within the microfluidic channels of scleral lenses in reflection and transmission imaging modes.
Experimental section
Materials
p(HEMA) mini scleral lenses (water content 45 vol%; SPH: −0.00; diameter: 14.00 mm; base curve: 8.60 mm) were purchased from Meralens GmbH (Erding, Germany). Poly(methyl methacrylate) (PMMA) (2 mm thickness; 30 × 1000 mm cut) was purchased from B&T Metall- und Kunststoffhandel GmbH (Kirchheim bei München, Germany). Rhodamine B was purchased from Sigma Aldrich.Equipment
A CO2 laser (VLS 4.60, 10.64 μm, 60 W) was purchased from Universal Laser Systems (Vienna, Austria). Leica DM750 with Leica ICC50 HD camera was used to image the microfluidic channels. Leica Acquire (3.4.1) was used to capture and process the microscopic images. Multiple microscopic images were merged and assembled to create wide-view microchannel images using Image J (1.52e, National Institutes of Health).Laser micromilling of PMMA substrates and scleral lenses
Microfluidic patterns were designed as lines and surfaces in Adobe Illustrator CC (2018). A CO2 laser cutter (10.64 μm, 60 W) was used to pattern microchannels on a PMMA sheet and p(HEMA) scleral lenses. The power of laser beam was varied from 1.2 W to 3.6 W at beam speeds ranging from 38 to 100 mm s−1.Microfluidic flow in scleral lenses
To visualize the fluid flow in the microchannels on scleral lenses, rhodamine B dye solution was prepared in deionized water (wt/vol, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10). A syringe with 23G needle was used to inoculate the rhodamine B solution (10 μl) at the inlet of the microchannels on the scleral lens. Capillary forces acting within the laser patterned microchannels wicked the rhodamine B solution and allowed the flow within a single channel leading to an outlet. The rhodamine B fluid flow was contained within the microchannels and no significant leakage was noted. The microfluidic channels were simultaneously imaged in reflection and transmission modes.
10). A syringe with 23G needle was used to inoculate the rhodamine B solution (10 μl) at the inlet of the microchannels on the scleral lens. Capillary forces acting within the laser patterned microchannels wicked the rhodamine B solution and allowed the flow within a single channel leading to an outlet. The rhodamine B fluid flow was contained within the microchannels and no significant leakage was noted. The microfluidic channels were simultaneously imaged in reflection and transmission modes.
Results and discussion
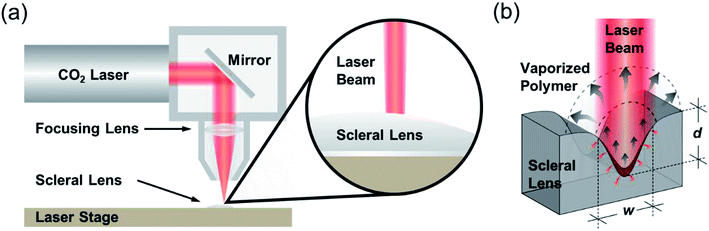
CO2 laser micromilling of polymers is a photothermal process. Excited CO2 molecules in a resonant cavity amplify any electromagnetic wave associated with the bending energy transition of the CO2 molecules, thus producing a photon. The photons then produce a laser beam until the gain medium is saturated and the beam is focused on the scleral lens (Fig. 1a). Laser ablation involves exposure of a highly-intense laser beam to the polymer surface leading to a shock wave, polymer vaporization, and ejecting particles from the substrate. This ablation process creates a microconcavity in the polymeric substrate (Fig. 1b). The beam spot size of the laser as well as the thermal capacity and density of the polymer affect the ablation efficiency. The polymer substrate (e.g. PMMA) transitions from a glassy state to a rubbery state above 115 °C.16 As the laser beam induced temperature increases from 170 °C to 210 °C, molecule chains begin deforming by releasing methyl methacrylate. At 360 °C, depolymerization initiated by the vinyl end groups, saturated C–C bonds, and –CH end groups.The ablation process has been simulated in MATLAB to rationally design the geometrical characteristics of the concavity of the microchannel in the PMMA substrate. The concept behind the fabrication of the concavity consisted of applying thermal energy to increase the temperature at the surface of the polymer. When the temperature at the surface of the polymer increases to a value higher than the ablation threshold, the polymer is removed leaving a concavity at the surface, where the ablation temperature of PMMA was estimated as 700 K.17 In the simulation, this process was repeated iteratively while the beam moved through the polymer surface. The increment in temperature ΔT was found with the increment in thermal energy ΔU, the density ρ, and the volumetric heat capacity cp of PMMA:
| ΔT = ΔUρcp | (1) |
The thermal energy was retrieved during each iteration of the simulation through the absorption of the laser light. In this case, the conversion of optical energy to thermal energy was calculated with the loss produced in the propagation path of the laser beam. Simplifying the analysis for a perfectly collimated laser beam with an intensity normalized Gaussian profile:18
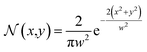 | (2) |
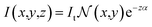 | (3) |
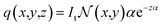 | (4) |
As in the case of the optical power, the heating rate per unit of volume was integrated to obtain the total energy introduced to the system. The total increment of energy was obtained by adding heating rate per unit of volume in each iteration while the beam was moving. Furthermore, the dissipation of the heat produced by the source can also be retrieved with the numerical solution of the diffusion equation:
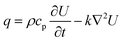 | (5) |
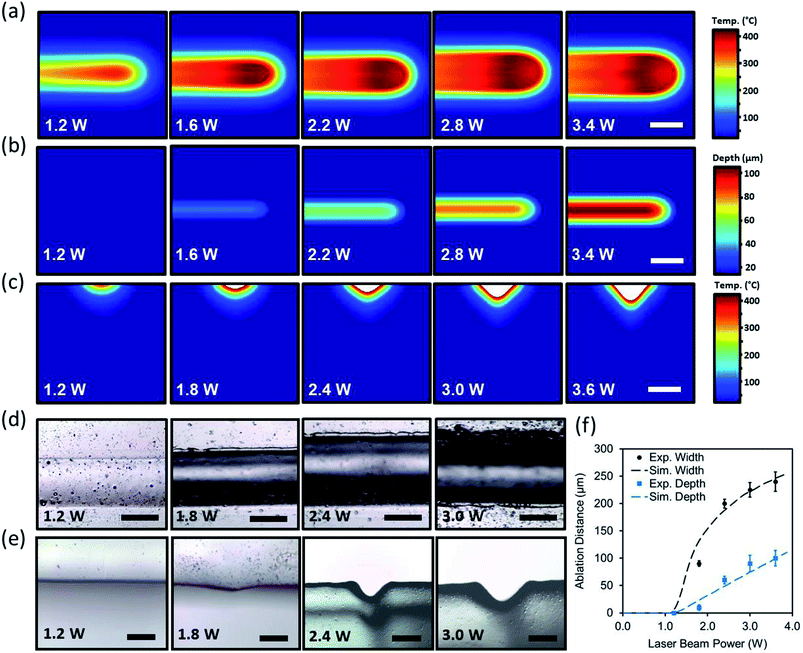
In experimental studies, a PMMA sheet was engraved with a CO2 laser to form concave microchannels. The beam power was varied from 1.2 W to 3.6 W when the beam speed was set constant (75 mm s−1). Fig. 2d and e shows the optical microscopic images of the top views and cross-section of the laser ablated channels as the laser power increased. As the laser power increased, the ablation depth and width also increased. Increasing the power in range of 1.2 W to 1.8 W produced subtle microconcavities. However, increasing the beam power above 2.4 W produced deeper microconcavities while maintaining its concave geometry. Fig. 2f depicts the computational and experimental results of the ablation depths and widths as a function of the applied beam power. At a constant beam speed of 75 mm s−1, 3.6 W of beam power produced an ablation depth of 90 μm while the ablation width reached 225 μm. The computational and experimental results showed that both curves follow a similar pattern, where the ablation width had larger margins of increase as the power increased. The experimental studies agreed with the simulated model, showing that the concavity depth could be accurately predicted based on the beam power variation.
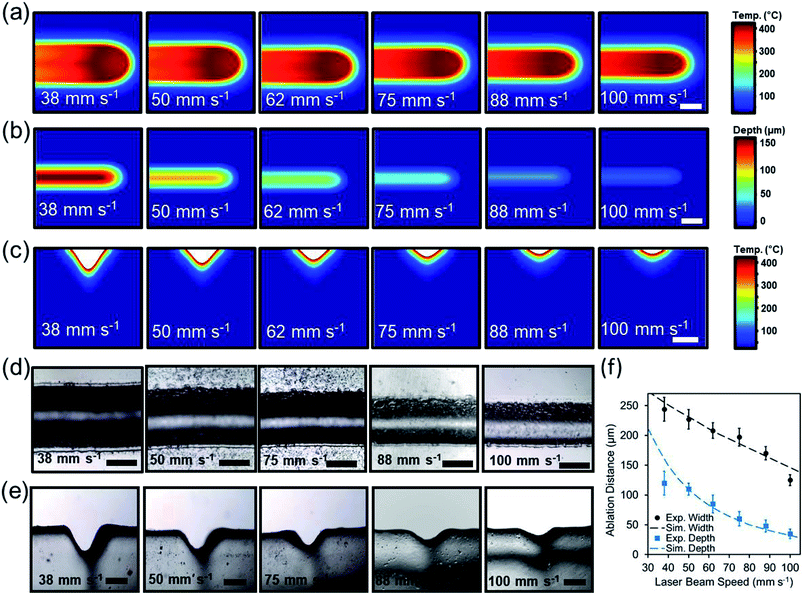
To understand the effect of beam exposure time on the laser micromilling process, the beam speed was computationally varied from 38 mm s−1 to 100 mm s−1 while the beam power was held constant at 3.6 W. Fig. 3a illustrates the simulated 2D top view temperature distribution as a function of laser beam speed. Increasing beam speed from 38 mm s−1 to 100 mm s−1 while having a constant beam power of 3.6 W decreased the ablation depth from 212 μm to 26 μm and the width from 274 μm to 134 (Fig. 3b). Fig. 3c illustrates the computational temperature distribution and 2D profiles of the ablated concavities as a function of laser beam exposure time.
In experimental studies, the influence of the beam speed on the ablation depth and width of microconcavities was investigated. Fig. 3d displays the microscopic cross-section view images of the laser ablated microconcavities as the beam speed increased from 38 mm s−1 to 100 mm s−1 as the beam power was set to 3.6 W. Fig. 3d displays top view images of the cross-section cuts of the channels with varying beam speed. Using higher speed values (100 mm s−1) produced a subtle microconcavity (Fig. 3e). The ablation depth and width were 120 μm and 244 μm at 38 mm s−1 beam speed and decreased to 35 μm and 125 μm at 100 mm s−1 beam speed respectively (Fig. 3f). The experimental studies agreed with the simulated model, showing that the concavity depth could be accurately predicted based on the beam speed variation.
Fabrication of microchannels on scleral lenses
Microchannels were engraved on p(HEMA) scleral lenses to form microfluidic components that may enable tear sample collection and multiplexed analyses in continuous monitoring applications. Fig. 4a–f shows the basic and complex microchannel patterns on p(HEMA) scleral lenses, and the insets display optical microscopic top view images of the microchannels. Fig. 4a illustrates a basic line microchannel with one inlet and one outlet on the scleral lens. Fig. 4b shows a T-junction microchannel as a combination of two perpendicular line components. The T-junction microchannel can be utilized as 2 inlet 1 outlet component or as 1 inlet 2 outlet schemes. A Y-junction microchannel was also created as a basic component on a scleral lens for multiplexing the fluid from one branch to the other (Fig. 4c). Combining Y components together could achieve complex tree like microfluidic systems for highly multiplexed operations. Fig. 4d depicts a four-plexed pattern on the scleral lens, where the inlet branches out to four outlets. Microchannels featuring curves can also be used to achieve mixing functionality as the micropattern curves toward the inside and then outside in a cyclic motion that allows the mixing the fluid in the microchannel (Fig. 4e). A spiral microchannel could achieve separation of fluids or microscale solids with different densities (Fig. 4f). The inlet shown in outer circle swirls into smaller circles and ultimately to into the outlet. Fluids with different densities could be separated as the circles get smaller to pass the least dense fluid or filter out a microscale solid. For example, microcontaminants could be extracted from the tear fluid using the spiral microchannel.To provide complex microfluidic functions, wider available area over the scleral lenses was utilized. Fig. 4g shows a mixer system with a number of crown-patterned channels running around the whole scleral lens surface. Fig. 4h illustrates a channel with one the inlet and outlet expanding over the scleral lens surface. This system could be used to separate microparticles from the fluid as some solids will be filtered out in the microchannel. Fig. 4i shows a microchannel system with two inlets that could mix different fluids at the overlapping region of the microchannels leading to an outlet. Fig. 4j shows a multiplexer system with four outlets over the scleral lens. Fig. 4k shows three reaction chambers connected with one inlet and outlet, where tear fluid can be stored or reactions can occur on the scleral lens. Fig. 4l shows a microchannel system having one inlet connected to a mixer component which leads to a reaction chamber subsequently directed to 2 outlets. Such microchannels systems can carry out multistep reactions, processes, and multiplexed analyses on the scleral lens. Based on the Rayleigh length for a CO2 laser, the Gaussian distribution of beam width was consistent within ±2.0 mm from the focal point. The base curve radius of the contact lens used in this work was less than 2.0 mm; hence, the widths of the channels formed along the surface of the contact lenses were precise.
Fluid flow in microfluidic scleral lens components
To visualize the fluid flow in the microchannels on scleral lenses, rhodamine B dye solution in deionized water was utilized (wt/vol, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10). A syringe with 23G needle was used to introduce the rhodamine B solution (10 μl) at the inlet of the microchannels on the scleral lens. Fig. 5 illustrates rhodamine B solution (in pink) flow in basic line component, T/Y-junction components, multiplexed microchannel, mixer component, and spiral microchannel, and the insets show the magnified images of the fluid flow. The liquid flow was attained along the microchannels due to the capillary action of the water on the scleral lens. Fig. 5a shows the flow of the rhodamine dye into a microconcavity. Such microconcavities could be used as reaction chambers in scleral lenses. Fig. 5b shows the dye flow into a T junction from two inlets merging to a single inlet; such devices can be used as microfluidic timers, in which different dye flow can be sequentially delivered to a reaction chamber. Fig. 5c shows a Y component that consists of three reaction chambers that may be utilized as a multiplexed assay. Fig. 5d illustrates a multiplexed array that distributes the dye into four reaction chambers for multiplexed analysis. Fig. 5e shows the flow of the rhodamine B dye in a microfluidic mixer system consisting of one inlet and outlet. Fig. 5f displays rhodamine dye flow in a spiral microfluidic component. Hence, complex fluid flows can be attained by capillary flow in scleral lens microfluidics. The flow of the fluids in the channels can be controlled by modifying the wettability characteristics of the channels. For example, hierarchical microcone arrays and pillars can be formed using water-assisted femtosecond laser irradiation21,22
10). A syringe with 23G needle was used to introduce the rhodamine B solution (10 μl) at the inlet of the microchannels on the scleral lens. Fig. 5 illustrates rhodamine B solution (in pink) flow in basic line component, T/Y-junction components, multiplexed microchannel, mixer component, and spiral microchannel, and the insets show the magnified images of the fluid flow. The liquid flow was attained along the microchannels due to the capillary action of the water on the scleral lens. Fig. 5a shows the flow of the rhodamine dye into a microconcavity. Such microconcavities could be used as reaction chambers in scleral lenses. Fig. 5b shows the dye flow into a T junction from two inlets merging to a single inlet; such devices can be used as microfluidic timers, in which different dye flow can be sequentially delivered to a reaction chamber. Fig. 5c shows a Y component that consists of three reaction chambers that may be utilized as a multiplexed assay. Fig. 5d illustrates a multiplexed array that distributes the dye into four reaction chambers for multiplexed analysis. Fig. 5e shows the flow of the rhodamine B dye in a microfluidic mixer system consisting of one inlet and outlet. Fig. 5f displays rhodamine dye flow in a spiral microfluidic component. Hence, complex fluid flows can be attained by capillary flow in scleral lens microfluidics. The flow of the fluids in the channels can be controlled by modifying the wettability characteristics of the channels. For example, hierarchical microcone arrays and pillars can be formed using water-assisted femtosecond laser irradiation21,22
A continuous wave CO2 laser was employed to engrave microchannels on scleral lenses. With the development of high-energy lasers with rapid scan head platforms, precise micromilling operations can be carried out using ultrashort light pulses. Femtosecond laser milling has emerged as a precise approach for laser ablation in microfluidic device fabrication.23 An advantage of femtosecond lasers is the absence of thermal effects, where structural polymer characteristics do not significantly change as there is subtle thermal tension, shock waves and melting effects.24 These ultrashort laser pulses have enough high peak power to drive nonlinear multiphoton absorption, leading to laser ablation at wavelengths where the polymer has low absorption. Ultrashort pulse laser ablation is preferred to that of longer pulse sources, where the photon energy must be greater than the bandgap to deposit energy via linear absorption.14 Laser ablation can also be used to generate 3D microfluidic channels inside bulk PMMA substrates.25 This approach uses femtosecond pulses to produce nonlinear absorption inside the focal volume, triggering a polymer modification. Such laser fabrication approaches could be adopted to construct 3D channels in scleral lenses. Furthermore, in the present work, contact lenses made of pHEMA were demonstrated; however, other contact lens materials including silicone acrylates and other co-polymers can also be used to form channels with the laser ablation method. The intensity and the speed of laser beam can be controlled to pattern any polymer matrix depending on thermal conductivity, water content, absorbance, and density. Creating a microfluidic system is vital for continuous tear fluid sampling and multiplexed analysis at point-of-care settings. Furthermore, autonomous pumps consisting of micropillars could be fabricated on the microfluidic channels to rapidly sample tear fluid.26,27
Conclusions
Microfluidic components were developed in scleral lenses, where laser ablation has been chosen to machine microchannels on scleral lenses. A numerical model was developed to predict the depth and width of microscale channels in scleral lenses. Additionally, the physical heat phenomena behind laser ablation has been described. Beam power and speed was optimized to create microchannels in polymers. Upon optimizing the beam speed and power, basic and complex microstructures have been engraved on scleral lenses, including basic line components with inlets and outlets, multiplexed channels, Y/T junctions, spiral components, and microfluidic mixers. Rhodamine B solution was introduced to the microchannels where capillary flow guided the flow in the channels. Fabricated microfluidic channels will serve a platform role in the fabrication of lab-on-a-chip functionalities in scleral lenses for sample collection, storage, and analyses in real-time biomarker monitoring in tear fluid.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This research was funded by the Alexander von Humboldt Foundation and Carl Friedrich von Siemens Foundation.References
- N. M. Farandos, A. K. Yetisen, M. J. Monteiro, C. R. Lowe and S. H. Yun, Adv. Healthcare Mater., 2015, 4, 792–810 CrossRef CAS.
- B. Otis and B. Amirparviz, Contact lenses, US Pat., US8798332B2, 2014.
- M. X. Chu, K. Miyajima, D. Takahashi, T. Arakawa, K. Sano, S.-i. Sawada, H. Kudo, Y. Iwasaki, K. Akiyoshi and M. Mochizuki, Talanta, 2011, 83, 960–965 CrossRef CAS.
- J. Kim, M. Kim, M.-S. Lee, K. Kim, S. Ji, Y.-T. Kim, J. Park, K. Na, K.-H. Bae and H. K. Kim, Nat. Commun., 2017, 8, 14997 CrossRef PubMed.
- K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J.-H. Ahn, P. Kim, J.-Y. Choi and B. H. Hong, Nature, 2009, 457, 706 CrossRef CAS PubMed.
- H. Yao, A. J. Shum, M. Cowan, I. Lähdesmäki and B. A. Parviz, Biosens. Bioelectron., 2011, 26, 3290–3296 CrossRef CAS PubMed.
- H. Yao, C. Marcheselli, A. Afanasiev, I. Lähdesmäki and B. Parviz, presented in part at the 25th IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Paris, France, 2012, pp. 769–772 Search PubMed.
- J. Park, J. Kim, S.-Y. Kim, W. H. Cheong, J. Jang, Y.-G. Park, K. Na, Y.-T. Kim, J. H. Heo and C. Y. Lee, Sci. Adv., 2018, 4, eaap9841 CrossRef PubMed.
- M. Elsherif, M. U. Hassan, A. K. Yetisen and H. Butt, ACS Nano, 2018, 12, 5452–5462 CrossRef CAS PubMed.
- M. Elsherif, M. U. Hassan, A. K. Yetisen and H. Butt, ACS Nano, 2018, 12, 2283–2291 CrossRef CAS PubMed.
- L. E. Locascio, D. J. Ross, P. B. Howell and M. Gaitan, in Microchip Capillary Electrophoresis, Springer, 2006, pp. 37–46 Search PubMed.
- M. A. Roberts, J. S. Rossier, P. Bercier and H. Girault, Anal. Chem., 1997, 69, 2035–2042 CrossRef CAS PubMed.
- H. Becker and L. E. Locascio, Talanta, 2002, 56, 267–287 CrossRef CAS PubMed.
- R. Suriano, A. Kuznetsov, S. M. Eaton, R. Kiyan, G. Cerullo, R. Osellame, B. N. Chichkov, M. Levi and S. Turri, Appl. Surf. Sci., 2011, 257, 6243–6250 CrossRef CAS.
- N. Jiang, Y. Montelongo, H. Butt and A. K. Yetisen, Small, 2018, 14, 1704363 CrossRef PubMed.
- D. Yuan and S. Das, J. Appl. Phys., 2007, 101, 024901 CrossRef.
- M. Shulepov, N. Bulgakova, L. Zakharov, A. Panchenko and A. Telminov, CO2 laser ablation of poly (methyl methacrylate) and polyimide: experiment and theory, Proceedings of the 10th international conference on modification of materials with particle beams and plasma flow, Tomsk, Russia, 2010, pp. 132–135 Search PubMed.
- O. Svelto and D. C. Hanna, Principles of lasers, Springer, 1998 Search PubMed.
- N. C. Nayak, Y. Lam, C. Yue and A. T. Sinha, J. Micromech. Microeng., 2008, 18, 095020 CrossRef.
- H. P. Langtangen and S. Linge, Finite Difference Computing with PDEs: A Modern Software Approach, Springer, 2017 Search PubMed.
- G. Li, Y. Lu, P. Wu, Z. Zhang, J. Li, W. Zhu, Y. Hu, D. Wu and J. Chu, J. Mater. Chem. A, 2015, 3, 18675–18683 RSC.
- J. Xu, D. Wu, J. Y. Ip, K. Midorikawa and K. Sugioka, RSC Adv., 2015, 5, 24072–24080 RSC.
- C. De Marco, S. M. Eaton, R. Suriano, S. Turri, M. Levi, R. Ramponi, G. Cerullo and R. Osellame, ACS Appl. Mater. Interfaces, 2010, 2, 2377–2384 CrossRef CAS PubMed.
- X. Liu, D. Du and G. Mourou, IEEE J. Quantum Electron., 1997, 33, 1706–1716 CrossRef CAS.
- G.-L. Roth, C. Esen and R. Hellmann, Opt. Express, 2017, 25, 18442–18450 CrossRef CAS PubMed.
- B. Xu, Y. Shi, Z. Lao, J. Ni, G. Li, Y. Hu, J. Li, J. Chu, D. Wu and K. Sugioka, Lab Chip, 2018, 18, 442–450 RSC.
- Z.-X. Lao, Y.-L. Hu, D. Pan, R.-Y. Wang, C.-C. Zhang, J.-C. Ni, B. Xu, J.-W. Li, D. Wu and J.-R. Chu, Small, 2017, 13, 1603957 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2019 |