Open Access Article
Open Access ArticleRedox activity of nickel and vanadium porphyrins: a possible mechanism behind petroleum genesis and maturation?†
G. Munoz,
B. K. Gunessee,
D. Bégué ,
B. Bouyssiere,
I. Baraille,
G. Vallverdu and
H. Santos Silva
,
B. Bouyssiere,
I. Baraille,
G. Vallverdu and
H. Santos Silva *
*
CNRS/Univ Pau & Pays Adour, Institut des Science Analytiques et Physico-Chimie pour l’Environnement et les Materiaux, UMR 5254, 64000, Pau, France. E-mail: hugo.santos-silva@univ-pau.fr
First published on 26th March 2019
Abstract
The presence of metalloporphyrins in crude oil has been known for many years. In contrast, their role on the physical–chemical properties is only now beginning to be understood. In this study, we test using high-level ab initio calculations, the hypothesis of a possible redox catalytic activity of vanadium and nickel metalloporphyrins in crude oil, illustrated by the oxidation of methanol to formaldehyde and hydrogen dissociation, respectively. This process which may take place during petroleum genesis and maturation, explains some of its physical–chemical properties, such as polar chains, the absence of alcohols, the trapping of porphyrins within macromolecular aggregates.
1 Introduction
Processing heavy crude oil has become of utmost importance in the oil industry. Low-molecular weight distillates may be obtained from refining heavy fractions by catalytic and non-catalytic conversions.1 The presence of metals in these fractions has been known since the early ’50s.2 They are complexed in tetrapyrolic macrocycles (porphyrin derivatives – see Fig. 1) and have a major negative impact during oil processing, since they can contaminate and deactivate the catalysts used in the refinery.3 The presence of such compounds in crude oil was first reported by Treibs,4 and it is legitimized since porphyrin derivatives are naturally abundant in the world, therefore in biomass which, following sedimentation and ripening stages, allows the formation of oil present in the oil reservoirs. During petrogenesis, biological metallo-porphyrins are degraded. Only the pyrrolic core is resistant to chemical degradation, which explains the structural difference (absence of side chains) between the metalloporphyrin (MP) oil and the biological MP. Fourier transform ion cyclotron resonance mass spectroscopy (FT-ICR-MS) results indicate that porphyrins found in crude oil can bear either nickel, vanadium, chromium or iron as metallic centers.5,6 Their content is not constant across different oil sources.7Several series of porphyrins have been identified in fossil fuels using mass spectrometry which contain a core structure of the N4VO type. Among them, etioporphyrins (ETIO) and deoxophylloerythroetio porphyrins (DPEP) are the two most common porphyrins found in petroleum.8 Vanadium and nickel are the two most abundant and problematic metals in this phase with vanadium commonly reaching concentrations up to 1200 ppm and nickel up to 150 ppm depending on the origin of the petroleum.9 It was found that the majority of vanadium is enriched in residue fractions (>500 °C) and only a little vanadium is contained in the distillates (350–500 °C).10 By separation of some atmospheric residue to SARA (saturate, aromatic, resin, and asphaltene) it was found that the majority of vanadium and nickel were in the polar fractions, both resin and asphaltene.11 It was found that about half of the vanadium and nickel in the vacuum residual oils from different origins is concentrated in the C7-asphaltenes, while the other half of the metal content is concentrated in the C7 deasphalted oil.12 Given this, the ratio of DPEP/(ETIO + DPEP) has been used as a maturity indicator13–15 and it generally ranges from 0.8 in the least mature oils to 0 in the most mature oils.8
On the other hand, crude oil also presents a variable quantity of asphaltenes, which impacts on oil extraction and refining due to their tendency to aggregate, being able to block pipes and refineries.16 There is a recent growing consensus on the fact that vanadium and nickel porphyrins are essentially detected with asphaltene aggregates, which may also be linked to the increase in the viscosity of the crude and gives rise to aggregation phenomena, even if this behavior is not yet fully defined.17 This preferential positioning of the porphyrins of nickel and vanadium does not seem to be intuitive, which suggests that privileged physicochemical interactions exist.
In previous work based on molecular dynamics simulations, we have shown that (i) polar acidic lateral chains play a major role favoring this aggregation pattern18,19 and (ii) porphyrins are inherently present in these molecular aggregates forming multiple H-bonds with asphaltenes and water.20 More particularly, we have also shown that vanadium porphyrins play an important role on asphaltene aggregation and water/oil interfacial activity.21 Noteworthy, such new pieces of information corroborate the acceptance of an asphaltene supramolecular self-assembly model instead of a colloidal one.22
To this point, electron-spin resonance (ESR) can quantitatively measure levels of the paramagnetic vanadyl ions VO2+ in crude oil.23 According to both ESR and high-resolution mass spectroscopy, around 2/3 of the VO2+ are trapped in porphyrins embedded within the asphaltenic phase while the remaining 1/3 were retained in the bulk. Nuclear Magnetic Relaxation Dispersion (NMRD) profiles of proton’s 1/T1 have shown an intermittent surface dynamics of proton species asphaltene nanoaggregates and bulk dynamics in between the slowly rotating metallic clusters (vanadyl centers) of these nanoaggregates.24 The direct consequence of this 2D diffusion of hydrocarbons (maltenes) at the proximity of the surface of the asphaltene nanoaggregates is the existence of an attractive potential interaction between the maltene and asphaltene nanoaggregates mediated by the vanadyl paramagnetic centers. In a recent study, this potential was found to be about 50 kcal mol−1.21
The role of nickel porphyrins is much less explored and despite the consensus on their presence within asphaltene aggregates. In our recent studies, we have showed that, indeed, these porphyrins only interact strongly with asphaltene aggregates and water interfaces when they are grafted with polar lateral chains.20
Conversely, for a long time, porphyrins have been known to play a major role as gas transporters and also as catalysts in oxidizing several organic and inorganic species. The first is exemplarily demonstrated by hemoglobin in which the metallic iron center in a heme group can bind an oxygen molecule (O2).25 We can also cite other examples such as the case of plants, which have a magnesium center, the B12 vitamin which has a cobalt center, and many others.26 In other words, the tetrapyrolic macrocycle and its facility to bear metals can be considered as one of the most important players in aerobic life on Earth.
Nonetheless, the catalytic faculty of these moieties is not the subject of discussion.27 In living organisms, several enzymes are known to catalyze oxidation and reduction reactions of saturated and unsaturated small organic molecules. As an example, Cytochrome P450 can (i) oxidize carbon (from a saturated chain towards a carboxylic acid) (ii) oxidize heteroatoms such as nitrogen and sulfur (iii) dealkylate ether groups and amine groups, form alcohols or amines and aldehydes as sub-products and form epoxides on unsaturated moieties; amongst others.28
The reactivity of vanadium, and particularly of its oxide (VO), is well documented in solid state chemistry. Vanadium oxide surfaces and clusters are known for being good catalysts in oxidizing methanol into formaldehyde29 as well as efficiently oxidizing olefins.30 The mechanism of oxidation involves the abstraction of two hydrogen atoms forming two hydroxyl surface groups, releasing the formaldehyde molecule with a good yield.29
Nickel porphyrins also have very specific catalytic activities. Oxidation reactions can also be obtained with nickel(II)-modified surfaces31 and even polymers bearing nickel-porphyrins.32
Given this, it is therefore natural to think that an extrapolation of the reactivity of the solid to the organometallic compound is possible. In this way, the porphyrins in crude oil would also display a catalytic activity that could help explain some of the properties of oil that were only acquired due to their presence.
One could imagine that vanadium porphyrins may also play an oxidizer role in crude oil, as well as nickel porphyrins which may become chemically active by interacting with other molecules in oil. In the presence of an excess of ligands, it is known that such porphyrins, particularly nickel ones, can be forced to accept one or two axial ligands33 that may activate the metal center and increase its catalytic properties.
Taking all this into account, led us to propose a hypothesis that porphyrins may play the same roles in petroleum: gas transporters and catalysts. In this way, during petroleum genesis and maturation, they could produce new species and newly oxidized moieties that can be grafted to themselves or to other neighboring molecules. Then, they can participate in the formation of tightly bound H-bond interactions, forming clusters of molecules in solution. In the end, this may then lead to the trapping of the porphyrins inside macromolecule (such as asphaltenes) aggregates. The variety of petroleum mixtures can also be, in some parts, explained by this catalytic role. Finally, the absence of alcohols in crude oil, for instance, and the presence of polar groups grafted to high-molecular weight molecules, such as asphaltenes, can also be supported by this hypothesis.
In this way, the main objective of this work was to explore this hypothesis using a multi methodology quantum chemical calculation strategy to investigate the oxidation mechanism of a single methanol molecule by a vanadium porphyrin, and the dissociation of a hydrogen molecule by a nickel porphyrin. Even though molecular hydrogen is not expected to be found in crude oil, given its high stability, if nickel porphyrin displays any catalytic activity towards this molecule, it certainly also does towards other labile hydrogen-containing molecules. This study aims to be a proof-of-concept that can help geochemists to gain knowledge into crude oil origin and maturation.
2 Computational details
Both density functional theory (DFT), Møller–Plesset many-body perturbation theory (MP2), complete active space self consistent field (CASSCF), and n-electron valence state perturbation theory (NEVPT2) methodologies were used in this study, all of them using the ORCA 4.0.0.1 package.34 The MP2 method was used to get reasonable wave function as starting points for CASSCF and NEVPT2 calculations.DFT calculations were performed at the B3LYP/def2-TZVPP level of theory,35–39 using the D3BJ dispersion correction scheme in order to account for missing van der Waals interactions.40,41 Moreover, the RIJCOSX approximation was employed alongside the def2-TZVPP/C auxiliary basis set in order to reduce computational cost.42
Multi-reference (MR) (CASSCF and NEVPT2) calculations were needed to treat particularly some structures present in the reaction path of vanadium porphyrins. The contamination of the wavefunction by higher-order spin states and the variability of the multiplicity within the reaction path obtained by DFT calculations led us to envisage the MR character of the system. As a reminder, the CASSCF method is based on the configuration of interactions (CI) method for a given number of electrons within a fixed number of frontier orbitals. The choice of this number (the active space) can be particularly troublesome since it must be high enough to capture all the electronic properties of the system, keeping the computational costs as low as possible.
Needless to say, for each slightly different system, a different active space is required and the energies also depend heavily on this parameter. That being said, producing reaction paths using this methodology is a difficult task that demands careful attention. In order to support our estimations, the NEVPT2 method was employed to correct the CASSCF energies. However, the high computational cost of NEVPT2 methodology only allows single point calculations and no geometry optimization (gradient calculation) can be performed. Finally, in such calculations, the def2-SVP basis set was used for hydrogen, carbon and nitrogen atoms, and def2-TZVPP used for oxygen and metal atoms.
Regardless of the method in use, tight convergence criteria were imposed for both energies and geometries. Transition states were characterized by a single imaginary frequency calculated numerically corresponding to the reaction coordinate. In CASSCF, due to computation limitations, we had to employ the hybrid Hessian method, as implemented in the Orca code. Energies were characterized by total energy (E), enthalpy (H) and Gibbs free enthalpy (G), whenever applicable and feasible. The latter two were calculated at 298.15 K.
3 Results and discussion
3.1 Vanadium porphyrins
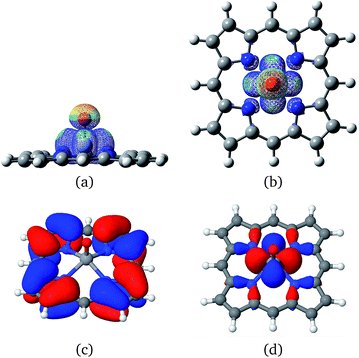
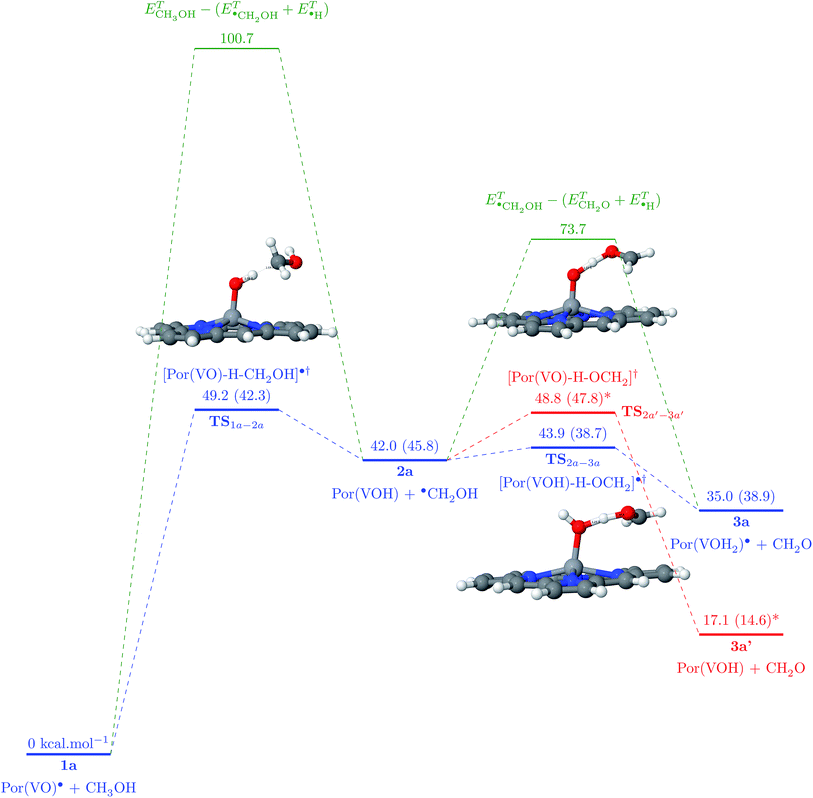
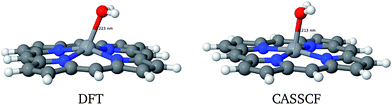
Vanadium porphyrins are vanadyl-complexed ions within a tetrapyrolic cycle. This structure bears an unpaired electron localized in the surroundings of a VO bond, as can be seen in Fig. 2(a) and (b).Earlier, we estimated the interaction energy between a hydrogen atom and the vanadyl group to be around 50 kcal mol−1 (ref. 21) (see Fig. S5†). This result explains the experimental results showing that there must be an attractive potential between the paramagnetic source of relaxation in the NMRD experiments and maltenes, as mentioned previously. In order to estimate if this is enough to trigger the abstraction of hydrogen atoms from surrounding molecules, we were inspired by the solid state results describing the oxidation reaction of methanol into methanal by V2O5.29 To test this hypothesis, we propose to study the following general mechanism:
| Por(VO)˙ + CH3OH → [Por(VO)–H–CH2OH]˙† → Por(VOH) + ˙(CH2OH) | (1) |
This reaction passes necessarily via a transition state (TS) in which the methyl hydrogen atom is bound both to carbon and vanadyl’s oxygen. If there is enough energy, this results in an unpaired electron on the methanol molecule, whereas PorVO gains a closed-shell electronic configuration. Then, the hydroxyl hydrogen can also be abstracted by either the same porphyrin (reaction (2)) or another porphyrin (reaction (3)):
| Por(VOH) + ˙(CH2OH) → [Por(VOH)–H–OCH2]˙† → Por(VOH2)˙ + CH2O | (2) |
| Por(VO)˙ + ˙(CH2OH) → [Por(VO)–H–OCH2]† → Por(VOH) + CH2O | (3) |
The starting state 1a is composed of a PorVO porphyrin in the D0 state and a methanol molecule in the S0 state. The abstraction of a hydrogen from the methyl group of the methanol leads to a D0 transition state with an energy barrier of 49.2 kcal mol−1 which is a factor of two lower than the activation energy needed for the same abstraction in the absence of PorVO (100.7 kcal mol−1). Then, the TS yields a PorVOH T0 molecule in a triplet state (ΔE(T0 − S0) = 23.4 kcal mol−1, ΔE(T0 − S0) = 23.2 kcal mol−1, ΔE(T0 − S0) = 23.9 kcal mol−1) and a methoxymethyl radical D0.
The continuation of the reaction can follow two distinct mechanisms: either the methoxymethyl radical reacts with the same porphyrin, yielding the hydroxyl hydrogen, leading to the formation of porphyrin bearing a VOH2 group and the formaldehyde molecule (2); or it reacts with a new (second) PorVO molecule, leading to the formation of a second PorVOH molecule alongside formaldehyde (3).
For the first hypothesis, there is a T0 TS (TS2a–3a) with a barrier of 1.9 kcal mol−1 which finally yields 3a with a PorVOH2 molecule in the quadruplet ground state (Q0 − ΔE(Q0 − D0) = 13.4 kcal mol−1, ΔE(Q0 − D0) = 13.2 kcal mol−1, ΔE(Q0 − D0) = 13.9 hydrogen abstraction in the absence of the porphyrin (ΔE = 37.5 kcal mol−1, ΔH = 30.5 kcal mol−1). This represents a reduction of ∼95% of the energy needed to accomplish this reaction in the absence of a porphyrin molecule. In the scenario of the second hypothesis, the TS required for this mechanism has an energy barrier of only 6.8 kcal mol−1, that is still very small compared to the initial 37.5 kcal mol−1 value without any porphyrin involved in the mechanism.
Regardless of the scenario adopted, the hydrogen of the methyl group is the first to be abstracted since it corresponds to a lower C–H bond dissociation energy (ΔE = 100.7 kcal mol−1, ΔH = 92.0 kcal mol−1) whereas the O–H bond dissociation energy equals 107.7 kcal mol−1 (ΔH = 98.4 kcal mol−1). The fact that the reaction starts by an abstraction of the methyl’s hydrogen is also in agreement with the results published by Chenoweth et al.29
At the end of these reactions, a formaldehyde molecule is obtained as well as Por(VOH2)˙ (Q0) and/or PorVOH (T0) ones. The energy barriers to abstraction of methyl hydrogen atoms from methanol molecules are lowered showing how the Por(VO)˙ porphyrin can indeed act as a catalyst during oil formation. Moreover, this cascade of reactions characterizes the vanadium oxide porphyrins as hydrogen acceptors and transporters during crude oil formation.
The porphyrins formed in both steps (2) and (3) can be, respectively, deactivated following the mechanisms proposed in (4) and (5), for instance. The calculated ΔG0 for the reaction (4) was found to be −9.7 kcal mol−1 (ΔE = −20.8 kcal mol−1, ΔH = −19.2 kcal mol−1). It means that the Por(VOH2)˙ species is more stable than Por(V)˙ and H2O separately. Beyond this result, the low energy of this bond indicates that it can be broken, releasing water and a reactive Por(V)˙ center able to trap other radical or neutral species, probably CO2. On the other hand, the dissociation of the PorVOH into Por(VO)˙ and H˙ has a ΔE of −55.1 kcal mol−1 (ΔH = −48.5 kcal mol−1), which is significantly more difficult to dissociate than the aforementioned case. It is worth noting that this energy corresponds exactly to the attractive potential that exists between PorVO porphyrins and hydrogen atoms, as was found in our recent work.21 The regeneration method, amongst others, will be studied in more detail in the next section.
| Por(VOH2)˙ → Por(V)˙ + H2O | (4) |
| Por(VOH) → Por(VO)˙ + H˙ | (5) |
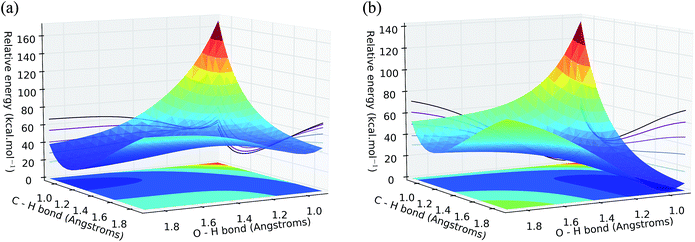
Concerning convergence difficulties when searching for transition states, the problem lies particularly in the multiplicity of the second transition state (TS2). Indeed, the potential energy surfaces (PES) of the doublet states and quadruplet (Fig. 4) intersect at the TS2 level. This is translated into a spin contamination and is a typical indication of a multi-determinative wave function. In other words, the wavefunction describing the system cannot be described by a single Slater determinant (hence a single spin multiplicity), but by a linear combination of several determinants.
Given these results, even if the reaction path produced by DFT is acceptable and proves a catalytic activity of the vanadyl group present in the center of porphyrins, it is necessary to explore the possibility of the reaction path containing plurideterminantal points, and if this happens to be the case, whether or not the DFT results can be supported by these MR data. This could lead to a better trend in the value of energy barriers and assess the relevance of DFT in addressing this problem. It was therefore chosen to study the reaction path by the post-HF CASSCF method in order to be free from the constraints due to a multiplicity of ambiguous spin of certain geometries of the reaction path.
Given the impossibility to perform NEVPT2 geometry optimizations, CASSCF (5,5) and (11,10) methods were used to refine the DFT geometries. The energies and perturbations of the wavefunction of each state are presented in Table 1. The particularity of such a methodology is finding the HOMO orbital as the one bearing the radical, instead of that found by DFT calculations (Fig. S6†).
| PorVOHx and CHyOHz multiplicities | ΔE(kcal mol−1NEVPT2) | |
|---|---|---|
| 1a | D0 and S0 | — |
| TS1a−2a | D0 + D1 + T0 | +77.4 |
| 2a | T0 and D0 | +84.3 |
| TS2a−3a | D0 + D1 + T0 | +73.7 |
| 3a | D0 + D1 + T0 and S0 | +93.1 |
It is interesting to note that the origin of the MR character of TS1a–2a comes from the fact that the 1a reactants are in a D0 (porphyrin) and S0 (formaldehyde) state whereas the products 2a are in a T0 (porphyrin) and D0 (methoxymethyl radical). The energies displayed in this table are NEVPT2-corrected ones in order to be free from the CASSCF-size dependence phenomenon. However, one can see clearly that the energies of the transition states are lower than the products they lead to. But if one takes a look at Fig. 3, this is also the case for DFT when one only compares energy (E) without taking into account entropic corrections. Even with the impossibility to calculate such contributions at the NEVPT2 level of theory, it is highly probable that the same happens to such energy values, i.e., the entropic corrections lead to a logic and valid reaction path.
However, the energy of 3a (PorVOH2) is intriguing: it is relatively high compared to the other systems and studying it further may also hint at the catalyst recovery problem. In the solid state case,29 after the abstraction of the second hydrogen by the VO group, a H2O molecule is released, leaving behind a V˙ radical. First of all, the DFT and CASSCF geometries for this system are considerably different, as presented in Fig. 5 and Table 2.
| RVO (Å) | ΔRVO (%) | |
|---|---|---|
| PorVO | 1.53 | — |
| PorVOH | 1.77 | +16 |
| PorVOH2 | 2.13 | +39 |
From these data, one can clearly note that H2O has a high tendency to leave the porphyrin molecule. Indeed, the O–H bond and H–O–H angles are very close to those of a water molecule. If this happens to be the case, the PORV˙ radical could be regenerated by capturing an oxygen atom from a CO2 molecule, which is highly probable to be found in the crude oil.43
| PorV˙ + CO2 → PorVO˙ + CO |
NEVPT2 energies show that this reaction is highly probable thermodynamically (−66 kcal mol−1), even if, for the time being, it is not possible to estimate the energy barrier of the transition state in this reaction step. Otherwise, the reaction can also stop at the 2a product. In this case, a homolytic scission of the O–H bond would be needed. One can imagine that this hydrogen radical could be easily transferred to a double bond, where it can be stabilized, restoring the departing structure of PorVO˙.
PorVOH + R–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–R → PorVO˙ + R–CH2–CH˙–R CH–R → PorVO˙ + R–CH2–CH˙–R |
In both scenarios, one can recover at the end of the reaction the initial vanadyl porphyrin, which served as a hydrogen transporter, oxidizing alcohols and reducing either CO2 and/or alkyl compounds. This occurrence could be considered as a game-changer in the state-of-art of the role of vanadyl porphyrins in petroleum fluids: besides being capable of strongly interacting with asphaltenes, it also plays a role in petroleum genesis and maturation processes.
3.2 Nickel porphyrins
In order to demonstrate a catalytic activity of the nickel porphyrin, the dissociation of H2 in the presence of PorNi is chosen, both in its ground or first anionic stated (that mimics a possible charge input from a ligand). Given the MR difficulties found in the study of vanadyl porphyrin, we first estimated the need to use CASSCF methods to study the catalytic activity of the nickel porphyrin. Both geometries and energies are essentially identical under DFT and CASSCF methods. Having said this, the former will be used next.The first step is to screen the possibility of the nickel atom to receive charge inputs from ligands present in the crude oil environment. Table 3 presents the Loewdin charges on the nickel atom if the system is negatively charged, if it has a SH–, CH3CH2COO– or a pyridine ligand (see Fig. S7† for further information).
| System | RNi–ligand (Å) | ΔG (kcal mol−1) | Lowdin charges on Ni |
|---|---|---|---|
| PorNi | — | — | −0.09 |
| PorNi− | — | +45.08 | −0.44 |
| PorNi–SH− | 2.48 | −11.93 | −0.34 |
| PorNi–CH3CH2COO− | 2.26 | −3.23 | −0.08 |
| PorNi–pyridine | 2.50 | +2.36 | −0.10 |
It is interesting to note that the addition of a ligand is possible on the metal center. This addition is more favorable for the ligands with very localized charges. Given that the charge on the nickel atom is of the same order of magnitude as the charge input of a ligand, we chose to start studying this system in particular. In this way, the following reactions were studied:
| PorNi + H2 ↔ PorNiH˙ + H˙ |
| PorNi− + H2 ↔ [PorNiH]−˙ + H˙ |
The exploration of the potential energy surface for the first reaction was performed by screening the H–H and Ni–H distance at the same time and it is presented in Fig. S8 and S9,† where one can clearly distinguish a probable transition state for the dissociation of the H–H bond at 91 kcal mol−1. The relaxation of this geometry following the PES uphill for both the neutral and the charged systems allowed us to identify the two respective transition states (Fig. S10†), whose energies are reported in Table 4.
| Neutral system | Multiplicity | ΔE(kcal mol−1DFT) |
|---|---|---|
| PorNi + H2 | S0 | 0 |
| PorNi–H–H | T0 | +66.09 |
| Explicit negative charge | Multiplicity | ΔE(kcal mol−1DFT) |
|---|---|---|
| PorNi + H2 | D0 | 0 |
| PorNi–H–H | D0 | +37.53 |
This being said, the nickel-catalyzed hydrogen dissociation requires a relatively low-energy for both systems. The energy of the transition state of the charged system is around a half of the energy required for the neutral system. Both of these facts indicate that nickel porphyrins can indeed act as catalysts in dissociating bonds in crude oil. Of course no H2 can be found in such conditions, but if such a reaction can take place for this molecule, it means that it could easily also be the case for other bonds, such as C–H ones. Another possibility that can also be considered is a joint action with vanadyl porphyrins: in such a scenario, nickel porphyrins can assist with recovering the former after it abstracts hydrogens from alcohol molecules, for instance.
4 Conclusions
In this paper, quantum chemistry calculations were used to test the possible redox activity of both nickel and vanadium porphyrins present in crude oil. Our results validated this hypothesis based on the analysis of both DFT and CASSCF levels of theory.The catalytic activity of vanadium porphyrin has one last issue to be resolved: the regeneration of the initial porphyrin. In this case, we have proposed a couple of hypotheses, one based on an O–H bond dissociation, and another based on the release of water, capture of CO2 with the consequent release of CO. Both levels of theory show that the latter is the most likely to take place. If the former happens to be the case, the hydrogen radical could easily be captured by an alcene, which are also present in crude oil.
On the other hand, nickel porphyrin also proved to be successful in dissociation of a H2 molecule when the nickel atoms received an electronic charge from its environment (via an axial ligand, for instance). In this case, the porphyrin reduces the dissociation energy to ∼2/3 of the original. This can be even higher for lower-energy dissociations, such as C–H bonds.
Finally, these observations serve as a proof-of-concept of our initial hypothesis: porphyrins play a role as catalysts in crude oil. This phenomenon could explain some physical–chemical properties of the heavy fractions, wherein they are found. We encourage geo- and petroleum chemists to take into account this behavior in forthcoming models.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the DN (Direction du Numérique) from Université de Pau et des Pays de l’Adour, MCIA (Mésocentre de Calcul Intensif Aquitain) and GENCI-CINES (Grant 2017-c2016087698) for providing computation power needed for this project. Isifor-Carnot Institute and Total Refining & Chemicals are also acknowledged for their financial support to this research project. We thank Drs J.-P. Korb, Ahmad Alfarra, Agnès Rivaton, and Mohamed Sarakha for fruitful discussions.References
- G. Que, C. Men, C. Meng, A. Ma, J. Zhou, W. Deng, Z. Wang, B. Mu, C. Liu, D. Liu, S. Liang and B. S. Shi, US Pat., US20020125172A1, 2003.
- H. Dunning, J. Moore and M. Denekas, Ind. Eng. Chem., 1953, 45, 1759–1765 CrossRef CAS.
- K. Qian, A. S. Mennito, K. E. Edwards and D. T. Ferrughelli, Rapid Commun. Mass Spectrom., 2008, 22, 2153–2160 CrossRef CAS PubMed.
- A. Treibs, Justus Liebigs Ann. Chem., 1934, 510, 42–62 CrossRef CAS.
- G. Caumette, C.-P. Lienemann, I. Merdrignac, B. Bouyssiere and R. Lobinski, J. Anal. At. Spectrom., 2009, 24, 263–276 RSC.
- H. Liu, J. Mu, Z. Wang, A. Guo and K. Chen, Energy Fuels, 2016, 30, 1997–2004 CrossRef CAS.
- K. Qian, K. E. Edwards, A. S. Mennito, C. C. Walters and J. D. Kushnerick, Anal. Chem., 2010, 82, 413–419 CrossRef CAS.
- X. Zhao, C. Xu and Q. Shi, Structure and modeling of complex petroleum mixtures, Springer, 2015, pp. 39–70 Search PubMed.
- R. Agrawal and J. Wei, Ind. Eng. Chem. Process Des. Dev., 1984, 23, 505–514 CrossRef CAS.
- A. Barwise and E. Whitehead, Phys. Chem. Earth, 1980, 12, 181–192 CrossRef CAS.
- J. G. Reynolds, Liq. Fuels Technol., 1985, 3, 73–105 CrossRef CAS.
- D. Stratiev, I. Shishkova, T. Tsaneva, M. Mitkova and D. Yordanov, Fuel, 2016, 170, 115–129 CrossRef CAS.
- R. H. Filby and J. F. Branthaver, Metal Complexes in Fossil Fuels: Geochemistry, Characterization, and Processing, ACS Symposium Series, American Chemical Society, 1987, vol. 344 Search PubMed.
- P. Sundararaman and L. D. Raedeke, Appl. Geochem., 1993, 8, 245–254 CrossRef.
- P. Sundararaman, Geochim. Cosmochim. Acta, 1993, 57, 4517–4520 CrossRef CAS.
- J. J. Adams, Energy Fuels, 2014, 28, 2831–2856 CrossRef CAS.
- Y. Y. Borisova, E. G. Tazeeva, N. A. Mironov, D. N. Borisov, S. G. Yakubova, G. R. Abilova, K. O. Sinyashin and M. R. Yakubov, Energy Fuels, 2017, 31, 13382–13391 CrossRef CAS.
- A. C. R. Sodero, H. Santos Silva, P. Guevara Level, B. Bouyssiere, J.-P. Korb, H. Carrier, A. Alfarra, D. Bégué and I. Baraille, Energy Fuels, 2016, 30, 4758–4766 CrossRef CAS.
- H. S. Silva, A. C. Sodero, B. Bouyssiere, H. Carrier, J.-P. Korb, A. Alfarra, G. Vallverdu, D. Bégué and I. Baraille, Energy Fuels, 2016, 30, 5656–5664 CrossRef CAS.
- H. Santos Silva, A. Alfarra, G. Vallverdu, D. Bégué, B. Bouyssiere and I. Baraille, Energy Fuels, 2018, 32, 11153–11164 CrossRef CAS.
- H. Santos Silva, A. C. Sodero, J.-P. Korb, A. Alfarra, P. Giusti, G. Vallverdu, D. Bégué, I. Baraille and B. Bouyssiere, Fuel, 2017, 188, 374–381 CrossRef CAS.
- M. R. Gray, R. R. Tykwinski, J. M. Stryker and X. Tan, Energy Fuels, 2011, 25, 3125–3134 CrossRef CAS.
- L. Benamsili, J.-P. Korb, G. Hamon, A. Louis-Joseph, B. Bouyssiere, H. Zhou and R. G. Bryant, Energy Fuels, 2014, 28, 1629–1640 CrossRef CAS.
- J.-P. Korb, N. Vorapalawut, B. Nicot and R. G. Bryant, J. Phys. Chem. C, 2015, 119, 24439–24446 CrossRef CAS.
- J. P. Collman, J. I. Brauman, B. L. Iverson, J. L. Sessler, R. M. Morris and Q. H. Gibson, J. Am. Chem. Soc., 1983, 105, 3052–3064 CrossRef CAS.
- S. Aime, M. Botta, E. Gianolio and E. Terreno, Angew. Chem., 2000, 112, 763–766 CrossRef.
- L. M. Slaughter, J. P. Collman, T. A. Eberspacher and J. I. Brauman, Inorg. Chem., 2004, 43, 5198–5204 CrossRef CAS PubMed.
- J. T. Groves, J. Inorg. Biochem., 2006, 100, 434–447 CrossRef CAS.
- K. Chenoweth, A. C. v. Duin, P. Persson, M.-J. Cheng, J. Oxgaard and W. A. Goddard III, J. Phys. Chem. C, 2008, 112, 14645–14654 CrossRef CAS.
- C. D. Nunes, P. D. Vaz, V. Félix, L. F. Veiros, T. Moniz, M. Rangel, S. Realista, A. C. Mourato and M. J. Calhorda, Dalton Trans., 2015, 44, 5125–5138 RSC.
- V. Ritleng, M. Henrion and M. J. Chetcuti, ACS Catal., 2016, 6(2), 890–906 CrossRef CAS.
- A. Ciszewski and G. Milczarek, J. Electroanal. Chem., 1997, 426, 125–130 CrossRef CAS.
- J. Buchler, Porphyrins, 1978, 1, 389–483 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- P. Stephens, F. Devlin, C. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- R. Alston, G. Kokolis and C. James, Soc. Pet. Eng. J., 1985, 25, 268–274 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra01104h |
| This journal is © The Royal Society of Chemistry 2019 |