Open Access Article
Open Access ArticleTheoretical study on the electronic structure and second-order nonlinear optical properties of benzannulated or selenophene-annulated expanded helicenes†
Li-jing Gong‡
 *a,
Chun-yu Liu‡b,
Cheng Maa,
Wan-feng Lina,
Jin-kai Lva and
Xiang-yu Zhanga
*a,
Chun-yu Liu‡b,
Cheng Maa,
Wan-feng Lina,
Jin-kai Lva and
Xiang-yu Zhanga
aAviation University of Air Force, Changchun, 130022 Jilin, China. E-mail: gonglijing@126.com
bInstitute of Functional Material Chemistry, National & Local United Engineering Lab for Power Battery, Faculty of Chemistry, Northeast Normal University, Changchun, 130024 Jilin, China
First published on 3rd June 2019
Abstract
Currently, discovering new materials with superior second-order nonlinear optical (NLO) performance has become a very hot research topic in the fields of chemistry and materials science. Now, density functional theory (DFT) has become a powerful tool to predict the performance of novel materials. In this paper, based on benzannulated and selenophene-annulated expanded helicenes, twenty-six helicenes are designed by introduction donor/acceptor moieties and their combinations at different substituent positions. The geometrical/electronic structures, electronic transition, and second-order NLO properties of these helicenes are full investigated by DFT/TDDFT theory. The investigations show that these helicenes have large first hyperpolarizability values (βHRS). For instance, the βHRS value (29.95 × 10−30 esu) of helicene H24 is about 7 times larger than that of the highly π-delocalized phenyliminomethyl ferrocene complex. In addition, the introduction of acceptor NO2 unit at R7 and R8 positions for helicenes H1 and H15 can obtain the largest βHRS value, which is attributed to the enhancement of electron acceptor ability. In view of large NLO response and intrinsic asymmetric structures, the studied helicenes have the possibility to be excellent second-order NLO materials.
I. Introduction
Helicenes have been defined as polycyclic aromatic hydrocarbons with nonplanar screw-shaped structures formed by ortho-fused benzene or other aromatic rings. These helicenes possess many fascinating properties because of their helical molecular geometries, such as large nonlinear optical responses, chiroptical, circular polarized absorption and emission, and relatively high solubility.1–7 Therefore, they are now sparking extensive attention in the areas of electronics and optoelectronics, nonlinear optics, switches and molecular recognition.8–14In general, the currently studied helicenes can be divided into three types from the perspective of the fused rings arrangement. One type only contains angularly fused rings. The second is the combinations of angular with linear fusion of benzene rings, are viewed as expanded helicenes. The third is laterally π-extended helicenes based on the first type. The latter two types may lead to novel electronic, photophysical and chiroptical properties due to the size increase of a helicene.15
A large number of laterally extended helicenes have been well-characterized.16–19 For example, Collins et al. reported that pyrene and [4]- or [5]helicene with an increased π surface displayed significant red-shifts compared to the parent [5]helicene in both the UV/Vis and the fluorescence spectra, and adopts co-planar or stacked arrangements in the solid state.20 The pyrene-based dibenzo[7]helicene and 2H-pyran[7]helicene lateral derivatives with the fluorescent quantum yields in dichloromethane of FF = 0.10 and 0.17 have been reported.21 They form remarkably stabilised intramolecular excimer states upon excitation and exhibit large Stokes shifts respectively. Nuckolls et al.22 demonstrated that perylenediimide (PDI)-based π-extended helicenes results in the collision of π-electron clouds between two PDI subunits, which enhance the delocalization of electrons. However, the studies of expanded helicenes are very few, especially the study on the modification of their structure.
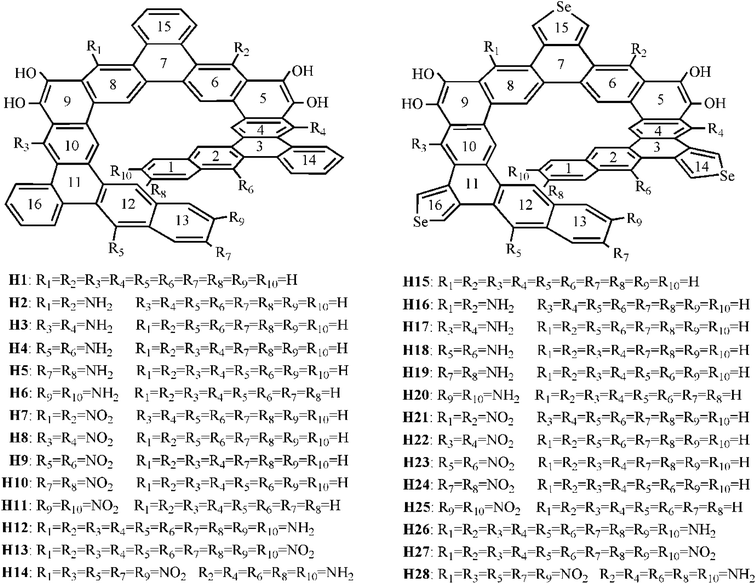
Recently, Tilley et al.23 reported a benzannulated or selenophene-annulated expanded helicenes, which is named helicenes H1 and H15, respectively (Fig. 1). They are composed of alternating linearly and angularly fused rings and contain larger π-systems than typical helicenes, and possess an internal cavity. The H1 forms dimeric structure in the solid state, and no π-stacking interactions between dimers, while helicene H15 exhibits long-range π-stacking in the solid state. These properties may result in a certain application in the field of organic electronics. Moreover, their unique helical structure arising from the chirality can meet the basic requirement of second-order NLO material. Accordingly, helicenes H1 and H15 are likely to be the potential second-order NLO material.
It is well known that macroscopic properties strongly related to microcosmic electron structures, especially for electronic transition properties upon excitation. By all appearances, it is necessary to systemically investigate the photophysical properties and establish structure–property relationships at the quantum chemistry level of theory, so that their performance further improve. To achieve this purpose, twenty-six benzannulated or selenophene-annulated expanded helicenes H2–H14 and H16–H28 were designed. The introduction of donor NH2 unit or acceptor NO2 unit at R1 and R2, or R3 and R4, or R5 and R6, or R7 and R8, or R9 and R10 positions was named as helicenes H2–H11 and H16–H25, respectively. Helicenes H12, H13, H26, H27 are the simultaneously introduction of donor NH2 unit or acceptor NO2 unit at R1–R10 positions. For helicenes H14 and H28, NO2 unit is at R1, R3, R5, R7 and R9 positions, and NH2 unit is at R2, R4, R6, R8 and R10 positions. In order to more clearly describe the structure and charge transfer properties, we numbered the benzene ring in the helicenes, as shown in Fig. 1. In this paper, our main goal is to shed light with the help of DFT/TDDFT calculations to (i) investigate the frontier molecular orbitals (FMOs) (ii) analyze electronic transition mechanism and (iii) study NLO properties.
II. Computational details
All quantum chemistry calculations were carried out with Gaussian 09 Software.24 The ground-state geometries of the studied helicenes were optimized using the B3LYP25 functional. The B3LYP functional is a combination of Becke's three-parameter hybrid exchange functional26 and the Lee–Yang–Parr27 correlation functional. Basis sets of the effective core potential (ECP) double-ζ (DZ) LANL2DZ containing relativistic effects for Se and 6-31G(d) for O, N, C and H atoms were employed. Harmonic vibration frequency calculations were used to ensure the optimized structure is the most stable configuration. During the optimization process, there are no symmetry or internal coordination constraints.The calculated excitation energies, absorption wavelengths, and oscillator strengths the studied helicenes H1–H14 were calculated at the TD-B3LYP/6-31+G(d) level and those of the studied helicenes H15–H28 were calculated at the TD-B3LYP/6-31+G(d)/LANL2DZ level (6-31+G(d) for O, N, C and H atoms; LANL2DZ basis set for Se atom).
It is noted that first hyperpolarizability is an important parameter to evaluate the second-order NLO property. In this paper, the second-order NLO response was determined by hyper-Rayleigh scattering (βHRS), as follows:28,29
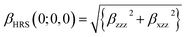 | (1) |
The associated depolarization ratio (DR), which gives the shape information of the NLO-phore, reads as follows:30
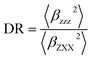 | (2) |
β is also typically decomposed into the sum of dipolar (J = 1) and octupolar (J = 3) tensorial components:31
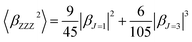 | (3) |
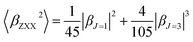 | (4) |
The βHRS values (×10−30 esu) of helicenes H1–H14 are calculated by using CAM-B3LYP functionals associated with the 6-31+G(d) basis set and the βHRS values (×10−30 esu) of helicenes H15–H28 are calculated by using CAM-B3LYP associated with the 6-31+G(d) for O, N, C and H atoms and LANL2DZ basis set for Se atom.
III. Results and discussion
3.1 Molecular structures
In this paper, twenty-eight expanded helicenes were investigated, as shown in Fig. 1. Their ground state geometrical structures have been fully optimized at B3LYP/6-31G(d) or B3LYP/6-31G(d)/LANL2DZ level. The positive vibrational frequencies confirmed that our studied helicenes are dynamically stable. Helicenes H1 and H15 has been synthesized and characterized, which possess typical helical structure.23 It consists of alternating linearly and angularly fused rings, H atom at R1–R10 positions. The X-ray crystal structure unambiguously demonstrated it is helical structures. Taking the helicene H1 as an example to test the feasibility of the selected functional. Several selected geometric structural parameters are compared with the experimental ones (Table S1†), and it is found that the theoretical values are in good agreement with the experimental ones, indicating that our adopted method is suitable to describe the ground state geometrical structure of the studied helicenes.3.2 Frontier molecular orbital analysis
For organic helicenes, their frontier molecular orbitals (FMOs) distributions and energy gaps (HOMO–LUMO gap) are closely related to the electronic and optical properties. The sketch of the HOMO and LUMO orbitals, the calculated HOMO/LUMO energy levels, and energy gaps of helicenes H1–H28 are shown in Fig. 2 and S1.†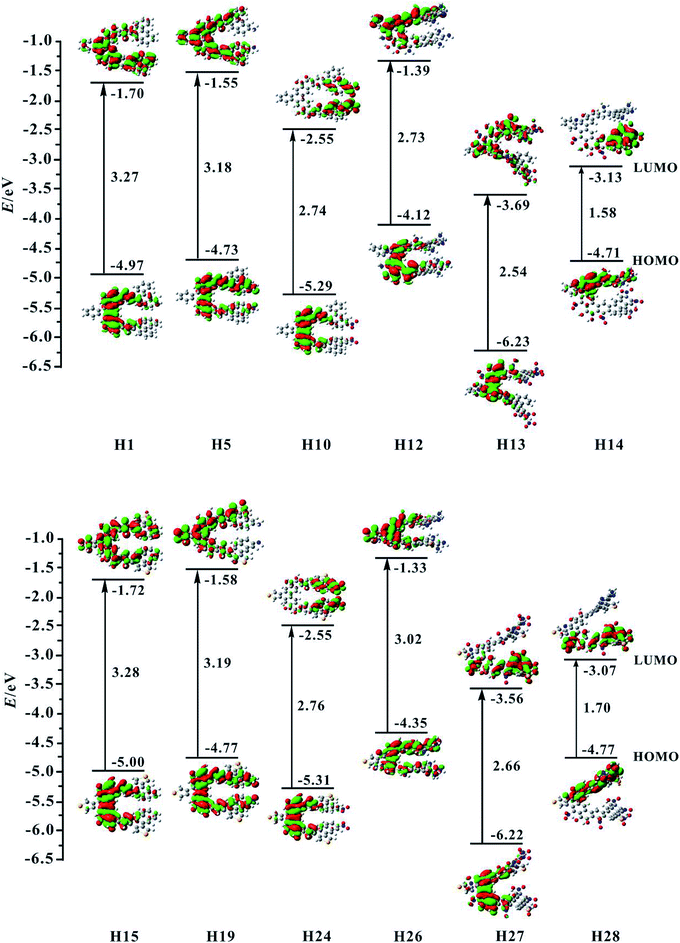 | ||
| Fig. 2 Contour plots of the HOMO and LUMO for the studied helicenes H1, H5, H10, H12–H15, H19, H24, and H26–H28. | ||
For helicene H1, its HOMO mainly localizes on rings 4–6, 8–10 and oxygen atoms, and its LUMO mostly localizes on rings 4–13, 15 and 16. For helicenes H2 and H3, their HOMO distributions are almost the same as that of helicene H1, but the LUMO of helicene H2 primary distributes on the inner rings, and that of helicene H3 largely distributes on rings 6–13, 15 and 16, indicating that the introduction of donor NH2 unit at R1 and R2 or R3 and R4 positions has a certain influence on the LUMO distribution of helicene H1. For helicenes H4–H6, their LUMO distributions are nearly the same as that of helicene H1, however, the HOMO distributions of helicenes H4 and H5 almost delocalize throughout the inner rings, and that of helicene H6 mainly localizes on rings 1–6, demonstrating that the introduction of donor NH2 unit at R5 and R6, R7 and R8 or R9 and R10 positions in helicene H1 may change the HOMO distribution. For helicenes H7–H11, their HOMO distributions are almost the same as that of helicene H1. However, their LUMO distributions are rather sensitive to the position of NO2 unit. The LUMO distribution of helicene H7 mainly localizes on rings 8–9 and NO2 unit attached to ring 8, and that of helicene H8 localizes on rings 4–5 and NO2 attached to ring 4, and that of H9 localizes on rings 1–3 and NO2 units, while the LUMO distributions of helicenes H10 and H11 largely localize on rings 1, 2, 12, 13 and NO2 units. These signify that acceptor NO2 unit at different substituent positions may have remarkably influence on LUMO distribution of helicene H1. For helicene H12 with the donor NH2 unit, its HOMO orbital mainly distributes on rings 5, 6, 8–10 and O atoms, and its LUMO localizes on rings 4–9, 14 and 15, which indicating that the distributions of HOMO and LUMO partially overlap. The HOMO of helicene H13 locates on rings 4–6, 8–10 and O atoms attached to rings 5 and 9, while the LUMO distributes on the whole molecule. Compared with helicene H12, the HOMO and LUMO orbitals distributions of helicene H14 are clearly separated. Its HOMO distribution mainly localizes on rings 1, 2, 4–6, and N and O atoms attached to rings 1–6, and the LUMO distribution mostly localizes on rings 10–13, 16 and NO2 units attached to rings 12–13. The changes of FMO distributions, indicating that the introduction of the electron-withdraw units (NO2) facilitates charge separation of frontier molecular orbital, which is beneficial to realize intramolecular charge transfer from HOMO to LUMO.
For helicene H15, its HOMO distribution is almost the same as helicene H1. However, its LUMO distribution almost delocalizes over the inner rings and ring 15. For helicene H16, its FMOs are nearly the same as that of helicene H15. The LUMO distributions of helicenes H17–H20 are almost the same, distributed on rings 4–10 and 15. However, the HOMO distribution of helicene H17 is nearly the same as that of helicene H15, the HOMOs of helicenes H18 and H19 mainly delocalize on inner rings, and the HOMO of helicene H20 mostly localizes on rings 12, 13, 16 and NH2 unit attached to ring 13. By observing the FMOs of helicenes H21–H25, it can be concluded that the effect of NO2 unit at different substituent positions on the FMOs of helicene H15 is almost the same as its effect on the FMOs of helicene H1. For helicenes H26–H28, their FMOs distributions have significant changes compared with helicene H15.
Subsequently, we investigate the effect of the different substituents and substituent positions on energy gap. Compared with helicene H1, the HOMO and LUMO energy level of helicenes H2–H6 slightly increase. However, the increase in HOMO energy levels is greater than the increase in LUMO energy levels, so the bands gap of the five substituted helicenes slightly reduce. It is worth mentioning that the band gap of helicene H3 is the smallest of the five substituted helicenes, so it can be concluded that the band gap of helicene H1 can be effectively reduced when the R3 and R4 positions are substituted with donor NH2 unit. For helicenes H7–H11, their HOMO and LUMO energy level significantly reduce relative to helicene H1. However, the LUMO energy level decreases more rapidly than the HOMO energy level, their band gaps are significantly reduced, which is closely related to the introduction of the NO2 unit affects the distribution of LUMO in the above analysis. This indicates that the introduction of acceptor NO2 unit in helicene H1 can effectively reduce the band gap. In particular, the band gap of helicene H7 which introduces acceptor NO2 unit at R1 and R2 positions has been reduced to 2.49 eV. For helicene H12, its band gap significantly reduces relative to helicenes H1–H6, indicating that when the R1–R10 positions are all substituted with donor NH2 unit, the band gap can be effectively reduced. For helicene H13, its band gap also significantly reduced relative to helicene H1, but does not much change compared to helicenes H7–H11, except that both its HOMO and LUMO energy level greatly reduce. For helicene H14, its band gap is the smallest of helicenes H1–H14, which results from the electronic distributions of HOMO and LUMO are obviously separated. This indicates that the introduction of the combination of donor NH2 and acceptor NO2 unit is an effective method for reducing the band gap of helicene H1.
For the homologue H15 of helicene H1, the same substituted way was used in helicene H15, which obtained helicenes H16–H28. The research found that the HOMO/LUMO energy level and energy gaps of helicenes H15–H28 have the same conclusions as helicenes H1–H14, for example, helicene H28 which is the introduction of acceptor NO2 unit at R1, R3, R5, R7 and R9 positions and donor NH2 unit at R2, R4, R6, R8 and R10 positions, has the smallest energy gap in helicenes H15–H28. In addition, the electronic structure shows that the visible charge transfer from top (rings 1, 2, 4–6 and N atoms at R2, R4, R6 and R8 positions) to bottom (rings 8–13 and NO2 units at R1, R5 and R7 positions) of whole molecule. Overall, FMOs and energy gaps of helicenes H1 and H15 can be effectively tuned through introduction of different substituents at proper positions.
3.3 Electronic absorption of helicenes H1–H28
In recent years, the TDDFT method has been widely used in the calculations of electronic transition properties.32–36 However, proper selection of the functional and basis set is rather important for accurately describing the electronic transition because each functional or basis set has its own merit. Firstly, four Pople's basis sets (e.g. 6-31G(d), 6-31G(d,p), 6-31+G(d), and 6-311+G(d)) were selected to evaluate the effect of basis set extension on the electronic absorption wavelength by using B3LYP functional. The calculated main absorption bands of helicene H1 at the different basis set levels were listed in Table S2.† It is interesting to find that the difference between the absorption wavelengths of the largest basis set and the smallest basis set is about 8 nm. It means that the effect of the basis set size on the calculated absorption wavelength is negligible. Many studies demonstrate that diffuse functions can accurately calculate absorption wavelengths and successfully describe the electronic transition properties.37,38 Considering the performance and reasonable computational resource, 6-31+G(d) basis set was selected in the following calculation. Subsequently, the B3LYP,26 M06-2X,39,40 CAM-B3LYP,41,42 and BH&HLYP43 functionals were chosen to test the influence of different functionals on the absorption wavelengths. The results show that the calculated absorption wavelengths of M06-2X, CAM-B3LYP, and BH&HLYP functionals are similar (Table S3†). And, the B3LYP functional slightly underestimates the excitation energy. However, previous studies have shown that the B3LYP functional is the most suitable functional for organic conjugated systems.44–46 Thus, the B3LYP functional combined with 6-31+G(d) basis set was employed in the following electronic excitation calculations. For the helicenes H15–H28, the LANL2DZ basis set was used for Se atom.Based on the above results of functional or basis set, the 60 lowest electronic excitation energies of the studied helicenes H1–H14 were calculated at the TD-B3LYP/6-31+G(d) level and those of the studied helicenes H15–H28 were calculated at the TD-B3LYP/6-31+G(d)/LANL2DZ(6-31+G(d) for O, N, C and H atoms; LANL2DZ basis set for Se atom) level. The calculated excitation energies, absorption wavelengths, and oscillator strengths are summarized in Table 1. To better understand the nature of electronic absorption, electron density difference maps (EDDMs) involved into the most intense band were shown in Fig. 3 and S2.†
| Compound | ΔEge | λ | f | Compound | ΔEge | λ | f |
|---|---|---|---|---|---|---|---|
| H1 | 3.90 | 318.21 | 0.470 | H15 | 3.71 | 334.41 | 0.911 |
| H2 | 3.95 | 313.64 | 0.301 | H16 | 4.12 | 300.82 | 0.324 |
| 3.61 | 343.00 | 0.216 | 2.99 | 414.39 | 0.172 | ||
| 2.58 | 479.76 | 0.156 | 2.61 | 475.71 | 0.185 | ||
| H3 | 4.00 | 310.00 | 0.357 | H17 | 3.94 | 314.99 | 0.161 |
| 3.54 | 349.96 | 0.286 | 3.35 | 370.15 | 0.397 | ||
| 2.54 | 487.71 | 0.147 | 2.81 | 440.77 | 0.195 | ||
| H4 | 3.88 | 319.32 | 0.790 | H18 | 3.65 | 339.48 | 0.621 |
| H5 | 3.84 | 322.64 | 0.670 | H19 | 3.94 | 314.49 | 0.430 |
| 3.18 | 389.41 | 0.162 | |||||
| H6 | 3.88 | 319.90 | 0.613 | H20 | 3.65 | 339.52 | 0.574 |
| 3.28 | 378.13 | 0.214 | |||||
| H7 | 3.92 | 316.31 | 0.606 | H21 | 3.66 | 338.81 | 0.395 |
| 3.32 | 373.00 | 0.102 | 2.72 | 465.57 | 0.135 | ||
| 2.75 | 451.32 | 0.175 | |||||
| H8 | 3.87 | 320.15 | 0.575 | H22 | 3.72 | 333.53 | 0.529 |
| 3.53 | 350.82 | 0.118 | |||||
| H9 | 3.62 | 342.09 | 0.326 | H23 | 3.72 | 333.15 | 0.432 |
| H10 | 3.68 | 336.69 | 0.560 | H24 | 3.78 | 328.22 | 0.918 |
| 3.17 | 390.82 | 0.180 | 2.67 | 464.57 | 0.144 | ||
| H11 | 3.75 | 330.25 | 0.554 | H25 | 3.67 | 337.52 | 0.508 |
| H12 | 3.53 | 358.80 | 0.184 | H26 | 3.60 | 344.41 | 0.199 |
| 2.96 | 419.10 | 0.238 | 3.13 | 396.23 | 0.248 | ||
| 2.50 | 495.16 | 0.100 | |||||
| H13 | 3.04 | 407.95 | 0.124 | H27 | 2.99 | 414.98 | 0.096 |
| 2.08 | 596.13 | 0.121 | |||||
| H14 | 2.96 | 418.79 | 0.077 | H28 | 2.99 | 414.11 | 0.093 |
| 2.68 | 463.13 | 0.096 |
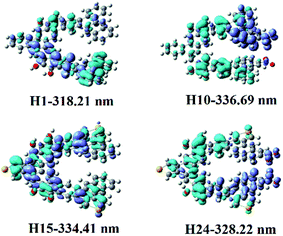 | ||
| Fig. 3 Electron density difference maps of helicenes H1, H10, H15 and H24. Blue and purple colours indicate depletion and accumulation of electron density, respectively. | ||
Helicene H1 exhibits one main absorption band with the charge transfer (CT) from rings 4, 5, 12, 13 and 16 to rings 7–11. Helicenes H2 and H3 shows three main absorption bands. The most intense absorption band of helicene H2 is at 313.64 nm, mainly coming from rings 1, 2, 8–10, 12 and 14 to rings 5–7 charge transfer, while that of helicene H3 mainly originates from the π → π* character on the entire skeleton. For helicene H4, there is one main absorption band, the electronic transition is assigned as a CT from rings 2–5, 10, 12, N and O atoms to rings 6–8 and 16. With respect to helicene H5, it is interesting to find that there is a CT from rings 11–13 and 16 to the other inner rings, besides π → π* character with rings 7–10. For helicene H6, the absorption band locates at 319.90 nm, with the largest oscillator strength, mainly arises from the π → π* character on the entire skeleton. For helicenes H7 and H8, the electronic transition mainly ascribed to the π → π* character on the entire skeleton, while the most intense absorption band of helicene H9 originates from rings 1, 2, 12, 13 and 16 to the other rings and NO2 unit attached to ring 12 charge transfer, and that of helicene H10 is ascribed to a CT from rings 4, 5, 9, 10, 16 and O atoms attached to rings 5 and 9 to rings 1, 2 and NO2 attached to ring 1, and that of helicene H11 comes from rings 12, 13, 16 and C atoms connected to OH units to the other inner rings and NO2 units CT. For helicene H12, it displays three main absorption bands. It is worth mentioning that the oscillator strengths of the second absorption band is largest, this most intense absorption peak at 419.10 nm attributes from rings 5, 6, 9, 10, 12, 13, O atoms and N atoms at R2, R3, R5–R7 positions to the other rings CT. For helicene H13, it has two absorption bands, and its absorption wavelength extended to 596 nm. Its electronic transition arises from rings 8, 10, 15, 16 and C atoms connected to OH units to the NO2 units at R1, R3–R5, R7, R9 and R10 positions CT. For helicene H14, the oscillator strength of the absorption band is very small, less than 0.1. The most intense absorption band at 463.13 nm has a charge transfer from rings 1, 2, 5, 6, N atoms at R2, R4, R6, R8, R10 positions and O atoms attached to ring 5 to the other inner rings and NO2 units at R3, R5, R7, R9 positions, and π → π* character on rings 4 and 9.
For helicene H15, it shows one main absorption band, mainly assigned as π → π* character on the entire skeleton. The same as helicene H15, that of helicene H19 also ascribed to the π → π* character on the entire skeleton. Unlike helicene H15, that of helicene H16 comes from rings 12, 13, 15 and 16 to the other rings CT, and that of helicene H17 originates from rings 1, 2, 11–13, 14 and 16 to the other rings CT, and that of helicene H18 arises from rings 2, 5–9, 14, O atoms and N atoms to rings 11–13 and 16 CT, and that of helicene H20 attributes from rings 1, 2 and the N atom at R10 position to the other rings CT. For helicene H21, the most intense electronic transition is the same as that of helicene H15. Unlike helicene H15, that of helicene H22 comes from rings 12, 13, 15 and 16 to NO2 units CT, and that of helicene H23 mainly originates from rings 16 to the other rings CT, and that of helicene H24 arises from rings 4–9 and 14–16 to rings 10–13 and NO2 units CT, and that of helicene H25 attributes from rings 14, 15, C atoms connected to OH units to the other rings CT. For helicene H26, the second band at 396.23 nm is the most intense absorption, this absorption has a CT and π → π* character on ring 1–11, 14 and 15. With respect to helicene H27, the electronic transition originates from rings 4, 5, 9, 14 and O atoms at rings 5 and 9 to NO2 units at R5-R8 positions CT, besides the π → π* character within rings 6–8. For helicene H28, the electronic transition mainly arises from rings 1, 2, 4, 14 and N atoms attached to rings 1, 2 and 4 to the other rings and NO2 units attached to ring 13.
Overall, compared with helicene H1, the wavelengths of the high-energy absorption band of helicene H3 are slightly blue-shifted, while those of helicenes H2, H4–H6, H7 and H8 remain essentially unchanged. But those of helicenes H9–H11 are red-shifted, and those of helicenes H12–H14 are obviously red shifted (Δλ = 40 nm for helicene H12, Δλ = 89 nm for helicene H13 and Δλ = 100 nm for helicene H14). For helicene H15, its absorption wavelength is 334.41 nm. Compared with helicene H15, the wavelength of the high-energy absorption band of helicenes H16, H17 and H19 are blue-shifted. The absorption wavelengths of helicenes H18 and H20–H25 are close to helicene H15. The absorption wavelengths of helicenes H26–H28 are obviously red-shifted compared with helicene H15. In general, the electronic transition properties, absorption wavelength and the number of absorption bands of helicenes H1 and H15 can be changed through introduction of different substituents at proper positions.
3.4 Second-order NLO properties
Based on the above analysis, the asymmetric electronic structures of studied helicenes meet the basic requirements for second-order NLO materials. At the same time, the obvious intramolecular CT of these helicenes may result in the large first hyperpolarizability (βHRS). These unique features motivate us to investigate their second-order NLO response.As we all known, the βHRS is very sensitive to the adopted functionals. Therefore, four popular DFT functionals (i.e. B3LYP,26 CAM-B3LYP,41,47 M06-2X,39 and BH&HLYP48) were chosen to strengthen the reliability of our calculation results. The calculated βHRS values of helicenes H1–H28 by four different functionals are given in Table S7.† Among the considered functionals, the βHRS value calculated by B3LYP functional is the largest, whereas the βHRS values obtained by other three functionals are relatively close. Previous studies have shown that the long-range corrected functional CAM-B3LYP is a reliable method to calculate the βHRS,49,50 and B3LYP functional overestimates the βHRS.51,52 Thus, the βHRS values obtained from CAM-B3LYP were used in the following discussion (Table 2).
| Compound | βHRS | DR | |βJ=1| | |βJ=3| |
|---|---|---|---|---|
| H1 | 5.26 | 3.91 | 1045.33 | 1159.44 |
| H2 | 10.57 | 6.56 | 2451.93 | 1301.30 |
| H3 | 4.86 | 2.18 | 635.11 | 1541.19 |
| H4 | 5.02 | 2.83 | 838.51 | 1381.68 |
| H5 | 9.41 | 5.68 | 2111.06 | 1436.33 |
| H6 | 5.59 | 1.71 | 436.40 | 1987.46 |
| H7 | 8.39 | 4.56 | 1764.52 | 1623.98 |
| H8 | 11.04 | 6.05 | 2516.43 | 1543.56 |
| H9 | 9.70 | 5.76 | 2182.60 | 1454.95 |
| H10 | 28.88 | 6.35 | 6650.65 | 3757.64 |
| H11 | 14.11 | 5.78 | 3178.59 | 2104.02 |
| H12 | 10.16 | 3.13 | 1808.64 | 2624.92 |
| H13 | 22.23 | 6.27 | 5106.31 | 2949.23 |
| H14 | 18.21 | 5.31 | 4012.12 | 3018.81 |
| H15 | 5.89 | 3.81 | 1158.22 | 1325.11 |
| H16 | 8.50 | 4.68 | 1790.83 | 1640.37 |
| H17 | 5.79 | 2.57 | 898.50 | 1682.94 |
| H18 | 5.72 | 2.78 | 945.12 | 1588.10 |
| H19 | 10.11 | 5.69 | 2268.77 | 1540.48 |
| H20 | 5.90 | 2.63 | 934.23 | 1692.44 |
| H21 | 7.89 | 3.42 | 1474.83 | 1918.88 |
| H22 | 7.96 | 4.89 | 1712.48 | 1441.10 |
| H23 | 7.82 | 4.79 | 1671.75 | 1445.51 |
| H24 | 29.95 | 6.32 | 6892.77 | 3920.86 |
| H25 | 15.10 | 5.11 | 3290.10 | 2611.43 |
| H26 | 8.30 | 2.88 | 1405.00 | 2255.36 |
| H27 | 26.10 | 5.35 | 5762.05 | 4282.72 |
| H28 | 15.29 | 5.56 | 3410.00 | 2395.30 |
The calculated βHRS values of our studied helicenes are large. For example, the βHRS value of the helicene H24 is (29.95 × 10−30 esu) is about 7 times larger than that of the highly π-delocalized phenyliminomethyl ferrocene complex.53 Thus, our studied helicenes may be the excellent candidates for second-order NLO materials from the stand point of their large NLO response and intrinsic asymmetric structures. For helicenes H3, H4 and H6, their βHRS values are close to the value of helicene H1, which indicates that when the R3 and R4, R5 and R6, or R9 and R10 positions are replaced by donor NH2 unit, respectively, their effect on the βHRS value is not significant. For helicenes H2 and H5, their βHRS values are about twice that of helicene H1, which signifies that the introduction of donor NH2 unit at R1 and R2 or R7 and R8 positions can increases the βHRS value. For helicenes H7–H11, their βHRS values are larger than helicene H1, which shows that the introduction of acceptor NO2 unit can effective enhance βHRS value. Comparing helicenes H8–H11 and helicenes H3–H6, it is found that the βHRS values of helicene substituted by acceptor NO2 unit is larger than that of helicene substituted by donor NH2 unit at the same substituent position, for example, helicene H8 > helicene H3. For helicenes H12–H14, their βHRS values are also larger than that of helicene H1, which manifests that these three substitution methods are also ways to obtain larger βHRS value. In addition, from helicenes H1 to H14, it can be concluded that the βHRS value of helicene H10 is the largest of all. This indicates that the maximum βHRS value can be obtained by the introduction of acceptor NO2 unit at R7 and R8 positions for helicene H1, which is attributed to the enhancement of electron acceptor ability. For the homolog H15 of helicene H1, the same substituted way was used in helicene H15, which obtained helicenes H16–H28. It is found that helicenes H15–H28 have the same conclusions as helicenes H1–H14, for example, helicene H24 which is the introduction of acceptor NO2 unit at R7 and R8 positions, has the largest βHRS value in helicenes H15–H28. Comparing helicenes H15–H28 with H1–H14, it can be seen that helicenes H15–H28 does not have much improvement in NLO response, for example, the βHRS value of helicene H10 is relatively close to that of helicene H24.
The depolarization ratio (DR) is also an important parameter of the NLO material, which can be used to reveal the contribution of the βHRS response. Specifically, when the DR is larger than 4.26, the dipolar component makes a major contribution. Reversely, the βHRS response is dominantly from octupolar. For our studied helicenes H3, H4, H6, H12, H17, H18, H20, H21 and H26, the octupolar component is dominant. For helicenes H2, H5, H8–H11, H13, H14, H19, H24, H25, H27 and H28 the dipolar part is larger than the octupolar, which becomes more clearly from dipolar (J = 1) and octupolar (J = 3) tensorial components. However, for helicenes H1, H7, H15, H16, H22 and H23, the dipolar part is comparable to the octupolar. Thus, the contribution of dipolar (J = 1) and octupolar (J = 3) components to the NLO response of helicenes H1, H7, H15, H16, H22 and H23 are nearly equal.
To better understand their NLO origins, the corresponding electron density difference maps (EDDMs) of helicenes H1, H10, H15 and H24 were shown in Fig. 3. It can be seen that the NLO origin of helicene H1 attributes to charger transfer (CT) from rings 4, 5, 12, 13 and 16 to rings 7–11, and that of helicene H15 mainly derives from the localized CT on entire skeleton. Obviously, the CT characters of helicenes H10 and H24 are different from helicenes H1 and H15. For instance, the NLO origin of helicene H10 mainly because of the obvious CT from rings 4, 5, 9, 10, 16 and O attached rings 5 and 9 to rings 1, 2 and NO2 with ring 1, while that of helicene H24 originates a CT from rings 4–9 and 14–16 to rings 10–13 and the donor NO2 parts.
IV. Conclusions
In this paper, we employed DFT/TDDFT theory to investigate photophysical properties of twenty-eight benzannulated or selenophene-annulated expanded helicenes. The investigations show that different substituents at different substituent positions have great effects on electronic structure, electronic absorption and the second-order NLO properties. The introduction of the combination of donor and acceptor units can effectively reduce band gap, and the introduction of donor or acceptor unit at R1–R10 positions enables a large red shift in the absorption wavelength, and the introduction of a NO2 acceptor unit at R7 and R8 positions may obtain the largest first hyperpolarizability values. All these benzannulated or selenophene-annulated expanded helicenes have large first hyperpolarizability values, indicating that the second-order NLO response can be effectively tuned by the introduction of donor or acceptor units or their combination. In view of large NLO response and intrinsic asymmetric structures, these studied helicenes may become the excellent candidates for second-order NLO materials, which will further promote the development of high technological applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Education Department of Jilin Province, China, under Grant number 2016511.Notes and references
- Y. Shen and C. Chen, Chem. Rev., 2012, 112, 1463–1535 CrossRef CAS PubMed.
- M. Richard Henri, Angew. Chem., Int. Ed. Engl., 2003, 13, 649–660 Search PubMed.
- J. Katz Thomas, Angew. Chem., Int. Ed., 2000, 39, 1921–1923 CrossRef.
- A. Urbano, Angew. Chem., Int. Ed., 2003, 42, 3986–3989 CrossRef CAS PubMed.
- M. Daigle, D. Miao, A. Lucotti, M. Tommasini and J. Morin, Angew. Chem., Int. Ed., 2017, 56, 5946 CrossRef CAS.
- M. Gingras, Chem. Soc. Rev., 2013, 42, 968–1006 RSC.
- M. Gingras, Chem. Soc. Rev., 2013, 42, 1051–1095 RSC.
- T. Fujikawa, Y. Segawa and K. Itami, J. Am. Chem. Soc., 2016, 138, 3587–3595 CrossRef CAS PubMed.
- T. Wohrle, I. Wurzbach, J. Kirres, A. Kostidou, N. Kapernaum, J. Litterscheidt, J. Haenle, P. Staffeld, A. Baro, F. Giesselmann and S. Laschat, Chem. Rev., 2016, 116, 1139–1241 CrossRef PubMed.
- R. Pascal, Chem. Rev., 2006, 106, 4809–4819 CrossRef CAS PubMed.
- S. Choudhary, C. Gozalvez, A. Higelin, I. Krossing, M. Melle-Franco and A. Mateo-Alonso, Chem.–Eur. J., 2014, 20, 1525–1528 CrossRef CAS PubMed.
- S. More, S. Choudhary, A. Higelin, I. Krossing, M. Melle-Franco and A. Mateo-Alonso, Chem. Commun., 2014, 50, 1976–1979 RSC.
- D. Cortizo-Lacalle, A. Pertegas, L. Martinez-Sarti, M. Melle-Franco, H. Bolink and A. Mateo-Alonso, J. Mater. Chem. C, 2015, 3, 9170–9174 RSC.
- J. Luo, X. Xu, R. Mao and Q. Miao, J. Am. Chem. Soc., 2012, 134, 13796–13803 CrossRef CAS PubMed.
- R. Rieger and K. Müllen, J. Phys. Org. Chem., 2010, 23, 315–325 CAS.
- T. Fujikawa, Y. Segawa and K. Itami, J. Org. Chem., 2017, 82, 7745–7749 CrossRef CAS PubMed.
- T. Fujikawa, Y. Segawa and K. Itami, J. Am. Chem. Soc., 2016, 138, 3587–3595 CrossRef CAS PubMed.
- Y. Zhu, Z. Xia, Z. Cai, Z. Yuan, N. Jiang, T. Li, Y. Wang, X. Guo, Z. Li, S. Ma, D. Zhong, Y. Li and J. Wang, J. Am. Chem. Soc., 2018, 140, 4222–4226 CrossRef CAS PubMed.
- T. Hosokawa, Y. Takahashi, T. Matsushima, S. Watanabe, S. Kikkawa, I. Azumaya, A. Tsurusaki and K. Kamikawa, J. Am. Chem. Soc., 2017, 139, 18512–18521 CrossRef CAS PubMed.
- A. Bédard, A. Vlassova, A. C. Hernandez-Perez, A. Bessette, G. S. Hanan, M. A. Heuft and S. K. Collins, Chem.–Eur. J., 2013, 19, 16295–16302 CrossRef PubMed.
- M. Buchta, J. Rybáček, A. Jančařík, A. A. Kudale, M. Buděšínský, J. V. Chocholoušová, J. Vacek, L. Bednárová, I. Císařová and G. J. Bodwell, Chem.–Eur. J., 2015, 21, 8910–8917 CrossRef CAS PubMed.
- N. J. Schuster, D. W. Paley, S. Jockusch, F. Ng, M. L. Steigerwald and C. Nuckolls, Angew. Chem., Int. Ed., 2016, 55, 13519–13523 CrossRef CAS PubMed.
- G. R. Kiel, S. C. Patel, P. W. Smith, D. S. Levine and T. D. Tilley, J. Am. Chem. Soc., 2017, 139, 18456–18459 CrossRef CAS PubMed.
- M. W. Evans and G. Wagnière, Phys. Rev. A, 1990, 42, 6732–6736 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- F. Mançois, L. Sanguinet, J.-L. Pozzo, M. Guillaume, B. Champagne, V. Rodriguez, F. Adamietz, L. Ducasse and F. Castet, J. Phys. Chem. B, 2007, 111, 9795–9802 CrossRef PubMed.
- A. Plaquet, M. Guillaume, B. Champagne, F. Castet, L. Ducasse, J.-L. Pozzo and V. Rodriguez, Phys. Chem. Chem. Phys., 2008, 10, 6223–6232 RSC.
- M. de Wergifosse, J. de Ruyck and B. Champagne, J. Phys. Chem. C, 2014, 118, 8595–8602 CrossRef CAS.
- P. Beaujean, F. Bondu, A. Plaquet, J. Garcia-Amorós, J. Cusido, F. M. Raymo, F. Castet, V. Rodriguez and B. Champagne, J. Am. Chem. Soc., 2016, 138, 5052–5062 CrossRef CAS PubMed.
- G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi and V. Barone, J. Chem. Phys., 2006, 124, 094107 CrossRef PubMed.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2004, 121, 12772–12773 CrossRef CAS.
- C. Liu, Y. Si, S. Shi, G. Yang and X. Pan, Dalton Trans., 2016, 45, 7285–7293 RSC.
- D. Jacquemin, B. Mennucci and C. Adamo, Phys. Chem. Chem. Phys., 2011, 13, 16987–16998 RSC.
- C. Guido, D. Jacquemin, C. Adamo and B. Mennucci, J. Chem. Theory Comput., 2015, 11, 5782–5790 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- L. Wang, W.-Y. Wang, Y.-Q. Qiu and H.-Z. Lu, J. Phys. Chem. C, 2015, 119, 24965–24975 CrossRef CAS.
- J.-L. Chen, J.-T. Hong, K.-J. Wu and W.-P. Hu, Chem. Phys. Lett., 2009, 468, 307–312 CrossRef CAS.
- E. G. Hohenstein, S. T. Chill and C. D. Sherrill, J. Chem. Theory Comput., 2008, 4, 1996–2000 CrossRef CAS PubMed.
- A. Pedone, J. Chem. Theory Comput., 2013, 9, 4087–4096 CrossRef CAS PubMed.
- A. B. Tathe, L. Rhyman, P. Ramasami and N. Sekar, J. Fluoresc., 2015, 25, 1117–1126 CrossRef CAS PubMed.
- A. Sorkin, M. A. Iron and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 307–315 CrossRef CAS PubMed.
- L. Y. Zou, A. M. Ren, J. K. Feng, Y. L. Liu, X. Q. Ran and C. C. Sun, J. Phys. Chem. A, 2008, 112, 12172–12178 CrossRef CAS PubMed.
- Y. He, Y. Huang, J. Li, X. Pang and G. Yang, Org. Electron., 2017, 50, 220–227 CrossRef CAS.
- C. Liu, Y. Si, X. Pan and G. Yang, RSC Adv., 2015, 5, 72907–72915 RSC.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- I. H. Nayyar, A. E. Masunov and S. Tretiak, J. Phys. Chem. C, 2013, 117, 18170–18189 CrossRef CAS.
- M. Torrent-Sucarrat, J. Anglada and J. Luis, J. Chem. Theory Comput., 2011, 7, 3935–3943 CrossRef CAS PubMed.
- M. de Wergifosse and B. Champagne, J. Chem. Phys., 2011, 134, 074113 CrossRef PubMed.
- H. Sun and J. Autschbach, ChemPhysChem, 2013, 14, 2450–2461 CrossRef CAS PubMed.
- S. J. A. Van Gisbergen, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1998, 109, 10657–10668 CrossRef CAS.
- S. K. Pal, A. Krishnan, P. K. Das and A. G. Samuelson, J. Organomet. Chem., 2000, 604, 248–259 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: The selected bond lengths for helicene H1 between experiment and calculation, the contour plots of the HOMO and LUMO for the studied helicenes H2–H4, H6–H9, H11, H16–H18 and H20–H23, and H25, the computed main energy absorption band (λ, nm) at the different basis sets level for helicene H1, the computed main energy absorption band (λ, nm) using the different functionals for helicene H1, the electron density difference maps of helicenes H2–H9, H11–H14, H16–H23 and H25–H28, and the calculated βHRS values (×10−30 esu) of helicenes H1–H28 by using four DFT functionals are shown. See DOI: 10.1039/c9ra01136f |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |