Open Access Article
Open Access ArticleModel-based temperature control for improving lactic acid production from glycerol†
Ke-Ke Cheng *a,
Jing Zengb,
Jing-Hai Jianb,
Jun-Fan Zhua,
Gui-Xing Zhanga and
De-Hua Liuc
*a,
Jing Zengb,
Jing-Hai Jianb,
Jun-Fan Zhua,
Gui-Xing Zhanga and
De-Hua Liuc
aChina-Latin America Joint Laboratory for Clean Energy and Climate Change, School of Chemical Engineering and Energy Technology, Dongguan University of Technology, Dongguan, 523808, China. E-mail: chengkeke@dgut.edu.cn
bTsinghua Innovation Center in Dongguan, Dongguan 523808, China
cDepartment of Chemical Engineering, Tsinghua University, Beijing 100084, China
First published on 12th April 2019
Abstract
To maximize the final lactic acid productivity and concentration, temperature control was optimized using a mathematical modelling approach. A kinetic model, including cell growth, product formation and substrate consumption equations, was proposed to describe the lactic acid production process by Escherichia coli AC-521 with glycerol as the substrate. By constructing four functions, the temperature effect was introduced on the fermentation process, where four parameters (Xmax, μmax, Yps and β) were observed to be significantly affected by the temperature. For the convenience of application, the temperature control strategies were simplified by dividing the whole fermentation process into several units. In each unit, the temperature was controlled constantly. Based on the model, the optimal temperature for each unit was determined to maximize the final lactate productivity. This temperature control strategy can be effectively applied in batch and fed-batch cultures, and the verified experimental evaluation showed a good correlation with the model data. Under improved temperature control conditions, a maximal lactic acid concentration of 90.4 g L−1 was obtained after 80 h of fed-batch fermentation, giving a productivity of 1.13 g L−1 h−1, which is 1.2 times more than that in the conventional constant temperature during the cultivation course.
1 Introduction
Lactic acid has a wide range of applications in various fields such as polymers, cosmetics, food, agriculture, and medicine.1 At first, lactic acid was usually produced globally from glucose or starch by fermentation.2 Xylose, sugar beet juice, waste office paper, cellobiose and lignocellulosic materials, including Jerusalem artichoke tubers, corn stover and mixed sugars derived from lignocellulosic biomass, were also tested for their suitability as substrates for lactic acid fermentation.3–15 In recent years, a rapid expansion in biodiesel production capacity has been reported worldwide, which led to more and more glycerol production in the market (about 10% of biodiesel capacity). Glycerol obtained as a by-product from biodiesel production is an abundant and cheap feedstock, which can also be used as a substrate for lactic acid production by fermentation.16 In our previous study, a highly efficient strain of Escherichia coli AC-521 was screened for the production of lactic acid from glycerol in high yields.17In most of the regular fermentation processes, optimization of the culture temperature is usually based on the theory that the temperature should be kept constant during the whole process of cultivation.18–20 However, this constant temperature may not be optimal because effective cell growth, substrate consumption and product formation cannot be achieved simultaneously at the same temperature. It was found that lower temperatures (33–35 °C) are more favorable for the growth of E. coli AC-521, whereas a high temperature (45 °C) maximizes the rates of lactic acid synthesis, although the conventional culture is carried out at a constant temperature of 42 °C.17 Therefore, the intentional variation of temperature during the fermentation process can probably give larger lactic acid yields than when the temperature is kept constant.
The effect of variation of temperature on the lactic acid production has not yet been fully explored. In this work, a kinetic model containing temperature as a variable was proposed to study the effects of temperature on the kinetic behavior of lactic acid fermentation. First, the kinetic model was used to describe the lactic acid fermentation profiles at a constant temperature. Further, the model was improved to simulate the data under different temperatures. In the end, the developed model was used to predict glycerol consumption and product formation in different temperature programs. An optimal temperature profiling determined by a dynamic optimization method was developed to improve the final lactic acid concentration and productivity.
2 Experimental
2.1 Microorganism and fermentation experiments
Escherichia coli AC-521 was grown on the preculture medium containing 2 g K2HPO4·7H2O L−1, 2 g (NH4)2SO4 L−1, 0.5 g KH2PO4 L−1, 2 g yeast extract L−1, and 20 g glycerol L−1. The seed cells for the bioreactor were prepared in 500 mL flasks containing 40 mL preculture medium. The flasks were incubated at 35 °C and 150 rpm for 14 h and subsequently inoculated into a bioreactor at 2% (v/v). The batch or fed-batch cultivations were conducted in a 3 L stirred-vessel bioreactor (BLBIO-3GC, Bailun, China) containing 2 L of fermentation medium under 0.5 vvm air flow. The maximum temperature steady-state error was ±0.23 °C. The fermentation medium contains 2 g K2HPO4·7H2O L−1, 4 g (NH4)2SO4 L−1, 0.5 g KH2PO4 L−1, 3 g yeast extract L−1, and 50–70 g glycerol L−1.For regressing the model parameters, batch cultivations were carried out at 35, 37, 40, 42 and 45 °C, respectively. In lactic acid fed-batch fermentation, the glycerol concentration in the bioreactor was controlled between 10 and 20 g L−1 in 28–72 h by continuous dropwise addition of sterilized glycerol with a precise peristaltic pump (BT101L, Lead Fluid). The experimental values were the means of two independent samples. The biomass concentration in the bioreactor at the beginning of the fermentation ranged from 0.07 g L−1 to 0.08 g L−1. The pH was adjusted to 6.5 before inoculation and maintained at 6.5 throughout the cultivations. All fermentation experiments were carried out at 350 rpm and the broth was sampled every 6–12 h to monitor the lactic acid concentration.
2.2 Kinetic model development
A kinetic model was proposed to simulate the lactic acid fermentation profiles, including cell growth, product accumulation, and substrate consumption. Development of the model was based on the following assumptions:17,21(1) Glycerol is the only limiting substrate. There is no other nutriment (including nitrogen, phosphorous and yeast extract) limitation in the medium and these are excessive in the fermentation medium.
(2) There is no change in the stirring velocity, aeration and pH during the whole process.
During lactic acid production, the growth of bacteria had a maximum saturated concentration, and hence, the cell growth rate of AC521 is described by the logistic equation.22 Moreover, with the increase in the initial glycerol concentration, the growth rate of bacteria decreased, which indicates that the cell growth rate was inhibited by the substrate concentration.17,23,24 The cell growth model considering the inhibitions of glycerol is proposed as follows:
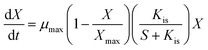 | (1) |
The formation rate of lactic acid is described by eqn (2), which indicates that the product accumulation is correlated with both the cell concentration and the cell growth rate. It has been found that lactic acid accumulation occurs to a certain degree, after which the lactic acid productivity gradually decreases; so the product inhibition item is introduced to the equation:22,25,26
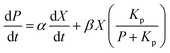 | (2) |
Furthermore, the substrate glycerol consumption rate can be described using eqn (3), which shows that glycerol was consumed for biomass growth, product accumulation and cell metabolic activity:27–29
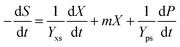 | (3) |
2.3 Data processing methods
The 4th-order Runge–Kutta method was used for the numerical solution of all kinetic equations. The model parameters were solved by minimizing the quadratic sum of the difference between the experimental data and the calculated data using Matlab 6.5 software.262.4 Analytical methods
The liquid samples were analyzed using Shimadzu LC20 HPLC, equipped with a refractive index detector (RID-20A). Glycerol, lactic acid, acetate, succinate and ethanol were analyzed using an Aminex HPX-87H column at 65 °C with 5 mM H2SO4 as the mobile phase at a rate of 0.8 mL min−1. The cell concentration was monitored at 600 nm and converted into dry cell weight (DCW) by a calculated calibration curve.3 Results
3.1 Lactic acid production kinetic model at different temperatures
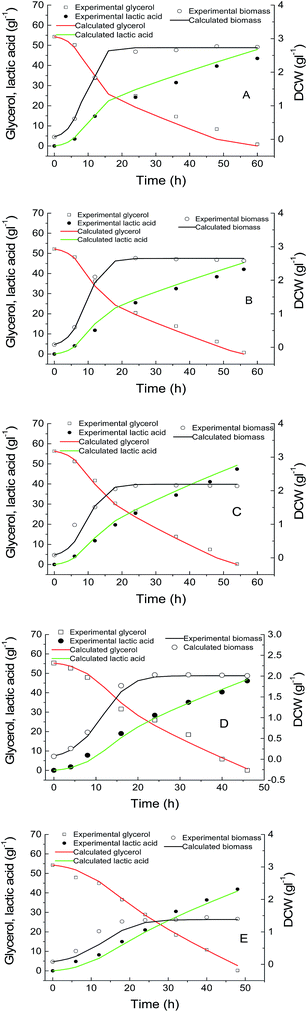
Batch cultivations at different temperatures (from 35 to 42 °C) with around 50 g L−1 initial glycerol concentration were compared in Fig. 1. The lactic acid concentration increased gradually when the fermentation temperature was increased from 35 to 42 °C. The ability of lactic acid production has been associated with the ability to reduce pyruvate by lactate dehydrogenase. The lower the temperature was, the lower the potential lactic acid yield. It was probably because the lactate dehydrogenase of AC-521 was mesophilic.30 However, the μmax value and biomass concentration increased with the decrease in the temperature; the biomass concentration at 35 °C was about 1.5 times higher than that at 42 °C (Fig. 1).Purified lactate dehydrogenase of AC-521 showed the optimal catalytic temperature to be 45 °C, and the relative activities were 79% and 21% at 35 °C and 65 °C, respectively (Fig. S1†). The lactate dehydrogenase lost only 3% of its initial activity when the enzyme was exposed at 35 °C for 4 h, and lost 18.9% of the initial activity at 45 °C for 4 h (Fig. S2†).
For regressing these mathematical model parameters for eqn (1)–(3), batch kinetic data of lactic acid production at 35–45 °C were utilized. The kinetic parameters at different temperatures were estimated by minimizing the residual sum of squares between the experimental values at different temperatures and the corresponding simulated values. The regressed parameters are shown in Table 1. The quality of model regression and the significance were evaluated by the determination coefficient and P-value. It was found that the determination coefficient R2 ranged from 0.982 to 0.993 and the P value was less than 0.01, implying that the model was significant.
| Temperature (°C) | Variable parameters | Invariable parameters | |||||||
|---|---|---|---|---|---|---|---|---|---|
| μmax (h−1) | Xmax (g L−1) | Yps (g g−1) | β | Yxs (g L−1) | Kis (g L−1) | Kp (g L−1) | α | m | |
| 35 | 0.65 | 2.73 | 0.88 | 0.31 | 0.9 | 85.2 | 73.7 | 6.75 | 0.005 |
| 37 | 0.57 | 2.65 | 0.92 | 0.32 | 0.9 | 85.2 | 73.7 | 6.75 | 0.005 |
| 40 | 0.55 | 2.19 | 0.9 | 0.51 | 0.9 | 85.2 | 73.7 | 6.75 | 0.005 |
| 42 | 0.45 | 2.01 | 0.9 | 0.67 | 0.9 | 85.2 | 73.7 | 6.75 | 0.005 |
| 45 | 0.34 | 1.38 | 0.82 | 0.88 | 0.9 | 85.2 | 73.7 | 6.75 | 0.005 |
3.2 Kinetic model with temperature effect
To maximize the lactic acid concentration and productivity, a reasonable temperature scheme should start at a lower temperature in a former stage to improve cell growth, and then be maintained at a higher temperature for enhancing the lactic acid production. In order to introduce the temperature effects on the fermentation performance, some kinetic parameters, including Xmax, μmax, Yps, and β, were observed to be affected by the temperature significantly, which were classified as variable parameters. Unlike some invariable kinetic parameters such as Kis, α, m, Yxs, and Kp, these variable parameters in this model should be correlated with temperature.The temperature effect was described using a quadratic polynomial temperature function to substitute for the variable parameters.
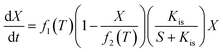 | (4) |
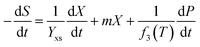 | (5) |
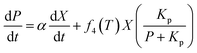 | (6) |
The parameters of the four functions at different temperatures were estimated by minimizing the residual sum of squares between the experimental values at different temperatures and the corresponding simulated values. The four equations are deduced from the fermentation results at different constant temperatures and listed as follows:
| f1(T) = −0.0012 × T2 + 0.0739 × T − 0.539 | (7) |
| f2(T) = −0.008 × T2 + 0.5003 × T − 4.962 | (8) |
| f3(T) = −0.0023 × T2 + 0.1792 × T − 2.556 | (9) |
| f4(T) = 0.0049 × T2 + −0.3322 × T + 6.046 | (10) |
The quality of the model with temperature effect and the significance were also evaluated by the determination coefficient and P-value. It was found that the determination coefficient R2 ranged from 0.955 to 0.993 and the P value was less than 0.01, implying that the model values agreed well with the experimental values. Thus, the model containing modified temperature functions can be used to optimize the lactic acid fermentation process.
The goal of our optimization was to find out the best values for the temperature and the best value for the duration during which the temperature should be controlled at the optimized value so that the volumetric productivity QP calculated at the point of time tN+1 as
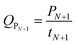 | (11) |
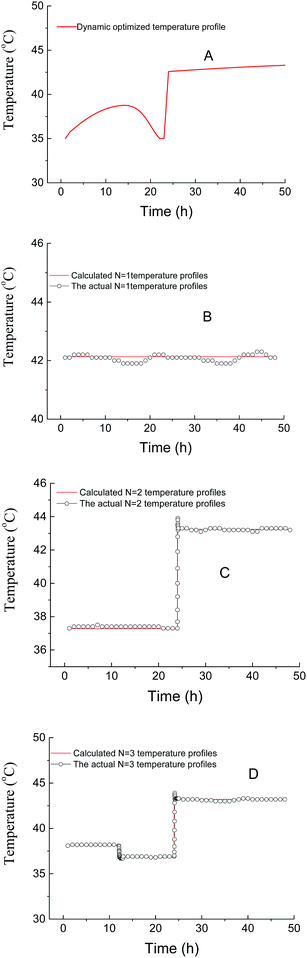
The optimal temperature profile obtained by the above-mentioned dynamic optimization method is a continuous change and time-dependent control strategy (Fig. 2A). This temperature profile is relatively multivariate and not easy to apply in the real fermentation process. Further, a simplified process was developed, in which the fermentation process was separated into only several time units. During each unit, the temperature was controlled constantly.31 Fig. 2 compares the temperature profiles of different units (N = 1, 2, 3) and the profile obtained by dynamic optimization. For N = 1, it was found that the optimal constant temperature was 42.1 °C, which agreed with the results in conventional optimization (42 °C).17 The actual temperature profiles are also shown in Fig. 2. With the increase in the units, the temperature profile gradually approached to that obtained by dynamic optimization. The experimental and the corresponding simulated lactic acid formation processes are shown in Fig. 3. It was found that when the temperature control strategy was N = 3 (0–12 h 38.1 °C, 12–24 h 36.8 °C, after 24 h 43.2 °C), lactic acid production could be greatly improved and the fermentation performance was very near to the simulated process by dynamic optimization (Fig. 3). So this simplified method for temperature control can be chosen during lactic acid batch fermentation.
 | ||
| Fig. 3 Comparison between lactic acid formation using different temperature-controlling processes and the corresponding calculated model values. | ||
3.3 Lactic acid production by fed-batch fermentation
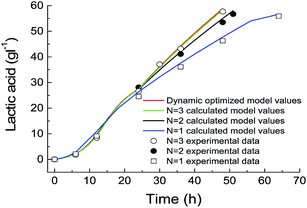
From the above-mentioned results, it was found that the N = 3 temperature control strategy was completed in the first 24 hours of the fermentation. So, if we can start the glycerol feeding after 24 hours, this improved temperature scheme can also be applied in fed-batch fermentation. A typical set of comparative experiments in which the initial concentration of glycerol was 60 g L−1, temperatures were controlled at a constant value (42.1 °C) and N = 3, temperature profiling showed that by changing the culture temperature at the given program, there were significant improvements in the lactic acid production and even in the glycerol consumption rate and cell growth. The cell growth rate at the optimized temperature was faster than that at a constant temperature of 42.1 °C (Fig. 4A). Moreover, it showed that a relatively higher cell density is helpful for glycerol consumption and lactic acid production. Therefore, the developed simplified process appeared to be effective in improving the lactic acid production. Under any conditions, there were always by-products, including acetate, succinate and ethanol, which were detected in the culture medium although their concentrations varied (Fig. 4B). At the end of the optimized temperature control process, a maximal lactic acid concentration of 90.4 g L−1 was obtained after 80 h of fed-batch fermentation, giving a yield of 0.88 g g−1 glycerol and a productivity of 1.12 g L−1 h−1, which is 1.2 times more than that obtained in the traditional process with a constant temperature during the cultivation course.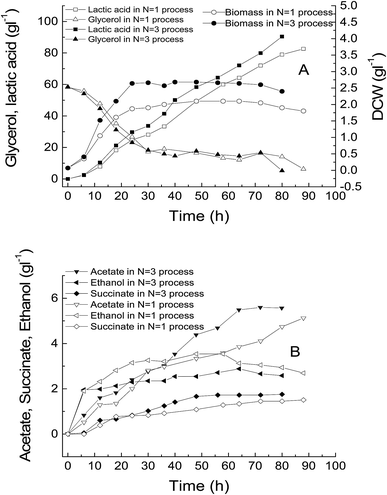 | ||
| Fig. 4 Comparison of lactic acid fed-batch fermentation using N = 3 temperature-controlling process and N = 1 temperature-controlling process. | ||
4 Discussion
Lactic acid production from glycerol has been studied because glycerol from the biodiesel industry is an ideal feedstock due to its availability and low price. Recent studies on lactic acid fermentation from glycerol are summarized and compared in Table 2. For most of the reported results, the obtained lactic acid yield is in the range of 0.7 to 0.89 g g−1 glycerol. E. coli AC-521 showed the highest lactic acid concentration and relatively higher yield.| Process, fermentation model and substrate | Strain | Lactic acid production | References | ||
|---|---|---|---|---|---|
| Concentration (g L−1) | Productivity (g L−1 h−1) | Yield (g g−1 glycerol) | |||
| Batch, glycerol with sodium pyruvate addition | Rhizopus oryzae 9363 | 1.33 | 0.013 | — | 32 |
| Batch, glycerol with lucerne green juice addition | Rhizopus oryzae NRRL 395 | 46.8 | 0.93 | 0.82 | 33 |
| Fed-batch, glycerol | Pichia pastoris GLS | 28 | 0.24 | 0.7 | 34 |
| Fed-batch, glycerol with acetate addition | Enterococcus faecalis QU11 | 44.9 | 0.72 | 0.75 | 35 |
| Fed-batch, glycerol | Escherichia coli LA20ΔlldD | 50 | 0.6 | 0.89 | 36 |
| Batch, glycerol | Lactobacillus sp. CYP4 | 30.7 | 1.28 | 0.71 | 37 |
| Fed-batch, glycerol | Escherichia coli AC-521 | 85.8 | 0.97 | 0.88 | 17 |
| Fed-batch, glycerol | Escherichia coli AC-521 | 90.4 | 1.12 | 0.88 | This study |
Considering the high energy consumption and high cost of operation of lactic acid recovery from the aqueous broth, economical production of lactic acid from glycerol requires the improvements of product concentration, yield and productivity. In our pervious study, the temperature in the whole cultivation process for lactic acid production was controlled at 42 °C, since the process at this “optimized” temperature would result in higher lactic acid yield and concentration than those at other constant temperatures. However, the most suitable temperatures respectively for cell growth, substrate consumption and product formation are not always constant during the whole process, which means that the best constant temperature is not the optimal selection. Compared with the maximal biomass concentration of 2.1 g L−1 in the process carried out at a constant temperature, the maximal biomass concentration increased to 2.68 g L−1 during the N = 3 temperature control process (Fig. 4A). In the N = 3 temperature mode, the culture temperature was controlled at a lower temperature in the former stage to improve cell growth, and then maintained at a higher temperature (43.2 °C) for retaining higher lactate dehydrogenase activity. This could be the reason for the higher lactic acid yield in the N = 3 temperature mode.
The fermentation model is a good tool for optimization of culture parameters, such as feeding strategy, temperature and product removal. Before the optimal temperature control strategy was determined, we must develop a model containing temperature as the variable. In this study, the effect of temperature was described by constructing functions substitute for some variables, which were affected by the temperature significantly. The optimal control profiles obtained by the dynamic optimization is a process with continuous change, thus relatively difficult to be performed in a practical cultivation process since very complicated control precision and devices are needed. For the convenient application in practical fermentation, the control strategy was simplified by dividing the whole process into several units. It can be found that the greater the units, the closer the final fermentation performance was to that of the dynamic control strategy. At the end of the optimized temperature control process, a maximal lactic acid concentration of 90.4 g L−1 was obtained after 80 h of fed-batch fermentation, giving a yield of 0.88 g g−1 glycerol and a productivity of 1.12 g L−1 h−1. Model-based temperature control can also be used in other fermentation processes. Based on kinetic parameters analysis, a temperature control strategy (30 °C to 28 °C for 0–43 h, 28 °C to 24 °C for 43–90 h, 24 °C for 90–161 h) was proposed to shorten the lag phase of mycelial growth, keep high flavonoid productivity and relieve inhibition of flavonoids. By this temperature control strategy, the maximum flavonoid yield reached 42.1 mg g−1 dry cell weight, which was 70.45% higher than that at a constant temperature of 26 °C.38 Using model-based temperature profile (0–20 h 30 °C, 20–72 h 40 °C), Xie et al. increased the glycerol yield by 12–14%, while the residual glucose was less than 1% (w/v).31 By programmed controlling of the incubation temperature (0–24 h 37 °C, 24–144 h 25 °C) and using the optimized medium, Shen et al. increased the alcohol concentration to 6.97 g L−1 in carbon monoxide-rich off-gas fermentation using Clostridium carboxidivorans. It showed that a dynamic temperature control strategy might be more attractive for practical fermentation.39
Besides that, the organic nitrogen source concentration (provided by yeast extract) and dissolved oxygen are also the key factors to cell growth rate, leading to a larger cell growth rate and a higher cell density. In the future investigation, further optimization of the kinetic model should be correlated with these two factors.
5 Conclusions
An optimal temperature profiling determined by the model can be effectively applied in batch and fed-batch lactic acid cultures and the verified experimental evaluation resulted in good correlation with the model data. Under improved temperature control conditions, a maximal lactic acid concentration of 90.4 g L−1 was obtained after 80 h of fed-batch fermentation, giving a productivity of 1.13 g L−1 h−1, which is 1.2 times greater than that obtained in the conventional process with a constant temperature during the cultivation course. It showed that a dynamic temperature control strategy might be more attractive for lactic acid production.Conflicts of interest
There are no conflicts to declare.Nomenclature
| X | Biomass concentration (g L−1) |
| S | Glycerol concentration (g L−1) |
| μmax | Maximum specific growth rate (h−1) |
| Kis | Glycerol inhibition constant (g L−1) |
| Kp | Product inhibition constant (g L−1) |
| α | Constant for lactic acid accumulation decided by cell growth rate |
| β | Constant for lactic acid accumulation decided by cell concentration |
| Yxs | Coefficient of biomass yield on glycerol |
| Yps | Coefficient of lactic acid yield on glycerol |
| m | Coefficient of substrate consumption using for cell metabolism activity |
| QP | Volumetric productivity (g L−1 h−1) |
| Send | Final glycerol concentration (g L−1) |
Acknowledgements
This study was supported by DongGuan Innovative Research Team Program (No. 201536000100033), and Guangdong Innovation Research Team for Higher Education (2017KCXTD030), High-level Talents Project of Dongguan University of Technology (KCYKYQD2017017).Notes and references
- V. Juturu and J. C. Wu, Crit. Rev. Biotechnol., 2016, 36, 967–977 CrossRef CAS PubMed.
- M. A. Abdel-Rahman, Y. Tashiro and K. Sonomoto, Biotechnol. Adv., 2013, 31, 877–902 CrossRef CAS PubMed.
- M. A. Abdel-Rahman, Y. Tashiro, T. Zendo, K. Sakai and K. Sonomoto, RSC Adv., 2016, 6, 17659–17668 RSC.
- R. H. W. Maas, R. R. Bakker, G. Eggink and R. A. Weusthuis, Appl. Microbiol. Biotechnol., 2006, 72, 861–868 CrossRef CAS PubMed.
- D. Visser, J. Van Breugel, J. M. De Bruijn and P. A'Campo, US Pat., 8211675B2, 2012.
- Y. Wang, M. Wang, D. Cai, B. Wang, Z. Wang, P. Qin and T. Tan, RSC Adv., 2016, 6, 35771–35777 RSC.
- K. Tokuhiro, N. Ishida, A. Kondo and H. Takahashi, Appl. Microbiol. Biotechnol., 2008, 79, 481–488 CrossRef CAS PubMed.
- Z. Y. Qiu, Q. Gao and J. Bao, Bioresour. Technol., 2017, 245, 1369–1376 CrossRef CAS PubMed.
- J. Tan, M. A. Abdel-Rahman, M. Numaguchi, Y. Tashiro, T. Zendo, K. Sakai and K. Sonomoto, RSC Adv., 2017, 39, 24233–24241 RSC.
- X. Y. Ge, H. Qian and W. G. Zhang, Bioresour. Technol., 2009, 100, 1872–1874 CrossRef CAS PubMed.
- J. Wang, M. Gao, Q. H. Wang, W. Y. Zhang and Y. Shirai, RSC Adv., 2016, 6, 104354–104358 RSC.
- D. M. Bai, S. Z. Li, Z. L. Liu and Z. F. Cui, Appl. Biochem. Biotechnol., 2008, 144, 79–85 CrossRef CAS.
- C. Gao, C. Ma and P. Xu, Biotechnol. Adv., 2011, 29, 930–939 CrossRef CAS PubMed.
- X. Shen and L. Xia, Appl. Biochem. Biotechnol., 2006, 33, 251–262 CrossRef.
- Y. Guo, Q. Yan, Z. Jiang, C. Teng and X. Wang, J. Ind. Microbiol. Biotechnol., 2010, 37, 1137–1143 CrossRef CAS PubMed.
- S. Apilak and W. Colin, Biochem. Eng. J., 2018, 137, 358–364 CrossRef.
- A. A. Hong, K. K. Cheng, F. Peng, S. Zhou, Y. Sun, C. M. Liu and D. H. Liu, J. Chem. Technol. Biotechnol., 2009, 84, 1576–1581 CrossRef CAS.
- J. L. Tang, X. C. Wang, Y. S. Hu, Y. M. Zhang and Y. Y. Li, Waste Manag., 2016, 52, 278–285 CrossRef CAS PubMed.
- P. Gokfiliz-Yildiz and I. Karapinar, Int. J. Hydrogen Energy, 2018, 43, 10655–10665 CrossRef CAS.
- K. Shibata, D. M. Flores, G. Kobayashi and K. Sonomoto, Enzyme Microb. Technol., 2007, 41, 149–155 CrossRef CAS.
- G. Kaur, A. K. Srivastava and S. Chand, Biochem. Eng. J., 2102, 68, 34–41 CrossRef.
- B. Abdallah, B. Beatrice and A. Abdeltif, Food Technol. Biotechnol., 2011, 49, 3–12 Search PubMed.
- V. H. Edwards, Biotechnol. Bioeng., 1970, 12, 679–712 CrossRef CAS PubMed.
- C. J. Zhu, B. S. Fang and S. Z. Wang, Bioresour. Technol., 2016, 212, 130–137 CrossRef CAS PubMed.
- R. Luedeking and E. L. Piret, Biotechnol. Bioeng., 1959, 67, 393–412 Search PubMed.
- L. He, X. B. Zhao, K. K. Cheng, Y. Sun and D. H. Liu, Appl. Biochem. Biotechnol., 2013, 169, 312–326 CrossRef CAS PubMed.
- J. M. Monteagudo, L. Rodriguez, J. Rincón and J. Fuertes, J. Chem. Technol. Biotechnol., 1997, 68, 271–276 CrossRef CAS.
- S. K. Avadhani, Z. Zhang and K. Shetty, Process Biochem., 1999, 35, 227–235 CrossRef.
- J. Mareš, J. Kukal, P. Hrnčiřík and J. Náhlík, Biochem. Eng. J., 2016, 112, 178–185 CrossRef.
- M. M. Kabir, P. Y. Ho and K. Shimizu, Biochem. Eng. J., 2005, 26, 1–11 CrossRef CAS.
- D. M. Xie, D. H. Liu and J. A. Zhang, J. Chem. Technol. Biotechnol., 2001, 76, 1057–1069 CrossRef CAS.
- X. Q. Wang, Z. H. Ruan, W. Guan, R. Kraemer, Y. Zhong and Y. Liu, Biotechnol. Appl. Biochem., 2015, 20, 389–395 CAS.
- D. C. Vodnar, F. V. Dulf, O. L. Pop and C. Socaciu, Microb. Cell Fact., 2013, 92, 12 Search PubMed.
- P. B. A. de Lima, K. C. L. Mulder, N. T. M. Melo, L. S. Carvalho, G. S. Menino, E. Mulinari, V. H. de Castro, T. F. dos Reis, G. H. Goldman, B. S. Magalhaes and N. S. Parachin, Microb. Cell Fact., 2016, 158, 15 Search PubMed.
- N. Murakami, M. Oba, M. Iwamoto, Y. Tashiro, T. Noguchi, K. Bonkohara, M. A. Abdel-Rahman, T. Zendo, M. Shimoda, K. Sakai and K. Sonomoto, J. Biosci. Bioeng., 2016, 121, 89–95 CrossRef CAS PubMed.
- S. Mazumdar, M. D. Blankschien, J. M. Clomburg and R. Gonzalez, Microb. Cell Fact., 2013, 12, 7 CrossRef CAS PubMed.
- Y. Prada-Palomo, M. Romero-Vanegas, P. Diaz-Ruiz, D. Molina-Velasco and C. Guzman-Luna, CT&F, Cienc., Tecnol. Futuro, 2012, 5, 57–65 Search PubMed.
- F. C. Jiang, H. N. Zhang, D. Wu, N. Feng, Z. Zhang, J. S. Zhang, J. Feng and Y. Yang, Biotechnol. Appl. Biochem., 2018, 65, 739–747 CrossRef CAS PubMed.
- S. H. Shen, Y. Gu, C. S. Chai, W. H. Jiang, Y. P. Zhuang and Y. H. Wang, Bioresour. Technol., 2107, 239, 236–243 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra01323g |
| This journal is © The Royal Society of Chemistry 2019 |