Open Access Article
Open Access ArticleThermoelectric and vibrational properties of Be2C, BeMgC and Mg2C using first-principles method
V. Mauryaa,
U. Paliwalb,
G. Sharmac and
K. B. Joshi *a
*a
aDepartment of Physics, Mohan Lal Sukhadia University, Udaipur-313001, India. E-mail: cmsmlsu@gmail.com
bDepartment of Physics, Jai Narain Vyas University, Jodhpur-342011, India
cDepartment of Pure & Applied Physics, University of Kota, Kota-324005, India
First published on 1st May 2019
Abstract
Transport coefficients are calculated combining first-principles calculations with the Boltzmann transport theory. Electronic states obtained in terms of the k-space eigen-energies from the crystalline orbital program, based on density functional theory, are Fourier transformed and interfaced with the transport equations modeled in the BoltzTraP. The calculations are performed for Be2C, Mg2C, and the BeMgC mixed crystal. The Seebeck coefficient, electronic thermal conductivity and the power factor are calculated. Further, the transport coefficients are linked to find the electronic fitness function to compare the performance with other thermoelectric materials. The procedure can also be applied to study the thermoelectric properties of other materials. The vibrational frequencies at the Brillouin zone centre are calculated generating a Hessian matrix from the analytical gradients of the energy with respect to atomic coordinates in the three antifluorite crystals. Moreover, the static, high frequency dielectric constants and Born effective charges are calculated to find splitting in the longitudinal optic and transverse optic modes. Results are compared with the data wherever available in the literature and a very good agreement is found in most cases.
1. Introduction
Clean energy is one of the central issues from scientific, economic and environmental points of view. Efforts have begun to look into sustainable and efficient sources of clean energy.1–7 Thermoelectric (TE) and photo-voltaic devices in conjunction with renewable energy sources play a vital role in this strategic area such as thermoelectric generators and space exploration.7,8 Like solar-energy conversion, the TE generators require enhanced energy efficiency and waste heat recovery from the exhaust. Reliable, silent or sustainable operations and small device size are the additional required features.7,9 The challenges are to find materials having specific and tailored thermoelectric properties.1–9 Combining quantum mechanical principles with computational power, it is possible to simulate and predict properties of materials.4,7,10 Density functional theory (DFT) has been the backbone of such techniques over the last several decades.11 Now it is also possible to calculate thermoelectric coefficients by coupling k-space eigen-energies from first-principles DFT methods with the Boltzmann transport equations (BTEs).12,13 No such provision lies for each computational method used in general by the community of computational materials scientists.14 These are highly needed because the performance of a TE material is quantified in terms of the figure of merit (zT), and the power factor (PF) which can be obtained theoretically vis-a-vis experimentally. Such an interface was published for the Linearized Augmented Plane Wave (LAPW) method recently.15 In this endeavor we couple the k-space eigen-vectors and eigen-energies calculated from the first-principles periodic Linear Combination of Atomic Orbitals (LCAO) with the second principle model based on the BTE embodied in the BoltzTraP.16–18 The periodic LCAO method is implemented in the CRYSTAL package.16,17 A series of this crystalline orbital program in several versions has appeared in literature. In these, the non-cellular periodic LCAO method enables to use the Hartree–Fock or the DF theory to find the E–k curve and several other properties of a crystal. The Hartree–Fock method treats the exchange part exactly and correlation part very poorly. The DFT treats both parts reasonably well but approximately.16 The multi-valley structures of E–k curves and the band gap of periodic solids largely depend on the theory applied and consequently the electronic and thermoelectric properties vary.18 Recent trends are to use hybrid functionals to get accurate values of the band gap and bands dispersion which works well in some solids.19–22 The hybrid functionals club merit of both approaches. Many methods use a number of hybrid functionals from the library of exchange and correlation (XC) functionals. On the contrary, one can devise a hybrid XC functional tuning percentage of mixing in the CRYSTAL98 and higher versions.16,17 Effect on the band gap and bands dispersion can also be examined. Therefore an interface of the periodic LCAO method with the BoltzTraP will be highly useful to predict the transport coefficients from the E–k dispersion spectra provided by the periodic LCAO method.16–18 This is the major objective of this paper.Hitherto, oxides cover major section (∼70%) of the explored TE materials. Half or full-Heusler compounds which owe spin-polarized band structure, skutterudites, clathrates and chalcogenides share major part of the residual section.2,4,7,23–25 Alkaline-earth metal methanides are technologically important carbides. The complex chemical synthetic process leads to either very low yield or very less stability.7,26 The Be2C, Mg2C and Al4C3 are among a few known alkaline-earth methanides.26–29 Interestingly, Mg2C is only recently synthesized28,29 whereas no ternary methanide is studied to our knowledge. The Be2C, used in the ceramic and nuclear technology, has attracted quite a few theoretical as well as experimental studies.30–38 On Mg2C, the band gap and the pressure coefficients are calculated employing local density approximation (LDA) in FP-LAPW method.39,40 Later it is synthesized and characterized by X-ray diffraction method.28,29 In our earlier work we have studied structural and bonding properties of Be2C, Mg2C and the hypothetical BeMgC deploying the periodic LCAO method.41,42 The thermal conductivity and band gap are proposed without specifying the carrier density or the chemical potential which is mandatory for practical purpose.43,44 Thus there are minimal efforts on the TE studies of carbides. So the second objective is to deploy the interface between periodic LCAO method and the BoltzTraP to find the thermoelectric coefficients of the Be2C, Mg2C and the BeMgC. Further, we compare the TE performance with other materials by means of the newly introduced electronic fitness function (EFF).45
While modeling the properties of particularly the ceramics, nuclear and refractory materials, some limitations remain for practical applications due to change in properties at high temperatures. Vibrational properties and nature of bonding are elemental to the thermal behavior of crystals. Moreover, the vibration frequencies carry information regarding symmetry driven structural stability under different conditions.1,44,47 The frequencies can be compared with the Infrared (IR) and Raman spectra. Essentially, the visible and infrared radiation used in conventional IR and Raman spectroscopies interact strongly with the phonon modes close to the Brillouin Zone (BZ) centre.1,46–48 Therefore, meaningful information can also be obtained from frequencies at the Γ point of the BZ in a crystal. Further, the Born effective charges (BEC) and the splitting in longitudinal optical (LO) and transverse optical (TO) modes provide additional features of the vibration spectra and dynamical behavior of crystals.16,17,49 Thus it is imperative to improve upon the current understanding on the vibrational behavior of the three methanides. Therefore, the third objective of this work is to present the vibrational frequencies at the BZ centre, the BEC, static and high frequency dielectric constants and the LO–TO splitting of vibrational frequencies in Be2C, Mg2C and BeMgC.
Following is the plan of the remaining part of the paper: calculations procedures are described in the second section. Three parts of this section contains computational details, a brief description to compute the TE properties followed by the description on zone centre frequencies along with the LO–TO splitting. Results are presented in the third section. The four sub-sections cover discussion of results on electronic, thermoelectric, vibrational and the dielectric properties. Results are summarized in the last section.
2. Methods and computational details
2.1 Periodic LCAO method
The first-principles periodic LCAO method is applied.16,17,49,50 The salient features can be found in our earlier work.41 The Perdew–Burke–Ernzerhof (PBE) ansatz based on the generalized gradient approximation (GGA) is applied to treat the XC part of the Kohn–Sham Hamiltonian.51 The structure is optimized with an iterative method based on the total energy gradients calculated analytically with respect to the nuclear coordinates and numerically with respect to the lattice constants. The convergence is checked from the root-mean-square and absolute value of the largest component of the gradients and displacements. The thresholds (in a.u.) for the maximum and the root-mean-square forces were set to 4.5 × 10−4, 3.0 × 10−4 and those for displacements the thresholds were 1.8 × 10−3, 1.2 × 10−3 respectively. The complete optimization was ensured when the four conditions are simultaneously satisfied for the fractional coordinates and cell parameters. For exact treatment of the Coulomb and exchange terms of the total energy operator, computation of integrals over an infinite series is mandatory.16,17,49,50 To achieve it in practice, each infinite series needs to be truncated by setting threshold values of controlling parameters. These tolerance (T) parameters ensure that beyond cutoff limits the contribution to the total sum is smaller than 10−T that can be neglected. In current calculations, five tolerances of the order of 10−7, 10−7, 10−7, 10−7 and 10−12 were undertaken to truncate Coulomb and exchange sum.17,49,50 The SCF process is stopped when two successive cycles differ in energy by less than 10−8 Hartree in geometry optimization and 10−12 Hartree in force calculations. The antifluorite structure belonging to the space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (#225) is taken for the three carbides. The lattice parameters and bulk modulii deduced from the equation of state E(V) are the same as described in our earlier work for this crystal structure of the three carbides.41
m (#225) is taken for the three carbides. The lattice parameters and bulk modulii deduced from the equation of state E(V) are the same as described in our earlier work for this crystal structure of the three carbides.41
2.2 Transport properties
The figure of merit zT, expressed above, depends on the thermal conductivity (κ) which contains both electronic (κe) and lattice (κl) contributions. The electronic part (κe) is usually low in semiconductors. However, band gaps and bandwidth in the vicinity of Fermi level affect the electronic part associated with TE properties. It is well known that many XC functionals are being used by the community which show variation in the band gap of semiconductors. Usage of hybrid functional brings the band gap values close to the many body GW calculations which are believed to give accurate band gap in semiconductors.19–21 Better agreement of band gap from quasi particle or GW calculations with the hybrid functional and also with experiments, in some cases, is ascribed to the fact that hybrid functionals essentially augment LDA or GGA by non-local exchange.19–21 The underestimation of band gap by DFT has commonly been attributed to the inappropriate treatment of the XC functional20–22,52 and the incomplete cancellation of the artificial self-interaction20,52 within the LDA (local) or GGA (semi-local) descriptions. The hybrid functional, generally, combines the ¼ non-local exchange, ¾ of the semi-local exchange with the correlation functional.16,17,20–22,50 The Kohn–Sham eigenvalues generated using such XC functionals are closer to those generated from many body perturbation theory. Here, therefore, we have also deduced band energies using a PBE0 hybrid functional.20–22,52Now it has become possible to unravel thermoelectric properties by combining first-principles methods with the BTE.15,18,53 The requisite formulation to find tensors of transport coefficients from band energies, εik of the ith band at a k point can be found elsewhere.12,13,15,18 Two approximations are made to simplify the calculation procedure. Firstly, in the constant relaxation time approximation τi,k = τ for all i,k and secondly, in the rigid-band approximation we assume that the band structure does not vary with temperature or doping. The formulation gives the electrical conductivity tensor σ, thermal conductivity tensor κe and the Seebeck coefficient S. The temperature and chemical potential (μ) dependent tensors determine the number of charge carriers.15,18,53 The thermoelectric quantities are obtained from the average of the diagonal components of the Seebeck and electrical conductivity tensors.
To compute these tensors, the band energies calculated from the converged electronic charge density using periodic LCAO method over a dense grid of k-points need to be linked with the BoltzTraP. To achieve this an interface is created. The interface arranges the E–k spectrum from the LCAO method and writes into the case.energy file required for processing by the BoltzTraP to compute the transport coefficients. The interface also takes care of the units conversion of the energy and the k-vectors. Lattice vectors and symmetry related information of the crystal under investigation are given in the case.struct file. Thereafter another required file namely case.intrans is generated to completely fill the basket of files BoltzTraP.def. A flowchart of the entire process can be found in our recent work where a similar interface is created to link the energy spectrum from the LAPW method with the BoltzTraP.15 In the current study the band energies are calculated over a dense grid size leading to ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 k-points in the irreducible BZ of the three crystals. The k-points were adequate to ensure convergence in Fourier expansion coefficients.
000 k-points in the irreducible BZ of the three crystals. The k-points were adequate to ensure convergence in Fourier expansion coefficients.
Performance of a TE material is quantified in terms of figure of merit (zT) defined as zT = (SσT)/κ where S is the Seebeck coefficient, σ is electrical conductivity, κ is thermal conductivity, and T is absolute temperature. The quantity S2σ, known as the power factor (PF) is of profound interest to characterize TE materials theoretically as well as experimentally. An ideal TE should follow an electron-crystal phonon-glass model because high zT requires a large S, high σ and low κ. First two transport coefficients also ensure high PF. For metals and semiconductors, the Seebeck coefficient is given by:54
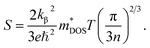 | (1) |
So for high power at certain temperature, a material should have high effective mass and low carrier density, which in turn reduces σ. The effective mass comes from the complexity of the electronic band structure. The degree to which the band structure can be decoupled with the electrical conductivity and S is quantified by means of the EFF. Otherwise these have counterpoising role in determining the figure of merit and the PF. The EFF (or the t function) is defined as45 t = (σ/τ)S2(N/V)2/3, where τ is the relaxation time, σ/τ and S are directly obtained from band structure and the BTE, (N/V) is the volumetric density of states directly proportional to the density of states effective mass 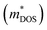 and the Fermi energy (EF) as:
and the Fermi energy (EF) as: 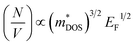 . The function captures the behaviour that quantifies the favourable thermoelectric performance that is useful to scrutinize on a scale. The unit of the t-function turns out to be
. The function captures the behaviour that quantifies the favourable thermoelectric performance that is useful to scrutinize on a scale. The unit of the t-function turns out to be 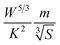 .
.
2.3 Zone centre frequencies and dielectric tensors
In periodic systems the phonon frequencies at the Γ point are calculated by diagonalizing the mass weighted Hessian matrix (Wij) within the harmonic approximation as:16,17,49,50,55–57
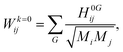 | (2) |
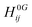 is the second derivative of the electronic and nuclear repulsive energy E at u = 0 with respect to displacement
is the second derivative of the electronic and nuclear repulsive energy E at u = 0 with respect to displacement 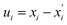 of atom A in the 0th cell, and displacement
of atom A in the 0th cell, and displacement 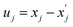 of atom B in the Gth cell from the equilibrium positions
of atom B in the Gth cell from the equilibrium positions 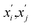 :
:
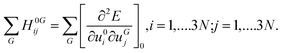 | (3) |
The Hessian at u = 0 is calculated by the analytical evaluation of the first derivative Φjof E with respect to the atomic displacements:
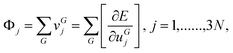 | (4) |
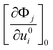 . Since the displacement step considered here is ui = 0.001 Å, the corresponding change in energy is very small and therefore tight tolerance in the self-consistent-field cycles is taken.
. Since the displacement step considered here is ui = 0.001 Å, the corresponding change in energy is very small and therefore tight tolerance in the self-consistent-field cycles is taken.
The effect of dynamical charge due to macroscopic electric field associated with the coherent displacement of crystal nuclei can be included in the Hessian as a correction.55–58 It takes care of the long range Coulomb interaction and results into LO–TO splitting. The LO frequencies are obtained by the additional non-analytic term to the dynamical matrix (eqn (2)):
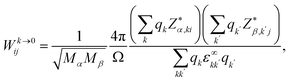 | (5) |
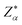 is the BEC tensor of atom α. The electronic dielectric tensor is evaluated using a finite field saw-tooth model50 and the BEC tensor is obtained from the localised Wannier functions.50,58 The ionic contribution deduced from frequency eigenvalues ωm, eigenvector V and Born tensor Z are added in ε∞ to find the static dielectric tensor:
is the BEC tensor of atom α. The electronic dielectric tensor is evaluated using a finite field saw-tooth model50 and the BEC tensor is obtained from the localised Wannier functions.50,58 The ionic contribution deduced from frequency eigenvalues ωm, eigenvector V and Born tensor Z are added in ε∞ to find the static dielectric tensor:
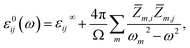 | (6) |
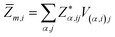 , ω is the electric field frequency, α labels the N atoms of the unit cell, and i and j indicate the three Cartesian components.
, ω is the electric field frequency, α labels the N atoms of the unit cell, and i and j indicate the three Cartesian components.
3. Results and discussion
3.1 Electronic states
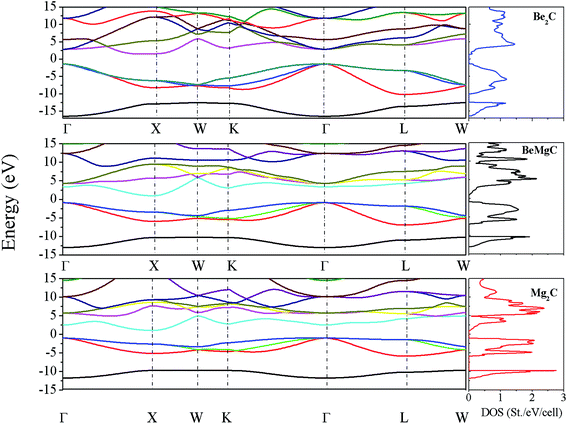
The lattice constant and bulk modulus reported in our earlier publication are well reproduced from the total energy curves of the three crystals.41 The bands dispersion curves delineating microscopic picture of electronic bands are described in Fig. 1. The bands structures show that each carbide has indirect band gap with the valence band maximum (VBM) at Γ and the conduction band minimum (CBM) at X. The Γ–X gaps, for Be2C, BeMgC and Mg2C, in order, are 2.90, 1.86 and 2.05 eV. Likewise Γ–Γ direct gaps are 4.24, 4.21 and 3.53 eV. Similar calculations using PBE0 hybrid functional21 suggest that Γ–X gaps, sequentially for Be2C, BeMgC and Mg2C are 4.37, 3.24 and 3.46 eV whereas the Γ–Γ direct gaps are 5.77, 5.59 and 5.19 eV. Thus PBE0 gives larger band energies and band gaps than the PBE. Band gap measurement is attempted only for the Be2C and Γ–X indirect band gap is reported.38,40 The authors did not propose definite value but concluded that the band gap may be more than at least 1.3 eV.37,38 Moreover, X1v and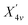 bands observed at −11.5 and−6.7 eV from VBM in LEED, ARPES and NEXAFS experiments are found at −11.46 and−6.79 eV by PBE calculations. The PBE0 functional locates these bands at−12.87 eV and−7.71 eV. Thus energies of these states are very well produced by PBE–GGA in case of Be2C. In case of Mg2C only a few calculations are available for comparison. The published calculations reveal that indirect (direct) band gap lies in the 0.67–0.97 eV (1.34–1.9 eV) range.28,40,43 So both PBE and PBE0 predict band gaps beyond the limits proposed by earlier workers. The LDA used by earlier workers may be the reason for this discrepancy.52 In BeMgC, interestingly PBE0 calculation gives a value of 5.6 (±0.1) eV for both Γ–K and Γ–Γ gaps. These two gaps are separated by 0.25 eV in the PBE bands structure. Current results follow the trends of compounds with identical crystal structure wherein the band gap is found more in the compound with lighter elements.59
bands observed at −11.5 and−6.7 eV from VBM in LEED, ARPES and NEXAFS experiments are found at −11.46 and−6.79 eV by PBE calculations. The PBE0 functional locates these bands at−12.87 eV and−7.71 eV. Thus energies of these states are very well produced by PBE–GGA in case of Be2C. In case of Mg2C only a few calculations are available for comparison. The published calculations reveal that indirect (direct) band gap lies in the 0.67–0.97 eV (1.34–1.9 eV) range.28,40,43 So both PBE and PBE0 predict band gaps beyond the limits proposed by earlier workers. The LDA used by earlier workers may be the reason for this discrepancy.52 In BeMgC, interestingly PBE0 calculation gives a value of 5.6 (±0.1) eV for both Γ–K and Γ–Γ gaps. These two gaps are separated by 0.25 eV in the PBE bands structure. Current results follow the trends of compounds with identical crystal structure wherein the band gap is found more in the compound with lighter elements.59
It is known that DOS gives the number of electronic states integrated over k-space in a finite energy interval. The curves showing electronic DOS are displayed on the right hand panels of Fig. 1. The occupied DOS can be divided into two parts. In first part, the occupied valence band below −10 eV is largely constituted by the C-2s state present in the three carbides. In the second part, the upper valence bands extend from −9.5 to 0 eV approaching to the Fermi level. The interacting cationic (Be and or Mg) 2s2p and C-2p states constitute states in this region. Additionally, the cationic 2p states interact in bonding and anti-bonding modes with C-2p state to form remaining valence bands as well as a few conduction bands in the vicinity of Fermi energy. There is a minor contribution of outer cation s states also. Difference in the DOS of three carbides can be marked by appearance of peaks. The peaks like structures are absent in Be2C and clearly visible in the other two compounds. These bands have typical character of C-2p states and play major role in the thermoelectric properties. Both DOS and dispersion curves reveal that the lowest valence band of Be2C is very deep having the largest width and least number of states. On the contrary, in Mg2C corresponding band has the shortest width and maximum number of states. This is a manifestation of flat bands in Mg2C. The flat bands are normally seen in materials with ionic character. So, the DOS of BeMgC indicate mixed ionic and covalent character.
3.2 Thermoelectric properties
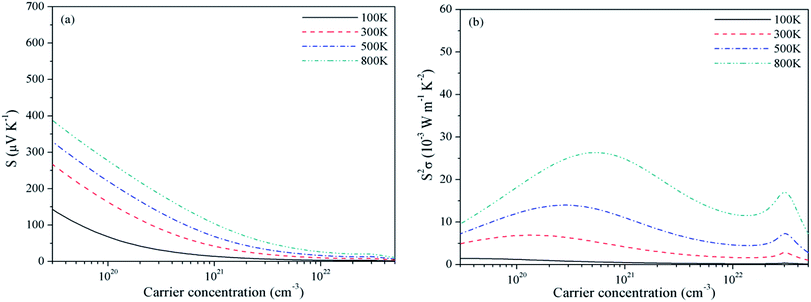
As discussed before, experimental studies of band energies and gaps are reported only for Be2C and the characteristic energies from PBE are in very good agreement compared to the PBE0 hybrid functional. Also, in a study on SrRuO3 several XC functionals were applied to compute the TE properties and PBE was found to be the most suitable.60 Therefore, we use the PBE eigen-energies at k points to compute the TE properties. Also these properties are studied under the constant relaxation time approximation wherein τ is a constant, and the band structure is independent of both temperature and doping. The relaxation time can be estimated from the experimental electrical conductivity σ at given carrier density and temperature. In case of Be2C, such a specified value of electrical conductivity is not available. So we have compared the optimum value of σ/τ deduced directly from the BTE with the reciprocal of the experimental resistivity ρ = 103 μΩ cm (ref. 61) at 300 K which gives τ = 4 × 10−14 s. In absence of such a data for three carbides, we take this as a representative value of relaxation time. On the availability of exact value of τ the transport coefficients can be readily calculated. Dependence of S and PF with chemical potential (μ) is displayed in Fig. 2–4. At four temperatures such a dependence for Be2C is shown in Fig. 2(a). Specific structures appear in S. It shows that by appropriate doping the Seebeck coefficient of the order of ∼2.74–1.54 × 10−3 V K−1 can be achieved. As the range of chemical potential over which this structure is visible expands with increase in temperature, the attainable doping level to achieve calculated S increases. One can see in Fig. 2(b) that optimum PF is ≅1.36 × 10−3 W mK−2 at 100 K and rises to 26.42 × 10−3 W mK−2 at 800 K where S ≅ 2.73 × 10−3 V K−1.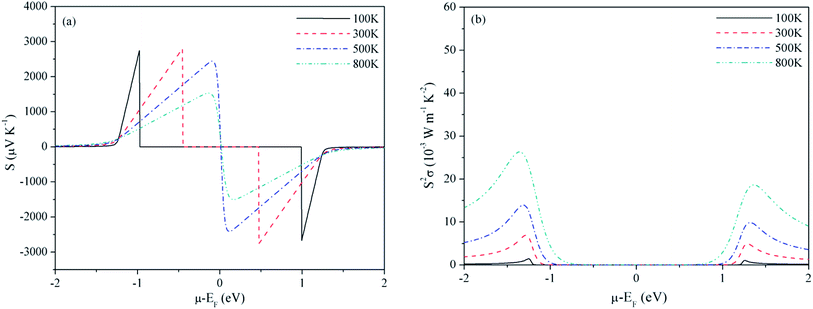 | ||
| Fig. 2 Variation of (a) Seebeck coefficient and (b) power factor of Be2C with chemical potential at τ = 4 × 10−14 s. | ||
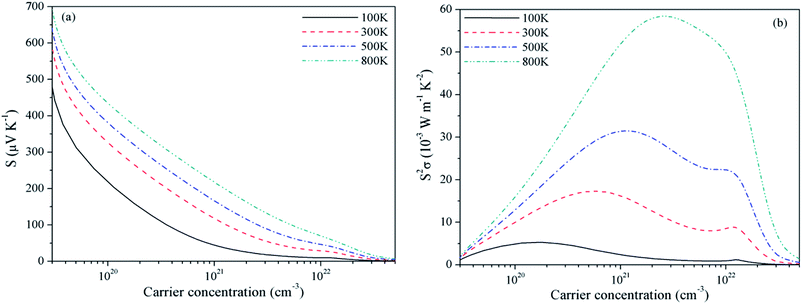
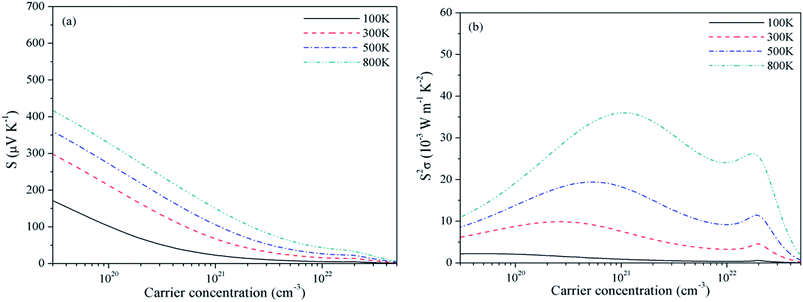
For Mg2C, variation of S and PF with chemical potential is shown in Fig. 3. It depicts that optimum values of S and PF are 2.94 × 10−3 V K−1 and 17.10 × 10−3 W mK−2 at 300 K. Corresponding values at 800 K are 1.344 × 10−3 V K−1 and 58.20 × 10−3 W mK−2. Similarly, at 300 K the S and PF of BeMgC are 2.91 × 10−3 V K−1 and 9.88 × 10−3 W mK−2. The S and PF lie in between the corresponding values of Be2C and Mg2C. It is well expected as bands dispersion and DOS in BeMgC is intermediate to those in Be2C and Mg2C. The microscopic variation in the curvature of bands determines the velocity and effective mass tensor and consequently trend with respect to chemical potential is somewhat different in BeMgC than in Mg2C visible in Fig. 3(b) and 4(b). In mixed compounds mass and concentration dependence affect thermal properties and the effect of mutual interaction of the sub lattices (Be and Mg in this case) on thermal properties is not well understood.6
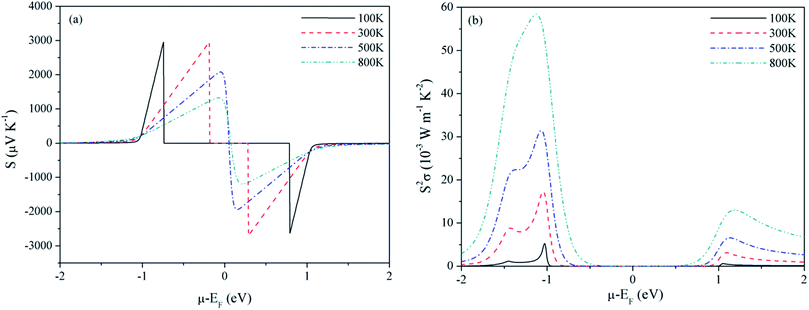 | ||
| Fig. 3 Variation of (a) Seebeck coefficient and (b) power factor of Mg2C with chemical potential at τ = 4 × 10−14 s. | ||
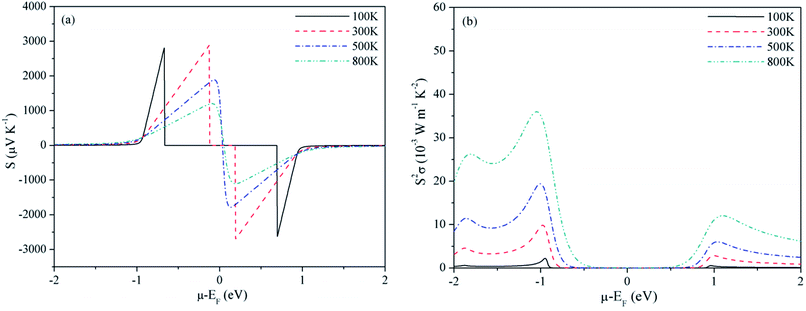 | ||
| Fig. 4 Variation of (a) Seebeck coefficient and (b) power factor of BeMgC with chemical potential at τ = 4 × 10−14 s. | ||
Effect of the electronic states exhibited through DOS can be clearly seen in the S2σ plotted in Fig. 2–4. Widths of the valence bands in the vicinity of Fermi level are 8.75, 4.844 and 6 eV respectively for the Be2C, Mg2C and BeMgC from the PBE calculations. Likewise width of the first conduction band is 4.36, 3.87 and 4.949 eV. The PF is more in Mg2C wherein bands are relatively flat that is normally found in compounds with prevalent ionic character. The Mulliken population analysis also pointed such ionic behaviour in Mg2C.20,35 Carriers in heavy band (flat band structure) have low velocity and large effective mass so Seebeck coefficient is somewhat higher in Mg2C. The overall effect is the maximum PF of Mg2C among the three carbides. The dependence of PF on μ is shown in Fig. 2(b)–4(b) reveal that PF depends strongly on the sign of chemical potential. The curves signify better performance of three carbides with p-type doping. The asymmetry with respect to sign is lowest in the Be2C and maximum in Mg2C. The asymmetry is sufficiently large in Mg2C and BeMgC to propose p-type majority carriers. So both Mg2C and the BeMgC could, in principle, make a good TE unlike Be2C.
In Fig. 5–7, we plot temperature and concentration dependence of S and PF. The optimum values of the S and PF are maximum for Mg2C followed by BeMgC and the Be2C. In the figures both coefficients increase with temperature. The value of S is comparable to the experimental values 147 μV K−1 in SrTiO3 which has band gap 3.25 eV.62 The difference in the relaxation time and band gap may cause the residual deviation.60,62
In the three cases the maximum PF is well around the experimentally realizable high doping (up to 1020 cm−3).4,7,54 The values of PF at three temperatures are listed in Table 1. We see that at a given temperature PF is maximum in Mg2C that increases with temperature. Though hole concentration corresponding to the maximum PF is higher in Mg2C (∼7 × 1020 cm−3) it is well within the achievable experimental limits. To predict the values of TE quantities, we need to consider the variation resulting from the relaxation time. We have taken τ = 4 × 10−14 s in all calculations reported above. However, in the case of Mg2C thermal conductivity ∼34 W mK−1 is reported at 300 K using plane wave pseudopotential (PP) method.43,44 The comparison with the optimum value obtained in the current calculations give τ = 4.4 × 10−15 s.43 It alters the relaxation time by a factor of ∼10−1. Therefore we calculated optimum values of PF and κe also at τ = 4.4 × 10−15 s, and give in Table 1. It furnishes the range of transport coefficients. Reviews on the basis of high-throughput calculations suggest that PF more than 3 × 10−3 W mK−2 at experimentally realizable doping are promising for the next generation thermoelectrics and less than 1 × 10−3 W mK−2 are of little use.4,7 In a few theoretical vis-a-vis experimental studies it is observed that calculations usually underestimate the PF.60,62 In view of these, we may infer that the values of PF will be more than those listed in Table 1. The predicted PF of Mg2C is better than the values suggested for TE materials on the basis of data mining techniques covering many thousand compounds.4,5,7,45 BeMgC may also be tried at higher temperatures once it is synthesized in the laboratory.
| Temp (K) | Transport coefficients | Be2C | BeMgC | Mg2C | |||
|---|---|---|---|---|---|---|---|
| 4 × 10−14 s | 4.4 × 10−15 s | 4 × 10−14 s | 4.4 × 10−15 s | 4 × 10−14 s | 4.4 × 10−15 s | ||
| 300 | PF(10−3 W mK−2) | 6.78 | 0.75 | 9.88 | 1.09 | 17.10 | 1.93 |
| κe (W mK−1) | 628 | 68 | 334 | 38.4 | 244 | 27.00 | |
| σ (106 S m−1) | 86.7 | 9.5 | 47 | 5.2 | 33 | 3.7 | |
| 500 | PF(10−3 W mK−2) | 13.93 | 1.52 | 19.40 | 2.13 | 31.00 | 3.43 |
| κe (W mK−1) | 1043 | 116 | 578.9 | 63.94 | 409 | 45.00 | |
| 800 | PF(10−3 W mK−2) | 26.33 | 2.88 | 35.94 | 3.96 | 58.20 | 6.47 |
| κe (W mK−1) | 1678 | 186 | 922.2 | 101.18 | 655 | 71 | |
In Table 1, optimum values of the electrical and thermal conductivity of the three carbides are also listed. At the three temperatures σ is almost same for the three carbides. It is maximum for Be2C and ∼2.6 times the conductivity of Mg2C. Note that these optimum values occur at different levels of carrier concentration. The electronic thermal conductivity also follow nearly the similar trend. In the three compounds κe is negligibly small below 1021 cm−3 and rises thereafter. Therefore the reported values are found at ∼1023 cm−3. In case of BeMgC both coefficients are in between the Be2C and Mg2C.
In a recent work on a quaternary mixed compound, the figure of merit (zT) is interpreted in terms of generalized material parameter which connects the thermal conductivity, band gap and the newly defined weighted mobility.6 It is proposed that for a good thermoelectric the weighted mobility and the band gap should be high and the zT is proportional to the band gap. It is also mentioned that the materials with wide band gap have modest theoretical PF.6 Though the carbides containing magnesium have band gap ∼ 2 eV, the PF is good as discussed before. It may be a consequence of the larger effective mass resulting from the non parabolic bands in eqn (1) which facilitate enhanced thermoelectric performance.63 To examine it further, measurement of transport coefficients shall be fruitful.
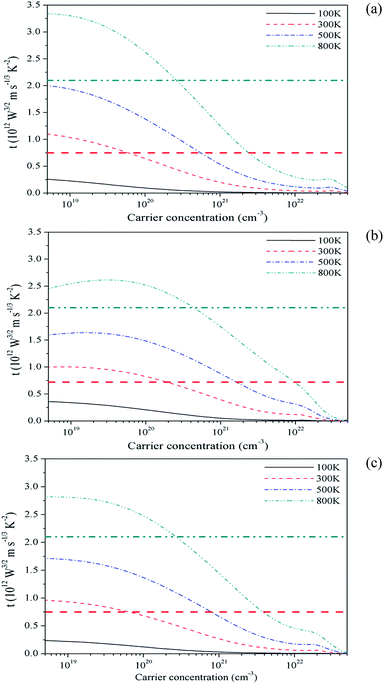
As discussed earlier, the transport function EFF i.e. t measures the extent to which a complex band structure decouples σ and S. It is proposed to find and screen materials that overcome reciprocal behaviour of σ and S in achieving a good thermoelectric behaviour. In order to compare the performance of the three carbides with the promising TE materials we have calculated the EFF i.e. t-function introduced recently.45 The EFF for three crystals are plotted in Fig. 8. The function gradually decreases and becomes negligible beyond 1022 cm−3. At higher temperature the EFF is more. According to the screening criteria, the p-type materials having EFF more than that of FeNbSb (0.75 × 1012 W5/2 ms−1/3 K−2 at 300 K and 2.10 × 1012 W5/2 ms−1/3 K−2 at 800 K, shown by horizontal lines in Fig. 8) are useful in TE applications.45 The optimum value of PF for this reference compound lies in the 4.3 to 5.5 × 10−3 W mK−2 range at 800 K. The Mg2C has the PF in this range and the EFF is more than FeNbSb up to a certain carrier concentration. Thus Mg2C fits into this criterion. Moreover, it turns out to be a better TE compared to the similar p-type compound Mg2Ge (t = 0.85). The Mg2Si (t = 1.18) is albeit better than the Mg2C.45 The EFF of Be2C also satisfies the screening criterion but the PF is somewhat lower and other type of carriers will also have some contribution which does not help to make it a good thermoelectric.
3.3 Vibrational frequencies and LO–TO splitting
The IR and Raman frequencies are calculated at the zone centre i.e. at Γ-point of the BZ. The classified active modes and corresponding frequencies are listed in Table 2. For the antifluorite crystals the group theory suggests either g or u type modes. The Be2C and Mg2C contain six optical modes at the Γ point. The irreducible presentation for the two crystals is:| Γ = 3F2g ⊕ 6F1u. | (7) |
| Be2C | Mg2C | BeMgC | ||||||
|---|---|---|---|---|---|---|---|---|
| This work | Others work | |||||||
| PPa | PAWb | PPc | ||||||
| a Calibrated from the graphical data of ref. 28.b Ref. 43.c Ref. 64. | ||||||||
| TO | IR | F1u | 632.52 | 421.78 (394.21) | 437.79 | 406.26 | 428 | 519.83 |
| Raman | F2g | 722.41 | 389.18 (374.12) | 387.76 | — | 387 | 565.59 | |
| LO | F1u | 965.85 | 635.99 (613.41) | — | 559.44 | 588 | 754.57 | |
| 547.91 | ||||||||
| LO-TO | F1u | 333.33 | 214.21 (219.20) | — | 153.18 | 160 | 234.74 | |
| −17.68 | ||||||||
The g and u indicate symmetric and anti symmetric normal modes. F1u arises from the Cation–C(apical) whereas F1g arises from the C(central)–C(apical) vibrations. In Be2C, excluding the three translational acoustic modes belonging to the F1u representation, there are 3 Raman active (3F2g) and 3 IR active (3F1u) optic modes. The Raman active modes vibrate at 722.41 cm−1 and IR active modes at 632.48 cm−1. In the long wavelength limit, optical phonons couple to the macroscopic electric fields in ionic crystals. It manifests in the difference in the frequency of LO and TO at the Γ-point and shows the LO–TO split. In Be2C, the LO, TO modes do not overlap and the anti-symmetric IR optical mode exhibits an LO–TO split of 333.34 cm−1.
In Mg2C, the three Raman active modes vibrate at 389.18 cm−1 while IR active modes vibrate at 421.78 cm−1. These are in very good agreement with 387.76 cm−1, 437.79 cm−1 reported by PP method28 and 387 cm−1, 428 cm−1 reported by Quantum Espresso using norm-conserving PP method.64 Calculations using LDA in the PAW method found these modes at 406.26 and 559.44 cm−1.43 So each calculation, except the one using PAW, gives nearly similar frequencies. It is observed that Mg2C is synthesized at 15 GPa and fully recoverable under ambient conditions. In view of this it is remarkable to see absence of negative zone centre frequencies in Mg2C calculations. The BeMgC mixed crystal shows the Γ = 9F irreducible representation with reduced symmetry and 9 modes. The first three IR and Raman active acoustic modes have zero frequencies. There are two sets of optic modes. In each set, the three TO modes have 519.83 cm−1 and 565.59 cm−1 frequencies. Both these sets are IR and Raman active and show mixing of the TO and LO modes. Although absence of imaginary frequencies alone does not ascertain stability of crystals, the non-appearance in BeMgC increases the chances of BeMgC synthesis in laboratory.
The vibrational frequencies and the active modes change with atoms and symmetry. The optical modes are sensitive to the inter-cellular interaction and therefore generalized trend (ωL)2 ![[right double angle bracket]](https://www.rsc.org/images/entities/char_27eb.gif) (ωT),2 is usually seen in the vibration spectra of the three materials. Unlike pure methanides, BeMgC shows mixing of the LO–TO modes. The replacement of Be by Mg reduces symmetry and the interaction between Be–Mg cations leads to the lowering of the LO frequency by 17.7 cm−1 from the TO mode of 565.59 cm−1 frequency. In fact, one of active Raman mode arises from the vibration of cations. The Be–Be bond length (dBe–Be ≅ a/2) and mass is lower than the Mg–Mg so the frequency is larger in Be2C. In BeMgC, both inter-cellular environment and appearance of Be–Mg bonds alter the frequencies of vibration. Further, electro-negativity of Be and Mg leads to asymmetry in polarization which causes mixing of the LO, TO modes in BeMgC.
(ωT),2 is usually seen in the vibration spectra of the three materials. Unlike pure methanides, BeMgC shows mixing of the LO–TO modes. The replacement of Be by Mg reduces symmetry and the interaction between Be–Mg cations leads to the lowering of the LO frequency by 17.7 cm−1 from the TO mode of 565.59 cm−1 frequency. In fact, one of active Raman mode arises from the vibration of cations. The Be–Be bond length (dBe–Be ≅ a/2) and mass is lower than the Mg–Mg so the frequency is larger in Be2C. In BeMgC, both inter-cellular environment and appearance of Be–Mg bonds alter the frequencies of vibration. Further, electro-negativity of Be and Mg leads to asymmetry in polarization which causes mixing of the LO, TO modes in BeMgC.
3.4 Born effective charges and dielectric properties
Now we present the calculated BEC, high frequency (ε∞) and the static dielectric tensors (ε0). BEC is the derivative of polarization with respect to atomic position at zero macroscopic electric field. Hence this and related quantities exhibit dynamical properties of crystals and categorized mathematically as tensor. The BEC captures change in polarization with respect to atomic displacement. The three crystals show isotropic behaviour and the values are given in Table 3. Calculated BEC on two cations and carbon is about 20% lower than the formal charge (+2|e|;−4|e|) in the two methanides. In BeMgC, the dynamical charges on the three atoms are less in comparison to the formal charge. We found the maximum reduction (∼30%) on the beryllium. Further, we note that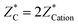 and the sum rule
and the sum rule 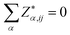 is very well followed. The BEC, dielectric constants and susceptibility reveal that the tendency of polarization under electric field is more in Be2C and less in the Mg2C. It leads to a larger contribution of vibrational part (Column-VII) in the ε0 (Column-V). The total contribution (ε0) decreases in the Be2C > BeMgC > Mg2C order. The available values of Mg2C taking LDA in the PP method64 are also given in Table 3. We note that our results well reconcile. A difference of ∼39% in the ε∞ is found. To check if this is due to the lattice constant, we calculated the dynamical tensors at the experimental lattice constant of Mg2C. These numbers, within parenthesis, are given in a row of Table 3. Only a marginal reduction in difference (∼38.5%) is observed. To check if this is due to the band gap we also calculated the dielectric constants and the refractive index using the empirical relations among band gap, high frequency dielectric constants and the refractive index proposed by Moss.65 The deviations in the dielectric constant and refractive index (n) from Moss formulation are about 13% and 7%. In case of the PP results deviation rises to 20% and 29%.
is very well followed. The BEC, dielectric constants and susceptibility reveal that the tendency of polarization under electric field is more in Be2C and less in the Mg2C. It leads to a larger contribution of vibrational part (Column-VII) in the ε0 (Column-V). The total contribution (ε0) decreases in the Be2C > BeMgC > Mg2C order. The available values of Mg2C taking LDA in the PP method64 are also given in Table 3. We note that our results well reconcile. A difference of ∼39% in the ε∞ is found. To check if this is due to the lattice constant, we calculated the dynamical tensors at the experimental lattice constant of Mg2C. These numbers, within parenthesis, are given in a row of Table 3. Only a marginal reduction in difference (∼38.5%) is observed. To check if this is due to the band gap we also calculated the dielectric constants and the refractive index using the empirical relations among band gap, high frequency dielectric constants and the refractive index proposed by Moss.65 The deviations in the dielectric constant and refractive index (n) from Moss formulation are about 13% and 7%. In case of the PP results deviation rises to 20% and 29%.
 , high frequency (ε∞) and static (ε0) dielectric constants together with the contribution of the vibrational part (εω). The refractive index and susceptibility are also given. The values given in parenthesis for Mg2C are calculated at the experimental lattice constant
, high frequency (ε∞) and static (ε0) dielectric constants together with the contribution of the vibrational part (εω). The refractive index and susceptibility are also given. The values given in parenthesis for Mg2C are calculated at the experimental lattice constant
| Dynamical charge (electrons) | Isotropic dielectric tensor | χ | n | |||||
|---|---|---|---|---|---|---|---|---|
| ε0 | ε∞ | εω | ||||||
| a Ref. 64.b Ref. 65. | ||||||||
| Be2C | This work | Be | 1.605 | 15.124 | 6.486 | 8.638 | 5.4856 | 2.547 |
| C | −3.210 | |||||||
| Mossb | — | — | 5.723 | — | — | 2.392 | ||
| Mg2C | This work | Mg | 1.588 (1.599) | 13.280 (14.211) | 5.839 (5.869) | 7.441 (8.342) | 4.839 (4.869) | 2.416 (2.423) |
| C | −3.175 (−3.197) | |||||||
| PPa | Mg | 1.57 | 15.4 | 8.15 | 7.25 | — | — | |
| C | −3.14 | |||||||
| Mossb | — | — | 6.807 | — | — | 2.609 | ||
| BeMgC | This work | Be | 1.409 | 12.278 | 6.209 | 6.069 | 5.209 | 2.492 |
| Mg | 1.569 | |||||||
| C | −2.978 | |||||||
| Mossb | — | — | 7.147 | — | — | 2.673 | ||
The Born effective charges and the LO–TO splitting are closely related. The more is the BEC the more is the LO–TO split. In Table 3, the isotropic BEC are listed. The non-zero value in each case signifies the LO–TO splitting. We note that the BEC is maximum on the constituent atoms in Be2C and the LO–TO split 333.34 cm−1 is the largest. This and the acquiescence of the BEC sum rule exhibited by the three carbides ensure reliability of our calculations. In Mg2C, the anti-symmetric mode shows LO–TO splitting of 214.28 cm−1. This is more than the 153 cm−1 obtained from the PAW method using LDA43 and 160 cm−1 obtained from the LDA-PP method.64 It may be noticed that absolute TO frequencies from LDA-PP method are in very good agreement while LO frequencies differ by 48 cm−1 leading to a less LO–TO split. The effect of LDA and GGA reflects in the lattice constant, volume and bulk modulus determination. Due to the over-binding tendency, the LDA underestimates the lattice constant, volume and overestimates the bulk modulus. This is one of the reason for the differences with the LDA-PP results. So, at the first place, we can see the effect of volume by computing the LO–TO split and the BEC in Mg2C at the experimental lattice constant. The LO–TO split and the dielectric constants are given in Tables 2 and 3 respectively. A difference of 5 cm−1 is found which is negligible in view of the fact that numerical inaccuracy in current calculations is 2 cm−1.57 The values of BEC, listed in Table 3, at experimental lattice constant are close to those at the equilibrium lattice constant. Thus role of LDA or GGA appearing in terms of volume estimation is not the only reason for the residual discrepancy. The Raman and the IR spectroscopic measurements are required for a fair comparison.
4. Conclusions
The Seebeck coefficient, power factor and thermal conductivity are calculated for the antifluorite crystals of Be2C, Mg2C and BeMgC using the first-principles calculations. Modelling of TE properties predict PF of Mg2C in the 5.17–58.20 × 10−3 W mK−2 range within 100 to 800 K. The better performance can be achieved at ∼2 × 1021 cm−3 p-type doping level. The PF is well above the 3 × 10−3 W mK−2 required at experimentally realizable doping level for the next generation thermoelectrics. The hypothetical BeMgC mixed compound also exhibits such properties above 300 K. The value of EFF for Mg2C is well above the threshold on the scale of a good thermoelectric. Moreover, major contribution of p-type carriers is observed in the energy transport. So Mg2C is a good candidate for the thermoelectric measurements and usage. It is found above Mg2Ge and below Mg2Si on the EFF scale. The BeMgC may probably be a good thermoelectric unlike Be2C. For a rigorous analysis measurements of transport coefficients shall be fruitful. Nevertheless, the current study demonstrates that the interface used in this study can be well applied to explore TE properties of other materials using the periodic LCAO method.For the three methanides, the zone centre vibration frequencies are in very good agreement with other calculations. The BEC, static as well as high frequency dielectric tensors, susceptibility and refractive index are isotropic in nature for the three crystals. A consistent trend and a good accord with available results is observed. Calculated BEC charges and susceptibility show that Be2C has the maximum tendency of polarization and hence exhibits largest LO–TO splitting. The band gap measurement and spectroscopic investigations of the vibrational properties of the methanides shall be helpful to examine our findings rigorously.
Conflicts of interest
Authors declare no conflicts of interest.Acknowledgements
VM is thankful to the UGC, New Delhi for the BSR fellowship. Partial support is also received from the grants of RUSA-Phase I. Authors gratefully acknowledge the assistance provided by S. Lemal and P. Ghosez, Université de Liège, Belgium at various stages of the thermoelectric calculations.References
- J. M. Skelton, L. A. Burton, A. J. Jackson, F. Oba, S. C. Parker and A. Walsh, Phys. Chem. Chem. Phys., 2017, 19, 12452 RSC.
- A. J. Hong, L. Li, R. He, J. J. Gong, Z. B. Yan, K. F. Wang, J.- M Liu and Z. F. Ren, Sci. Rep., 2016, 6, 22778 CrossRef CAS PubMed.
- T. D. Sparks, M. W. Gaultois, A. Oliynyk, J. Brgoch and B. Meredig, Scr. Mater., 2016, 111, 10 CrossRef CAS.
- W. Chen, et al., J. Mater. Chem. C, 2016, 4, 4414 RSC.
- C. G. Fu, T. J. Zhu, Y. T. Liu, H. H. Xie and X. B. Zhao, Energy Environ. Sci., 2015, 8, 216 RSC.
- W. Liu, J. Zhou, Q. Jie, Y. Li, H. S. Kim, J. Bao, G. Chen and Z. Ren, Energy Environ. Sci., 2016, 9, 530 RSC.
- A. Zevalkink, et al., Appl. Phys. Rev., 2018, 5, 021303 Search PubMed.
- J. Yang and T. Caillat, MRS Bull., 2006, 31, 224 CrossRef CAS.
- J.-P. Fleurial, M. A. Ryan, A. Borshchevsky, W. Phillips, E. A. Kolawa, G. J. Snyder, T. Caillat, T. Kascich and P. Mueller, US Pat. number 6787691, 2004.
- W. Setyawen and S. Curtarolo, Comput. Mater. Sci., 2010, 49, 299 CrossRef.
- D. S. Sholl and J. A. Steckel, Density Functional Theory, John Wiley & Sons, Hoboken, New Jersey, 2009 Search PubMed.
- S. Bhattacharya and G. K. H. Madsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 85205 CrossRef.
- K. P. Ong, D. J. Singh and P. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115110 CrossRef.
- J. Neugebauer and H. Tilmann, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 438 CAS.
- V. Maurya and K. B. Joshi, J. Alloys Compd., 2019, 779, 971 CrossRef CAS.
- R. A. Evarestov, Quantum Chemistry of Solids: The LCAO First Principles Treatment of Crystals, Springer-Verlag, Berlin, vol. 153, 2007 Search PubMed.
- R. Dovesi, et al., Int. J. Quantum Chem., 2014, 114, 1287 CrossRef CAS.
- G. K. H. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140 CrossRef CAS.
- K. B. Joshi, U. Paliwal and B. K. Sharma, Phys. Status Solidi B, 2011, 248, 1248 CrossRef CAS.
- F. Fuchs, J. Furthmuller and F. Bechsted, Phys. Status Solidi B, 2009, 246, 1877 CrossRef.
- A. D. Becke, J. Chem. Phys., 2014, 140, 18A301 CrossRef PubMed.
- F. Fuchs, J. Furthmüller, F. Bechstedt, M. Shishkin and G. Kresse, Phys. Rev. B, 2007, 76, 115109 CrossRef.
- B. Chen, J.-H. Xu, C. Uher, D. T. Morelli, G. P. Meisner, J.-P. Fleurial, T. Caillat and A. Borshchevsky, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 1476 CrossRef CAS.
- J. Martin, G. S. Nolas, H. Wang and J. Yang, J. Appl. Phys., 2007, 102, 103719 CrossRef.
- M. W. Gaultois, T. D. Sparks, C. K. H. Borg, R. Seshadri, W. D. Bonificio and D. R. Clarke, Chem. Mater., 2013, 25, 2911 CrossRef CAS.
- U. Ruschewitz, Coord. Chem. Rev., 2003, 244, 115 CrossRef CAS.
- R. O. G. Blachnik, P. Gross and C. Hyaman, Trans. Faraday Soc., 1970, 66, 1058 RSC.
- O. O. Kurakevych, Y. Le Godec, T. A. Strobel and D. Y. Kim, J. Mater. Chem. C, 2014, 118, 8128 CAS.
- O. O. Kurakevych, T. A. Strobel, D. Y. Kim and G. D. Cody, Angew. Chem., 2013, 52, 8930 CrossRef CAS PubMed.
- L. H. Rovner and G. R. Hopkins, Nucl. Technol., 1976, 29, 274 CrossRef CAS.
- H. Migge, J. Nucl. Mater., 1981, 103, 687 CrossRef CAS.
- W.-S. Shish, R. B. Stephens and W. J. James, Fusion Sci. Technol., 2000, 37, 24 CrossRef.
- H. Kleykamp, J. Nucl. Mater., 2001, 294, 88 CrossRef CAS.
- A. Anghel, C. Porosnicu, C. P. Lungu, K. Sugiyama, C. Kriger and J. Roth, J. Nucl. Mater., 2011, 416, 9 CrossRef CAS.
- M. M. Disko, J. C. H. Spence, O. F. Sankey and D. Saldin, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 5642 CrossRef CAS.
- J. L. Corkill and M. L. Cohen, Phys. Rev. B, 1993, 48, 17138 CrossRef CAS.
- C. H. Lee, W. R. L. Lambrecht and B. Segall, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 10392 CrossRef CAS.
- C.-T. Tzeng, K.-D. Tsuei and W.-S. Lo, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 6837 CrossRef CAS.
- F. Kalarasse and B. Bennecer, J. Phys. Chem. Solids, 2008, 69, 1775 CrossRef CAS.
- S. Laref and A. Laref, Comput. Mater. Sci., 2008, 44, 664 CrossRef CAS.
- K. B. Joshi, D. K. Trivedi, U. Paliwal and K. L. Galav, Mater. Res. Express, 2016, 3, 55601 CrossRef.
- U. Paliwal, D. K. Trivedi, K. L. Galav and K. B. Joshi, AIP Conf. Proc., 2013, 1536, 395 CrossRef CAS.
- A. Chernatynskiy and S. R. Phillpot, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 64303 CrossRef.
- K. Kaur and R. Kumar, Chin. Phys. B, 2016, 25, 26402 CrossRef.
- G. Xing, J. Sun, Y. Li, X. Fan, W. Zheng and D. J. Singh, Phys. Rev. Mater., 2017, 1, 65405 CrossRef.
- J. M. Skelton, S. C. Parker, A. Togo, I. Tanaka and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205203 CrossRef.
- L. Valenzano, F. J. Torres, K. Doll, F. Pascale, C. M. Zicovich-Wilson and R. Dovesi, Z. Phys. Chem., 2006, 220, 893 CrossRef CAS.
- U. Paliwal, G. Sharma and K. B. Joshi, J. Mat. Sci., 2019, 54, 1382 CrossRef CAS.
- F. Pascle, C. M. Zicovich-Wilson, G. Lopez, B. Civalleri, R. Orlando and R. Dovesi, J. Comp. Chem., 2004, 25, 888 CrossRef PubMed.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalerri, K. Doll, N. M. Harrison, I. J. Bush, Ph. D'Arco and M. Llunell, CRYSTAL14 User's Manual, Turin:University of Torino, 2014 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048 CrossRef CAS.
- K. Seeger, Semiconductor Physics, Springer-Verlag, Heidelberg, 2004 Search PubMed.
- Y. Pei, H. Wang and G. J. Snyder, Adv. Mater., 2012, 24, 6125 CrossRef CAS PubMed.
- K. Doll, N. M. Harrison and V. C. Saunders, Int. J. Quantum Chem., 2001, 82, 1 CrossRef CAS.
- K. Doll, Comput. Phys. Commun., 2001, 137, 74 CrossRef CAS.
- C. M. Zicovich-Wilson, F. Pascale, E. Roetti, V. R. Saunders, R. Orlando and R. Dovesi, J. Comp. Chem., 2004, 25, 1874 CrossRef PubMed.
- C. M. Zicovich-Wilson, A. Bert, C. Roetti, R. Dovesi and V. R. Saunders, J. Chem. Phys., 2002, 116, 1120 CrossRef CAS.
- D. M. Rowe and C. M. Bhandari, Modern Thermoelectrics, Reston Publishing Company, Reston Virginia, 1983 Search PubMed.
- N. Miao, B. Xu, N. C. Bristowe, D. I. Bilc, M. J. Verstraete and P. Ghosez, J. Phys. Chem. C, 2016, 120, 9112 CrossRef CAS.
- S. T. Oyama and R. Kieffer, Carbides, Kirk-Othmer Encycl. Chem. Technol., 2000, 4, 647 Search PubMed.
- D. I. Bilc, C. G. Floare, L. P. Zarbo, S. Garabagiu, S. Lemal and P. Ghosez, J. Phys. Chem. C, 2016, 120, 25678 CrossRef CAS.
- H. Shi, D. Parker, M.-H. Du and D. J. Singh, Phys. Rev. Appl., 2015, 014004 CrossRef.
- T. Li, W. Ju, H. Liu, H. Cui, X. Zhao, Y. Yong and Z. Feng, Comput. Mater. Sci., 2014, 93, 234 CrossRef CAS.
- T. S. Moss, Proc. Phys. Soc., London, Sect. B, 1950, 63, 167 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |