Open Access Article
Open Access ArticleImportance of protein flexibility in ranking ERK2 Type I1/2 inhibitor affinities: a computational study†
Yuzhen Niu *a,
Xiaojun Yaob and
Hongfang Ji*a
*a,
Xiaojun Yaob and
Hongfang Ji*a
aShandong Provincial Research Center for Bioinformatic Engineering and Technique, College of Life Sciences, Shandong University of Technology, Zibo 255049, China. E-mail: niuyzh12@lzu.edu.cn; jhf@sdut.edu.cn
bState Key Laboratory of Applied Organic Chemistry, Department of Chemistry, Lanzhou University, Lanzhou 730000, China
First published on 23rd April 2019
Abstract
Extracellular-regulated kinase (ERK2) has been regarded as an essential target for various cancers, especially melanoma. Recently, pyrrolidine piperidine derivatives were reported as Type I1/2 inhibitors of ERK2, which occupy both the ATP binding pocket and the allosteric pocket. Due to the dynamic behavior of ERK2 upon the binding of Type I1/2 inhibitors, it is difficult to predict the binding structures and relative binding potencies of these inhibitors with ERK2 accurately. In this work, the binding mechanism of pyrrolidine piperidines was discussed by using different simulation techniques, including molecular docking, ensemble docking based on multiple receptor conformation, molecular dynamics simulations and free energy calculations. Our computational results show that the traditional docking method cannot predict the relative binding ability of the studied inhibitors with high accuracy, but incorporating ERK2 protein flexibility into docking is an effective method to improve the prediction accuracy. It is worth noting that the binding free energies predicted by MM/GBSA or MM/PBSA based on the MD simulations for the docked poses have the highest correlation with the experimental data, which highlights the importance of protein flexibility for accurately predicting the binding ability of Type I1/2 inhibitors of ERK2. In addition, the comprehensive analysis of several representative inhibitors indicates that hydrogen bonds and hydrophobic interactions are of significance for improving the binding affinities of the inhibitors. We hope this work will provide valuable information for further design of novel and efficient Type I1/2 ERK2 inhibitors.
1. Introduction
The Ras/MAPK (RAF/MEK/ERK) signaling transduction is a key pathway of cellular proliferation, differentiation and survival downstream of RAS activation.1–3 Not surprisingly, this pathway is frequently deregulated in human cancers, such as melanoma.4,5 The extracellular-regulated kinases (ERK1 and ERK2) are central in the pathway downstream of Ras, Raf, and MEK kinases, while ERK1 and ERK2 show 89% sequence identity within the kinase domains. Activation/phosphorylation of ERK promotes tumor growth, cell cycle progression and survival through transcriptional activation, for example, ERK1/2 was found constitutively activated in 60% of melanoma cells.6 Therefore, the ERK1/2 kinase is the central node of the RAS/MAPK pathway. The greatest advantage of targeting ERK1/2 is that no mutations have been found in ERK1/2.7,8Despite ERK1/2 inhibitors playing an important role in the MAPK pathway, few ERK1/2 inhibitors have been reported in the literature, and no known ERK1/2 inhibitor has entered advanced clinical trials.9–11 So, development of potential ERK1/2 inhibitors is extremely urgent. The majority of reported ERK1/2 inhibitors are ATP competitive inhibitors, which belong to Type I kinase inhibitors, such as VTX-11e,10 FR180204 (ref. 12) and GDC-0994.13 Apirat et al. reported that inhibitor SCH772984 simultaneously binds to the ATP binding pocket and the allosteric pocket. The allosteric pocket is adjacent to the ATP binding pocket, which located between P-loop and αC helix. As a Type I1/2 kinase inhibitor, SCH772984 is a promising inhibitor targeting ERK1/2 with high bioactivity, and we have previously studied the interaction mechanisms of SCH772984 with ERK2.14 Afterwards, Deng and coworkers discovered compound 1 as an effective selective ERK2 inhibitor through the automated ligand identification system (ALIS),15 and meanwhile they obtained the crystal structure of human ERK2 bound compound 1 (PDB ID: 4QYY16). As shown in Fig. 1, the binding mode of compound 1 to ERK2 is similar with that of SCH772984 to ERK2. In detail, ERK2 adapts a “DFG in” mode, and compound 1 forms hydrogen-bonding interaction with the residues Lys52, Gln103, Asp104 and Met106. Chlorophenyl forms hydrophobic interaction with the hinge region and catalytic loop region of ERK2. Besides, the acetyl phenyl interacts “face to face” with the Tyr62 side chain through an aromatic π–π interaction, which may be critical to improve the potencies of ERK2 Type I1/2 inhibitors.
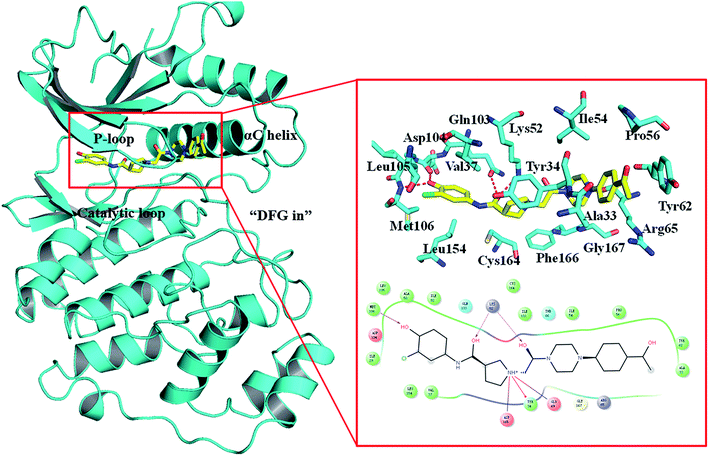 | ||
| Fig. 1 Binding mode of ERK2 with compound 1. The key residues in the binding pocket of ERK2 and the interactions between compound 1 and ERK2 are highlighted. | ||
Based on the structures of the compounds already reported, investigating the interaction mechanisms of these compounds with ERK2 is of great significance for discovering efficient and potential ERK2 inhibitors. Therefore, in this study, a combined computational modeling strategy, based on molecular docking, molecular dynamics (MD) simulations, free energy calculations and free energy decomposition analysis, was employed to understand the interaction between ERK2 and Type I1/2 inhibitors and identify several key structures that are important to the efficiency of inhibitors.
The use of rigid protein structures may hinder the correct prediction of ligand binding posture and relative binding capacity due to the dynamic behavior of kinase in binding of Type I1/2 inhibitors.17–19 Herein, various molecular modeling techniques were used to handle the flexibility of ERK2, including ensemble docking and MD simulations and induced-fit docking (IFD), IFD simulates the induced fit by refining the side chain conformation of important residues located in active site. Ensemble docking is based on the use of multiple receptor conformation (MRC) in molecular docking to combine protein flexibility.20,21 In this study, MD simulations and structural generate an ensemble of MRC for ERK2, and then was utilized for ERK2 docking with Type I1/2 inhibitors. The complex structure of ERK2 with Type I1/2 inhibitors after docking were carried out MD simulations to get the stable conformations. Then both Molecular Mechanics/Poisson–Boltzmann Surface Area (MM/PBSA) and Molecular Mechanics/Generalized Born Surface Area (MM/GBSA) technologies were employed to predict the binding potencies of these 27 inhibitors with ERK2. We expect that the detailed analysis of the structural and energetic binding mode of ERK2 and Type I1/2 inhibitors will provide valuable information for designing novel, effective and selective inhibitors with controllable activity.
2. Materials and methods
2.1 Preparing systems
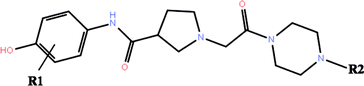
The co-crystallized structures of two known inhibitors bound with ERK2 were retrieved from the RCSB Protein Data Bank (PDB ID codes: 4QTA22 and 4QYY16). The missing residues were added using the Prime module in Schrodinger 2009.23 After that the two structures were prepared by the Protein Preparation Wizard in Schrodinger 2009, including adding assigning protonation states, side chains of residues and hydrogen atoms, and relaxing the amino residue side chains of the proteins.The 3D structures of all the 27 inhibitors16,24 were sketched by Maestro and preprocessed by LigPrep, which generated the low energy 3D conformers for each compound with the OPLS-2005 force field. The ionized state was assigned by using Epik at a target pH value of 7.0 ± 2.0. Default settings were used for the other parameters. The 2D structures of all the 27 compounds and their biological activities against ERK2 are summarized in Table 1.
| No. | R1 | R2 | IC50a (μM) | pIC50 | RRD | IFD | QPLD |
|---|---|---|---|---|---|---|---|
| a Refer to the ref. 16 and 24. | |||||||
| 1 | 3-Cl |  |
2.6 | 5.58 | −13.84 | −14.20 | −14.11 |
| 1a | 3-Cl | 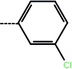 |
2.1 | 5.68 | −13.50 | −14.09 | −13.28 |
| 1b | 3-Cl |  |
8.2 | 5.09 | −12.97 | −12.50 | −13.51 |
| 2 | 3-Cl | 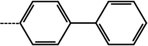 |
4.4 | 5.36 | −11.71 | −13.37 | −17.01 |
| 2a | 3-Cl | 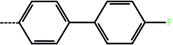 |
100 | 4.00 | −8.77 | −9.59 | −14.78 |
| 2b | 3-Cl | 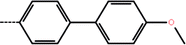 |
50 | 4.30 | −11.83 | −11.98 | −11.83 |
| 3 | 3-Cl |  |
20 | 4.70 | −11.30 | −13.74 | −16.87 |
| 3a | 3-Cl |  |
5.5 | 5.26 | −11.51 | −10.52 | −14.75 |
| 3b | 3-Cl |  |
20 | 4.70 | −11.53 | −13.80 | −17.27 |
| 3c | 3-Cl |  |
12 | 4.92 | −10.74 | −11.34 | −14.66 |
| 3d | 3-Cl | 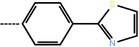 |
9.34 | 5.03 | −12.88 | −9.33 | −14.52 |
| 4 | 3-Cl | 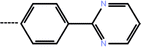 |
0.41 | 6.39 | −13.72 | −12.04 | −14.58 |
| 4a | 3-Cl | 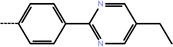 |
0.10 | 7.00 | −13.41 | −14.08 | −16.45 |
| 4b | 3-Cl |  |
1.76 | 5.75 | −8.28 | −9.20 | −16.22 |
| 5 | 3-Cl | 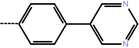 |
1.8 | 5.74 | −12.34 | −10.10 | −14.84 |
| 5a | 3-Cl | 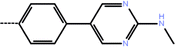 |
2.67 | 5.57 | −7.68 | −11.97 | −16.51 |
| 6 | 3-Cl | 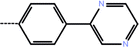 |
0.13 | 6.89 | −12.90 | −14.39 | −14.65 |
| 7 | 3-CF3 | 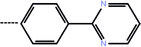 |
0.10 | 7.00 | −14.15 | −14.36 | −14.95 |
| 7a | 3-Cyclopropyl | 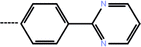 |
1.76 | 5.75 | −14.44 | −14.59 | −15.88 |
| 7b | 3-Isopropyl | 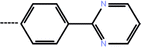 |
1.80 | 5.74 | −13.95 | −14.28 | −15.76 |
| 7c | 3-(4-Fluoro phenyl) | 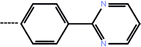 |
2.67 | 5.57 | −7.44 | −12.78 | −17.33 |
| 8 | 3-Cl | 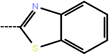 |
1.6 | 5.80 | −12.18 | −12.63 | −13.03 |
| 9 | H | 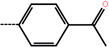 |
18.6 | 4.73 | −13.17 | −10.74 | −13.14 |
| 9a | 2-Cl |  |
50 | 4.30 | −13.32 | −12.68 | −13.66 |
| 9b | 3-Br |  |
3.6 | 5.44 | −13.89 | −14.96 | −14.03 |
| 9c | 3-F |  |
11.8 | 4.93 | −13.74 | −12.91 | −14.25 |
| 9d | 3-Methyl | 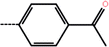 |
2.5 | 5.60 | −13.70 | −13.53 | −14.00 |
2.2 Generation of multiple representative ERK2 protein conformations
Based on the two resolved crystal structures (PDB codes: 4QTA and 4QYY), the representative ERK2 conformations for ensemble docking were generated by molecular dynamics (MD) simulations. The partial charges of the two inhibitors in 4QTA and 4QYY were fitted using the RESP methodology based on the electrostatic potentials computed at the HF/6-31G(d) level of theory.25–27 The AMBER99SB28 and GAFF force fields were used for the proteins and inhibitors, respectively.29 Then, Na+ ions were added to neutralize the net charge of the two complexes, and last the two systems were solvated into a 10 Å cubic TIP3P water30 box.All of the MD simulations were performed with the NAMD 2.9 simulation package.31 The specific parameter settings refer to our previous work.32 Particle Mesh Ewald (PME) algorithm33 was employed to treat long-range electrostatic interactions, while the cutoff for the short-range non-bonded interactions were set to 10 Å. All bonds involving hydrogen atoms were restrained using the SHAKE34 algorithm, and the time step was set to 2 fs. During the sampling process, the coordinates of each complex were saved every 1 ps.
For each complex structure, 200 conformations were evenly extracted from the final stable 10 ns MD trajectories, and then clustered into 10 categories using the k-means clustering method based on the RMSDs within 5 Å in the ligand binding pocket in the extracted MD conformations. At last, 10 representative structures chosen from 10 clusters were generated.
2.3 Docking protocols
According to the two crystal structures 4QTA and 4QYY, the studied 27 inhibitors were docked into the binding pocket of ERK2 using Glide in Schrodinger 9.0. For each system, the binding site was defined based on the known ligand (SCH772984 in 4QTA and compound 1 in 4QYY), and the receptor grid box for docking was set to 25 Å × 25 Å × 25 Å using the Receptor Grid Generation protocol of Schrodinger 9.0. Default settings were used for the other parameters.2.4 Molecular dynamics (MD) simulations
The 27 ERK2-inhibitor complexes obtained by RRD based on the crystal structure of 4QYY were submitted to 5 ns NPT MD simulations (T = 300 K and P = 1 atm). For the details parameters setting of the MD simulations, please see the previous section ‘‘Generation of multiple representative ERK2 protein conformations’’. The trajectory for each system was saved every 1 ps for the sampling process.2.5 MM/PB(GB)SA binding free energy calculations and residue decomposition
The Molecular Mechanics/Poisson–Boltzmann Surface Area (MM/PBSA) and Molecular Mechanics/Generalized Born Surface Area (MM/GBSA) method,35,36 widely used in elucidating receptor–ligand binding mechanisms,37–48 were employed to estimate the ERK2-inhibitor binding free energies in AMBER14. In MM/PB(GB)SA, the binding free energy can be decomposed into several terms and 200 snapshots were extracted from the last 3 ns MD trajectory for the free energy calculations. In MM/GBSA, the binding free energy can be calculated as follows:| 〈ΔGbind〉 = 〈ΔEMM〉 + 〈ΔGsolvation〉 − T〈ΔSMM〉 | (1) |
| 〈ΔEMM〉 = 〈ΔEbond〉 + 〈ΔEangle〉 + 〈ΔEtors〉 + 〈ΔEvdW〉 + 〈ΔEelec〉 | (2) |
| 〈ΔGsolvation〉 = 〈ΔGPB(GB)〉 + 〈ΔGSA〉 | (3) |
Exploring the energy contribution of individual residue to the total binding free energy between the inhibitors and ERK2 is crucial, so the MM/GBSA binding free energy decomposition process52,53 was used to decompose the interaction energy to each residue involved in the interaction by considering molecular mechanics and solvation energy without consideration of the contribution of entropy.
3. Results and discussion
3.1 Molecular docking based on the crystal structure
Redocking was used to verify the accuracy of our docking protocols for the two crystal structure 4QTA or 4QYY, which was implied by Glide with XP scoring mode in Schrodinger 2009. The RMSD between the binding pose and the corresponding experimental structure was 0.57 and 0.41 Å for 4QTA and 4QYY, respectively, indicating that the Glide RRD has high accuracy to reproduce the experimental binding poses.Then, we docked all the 27 compounds into the active site of ERK2 (4QYY) in Schrodinger 2009, and three different docking protocols RRD, IFD and QPLD were implied. The corresponding docking scores are summarized in Table 1. The linear correlation between the experimental pIC50 values and the docking scores was used to evaluate the performance of each docking protocol. As shown in Fig. 2, the correlation coefficient squares (R2) for RRD, IFD and QPLD are 0.08, 0.16 and 0.04, respectively. The performance of IFD is better than those of RRD and QPLD, which mean that considering protein flexibility is a well method to enhance the docking accuracy. However, IFD can only considers the flexibility of residues around the active site, rather than the whole protein. Based on the above analysis, any of the traditional docking methods used above could not correctly rank the binding potencies with a high confidence.
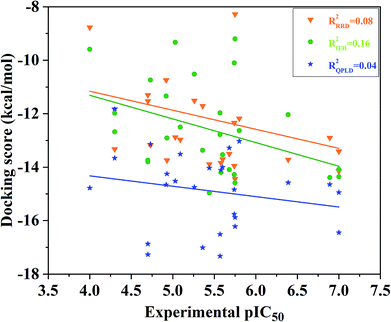 | ||
| Fig. 2 Correlation between the docking scored predicted by RRD, IFD or QPLD and the experimental data. | ||
3.2 Incorporating flexibility and dynamics into the receptor
The k-means clustering algorithm were used to cluster 200 conformations extracted from the last stable 10 ns trajectory for each ERK2-inhibitors complex, at last 10 representative structures were eventually resolved for each complex (Fig. 3 and S2†). Then the 10 representatives as the receptor, 27 inhibitors were docked into the active site of ERK2 by using RRD. MD simulations generated most of conformations have better binding capability to rank the binding potency than the crystal structures (Fig. S3†), which indicates that the protein backbones of the conformations extracted from the MD simulations have obvious conformational rearrangement. Above analysis confirms the importance of protein flexibility on the prediction of protein–ligand interactions.
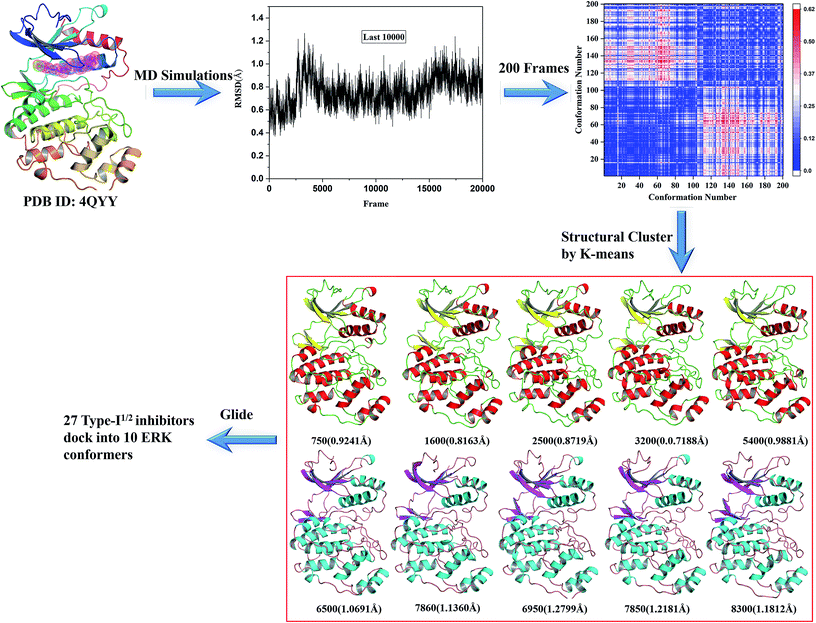 | ||
| Fig. 3 Generation of the representative conformational ensembles base on 4QYY. | ||
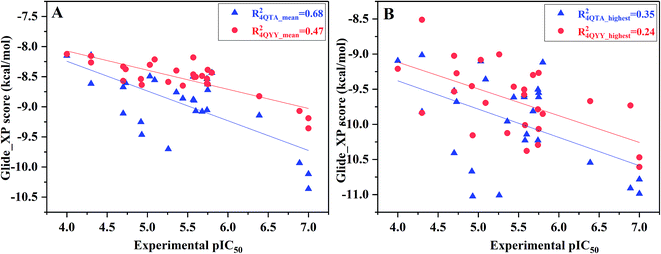
However, not all the binding capability of MD conformations is superior to the crystal structure (R4QTA_42002 = 0.07, R4QYY_16002 = 0.00, and R4QYY_54002 = 0.06), which makes us wonder how to choose the reasonable conformation. In fact, it is difficult to determine the reasonable structures beforehand. Therefore, the highest and average docking scores of all the 10 representative conformations for each inhibitor were used to rank the binding affinities of the inhibitors (Fig. 4), which have better correlations (R4QTA_mean2 = 0.68, R4QYY_mean2 = 0.47, R4QTA_highest2 = 0.35, and R4QTA_highest2 = 0.24) with the experimental data for the two crystal structures (4QTA and 4QYY). Obviously, the above results illustrate that the set of protein structures used in molecular docking can indeed improve the prediction accuracy.
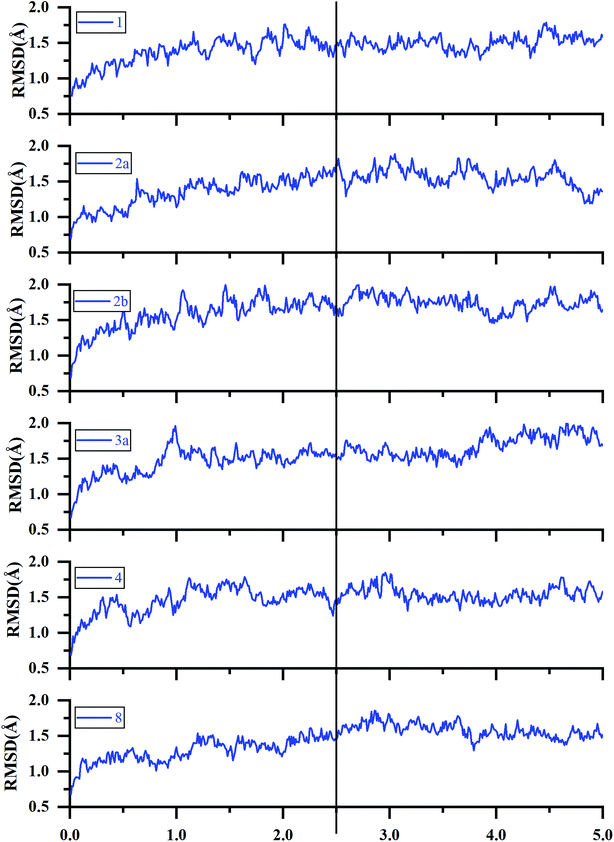 | ||
| Fig. 5 RMSDs of the backbone Cα atoms of the representative ERK2-inhibitors complexes (1, 2a, 2b, 3a, 4 and 8) as a function of simulation time. | ||
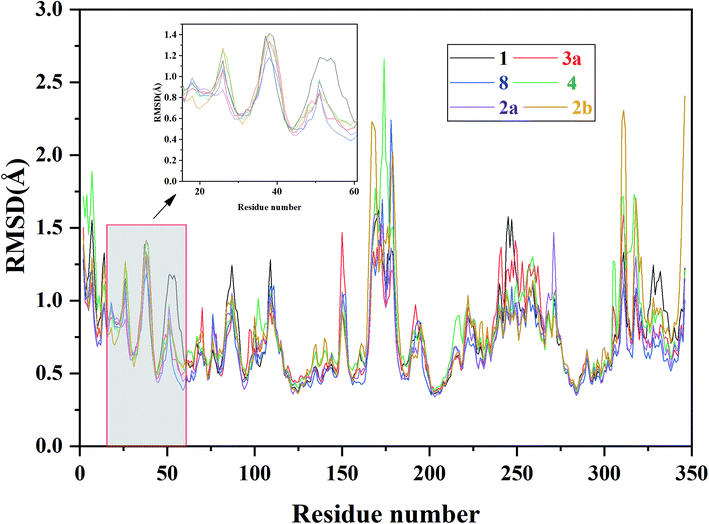 | ||
| Fig. 6 RMSF of each residue of the selected ERK2-inhibitors complexes (1, 2a, 2b, 3a, 4 and 8) obtained from the MD simulations. | ||
The binding free energies and the energy components for each inhibitor-ERK2 system were predicted based on the 200 snapshots using the MM/PBSA and MM/GBSA approaches. Fig. 7 the shows that MM/PBSA (R2 = 0.43) is superior than that of MM/GBSA (R2 = 0.33) in predicting receptor and ligand binding affinity, but both methods perform better than RRD, IFD, QPLD and even ensemble docking. In addition, the correlations between the individual energy terms and the experimental activities were compared (Fig. S4†). The results show that the linear correlations between the non-polar (ΔEvdW + ΔGSA; MM/PBSA: R2 = 0.33) contributions and the experimental data is significantly higher than that of the polar contributions (ΔEele + ΔGPB; MM/GBSA: R2 = 0.06) and the experimental data. As a conclusion, the non-polar contributions are possibly more important than the polar contributions to determine the discrepancy of the binding affinities of the 27 inhibitors.
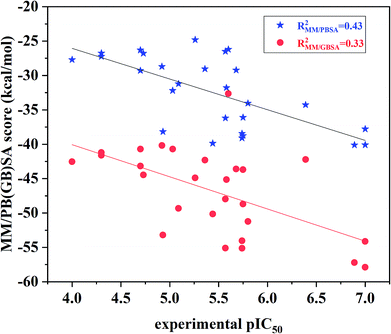 | ||
| Fig. 7 Correlation between the binding free energies calculated by MM/PBSA or MM/GBSA and the experimental data. | ||
Furthermore, as shown in Table 2, the predicted binding affinity of compound 1 (−32.78 kcal mol−1) is stronger than those of the derivatives bound with the allosteric pocket (2–3d) or ATP binding pocket (1a, 9–9d) and modifications, which is consistent with the experimental results. In addition, the compounds with different terminal substitutions located in the allosteric pocket (2–2b, 3, 4 and 5) display different binding affinities compared with compound 1. The above results predicted by MM/PBSA are basically accordant to the experimental data.
| System | ΔEele | ΔEvdW | ΔGPB | ΔGSA | ΔGnonpolara | ΔGpolarb | ΔGbind,PB | pIC50 |
|---|---|---|---|---|---|---|---|---|
| a ΔGpolar = ΔEele + ΔGPB.b ΔGnonpolar = ΔEvdW + ΔGSA. | ||||||||
| ERK2/1 | −74.22 | −54.34 | 104.88 | −9.10 | −63.44 | 30.66 | −32.78 | 5.58 |
| ERK2/1a | −73.13 | −52.84 | 104.97 | −7.64 | −60.48 | 31.84 | −28.64 | 5.68 |
| ERK2/1b | 47.81 | −53.31 | 98.02 | −8.11 | −61.42 | 30.21 | −31.21 | 5.09 |
| ERK2/2 | −52.89 | −61.56 | 94.26 | −8.86 | −70.42 | 41.37 | −29.05 | 5.36 |
| ERK2/2a | −59.32 | −51.26 | 91.88 | −9.00 | −60.26 | 32.56 | −27.70 | 4.00 |
| ERK2/2b | −66.49 | −54.66 | 103.00 | −8.61 | −63.27 | 36.51 | −26.76 | 4.30 |
| ERK2/3 | −66.77 | −50.93 | 98.08 | −8.74 | −59.67 | 33.36 | −26.31 | 4.70 |
| ERK2/3a | −64.72 | −57.09 | 105.51 | −8.52 | −65.61 | 40.79 | −24.82 | 5.26 |
| ERK2/3b | −51.96 | −69.80 | 92.47 | −8.68 | −78.48 | 40.51 | −29.28 | 4.70 |
| ERK2/3c | −63.20 | −67.42 | 114.09 | −8.53 | −75.95 | 46.67 | −28.69 | 4.92 |
| ERK2/3d | −58.44 | −61.09 | 95.26 | −7.92 | −69.01 | 36.82 | −32.19 | 5.03 |
| ERK2/4 | −78.24 | −65.10 | 117.55 | −8.46 | −73.56 | 39.31 | −34.26 | 6.39 |
| ERK2/4a | −68.93 | −64.12 | 103.23 | −7.97 | −72.09 | 34.30 | −37.79 | 7.00 |
| ERK2/4b | −67.89 | −73.49 | 104.63 | −8.63 | −82.12 | 43.37 | −38.75 | 5.75 |
| ERK2/5 | −57.65 | −65.72 | 93.18 | −8.92 | −74.64 | 35.54 | −39.10 | 5.74 |
| ERK2/5a | −58.80 | −64.89 | 96.57 | −9.07 | −73.96 | 37.77 | −36.19 | 5.57 |
| ERK2/6 | −64.70 | −71.80 | 104.94 | −8.55 | −80.35 | 40.24 | −40.11 | 6.89 |
| ERK2/7 | −67.42 | −73.76 | 107.69 | −8.41 | −82.17 | 40.27 | −40.10 | 7.00 |
| ERK2/7a | −58.99 | −64.88 | 96.46 | −9.21 | −74.09 | 37.47 | −36.62 | 5.75 |
| ERK2/7b | −73.65 | −68.07 | 112.38 | −9.10 | −77.17 | 38.73 | −38.44 | 5.74 |
| ERK2/7c | −58.29 | −58.20 | 97.91 | −7.62 | −65.82 | 39.32 | −26.50 | 5.57 |
| ERK2/8 | −56.50 | −63.96 | 94.39 | −7.97 | −71.93 | 37.89 | −34.04 | 5.80 |
| ERK2/9 | −68.36 | −58.89 | 108.38 | −7.91 | −66.80 | 35.02 | −31.78 | 4.73 |
| ERK2/9a | −67.01 | −51.33 | 99.44 | −8.33 | −59.66 | 32.43 | −27.23 | 4.30 |
| ERK2/9b | −70.46 | −71.94 | 111.46 | −8.93 | −80.87 | 41.00 | −39.87 | 5.44 |
| ERK2/9c | −55.37 | −63.32 | 88.74 | −8.22 | −71.54 | 33.37 | −38.17 | 4.93 |
| ERK2/9d | −71.09 | −60.30 | 103.28 | −8.10 | −68.40 | 32.19 | −26.21 | 5.60 |
3.3 Identification of key residues responsible for inhibitor binding
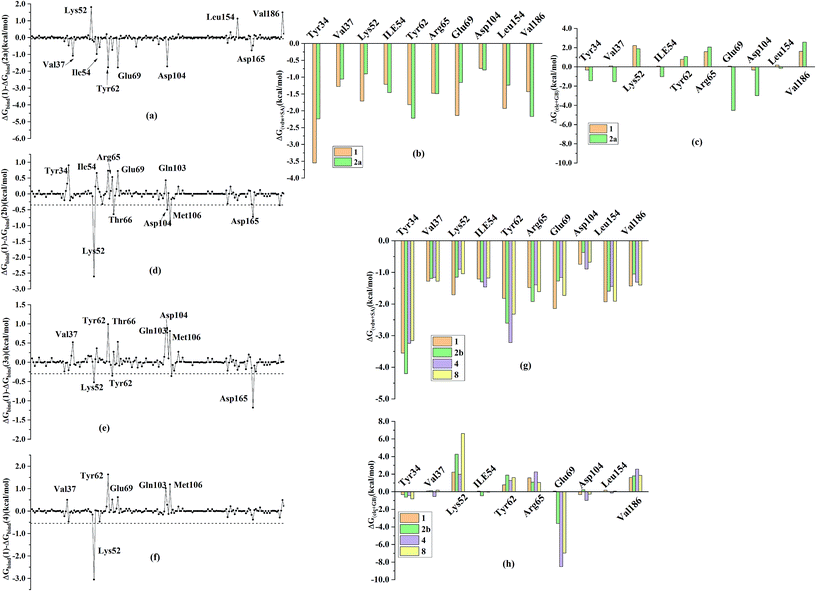
In order to further identify the key residues for ERK2 binding to inhibitors, as well as understand the possible molecular mechanism of the important substituents that can improve the binding affinity with ERK2, the enthalpy (ΔGbind,PB) of representative inhibitors (1, 2a, 2b, 4 and 8) was decomposed into a per-residue depicted in Fig. 8. According to Fig. 8, the key residues contributing to the binding progress is: Val37, Lys52, Ile82, Gln103, Leu105, Met106 and Leu154 (the ATP binding pocket) and Tyr34, Pro56, Tyr62, Asp165, Phe166 and Val186 (the allosteric pocket), and the main role of these residues for ERK2 binding inhibitors are hydrogen bonding and hydrophobic interaction. The contributions of the non-polar residues are a very important part of the binding free energies, especially the residues Val37, Lys52, Tyr62, Arg65, Glu69, Met106 and Leu154. The contributions of the polar residues (e.g. Tyr34, Ile54, Met106 and Asp165) are relatively insignificant except for the residues Lys52 and Tyr62, and there is a slight energetic difference between different inhibitors. The pIC50 values of the compounds 2b, 4 and 8 are about 20 times higher than that of compound 1, while compound 2a shows the lowest activity. Structural analysis shows that these compounds have different substituents interacting with the allosteric pocket region. By further comparing the binding characteristics of the selected inhibitors, we can understand the structural requirements of inhibitors for enhancing binding affinity, which will guide the rational design of more effective and selective ERK2 Type I1/2 inhibitors.3.4 Suggestions for designing of improved Type I1/2 ERK2 inhibitors
Based on the binding free energy calculations and structural analysis, we could propose several improved design criterions for Type I1/2 ERK2 inhibitors.(1) Considering the flexibility and dynamics behavior of ERK2 is quite important to correctly predict the binding potencies of Type I1/2 inhibitors. MD simulations is an important way to improve protein flexibility, and the results indicate that the protein structures obtained from the MD simulations show better tolerance to the ligands. Meanwhile, MD simulations can obviously improve the ranking ability of the binding potencies of the studied ERK2 inhibitors. The binding affinities give the best correlation with the experimental data, which highlighting the importance of incorporating protein flexibility in predicting ERK2-inhibitors interactions.
(2) The hydrogen bonds between the side chain of residues Lys52 and Gln103 with inhibitors play a key role in stabilizing the interaction between inhibitors and ERK2. The favorable van der Waals contribution (ΔEvdW) is important for improving the interaction between ERK2 and inhibitors, which mainly contributes the non-polar interaction. The hydrophobic contributions may be highly helpful to improve the binding ability of ERK2 inhibitors, and the hydrophobic contributions are mainly from some surrounding key residues, such as Val37, Gln103, Asp104 and Met106. Therefore, potential improved ERK2 inhibitors can be designed by increasing hydrophobic interactions, as well as keeping the hydrogen bounds between ERK2 and ERK2 inhibitors.
(3) The terminal substitute interacts “face to face” with the residue Tyr62 side chain through an aromatic π–π interaction is of significant importance for improving activities of ERK2 inhibitors. The results given by our calculations and the experimental data show that large terminal substitute is unfavorable for inhibitors, for example compound 2a.
4. Conclusions
In this work, the binding mechanisms of ERK2 with the Type I1/2 inhibitors were investigate by molecular docking, ensemble docking, MD simulations and binding free energy calculations. Our prediction results show that it is necessary to consider the flexibility of receptor before performing molecular docking to improve the prediction accuracy of traditional docking methods, such as Glide docking, IFD and QPLD. In particular, MD simulations is a well way to improve the flexibility and the binding free energies predicted by MM/PBSA protocols show the highest correlation with the experimental data, which investigates the importance of protein flexibility to predict ERK2 with the Type I1/2 inhibitors interactions. The results of binding free energy calculations predicted by MM/PBSA show that the non-polar interactions play determinative roles in the binding of ERK2 inhibitors, which leads to the difference of the binding affinities of the inhibitors. Several possible key residues for inhibitors binding are identified by the binding free energy decomposition analysis. In addition, the comprehensive analysis of several representative inhibitors also demonstrates the importance of hydrophobic and hydrogen bonds interactions between the residues located in the ATP binding pocket and the allosteric pocket and the inhibitors in improving the binding affinities of the inhibitors. We hope our results will provide a deeper understanding of the interaction between the Type I1/2 inhibitors and ERK2 more valuable information for the further design of new potent ERK2 inhibitors.Conflicts of interest
The authors declare that there is no conflict of interest in this work.Acknowledgements
This work was supported by the Natural Foundation of Shandong Province (Grant No. ZR2018BB055).References
- O. K. Mirzoeva, D. Das and L. M. Heiser, et al., Basal Subtype and MAPK/ERK Kinase (MEK)-Phosphoinositide 3-Kinase Feedback Signaling Determine Susceptibility of Breast Cancer Cells to MEK Inhibition, Cancer Res., 2009, 69, 565–572 CrossRef CAS PubMed.
- N. Sawe, G. Steinberg and H. Zhao, Dual roles of the MAPK/ERK1/2 cell signaling pathway after stroke, J. Neurosci. Res., 2008, 86, 1659 CrossRef CAS PubMed.
- P. Y. Yeh, S. E. Chuang and K. H. Yeh, et al., Increase of the resistance of human cervical carcinoma cells to cisplatin by inhibition of the MEK to ERK signaling pathway partly via enhancement of anticancer drug-induced NF kappa B activation, Biochem. Pharmacol., 2002, 63, 1423–1430 CrossRef CAS PubMed.
- P. J. Roberts and C. J. Der, Targeting the Raf-MEK-ERK mitogen-activated protein kinase cascade for the treatment of cancer, Oncogene, 2007, 26, 3291–3310 CrossRef CAS PubMed.
- S. Schubbert, K. Shannon and G. Bollag, Hyperactive Ras in developmental disorders and cancer, Nat. Rev. Cancer, 2007, 7, 295–308 CrossRef CAS PubMed.
- S. Wilhelm, C. Carter and M. Lynch, et al., Discovery and development of sorafenib: a multikinase inhibitor for treating cancer, Nat. Rev. Drug Discovery, 2006, 5, 835 CrossRef CAS.
- F. Romerio and D. Zella, MEK and ERK inhibitors enhance the antiproliferative effect of interferon-a2b, FASEB J., 2002, 16, 1680 CrossRef CAS PubMed.
- M. S. Carlino, J. R. Todd and K. Gowrishankar, et al., Differential activity of MEK and ERK inhibitors in BRAF inhibitor resistant melanoma, Mol. Oncol., 2014, 8, 544–554 CrossRef CAS PubMed.
- A. M. Aronov, C. Baker and G. W. Bemis, et al., Flipped out: structure-guided design of selective pyrazolylpyrrole ERK inhibitors, J. Med. Chem., 2007, 50, 1280–1287 CrossRef CAS PubMed.
- M. Ohori, T. Kinoshita and M. Okubo, et al., Identification of a selective ERK inhibitor and structural determination of the inhibitor-ERK2 complex, Biochem. Biophys. Res. Commun., 2005, 336, 357–363 CrossRef CAS PubMed.
- E. J. Morris, S. Jha and C. R. Restaino, et al., Discovery of a novel ERK inhibitor with activity in models of acquired resistance to BRAF and MEK inhibitors, Cancer Discovery, 2013, 3, 742–750 CrossRef CAS PubMed.
- A. M. Aronov, Q. Tang and G. Martinez-Botella, et al., Structure-guided design of potent and selective pyrimidylpyrrole inhibitors of extracellular signal-regulated kinase (ERK) using conformational control, J. Med. Chem., 2009, 52, 6362–6368 CrossRef CAS PubMed.
- J. F. Blake, M. Burkard and J. Chan, et al., Discovery of (S)-1-(1-(4-chloro-3-fluorophenyl)-2-hydroxyethyl)-4-(2-((1-methyl-1H-pyrazol-5-yl)amino)pyrimidin-4-yl)pyridin-2(1H)-one (GDC-0994), an extracellular signal-regulated kinase 1/2 (ERK1/2) inhibitor in early clinical development, J. Med. Chem., 2016, 59, 5650–5660 CrossRef CAS PubMed.
- Y. Niu, D. Pan and Y. Yang, et al., Revealing the molecular mechanism of different residence times of ERK2 inhibitors via binding free energy calculation and unbinding pathway analysis, Chemom. Intell. Lab. Syst., 2016, 158, 91–101 CrossRef CAS.
- T. Zhang, Y. Liu and X. Yang, et al., Definitive Metabolite Identification Coupled with Automated Ligand Identification System (ALIS) Technology: A Novel Approach to Uncover Structure-Activity Relationships and Guide Drug Design in a Factor IXa Inhibitor Program, J. Med. Chem., 2016, 59, 1818 CrossRef CAS PubMed.
- Y. Deng, G. W. Shipps and A. Cooper, et al., Discovery of Novel, Dual Mechanism ERK Inhibitors by Affinity Selection Screening of an Inactive Kinase, J. Med. Chem., 2014, 57, 8817–8826 CrossRef CAS PubMed.
- X. Kong, P. Pan and D. Li, et al., Importance of protein flexibility in ranking inhibitor affinities: modeling the binding mechanisms of piperidine carboxamides as Type I1/2 ALK inhibitors, Phys. Chem. Chem. Phys., 2015, 17, 6098–6113 RSC.
- X. Kong, H. Sun and P. Pan, et al., Importance of protein flexibility in molecular recognition: a case study on Type-I1/2 inhibitors of ALK, Phys. Chem. Chem. Phys., 2018, 20, 4851–4863 RSC.
- P. Pan, H. Yu and Q. Liu, et al., Combating Drug-Resistant Mutants of Anaplastic Lymphoma Kinase with Potent and Selective Type-I1/2 Inhibitors by Stabilizing Unique DFG-Shifted Loop Conformation, ACS Cent. Sci., 2017, 3, 1208–1220 CrossRef CAS PubMed.
- S. Tian, H. Sun and Y. Li, et al., Development and evaluation of an integrated virtual screening strategy by combining molecular docking and pharmacophore searching based on multiple protein structures, J. Chem. Inf. Model., 2013, 53, 2743–2756 CrossRef CAS PubMed.
- S. Tian, H. Sun and P. Pan, et al., Assessing an ensemble docking-based virtual screening strategy for kinase targets by considering protein flexibility, J. Chem. Inf. Model., 2014, 54, 2664–2679 CrossRef CAS PubMed.
- A. Chaikuad, E. M. C. Tacconi and J. Zimmer, et al., A unique inhibitor binding site in ERK1/2 is associated with slow binding kinetics, Nat. Chem. Biol., 2014, 10, 853 CrossRef CAS PubMed.
- Prime, version 2.0, Schrödinger, LLC, New York, 2008 Search PubMed.
- Y. Zhu, J. Desai and y. Deng, et al., Discovery of hydroxyaniline amides as selective extracellular regulated kinase (Erk) inhibitors, Bioorg. Med. Chem. Lett., 2015, 25, 1627–1629 CrossRef PubMed.
- G. A. K. And, R. A. Friesner and T. R. And, et al., Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides, J. Phys. Chem. B, 2001, 105, 6474–6487 CrossRef.
- P. Cieplak, W. D. Cornell and C. Bayly, et al., Application of the multimolecule and multiconformational RESP methodology to biopolymers: charge derivation for DNA, RNA, and proteins, J. Comput. Chem., 1995, 16, 1357–1377 CrossRef CAS.
- C. I. Bayly, P. Cieplak and W. Cornell, et al., A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- T. Fox and P. A. Kollman, Application of the RESP Methodology in the Parametrization of Organic Solvents, J. Phys. Chem., 1998, 102, 8070–8079 CrossRef CAS.
- K. Lindorff-Larsen, S. Piana and K. Palmo, et al., Improved side-chain torsion potentials for the Amber ff99SB protein force field, Proteins: Struct., Funct., Bioinf., 2010, 78, 1950–1958 CAS.
- J. Wang, R. M. Wolf and J. W. Caldwell, et al., Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar and J. D. Madura, et al., Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- Y. Niu, D. Shi and L. Li, et al., Revealing inhibition difference between PFI-2 enantiomers against SETD7 by molecular dynamics simulations, binding free energy calculations and unbinding pathway analysis, Sci. Rep., 2017, 7, 46547 CrossRef CAS PubMed.
- J. C. Phillips, R. Braun and W. Wang, et al., Scalable molecular dynamics with NAMD, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- P. A. Kollman, I. Massova and C. Reyes, et al., Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models, Acc. Chem. Res., 2000, 33, 889–897 CrossRef CAS.
- P. D. Lyne, M. L. Lamb and J. C. Saeh, Accurate prediction of the relative potencies of members of a series of kinase inhibitors using molecular docking and MM-GBSA scoring, J. Med. Chem., 2006, 49, 4805–4808 CrossRef CAS PubMed.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- A. Weis, K. Katebzadeh and P. Söderhjelm, et al., Ligand affinities predicted with the MM/PBSA method: dependence on the simulation method and the force field, J. Med. Chem., 2006, 49, 6596 CrossRef CAS PubMed.
- P. A. Kollman, I. Massova and C. Reyes, et al., Calculating structures and free energies of complex molecules: Combining molecular mechanics and continuum models, Acc. Chem. Res., 2000, 33, 889–897 CrossRef CAS.
- J. Galvez, S. Polo and B. Insuasty, et al., Design, facile synthesis, and evaluation of novel spiro- and pyrazolo1,5-c quinazolines as cholinesterase inhibitors: molecular docking and MM/GBSA studies, Comput. Biol. Chem., 2018, 74, 218–229 CrossRef CAS PubMed.
- H. Sun, L. Duan and F. Chen, et al., Assessing the performance of MM/PBSA and MM/GBSA methods. 7. entropy effects on the performance of end-point binding free energy calculation approaches, Phys. Chem. Chem. Phys., 2018, 20, 14450–14460 RSC.
- T. Hou, J. Wang and Y. Li, et al., Assessing the performance of the molecular mechanics/Poisson Boltzmann surface area and molecular mechanics/generalized Born surface area methods. II. The accuracy of ranking poses generated from docking, J. Comput. Chem., 2011, 32, 866–877 CrossRef CAS PubMed.
- H. Sun, Y. Li and S. Tian, et al., Assessing the performance of MM/PBSA and MM/GBSA methods. 4. Accuracies of MM/PBSA and MM/GBSA methodologies evaluated by various simulation protocols using PDBbind data set, Phys. Chem. Chem. Phys., 2014, 16, 16719–16729 RSC.
- J. Wang, T. Hou and X. Xu, Recent Advances in Free Energy Calculations with a Combination of Molecular Mechanics and Continuum Models, Curr. Comput.-Aided Drug Des., 2006, 2, 95–103 CrossRef.
- L. Xu, H. Sun and Y. Li, et al., Assessing the performance of MM/PBSA and MM/GBSA methods. 3. The impact of force fields and ligand charge models, J. Phys. Chem. B, 2013, 117, 8408–8421 CrossRef CAS PubMed.
- H. Sun, Y. Li and S. Tian, et al., P-loop conformation governed crizotinib resistance in G2032R-mutated ROS1 tyrosine kinase: clues from free energy landscape, PLoS Comput. Biol., 2014, 10, e1003729 CrossRef PubMed.
- H. Sun, Y. Li and M. Shen, et al., Assessing the performance of MM/PBSA and MM/GBSA methods. 5. Improved docking performance using high solute dielectric constant MM/GBSA and MM/PBSA rescoring, Phys. Chem. Chem. Phys., 2014, 16, 22035–22045 RSC.
- N. Homeyer and H. Gohlke, Free Energy Calculations by the Molecular Mechanics Poisson-Boltzmann Surface Area Method, Mol. Inf., 2012, 31, 114–122 CrossRef CAS PubMed.
- A. Onufriev, D. Bashford and D. A. Case, Exploring protein native states and large-scale conformational changes with a modified generalized born model, Proteins: Struct., Funct., Bioinf., 2004, 55, 383–394 CrossRef CAS PubMed.
- Q. Lu and R. Luo, Analyzing the biopolymer folding rates and pathways using kinetic cluster method, J. Chem. Phys., 2003, 119, 11035–11048 CrossRef CAS.
- T. Hou, J. Wang and Y. Li, et al., Assessing the performance of the MM/PBSA and MM/GBSA methods. 1. The accuracy of binding free energy calculations based on molecular dynamics simulations, J. Chem. Inf. Model., 2011, 51, 69–82 CrossRef CAS PubMed.
- T. Hou, N. Li and Y. Li, et al., Characterization of domain-peptide interaction interface: prediction of SH3 domain-mediated protein-protein interaction network in yeast by generic structure-based models, J. Proteome Res., 2012, 11, 2982–2995 CrossRef CAS PubMed.
- G. Holger, K. Christina and A. C. David, Insights into protein-protein binding by binding free energy calculation and free energy decomposition for the Ras-Raf and Ras-RalGDS complexes, J. Mol. Biol., 2003, 330, 891–913 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra01657k |
| This journal is © The Royal Society of Chemistry 2019 |