Open Access Article
Open Access ArticleThe solid-state proton NMR study of bone using a dipolar filter: apatite hydroxyl content versus animal age†
Agnieszka Kaflak *a,
Stanisław Moskalewskib and
Waclaw Kolodziejskia
*a,
Stanisław Moskalewskib and
Waclaw Kolodziejskia
aMedical University of Warsaw, Faculty of Pharmacy, Department of Analytical Chemistry and Biomaterials, ul. Banacha 1, Warsaw 02-097, Poland. E-mail: akaflak@wum.edu.pl; Fax: +48 22 5720784; Tel: +48 22 5720784
bMedical University of Warsaw, Department of Histology and Embryology, Chalubinskiego 5, Warsaw 02-004, Poland
First published on 29th May 2019
Abstract
The hydroxyl content of bone apatite mineral has been measured using proton solid-state NMR performed with a multiple-pulse dipolar filter under slow magic angle spinning (MAS). This new method succeeded in resolving and relatively enhancing the main hydroxyl peak at ca. 0 ppm from whole bone, making it amenable to rigorous quantitative analysis. The proposed methodology, involving line fitting, the measurement of the apatite concentration in the studied material and adequate calibration, was proved to be convenient and suitable for monitoring bone mineral hydroxylation in different species and over the lifetime of the animal. It was found that the hydroxyl content in the cranial bone mineral of pig and rats remained in the 5–10% range, with reference to stoichiometric hydroxyapatite. In rats, the hydroxyl content showed a non-monotonic increase with age, which was governed by biological processes rather than by chemical, thermodynamically driven apatite maturation.
Introduction
Nanoapatite is the major inorganic component of osseous tissue.1–3 The chemical composition of this mineral, the internal structure of its crystals, its crystallinity (crystal size and perfection), maturity, solubility and surface properties (all being mutually related features), are crucial for the biological functions of bone.4–14 Unlike a reference apatite mineral, that is, monoclinic stoichiometric calcium hydroxyapatite Ca10(PO4)6(OH)2, bone apatite is hexagonal, contains various extraneous ions and is deficient in structural hydroxyl ions.This latter aspect is still studied and debated, because the ionic and water filling of the crystal channels containing apatite hydroxyl ions is crucial for the bone mineral structure and its properties.15–17 It is known that the OH− concentration in the apatite crystals decreases with increase of the carbonate content caused by A-type (CO32− for OH−) and/or B-type (CO32− for PO43−) substitution,18–21 and with the decreasing size of apatite nanocrystals4,15,22,23 and with increasing disorder in their crystal lattice.4,15 Maturation of bone apatite, which is a chemical, thermodynamically driven process,24 increases the apatite OH− content.25 In bone, the lifetime of apatite nanocrystals over which the maturation can proceed and advance the hydroxylation, is limited by bone turnover,6,10,11 which is a biological, age-dependent process. So far, the available quantitative results on bone mineral hydroxylation are inconsistent and their relationship to animal age has been mentioned in only one publication; namely, in tibia of a 7 week and 28 week old mouse, the apatite OH− content was estimated at 33 ± 1 and 29 ± 1%, respectively, by reference to stoichiometric hydroxyapatite.26 In our study, we wish to prove that reliable information on apatite hydroxylation and on its evolution with animal age can be obtained using an adequate proton solid-state NMR technique. For this work, rat cranial bone was chosen, because its growth and concomitant changes in chemical composition have already been well characterized.27,28 The chemical and biological aspects of apatite hydroxylation are discussed.
Information on the hydroxyl content of bone and dental mineral can be obtained from various methods. The simplest is to explore the analytical chemical formulae developed for the crystallographic unit cell of apatite.5,13,14,29,30 For human bone, dentin and enamel these formulae give 0.3, 0.4 and 0.9 OH− per unit cell, respectively. This corresponds to about 15, 20 and 45% of the OH− concentration in stoichiometric hydroxyapatite. There is a problem with this estimation because the hydroxyl content is not experimentally measured but obtained indirectly. Therefore, it lacks accuracy and it is better to use spectroscopic methods.
The degree of apatite hydroxylation can be determined using vibrational infrared (IR) and Raman (R) spectroscopy methods from the stretching OH band at 3572 cm−1 (IR and R active) and the librational OH band at 632 cm−1 (IR active, R unobserved).31 First, Biltz and Pellegrino found that those IR bands are absent from the infrared spectra of bone mineral.32 Then, it was demonstrated that the mineral hydroxyl bands are also missing from the Raman spectra.15,33 Recently, Rey and Combes concluded that the content of the OH− ions measured with Raman in the bone mineral of vertebrates is below 5% relative to stoichiometric hydroxyapatite.13 The inelastic neutron scattering results for bone mineral appeared inconsistent and were unsuccessful, because the relative concentrations of the OH− ions presented in two independent reports34,35 were estimated at 0% (bovine and rat cortical bone) and about 40% (ox femur bone), respectively.
It would seem that solid-state NMR is well suited to observe the OH− ions, especially by inspecting proton resonance spectra of samples subjected to magic angle spinning (MAS). In the 1H MAS NMR spectrum of stoichiometric hydroxyapatite, an easily discernible OH− peak appears at 0 ppm on the tetramethylsilane (TMS) scale.36–38 Curiously enough, Rey et al. failed to detect such a peak from powdered rat bone.37 Nonetheless, the structural hydroxyl ions do exist in apatite, since they constitute a proton polarization source in the polarization transfer (cross-polarization; CP) to phosphorus-31.38–40 The problem with the detection of the hydroxyl ions is that their faint peak is located at the lower-frequency side of overwhelming and interfering resonances from the bone organic constituents.
To overcome this difficulty various solid-state MAS NMR techniques have been proposed and tested on bone and dental apatites. Cho et al.41 applied 2D correlation MAS NMR experiments (HETCOR) based on the 1H → 31P CP. An increased resolution in the proton dimension allowed them to measure the hydroxyl content of apatite mineral in human cortical bone. It was roughly estimated at 20% relative to stoichiometric hydroxyapatite. Kaflak and Kolodziejski40 showed that the reverse 31P → 1H CP is possible and leads to proton MAS NMR spectra free of signals from the organic matrix, with an exposed, clearly seen hydroxyl peak of the bone mineral. This method was then applied to dental hard tissues, giving OH− contents of 73, 18 and 18% for enamel, dentin and cementum, respectively.42 Taylor et al.26 determined individual contributions of water and OH− to the 1H → 31P CP by analyzing the kinetics (CP signal intensity versus contact time) of this process. Then, from their relative magnitudes, they derived the specific surface area and hydroxyl content of bone apatite nanocrystals. For chicken bone, the OH− results were in the range 19–26% relative to stoichiometric hydroxyapatite and were dependent on the kind of bone (tibia vs. radius). For tibia of a young adult and adult mouse, the OH− content was about 30%. All three CP methods, that is, conventional CP HETCOR,41 inverse CP40,42 and that based on conventional CP kinetics,26 are time consuming and dependent on various factors and thus prone to experimental errors. There was also a double CP technique proposed by Duer et al.43,44 to get rid of the unwanted proton signals from the organic substance, and this was illustrated on single spectra of calcified cartilage and bone. They used the regular 1H → 31P CP followed by the Lee-Goldburg 31P → 1H CP. The method looks rather fast, because rapid longitudinal proton relaxation allows the use of short recycle delays. However, there still remains the problem that the CP technique, especially its double back-and-forth version, is difficult to make quantitative and therefore this strategy has not been explored further. Then, Vyalikh et al.45 applied high-resolution proton NMR using combined sample rotation and multiple-pulse sequences to sharpen 1H peaks, enhance their resolution and, in this manner, render the OH− peak visible. This technique was quite successful for enamel (40% of OH− found), but the hydroxyl peaks in the spectra of dentin (14% of OH−) and cementum (called root dentin in that study; 9% of OH−) were still severely overlapped with the peaks of the organic matrix, thereby requiring involved deconvolutions.
The above survey of analytical methods indicates that solid-state NMR is more sensitive than the IR and Raman methods in the study of bioapatite hydroxylation. However, NMR results are generally higher, while those from vibrational spectroscopy are significantly lower, than the hydroxyl content deduced from analytical chemical formulae.13,14 Furthermore, previously used NMR techniques suffer from various problems, as indicated. Therefore, a dependable, convenient NMR technique is needed to continue studies on the OH− content of biological apatites, and to reconcile and explain previous divergent results. This task is not trivial, because ultra-high speed MAS is not capable of resolving and exposing the proton hydroxyl peak from bone.46,47 A successful use of the HARDSHIP NMR pulse sequence to measure internuclear distances in biological solids48–51 and the spin-echo pulse sequence with adequately selected echo time to promote desired proton resonances47 have encouraged us to experiment with a proton T2-filter formerly used for polymers.52–55 The multiple-pulse sequence shown in Fig. 1 has been adapted and tuned by us for bone study, to select the proton magnetization from relatively mobile groups with corresponding long transverse relaxation times. In this way, the apatite proton hydroxyl peaks became better seen and prepared for quantitative analysis.
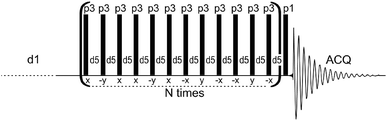 | ||
| Fig. 1 The dipolar filter pulse sequence used in this work to acquire proton solid-state NMR spectra of apatite biomaterials. | ||
Thus, our goal in this work is to propose this new proton NMR methodology, based on the multiple-pulse dipolar filter, to directly measure the hydroxyl content in the mineral of whole bone. This methodology is tested on specimens of cranial bone from two species (pig and rat), and rat bone mineral is examined as a function of animal age. So far, such studies are virtually missing. The results for the hydroxyl content will be discussed, together with supporting data on carbonates and crystallinity.
Materials and methods
Animals, bone specimens and reference materials
The study was done on cranial bone of female rats (inbred strain LEW/Han) at different ages, and of a one-day female pig obtained from the Animal Unit of the Medical University of Warsaw. All the animal experiments were carried out in accordance with the EU Directive 2010/63/EU and the study, including experimentation, transportation and care of the animals, was approved by the Animal Ethical Committee of the Medical University of Warsaw (Permission No. 24 issued on 19.09.2006). The rats were housed in an air-conditioned room (temperature maintained at 22–24 °C, relative humidity of 65%) with artificial circadian light cycles (lights on over 13 h). Food (Labofeed H from the Animal Feed Manufacturing Plant in Kcynia, Poland) and water were freely available. At the different ages, the animals were anaesthetized and euthanized by cervical dislocation, then the specimens of cranial bone were excised and collected, lyophilised, gently crushed (no grinding) and used in the MAS NMR experiments. The rat samples are designated by R followed by the age of the animal expressed in days (R1, R30, R90 and R180). To ensure proper sampling and to obtain enough material to fill the MAS NMR rotor, pieces of bone for R1 were collected from 40 animals and the other samples were gathered from four animals each. Collagen type I from kangaroo tail was purchased from Sigma-Aldrich. The hydroxyapatite (HA)/chitosan composite was synthesized according to the work described previously.56Analytical methods
The proton NMR spectra were recorded with MAS at 7 kHz using a Bruker Avance 400 WB spectrometer and a Bruker 4 mm MAS probe. The measurements were done at 295 K in ZrO2 rotors driven by dry air. The single pulse-acquire (Bloch decay; denoted BD) and dipolar filter (DF) spectra were recorded with 8 and 360 scans, respectively, using a π/2 pulse of 3.2 μs and a recycle delay of 30 s. A spectral background from the rotor and the probe was carefully subtracted. The DF pulse sequence (Fig. 1) consists of the multiple-pulse DF, followed by a detection π/2 pulse (p1). The long recycle delay of 30 s (d1) was used for all the measurements to ensure that all proton sites and groups in all the studied samples were able to rebuild their magnetization after each DF pulse sequence by means of longitudinal relaxation. The dipolar filter eliminates magnetization from protons with stronger homonuclear dipole–dipole couplings (shorter TH2), leaving that from mobile protons with weaker interactions (longer TH2).52–55 The DF consists of N trains of 12 pulses p3 with the interpulse period d5. By appropriate tuning of the parameters N, p3 and d5, the OH− signals of apatite were sufficiently exposed to be applied for quantitative determination of OH− ions (Fig. 1S†). In this work, we used N = 3, d5 = 25 μs and p3 corresponding to the pulse angle of 71°. Selected proton BD NMR spectra were also recorded with MAS of 60 kHz using a Bruker Avance III HD 600 spectrometer and a Bruker 1.3 mm MAS probe. The measurements were done in ZrO2 rotors driven by dry air, with 32 scans using a π/2 pulse of 1.2 μs and a recycle delay of 10 s. In all the proton spectra, the chemical shifts were externally referenced to TMS.The powder X-ray diffraction (PXRD) analysis was performed using a Bruker D8 Discovery diffractometer (with a step size of 0.024° in the 2θ range from 1.5–10° and 10–60°). The FT-IR measurements were carried out from KBr pellets using a Spectrum 1000 spectrometer (PerkinElmer). The mineral content of bone was measured using thermogravimetric analysis (TGA) in air flow by comparing the sample mass at 600 °C to that at 25 °C.57,58
Data processing and statistical analysis
The proton MAS NMR free induction decays (FIDs) were processed with NUTS (NutsPro – NMR Utility Transform Software, Acorn NMR 2007), wherein the proton background from the rotor and the probe was also subtracted, and the resulting spectra were then exported to GRAMS (GRAMS/AI Version 9.00 R2, Thermo Fischer Sci. Inc. 2009). In GRAMS, a linear spectral background was adjusted, then the spectra were divided by the sample mass in the rotor (in mg), and the spectral region containing lipid and hydroxyl peaks (from −2.0 to 3.1 ppm) was extracted and deconvoluted using Gaussian lines (Fig. 2S†). This procedure was repeated seven times for each sample to calculate a mean area of the OH− peak and its standard error. This experience made it clear that the proton background subtraction and the final deconvolution (line fitting) are two influential steps that generate random errors, so both have been given special attention. The deconvolution step requires a good signal-to-noise (S/N) ratio, which should be attained by performing an adequate number of scans. In our procedure, the NMR acquisition and processing parameters were the same for each sample and for each processing course for a given sample. The mean values of the hydroxyl peak areas were then recalculated to the unit mass of the bone mineral (in mg), the content of which in bone had been previously determined using TGA. Finally, the hydroxyl ion concentration was calculated from a linear calibration function (Fig. 3S†), which was derived using reference materials of precisely determined hydroxyl content in the apatite lattice. To perform the calibration we applied such materials from earlier studies carried out in our group: apatite HA12,22 dentin42 and apatite HA800.42 Any inaccuracy of the calibration may introduce only a systematic error into the hydroxyl determination. Further details of the entire analytical methodology are given in the ESI.† The GRAMS program was also used to process Fourier transform (FT)-IR spectra and to perform line fitting of the (001) reflection in the PXRD diffractograms (Fig. 4S†). The calculations, statistics and drawings were done with the KaleidaGraph program (Version 3.5, Synergy Software 2000).Results and discussion
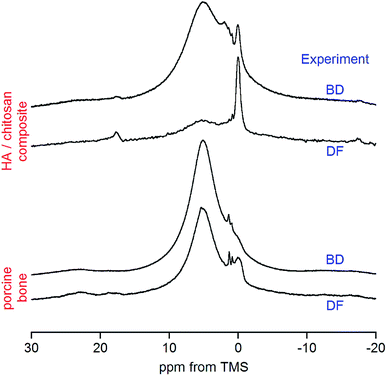
The dipolar filter pulse sequence (Fig. 1) works well on both synthetic and biological composites containing organic components and the apatite mineral (Fig. 2). It is easy to tune (Fig. 1S†) and gives reproducible proton spectra under slow MAS, which can feasibly be acquired with regular solid-state NMR probes and are amenable to quantitative analysis. Although the dipolar filter strongly reduces spectrum intensity (Fig. 1S†), this is not a problem because of the high sensitivity of the proton NMR.In the case of the HA/chitosan composite (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 weight ratio) the regular BD spectrum (Fig. 2) reveals a tiny peak at 0.0 ppm from apatite structural OH− ions,36–38 sitting on the lower-frequency shoulder of a huge water signal. Some organic features are visible between the water and OH− resonances, but the main contribution from chitosan is to a massive background formed of highly overlapped sidebands (Fig. 5S†). This background, resulting also from strongly adsorbed water, is apparently reduced with the DF sequence (Fig. 5S†), and the hydroxyl peak becomes effectively enhanced and exposed over the water signal (Fig. 2).
7 weight ratio) the regular BD spectrum (Fig. 2) reveals a tiny peak at 0.0 ppm from apatite structural OH− ions,36–38 sitting on the lower-frequency shoulder of a huge water signal. Some organic features are visible between the water and OH− resonances, but the main contribution from chitosan is to a massive background formed of highly overlapped sidebands (Fig. 5S†). This background, resulting also from strongly adsorbed water, is apparently reduced with the DF sequence (Fig. 5S†), and the hydroxyl peak becomes effectively enhanced and exposed over the water signal (Fig. 2).
Our attention has been primarily focused on bone. A typical BD proton spectrum of whole bone is shown in Fig. 2. It was acquired from the porcine cranial bone, which was a mixture of compact cortical tissue (outer and inner tables of the skull) and trabecular tissue (intervening cancellous diploë). Again, the water signal is overwhelming and the apatite hydroxyl peak is hardly detectable. With the DF technique the OH− peak becomes nicely enlarged and suitable for quantitative evaluation. The two small peaks at 0.9 and 1.3 ppm are from accompanying adipose tissue (see later discussion).
Bone is a highly complex biological composite, so its proton NMR spectrum comprises many resonances, which require adequate comment and assignment (Table 1). The appearance of the spectrum is strongly dependent on the MAS rate.46,47 With the advent of ultra-high speed MAS there is an obvious trend to use it to attain a maximum possible spectral resolution. A visual inspection of the porcine bone spectra in Fig. 2 poses a question, where are the signals from collagen and other organic constituents present in the osseous tissue?
| Peak | Chemical shift/ppm | Assignment |
|---|---|---|
| a Two alternative assignments: either hydroxyl groups at surface calcium sites59 or structured and stacked water at the entrances to the hydroxyl channels.60b Large, broad, asymmetric signal with a sizable high-frequency shoulder expanding beyond 10 ppm.c Complex signal, with shoulders at 0.8 and 1.9 ppm.d Complex region, a sharper peak at 3.1 ppm and a broader peak at 3.5 ppm. | ||
| 1 | −0.1 to 0.0 | Apatite hydroxyl groups residing in crystal channels (main signal) |
| 2 | 0.8–1.3 | Apatite surface: either specific hydroxyl groups or atypical water (minor pool)a |
| 3 | 5.8b | Apatite surface: adsorbed water (main pool) |
| 4 | 1.2c | Collagen Hβ and Hγ protons |
| 5 | 3.0 to 3.7d | Collagen Hα protons and –C![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) 2–NH– protons (Hδ in Pro and Hyp) 2–NH– protons (Hδ in Pro and Hyp) |
| 6 | 4.6 | Collagen water |
| 7 | 7.4–8.2 | Collagen amide NH protons |
| 8 | 0.9 | Adipose tissue: C![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) 3–(CH2)n– 3–(CH2)n– |
| 9 | 1.3 | Adipose tissue: –(C![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) 2)n– 2)n– |
| 10 | 2.1 | Adipose tissue: –CH2–C![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) 2–CH 2–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– and –CH2–O–CO–C CH– and –CH2–O–CO–C![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) 2–CH2– 2–CH2– |
| 11 | 2.9 | Adipose tissue: –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–C CH–C![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) 2–CH 2–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– CH– |
| 12 | 4.8 | Adipose tissue water |
| 13 | 5.4 | Adipose tissue: –C![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) – and – and ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) C C![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) –CH2–O–CO–CH2–CH2– –CH2–O–CO–CH2–CH2– |
| 14 | 0.12 | OCP hydroxyl groups |
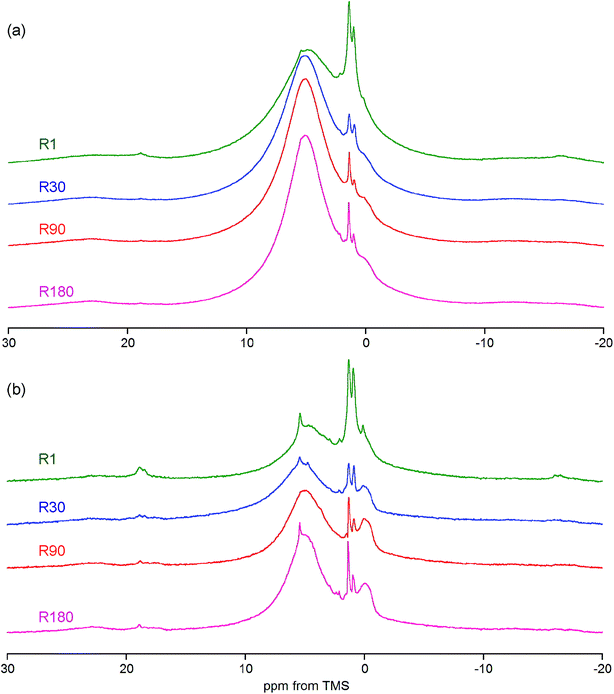
The answer is that under MAS at 7 kHz the collagen peaks are practically invisible. In principle, they are hidden in the huge background observed only for a broad chemical shift range (Fig. 5S†). By contrast, the bone spectrum acquired under MAS at 60 kHz (e.g. R90 in Fig. 3a) does not contain this background and it is thoroughly dominated by collagen peaks (see Table 1 for assignments). Unfortunately, the OH− peak of apatite at 0 ppm, yet detectable under MAS at 7 kHz, is completely unrevealed in the proton BD spectrum of bone measured with MAS at 60 kHz (Fig. 3a). Thus, the ultra-high speed MAS fails to resolve the OH− peak.
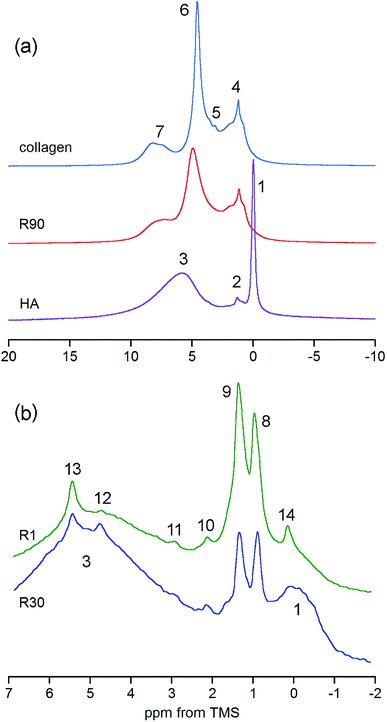 | ||
| Fig. 3 Details of the proton spectra of whole bone and its components. (a) Comparison of the R90 rat bone spectrum with the spectra of collagen and hydroxyapatite (HA), all acquired with the BD pulse sequence under MAS at 60 kHz and scaled to the same spectrum area. (b) Expanded regions of the DF spectra of rat bone showing discrete peaks from adipose tissue and OCP (R1 and R30, the same sample mass, MAS at 7 kHz). For assignments, see Table 1. | ||
The previously mentioned adipose tissue is a part of the marrow contained in the trabecular bone and, to a lesser extent, it is also present in the cortical bone. As has already been noted, the whole cranial bone studied is a mixture of the two bone types, so it includes the adipose tissue, the presence of which is reflected in the discussed proton NMR spectra recorded with MAS at 7 kHz (Fig. 3b and 4, Table 1).62–64 This adipose tissue contains various triacylglycerols, giving proton peaks that are relatively sharp and easy to discern. The most prominent peaks show at 0.9 (–CH3) and 1.3 (–CH2–) ppm, and even water located in the adipose tissue can sometimes be detected at 4.8 ppm (peak 12 in Fig. 3b). Generally, the full set of adipose peaks is better observed with MAS at 7 kHz than at 60 kHz (compare Fig. 3b and R90 in Fig. 3a). It is spectacular that the adipose peaks are clearly most intensive for the one-day-old rat (R1 in Fig. 4), that is, the youngest animal had the highest content of triacylglycerols in its cranial bone. The high level of bone marrow adipose tissue (BMAT) in R1 probably originates from the distinctly lower mineral content in this sample (see Table 2), because BMAT is elevated with low bone mineral density (BMD).69 That relationship is called an inverse relationship between BMD and BMAT.70,71 It is also worth considering that the intensity ratio of the methylene and methyl peaks should increase with increase of the mean length of the acyl chains. In our work, this ratio is slightly higher for R1 than for R30, and then from R30 it increases with animal age (Fig. 4 and 5). Accordingly, the related ratio of longer-chain to shorter-chain triacylglycerols follows the order: R1 ≳ R30 < R90 < R180, which is roughly consistent with the already observed, increasing trend on aging.72,73 Recent studies offer us a probable, deeper understanding of this effect. Namely, the higher level of BMAT in R1 and the discussed proportion of triacylglycerols may both be controlled by underlying constitutive and regulated forms of BMAT in the rat bone, considering that concentrations of those forms are dependent on animal age.74,75
| Sample | Pig | R1 | R30 | R90 | R180 |
|---|---|---|---|---|---|
| a Along the crystal c-axis, calculated from the PXRD (002) reflection using Scherrer's equation.65b Splitting factor of Weiner and Bar-Yosef calculated from the ν4(PO4) IR spectral region.66,67c From the ratio [area ν3(CO3)]/[area ν1ν3(PO4)] of the IR spectral regions.68d Sample mass at 600 °C compared to that at 25 °C, measured using TGA under air flow.57,58.e The results contain only significant figures that are justified by the precision of the method of analysis used.f From proton DF MAS NMR; by reference to stoichiometric hydroxyapatite; standard errors in parentheses. | |||||
| Animal age/days | 1 | 1 | 30 | 90 | 180 |
| Apatite crystal size/nma | 16.6 | 12.5 | 17.9 | 18.5 | 20.4 |
| Crystallinity indexb | 2.90 | 2.85 | 2.89 | 2.98 | 2.95 |
| Carbonate content/wt%c | 8.6 | 4.0 | 7.0 | 7.1 | 8.4 |
| Bone mineral content/wt%d | 59.6 | 42.1 | 61.1 | 62.4 | 60.9 |
| Hydroxyl content of the mineral/%f | 5.14 (0.07) | 7.95 (0.20) | 7.48 (0.09) | 10.23 (0.09) | 10.07 (0.06) |
The rat model is often used to study human diseases. In the case of skeletal diseases this model may be inadequate, because osteonal bone remodeling is absent in the murine cortical bone.76,77 However, this particular possibility gives a better chance to observe age-related maturation effects in the cortical bone mineral in rats. Even that in our case it was impossible to separate cortical from trabecular bone components of the tiny cranial bone pieces, so the R1–R180 samples also contained trabecular bone tissue. The amount and structure of the bone mineral must be dependent on the rat development,78 so the samples studied should be related to the stages of development. Rats grow very fast after birth and are weaned at 21 days. Our one-day-old rats (R1) correspond to nine-day-old human neonates. The sample R30 was collected from female rats just before reaching sexual maturity (32–34 days), which equates to human girls from about 10 years of age. The 90 day-old rats (R90) and 180 day-old rats (R180) can be considered as typical teenagers and adults, respectively.
The results obtained for the hydroxyl content (Table 2) range from 5 to 10%, with reference to stoichiometric hydroxyapatite. These values are lower than the 15% predicted for bone mineral from analytical chemical formulae5,13,14,29,30 or the 21% measured by CP MAS NMR in human bone mineral.41 However, the values all are above those for Raman, which are below 5%.13 It must be emphasized that the Raman OH− bands were missing from our animal bone spectra. We submit that the DF MAS NMR method allowed us to confidently correct the hydroxyl level in the same human enamel sample that had been studied in previous work42 and estimated at that time with OH− at 73%. The present, new value of 43% agrees well with the value of 45% resulting from the analytical chemical formula and that of 40% obtained by Vyalikh et al.14,45 Furthermore, the OH− concentration in the human cortical bone sample B1 studied in previous work40 has now been measured as 24% by reference to stoichiometric hydroxyapatite, which is very close to the value of 21% obtained by Cho et al.41 Thus, our DF MAS NMR method yields accurate results and is also sufficiently precise (cf. standard errors) to determine interspecies differences in the OH− concentration (pig vs. rats), as well as to monitor subtle changes in OH− content with aging (Table 2).
Interspecies comparison of the OH− concentration is difficult because of uncertainty about matching the age of animals to be examined.78 It is clear from Table 2 that, for the one-day-old pig, apatite mineral characteristics such as crystal size, crystallinity and carbonate content, together with the mineral content of bone, correspond to 30 day-old rather than to one-day-old rats. However, no matter which rat samples are chosen for the comparison, the hydroxyl content in the murine mineral is significantly higher than that in the porcine mineral.
The dependence of apatite OH− concentration on age was studied in the female rat model (R1–R180 in Table 2). The specimens of cranial bone comprised both cortical and trabecular tissues, the former lacking of osteonal remodeling and the latter having the remodeling period of about 2 weeks (inferred from studies of distal femurs of eight month old male mice).76 Because of a decrease in remodeling rate with aging, aging bone is expected to increase its mineral/matrix ratio and gradually acquire a higher percentage of older, more mature mineral crystals with better crystallinity, higher carbonate and lower hydrogen phosphate content.6,11 Such trends are generally confirmed by our results shown in Table 2. The peak values of crystallinity, bone mineral content and mineral hydroxyl content for R90 are perhaps associated with the fact that age-related cancellous bone loss begins at about three months of age for rodents.76 We note a lower hydroxyl level of about 8.0–7.5% for R1 and R30, followed by a spectacular jump to about 10% for R90 and R180. Thus, the lower hydroxyl level is maintained in the bone mineral during a fast increase of cortical thickness in female rats, which occurs approximately during the first 30 days after birth.27 The sudden jump in OH− between R30 and R90 we tentatively ascribe to female rats reaching sexual maturity at the age of 32–34 days.78 It appears that later on (R90 and R180), during transition from the adolescent to the adult period of life, the OH− level in the rat bone mineral remains relatively constant. All the above findings on OH− indicate that the hydroxyl content of the apatite bone mineral is mostly regulated in rats by biological processes, not by chemical, thermodynamically driven apatite maturation, which would have caused its monotonic evolution.79 Although the more mature apatite crystals for R90 and R180, bigger in size and with better crystallinity, certainly contain significantly higher levels of OH− than R1 and R30. The coincident increase in crystallinity and carbonates of the apatite mineral with animal age observed by us (Table 2) and others looks troublesome.6,11 We submit that carbonates may accumulate in the hydrated surface layer of the apatite crystals, so they do not deteriorate their crystal lattice.
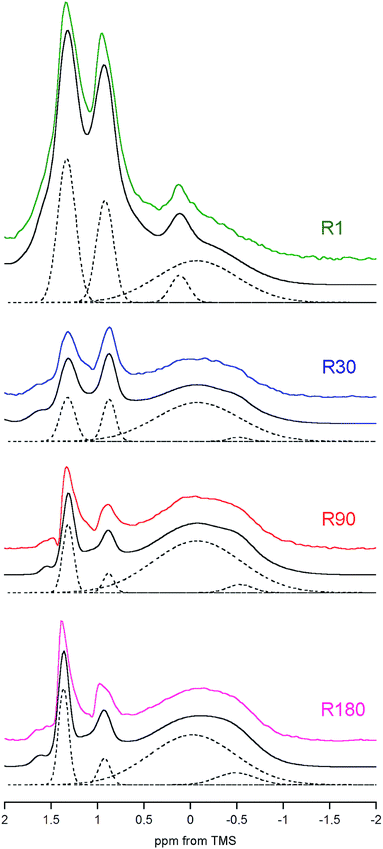
We have already shown that the DF MAS NMR method is capable of providing reliable results, suitable for the discussion of interspecies and age-related differences in the hydroxyl concentration of bone mineral. In addition, it is also useful to observe a heterogeneous nature of the apatite hydroxyl 1H MAS NMR signal (Fig. 5). The composite structure of the OH− signal was found in synthetic nanocrystalline apatites80 and was then explained by up and down orientation of columnar hydroxyl ions and by their interaction with water molecules at surface terminations.60 In bone, such component lines cannot be resolved, because they are too broad. However, in the R1 spectrum there was a distinct, single extra peak at 0.12 ppm, accompanying the major OH− signal at −0.1 ppm (Fig. 5; chemical shifts from deconvolutions). A peak like that has been observed for octacalcium phosphate (OCP) and explained by formation of hydroxyl ions by hydrolysis of phosphates associated with P2 and P4 crystallographic sites.81 Since OCP has been found in rat calvarial tissue82 and rat tibia83 during mineralization, we assign this R1 extra peak at 0.12 ppm to hydroxyl ions in OCP.
In the R30, R90 and R180 spectra there are also small peaks at about −0.5 ppm (Fig. 5), with growing contributions of 2.5, 4.3 and 9.1%, respectively, to the total OH− intensity from both major (−0.1 ppm) and minor (−0.5 ppm) resonances. Respective full width at half maximum (FWHM) values (±SE) for the minor peak are 100 ± 14, 134 ± 3 and 184 ± 4 Hz, while the major signal has a quite stable FWHM as it is limited to the 416–440 Hz range. In the pig bone spectrum the minor peak is also present, it has the same chemical shift of −0.5 ppm and an intensity of 9.4% (FWHM = 168 ± 4 Hz). The chemical shift of −0.5 ppm indicates that the corresponding OH− ions are much less involved in molecular interactions than those attributed to the main hydroxyl signal at −0.1 ppm. At the present stage of research, any assignment of the minor peak at −0.5 ppm must be speculative. It may very well be that this peak is from terminal hydroxyl ions in the columnar arrangements15–17 OH OH⋯OH OH  , like that highlighted in the preceding scheme. The remaining hydroxyl ions would contribute to the main signal at −0.1 ppm. With aging, the apatite crystals grow and organize their crystal lattice (Table 2), so the terminal OH− ions become less mobile (more confined) as far as their hindered rotations (librations) are concerned and hence the FWHM of their peak at −0.5 ppm increases. Then, one should bear in mind that the apatite mineral remains highly deficient in structural OH− ions over the whole rat life, regardless of the already discussed jump in concentration between the 30 and 90 days of age. In such circumstances, on maturation, it may be thermodynamically favorable for the apatite crystals to have more defragmented OH− columns, that is, a variety of short OH− strips disposed along the crystallographic c-axis (higher crystal entropy). In consequence, the population of those terminal hydroxyl ions would grow and so would their potential peak at −0.5 ppm (cf. the increase from R30 to R180 in Fig. 5). Other assignments of the minor hydroxyl peaks are still open to debate.
, like that highlighted in the preceding scheme. The remaining hydroxyl ions would contribute to the main signal at −0.1 ppm. With aging, the apatite crystals grow and organize their crystal lattice (Table 2), so the terminal OH− ions become less mobile (more confined) as far as their hindered rotations (librations) are concerned and hence the FWHM of their peak at −0.5 ppm increases. Then, one should bear in mind that the apatite mineral remains highly deficient in structural OH− ions over the whole rat life, regardless of the already discussed jump in concentration between the 30 and 90 days of age. In such circumstances, on maturation, it may be thermodynamically favorable for the apatite crystals to have more defragmented OH− columns, that is, a variety of short OH− strips disposed along the crystallographic c-axis (higher crystal entropy). In consequence, the population of those terminal hydroxyl ions would grow and so would their potential peak at −0.5 ppm (cf. the increase from R30 to R180 in Fig. 5). Other assignments of the minor hydroxyl peaks are still open to debate.
We are aware of several research limitations: only four bone samples were studied from rats of various ages, male rats should also be included, other vertebrates are necessary for comparisons and bones other than cranial should be considered, preferably with a clear distinction between the cortical and trabecular tissue. However, we offer this DF MAS NMR method, which is accurate for the determination of hydroxyl ions in biological apatites in the presence of the organic matrix, and with it all the envisaged research routes that can be followed in the future.
Conclusions
Ultra-high speed MAS fails to resolve the proton NMR hydroxyl peak in biological apatites in the presence of the organic matrix. Under such circumstances, we have proposed the application of a multiple-pulse dipolar filter in order to differentiate various environments in bone and other apatite-containing tissues on the basis of their different proton spin–spin relaxation. The dipolar filter is easy to tune, works well under slow MAS with regular solid-state NMR probes and allows relative enhancement of the major proton hydroxyl peak at −0.1 ppm over interfering neighboring resonances, exposing it to reliable quantitative analysis. We have suggested an adequate and convenient methodology to determine the hydroxyl content, which yields accurate and sufficiently precise results to monitor bone mineral hydroxylation in different species and over the animal lifetime. The dipolar filter spectra are also useful to study details of hydroxyl peaks and the structure of bone marrow adipose tissue.The hydroxyl content was determined in the cranial bone mineral of pig and rats to be in the 5–10% range by reference to stoichiometric hydroxyapatite. It was found to be dependent on species (pig vs. rats) and animal age in rats. The hydroxyl content in murine mineral is significantly higher than that in porcine mineral. In rats, the hydroxyl content shows a stepwise increase with age, which is governed by biological processes rather than by chemical, thermodynamically driven apatite maturation. In the neonate rat bone, octacalcium phosphate has been detected (peak at 0.12 ppm). Two significant processes that progress with rat age have been inferred: defragmentation of hydroxyl columns in the bone mineral, when the hydroxyl-deficient biological apatite undergoes maturation (considering the peak at −0.5 ppm), and accumulation of carbonates in the hydrated surface layer of the apatite crystals, as those ions do not affect apatite crystallinity. Our results are consistent with the inverse relationship between bone mineral density and bone marrow adipose tissue. Besides, they demonstrate that the related ratio of longer-chain to shorter-chain triacylglycerols increases with aging.
When testing the dipolar filter method, we also returned to previously studied human samples of enamel and bone. The hydroxyl content in enamel was corrected at 43%, while that in cortical bone mineral was measured at 24%, both values in reference to stoichiometric hydroxyapatite. Overall, proton MAS NMR spectroscopy used with the dipolar filter, as proposed in this work, was found to be suitable for monitoring the hydroxyl level in the apatite mineral of calcified tissues.
Finally, one may anticipate a broader chemical context and outcome for this work. Hydroxyl groups can take part in the structure-forming of geological minerals (e.g. clays) and novel synthetic materials, nanostructured or mesoporous, designed for various purposes. Furthermore, hydroxyl groups can participate in interfacial and interstitial phenomena (formation of a surface layer, adsorption, particle aggregation, intercalation, occlusion, confinement of various molecules in intracrystalline spaces and inside mesopores), which affect and/or determine the functions of those solids. Thus, a potential application of proton MAS NMR used with the dipolar filter can be expected to be the study of OH-involving interactions in geochemistry, environmental and material science, heterogeneous catalysis, host–guest chemistry, and pharmaceutical (specific drug carriers) and medicinal chemistry (dental and prosthetic materials).
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
The Medical University of Warsaw is acknowledged for the research grant FW23/N/18. The authors are grateful to Dr Janusz Skonieczny for recording the proton spectra of collagen, R90 and HA with MAS at 60 kHz.References
- R. Z. LeGeros, Calcium phosphates in oral biology and medicine, Monogr. Oral Sci., S. Karger, Basel, 1991, vol. 15 Search PubMed.
- H. Aoki, Science and Medical Applications of Hydroxyapatite, Takayama Press, Tokyo, 1991 Search PubMed.
- J. C. Elliot, Structure and Chemistry of the Apatites and Other Calcium Orthophosphates, Studies in inorganic chemistry, Elsevier, Amsterdam, 1994, vol. 18 Search PubMed.
- B. Wopenka and J. D. Pasteris, Mater. Sci. Eng., C, 2005, 25, 131–143 CrossRef.
- C. Rey, C. Combes, C. Drouet and H. Sfihi, Adv. Sci. Technol., 2006, 49, 27–36 CAS.
- M. J. Glimcher, Rev. Mineral. Geochem., 2006, 64, 223–282 CrossRef CAS.
- M. J. Olszta, X. Cheng, S. S. Jee, R. Kumar, Y.-Y. Kim, M. J. Kaufman, E. P. Douglas and L. B. Gower, Mater. Sci. Eng., R, 2007, 58, 77–116 CrossRef.
- C. Rey, C. Combes, C. Drouet, A. Lebugle, H. Sfihi and A. Barroug, Materialwiss. Werkstofftech., 2007, 38(12), 996–1002 CrossRef CAS.
- D. Farlay and G. Boivin, in Osteoporosis, ed. Y. Dionyssiotis, In Tech Europe, Rijeka, Croatia, 2012, ch. 1, pp. 1–32, DOI:10.5772/29091, https://www.intechopen.com/books/osteoporosis/bone-mineral-quality, accessed February 2019.
- Y. Bala, D. Farlay and G. Boivin, Osteoporosis Int., 2012, 24(8), 2153–2166 CrossRef PubMed.
- A. L. Boskey, BoneKEy Rep., 2013, 2, 447–458 Search PubMed.
- Y. Bala and E. Seeman, Calcif. Tissue Int., 2015, 97, 308–326 CrossRef CAS PubMed.
- C. Rey and C. Combes, in Biomineralization and Biomaterials: Fundamentals and Applications, Woodhead Publishing Series in Biomaterials 104, ed. C. Aparicio and M. P. Ginebra, Woodhead Publishing, Sawston, Cambridge, U.K., 2016, ch. 3, pp. 95–127 Search PubMed.
- C. Combes, S. Cazalbou and C. Rey, Minerals, 2016, 6, 34–58, DOI:10.3390/min6020034.
- J. D. Pasteris, B. Wopenka, J. J. Freeman, K. Rogers, E. Valsami-Jones, J. A. M. van der Houwen and M. J. Silva, Biomaterials, 2004, 25, 229–238 CrossRef CAS PubMed.
- J. D. Pasteris, C. H. Yoder and B. Wopenka, Am. Mineral., 2014, 99(1), 16–27 CrossRef CAS.
- V. Uskoković, RSC Adv., 2015, 5, 36614–36633 RSC.
- M. E. Fleet and X. Liu, Biomaterials, 2005, 26, 7548–7554 CrossRef CAS PubMed.
- J. D. Pasteris, C. H. Yoder, M. P. Sternlieb and S. Liu, Mineral. Mag., 2012, 76(7), 2741–2759 CrossRef CAS.
- J.-D. P. McElderry, P. Zhu, K. H. Mroue, J. Xu, B. Pavan, M. Fang, G. Zhao, E. McNerny, D. H. Kohn, R. T. Franceschi, M. M. Banaszak Holl, M. M. J. Tecklenburg, A. Ramamoorthy and M. D. Morris, J. Solid State Chem., 2013, 206, 192–198 CrossRef CAS PubMed.
- M. Wang, R. Qian, M. Bao, C. Gu and P. Zhu, Mater. Lett., 2018, 210, 203–206 CrossRef CAS.
- L. Pajchel and W. Kolodziejski, J. Nanopart. Res., 2013, 15, 1868–1882 CrossRef PubMed.
- S. Krukowski, N. Lysenko and W. Kolodziejski, J. Solid State Chem., 2018, 264, 59–67 CrossRef CAS.
- S. Rollin-Martinet, A. Navrotsky, E. Champion, D. Grossin and C. Drouet, Am. Mineral., 2013, 98, 2037–2045 CrossRef CAS.
- J. L. Meyer, Calcif. Tissue Int., 1979, 27, 153–160 CrossRef CAS PubMed.
- A. J. Taylor, E. Rendina, B. J. Smith and D. H. Zhou, Chem. Phys. Lett., 2013, 588, 124–130 CrossRef CAS PubMed.
- M. C. Diamond, Brain Res. Rev., 1987, 12, 235–240 CrossRef CAS.
- C. Tarnowski, M. A. Ignelzi Jr and M. D. Morris, J. Bone Miner. Res., 2002, 17(6), 1118–1126 CrossRef PubMed.
- R. Legros, N. Balmain and G. Bonel, J. Chim. Phys. Phys. Chim. Biol., 1986, 1, 8–9 Search PubMed.
- R. Legros, N. Balmain and G. Bonel, Calcif. Tissue Int., 1987, 41, 137–144 CrossRef CAS PubMed.
- S. Koutsopoulos, J. Biomed. Mater. Res., 2002, 62(4), 600–612 CrossRef CAS PubMed.
- R. M. Biltz and E. D. Pellegrino, Calcif. Tissue Res., 1971, 7, 259–263 CrossRef CAS PubMed.
- G. Penel, E. Cau, C. Delfosse, C. Rey, P. Hardouin, J. Jeanfils, C. Delecourt, J. Lemaitre and G. Leroy, Dent. Med. Probl., 2003, 40(1), 37–43 Search PubMed.
- C.-K. Loong, C. Rey, L. T. Kuhn, C. Combes, Y. Wu, S.-H. Chen and M. J. Glimcher, Bone, 2000, 26, 599–602 CrossRef CAS PubMed.
- M. G. Taylor, S. F. Parker, K. Simkiss and P. C. H. Mitchell, Phys. Chem. Chem. Phys., 2001, 3, 1514–1517 RSC.
- J. P. Yesinowski and H. Eckert, J. Am. Chem. Soc., 1987, 109, 6274–6282 CrossRef CAS.
- C. Rey, J. L. Miquel, L. Facchini, A. P. Legrand and M. J. Glimcher, Bone, 1995, 16, 583–586 CrossRef CAS PubMed.
- W. Kolodziejski, Top. Curr. Chem., 2005, 246, 235–270 CrossRef CAS PubMed.
- A. Kaflak, D. Chmielewski, A. Górecki and W. Kolodziejski, Solid State Nucl. Magn. Reson., 1998, 10, 191–195 CrossRef CAS PubMed.
- A. Kaflak and W. Kolodziejski, Magn. Reson. Chem., 2008, 46, 335–341 CrossRef CAS PubMed.
- G. Cho, Y. Wu and J. L. Ackerman, Science, 2003, 300, 1123–1127 CrossRef CAS PubMed.
- J. Kolmas and W. Kolodziejski, Chem. Commun., 2007, 4390–4392 RSC.
- M. J. Duer, T. Friscić, R. C. Murray, D. G. Reid and E. R. Wise, Biophys. J., 2009, 96, 3372–3378 CrossRef CAS PubMed.
- M. J. Duer, J. Magn. Reson., 2015, 253, 98–110 CrossRef CAS PubMed.
- A. Vyalikh, R. Mai and U. Scheler, Bio-Med. Mater. Eng., 2013, 23, 507–512 CAS.
- K. H. Mroue, Y. Nishiyama, M. K. Pandey, B. Gong, E. McNerny, D. H. Kohn, M. D. Morris and A. Ramamoorthy, Sci. Rep., 2015, 5, 11991–12000 CrossRef PubMed.
- C. Singh, R. K. Rai, A. M. Kayasthab and N. Sinha, Magn. Reson. Chem., 2016, 54, 132–135 CrossRef CAS PubMed.
- K. Schmidt-Rohr, A. Rawal and X.-W. Fang, J. Chem. Phys., 2007, 126, 054701–054716 CrossRef CAS PubMed.
- Y.-Y. Hu, X. P. Liu, X. Ma, A. Rawal, T. Prozorov, M. Akinc, S. K. Mallapragada and K. Schmidt-Rohr, Chem. Mater., 2011, 23(9), 2481–2490 CrossRef CAS.
- M. Hong and K. Schmidt-Rohr, Acc. Chem. Res., 2013, 46(9), 2154–2163 CrossRef CAS PubMed.
- W. T. Tsai and J. C. C. Chan, Annu. Rep. NMR Spectrosc., 2011, 73, 1–61 CrossRef.
- N. Egger, K. Schmidt-Rohr, B. Blümich, W.-D. Domker and B. Stapp, J. Appl. Polym. Sci., 1992, 44, 289–295 CrossRef CAS.
- P. Sun, Q. Dang, B. Li, T. Chen, Y. Wang, H. Lin, Q. Jin and D. Ding, Macromolecules, 2005, 38, 5654–5667 CrossRef CAS.
- X. Wang, Q. Gu, Q. Sun, D. Zhou, P. Sun and G. Xue, Macromolecules, 2007, 40, 9018–9025 CrossRef CAS.
- X. Wang, F. Tao, P. Sun, D. Zhou, Z. Wang, Q. Gu, J. Hu and G. Xue, Macromolecules, 2007, 40, 4736–4739 CrossRef CAS.
- S. N. Danilchenko, O. V. Kalinkevich, M. V. Pogorelov, A. N. Kalinkevich, A. M. Sklyar, T. G. Kalinichenko, V. Y. Ilyashenko, V. V. Starikov, V. I. Bumeyster, V. Z. Sikora, L. F. Sukhodub, A. G. Mamalis, S. N. Lavrynenko and J. J. Ramsden, J. Biol. Phys. Chem., 2009, 9, 119–126 CrossRef CAS.
- M. Figueiredo, A. Fernando, G. Martins, J. Freitas, F. Judas and H. Figueiredo, Ceram. Int., 2010, 36(8), 2383–2393 CrossRef CAS.
- L. D. Mkukuma, J. M. S. Skakle, I. R. Gibson, C. T. Imrie, R. M. Aspden and D. W. L. Hukins, Calcif. Tissue Int., 2004, 75, 321–328 CrossRef CAS PubMed.
- M. Jarlbring, D. E. Sandstrom, O. N. Antzutkin and W. Forsling, Langmuir, 2006, 22, 4787–4792 CrossRef CAS PubMed.
- M. B. Osman, S. Diallo-Garcia, V. Herledan, D. Brouri, T. Yoshioka, J. Kubo, Y. Millot and G. Costentin, J. Phys. Chem. C, 2015, 119, 23008–23020 CrossRef.
- R. K. Rai, C. Singh and N. Sinha, J. Phys. Chem. B, 2015, 119, 201–211 CrossRef CAS PubMed.
- K. Strobel, J. van den Hoff and J. Pietzsch, J. Lipid Res., 2008, 49, 473–480 CrossRef CAS PubMed.
- D. K. W. Yeung, S. L. Lam, J. F. Griffith, A. B. W. Chan, Z. Chen, P. H. Tsang and P. C. Leung, Chem. Phys. Lipids, 2008, 151, 103–109 CrossRef CAS PubMed.
- J. Ren, I. Dimitrov, A. D. Sherry and C. R. Malloy, J. Lipid Res., 2008, 49, 2055–2062 CrossRef CAS PubMed.
- Y. X. Pang and X. Bao, J. Eur. Ceram. Soc., 2003, 23, 1697–1704 CrossRef CAS.
- S. Weiner and O. Bar-Yosefa, J. Archaeol. Sci., 1990, 17, 187–196 CrossRef.
- T. A. Surovell and M. C. Stiner, J. Archaeol. Sci., 2001, 28, 633–642 CrossRef.
- A. Grunewald, C. Keyser, A. M. Sautereau, E. Crubezy, B. Ludes and C. Drouet, J. Archaeol. Sci., 2014, 49, 134–141 CrossRef.
- K. J. Suchacki and W. P. Cawthorn, Curr. Mol. Biol. Rep., 2018, 4, 41–49, DOI:10.1007/s40610-018-0096-8.
- M. Elia, Eur. J. Clin. Nutr., 2012, 66, 979–982 CrossRef CAS PubMed.
- A. V. Schwartz, Front. Endocrinol., 2015, 6, 40–45, DOI:10.3389/fendo.2015.00040.
- R. H. Houtkooper, C. Argmann, S. M. Houten, C. Canto, E. H. Jeninga, P. A. Andreux, C. Thomas, R. Doenlen, K. Schoonjans and J. Auwerx, Sci. Rep., 2011, 1, 134–144 CrossRef PubMed.
- K. M. Connor, Y. Hsu, P. K. Aggarwal, S. Capone, A. R. Colombo and G. Ramsingh, Exp. Hematol. Oncol., 2018, 7, 13–23 CrossRef PubMed.
- Z. Li, J. Hardij, D. P. Bagchi, E. L. Scheller and O. A. MacDougald, Bone, 2018, 110, 134–140 CrossRef CAS PubMed.
- C. Gillet and J. Rasschaert, Cur. Mol. Biol. Rep., 2018, 4, 8–15, DOI:10.1007/s40610-018-0086-x.
- R. L. Jilka, J. Gerontol., Ser. A, 2013, 68(10), 1209–1217 CrossRef PubMed.
- E. Bonucci and P. Ballanti, Toxicol. Pathol., 2014, 42, 957–969 CrossRef CAS PubMed.
- P. Sengupta, Int. J. Prev. Med., 2013, 4(6), 624–630 Search PubMed.
- S. Rollin-Martinet, A. Navrotsky, E. Champion, D. Grossin and C. Drouet, Am. Mineral., 2013, 98, 2037–2045 CrossRef CAS.
- L. Pajchel, V. Kowalska, D. Smolen, A. Kedzierska, E. Pietrzykowska, W. Lojkowski and W. Kolodziejski, Mater. Res. Bull., 2013, 48, 4818–4825 CrossRef CAS.
- Y.-H. Tseng, J. Zhan, K. S. K. Lin, C.-Y. Mou and J. C. C. Chan, Solid State Nucl. Magn. Reson., 2004, 26, 99–104 CrossRef CAS PubMed.
- N. J. Carane, V. Popescu, M. D. Morris, P. Steenhuis and M. A. Ignelzi Jr, Bone, 2006, 39, 434–442 CrossRef PubMed.
- P. Simon, D. Grüner, H. Worch, W. Pompe, H. Lichte, T. E. Khassawna, C. Heiss, S. Wenisch and R. Kniep, Sci. Rep., 2018, 8, 13696–13712 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra01902b |
| This journal is © The Royal Society of Chemistry 2019 |