 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Investigating the draw ratio and velocity of an electrically charged liquid jet during electrospinning
Chenhui Dinga,
Hong Fanga,
Gaigai Duan *b,
Yan Zouc,
Shuiliang Chen
*b,
Yan Zouc,
Shuiliang Chen a and
Haoqing Hou
a and
Haoqing Hou *a
*a
aCollege of Chemistry and Chemical Engineering, Jiangxi Normal University, Nanchang 330027, China. E-mail: haoqing@jxnu.edu.cn; Tel: +86 791 8812 0389
bCollege of Materials Science and Engineering, Nanjing Forestry University, Nanjing 210037, China. E-mail: duangaigai@njfu.edu.cn; Tel: +86 25 85428090
cDepartment of Mechanics, Huazhong University of Science and Technology, Wuhan 430074, China
First published on 2nd May 2019
Abstract
The investigation of the draw ratio and velocity of an electrospinning polymer solution jet is of great interest for understanding the formation of nanofibers. During the electrospinning process, the charged polymer solution jets were stretched by electric force, resulting in the formation of ultrathin fibers. In this study, theoretical deduction and experimental calculation were applied to evaluate the velocities and draw ratios of the charged jets at different electrospinning stages. Depending on the diameter of the charged jets at different electrospinning stages, the velocities and draw ratios of the charged jets were calculated with values far lower than the data in a previous report. The theoretical calculation was compared with experimental data using polyamic acid as a model polymer for electrospinning. The results indicated that during electrospinning, as the collecting distance was increased from 0 to 30 cm, the diameter of the electrospinning jet decreased from 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 nm to a constant value of around 245 nm, the solvent in the jet decreased from 96.50 wt% to 25.45 wt%, and the density of the jet increased from 0.9504 to 1.0995 g cm−3. These parameters led to the draw ratio and velocity of the jet experiencing first an increase and then a decrease in the value, and the highest draw ratio and velocity were 869 and 867 m s−1, respectively, which are quite different from the data in previous reports.
800 nm to a constant value of around 245 nm, the solvent in the jet decreased from 96.50 wt% to 25.45 wt%, and the density of the jet increased from 0.9504 to 1.0995 g cm−3. These parameters led to the draw ratio and velocity of the jet experiencing first an increase and then a decrease in the value, and the highest draw ratio and velocity were 869 and 867 m s−1, respectively, which are quite different from the data in previous reports.
1. Introduction
As one of the effective technologies for producing fibers with an ultrathin fiber diameter, electrospinning has attracted much attention recently1,2 due to new perspectives for numerous applications in a broad range of areas, such as tissue engineering,3,4 heavy metal detection,5 filtration,6–10 oil/water separation,11–14 catalysts,15–19 sensitive and responsive materials,20–24 nanofiber reinforced composites,25,26 high efficiency electrodes in electrochemical cells,27–30 heat resistant materials,31 white light-emitting materials,32,33 and sponge materials.34–36 During the electrospinning process, an electrically charged jet is created from a pendant droplet of polymer solution. After forming a nearly straight line, it is bent into a complex path and other changes in shape occur under the stretch of electric forces. Surprisingly, the liquid jet can be drawn in a strong electric field during the electrospinning process.37–40 Polymer chains in electrospun polymer fibers are oriented under the induction of an electric field.41 The orientation of the polymer chains depends on the draw ratio.42 It is very important to investigate the draw ratio of the electrospinning charged jet because the draw ratio will significantly affect the molecular orientation, and therefore influence the physical properties, especially the mechanical properties.43–46 There are some studies aimed at deducing the velocity of jet and the draw ratio.38,47–53 However, because of the complexity of the electrospinning process, too many electrospinning parameters, such as polymers, concentration, evaporation of solvent, flow rate, should be considered, which leads to the difficulties in proposing a universal model to deduce the draw ratio and velocity of the electrospinning jet. For example, in a very early study, the draw ratio of electrospun fibers was evaluated using an aqueous solution of polyethylene oxide (PEO).38 In that study, the starting diameter of a PEO solution jet with a concentration of 6% was assumed to be 100 μm and the final diameter of the fibers was 100 nm. Then, the draw ratio would be 106 without accounting for the evaporation of solvent. If considering the evaporation of the solvent, the draw ratio would be 0.06 × 106 = 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Furthermore, the velocity at the nanofiber end of the jet was deduced to be about 60
000. Furthermore, the velocity at the nanofiber end of the jet was deduced to be about 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m s−1, which was 176 times faster than the speed of sound in air, which is more than five times faster than the speed that objects need to get out of the Earth's atmosphere (second cosmic velocity = 11
000 m s−1, which was 176 times faster than the speed of sound in air, which is more than five times faster than the speed that objects need to get out of the Earth's atmosphere (second cosmic velocity = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 m s−1).38 However, it is well-known that the draw ratio of conventional fibers is in the range of 5 to 40.54 Even for the ultra-high molecular weight polyethylene fibers, the draw ratio is merely 35
200 m s−1).38 However, it is well-known that the draw ratio of conventional fibers is in the range of 5 to 40.54 Even for the ultra-high molecular weight polyethylene fibers, the draw ratio is merely 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0,55 which is much lower than the draw ratio in a previous report.38 In another recent research, Zheng et al. developed a model to simulate the dynamic processes that occurs during electrospinning.47 Their simulation demonstrated that when the simulation voltage was 5 kV, the maximum velocity was about 2 m s−1; which was quite inconsistent with 60
0,55 which is much lower than the draw ratio in a previous report.38 In another recent research, Zheng et al. developed a model to simulate the dynamic processes that occurs during electrospinning.47 Their simulation demonstrated that when the simulation voltage was 5 kV, the maximum velocity was about 2 m s−1; which was quite inconsistent with 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m s−1.
000 m s−1.
Therefore, it is still necessary to develop a new way to evaluate the draw ratios and velocities of charged jets during electrospinning. In the present study, the draw ratio and velocity of jet were deduced based on the mass conservation of the polymer in the initial selected jet with a certain length. The mass of the polymer in the initial selected length remains constant even when the selected jet is elongated at different electrospinning times. Therefore, the model does not need to consider all of the complex electrospinning parameters but to consider the concentration and the diameter of the jet, which can be easily obtained as shown in the following sections. To show the application of the model in this study, a typical example is applied, in which the polyamic acid (PAA) is electrospun into nanofibers. The corresponding draw ratios and velocities of the charged jets during electrospinning are also calculated.
2. Materials and methods
2.1. Materials
3,3′,4,4′-Biphenyltetracarboxylic dianhydride (BPDA) was supplied by Hebei Jida Plastic Products Co., China and 4,4′-diaminodiphenyl ether (ODA) was bought from Quzhou Kaiyuan Fine Chem. Co., China. These two monomers were purified by sublimation before use. N,N′-Dimethylacetamide (DMAc, 99%) was supplied by Tianjin Fu Chen Chemical Reagent Factory, China. It was used as received.2.2. Preparation of polyamic acid (PAA) solution
The precursor of polyimide, polyamic acid (PAA) of BPDA/ODA was synthesized from an equal molar of dianhydride BPDA with diamine ODA. The polycondensation was performed in DMAc at −4–0 °C for 24 h and the solid contents of PAA solution was maintained to 10 wt%. The intrinsic viscosity of PAA was 4.5 dL g−1.2.3. Electrospinning
Before electrospinning, the 10 wt% PAA solution was diluted to 3.5 wt% by DMAc. During electrospinning, the voltage applied to the pendant drop and grounded collector was set to +20 kV and −5 kV. The flow rate was set to 1 mL h−1. The temperature and humidity for electrospinning were 20 °C and 30%, respectively. PAA nanofibers were collected by a water bath with different collecting distances. The obtained PAA fibrous mats were dried in a vacuum oven at 70 °C for 24 h to completely remove the solvent inside. The weights of the PAA fibrous mats at different collecting distances were measured before and after drying to give the concentration of polymers in the fibers.2.4. Characterization
A scanning electron microscope (SEM, FEI Quanta 200 FEG) was used to observe the morphology of the electrospun fibers. The fiber diameter was measured using the Image J software. The intrinsic viscosity of PAA was measured by an Ubbelohde viscosity meter at 25 °C using DMAc as solvent.3. Results and discussion
3.1. Symbols used in this work
In this study, many symbols are used. Their definitions and corresponding units are listed in Table 1.| Symbol | Definition | Unit |
|---|---|---|
| S1 | Cross-sectional area of straight segment | μm2 |
| S2 | Cross-sectional area of final nanofiber jets | μm2 |
| Δl1 | Differential length of straight segment jet | nm |
| Δl2 | Differential length of charged bending fiber jet | nm |
| υ1 | Velocity of straight segment of jet | m s−1 |
| υ2 | Velocity of charged bending fiber jet | m s−1 |
| Qs | Consumption of spinning solution | mL |
| Qp | Consumption of polymer | g |
| Vs | Flow rate of spinning solution | mL h−1 |
| t | Electrospinning time | h |
| d1 | Diameter of the straight segment of jet | μm |
| d2 | Diameter of charged bending fiber jet | nm |
| C1 | Concentration of polymer solution | |
| C2 | Percentage of polymer in bending fiber jet | |
| ρ1 | Density of straight segment of jet | g cm−3 |
| ρ2 | Density of charged bending fiber jet | g cm−3 |
| @ | Draw ratio |
3.2. Diameter in the straight segment of jets
In an electrospinning process, the pendant drop of polymer solution is first stretched into a straight linear part with a length of several millimeters to a few centimeters due to the electrical force, then it is bent and forms a loop-shaped fiber jet, as shown in Fig. 1. If the jet including the linear part and the loop-shaped part is an uninterrupted single jet and the electrospinning solution is only from the single jet, then the consumption of spinning solution is equal to the volume of spinning solution. Denoting the cross-sectional area of the straight segment of charged jet by S1, velocity by υ1, spinning time by t, the consumption of spinning solution Qs is given by:| Qs = υ1tS1 | (1) |
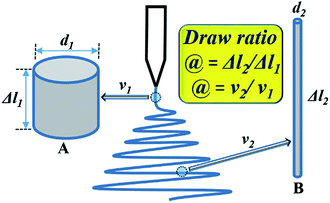 | ||
| Fig. 1 Schematic of an electrospinning jet model. (A) Straight segment and (B) charged bending fiber jet. | ||
The flow rate of the solution, Vs, is therefore:
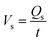 | (2) |
Combining eqn (1) and (2), and accounting for the fact that S1 = π(d1/2)2, we obtained eqn (3) for the initial diameter of the jet,
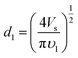 | (3) |
If the velocity along the straight segment υ1 is known, then it is possible to calculate the diameter d1. Warner et al.56 measured the velocities along the straight segment υ using laser Doppler velocimetry and reported that the velocity ranged from 1 to 15 m s−1. Therefore, according to eqn (3), the diameter of the straight segment decreases from 18.8 Vs1/2 to 4.9 Vs1/2 μm. The diameter of the straight jet is large at the beginning and small at the end.
3.3. Draw ratio of jet in electrospinning
In the previous section, the diameter of the straight segment jet can be easily calculated, varying from 4.9 Vs1/2 to 18.8 Vs1/2 μm. Here, we assume that the flow rate of the spinning solution Vs is 1 mL h−1, so the biggest diameter is 18.8 μm. When the flow rate Vs reaches up to 2 mL h−1, the diameter is no more than 26.6 μm, which is still much less than that of 100 μm estimated in a previous report.38Electrospun fibers experience quite a different fiber drawing process from the conventional dry-spinning fibers. The dry-spinning process begins with one solid state and ends with the other solid state. The densities of the two solid states are different, but the quantity of the solid remains the same. However, due to the very fast evaporation and removal of solvent in electrospinning, there is a change in the quantity from a liquid jet to solidified fibers. So, the mass of polymer in the two parts is equal,
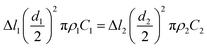 | (4) |
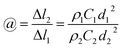 | (5) |
Combining this expression with eqn (3) gives
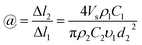 | (6) |
In a previous study,38 the mass concentration of 6% PEO was treated as a volume mass concentration, which is defined as the weight of the solute in a 100 mL solution. The flow rate of the spinning solution is 1 mL h−1, the velocity of jet in a straight segment is 1 m s−1, assuming that the density of the PEO nanofibers was 1.3 g cm−3. According to eqn (6), the draw ratio is 1632 and the final velocity of the PEO nanofiber jet achieved is only 1632 m s−1, which is far below the draw ratio (60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) and the velocity (60
000) and the velocity (60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m s−1) in the previous report.38
000 m s−1) in the previous report.38
3.4. Estimation of jet velocity
The investigation of the velocity of jet is to estimate the draw ratio during the electrospinning process and obtain information about the macromolecular chain orientation. The draw ratio in eqn (6) is deduced from one point of the initial jet to the other point of solidified jet. The velocity of the nanofiber jet υ2 (Δl2 = υ2t) is the product of the draw ratio @ (@ = Δl2/Δl1, eqn (5)) and the starting velocity υ1 (Δl1 = υ1t) of the jet. Therefore,
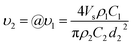 | (7) |
Eqn (7) can also be deduced from another aspect. If we similarly assume that electrospinning under a strong electric field is an uninterrupted single-jet process at all times and that the polymer is consumed completely through the virtual micro-nozzle with a diameter d, then the consumption speed Qp (g) of the polymer can be obtained from the parameters of the velocity of the charged bending fiber jet (υ2, m s−1), the density of the charged bending fiber jet (ρ2, g cm−3), the percentage of polymer in the bending fiber jet (C2), and the cross-sectional area of the final nanofiber jets,
| QP = ρ2(υ2tS2)C2 | (8) |
The consumption of polymer can also be derived from the parameters of consumption of the spinning solution (Qs, mL), the density of the straight segment jet (ρ1, g cm−3), and the concentration of the polymer solution (C1), expressed as the product of the solution concentration C and solution volume, which is given by:
| QP = ρ1QsC1 | (9) |
The flow rate of the spinning solution Vs can be replaced by Qs/t, and S2 is equal to π(d2/2)2. Combining eqn (8) and (9), the velocity of the nanofibers υ2 can be given by:
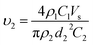 | (10) |
Based on our calculations and derivations, we found that the main unreasonable aspect in ref. 38 was the velocity of the jet at a diameter of 100 μm. When the flow rate of the polymer solution was 1 mL h−1, according to eqn (3), the velocity of the jet with a diameter of 100 μm was 0.0353 m s−1 rather than 1 m s−1. Putting the parameters of the initial jet velocity of 0.0353 m s−1, diameter of 100 μm, final diameter of the fibers of 200 nm density of 1.3 g cm−3, and the solution concentration of 0.06 g mL−1 into eqn (7) gives the final velocity of the nanofibers as 408 m s−1, which is far smaller than 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m s−1.38
000 m s−1.38
3.5. Electrospinning of PAA solution
PAA could immediately be precipitated by dropping PAA solution into water. Herein, in order to get detailed information about the changes in the jet diameter during electrospinning, a water bath is used to collect nanofibers at different collecting distances. The corresponding fiber morphology and the fiber diameter are shown in Fig. 2 and Table 2, respectively. Ribbon-like fibers are formed when the collecting distance is below 8 cm. When the collecting distance is too short, there is still too much solvent in the fibers (more than 90 wt%, Table 2), leading to the collapse of the fiber jets.57,58 The widths of the belts are about 640 nm and 580 nm, which were assumed to be the diameter of the fiber jets at collecting distances of 6 cm and 8 cm, respectively. As the collecting distance increased, the resultant fibers become round and uniform, and the diameter of the fiber jets becomes smaller. When the collecting distance is longer than 15 cm, due to the complete solidification of the jet, the diameter of the resultant PAA fibers are almost constant at around 245 nm.| Collecting distance (cm) | Diameter of jet (nm) | Amount of solvent (%) | Density of jet (g cm−3) | Draw ratioa | Velocityb (m s−1) | |
|---|---|---|---|---|---|---|
| υ1 | υ2 | |||||
| a Draw ratio was calculated from eqn (5).b Velocity υ1 was calculated from eqn (1) and υ2 was calculated from eqn (7). | ||||||
| 0 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
96.50 | 0.9504 | — | 0.998 | |
| 6 | 640 ± 132 | 91.40 | 0.9611 | 347 | 346 | |
| 8 | 580 ± 155 | 90.39 | 0.9632 | 378 | 377 | |
| 10 | 345 ± 106 | 88.24 | 0.9677 | 869 | 867 | |
| 11 | 325 ± 87 | 85.68 | 0.9731 | 799 | 797 | |
| 13 | 256 ± 31 | 74.36 | 0.9968 | 703 | 701 | |
| 15 | 260 ± 29 | 70.38 | 1.0052 | 585 | 584 | |
| 20 | 247 ± 17 | 53.76 | 1.0401 | 401 | 400 | |
| 25 | 243 ± 22 | 26.86 | 1.0965 | 248 | 248 | |
| 30 | 245 ± 15 | 25.45 | 1.0995 | 239 | 239 | |
The densities of polymer PAA (BPDA-PDA) and solvent DMAc are 1.153 g cm−3 and 0.943 g cm−3, respectively. The concentration of the PAA electrospinning solution is 3.5 wt% and the flow rate of the solution is 1 mL h−1. According to eqn (7), the velocity of the final nanofiber jet υ2 can be calculated by:
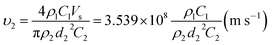 | (11) |
| ρ2 = φDMAcρDMAc + φPAAρPAA | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m s−1 from a previous report.38 Such a high velocity value in the previous report could be attributed to an overestimated initial jet diameter of 100 μm and the velocity of the straight segment at 1 m s−1. First, according to eqn (2), if the flow rate of the spinning solution is 1 mL h−1, the velocity of the jet at a diameter of 100 μm will not be 1 m s−1 but 0.0353 m s−1. Second, according to eqn (3), if the initial flow rate is 1 mL h−1, the jet diameter will be 18.8 μm and the initial jet velocity will be 0.998 m s−1. Then, the draw ratio of the jet can be calculated and is listed in Table 2. When the collecting distance was 10 cm, the draw ratio of the jet was 869, which was highest among other collecting distances, but much lower than the draw ratio of 60
000 m s−1 from a previous report.38 Such a high velocity value in the previous report could be attributed to an overestimated initial jet diameter of 100 μm and the velocity of the straight segment at 1 m s−1. First, according to eqn (2), if the flow rate of the spinning solution is 1 mL h−1, the velocity of the jet at a diameter of 100 μm will not be 1 m s−1 but 0.0353 m s−1. Second, according to eqn (3), if the initial flow rate is 1 mL h−1, the jet diameter will be 18.8 μm and the initial jet velocity will be 0.998 m s−1. Then, the draw ratio of the jet can be calculated and is listed in Table 2. When the collecting distance was 10 cm, the draw ratio of the jet was 869, which was highest among other collecting distances, but much lower than the draw ratio of 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in the previous report.38 Considering that the eqn (7) is deduced under ideal conditions without the consideration of the resistant force of air and other possible factors, the actual value of the draw ratios and the velocities of the charged jets would be lower than those calculated in Table 2.
000 in the previous report.38 Considering that the eqn (7) is deduced under ideal conditions without the consideration of the resistant force of air and other possible factors, the actual value of the draw ratios and the velocities of the charged jets would be lower than those calculated in Table 2.
4. Conclusion
Simple and reasonable models were successfully constructed to predict the draw ratio and velocity of the charged polymer solution jet by considering the evaporation of solvent and the solidification of the jet. Further calculations based on the model experiment proved that the electrically charged polymer solution jet first experienced an acceleration process, followed by a deceleration process due to the stretching of the electric force and the resistance force from air, respectively. The calculation based on the experiment revealed that the draw ratio and the velocity of the charged jet was lower than 350 and 1000 m s−1, respectively, both of which were much lower than those (draw ratio of 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and velocity of 60
000 and velocity of 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m s−1) in the previous reports.
000 m s−1) in the previous reports.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This study was funded by the National Natural Science Foundation of China (21774053 and 21574060), Major Special Projects of Jiangxi Provincial Department of Science and Technology (20114ABF05100), and Technology Plan Landing Project of Jiangxi Provincial Department of Education (GCJ2011-24).References
- S. Agarwal and S. Jiang, in Encyclopedia of Polymeric Nanomaterials, ed. S. Kobayashi and K. Müllen, Springer Berlin Heidelberg, 2015, ch. 370-1, pp. 1323–1337, DOI:10.1007/978-3-642-36199-9_370-1.
- Z. M. Huang, Y. Z. Zhang, M. Kotaki and S. Ramakrishna, Compos. Sci. Technol., 2003, 63, 2223–2253 CrossRef CAS.
- S. Agarwal, J. H. Wendorff and A. Greiner, Adv. Mater., 2009, 21, 3343–3351 CrossRef CAS PubMed.
- X. Liu, D. Wei, J. Zhong, M. Ma, J. Zhou, X. Peng, Y. Ye, G. Sun and D. He, ACS Appl. Mater. Interfaces, 2015, 7, 18540–18552 CrossRef CAS PubMed.
- N. Zhang, R. Qiao, J. Su, J. Yan, Z. Xie, Y. Qiao, X. Wang and J. Zhong, Small, 2017, 13, 1604293 CrossRef PubMed.
- C. Liu, P.-C. Hsu, H.-W. Lee, M. Ye, G. Zheng, N. Liu, W. Li and Y. Cui, Nat. Commun., 2015, 6, 6205 CrossRef CAS PubMed.
- T. Hua, Y. Li, X. Zhao, X. Yin, J. Yu and B. Ding, Composites Communications, 2017, 6, 29–33 CrossRef.
- M. Zhu, J. Han, F. Wang, W. Shao, R. Xiong, Q. Zhang, H. Pan, Y. Yang, S. K. Samal, F. Zhang and C. Huang, Macromol. Mater. Eng., 2017, 302, 1600353 CrossRef.
- S. Jiang, H. Hou, S. Agarwal and A. Greiner, ACS Sustainable Chem. Eng., 2016, 4, 4797–4804 CrossRef CAS.
- M. Zhu, R. Xiong and C. Huang, Carbohydr. Polym., 2019, 205, 55–62 CrossRef CAS PubMed.
- W. Ma, M. Zhang, Z. Liu, M. Kang, C. Huang and G. Fu, J. Membr. Sci., 2019, 570–571, 303–313 CrossRef CAS.
- X. Wang, B. Ding, J. Yu and M. Wang, Nano Today, 2011, 6, 510–530 CrossRef CAS.
- W. Ma, M. Zhang, Z. Liu, C. Huang and G. Fu, Environ. Sci.: Nano, 2018, 5, 2909–2920 RSC.
- X. Yuan, W. Li, H. Liu, N. Han and X. Zhang, Composites Communications, 2016, 2, 5–8 CrossRef.
- Y. Bai, X. Mao, J. Song, X. Yin, J. Yu and B. Ding, Composites Communications, 2017, 5, 13–18 CrossRef.
- Y.-E. Miao, F. Li, H. Lu, J. Yan, Y. Huang and T. Liu, Composites Communications, 2016, 1, 15–19 CrossRef.
- S. Jian, T. Zuo, W. Yang, X. Guo and H. Hou, Journal of Jiangxi Normal University, Natural Sciences Edition, 2017, 41, 225–228 Search PubMed.
- Y. Zhang and S.-J. Park, Appl. Catal., B, 2019, 240, 92–101 CrossRef CAS.
- Y. Zhang and S.-J. Park, J. Mater. Chem. A, 2018, 6, 20304–20312 RSC.
- S. Agarwal, S. Jiang and Y. Chen, Macromol. Mater. Eng., 2019, 304, 1800548 CrossRef.
- P. Li, Y. Li, B. Ying and M. Yang, Sens. Actuators, B, 2009, 141, 390–395 CrossRef CAS.
- S. Jiang, N. Helfricht, G. Papastavrou, A. Greiner and S. Agarwal, Macromol. Rapid Commun., 2018, 39, 1700838 CrossRef PubMed.
- K. Molnar, A. Jedlovszky-Hajdu, M. Zrinyi, S. Jiang and S. Agarwal, Macromol. Rapid Commun., 2017, 38, 1700147 CrossRef PubMed.
- L. Liu, H. Bakhshi, S. Jiang, H. Schmalz and S. Agarwal, Macromol. Rapid Commun., 2018, 39, 1800082 CrossRef PubMed.
- S. Jiang, Y. Chen, G. Duan, C. Mei, A. Greiner and S. Agarwal, Polym. Chem., 2018, 9, 2685–2720 RSC.
- H. Hou, W. Xu and Y. Ding, Journal of Jiangxi Normal University, Natural Sciences Edition, 2018, 42, 551–564 Search PubMed.
- C. Kim, K. S. Yang, M. Kojima, K. Yoshida, Y. J. Kim, Y. A. Kim and M. Endo, Adv. Funct. Mater., 2006, 16, 2393–2397 CrossRef CAS.
- S. Reich, M. Burgard, M. Langner, S. Jiang, X. Wang, S. Agarwal, B. Ding, J. Yu and A. Greiner, npj Flexible Electronics, 2018, 2, 5 CrossRef.
- Y. Zhang and S.-J. Park, Carbon, 2017, 122, 287–297 CrossRef CAS.
- Z. Qin, Y. Yin, W. Zhang, C. Li and K. Pan, ACS Appl. Mater. Interfaces, 2019, 11, 12452–12459 CrossRef CAS PubMed.
- S. Jiang, B. Uch, S. Agarwal and A. Greiner, ACS Appl. Mater. Interfaces, 2017, 9, 32308–32315 CrossRef CAS PubMed.
- Z. Qin, Q. Wang, C. Wang, D. Xu, G. Ma and K. Pan, J. Mater. Chem. C, 2019, 7, 1065–1071 RSC.
- Z. Qin, P. Zhang, Z. Wu, M. Yin, Y. Geng and K. Pan, Mater. Des., 2018, 147, 175–181 CrossRef CAS.
- J. Zhu, S. Jiang, H. Hou, S. Agarwal and A. Greiner, Macromol. Mater. Eng., 2018, 303, 1700615 CrossRef.
- S. Jiang, S. Agarwal and A. Greiner, Angew. Chem., Int. Ed., 2017, 56, 15520–15538 CrossRef CAS PubMed.
- G. Duan, M. Koehn-Serrano and A. Greiner, Macromol. Rapid Commun., 2017, 38, 1600511 CrossRef PubMed.
- H. R. Darrell and C. Iksoo, Nanotechnology, 1996, 7, 216 CrossRef.
- D. H. Reneker, A. L. Yarin, H. Fong and S. Koombhongse, J. Appl. Phys., 2000, 87, 4531–4547 CrossRef CAS.
- A. Yarin, S. Koombhongse and D. Reneker, J. Appl. Phys., 2001, 89, 3018–3026 CrossRef CAS.
- S. F. Fennessey and R. J. Farris, Polymer, 2004, 45, 4217–4225 CrossRef CAS.
- M. V. Kakade, S. Givens, K. Gardner, K. H. Lee, D. B. Chase and J. F. Rabolt, J. Am. Chem. Soc., 2007, 129, 2777–2782 CrossRef CAS PubMed.
- W. C. Sheehan and R. E. Wellman, J. Appl. Polym. Sci., 1965, 9, 3597–3603 CrossRef CAS.
- H. Yang, S. Jiang, H. Fang, X. Hu, G. Duan and H. Hou, Spectrochim. Acta, Part A, 2018, 200, 339–344 CrossRef CAS PubMed.
- S. Jian, J. Zhu, S. Jiang, S. Chen, H. Fang, Y. Song, G. Duan, Y. Zhang and H. Hou, RSC Adv., 2018, 8, 4794–4802 RSC.
- S. Jiang, D. Han, C. Huang, G. Duan and H. Hou, Mater. Lett., 2018, 216, 81–83 CrossRef CAS.
- S. Jiang, G. Duan, L. Chen, X. Hu, Y. Ding, C. Jiang and H. Hou, New J. Chem., 2015, 39, 7797–7804 RSC.
- Y. Zheng, B. Xin and M. Li, Text. Res. J., 2018 DOI:10.1177/0040517518786280.
- A. Baji, Y.-W. Mai, S.-C. Wong, M. Abtahi and P. Chen, Compos. Sci. Technol., 2010, 70, 703–718 CrossRef CAS.
- A. L. Yarin, S. Koombhongse and D. H. Reneker, J. Appl. Phys., 2001, 89, 3018–3026 CrossRef CAS.
- L. M. Bellan, H. G. Craighead and J. P. Hinestroza, J. Appl. Phys., 2007, 102, 094308 CrossRef.
- T. Han, D. H. Reneker and A. L. Yarin, Polymer, 2007, 48, 6064–6076 CrossRef CAS.
- I. Greenfeld, K. Fezzaa, M. H. Rafailovich and E. Zussman, Macromolecules, 2012, 45, 3616–3626 CrossRef CAS.
- Y. Zheng, S. Xie and Y. Zeng, J. Mater. Sci., 2013, 48, 6647–6655 CrossRef CAS.
- D. M. Bigg, Polym. Eng. Sci., 1976, 16, 725–734 CrossRef CAS.
- R. S. Porter, T. Kanamoto and A. E. Zachariades, Polymer, 1994, 35, 4979–4984 CrossRef CAS.
- S. B. Warner, A. Buer, M. Grimler, S. C. Ugbolue, G. C. Rutledge and M. Y. Shin, National textile center annual report (M98-D01), 1998, available from:http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.384.8090%26rep=rep1%26type=pdf Search PubMed.
- H. Wang, Y. Zhang, H. Shao and X. Hu, J. Mater. Sci., 2005, 40, 5359–5363 CrossRef CAS.
- A. Stanishevsky, J. Wetuski, M. Walock, I. Stanishevskaya, H. Yockell-Lelievre, E. Kostakova and D. Lukas, RSC Adv., 2015, 5, 69534–69542 RSC.
| This journal is © The Royal Society of Chemistry 2019 |

