Open Access Article
Open Access ArticleThe formation mechanism of uranium and thorium hydride phosphorus: a systematically theoretical study†
Huifeng Zhaoa,
Peng Li *ac,
Meigang Duana,
Feng Xie
*ac,
Meigang Duana,
Feng Xie b and
Jie Maac
b and
Jie Maac
aSchool of Physics and Electronics Engineering, Shanxi University, Taiyuan 030006, China. E-mail: lip@sxu.edu.cn
bInstitute of Nuclear and New Energy Technology, Collaborative Innovation Center of Advanced Nuclear Energy Technology, Key Laboratory of Advanced Reactor Engineering and Safety of Ministry of Education, Tsinghua University, Beijing 100084, China
cCollaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China
First published on 31st May 2019
Abstract
Activation of prototypical bonds by actinide atoms is an important aspect of material activity, and the results can be used for the study of nuclear material storage. In this study, the activation of the P–H bonds of the PH3 molecule by U or Th to form uranium or thorium hydride phosphorus has been systematically explored using density functional theory. A detailed description of the reaction mechanism which includes the potential energy profiles and the properties of bond evolution is presented. There are two types of reaction channels, isomerization and dehydrogenation in U + PH3 and Th + PH3. The difference between the two reactions is the process of the first P–H bond dissociation. The evolution characteristics of the chemical bonds along reaction pathways is analyzed by using electron localization functions, quantum theory of atoms in molecules, Mayer bond orders and natural bond orbitals. The reaction rate constants are calculated at the variational transition state level, and rate-determining steps are predicted.
Introduction
Actinides, an important component of nuclear materials, have attracted extensive attention of researchers from both the experimental and theoretical perspectives because of their unique chemical and physical properties.1–5 Since the reaction of actinides with small molecules has important applications in actinide chemistry and nuclear fuel storage, an exhaustive understanding of the reactions will contribute to the safe storage of nuclear fuel.6,7 The focus of these studies is to systematically explore the reaction mechanism, kinetics and reaction rate of activation of prototypical chemical bonds by actinide elements. In addition, the analysis of electronic structures and chemical properties of actinides is also a crucial object of these studies.The experimental observations provide intuitive information for understanding such chemical reactions.8 The experiment of laser-ablated Th atoms and NH3 under excess argon to form thorimine (HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ThH2) have studied, and the infrared spectrum of products were detected.9 Very recently, analogous experiment to PH3 reacting with U and Th atoms using laser ablated in excess argon were reported, and the new absorption in the intense An–H stretching region was discovered.10 Therefore, the current understanding of the microstructure evolution for U, Th + PH3 reactions is not comprehensive.
ThH2) have studied, and the infrared spectrum of products were detected.9 Very recently, analogous experiment to PH3 reacting with U and Th atoms using laser ablated in excess argon were reported, and the new absorption in the intense An–H stretching region was discovered.10 Therefore, the current understanding of the microstructure evolution for U, Th + PH3 reactions is not comprehensive.
In theoretical researches, with the continuous development of computing technology and theoretical methods, quantum chemistry calculations can provide further information for understanding this type of reaction.11 The reaction of CH4 and actinides has studied at density functional theory (DFT) levels.12,13 Our team also studied the detailed reactions of An atoms and their cations reacting with NH3 and H2O molecules.14,15 These studies provide inspiration for exploring the reaction mechanisms, kinetics and thermodynamics of these title reactions.
The main objective of this work is to perform a detailed study of the activation of P–H bond in PH3 molecule by U and Th atom. Multiple analysis methods are used to explore the bond evolution, involving electron localization function (ELF),16 quantum theory of atoms in molecules (QTAIM),17 Mayer bond order18 and natural bond orbital (NBO).19,20 The reaction rate constants are calculated by using the variational transition state theory (VTST),21 and the one-dimensional tunneling effects (by Eckart22 and Wigner23) was considered.
Method of calculation
Density functional theory (DFT) computations were carried out using Gaussian 16 package.24 Fully geometry optimizations and frequency computations were completed using B3LYP,25 PW91PW91,26 and B3PW91,27 along with the Stuttgart–Dresden–Bonn relativistic effective core potential (SDD)28 for U and Th atoms, and the aug-cc-pVTZ29 basis set for P and H atoms. In addition, the M06-2X30 is used with the segmented all-electron relativistically contracted (SARC)31 basis set for the An atoms. The relativistic recontracted triple-ξ basis set (def2-TZVPP)32 for light P and H atoms. The zero-order regular approximation (ZORA)33 method is adopted. The minimum energy crossing point (MECP) between different spin potential energy surface is determined. These calculations are carried out using the ORCA 4.0.1 (ref. 34) package. These methods have been successfully applied in similar research.35 We guarantee that located transition states have only one imaginary frequency and the intrinsic reaction coordinate (IRC) results show that the corresponding vibration direction correctly connects the reactant and product. The vibrational zero-point energy (VZPE) is considered in all relative energies, and correction factors were used in vibration frequencies to take into account the influence of anharmonic effects.36–38Electron localization function (ELF), quantum theory of atoms in molecules (QTAIM) and Mayer bond order are carried out. These analyses are completed using Multiwfn package,39 the bond character, the charge distribution and metal valence population are completed using NBO in Gaussian 16 package.
The reaction rate constants with increasing temperature are accomplished by using VTST on the basis of the B3LYP/SDD/aug-cc-pVTZ energy with KiSThelP program.40
Result and discussion
In order to estimate the accuracy of methods and basis sets, we compared the calculated vibrational frequencies of the H2UPH and H2ThPH with the experimental values. Different levels and types of methods and basis sets are chosen, the results are shown in Tables S1 and S2.† In addition, we summarize the bond lengths and energy of H2UPH and H2ThPH and Andrews and coworkers' calculated values. The results are listed in ESI.† As can be seen that B3LYP results (1495.5 cm−1 and 1472.6 cm−1) are the closest to the experimental values (1473.7 cm−1 and 1456.5 cm−1), followed by B3PW91 (1508.6 cm−1 and 1482.9 cm−1), PW91PW91 (1518.3 cm−1 and 1493.0 cm−1), and M06-2X (1526.3 cm−1 and 1473.0 cm−1). In terms of the basis set, SDD/aug-cc-pVTZ performs better. The comparison of bond length and energy shows that our calculations are in good agreement with Andrews. Besides, these methods have been successfully used for the study of other similar reactions.5,7,8 Therefore, the subsequent calculations are accomplished by using B3LYP/SDD/aug-cc-pVTZ, PW91PW91/SDD/aug-cc-pVTZ, B3PW91/SDD/aug-cc-pVTZ and M06-2X/ZORA-def2-TZVPP methods.Reaction mechanism
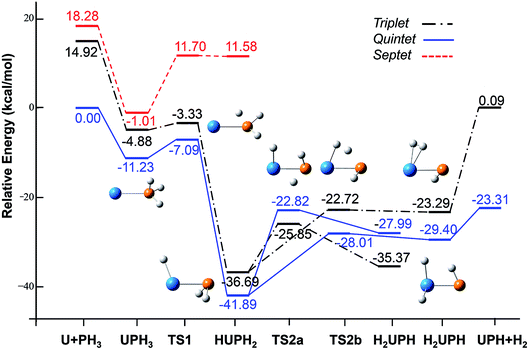 | ||
| Fig. 2 Potential energy profile for the reaction of U + PH3 computed at the B3LYP/SDD/aug-cc-pVTZ levels of theory. The energy in the figure is relative to the total energy of U + PH3 (quintet). | ||
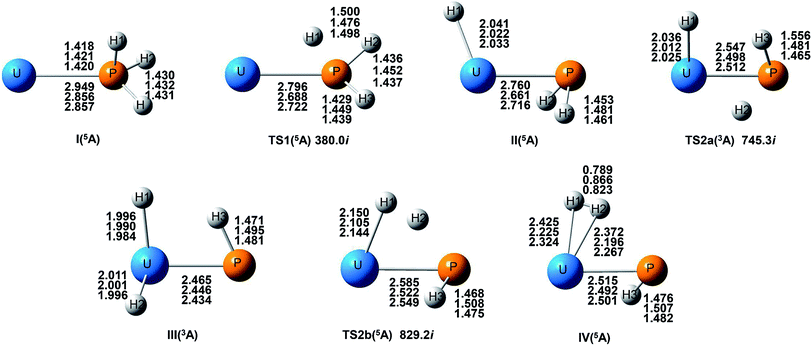
From the Fig. 2, we can clearly see that the lowest energy path of U + PH3 along the quintet state. For the first step of the reaction, the U atom attracts PH3, forming a stable complex U–PH3 (I), exothermic by approximately 11.23 kcal mol−1. Then, the reaction needs to overcome the first transition state (TS1) with an activation barrier of 4.14 kcal mol−1. The TS1 has an imaginary frequency of 398.0 cm−1, corresponding to the H1 atom close to the U atom, and the P–H1 bond length is elongated by about 0.070 Å. After crossed TS1, the system reaches the intermediate HU–PH2 (II). In this process, the P–H1 bond is completely broken and replaced by the U–H1 bond.
After the complex II, the reaction will proceed along two different pathways, isomerization and dehydrogenation. For isomerization channel, there is an intersystem crossing between the triplet and quintet PESs, after that the reaction will proceed along triplet. In this process, the second H atom will move toward the U, forming the non-planar isomerized products, the uranium dihydride phosphinidine H2U–PH (III). This process overcomes the energy barrier of 16.04 kcal mol−1, the corresponding transition state is TS2a with a 745.3 cm−1 imaginary frequency, corresponding to the H2 atom from the P atom to the U atom, and the whole reaction is endothermic.
The intersystem crossing is significant for the study of the reaction process, since it characterizes where the transition is most likely to take place.41 As mentioned above, there is a crossing between triplet and quintet states in the region from complex II to TS2a. Due to the crossing reduces the barrier of quintet, the reaction will proceed along the triplet. We can see from Fig. S3,† the MECP has a nonplanar geometry and is more similar to the complex II, the U–P, U–H bond lengths are 2.587 Å and 2.034 Å, respectively. It is noteworthy that intersystem crossing is thermodynamically favored, but it can also not happen in real experiments since the energy difference between different spin states is very small.
In the dehydrogenation channel, the second H atom is detached from the P atom and gradually approaches the first H forming the complex H2–UPH (IV). This process needs to climb a transition state TS2b with an activation barrier of 13.9 kcal mol−1, and the imaginary frequency is 829.2 cm−1. At this time, the bond length of U–H1 extended from 2.150 Å to 2.425 Å. After that, these two H atoms are getting farther away from the main frame, and the last complex IV decomposes into UPH and H2.
For the septet state, after the complex II, the subsequent reaction products are much higher than other spin multiplicity energy, and there is no crossing with other PES. We have also considered the case where H atoms continue to transfer from P atom to U, but our results indicate that the final product is relatively higher energy, and it is very difficult to achieve in terms of energy.
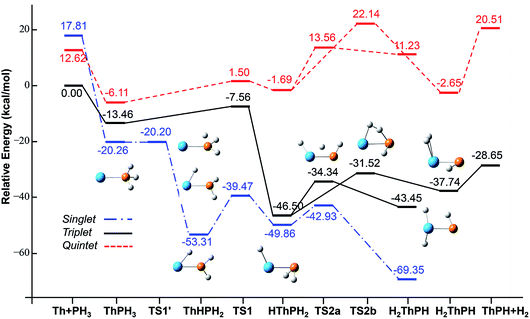 | ||
| Fig. 4 Potential energy profile for the reaction of Th + PH3 computed at the B3LYP/SDD/aug-cc-pVTZ levels of theory. The energy in the figure is relative to the total energy of Th + PH3 (triplet). | ||
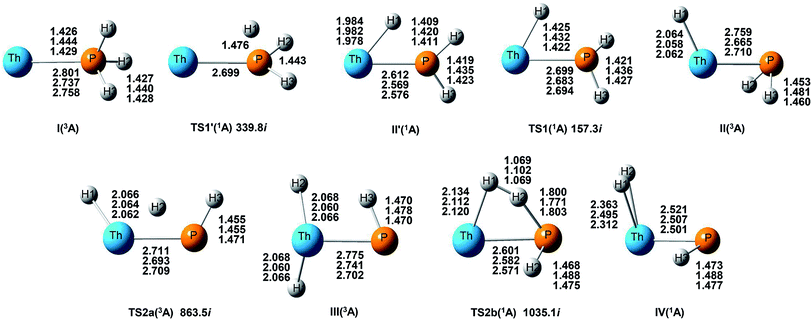
On the whole, the reaction mechanisms of Th + PH3 are very similar to that of U + PH3. It can be summarized as follows, the first step of the reaction is An atoms attracted the PH3 molecule to form complex I, then overcome TS1 and dissociate the first P–H bond to produce intermediate II. Dissociation of the second P–H bond has different spatial directionalities leading to two channels of isomerization and dehydrogenation.
Our results show that the difference between two reactions is the process of dissociating the first P–H bond. In the case of Th + PH3, the P–H1 bond cleavage of singlet reaction needs two steps. There are two transition states in this process, we named TS1′ and TS1. The activation barrier of the TS1′ is very shallow, only 0.06 kcal mol−1. The corresponding process is that the P–H1 bond is slightly elongated and forms an intermediate product II′ with a planar structure. Then the H atom continues to move toward the Th atom, and the molecular structure changes from plane to three-dimensional, the complex II formed. This process requires the system to pass through TS1 with a barrier height of 13.84 kcal mol−1, the imaginary frequency is 157.3 cm−1. Besides, for the dissociation of P–H1 bond, the different spin multiplicity corresponds to different situations. If the reaction proceeds along the singlet state, the above two steps are required to dissociate the P–H1 bond, if along the triplet state, this process is same as U + PH3, only one step is needed. It should be noted, the calculation of complex I and TS1′ for singlet state was successful only on B3LYP/SDD/aug-cc-pVTZ method. We have tried other methods, but failed. This may be due to the relatively small energy barrier of TS1′ and sensitive to the calculation method. From the above analysis, the reaction process of U + PH3 and Th + PH3 can be described as:
| U + PH3 → U–PH3 → TS1 → HU–PH2 → TS2a → H2U–PH, ΔE = −35.37 kcal mol−1 |
| U + PH3 → U–PH3 → TS1 → HU–PH2 → TS2b → H2–U–PH → H2 + UPH, ΔE = −23.31 kcal mol−1 |
| Th + PH3 → Th–PH3 → TS1′ → Th–H–PH2 → TS1 → HTh–PH2 → TS2a → H2Th–PH, ΔE = −81.36 kcal mol−1 |
| Th + PH3 → Th–PH3 → TS1 → HTh–PH2 → TS2b → H2–Th–PH → H2 + ThPH, ΔE = −28.65 kcal mol−1 |
The ELF shaded-surface-projected maps of complexes and transition states (lowest-energy spin state species) for U + PH3 and Th + PH3 are shown in Fig. 5 and 6. The QTAIM parameters of the (3, −1) bond critical points (BCPs) for the species involved in the reactions are gathered in Table 1 (U + PH3) and Table S9† (Th + PH3), including the electron density ρ(r) and Laplacian ∇2ρ(r), the potential energy density V(r), the electron kinetic energy density G(r) and the total electron energy density H(r). As the criteria proposed by Cremer and Kraka,42 H(r) > 0 corresponds to closed-shell interactions, and H(r) < 0 corresponds to covalent interactions.
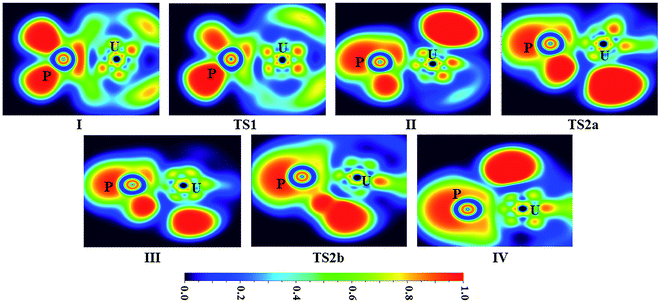 | ||
| Fig. 5 ELF shaded surfaces with projection maps of the stationary points on the U + PH3 reaction pathway at the B3LYP/SDD/aug-cc-pVTZ level theory. | ||
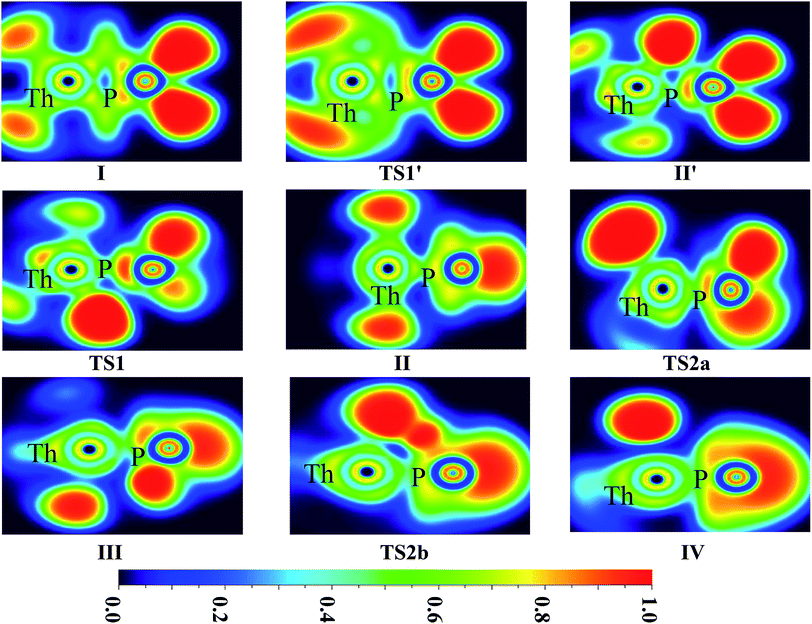 | ||
| Fig. 6 ELF shaded surfaces with projection maps of the stationary points on the Th + PH3 reaction pathway at the B3LYP/SDD/aug-cc-pVTZ level theory. | ||
| Species | ρ(r) | ∇2ρ(r) | G(r) | V(r) | H(r) | |
|---|---|---|---|---|---|---|
| a ρ(bcp) and ∇2ρ(bcp) in a.u. | ||||||
| I(5A) | U–P | 0.042 | 0.094 | 0.030 | −0.037 | −0.684 |
| P–H1 | 0.165 | −0.114 | 0.137 | −0.302 | −0.165 | |
| P–H2 | 0.163 | −0.161 | 0.124 | −0.288 | −0.164 | |
| P–H3 | 0.164 | −0.160 | 0.124 | −0.289 | −0.164 | |
| TS1(5A) | U–P | 0.052 | 0.063 | 0.029 | −0.041 | −0.013 |
| P–H1 | 0.144 | −0.271 | 0.062 | −0.192 | −0.130 | |
| P–H2 | 0.163 | −0.164 | 0.123 | −0.286 | −0.164 | |
| P–H3 | 0.164 | −0.155 | 0.126 | −0.290 | −0.165 | |
| II(5A) | U–P | 0.068 | 0.028 | 0.029 | −0.050 | −0.022 |
| U–H1 | 0.090 | 0.023 | 0.040 | −0.075 | −0.035 | |
| P–H2 | 0.147 | −0.081 | 0.117 | −0.255 | −0.137 | |
| P–H3 | 0.149 | −0.067 | 0.124 | −0.264 | −0.140 | |
| TS2a(3A) | U–P | 0.095 | 0.021 | 0.046 | −0.086 | −0.040 |
| U–H1 | 0.088 | 0.036 | 0.042 | −0.075 | −0.033 | |
| U–H2 | 0.075 | 0.062 | 0.040 | −0.064 | −0.024 | |
| P–H3 | 0.147 | −0.070 | 0.119 | −0.256 | −0.137 | |
| III(3A) | U–P | 0.109 | 0.027 | 0.058 | −0.110 | −0.051 |
| U–H1 | 0.097 | 0.012 | 0.043 | −0.083 | −0.040 | |
| U–H2 | 0.097 | 0.018 | 0.045 | −0.085 | −0.040 | |
| P–H3 | 0.141 | −0.049 | 0.115 | −0.241 | −0.127 | |
| TS2b(5A) | U–P | 0.088 | 0.034 | 0.044 | −0.079 | −0.035 |
| U–H1 | 0.063 | 0.104 | 0.041 | −0.056 | −0.015 | |
| U–H2 | 0.052 | 0.167 | 0.049 | −0.056 | −0.007 | |
| P–H3 | 0.141 | −0.065 | 0.111 | −0.238 | −0.127 | |
| H1–H2 | 0.140 | −0.306 | 0.026 | −0.129 | −0.103 | |
| IV(5A) | U–P | 0.100 | 0.028 | 0.051 | −0.095 | −0.044 |
| P–H3 | 0.138 | −0.063 | 0.107 | −0.229 | −0.123 | |
| H1–H2 | 0.241 | −0.960 | 0.008 | −0.257 | −0.240 | |
| Species | Bond character | qTh | qP | Metal valence populations | ||
|---|---|---|---|---|---|---|
| 7s | 5f | 6d | ||||
| I | BD(1) Occ. = 0.871 | 0.192 | −0.169 | 1.88 | 2.62 | 0.84 |
| TS1 | BD(1) Occ. = 0.827 | 0.987 | −0.203 | 0.87 | 2.99 | 0.20 |
| II | BD(1) Occ. = 0.997 | 1.072 | −0.399 | 1.03 | 3.00 | 0.96 |
| TS2a | BD(1) Occ. = 0.990 | 1.174 | −0.401 | 0.63 | 3.04 | 1.12 |
| BD(2) Occ. = 0.916 | ||||||
| III | BD(1) Occ. = 0.997 | 1.146 | −0.422 | 0.49 | 3.06 | 1.72 |
| BD(2) Occ. = 0.997 | ||||||
| TS2b | BD(1) Occ. = 0.992 | 0.639 | −0.356 | 0.96 | 3.12 | 1.23 |
| IV | BD(1) Occ. = 0.996 | 0.644 | −0.467 | 0.93 | 3.16 | 1.28 |
| BD(2) Occ. = 0.884 | ||||||
| Species | Bond character | qTh | qP | Metal valence populations | ||
|---|---|---|---|---|---|---|
| 7s | 5f | 6d | ||||
| I | BD(1) Occ. = 1.979 | 0.199 | −0.088 | 1.74 | 0.10 | 1.96 |
| BD(2) Occ. = 1.790 | ||||||
| TS1′ | BD(1) Occ. = 1.978 | 0.209 | −0.089 | 1.73 | 0.11 | 1.95 |
| BD(2) Occ. = 1.783 | ||||||
| II′ | BD(1) Occ. = 1.999 | 0.729 | −0.389 | 1.67 | 0.19 | 1.40 |
| BD(2) Occ. = 1.961 | ||||||
| TS1 | BD(1) Occ. = 1.963 | 0.790 | −0.417 | 1.63 | 0.17 | 1.39 |
| BD(2) Occ. = 1.988 | ||||||
| II | BD(1) Occ. = 1.995 | 0.922 | −0.309 | 1.49 | 0.21 | 1.35 |
| TS2a | BD(1) Occ. = 1.944 | 0.984 | −0.372 | 1.00 | 0.28 | 1.74 |
| BD(2) Occ. = 1.943 | ||||||
| BD(3) Occ. = 1.759 | ||||||
| III | BD(1) Occ. = 1.997 | 1.312 | −0.454 | 0.47 | 0.29 | 1.92 |
| BD(2) Occ. = 1.991 | ||||||
| BD(3) Occ. = 1.793 | ||||||
| TS2b | BD(1) Occ. = 0.998 | 0.690 | −0.267 | 0.77 | 0.26 | 2.14 |
| BD(2) Occ. = 0.726 | ||||||
| IV | BD(1) Occ. = 0.999 | 0.598 | −0.470 | 0.79 | 0.35 | 2.30 |
| BD(2) Occ. = 0.998 | ||||||
We calculated the electronic occupancy in order to investigate the multiple bonds between An and P atoms. As can be seen, on the whole, the An–P bond in Th species exhibit more multiple bond properties than in U species. For U + PH3, each BD has only one electron, the An–P bonds in all the species are partial multiple bonds that are not completely occupied. For Th + PH3, each BD have two electronic occupations, except for H2–Th–PH, the An–P bond in other species exhibit multiple bond features. This multiple bond phenomenon also exists in our previous studies of neptunimine (HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NpH2) and plutonimine (HN
NpH2) and plutonimine (HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PuH2).43
PuH2).43
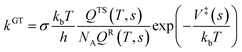 | (1) |
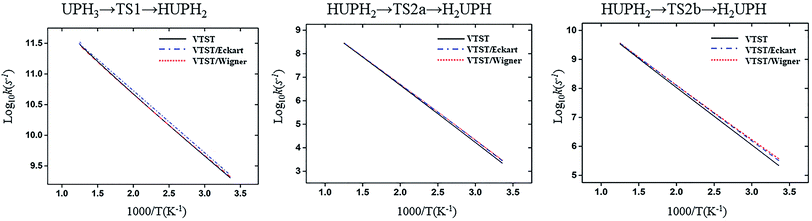
The structure and frequency results with the B3LYP/SDD/aug-cc-pVTZ level is used as the input for the KiSThelP program. It is expected that tunneling effects play an important role in the reaction which involves the transfer of hydrogen atoms.44 Therefore, in this study, the one-dimensional tunneling effects by Wigner and Eckart were considered. The rate constants at different temperatures (298 to 600 K) are shown in Tables 4 and 5. The log10k versus 1000/T plots are incorporated in experimental rate studies and depicted in Fig. 7 and 8.
| T, K | UPH3 → TS1 → HUPH2 | HUPH2 → TS2a → H2UPH | HUPH2 → TS2b → H2UPH | ||||||
|---|---|---|---|---|---|---|---|---|---|
| kVTST | kVTST/Eck | kVTST/W | kVTST | kVTST/Eck | kVTST/W | kVTST | kVTST/Eck | kVTST/W | |
| 298 | 2.03 × 109 | 2.13 × 109 | 3.40 × 109 | 2.20 × 105 | 3.75 × 105 | 3.27 × 105 | 2.23 × 103 | 3.00 × 103 | 2.86 × 103 |
| 300 | 2.14 × 109 | 2.23 × 109 | 3.56 × 109 | 2.43 × 105 | 4.12 × 105 | 3.60 × 105 | 2.53 × 103 | 3.40 × 103 | 3.24 × 103 |
| 350 | 6.34 × 109 | 6.48 × 109 | 9.45 × 109 | 2.14 × 106 | 3.14 × 106 | 2.90 × 106 | 3.77 × 104 | 4.69 × 104 | 4.55 × 104 |
| 400 | 1.45 × 1010 | 1.46 × 1010 | 2.00 × 1010 | 1.09 × 107 | 1.46 × 107 | 1.39 × 107 | 2.81 × 105 | 3.33 × 105 | 3.26 × 105 |
| 450 | 2.79 × 1010 | 2.77 × 1010 | 3.60 × 1010 | 3.87 × 107 | 4.87 × 107 | 4.70 × 107 | 1.33 × 106 | 1.52 × 106 | 1.49 × 106 |
| 500 | 4.73 × 1010 | 4.66 × 1010 | 5.86 × 1010 | 1.07 × 108 | 1.29 × 108 | 1.25 × 108 | 4.57 × 106 | 5.07 × 106 | 5.03 × 106 |
| 550 | 7.33 × 1010 | 7.18 × 1010 | 8.79 × 1010 | 2.46 × 108 | 2.88 × 108 | 2.82 × 108 | 1.25 × 107 | 1.36 × 107 | 1.35 × 107 |
| 600 | 1.06 × 1011 | 1.03 × 1011 | 1.23 × 1011 | 4.95 × 108 | 5.64 × 108 | 5.54 × 108 | 2.87 × 107 | 3.10 × 107 | 3.07 × 107 |
| T, K | HThPH2 → TS2a → H2ThPH | HThPH2 → TS2b → H2ThPH | ||||
|---|---|---|---|---|---|---|
| kVTST | kVTST/Eck | kVTST/W | kVTST | kVTST/Eck | kVTST/W | |
| a Rate constant in s−1. | ||||||
| 298 | 3.79 × 107 | 9.09 × 107 | 6.37 × 107 | 17.71 | 56.08 | 34.88 |
| 300 | 4.11 × 107 | 1.08 × 108 | 6.86 × 107 | 20.97 | 65.20 | 41.01 |
| 350 | 2.30 × 108 | 4.69 × 108 | 3.43 × 108 | 0.75 × 103 | 1.67 × 103 | 1.28 × 103 |
| 400 | 8.46 × 108 | 1.47 × 109 | 1.16 × 109 | 1.09 × 104 | 1.98 × 104 | 1.67 × 104 |
| 450 | 2.35 × 109 | 3.38 × 109 | 3.05 × 109 | 8.66 × 104 | 1.38 × 105 | 1.23 × 105 |
| 500 | 5.35 × 109 | 7.23 × 109 | 6.64 × 109 | 4.53 × 105 | 6.61 × 105 | 6.01 × 105 |
| 550 | 1.05 × 1010 | 1.36 × 1010 | 1.20 × 1010 | 1.75 × 106 | 2.38 × 106 | 2.25 × 106 |
| 600 | 1.86 × 1010 | 2.32 × 1010 | 2.18 × 1010 | 5.38 × 106 | 7.00 × 106 | 6.67 × 106 |
 | ||
| Fig. 7 Computed VTST rate constant and temperature plots of the reaction of U + PH3 obtained by using B3LYP/SDD/aug-cc-pVTZ energies and frequencies: log10k (s−1) versus 1000/T. | ||
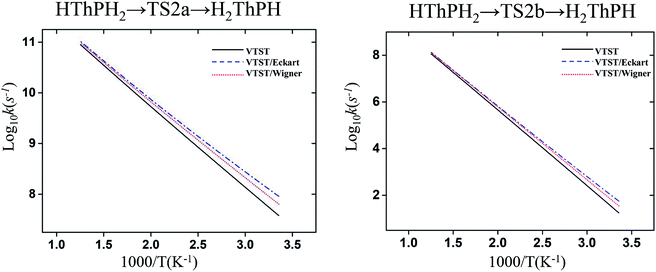 | ||
| Fig. 8 Computed VTST rate constant and temperature plots of the reaction of Th + PH3 obtained by using B3LYP/SDD/aug-cc-pVTZ energies and frequencies: log10k (s−1) versus 1000/T. | ||
From the table we can see that the process of dissociating the first P–H bond occur the fastest compared to the other steps. The effect of temperature on the reaction rate is also significant, and as the temperature increases, the reaction proceeds faster, especially when the P–H2 bond breaks. We also found that the isomerization channel reacts faster than the dehydrogenation channel at room temperature. For the reaction of Th + PH3, the dissociating process of the P–H1 bond requires two steps, and the energy barrier of the first step is very small (0.06 kcal mol−1), the exact reaction rate value is not obtained by this method. Even so, this process happens very quickly since the energy barrier is very small.
As for the impact of tunneling effects, it can be seen that the split of the curve at low temperature region are more obvious than that at the high temperature region. This indicates that the tunneling effect is more significant at low temperature region (room temperature), and the reaction rates are faster than expected. Take the HThPH2 → TS2a → H2ThPH process as an example. The reaction rates considering the tunneling effect are nearly doubled that of the unconsidered. In addition, we found that the tunneling effect is greater for the TS2a than that of other processes. This may due to the TS2a is the isomerization process, since the large-amplitude conformational motions that bring system centers in close proximity can promote this tunneling.44
Conclusions
In conclusion, we discuss the detailed reaction mechanisms of the gas-phase reaction of U and Th with PH3. Two types of reaction channels of the P–H bond activate by U and Th are discussed. Bonding evolution was analyzed by using several methods, including ELF, QTAIM and NBO calculations. The reaction rate constants are predicted by using VTST method with 1D tunneling effect. The main conclusions are summarized as follows. (1) The U + PH3 and Th + PH3 have similar reaction mechanisms. The reaction proceeds along two channels of isomerization and dehydrogenation. The difference between the two reactions is that the U + PH3 reaction needs one step to dissociate the P–H1 bond, while the reaction of Th + PH3 takes two steps. (2) Chemical bond evolution analysis results show that all the bonds involved in the reaction exhibit covalent bond characteristics, and the An–P bond in Th species exhibit more multiple bond properties than U species. (3) Based on the energies and frequencies, the rate constants are obtained by using the VTST method, and the 1D tunneling effect is considered. From the results, we know that as the temperature increases, the reaction rate increases. These results contribute to our growing knowledge of the chemistry of actinides, and establish a theoretical foundation for the study of activation of prototypical bonds by actinides atoms.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by National Natural Science Foundation of China (NSFC) (Grant No. 11604187), the Natural Science Young Foundation of Shanxi Province (Grant No. 201801D221004), the foundation for Outstanding Young Scholars of Shanxi Province, China (Grant No. 201601D021001), the fund for Shanxi “1331 Project” Key Subjects Construction, the Outstanding young academic leader of Shanxi Province, the Cooperation projects of Institute of Applied Physics and Computational Mathematics, and Open Fund of Key Laboratory of Advanced Reactor Engineering and Safety, Ministry of Education (Tsinghua University, China). We are very grateful to Dr Sobereva for many helpful discussions and providing us with the Multiwfn package. We would like to thank the reviewers for the valuable suggestions on improving our study.References
- T. W. Hayton, Chem. Commun., 2013, 49, 2956–2973 RSC.
- D. S. J. Arney, R. C. Schnabel, B. C. Scott and C. J. Bums, J. Am. Chem. Soc., 1996, 118, 6780–6781 CrossRef CAS.
- M. Ephritikhine, Coord. Chem. Rev., 2016, 319, 35–62 CrossRef CAS.
- A. C. Behrle, L. Castro, L. Maron and J. R. Walensky, J. Am. Chem. Soc., 2015, 137, 14846–14849 CrossRef CAS PubMed.
- X. Wang, L. Andrews, M. Knitter, P. A. Maimqvist and B. O. Roos, J. Phys. Chem. A, 2009, 113, 6064–6069 CrossRef CAS PubMed.
- L. Andrews, X. Wang, R. Lindh, B. O. Roos and C. J. Marsden, Angew. Chem., Int. Ed., 2008, 47, 5366–5370 CrossRef CAS PubMed.
- H. G. Cho and L. Andrews, Coord. Chem. Rev., 2017, 335, 76–102 CrossRef CAS.
- X. Wang, L. Andrews and C. Marsden, Chem.–Eur. J., 2008, 14, 9192–9201 CrossRef CAS PubMed.
- X. Wang, L. Andrews and C. Marsden, Chem.–Eur. J., 2007, 13, 5601–5606 CrossRef CAS PubMed.
- L. Andrews, H. G. Cho, K. S. Thanthiriwatte and D. A. Dixon, Inorg. Chem., 2017, 56, 2949–2957 CrossRef CAS PubMed.
- W. Niu, H. Zhang, P. Li and T. Gao, Int. J. Quantum Chem., 2015, 115, 6–18 CrossRef CAS.
- K. J. de Almeida and A. Cesar, Organometallics, 2006, 25, 3407–3416 CrossRef CAS.
- E. D. Santo, M. D. C. Michelini and N. Russo, Organometallics, 2009, 28, 3716–3726 CrossRef.
- P. Li, W. Niu and T. Gao, RSC Adv., 2014, 4, 29806–29817 RSC.
- P. Li, W. Niu, T. Gao and H. Wang, ChemPhysChem, 2015, 15, 3078–3088 CrossRef PubMed.
- A. D. Becke and K. E. Edgecombe, J. Phys. Chem., 1990, 92, 5397–5403 CrossRef CAS.
- R. F. W. Bader, A quantum theory. A quantum theory, Clarendon, Oxford, 1990, pp. 361–373 Search PubMed.
- I. Mayer, Chem. Phys. Lett., 1985, 97, 270–274 CrossRef.
- A. E. Reed and F. Weinhold, J. Chem. Phys., 1985, 83, 1736–1740 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- A. Fernandez-Ramos, B. A. Ellingson, B. C. Garrett and D. G. Truhlar, Rev. Comput. Chem., 2007, 23, 125–232 CAS.
- C. Eckart, Phys. Rev., 1930, 35, 1303–1309 CrossRef CAS.
- E. Wigner, Z. Phys. Chem., 1932, 19, 203–216 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc, Wallingford CT, 2016 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- W. Küchle, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1994, 100, 7535–7542 CrossRef.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 2975–2988 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Comput. Theor. Chem., 2008, 120, 215–241 CAS.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2011, 7, 677–684 CrossRef CAS.
- D. A. Pantazis, X. Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- M. E. Alikhani, M. C. Michelini, N. Russo and B. Silvi, J. Phys. Chem. A, 2008, 112, 12966–12974 CrossRef CAS PubMed.
- D. O. Kashinski, G. M. Chase, R. G. Nelson, O. E. Di. Nallo, A. N. Scales, D. L. Vanderley and E. F. C. Byrd, J. Phys. Chem. A, 2017, 121, 2265–2273 CrossRef CAS PubMed.
- N. M. Kreienborg and C. Merten, Phys. Chem. Chem. Phys., 2019, 21, 3506–3511 RSC.
- G. D. Liberto, R. Conte and M. Ceotto, J. Chem. Phys., 2018, 148, 104302 CrossRef PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- S. Canneaux, F. Bohr and E. Henon, J. Comput. Chem., 2013, 35, 82–93 CrossRef PubMed.
- K. M. Smith, R. Poli and J. N. Harvey, New J. Chem., 2000, 24, 77–80 RSC.
- D. Cremer and E. Kraka, Angew. Chem., Int. Ed., 1984, 23, 627–628 CrossRef.
- P. Li, W. Niu and T. Gao, J. Mol. Model., 2015, 21, 316 CrossRef PubMed.
- R. J. McMahon, Science, 2003, 299, 833 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The comparison of observed values and calculated harmonic frequencies for H2UPH and H2ThPH, comparison of the calculation results of the bond length and energy, the relative energy, the IRC curve and optimized Cartesian x, y, z coordinates about the complexes and transition state for the reactants ground state from different calculation methods. Structures and selected geometric parameters of MECP and Mayer bond order analysis along the reaction pathways. See DOI: 10.1039/c9ra02098e |
| This journal is © The Royal Society of Chemistry 2019 |