Open Access Article
Open Access ArticleQM/MM studies on luminescence mechanism of dinuclear copper iodide complexes with thermally activated delayed fluorescence†
Qian Wanga,
Yuan-Jun Gaoa,
Ting-Ting Zhang *ab,
Juan Han*a and
Ganglong Cui
*ab,
Juan Han*a and
Ganglong Cui a
a
aKey Laboratory of Theoretical and Computational Photochemistry, Ministry of Education, College of Chemistry, Beijing Normal University, Beijing 100875, P. R. China. E-mail: zhangtt@bnu.edu.cn; hanjuan@bnu.edu.cn
bKey Laboratory of Magnetic Molecules and Magnetic Information Materials of Ministry of Education, School of Chemistry and Materials Science, Shanxi Normal University, Linfen 041000, P. R. China
First published on 3rd July 2019
Abstract
The QM/MM method is employed to investigate the photophysical mechanism of two dinuclear copper iodide complexes with thermally activated delayed fluorescence (TADF). The S1–T1 energy differences (ΔEST) in these two complexes are small enough so that repopulating the S1 state from T1 becomes energetically allowed. Both forward and reverse intersystem crossing (ISC and rISC) processes are much faster than the corresponding radiative fluorescence and phosphorescence processes [kISC (108 s−1) > kFr (106 s−1), krISC (105 s−1) > kPr (103 s−1)]. The faster rISC process than the phosphorescence emission enables TADF. Moreover, the diphosphine ligands are found to play an important role in regulating the electronic structures and thereto the radiative and nonradiative rate constants. The present work rationalizes experimental phenomena and helps understand the intrinsic luminescence properties. The obtained insights could be useful for tuning the luminescence performance of dicopper-based luminescence materials.
1. Introduction
As third generation emitting materials, organic and inorganic compounds with thermally activated delayed fluorescence (TADF) have been extensively studied in recent decades.1–9 Due to the use of inexpensive Cu metal, a large variety of luminescent Cu(I) compounds have been investigated since TADF was observed in Cu(I) complexes by Blasse and co-workers in 1980.10 In addition, TADF Cu(I) materials exhibit certain superior luminescence properties, for example, they harvest all singlets and triplets for the generation of light in organic light emitting diodes (OLEDs). The first successful application as emitting materials in OLEDs was reported in 1999.11 Nowadays several classes of important structures that include three- and four-coordinated mononuclear, and four-coordinated dinuclear Cu(I) complexes have been applied in commercial OLEDs.12 These complexes usually have distorted tetrahedral geometries around central Cu(I) atoms with diimine and diphosphine ligands. These quasi-tetrahedral structures often lead to low quantum yields due to efficient non-radiative decays. To overcome this weakness a proposal of adopting binuclear Cu(I) complex structure was put forward, because similar structures between ground and emissive excited states in binuclear Cu(I) complexes result in an efficient emission.13As a result, dinuclear Cu(I) complexes with monodentate or chelating phosphines have gained high experimental attention in the past decade.14,15 In 2007 the first device using iodo-bridged complexes was reported.16,17 In 2010 Deaton et al. reported a diamond core dinuclear Cu(I) complex with high TADF emission, which is comparable to high-performance phosphorescent emitting complexes with rare metals.18 Yersin et al. synthesized another dinuclear complex, which has a butterfly-shaped metal-halide core that leads to a small ΔEST of 0.05 eV for TADF emission.19 Later, they further prepared some attractive shorter-lived halide-bridged dicopper TADF compounds with chelating aminophosphane ligands.20 The latest dinuclear Cu(I) TADF materials exhibit suitably short decay times and realize highly efficient OLEDs.20 These bridges are often unstable especially in fluid environments, which however can be enhanced by bridging two Cu(I) centers with additional bidentate ligands.21
On the other hand, it is commonly known that TADF is highly sensitive to structural details of emitting materials. To achieve better performance it is usually needed to effectively restrict certain vibration modes of emitting molecules, for example, recently reported efficient TADF of mononuclear tetradentate Cu(I) complexes.22 However, the corresponding studies on dinuclear copper complexes are less studied. It is not clear whether the introduced bidentate ligands restrict certain vibrational modes of dinuclear Cu(I) complexes leading to efficient TADF.
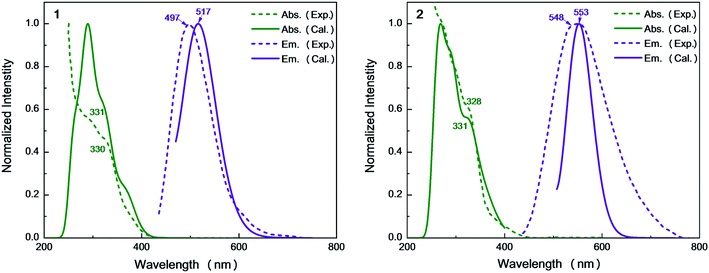
Recently, Kato et al. have synthesized solution-stable luminescent dinuclear Cu(I) complexes i.e. Cu2(μ-I)2(dpppy)2 [dpppy = 2,3-bis(diphenylphosphino)pyridine] (Cu-py) using chelating diphosphine ligands with heteroaromatic rings.9 These compounds were found to exhibit interesting TADF phenomena from mixed (M + X)LCT excited singlet and triplet states. Further analysis clearly shows the molecular structure is almost identical to the parent Cu2(μ-I)2(dppb)2 [dppb = 1,2-bis(diphenylphosphino)benzene] (Cu-bz).16 The emission quantum yields of Cu-bz and Cu-py are measured to be 0.99 and 0.48 in the solid state at 298 K, respectively. The 548 nm emission wavelength of Cu-py is also redshifted compared to the 497 nm one of Cu-bz. In previous studies, these emission properties are simply discussed, but, detailed excited-state properties and underlying photophysical processes related to TADF, for example, forward and reverse intersystem crossing rates, competition between radiative and nonradiative transitions, are elusive and not explored computationally.
In this work we have carried out a comprehensive computational study on two dinuclear Cu(I) complexes [Cu2(μ-I)2(dppb)2] (1) and [Cu2(μ-I)2(dpppy)2] (2) with chelating diphosphine ligands (see Fig. 1). Their excited-state geometric and electronic structures, forward and reverse intersystem crossing rates (ISC and rISC), fluorescence and phosphorescence emission rates are explored using both density functional theory (DFT) and time-dependent DFT (TD-DFT) methods in combination with the quantum mechanics/molecular mechanics (QM/MM) approach. In terms of the results, radiative and nonradiative rates and related TADF mechanism of these dinuclear Cu(I) TADF emitters are discussed in detail.
 | ||
| Fig. 1 Chemical structures of two Cu(I) complexes 1 and 2 studied in our present work. Also shown are two different substituent groups. | ||
2. Computational methods
Initial models are built based on X-ray crystal structures in experiments.9 Full optimizations of crystal structures including cell parameters and molecular geometric parameters are carried out at the PBE level with periodic boundary condition (PBC).23 The DNP basis set is used to expand electronic wavefunction and the default dispersion correction of Grimme is added to consider weak dispersion interaction.24,25 A Monkhorst–Pack k-point grids of 2 × 2 × 2 are used. Default convergence criteria on gradients and displacements are used in geometry optimizations. These calculations are performed using the DMol3 module in Materials Studio 2016.26–28In order to simulate excited-state properties of these Cu(I) complexes in crystals, a combined quantum mechanics/molecular mechanics (QM/MM) method is used.29,30 The central one molecule is chosen as the QM region; whereas, the surrounding twelve molecules are chosen as the MM region and frozen during geometry optimizations (see Fig. S1†). The universal force field (UFF) and QM methods are used for the MM and QM regions, respectively.31 This strategy has been demonstrated to work well in previous works.32–34 The minima are optimized by the DFT (S0) and TD-DFT (S1 and T1) methods with the hybrid exchange-correlation functional (PBE1PBE).35–37 In all these calculations, the Stuttgart relativistic pseudopotential and its accompanying basis set (SDD, ECP60MWB) are applied for the Cu and I atoms; the 6-31G* [6-31+G*] basis set is used for C, H and N [P] atoms.38–41 All QM/MM geometry optimizations are carried out using Gaussian 09 (ref. 42) and all vibrational frequencies are calculated using Gaussian 16.43 Oscillator strengths and spin–orbit coupling matrix elements that are used for rate constants of radiative fluorescence and phosphorescence emission and nonradiative ISC (kISC) and rISC (krISC) of compounds 1 and 2 are calculated using the Amsterdam density functional ADF program44–46 in which the TD-PBE1PBE method and the TZP basis set47,48 are used with the zero order regular approximation (ZORA).49–51
3. Results and discussion
3.1 Molecular structure
Important geometric parameters of two complexes in crystal as well as the corresponding experimental values are summarized in Table S1† and optimized molecular structures in the S0, S1, and T1 states are schematically shown in Fig. 2.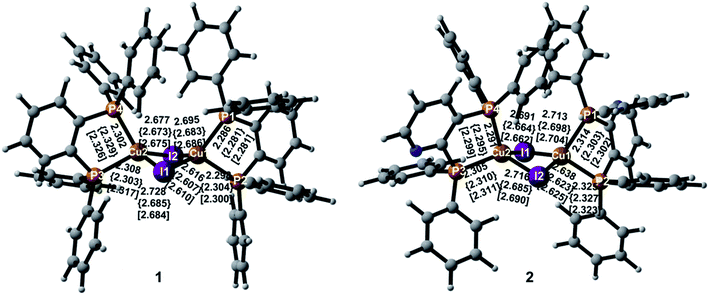 | ||
| Fig. 2 Optimized minimum-energy structures with atomic numbering and selected geometric parameters in the S0, S1 {curly brackets}, and T1 [square brackets] states. | ||
In the S0 state, two complexes have similar molecular structures and the structural parameters in crystal are consistent with experimental values.9 It also confirms the reliability of the PBE1PBE functional and the QM/MM method used. As shown in Fig. 2, the Cu atoms in the two complexes are coordinated with the two P atoms from the diphosphine ligands that form five-membered ring chelates and exhibit highly distorted tetrahedral coordination. The Cu–I and Cu–P bond lengths are comparable in the two complexes in crystal. The Cu⋯Cu distance is well-known to exert an evident impact on photophysical properties of the polynuclear Cu(I) halide complexes and the short Cu⋯Cu distance, less than 2.7 Å, usually generates emissive cluster-centered excited states.52 In crystal, they are 2.783 Å and 2.805 Å for 1 and 2, respectively. The distances are more or less equal to the sum of van der Waals radius of Cu(I) of 2.8 Å, indicating a small interaction between these two Cu atoms. The similar changes can be found in the I⋯I distances. These shortened distances should come from the influence of the surrounding molecules.
For 1, both I–Cu–I and P–Cu–P bond angles deviate largely from the usual tetrahedral value of 109.5°. In particular, the P–Cu–P bond angles are only 88.3° in crystal because of the small angle of the diphosphine ligand with respect to the five-membered ring chelate. The value 90.0° in crystal for compound 2 is larger slightly than that of compound 1. The chelate effect of diphosphine ligands may lead to stable complexes 1 and 2. In addition, two Cu(I) centers are bridged by two I atoms to form a dinuclear structure with a bent rhombic {Cu2I2} core. The four-membered butterfly Cu2I2 rings of the complexes are significantly distorted by bending along the I⋯I axis, which is different from most of halide-bridged Cu(I) complexes having a planar rhombic Cu2X2 geometry.53,54 The dihedral angles between the two CuI2 triangles in the {Cu2I2} core are 141.5° and 144.1° for 1 and 2 in crystal, respectively, implying a large steric hindrance of the diphenyl groups attached on the phosphines.
Different geometric changes of complexes 1 and 2 in the excited states are related to their luminescent properties. Comparing geometric parameters of S0, S1, and T1 minima in crystal, we can see that the Cu–I bond lengths and the I⋯I distances are shortened for 1 and 2. The changes of the Cu⋯Cu distances are different from those of the Cu–I bond lengths. For 1, they are computed to 2.918 Å and 2.934 Å in S1 and T1, respectively, which are longer than 2.783 Å in S0. There are negligible changes for the Cu–P bond lengths in S1 and T1. The same trend is also observed for compound 2. In addition, Fig. 3 displays the difference of geometric parameters for 1 and 2 between S0 and S1 (T1) states. It is worth mentioning that the S1 and T1 minima are structurally similar to each other, which may be caused by the dppb and dpppy ligands constructing a sterically bulky coordination environment around the Cu atoms. As a result, the structural distortion of the MLCT excited state may be suppressed,55 which will benefit the Cu(I) complex to achieve high emission quantum yield, 0.99 for 1 and 0.48 for 2 in crystal.9 This corroborates experimental studies focused on the design of TADF for heteroleptic Cu(I) complexes.54,55
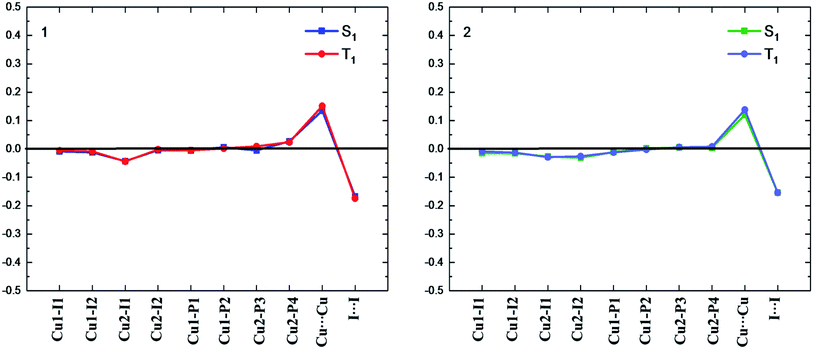 | ||
| Fig. 3 Bond length differences (in Å) of the S1 and T1 minima for complexes 1 and 2 relative to the counterparts of the S0 minimum (black line). | ||
3.2 Frontier molecular orbitals
Frontier orbital analysis for compound 1 and its related orbital energies at the S0 and S1 minima are shown in Fig. 4. The frontier orbital characters of 1 and 2 at the T1 minima as well as those of 2 at the S0 and S1 minima are displayed in Fig. S2 and S3,† respectively.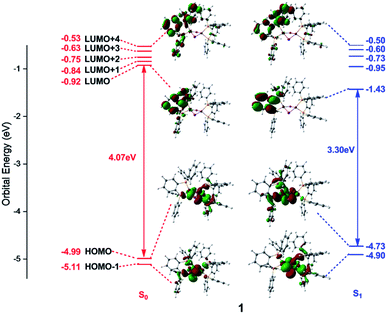 | ||
| Fig. 4 Frontier molecular orbitals and related orbital energies (in eV) at the S0 and S1 minima of complex 1. | ||
As shown in the left panel of Fig. 4, the highest occupied molecular orbital (HOMO) of compound 1 at the S0 minimum is mainly derived from the d orbitals of the Cu centers and the p orbitals of the bridging I atoms. In contrast, the lowest unoccupied molecular orbital (LUMO) is localized at one dppb moiety of the bridging diphosphine ligands. The nature of molecular orbitals of compound 1 at the S1 minimum are almost constant except a little different weights from the different fragment groups (see the right panel of Fig. 4). The minimum-energy structures at both S1 and T1 states of 1 are similar to each other, thus subtly changes are found in the orbital analysis for the T1 minimum compared with that for the S1 one (see Fig. S2†). In addition, the calculations reveal that compositions for compound 2 at the S0 and S1 minima are almost identical with those of compound 1 and are thus placed in Fig. S3.†
Since the photoexcited electron and the remaining hole are spatially separated in the π* orbital of the organic ligand and the 3d orbital of the Cu atom, the energy gap between HOMO and LUMO tends to be small enough to permit an inverse intersystem crossing process from the T1 to S1 states enabling TADF. At the S0 minima, the HOMO–LUMO energy gaps are 4.07 and 3.97 eV for compounds 1 and 2, respectively. However, they decrease to 3.30 and 3.14 eV at the S1 minima and 3.26 and 3.15 eV at the T1 minima for compounds 1 and 2. Obviously, this remarkable reduction of the HOMO–LUMO energy gaps from the S0 to S1 minima of compounds 1 and 2 is responsible for the large Stokes shift experimentally observed in the emission spectra (see below, Fig. 5). On the other hand, the energy gap becomes smaller in compound 2 than that of 1, which is caused by the introduction of the pyridyl N atom with large electronegativity to the aromatic ring that stabilizes the π* orbitals. The similar variation of the HOMO–LUMO energy gaps is also found in recent theoretical works on dinuclear TADF Cu(I) molecules.57
3.3 Absorption spectra
On the basis of the S0 minima of compounds 1 and 2, we have simulated the corresponding absorption spectra. As shown in Fig. 5, there is a broad shoulder at ca. 400 nm in compound 1. Electronic structure analysis shows that the absorption at 374 nm mainly stems from the S0 → S1 electronic excitation, for which the HOMO–LUMO electronic configuration contributes the most. The HOMO is mainly distributed over the Cu and I atoms, while the LUMO is localized on the dppb ligands. Thus, this absorption peak is of the mixed metal-to-ligand and halide-to-ligand charge transfer (M + X)LCT character. The origin of the lowest absorption of compound 2 is similar to that of 1 and the calculated absorption of 2 at 392 nm has a small redshift compared to that of 1 at 374 nm, which could be due to the stabilization of the π* orbitals of the bridging diphosphine ligands introduced by the pyridyl N atom.For 1, the computed 331 nm peak is very close to the experimentally measured 330 nm peak in crystal. The 332 nm peak of 2 is almost equal to that in 1 and also reproduces the experimental value of 328 nm.9 These peaks are mainly caused by the electronic excitation transitions of S0 → S8 for 1 and S0 → S10 for 2. Moreover, these two complexes have strong absorption peaks at 291 nm (see Table S3†), which are also assigned to the electronic transitions H → L+1 for 1 and H − 1 → L+7 for 2, respectively. They are of the same electronic transition character i.e. (M + L)CT (see Fig. S3†).
3.4 Emission properties
Vertical emission energies and related electronic configurations of compounds 1 and 2 in crystal from their S1 and T1 excited states are calculated and listed in Table 1, which also includes wavelengths and oscillator strengths. The corresponding fluorescence emission spectra based on the S1 minima are simulated in Fig. 5.| State | E (eV) | λ (nm) | f | Electronic configuration | Assignment | |
|---|---|---|---|---|---|---|
| 1 | S1 | 2.40 | 517 | 0.0157 | H ← L (94.4%) | (M + X)LCT |
| T1 | 2.19 | 567 | 0.0000 | H ← L (93.1%) | (M + X)LCT | |
| 2 | S1 | 2.24 | 553 | 0.0015 | H ← L (96.8%) | (M + X)LCT |
| T1 | 2.14 | 579 | 0.0000 | H ← L (93.3%) | (M + X)LCT |
In experiments, the emission spectrum of the dinuclear complex 1 in crystal is very similar to that of the mononuclear complex [CuI(dppb)PPh3] (λem = 492 nm).16 This can be understood very well taking into account that the Cu⋯Cu distance of 1 is close to the sum of the van der Waals radii of two Cu atoms (see above). This results in very weak interaction between two Cu atoms in both ground- and excited-states; thus, the emission from 1 resembles that of the mononuclear complex.16
From Table 1, we can find that the HOMO–LUMO electronic configuration is predominantly responsible for the S1 → S0 and T1 → S0 electronic de-excitation transitions, which are also of mixed metal-to-ligand and halide-to-ligand charge-transfer character (M + X)LCT. By contrast, the introduction of the N atoms to the cross-linking phenyl groups of the diphosphine ligands in 2 greatly shifts the emission from bright-greenish-blue (λem = 497 nm) to yellow (λem = 548 nm) as observed in experiments.9 The calculated λmax values of the dinuclear complexes 1 and 2 are in the order 1 (517 nm) < 2 (553 nm), which are consistent with the experimental values in crystal.9
3.5 Excited state properties
Excited-state properties play an important role in determining luminescence mechanism. In order to determine quantitatively related radiative and nonradiative processes of compounds 1 and 2, we have calculated rate constants of forward and inverse intersystem crossing processes between S1 and T1 [ISC (kISC) and rISC (krISC)] and those of fluorescence (kFr) and phosphorescence (kPr) from S1 and T1 in crystal.
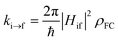 | (1) |
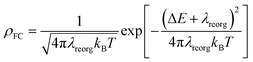 | (2) |
| At S1 | At T1 | |||
|---|---|---|---|---|
| 1 | 2 | 1 | 2 | |
| SOCMEs (cm−1) | 13.14 | 18.57 | 8.34 | 20.72 |
| λreorg (eV) | 0.0256 | 0.0108 | 0.0241 | 0.0096 |
| kISC/krISC (s−1) | 8.25 × 108 | 2.34 × 109 | 6.27 × 105 | 3.36 × 107 |
| kFr × 106 (s−1) | 3.91 | 0.33 | — | — |
| kPr × 103 (s−1) | — | — | 1.11 | 2.70 |
First, we focus on the SOCMEs values of compounds 1 and 2 calculated at the S1 and T1 minima in crystal (see Table 2). After comparing these values, one can find that the SOC value 13.14 cm−1 of compound 1 at the S1 minimum is a little larger than that 8.34 cm−1 at the T1 minimum; but, the SOC value 18.57 cm−1 of compound 2 at the S1 minimum is tinily smaller than 20.72 cm−1 at the T1 minimum. These SOCMEs values are comparable to other complexes with TADF and are large enough to ensure effective forward and reverse intersystem crossing processes.
Second, it is generally accepted that singlet-triplet energy difference (ΔEST) is an important parameter to regulate reverse ISC processes. Table 3 lists the energies of the S1 and T1 minima of compounds 1 and 2 in crystal. One can see the S1 and T1 states' energies of compound 2 are a little decreased compared to those of compound 1. For example, the values 2.75 eV in the S1 state and 2.66 eV in the T1 state of compound 2 are smaller than 2.89 eV and 2.74 eV in S1 and T1 for compound 1, respectively. Nevertheless, the ΔEST values are still small in both compounds, i.e. 0.15 eV in 1 and 0.09 eV in 2. Considering that both 1 and 2 have small ΔEST values, which make their rISC processes from the T1 to S1 states possible in the view of energy. Meanwhile, we have also calculated higher-lying triplet excited states to judge whether they are also involved in TADF. From Table S2,† it is clear that there is only a triplet state i.e. T1 lower than S1 in energy for compounds 1 and 2. In other words, no higher-lying triplet excited states are involved in the rISC processes.
| 1 | 2 | |
|---|---|---|
| S1 | 2.89 | 2.75 |
| T1 | 2.74 | 2.66 |
| ΔES1–T1 | 0.15 | 0.09 |
Finally, we analyze the changes of reorganization energies (λreorg), which can help us understand the radiationless processes either from S1 to T1 or from T1 to S1. The reorganization energy is calculated through the total Huang–Rhys factor S, which is collected as a sum of the Huang-Rhys factors of all vibrational frequencies Sj via the following equation:
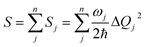 | (3) |
In order to calculate ΔQj, the following relationship for Cartesian coordinates is defined:
| qinit = qfinal + Δq | (4) |
| Qinit = LTinitLfinalQfinal + LTinitΔq | (5) |
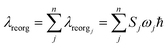 | (6) |
From Table 2, the reorganization energies λreorg for compound 1 either from S1 to T1 (0.0256 eV) or from T1 to S1 (0.0241 eV) are much close to each other. For compound 2, the λreorg values from S1 to T1 or from T1 to S1 are similar in crystal, 0.0108 eV from S1 to T1 vs. 0.0096 eV from T1 to S1. The reorganization energies λreorg of compound 1 either from S1 to T1 or from T1 to S1 are slightly larger than those of compound 2 in crystal phase. In addition, we have examined the distribution of the Huang–Rhys factors. Fig. S5† depicts the Huang–Rhys factor for each vibrational mode involved in the ISC and rISC processes of compounds 1 and 2 in crystal. The low-frequency vibrational modes related to the torsional motion of the dppb and dpppy groups are mainly responsible for these intersystem crossing processes between S1 and T1 (either ISC or rISC). Comparing these Huang–Rhys factors, one can find that the vibrational modes with large Huang–Rhys factors in the low-frequency region are suppressed to certain extent in compound 2. This is consistent with the results of λreorg discussed above.
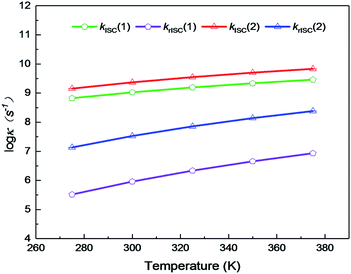
On the basis of SOC, ΔEST, and λreorg, we have calculated the related intersystem crossing rates kISC and krISC of these two Cu(I) dimers in crystal. The kISC and krISC values of compound 2 are larger than those of compound 1 at room temperature. For example, the kISC and krISC values of compound 2 (2.34 × 109 and 3.36 × 107 s−1) are larger than those of compound 1 (8.25 × 108 and 6.27 × 105 s−1), respectively. This change trend is in good agreement with that of involved SOC values (see Table 2). Moreover, the rates krISC of either compounds 1 or 2 are smaller than their forward intersystem crossing rates kISC in crystal. For example, the krISC and kISC values are predicted to be 6.27 × 105 [3.36 × 107] vs. 8.25 × 108 [2.34 × 109 s−1] for 1 [2]. This is because the forward ISC process is energetically favorable whereas the reverse one is merely active when the thermal energy provided by the temperature can overcome the related reverse barriers. Finally, we have checked the temperature effects on these intersystem crossing rates kISC and krISC (see Fig. 6). Obviously, both kISC and krISC rates of compounds 1 and 2 increase with higher temperature, which is caused by the fact that more vibrationally excited states are involved in the intersystem crossing processes when the temperature increases.58 Furthermore, one can see that the reverse intersystem crossing rate constants krISC are more sensitive to the temperature than those of the forward ones kISC in the temperature range of 275 to 375 K.
From above eqn (1) and (2), it is clear that kISC and krISC rate constants are dependent on not only SOC values but also (ΔE + λreorg)2. Fig. 7 shows the relationship of the forward and reverse ISC rate constants and ΔE for compounds 1 and 2 in crystal. In the equations, ΔE is defined as the difference between adiabatic energies of the final and initial states. For the reverse ISC processes from T1 to S1, ΔEST = (ES1 − ET1) is positive for our studied systems, so krISC decreases upon increasing ΔE because λreorg is a fixed positive value. By contrast, kISC is affected by both ΔE and λreorg through (ΔE + λreorg)2 because ΔETS = (ET1 − ES1) is negative for our studied systems. Specifically, when ΔEST is larger than the reorganization energy λreorg, kISC decreases upon increasing ΔETS. Because ΔETS = −ΔEST, kISC is found to decrease with decreasing ΔEST. More interestingly, the curvatures of parabolic functions for the kISC and krISC rate constants of compound 1 as a function of ΔEST are slightly smaller than those of compound 2 (see Fig. 7). This can be understood based on eqn (2) and (3). The logarithmic function of the rate constant k can be rewritten as follows
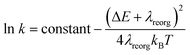 | (7) |
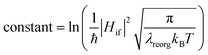 | (8) |
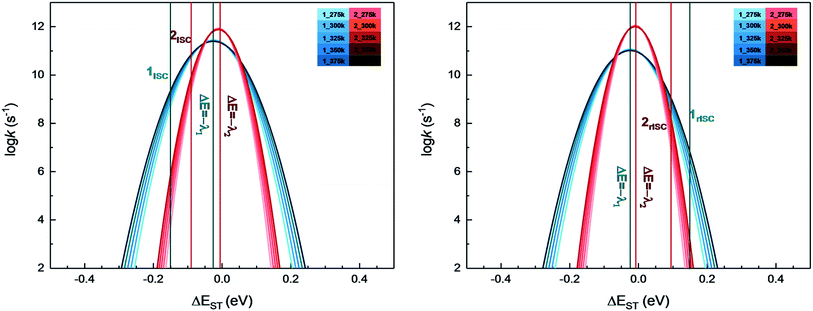 | ||
| Fig. 7 Forward (left) and reverse (right) intersystem crossing rate constants ISC and rISC as a function of ΔEST at different temperatures of complexes 1 (blue) and 2 (red). | ||
From this equation, it is clear that the function curvature is proportional to |1/λ| when the temperature is fixed. Because the λ values for compound 1 are larger than those of compound 2, as shown in Table 2, the former curvatures are smaller than the latter ones. In addition, one can find that the parabolic peaks are always at the points of ΔE = −λreorg where the logarithmic function in eqn (7) achieves a maximum value.
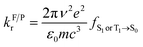 | (9) |
From Table 2, it can be found that the fluorescence and phosphorescence emission rates of compound 2 are smaller than those of compound 1 in crystal. The kFr rate of compound 2 is 0.33 × 106 s−1, which is smaller than 3.91 × 106 s−1 of compound 1. Moreover, one can see that the phosphorescence emission rates are much smaller than the fluorescence emission rates (ca. 103 vs. 106 s−1). Our presently calculated fluorescence radiative rates kFr are in good agreement with experiments, in which they are estimated to be 0.25 × 106 and 0.12 × 106 s−1 for compounds 1 and 2, respectively. These efficient radiative decay rates may overcome competitive nonradiative pathway from S1 to S0 to enable TADF.
3.6 TADF mechanism
The existence of TADF indicates not only that the S1/T1 SOC should be significant for efficient reverse ISC but also that the S1–T1 energy gap has to be small enough so that thermal energy can overcome this gap efficiently. In the following, we will discuss the TADF mechanism of compounds 1 and 2.A three-state model of the S0, S1, and T1 states is enough and used to study the TADF mechanism in these two Cu(I) dimer compounds because the T2 state is energetically higher than the S1 and T1 states at either S1 or T1 minima as discussed above. Fig. 8 summaries a reasonable speculation about the TADF working mechanism of compound 1. This compound can effectively convert its S1 to T1 states with an ISC rate constant of 8.25 × 108 s−1; importantly, the rISC process back to the S1 state is also very faster at the room temperature (6.27 × 105 s−1). These ISC and rISC rates are two orders of magnitude larger than the fluorescence and phosphorescence emission rates from the S1 and T1 states [kISC (108 s−1) > kFr (106 s−1), krISC (105 s−1) > kPr(103 s−1); see Table 2]. In addition, the phosphorescence emission rates are overall about 3 orders of magnitude smaller than the fluorescence emission rates. Thereby, compound 1 mainly fluoresces from the S1 state because the T1 population can be quickly transferred back to the S1 state through the fast rISC process. The internal conversion (IC) process from S1 to S0 and the ISC process from T1 to S0 are much slower due to huge energy gaps between S1 and S0 and between T1 and S0, so these nonradiative decay rates are neglected in our model.64 Even though the kFr rate of compound 2 is smaller than that of compound 1, the TADF mechanism of 2 is similar to that of 1. The present analysis gives in-depth understanding on the TADF properties of the two dinuclear Cu(I) iodide complexes.9
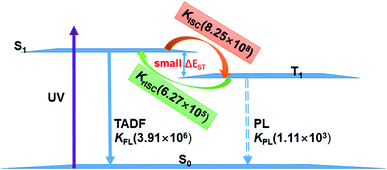 | ||
| Fig. 8 TADF working mechanism of complex 1 including related radiative and radiationless rates calculated by our present theoretical studies. | ||
The present results for the TADF of dinuclear Cu(I) iodide complexes also show that structural rigidity around the central Cu(I) atom is important. First, it benefits rapid intersystem crossing processes between singlets and triplets. Second, efficient deactivation pathways due to structural distortion are effectively suppressed. For example, the emission of dinuclear Cu(I) complexes with less-bulky ligands, i.e. [{Cu(PPh3)2(H2O)}(μ-MeOpyz){Cu(PPh3)2(H2O)}](BF4)2 with PPh3 = triphenylphosphine and MeOpyz = 2-methoxypyrazine, is observed at 580 nm with a remarkably lower quantum yield of 0.05, which has been proved due to efficient excited-state deactivation through structural distortion around the Cu atom from tetrahedral to quasi-square-planar coordination structures.56
Finally, TADF is very sensitive to subtle structural changes of emitting materials. Our studied two compounds are not similar because they have distinctly different ligands: one is related to pyridine and the other is related to benzene. Both ligands indeed brings us significant differences. First, the energy gap becomes smaller in compound 2 than that of compound 1, which is caused by the introduction of the pyridyl N atom with large electronegativity to the aromatic ring that stabilizes the π* orbitals. Second, the introduction of the N atom to the cross-linking phenyl groups of the diphosphine ligands in compound 2 greatly shifts the emission from bright-greenish-blue (497 nm) to yellow (548 nm). Third, the kISC and krISC values of compound 2 are larger than those of compound 1 at room temperature. For example, the kISC and krISC values of compound 2 are larger than those of compound 1, respectively (see Table 2). Fourth, the fluorescence and phosphorescence emission rates of compound 2 are smaller than those of compound 1 in crystal.
It should be noted that the TADF mechanism of copper-based organometallic compounds is rather different from those of pure organic TADF emitters. Recently, Penfold et al. have summarized many efficient organic TADF emitters and related TADF mechanisms.65 For example, different D–A–D molecules with very similar energy gaps exhibit large variations in krISC. They found that luminescence could be switched from TADF to phosphorescence by sterically hindering the motion of D and A group. Interested readers are referred to this literature.65
4. Conclusions
The structures, excited properties, and luminescence of two dinuclear Cu(I) complexes with dppb and dpppy ligands [Cu2(μ-I)2(dppb)2] (1) and [Cu2(μ-I)2(dpppy)2] (2) as potential TADF emitters have been comprehensively studied by means of combined QM/MM calculations. On the basis of ground and excited-state geometries we have found that the S1 and T1 states have very small energy gaps ΔEST, less than 0.15 eV, which makes the forward and reverse intersystem crossing ISC and rISC processes between S1 and T1 much efficient. We have also found that both ISC and rISC processes are much faster than the corresponding fluorescence and phosphorescence radiative processes [kISC (108 s−1) > kFr (106 s−1), krISC (105 s−1) > kPr (103 s−1)]. Since the reverse rISC rates are much faster than the phosphorescence emission rates, the T1 population can be quickly transferred to the S1 state leading to a delay fluorescence emission. Through analyzing the Huang–Rhys factors we have found that the low-frequency vibrational modes related to the torsional motion of the dppb and dpppy groups are mainly in charge of these intersystem crossing processes ISC or rISC. Our present calculations not only elucidate recent experimental phenomena but also help understand, and design similar TADF emitters, e.g. with rigid ligands to inhibit structural distortions of emitting states and nonradiative processes, etc.Conflicts of interest
The authors declared that they have no conflicts of interest to this work.Acknowledgements
This work was supported by the National Natural Science Foundation of China (G. C. 21522302) and China Postdoctoral Science Foundation (2018M641243); G. C. is also grateful for the financial support from “Fundamental Research Funds for Central Universities”.References
- J. Gibson, A. P. Monkman and T. J. Penfold, ChemPhysChem, 2016, 17, 2956 CrossRef CAS PubMed.
- G. Baryshnikov, B. Minaev and H. Ågren, Chem. Rev., 2017, 117, 6500 CrossRef CAS PubMed.
- J. Föller, M. Kleinschmidt and C. M. Marian, Inorg. Chem., 2016, 55, 7508 CrossRef PubMed.
- X.-K. Chen, S.-F. Zhang, J.-X. Fan and A.-M. Ren, J. Phys. Chem. C, 2015, 119, 9728 CrossRef CAS.
- Q. Peng, D. Fan, R. Duan, Y. Yi, Y. Niu, D. Wang and Z. Shuai, J. Phys. Chem. C, 2017, 121, 13448 CrossRef CAS.
- A. Stoïanov, C. Gourlaouen, S. Vela and C. Daniel, J. Phys. Chem. A, 2018, 122, 1413 CrossRef PubMed.
- J. Fan, L. Lin and C.-K. Wang, J. Mater. Chem. C, 2017, 5, 8390 RSC.
- T. Vikramaditya, M. Saisudhakar and K. Sumithra, RSC Adv., 2016, 6, 37203 RSC.
- Y. Okano, H. Ohara, A. Kobayashi, M. Yoshida and M. Kato, Inorg. Chem., 2016, 55, 5227 CrossRef CAS PubMed.
- G. Blasse and D. R. McMillin, Chem. Phys. Lett., 1980, 70, 1 CrossRef CAS.
- Y. G. Ma, W.-H. Chan, X.-M. Zhou and C.-M. Che, New J. Chem., 1999, 23, 263 RSC.
- J. L. Markus, M. Z. Danie, S. Alexander, B. Thomas, V. Daniel and Y. Hartmut, Top. Curr. Chem., 2016, 374, 25 CrossRef PubMed.
- Y. Tao, K. Yuan, T. Chen, P. Xu, H. Li, R. Chen, C. Zheng, L. Zhang and W. Huang, Adv. Mater., 2014, 26, 7931 CrossRef CAS PubMed.
- A. J. M. Miller, J. L. Dempsey and J. C. Peters, Inorg. Chem., 2007, 46, 7244 CrossRef CAS PubMed.
- J. Chen, T. Teng, J.-Y. Wang, L. Kang, X.-L. Chen, L.-J. Xu, R. Yu and C.-Z. Lu, Eur. J. Inorg. Chem., 2016, 2016, 3036 CrossRef CAS.
- A. Tsuboyama, K. Kuge, M. Furugori, S. Okada, M. Hoshino and K. Ueno, Inorg. Chem., 2007, 46, 1992 CrossRef CAS PubMed.
- H. Araki, K. Tsuge, Y. Sasaki, S. Ishizaka and N. Kitamura, Inorg. Chem., 2007, 46, 10032 CrossRef CAS PubMed.
- J. C. Deaton, S. C. Switalski, D. Y. Kondakov, R. H. Young, T. D. Pawlik, D. J. Giesen, S. B. Harkins, A. Miller, S. F. Mickenberg and J. C. Peters, J. Am. Chem. Soc., 2010, 132, 9499 CrossRef CAS PubMed.
- D. M. Zink, M. Bächle, T. Baumann, M. Nieger, M. Kühn, C. Wang, W. Klopper, U. Monkowius, T. Hofbeck, H. Yersin and S. Bräse, Inorg. Chem., 2013, 52, 2292 CrossRef CAS PubMed.
- M. J. Leitl, F.-R. Küchle, H. A. Mayer, L. Wesemann and H. Yersin, J. Phys. Chem. A, 2013, 117, 11823 CrossRef CAS PubMed.
- H. Araki, K. Tsuge, Y. Sasaki, S. Ishizaka and N. Kitamura, Inorg. Chem., 2005, 44, 9667 CrossRef CAS PubMed.
- G. Li, R. S. Nobuyasu, B. Zhang, Y. Geng, B. Yao, Z. Xie, D. Zhu, G. Shan, W. Che, L. Yan, Z. Su, F. B. Dias and M. R. Bryce, Chem.–Eur. J., 2017, 23, 11761 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- B. Delley, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155125 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- B. Delley, J. Chem. Phys., 1990, 92, 508 CrossRef CAS.
- B. Delley, J. Phys. Chem., 1996, 100, 6107 CrossRef CAS.
- B. Delley, J. Chem. Phys., 2000, 113, 7756 CrossRef CAS.
- F. Maseras and K. J. Morokuma, J. Comput. Chem., 1995, 16, 1170 CrossRef CAS.
- T. Vreven, K. Morokuma, Ö. Farkas, H. B. Schlegel and M. J. Frisch, J. Comput. Chem., 2003, 24, 760 CrossRef CAS PubMed.
- A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024 CrossRef.
- Y.-J. Gao, W.-K. Chen, Z.-R. Wang, W.-H. Fang and G. L. Cui, Phys. Chem. Chem. Phys., 2018, 20, 24955 RSC.
- L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Y. Liu, H.-B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678 CrossRef CAS PubMed.
- J. Fan, Y. Zhang, Y. Zhou, L. Lin and C.-K. Wang, J. Phys. Chem. C, 2018, 122, 2358 CrossRef CAS.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- M. A. L. Marques, C. A. Ullrich, F. Nogueira, A. Rubio, K. Burke and E. K. U. Gross, Time-dependent Density Functional Theory, Springer, 2006 Search PubMed.
- D. Andrae, U. Häuβermann, M. Dolg, H. Stoll and H. Preuβ, Theor. Chem. Acc., 1990, 77, 123 Search PubMed.
- J. M. L. Martin and A. Sundermann, J. Chem. Phys., 2001, 114, 3408 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chem. Acc., 1973, 28, 213 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgometry Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgometry Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A. 03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391 Search PubMed.
- E. J. Baerends, T. Ziegler, A. J. Atkins, J. Autschbach, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerritger, L. Cavallo, D. P. Chong, D. V. Chulhai, L. Deng, R. M. Dickson, J. M. Dieterich, D. E. Ellis, M. van Faassen, L. Fan, T. H. Fischer, C. Fonseca Guerra, M. Franchini, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. W. Götz, J. A. Groeneveld, O. V. Gritsenko, M. Grüning, S. Gusarov, F. E. Harris, P. van den Hoek, C. R. Jacob, H. Jacobsen, L. Jensen, J. W. Kaminski, G. van Kessel, F. Kootstra, A. Kovalenko, M. V. Krykunov, E. van Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, S. M. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, C. A. Peeples, P. H. T. Philipsen, D. Post, C. C. Pye, W. Ravenek,, J. I. Rodríguez P. Ros, R. Rüger, P. R. T. Schipper, H. van Schoot, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solà, M. Swart, D. Swerhone, G. te Velde, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakovlev, ADF2016, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, https://www.scm.com Search PubMed.
- E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142 CrossRef CAS PubMed.
- D. P. Chong, E. van Lenthe, S. van Gisbergen and E. J. Baerends, J. Comput. Chem., 2004, 25, 1030 CrossRef CAS PubMed.
- F. Wang and T. Ziegler, J. Chem. Phys., 2005, 123, 154102 CrossRef PubMed.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783 CrossRef CAS.
- E. van Lenthe, R. van Leeuwen, E. J. Baerends and J. G. Snijders, Int. J. Quantum Chem., 1996, 57, 281 CrossRef CAS.
- L. Kang, J. Chen, T. Teng, X.-L. Chen, R. Yu and C.-Z. Lu, Dalton Trans., 2015, 44, 11649 RSC.
- A. Kobayashi, K. Komatsu, H. Ohara, W. Kamada, Y. Chishina, K. Tsuge, H.-C. Chang and M. Kato, Inorg. Chem., 2013, 52, 13188 CrossRef CAS.
- P. Aslanidis, P. J. Cox, S. Divanidis and A. C. Tsipis, Inorg. Chem., 2002, 41, 6875 CrossRef CAS PubMed.
- A. Kobayashi, Y. Yoshida, M. Yoshida and M. Kato, Chem.–Eur. J., 2018, 24, 1 CrossRef.
- A. Kobayashi, R. Arata, T. Ogawa, M. Yoshida and M. Kato, Inorg. Chem., 2017, 56, 4280 CrossRef CAS PubMed.
- Y.-J. Gao, Z.-R. Wang, W.-K. Chen, W.-H. Fang and G. L. Cui, Chem. Phys., 2018, 515, 692 CrossRef CAS.
- R. A. Marcus, J. Phys. Chem., 1963, 67, 853 CrossRef CAS.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265 CrossRef CAS.
- I. Prigogine and S. A. Rice, Advances in Chemical Physics, John Wiley & Sons, 2003 Search PubMed.
- Y. X. Liu, M. S. Lin and Y. Zhao, J. Phys. Chem. A, 2017, 121, 1145 CrossRef CAS PubMed.
- J.-L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2014, 104, 4791 Search PubMed.
- Y. Gao, T. Su, L. Zhao, Y. Geng, Y. Wu, M. Zhang and Z. M. Su, Org. Electron., 2017, 50, 70 CrossRef CAS.
- H. Lin, X. P. Chang, D. Yan, W.-H. Fang and G. L. Cui, Chem. Sci., 2017, 8, 2086 RSC.
- T. J. Penfold, F. B. Dias and A. P. Monkman, Chem. Commun., 2018, 54, 3926 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra02256b |
| This journal is © The Royal Society of Chemistry 2019 |