Open Access Article
Open Access ArticleTesting density scaling in nanopore-confinement for hydrogen-bonded liquid dipropylene glycol
Katarzyna Chat *ab,
Grzegorz Szklarz
*ab,
Grzegorz Szklarz ab and
Karolina Adrjanowicz
ab and
Karolina Adrjanowicz *ab
*ab
aInstitute of Physics, University of Silesia, 75 Pulku Piechoty 1, 41-500 Chorzow, Poland. E-mail: kchat@us.edu.pl; kadrjano@us.edu.pl
bSilesian Center for Education and Interdisciplinary Research (SMCEBI), 75 Pulku Piechoty 1a, 41-500 Chorzow, Poland
First published on 4th July 2019
Abstract
Recently, it has been demonstrated that the glassy dynamics of the molecular liquids and polymers confined at the nanoscale level might satisfy the density scaling law (ργ/T) with the same value of the scaling exponent, γ, as that determined from the high-pressure studies of the bulk material. In this work, we have tested the validity of this interesting experimental finding for strongly hydrogen-bonded molecular liquid, dipropylene glycol (DPG), which is known to violate the ργ/T scaling rule in the supercooled liquid bulk state. The results of the independent dielectric relaxation studies carried out on increased pressure and in nanopores, have led to an important finding that when the density change induced by geometrical confinement is not very large, DPG can still obey the density scaling law with the same value of the scaling exponent as that found for the bulk sample. In this way, we confirm that the information obtained from the universal density scaling approach applied to nanoscale confined systems is somehow consistent with the macroscopic ones and that in both cases the same fundamental rules governs the glass-transition dynamics.
1 Introduction
The underlying nature of the glass transitions phenomena is a problem that has bothered scientists for many years.1–6 One of the concepts that might be helpful to understand it better is the density scaling which comes from the high-pressure studies of the bulk liquids and polymers. Numerous studies have shown that for many glass forming substances different dynamic quantities such as viscosity η or the characteristic time of the structural relaxation τα, measured at different thermodynamic conditions (T, p), can be expressed as function J(Γ) using a single scaling variable, Γ = T−1V−γ or Γ = ργ/T where T, V, and ρ denote the temperature, volume, and density, respectively. The γ exponent is a material constant which value does not depend on the thermodynamic conditions.7–14 It can be linked with the repulsive part of the Lennard–Jones potential.13,15–17 Furthermore, γ correlates with the thermodynamic quantities and can be identified with the Grüneisen constant.18–20 The density scaling idea has proven to work well for many molecular liquids, e.g. van der Waals liquids, ionic liquids, and polymers.11,13,14,21 However, it is also known to fail for strongly associated liquids.11,13,22–24 One of the most prominent example of such material is dipropylene glycol (DPG).25 Recently, Hansen and co-workers have demonstrated that the density scaling idea applies also for DPG, on the condition that the time scale of the α-relaxation refers to the equilibrium liquid far from the glass transition.26 Based on the experimental results it was suggested that the TVγ scaling works for most of the glass-forming systems only when considering a relatively small density changes.13,27 On the other hand, in the literature we can also find some evidence that it can be valid even up to 4.55 GPa (for cumene).28Apart from the high-pressure studies, a valuable source of information on the glass transition dynamics is the measurements carried out in confined geometry. It is well-established that the dynamics of the liquids confined to nanometer pores is much different from that in the bulk state.29–35 In the presence of nanoscale confinement, it has been observed that on cooling the temperature dependence of the structural relaxation time starts to depart from the bulk-behavior. This happens as due to verification of the interfacial layer, that is the fraction of molecules located in close proximity of the pore walls. Below that temperature, the dynamics of nanopore-confined liquid enters isochoric conditions. It has been also shown that in confined geometry the α-relaxation time measured below the glass transition temperature of the interfacial layer can obey the density scaling law, just like the bulk fluid. Surprisingly, to do that we use the same value of the scaling exponent γ as that found for substances measured in the bulk.29–31 What remains unclear, however, is whether the idea of the density scaling works in confined geometry for these glass-forming systems which for sure, does not scale in bulk supercooled liquid state.
In this work, we apply the concept of the density scaling to study the glass-transition dynamics of strongly hydrogen bonded liquid in the 2D nanoscale (hard) confinement. For that purpose, we have chosen dipropylene glycol (DPG) known as a modelled glass-former which fails to obey the density scaling law in the bulk, close to the glass transition. Our aim is to test whether, even in such case, the concept of the density scaling is still able to provide a consistent picture of the viscous liquid dynamics under varying thermodynamic conditions. To do that, dielectric relaxation studies have been carried out for DPG under high-pressure conditions (in the bulk liquid state) and when confined within alumina nanopores of pores diameter from 100 nm to 18 nm. The most important finding of this work is that using both approaches once can get consistent information about the characteristic ργ/T scaling behavior of various glass-forming systems, including strongly hydrogen bonding liquids. This provides new evidence that macro- and nanoscale glassy dynamics must be connected and governed by the same underlying principles.
2 Experimental section
2.1 Materials
Dipropylene glycol, DPG, (C6H14O3, MW 134.17 g mol−1) of purity greater than 99% was purchased from Sigma Aldrich and used as received. Based on calorimetric studies (Mettler-Toledo, CR 10 K min−1, HR 10 K min−1) the value of the glass transition temperature for a bulk sample at 0.1 MPa is 198 K (determined as the midpoint of the heat capacity increment). The glass transition temperature, Tg, found from the dielectric relaxation studies is typically defined as a temperature at which τα = 100 s. For DPG this gives Tg = 195 K, which is in agreement with the literature data (see for example ref. 26 and 36-38). As DPG can very easily absorb the moisture from the surrounding that causes a plasticizing effect (faster α-relaxation dynamics), we use freshly opened bottles from the same batch and handle them with care upon each stage of the sample preparation for high-pressure and confinement studies.2.2 Methods
Ambient pressure. Dielectric relaxation studies were carried out by using a Novocontrol Alpha analyzer. For bulk DPG, we use standard plate–plate electrodes of 10 mm in diameter separated by Teflon spacer of 30 μm thickness. Nanopores AAO templates (of 50 μm thickness and 13 mm diameter) filled with investigated sample were placed between two circular electrodes. Bulk and confined materials were measured as a function of temperature in the frequency range from 10−1 Hz to 106 Hz. The temperature was controlled with stability better than 0.1 K by Quatro system. The raw dielectric data of DPG confined to AAO nanopores represents a combined response of alumina matrix plus liquid embedded in the pores where the applied electric field is parallel to the long pore axes. This would mean that in order to get their individual contributions a deconvolution of both responses from the total dielectric signal of the composite is required. However, in such nanopore-composite scenario, the only variable which will be affected is the intensity of the dielectric signal of the confined liquid, while not the position of the maximum of the α-relaxation peak, neither the temperature evolution of the α-relaxation time (see for example ref. 39).
High pressure. For dielectric studies carried out at elevated pressure, we have utilized the high-pressure system with MP5 micropump and a control unit (Unipress, Institute of High-Pressure Physics, Warsaw, Poland). The pressure was exerted by using a silicon oil transmitted to the pressure chamber (MV1-30 vessel) by a system of capillary tubes (Nova Swiss). The real and imaginary parts of the complex permittivity were measured – within the same frequency range as the atmospheric pressure data – using impedance Alpha-A Analyzer (Novocontrol GmbH, Montabaur, Germany). The temperature was controlled by the highly dynamic temperature control system (Presto W85, Julabo). The sample capacitor composed of two stainless steel electrodes separated by quartz spacers (50 mm thickness) was sealed and mounted inside a Teflon capsule to separate it from pressure transmitting silicon oil. The schematic picture of the high-pressure plug used this study can be found in the literature (see pg. 75 in ref. 40).
3 Results and discussion
3.1 Ambient and high-pressure results
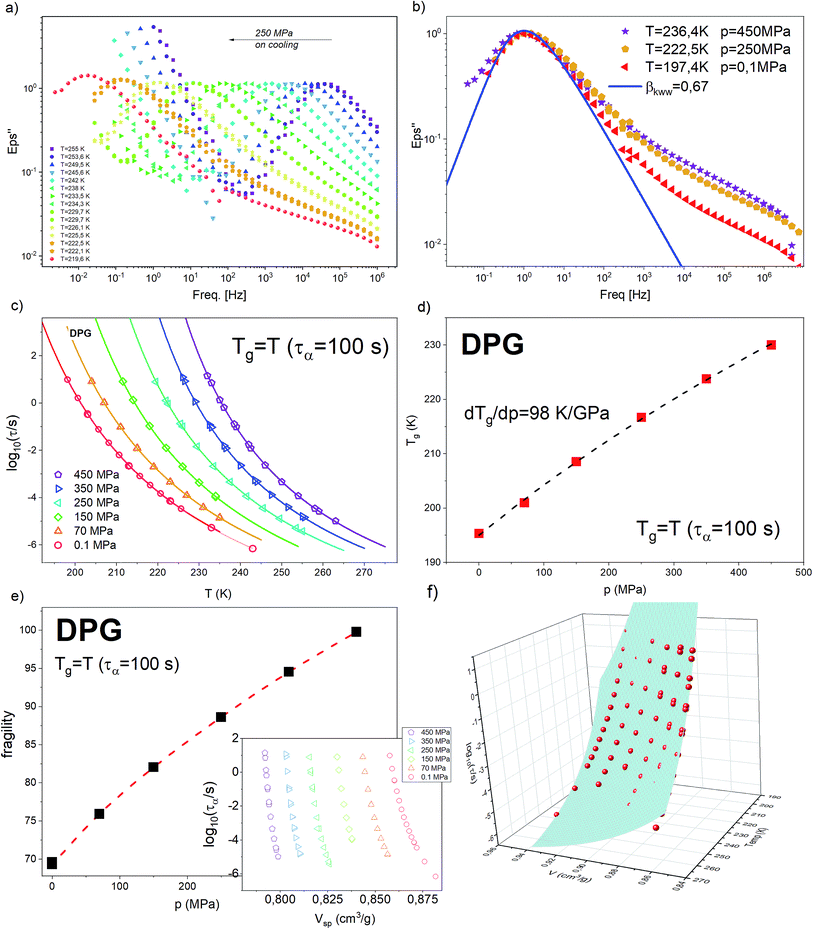
High-pressure behavior of DPG close to the glass transition was investigated in the past by Roland et al.41 along three isotherms (225.6 K, 216.8 K, and 238.4 K) as well as one isobar 0.1 MPa. Later studies by Paluch and co-workers,36 at 1.7 GPa, have explored in more details a peculiar behavior of DPG at elevated pressure. From abovementioned works, we know that as due to the change in the hydrogen-bonding structure an anomalous increase of the fragility parameter and broadening of the α-loss peak (lack of isochronal superposition) with increasing pressure are observed. Apart from that, a combination of the dielectric relaxation and PVT measurements has revealed a breakdown of the density scaling relation (the best match was achieved with γ ≅ 1.5).25 In the present study, we have re-measured the dielectric results for DPG on increased pressure. The purpose of that was to make sure that (i) the temperature dependences of the α-relaxation time that will be used to test the density scaling relation for the bulk liquid were collected by exactly the same experimental setup, precluding in this way unwanted effects associated e.g., with a bit different ways of applying pressure, various high-pressure equipment or accuracy in stabilization of temperature and pressure; (ii) the dielectric data in nanopore-confinement are collected on a sample taken from the same batch.The dielectric relaxation measurement for DPG on increased pressure was carried out along 6 isobars: 0.1 MPa, 70 MPa, 150 MPa, 250 MPa, 350 MPa, and 450 MPa. In Fig. 1a we show representative dielectric loss spectra collected upon cooling from 255 K down to 219.6 K, at a fixed pressure, p = 250 MPa. On lowering the temperature, cooperative α relaxation, seen as an intense peak, shifts towards lower frequencies, implying systematic slowing down of the molecular movements. The analysis of the breath of the α-relaxation at various combinations of temperature and pressure, while keeping the same peak position, is a common way of testing the isochronal superposition. For DPG, we show it in Fig. 1b. In agreement with the literature results, we found that the α-loss peak broadens when increasing temperature and pressure along an isochrone. The accompanying increase at the high-frequency flank of the α-relaxation signifies the presence of an additional – pressure independent – secondary relaxation termed in the literature as the γ-relaxation. The fit of the α-relaxation loss peak recorded at 197.4 K and atmospheric pressure by the one-sided Fourier transform of the KWW function:42,43
| ϕ(t) = exp[−(t/τα)βKWW], 0 < βKWW ≤ 1 | (1) |
In Fig. 1c we plotted temperature evolution of the α-relaxation time, τα, along all studied here isobars. The α-relaxation time at a given temperature and pressure conditions was determined from the frequency corresponding to the maximum of the loss peak, τα = 1/2(πfmax). The character of the obtained dependences was described with the use of Vogel–Fulcher–Tammann (VFT) equation44–46
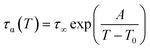 | (2) |
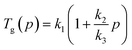 | (3) |
The other characteristic parameter that can be greatly affected by changes in the hydrogen-bonding structure of DPG is fragility index quantifying the degree of deviation of the τα(T) dependence from the Arrhenius behavior.49
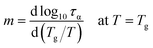 | (4) |
The values of m plotted as a function of pressure for the tested liquid can be found in Fig. 1e. Again, in agreement with the literature results, there is an increase in the fragility parameter with increasing pressure. This effect is explained in the literature as due to modification of the hydrogen bonding structures by pressure.36,41
Having verified that our high-pressure results are consistent with the literature, in the next step, we aim to test again the density scaling relation for DPG. Since in the experimental study we measure the evolution of the α-relaxation time as a function of temperature and pressure, Pressure–Volume–Temperature measurements are needed to get the interrelationship between these three thermodynamic variables. We use volumetric measurements reported by Roland et al.41 that covers the liquid state properties within the pressure range 10–200 MPa and temperature 323–443 K. Following Roland and co-workers, to parametrize the data the following set of the fitting parameters41 from Tait equation of state50 was used v0 = 0.910 cm3 g−1, v1 = 6.70 10−4 cm3 (g C)−1, v2 = 1.339 10−6 cm3 (g C2)−1, b0 = 184 MPa, b1 = 6.08 10−3 C−1. As a next step, τα(T) dependences measured under elevated pressure were expressed as a function of volume (see inset in Fig. 1e). To portray the evolution of τα in the entire T–V space, we use the modified version of the Avramov equation:18
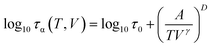 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ0 = −7.4, A = 198.3, D = 7.6 and γ = 1.9. The R2 value is equal to 0.987.
τ0 = −7.4, A = 198.3, D = 7.6 and γ = 1.9. The R2 value is equal to 0.987.
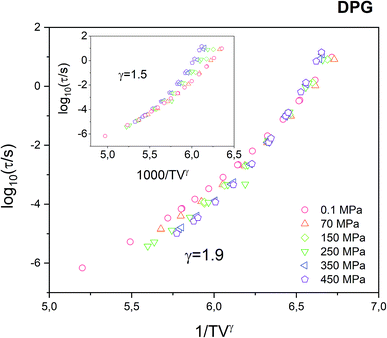
In Fig. 2 we plot all isobaric data as a function of 1000/TVγ with the scaling exponent γ = 1.9 as determined from the Avramov fit of the τα(T, V) dependence. It can be seen that the data does not collapse perfectly, as it is commonly observed for van der Waals liquids or polymers.
This is a clear indication that the density scaling indeed does not hold for the tested hydrogen bonding liquid. On the other hand, in this study, we were actually able to get a much better collapse of the α-relaxation times measured for DPG under varying thermodynamic conditions, compared with the results reported in the literature for γ = 1.5 (see Fig. 3 in ref. 25). As we suppose, the reason is that the previous study combines dielectric data that comes from the two sets of experiments utilizing high-pressure setups that differ e.g. in the way how the pressure/temperature is transferred to the sample. In contrast, in this study, all isobaric data were collected under the same sample environment. Therefore, the accuracy in determining τα for a particular (T, p) condition is greatly reduced. As a result of that, it was possible to achieve, to some degree better, superposition the dielectric relaxation data measured under varying thermodynamic conditions. We note here that the use of the scaling exponent γ = 1.5 in case of our data makes the 1000/TVγ scaling to work even worse (see inset in Fig. 2).
Summarizing this part, we have validated that the glass-transition dynamics of bulk DPG indeed shows typical attributes characteristic for strongly hydrogen bonded liquids such as very weak pressure sensitivity, lack of the isochronal superposition and evident problems with the density scaling. However, in contrast to the previous study, we also found that the deviation from the perfect scaling of the α-relaxation times measured for DPG under varying thermodynamic conditions is not as that pronounced as reported in the literature.
3.2 Confinement results
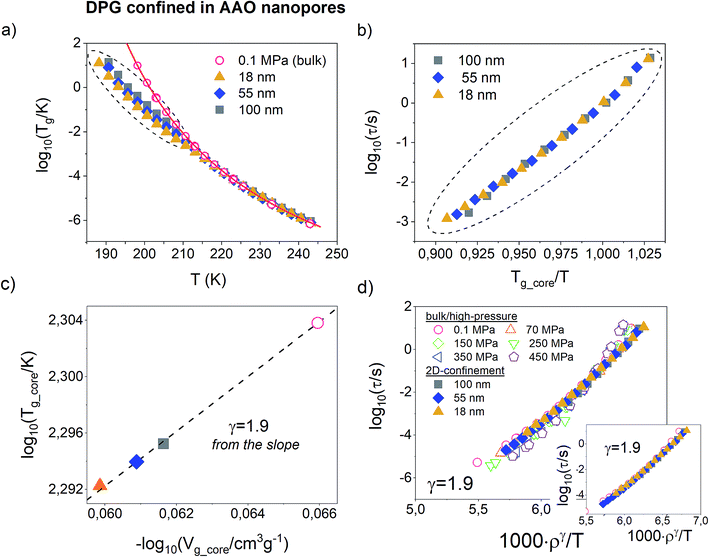
Before testing the density scaling law for DPG embedded within AAO nanopores, we will focus on much different sensitivity of various glass-forming systems to confinement effects. Fig. 3 presents temperature evolution of α-relaxation time recorded for two glass-formers, DPG and PMPS, i.e. polymethylphenylsiloxane embedded in AAO nanopores of approximately the same size (20 nm ± 3 nm and 18 nm ± 3 nm, respectively). The results demonstrate that the confinement effect seen in the evolution of τα(T) is more pronounced for nanopore-confined PMPS than DPG. In this case, a characteristic departure of the α-relaxation times from the bulk-like behavior shows up already at much faster relaxation times. We relate this effect to kinetic freezing of the interfacial layer at Tg_interface on the experimental time-scale which is accompanied by entering quasi-isochoric (constant volume) conditions. Therefore, τα(T) dependences recorded below Tg_interface was described by isochores generated with the use of high-pressure data for the bulk material. Interestingly, for PMPS, just by varying with the cooling rate it is possible to greatly affect the temperature at which the molecules located in close proximity of the pore walls vitrify. Hence, also the evolution of the α-relaxation times measured within Tg_core and Tg_interface. Although DPG in nanopores shows also a clear departure from the bulk-like dynamics, this effect is not as that pronounced as for PMPS. A characteristic change in the character of the τα(T) dependence occurs for a bit longer relaxation times (log10(τα/s) ≅ −3), and it is barely changed by the thermal history of the sample.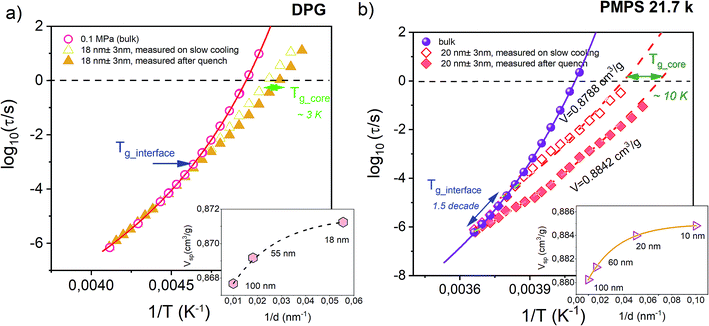 | ||
| Fig. 3 Temperature dependence of the α-relaxation time measured in the bulk and confined to AAO nanopores of approx. The same pore size for the hydrogen bonding liquid DPG (dTg/dp = 98 K GPa−1 – present study) and a siloxane polymer PMPS (dTg/dp = 289 K GPa−1).51 Solid lines denote VFT fits of τα(T) dependence for the bulk materials. Data were recorded by following the same thermal protocols (on slow cooling with 0.2 K min−1 and after quench with 10 K min−1). Dashed lines are isochoric dependencies of α-relaxation times determined based on the pressure-dependent dynamics. The same insets show the change in the volume frozen at the glass transition temperature of the interfacial layer (Tg_interface) as a function of the inverse pore diameter. | ||
To explain this finding we take advantage of the information that comes from the high-pressure studies of the bulk materials. The main difference between DPG and PMPS is the sensitivity of their glass-transition dynamics to pressure/density effects. The former one is very weakly sensitive to compression (dTg/dp = 98 K GPa−1), as commonly observed for strongly hydrogen-bonded systems. On the other hand, the segmental dynamics of PMPS – just like for the most of the polymer glass-formers – is fairly sensitive to compression/density changes as quantified by the coefficient dTg/dp = 289 K GPa−1.51 Almost 3-fold difference in the value of dTg/dp coefficient is a clear indication that the density fluctuations exert more important role on the glass-transition dynamics of PMPS than DPG. Indeed, we can also see in the presence of nanoscale confinement, where only a slight perturbation in volume is able to affect greatly the τα(T) for PMPS. On the other hand, for DPG – which dynamics is primarily controlled by the temperature while not density effects – such minimal frustration in volume is not enough to produce any noticeable changes in the evolution of the α-relaxation time.
In order to make our postulate more robust we present in the insets of Fig. 3 estimated – using volumetric data for DPG41 and PMPS52 – changes in the volume frozen at the glass transition temperature of the interfacial layer (Tg_interface) as a function of the inverse pore diameter. The volume for nanoconfined liquid is expected to increase with decreasing the pore size.53 However, more importantly, we also found that for both glass-formers the volume change which accompanies lowering the pore diameter from 100 nm to ∼20 nm is comparable, and does not exceed more than ∼0.5%. Hence, it is evident that the sensitivity of the α-relaxation dynamics to pressure might give us a quick outlook on whether a particular glass-former show significant deviation from the bulk behavior under nanoscale confinement. A similar conclusion has been recently reached in the study of various glass-formers characterized by different behavior under geometrical confinement.54
Fig. 4a present temperature dependence of α-relaxation time measured for DPG in AAO nanopores of pore sizes from 100 nm to 18 nm. The bulk τα(T) dependence was given as a reference. It can be seen that at higher temperatures the α-relaxation time for all pore sizes matches with that of the bulk liquid. However, as the temperature decrease, the mean relaxation rate for nanopore-confined DPG starts to deviate from the bulk behavior. At any given temperature below Tg_interface, the dynamics of DPG confined to AAO nanopores is faster compared to the bulk with the magnitude that increases with lowering the pore diameter. As noted above, the temperature at which a characteristic departure of the τα(T) dependence from the VFT bulk behavior occurs signifies the glass-transition temperature of the interfacial layer.
So far, for all glass-forming liquids and polymers studied under nanopore-confinement, we were able to describe τα(T) recorded below Tg_interface with the use of isochoric curves (see e.g. ref. 29, 35, 53 and 55). However, these systems – in contrast to DPG – are also known to satisfy the density scaling law in the bulk. In such a case, isochores can be generated using parametrized T–V version of the Avramov equation (eqn (5)). Herein, we use a model-independent approach to verify if DPG confined to AAO nanopores still follows isochoric dependences. This approach takes from the empirical finding that isochores scales onto a single master curve when plotted versus Tg/T.56 In Fig. 4b, we demonstrate such scaling plot for DPG confined to AAO nanopores of different pore sizes. The data includes τα(T) measured within Tg_interface and Tg_core plotted versus Tg_core/T, where Tg_core is defined as a temperature at which τα = 1 s. From the obtained results we conclude that the dependences of α-relaxation time measured for DPG in nanopores are also isochoric. Note that in order to avoid extrapolation of the confinement data, τα = 1 s instead of 100 s was used to define the glass-transition temperature for the core molecules.
In order to ascribe volume values for different pore sizes, we make use of the volumetric data for DPG. First, we determine the temperature at which a characteristic kink in τα(T) dependence occurs and then using volumetric data recorded at ambient pressure determine specific volume which corresponds to this particular ‘kink’ temperature. The same procedure was applied for DPG infiltrated into AAO with the averaged pores diameter in the range from 100 nm to 18 nm. The next step is to determine the value of the scaling exponent γ from the confinement data. For this purpose, we analyzed the relationship between Tg_core and Vg_core for DPG confined to nanopores of different sizes. Herein, Vg_core is basically a particular isochoric volume frozen for confined liquid below Tg_interface. Then, the slope of Tg(Vg) in a double logarithmic plot provides a direct estimate of the γ parameter.57 As presented in Fig. 4c, the value of the scaling exponent obtained in this way corresponds perfectly well to that determined from the high-pressure studies of the bulk material (γ = 1.9). Therefore, our results provide new arguments that from the analysis of the confinement data (and with only access to volumetric data at ambient pressure) we are able to obtain consistent information on the density scaling of the α-relaxation dynamics so as from the high-pressure studies.
As the last point, using the obtained value of the scaling parameter γ we have tested the density scaling law for nanopore-confined DPG. The results are demonstrated in Fig. 4d. Note, that for the analysis of the nanopore data we have used τα(T) measured below Tg_interface. In this temperature region, they are isochores, so the volume for the confined liquid can be easily estimated. For comparison, we have also included ργ/T scaling plot obtained for DPG in a standard way, i.e. using isobaric dielectric relaxation times measured at ambient and elevated pressure (results presented in Fig. 2). By combining high-pressure and confinement data we see that the density scaling breaks down meaning that we cannot describe accurately the dynamics of supercooled liquid DPG as a function of single scaling parameter 1000ργ/T in the entire T–V thermodynamic space. On the other hand, it can be also observed that isochoric dependences of the α-relaxation times for confined DPG can be made to collapse to a single master curve when plotted versus ργ/T with γ = 1.9 (see inset in Fig. 4d). Before taking this surprising finding to stand in disagreement with the bulk results, one needs to take into account the change of the density which accompanies confining investigated liquid to nanometer size pores and its pressurization. As noted before, the expected frustration in density for DPG in 18 nm pores is less than 0.5%. In contrast, compression of supercooled liquid DPG from 0.1 MPa to 450 MPa will change its density by roughly 7–8%. From the literature results, it is also known that the power-law density scaling breaks down for large variations in the density, while it still works at a very narrow density range.27 This seems to be the case in the present study. For DPG, the density change which accompanies the increase of pressure from by 100 MPa is ∼1.5%. Note in Fig. 2 that even the neighboring pairs of isobars: (i) 0.1 MPa and 70 MPa, (ii) 150 MPa and 250 MPa, (iii) 350 MPa and 450 MPa can be made to collapse individually while never all together. As we suppose, when the density scaling concept does not apply for bulk material, it should not apply either in nano-confinement. The same value of the scaling exponent γ obtained from the independent analysis of the high-pressure and confinement data suggests that the information obtained from both approaches is consistent. And, that they both should follow the same rules. However, for the hydrogen-bonded liquid DPG changes in the density induced in the presence of 2D geometrical constraints seems to be surprisingly far too small to violate the density scaling law.
4 Conclusions
Our results have confirmed that DPG in bulk exhibits lack of the isochronal superposition and it is a substance weakly sensitive to pressure. Besides, the fragility index for DPD increases with increasing pressure. Furthermore, DPG in bulk is not subject to the concept of density scaling. However, as opposed to previous studies, we have observed that relaxation times measured under different thermodynamic conditions can be better imposed on a single master curve.As shown, we have compared the temperature dependence of relaxation times for DPG and polymethylphenylsiloxane (PMPS) confined in nanopores and we have shown that in the case of DPG, confinement effect is less pronounced than for PMPS. Based on these observations, we have shown that the sensitivity of dynamics to pressure allows determining whether a particular substance in nanoconfined shows a pronounced deviation from the bulk behavior. For DPG, confined in nanopores, dynamics become faster with decreasing pore diameter. Interestingly, the relaxation times τα above the glass transition temperature of the interfacial layer can be described using isochores, as in the case of substances subject to the density scaling law. Based on the temperature of the core molecule (Tg_core) and the isochoric volume (Vg_core), we estimated the scaling parameter γ, which very well coincides with the parameter obtained for DPG in bulk. Moreover, the use of this parameter allows imposing the isochoric relaxation times to a single master curve. This is not possible with combined data for bulk materials and nanoscale. We believe that if the concept of density scaling does not apply to the bulk material, it should not apply to confinement systems. However, in the case of DPG, the changes in density caused by the nano-confinement are too small to disturb the density scaling law. On the other hand, both high-pressure data and the analysis of the confined dynamics suggest that the information obtained from both approaches is consistent, as evidenced by the same value of the scaling parameter.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
K. A. acknowledge financial support from the Ministry of Science and Higher Education within ‘Iuventus Plus’ project (0001/IP3/2016/74). K. C. is grateful for the financial assistance from National Science Centre (Poland) within the Project OPUS 14 nr. UMO-2017/27/B/ST3/00402.Notes and references
- C. A. Angell, Science, 1995, 267, 1924–1935 CrossRef CAS PubMed.
- P. G. Debenedetti and F. H. Stillinger, Nature, 2001, 410, 259–267 CrossRef CAS PubMed.
- M. D. Ediger, C. A. Angell and S. R. Nagel, J. Phys. Chem., 1996, 100, 13200–13212 CrossRef CAS.
- E. Leutheusser, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 29, 2765–2773 CrossRef CAS.
- P. G. Debenedetti, T. M. Truskett, C. P. Lewis and F. H. Stillinger, Adv. Chem. Eng., 2004, 28, 21–79 Search PubMed.
- C. A. Angell, K. L. Ngai, G. B. McKenna, P. F. McMillan and S. W. Martin, J. Appl. Phys., 2000, 88, 3113–3157 CrossRef CAS.
- A. Tölle, Rep. Prog. Phys., 2001, 64, 1473–1532 CrossRef.
- C. Dreyfus, A. Aouadi, J. Gapinski, M. Matos-Lopes, W. Steffen, A. Patkowski and R. M. Pick, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 11 CrossRef PubMed.
- C. Dreyfus, A. Le Grand, J. Gapinski, W. Steffen and A. Patkowski, Eur. Phys. J. B, 2004, 42, 309–319 CrossRef CAS.
- C. Alba-Simionesco, A. Cailliaux, A. Alegría and G. Tarjus, Europhys. Lett., 2004, 68, 58–64 CrossRef CAS.
- G. Floudas, M. Paluch, A. Grzybowski and K. Ngai, Molecular Dynamics of Glass-Forming Systems, Springer Berlin Heidelberg, Berlin, Heidelberg, 2011 Search PubMed.
- R. Casalini and C. M. Roland, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 3 CrossRef PubMed.
- F. Kremer and A. Loidl, The Scaling of Relaxation Processes—Revisited, Springer International Publishing, Cham, 2018 Search PubMed.
- A. Grzybowski, K. Grzybowska, M. Paluch, A. Swiety and K. Koperwas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 041505 CrossRef CAS PubMed.
- U. R. Pedersen, N. P. Bailey, T. B. Schrøder and J. C. Dyre, Phys. Rev. Lett., 2008, 100, 015701 CrossRef PubMed.
- C. M. Roland, S. Bair and R. Casalini, J. Chem. Phys., 2006, 125, 124508 CrossRef CAS PubMed.
- D. Coslovich and C. M. Roland, J. Phys. Chem. B, 2008, 112, 1329–1332 CrossRef CAS PubMed.
- R. Casalini, U. Mohanty and C. M. Roland, J. Chem. Phys., 2006, 125, 014505 CrossRef CAS PubMed.
- P. Mausbach and H. O. May, Fluid Phase Equilib., 2014, 366, 108–116 CrossRef CAS.
- P. Mausbach, A. Köster, G. Rutkai, M. Thol and J. Vrabec, J. Chem. Phys., 2016, 144, 244505 CrossRef PubMed.
- S. Pawlus, R. Casalini, C. M. Roland, M. Paluch, S. J. Rzoska and J. Ziolo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 4 CrossRef PubMed.
- C. M. Roland, S. Bair and R. Casalini, J. Chem. Phys., 2006, 125, 124508 CrossRef CAS PubMed.
- C. M. Roland, R. Casalini, R. Bergman and J. Mattsson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 012201 CrossRef.
- C. M. Roland and R. Casalini, J. Non-Cryst. Solids, 2005, 351, 2581–2587 CrossRef CAS.
- R. Casalini and C. M. Roland, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 041503 CrossRef PubMed.
- H. W. Hansen, B. Frick, S. Capaccioli, A. Sanz and K. Niss, J. Chem. Phys., 2018, 149, 214503 CrossRef PubMed.
- L. Bohling, T. S. Ingebrigtsen, A. Grzybowski, M. Paluch, J. C. Dyre and T. B. Schroder, New J. Phys., 2012, 14, 113035 CrossRef.
- T. C. Ransom and W. F. Oliver, Phys. Rev. Lett., 2017, 119, 025702 CrossRef CAS PubMed.
- K. Adrjanowicz, K. Kaminski, M. Tarnacka, G. Szklarz and M. Paluch, J. Phys. Chem. Lett., 2017, 8, 696–702 CrossRef CAS PubMed.
- K. Adrjanowicz, K. Kaminski, K. Koperwas and M. Paluch, Phys. Rev. Lett., 2015, 115, 265702 CrossRef CAS PubMed.
- K. Adrjanowicz, K. Kolodziejczyk, W. K. Kipnusu, M. Tarnacka, E. U. Mapesa, E. Kaminska, S. Pawlus, K. Kaminski and M. Paluch, J. Phys. Chem. C, 2015, 119, 14366–14374 CrossRef CAS.
- W. K. Kipnusu, M. Elsayed, R. Krause-Rehberg and F. Kremer, J. Chem. Phys., 2017, 146, 203302 CrossRef PubMed.
- R. Richert, Annu. Rev. Phys. Chem., 2011, 62, 65–84 CrossRef CAS PubMed.
- M. Alcoutlabi and G. B. McKenna, J. Phys.: Condens. Matter, 2005, 17, R461–R524 CrossRef CAS.
- G. Szklarz, K. Adrjanowicz, M. Tarnacka, J. Pionteck and M. Paluch, J. Phys. Chem. C, 2018, 122, 1384–1395 CrossRef CAS.
- K. Grzybowska, S. Pawlus, M. Mierzwa, M. Paluch and K. L. Ngai, J. Chem. Phys., 2006, 125, 144507 CrossRef CAS PubMed.
- H. W. Hansen, A. Sanz, K. Adrjanowicz, B. Frick and K. Niss, Nat. Commun., 2018, 9, 518 CrossRef CAS PubMed.
- C. León, K. L. Ngai and C. M. Roland, J. Chem. Phys., 1999, 110, 11585–11591 CrossRef.
- S. Alexandris, P. Papadopoulos, G. Sakellariou, M. Steinhart, H. J. Butt and G. Floudas, Macromolecules, 2016, 49, 7400–7414 CrossRef CAS.
- M. Paluch, Dielectric Properties of Ionic Liquids, Springer, 2016 Search PubMed.
- R. Casalini and C. M. Roland, J. Chem. Phys., 2003, 119, 11951–11956 CrossRef CAS.
- R. Kohlrausch, Ann. Phys., 1847, 72, 393 Search PubMed.
- G. Williams and D. C. Watts, Trans. Faraday Soc., 1970, 66, 80–85 RSC.
- H. Vogel, Phys. Z., 1921, 22, 645–646 CAS.
- G. S. Fulcher, J. Am. Ceram. Soc., 1925, 8, 339–355 CrossRef CAS.
- G. Tammann and W. Hesse, Z. Anorg. Allg. Chem., 1926, 156, 245–257 CrossRef CAS.
- S. P. Andersson and O. Andersson, Macromolecules, 1998, 31, 2999–3006 CrossRef CAS.
- C. M. Roland, S. Hensel-Bielowka, M. Paluch and R. Casalini, Rep. Prog. Phys., 2005, 68, 1405–1478 CrossRef CAS.
- R. Böhmer, K. L. Ngai, C. A. Angell and D. J. Plazek, J. Chem. Phys., 1993, 99, 4201–4209 CrossRef.
- P. G. Tait, in Physics and Chemistry of the Voyage of H.M.S., HMSO, London, 1888 Search PubMed.
- S. Pawlus, S. J. Rzoska, J. Ziolo, M. Paluch and C. M. Roland, Rubber Chem. Technol., 2003, 76, 1106–1115 CrossRef CAS.
- M. Paluch, R. Casalini, A. Patkowski, T. Pakula and C. M. Roland, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 5 CrossRef PubMed.
- K. Adrjanowicz and M. Paluch, Phys. Rev. Lett., 2019, 122, 176101 CrossRef CAS PubMed.
- A. Talik, M. Tarnacka, M. Geppert-Rybczynska, A. Minecka, E. Kaminska, K. Kaminski and M. Paluch, J. Phys. Chem. C, 2019, 123, 5549–5556 CrossRef CAS.
- K. Adrjanowicz, K. Kaminski, K. Koperwas and M. Paluch, Phys. Rev. Lett., 2015, 115, 265702 CrossRef CAS PubMed.
- M. Paluch, E. Masiewicz, A. Grzybowski, S. Pawlus, J. Pionteck and Z. Wojnarowska, J. Chem. Phys., 2014, 141, 134507 CrossRef CAS PubMed.
- M. Paluch, K. Grzybowska and A. Grzybowski, J. Phys.: Condens. Matter, 2007, 19, 205117 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |