Open Access Article
Open Access ArticleCharacterizing the bifurcating configuration of hydrogen bonding network in interfacial liquid water and its adhesion on solid surfaces†
Lei Zhao and
Jiangtao Cheng *
*
Department of Mechanical Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA 24061, USA. E-mail: chengjt@vt.edu; Tel: +1 (540) 231 4161
First published on 24th May 2019
Abstract
The interfacial structures of liquid water molecules adjacent to a solid surface contribute significantly to the interfacial properties of aqueous solutions, and are of prime importance in a wide spectrum of applications. In this work, we use molecular dynamics (MD) simulations to explore the interfacial structures, mainly in term of hydrogen bonding network, of a liquid water film interacting intimately with solid surfaces, which are composed of [100] face centered cubic (FCC) lattices. We disclose the formation of a bifurcating configuration of hydrogen bonds in interfacial liquid water and ascribe its occurrence to the collective effects of water density depletion, hydrogen bonds and local polarization. Such bifurcating configuration of interfacial water molecules consists of repetitive layer by layer water sheets with intra-layer hydrogen bonding network being formed in each layer, and inter-layer defects, i.e., hydrogen bonds formed between two neighboring layers of interfacial water. A lower bound of 2.475 for the average number of hydrogen bonds per interfacial water molecule is expected. Our MD study on the interfacial configuration of water on solid surfaces reveals a quadratic dependence of adhesion on the solid–liquid affinity, bridging the gap between the macroscopic interfacial property Wadh and the microscopic parameter εSL of the depth of the Lennard-Jones solid–liquid potential.
1. Introduction
The wettability of water or aqueous solutions on solid surfaces is crucially dependent on the interfacial properties of water interacting intimately with the surface materials. In the past decades, rapid developments in nanomaterials and microfabrication create an increasing demand for insightful understanding of both the static and the dynamic behaviors of liquid water near solid surfaces, due to its critical importance in a wide spectrum of applications, such as surface coating,1,2 micro/nano-fluidic devices,3–5 phase change heat transfer,6,7 and various biological occasions.8 For liquid water residing on a solid surface, the adhesive force applied by the solid surface, as well as the cohesive character of water, induces the reconfiguration of water molecules adjacent to the solid surface and in a large part determines the interfacial properties.9 For example, the parallel dipole alignment of water molecules near solid surfaces has been demonstrated to minimize the loss of hydrogen bonds and in the meantime contribute substantially to the interfacial tension.10Depending on the strength of adhesion, solid surfaces can be categorized into two main groups: hydrophobic and hydrophilic.11,12 A facile way to reflect the surface wettability is via its contact angle derived from the Young's equation:  , where γ is the interfacial tension and the subscripts of S, L and V represent solid, liquid and vapor phases, respectively. However, this equation does not provide any insightful information on the microscopic details near the solid–liquid interface, especially the structural change of liquid water in response to surface wettability.13,14 Increasing interests in micro/nanofluidics have inspired studies on solid–liquid interfaces whose characteristic length drops down to nanometers. First and foremost, a depletion region of liquid water is formed near a solid surface and such density deficit becomes more prominent for hydrophobic surfaces.15,16 Above the depletion region, wave-like spatial undulations of liquid density have been reported,17–19 implying a new mechanism of energy dissipation in the form of layer-by-layer friction during the process of dynamic wetting.20–22 It was also reported that such spatial undulations can break the ideal tetrahedron geometry of hydrogen bonds,23 which is usually formed in bulk water, and may give rise to the polarity of interfacial water.24,25 In this respect, the identification of truly interfacial molecules (ITIM) analyses revealed that the effect of structural change on interfacial properties may be limited to the close vicinity of the interface, i.e., the first molecular layer.26,27 Furthermore, when electrostatic interactions are taken into account, the balance or symmetry of accepting and donating hydrogen bonds is broken in the interfacial layer, leading to surface charging.28
, where γ is the interfacial tension and the subscripts of S, L and V represent solid, liquid and vapor phases, respectively. However, this equation does not provide any insightful information on the microscopic details near the solid–liquid interface, especially the structural change of liquid water in response to surface wettability.13,14 Increasing interests in micro/nanofluidics have inspired studies on solid–liquid interfaces whose characteristic length drops down to nanometers. First and foremost, a depletion region of liquid water is formed near a solid surface and such density deficit becomes more prominent for hydrophobic surfaces.15,16 Above the depletion region, wave-like spatial undulations of liquid density have been reported,17–19 implying a new mechanism of energy dissipation in the form of layer-by-layer friction during the process of dynamic wetting.20–22 It was also reported that such spatial undulations can break the ideal tetrahedron geometry of hydrogen bonds,23 which is usually formed in bulk water, and may give rise to the polarity of interfacial water.24,25 In this respect, the identification of truly interfacial molecules (ITIM) analyses revealed that the effect of structural change on interfacial properties may be limited to the close vicinity of the interface, i.e., the first molecular layer.26,27 Furthermore, when electrostatic interactions are taken into account, the balance or symmetry of accepting and donating hydrogen bonds is broken in the interfacial layer, leading to surface charging.28
In this study, we use molecular dynamics (MD) simulations to explore the interfacial structures and in particular the hydrogen bonding network of a liquid water film interacting with solid surfaces. We show that the bifurcating configuration of interfacial water, which is jointly determined by water density depletion, hydrogen bonds and local polarization, contribute significantly to the interfacial properties of liquid water. Importantly, this MD study reveals a quadratic dependence of work of adhesion Wadh, a macroscopic and experimentally accessible value, on the microscopic parameter εSL of the depth of the Lennard-Jones solid–liquid potential, indicative of solid–liquid affinity. Our findings can advance the fundamental understanding on the properties of solid–water interface.
2. Materials and methods
In our MD simulations, a water film of 10 nm wide and 5 nm thick was placed on a solid surface. Water molecules were modeled as a rigid planar four-site system, i.e., the TIP4P water model,29,30 which consists of the 12-6 Lennard-Jones interaction among oxygen atoms with the energy parameter εOO and the distance parameter σOO, as well as partial charges on oxygen and hydrogen atoms. We also tested the influences of water models by comparing the results based on the TIP4P model to those based on the SPC/E model (ESI†), and the results of both models are generally identical. The solid surface consisted of two layers of [100] face centered cubic (FCC) lattices and a refined Lennard-Jones model (εSS, σSS), which is able to accurately reproduce gold–water interface, was used to model the interactions among solid atoms.31 During the simulations, solid atoms were tethered to their initial positions via a harmonic potential, such that their mean displacement was small enough to mimic a rigid wall.32 The first layer of solid atoms in contact with the water film were slightly randomized in the surface normal direction with an amplitude of 0.3σSS to avoid the unrealistic large slip length observed in previous MD simulations.21,33 At first, the solid–water interactions were modeled via the 12-6 Lennard-Jones potential (εSL, σSL) with geometrical combination rule, i.e., εSL = 3.8 kJ mol−1 and σSL = 0.298 nm. In order to study the structural response of water molecules to surface wettability, we tuned εSL from 3.8 kJ mol−1 to 1.0 kJ mol−1 in this study. It has been shown that decreasing εSL can effectively enhance surface hydrophobicity and this method has been widely used in previous studies.34,35All of our MD simulations were carried out on Gromacs 5.1.2.36 Provided that the realistic density of liquid water is 996.5 kg m−3 at 300 K, there were 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 water molecules included in the modeling domain. The time step was set to be 1 femtosecond (fs). Short range interactions were cut-off at 1.2 nm with the Verlet scheme. The particle mesh Ewald method with cubic interpolation and grid spacing of 0.12 nm was adopted to handle the long range Coulombic interaction.37 An NVT ensemble with Nose–Hoover thermostat was used to maintain the system temperature at 300 K. Firstly, the system was equilibrated for 10 ns and then the simulation was continued for another 10 ns for data collection. In our simulations, the criteria for determining a hydrogen bond are based on the following geometrical conditions:38
300 water molecules included in the modeling domain. The time step was set to be 1 femtosecond (fs). Short range interactions were cut-off at 1.2 nm with the Verlet scheme. The particle mesh Ewald method with cubic interpolation and grid spacing of 0.12 nm was adopted to handle the long range Coulombic interaction.37 An NVT ensemble with Nose–Hoover thermostat was used to maintain the system temperature at 300 K. Firstly, the system was equilibrated for 10 ns and then the simulation was continued for another 10 ns for data collection. In our simulations, the criteria for determining a hydrogen bond are based on the following geometrical conditions:38
(1) The distance between two oxygen atoms is not greater than RcOO = 0.34 nm;
(2) The distance between the acceptor oxygen and the donor hydrogen is not greater than RcOH = 0.2425 nm;
(3) The H–O⋯O angle is less than αcH−O⋯O = 30°.
3. Results and discussion
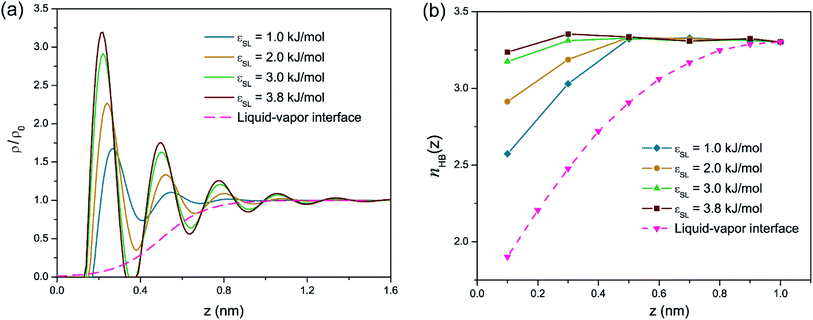
Fig. 1(a) presents the density profiles of oxygen atoms for interfacial water molecules in response to varied wettability. The density of oxygen atoms ρ is normalized by its value ρ0 in bulk water. For a liquid–vapor interface, water density shows a monotonic increase from zero in the vapor phase to its bulk value in the liquid phase. Thus-formed density profile can be accurately predicted by a hyperbolic tangent function indicative of a diffusion-governed mass transport.39,40 However, the density distribution at the solid–liquid interface exhibits a non-monotonic configuration, in spite of different εSL. The local density rapidly increases to a peak value, then oscillates around the bulk value ρ0 with decaying amplitude and eventually settles to ρ/ρ0 = 1. The strong density undulations in Fig. 1(a) provide a clear evidence of near-surface water layering, i.e., water molecules are mainly trapped within each spike in the density profile. Such layering effect extends about 1 nm into the water film. Within this range, the resultant layer-by-layer structure implies a mass transport mechanism jointly governed by phase transition,20,41 convective mass transfer42 and self-diffusion.43 In addition, lowering εSL mitigates the water layering and may lead to a smooth transition to a liquid–vapor like interface when the solid surface becomes more hydrophobic.We then estimated nHB, the number of hydrogen bonds shared by each water molecule, as a function of the distance z from the solid surface with different εSL. In bulk water, water molecules at equilibrium are apt to retain a local ice-like tetrahedral structure and each water molecule is expected to form 4 hydrogen bonds with its adjoining neighbors. In reality, nHB is smaller than 4 and varies from 3.2 to 3.5, since hydrogen bonds in liquid water are constantly breaking and reforming.10,19 In our MD simulations, nHB is found to be 3.3 on average in the bulk water. Fig. 1(b) demonstrates that liquid water experiences a loss of hydrogen bonds when it moves closer to the solid surface and increasing εSL can effectively reduce the loss of hydrogen bonds. For the standard case of εSL = 3.8 kJ mol−1 (strong hydrophilicity), the number of hydrogen bonds is almost unchanged comparing to that in the bulk water.
Hydrogen bonding in water is in fact a coulombic attraction between partially charged oxygen and hydrogen atoms. Therefore, the mathematical expectation of nHB for a water molecule can be summarized as:
| E(nHB) = p0(ρO1 + ρO2 + 2ρH) | (1) |
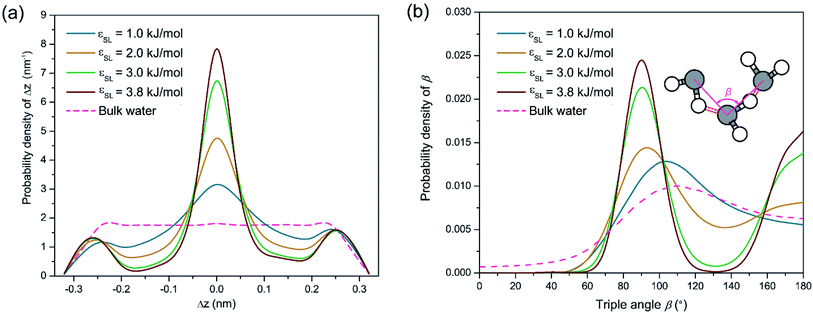
To testify this hypothesis, we examined the height difference Δz between the donating and accepting oxygen atoms for each pair of water molecules connected by hydrogen bonds near the solid surface. Hereafter, hydrogen bonds are considered to be near the solid surface if those connected water molecules are located within the first two layers indicated by Fig. 1(a). Fig. 2(a) presents the probability density distribution of Δz ranging from −RcOO to RcOO. In bulk water, the probability density profile of Δz is uniform, suggesting that a water molecule is equally probable to form hydrogen bonds with peers from all directions. In contrast, the probability density of Δz near the solid surface exhibits a pulse-like profile peaking at Δz = 0, indicating that water molecules in each spike of Fig. 1(a) are preferably aligned in parallel to the solid surface and form a planar sheet. In addition, increasing surface wettability intensifies the layering effect and subsequently stabilizes the planar configuration of each water layer, as shown in Fig. 2(a). To provide a detailed view of the as-formed planar water sheet, we analyzed the triple angle β, which is defined as the angle formed between two neighboring oxygen atoms connected by intra-layer hydrogen bonds (illustrated in the inlet of Fig. 2(b)). Fig. 2(b) presents the probability density distribution of β and highlights two most probable values at β = 90° or 180°. Therefore, the planar network of interfacial water molecules can be represented as a water sheet comprised of square cells. Although the layering structure of interfacial water has been widely observed, the planar geometry of each water layer (sheet) is not unambiguously a square grid system and may vary depending on the lattice structures of the solid surface. For example, a hexagonal configuration rather than a square grid is expected for interfacial water molecules close to a graphene surface.45
Despite the stabilization effect of strong confinement from the solid surface atoms, as-formed water sheets with square cells can still be distorted by viscous interactions among water molecules, mostly in the form of hydrogen bonds. A secondary configuration of interfacial water implied by Fig. 1(a) is hydrogen bonds bridging two neighboring water sheets. Since the distance between neighboring density peaks is around 0.28 nm (smaller than RcOO = 0.34 nm) in Fig. 1(a), the donating hydrogen atoms can be attracted by the accepting oxygen atoms from the adjacent layers. In this case, inter-layer hydrogen bonds may probably form, disturbing the otherwise planar geometry of each water sheet. In this respect, we name such secondary configuration of hydrogen bond as inter-layer defect. Those inter-layer defects are manifest in Fig. 2(a) as the two minor peaks located at Δz = ±0.28 nm and become more prominent with increasing εSL. Although such inter-layer defects are seemingly consistent with those perpendicular hydrogen bonds proposed by Velasco-Velez et al.,44 the asymmetric profiles in Fig. 2(a) reveal a directional preference of as-formed inter-layer defects. Since Δz is more likely to be positive, the inter-layer defects tend to connect donors within the current layer to acceptors from the subsequent layer.
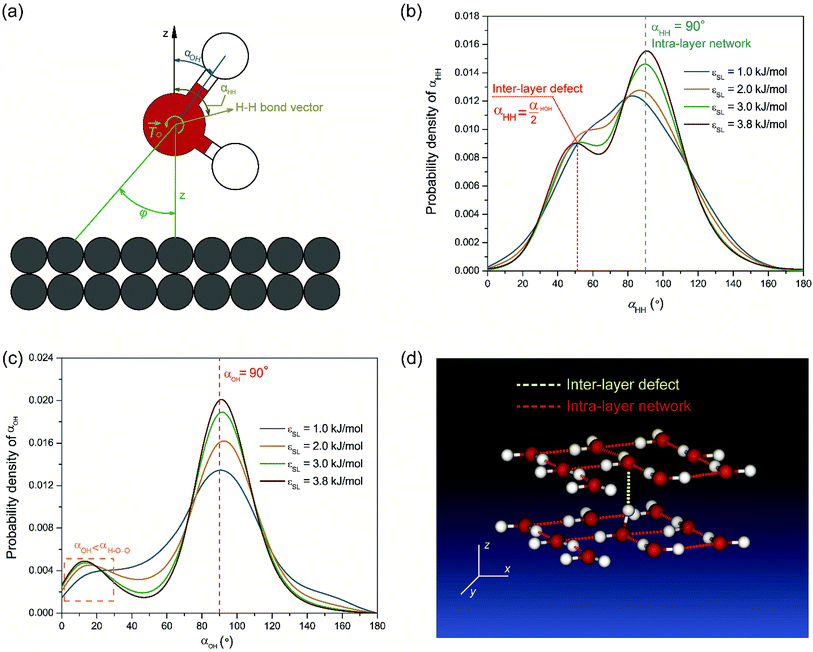
We show that the directional preference of inter-layer defects can be explained by the local polarization of interfacial water. A force analysis on a water molecule interacting with the solid surface is illustrated in Fig. 3(a). FH and FO denote the forces that the gold substrate applies to the oxygen and hydrogen atoms of a water molecule, respectively. In most cases, FH is negligible comparing to FO and is taken to be zero in this study. Therefore, the interaction between a water molecule and the solid substrate can be simplified as a force FO acting at the center of mass (COM) of the water molecule together with a resultant torque ![[T with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0054_20d1.gif) O =
O = ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) O ×
O × ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) OC, where
OC, where ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) OC is the vector connecting the oxygen atom and the COM. Here, FO can be evaluated as:
OC is the vector connecting the oxygen atom and the COM. Here, FO can be evaluated as:
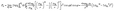 | (2) |
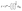 , FO is positive and water molecules within this region is hence repulsed away, leading to a depletion region with a thickness of z*. In this scenario, the water film is seemingly suspending z* from the gold surface. As FO is attractive for z > z*,
, FO is positive and water molecules within this region is hence repulsed away, leading to a depletion region with a thickness of z*. In this scenario, the water film is seemingly suspending z* from the gold surface. As FO is attractive for z > z*, ![[T with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0054_20d1.gif) O will force the water molecule in Fig. 3(a) to spin in the counterclockwise direction and subsequently induces the local polarization of interfacial water.
O will force the water molecule in Fig. 3(a) to spin in the counterclockwise direction and subsequently induces the local polarization of interfacial water.
We examined the orientation of a water molecule close to the solid surface in terms of two vectors, i.e., the H–H bond vector, which points to the opposite direction of its dipole moment, and the O–H vector, which connects the oxygen atom to one of the hydrogen atoms that are bonded to it. In this way, the orientation of a water molecule can be determined by two angles, i.e., αHH between the H–H bond vector and z axis, and αOH between the O–H vector and the z axis. Fig. 3(b) and (c) present probability density profiles of αHH and αOH for different surface wettability. Without the strong confining effect of the solid surface, the probability density distributions for both αHH and αOH ought to be homogenous, since a water molecule shows no orientational bias in the bulk. However, the highly distorted profiles in Fig. 3(b) and (c) provide unambiguous evidences for the orientational change of interfacial water molecules.44 The central peaks imply that interfacial water molecules are mostly aligned in parallel to the solid surface and hence form a planar sheet. In the meantime, a closer look at Fig. 3(b) and (c) reveals a preferential orientation of αHH, αOH ≤ 90°, which agrees with our force analysis on the local polarization. Moreover, such polarization favors the upright orientation of water molecules, and is responsible for the directional preference of inter-layer defects. We also notice that there are irregular wiggles that fall within the left sides of Fig. 3(b) and (c). These wiggles produce a secondary peak of the probability density profile, which corresponds to the inter-layer defects. Considering the H–O–H bond angle αHOH within a TIP4P water molecule is taken as 104.52°, those secondary peaks occur right at  and αOH = αHOH − 90°. Therefore, a typical configuration of inter-layer defects and intra-layer network is illustrated in Fig. 3(d).
and αOH = αHOH − 90°. Therefore, a typical configuration of inter-layer defects and intra-layer network is illustrated in Fig. 3(d).
So far, we perceive a bifurcating configuration of interfacial water, i.e., lateral water sheets and perpendicular inter-layer defects, as shown in Fig. 3(d), due to the collective effects of water density depletion, hydrogen bonds and local polarization. According to eqn (2), the first layer of water molecules is formed in such a fashion that the strong repulsive force leads to a depletion region and water molecules above it are attracted toward the upper edge of the depletion zone. The aggregation of water molecules in this layer produces a cloud of oxygen atoms, which drives the originally randomly oriented O–H bonds to be aligned laterally so as to form intra-layer bonds. Eventually, the aggregated water molecules in each spike are fashioned into a planar water sheet. For the [100] FCC lattice structures of the solid surface used in this work, the water sheet is ideally comprised of square-like lattices and one water molecule is expected to form 4 (2 donating and 2 accepting) hydrogen bonds with its in-plane neighbors. However, the local polarization may break one of the donating hydrogen bonds and expel one hydrogen atom to the upper space. This dispersed hydrogen atom may or may not form a hydrogen bond with subsequent water molecules. Given that  in the interfacial layer, a lower bound for the average number of hydrogen bonds per water molecule can be estimated as:
in the interfacial layer, a lower bound for the average number of hydrogen bonds per water molecule can be estimated as:
| E(nHB) ≥ p0(ρO1 + 2ρH) ≥ 2.475 | (3) |
Eqn (3) implies that the contribution of hydrogen bonds to the solid–liquid interfacial tension γSL is relatively trivial comparing with that to the liquid–vapor interface. Following the first layer formation, a second layer of water molecules comes into being once the inter-layer hydrogen bonds are formed between the dispersed hydrogen atoms and the subsequent water molecules. Similar to the first layer, the second layer is connected by intra-layer hydrogen bonds and inextricably expel hydrogen atoms into the upper space as well, giving rise to the third layer formation and vice versa. Therefore, a repetitive pattern of water sheets straddled by inter-layer defects is formed. Due to the fact that the polarization effect ![[T with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0054_20d1.gif) O decays rapidly as
O decays rapidly as ![[T with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0054_20d1.gif) O ∼ 1/z4, the amplitudes of the resultant density peaks in density profiles diminish successively and gradually settle at ρ = ρ0.
O ∼ 1/z4, the amplitudes of the resultant density peaks in density profiles diminish successively and gradually settle at ρ = ρ0.
We hereby propose a damped harmonic oscillator function to describe the non-monotonic density profiles of interfacial water and quantify the bifurcating configuration of hydrogen bonds as:
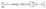 | (4) |
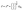 is expected for all cases. However, it is found that the depletion length decreases with increasing εSL, as shown in Fig. 4(a). This is because the cohesive force FLL of water must be taken into consideration in determining δ. Since FLL arises from the interactions among water molecules, it can be taken as constant regardless of εSL. Therefore δ can be solved by equating the right hand side of eqn (2) to FLL:
is expected for all cases. However, it is found that the depletion length decreases with increasing εSL, as shown in Fig. 4(a). This is because the cohesive force FLL of water must be taken into consideration in determining δ. Since FLL arises from the interactions among water molecules, it can be taken as constant regardless of εSL. Therefore δ can be solved by equating the right hand side of eqn (2) to FLL:
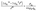 | (5) |
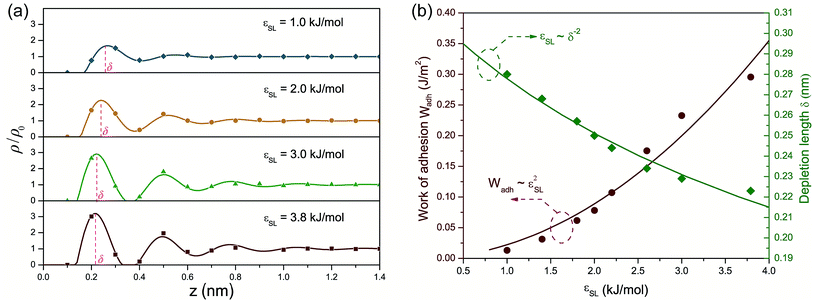 | ||
Fig. 4 (a) Density profiles fitted to 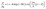 . (b) Work of adhesion Wadh and depletion length δ with respect to εSL. The quadratic increase of Wadh with εSL is attributed to εSL ∼ δ−2. . (b) Work of adhesion Wadh and depletion length δ with respect to εSL. The quadratic increase of Wadh with εSL is attributed to εSL ∼ δ−2. | ||
Apparently a smaller δ is expected for increasing εSL. Note that eqn (5) can not be solved explicitly. Therefore, by pinpointing the locations of first density peaks associated with different values of εSL, a simple scaling law relating δ to εSL as shown in Fig. 4(b) is unveiled:
| εSL ∼ δ−2 | (6) |
As-formed bifurcating configuration also has a profound influence on the interfacial properties of water. We consider the effect of such interfacial molecular structures by evaluating work of adhesion as:
Wadh = γLV(1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0) = γLV + γSV − γSL = USL + UHB θ0) = γLV + γSV − γSL = USL + UHB
| (7) |
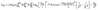 | (8) |
| Wadh ∼ εSL2 | (9) |
Eqn (9) bridges the gap between the macroscopic interfacial property of Wadh, which is experimentally accessible, and the microscopic parameter εSL of the depth of the Lennard-Jones potential well. Following the standard algorithm to calculate each component of interfacial tensions,46 we calculated Wadh for different εSL. Fig. 4(b) presents Wadh for different εSL and coincides with our prediction of the quadratic dependence of Wadh on εSL.
4. Conclusion and perspectives
In this work, we study the interfacial structures of liquid water interacting intimately with a solid surface with varied wettability via MD simulations. Both our simulation results and theoretical analyses unveil the bifurcating configuration of interfacial hydrogen bonds, due to the collective effects of water density depletion, hydrogen bonds and local polarization. Such bifurcating configuration, which is stabilized by the strong confining effect of the solid surface, is comprised of planar water sheets piled up in the perpendicular direction and inter-layer defects of hydrogen bonds bridging two adjacent sheets. As a result, a minimum number of 2.475 hydrogen bonds per water molecule is warranted and a quadratic dependence of work of adhesion on the surface–liquid affinity εSL is disclosed.In our simulations, the gold surface is essentially set to be electrically neutral and the coulombic interactions between the solid surface and the water film are hence neglected. However, possible surface charge and dielectric polarization may play a certain role in the interfacial properties of water as well, since the dipole moment of water molecules are exceptionally sensitive to the direction of an external electrical field. The introduction of an external electrical field is typically associated with the enhancement of surface wettability, since the electrostatic energy at the solid–liquid interface can be treated as part of the surface free energy. However, it may also alter the water density profile and the formation of hydrogen bonds by tuning the energetically favorable orientation of interfacial mean dipoles. In this respect, the proposed bifurcating configuration can be either stabilized or destabilized, depending on the strength and direction of the external electrical field. The interfacial structures of water molecules, especially the hydrogen bonding formation, on charged and electrically polarizable surfaces or under an external electrical field, warrant further investigation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is financially supported by NSF CBET under grant number 1550299, NSF ECCS under grant number 1808931, and Institute for Critical Technology and Applied Science at Virginia Tech. The authors also acknowledge Advanced Research Computing at Virginia Tech for providing computational resources and technical support to this work.References
- X. Hou, Y. S. Zhang, G. T. D. Santiago, M. M. Alvarez, J. Ribas, S. J. Jonas, P. S. Weiss, A. M. Andrews, J. Aizenberg and A. Khademhosseini, Interplay between materials and microfluidics, Nat. Rev. Mater., 2017, 2, 17016 CrossRef CAS.
- M. J. Kreder, J. Alvarenga, P. Kim and J. Aizenberg, Design of anti-icing surfaces: smooth, textured or slippery?, Nat. Rev. Mater., 2016, 1, 15003 CrossRef CAS.
- Q. M. Wang, Z. G. Suo and X. H. Zhao, Bursting drops in solid dielectrics caused by high voltages, Nat. Commun., 2012, 3, 1157 CrossRef PubMed.
- J.-T. Cheng and C. L. Chen, Adaptive beam tracking and steering via electrowetting-controlled liquid prism, Appl. Phys. Lett., 2011, 99, 191108 CrossRef.
- F. Mugele and J.-C. Baret, Electrowetting: from basics to applications, J. Phys. Condens. Matter, 2005, 17(28), R705–R774 CrossRef CAS.
- N. Miljkovic, R. Enright and E. N. Wang, Effect of Droplet Morphology on Growth Dynamics and Heat Transfer during Condensation on Superhydrophobic Nanostructured Surfaces, ACS Nano, 2012, 6(2), 1776–1785 CrossRef CAS PubMed.
- A. Bisetto, D. Torresin, M. K. Tiwari, D. Del Col and D. Poulikakos, Dropwise condensation on superhydrophobic nanostructured surfaces: literature review and experimental analysis, J. Phys. Conf. Ser., 2014, 501, 012028 CrossRef.
- M. M. Alvarez, J. Aizenberg, M. Analoui, A. M. Andrews, G. Bisker, E. S. Boyden, R. D. Kamm, J. M. Karp, D. J. Mooney, R. Oklu, D. Peer, M. Stolzoff, M. S. Strano, G. T. D. Santiago, T. J. Webster, P. S. Weiss and A. Khademhosseini, Emerging Trends in Micro- and Nanoscale Technologies in Medicine: From Basic Discoveries to Translation, ACS Nano, 2017, 11(6), 5195–5214 CrossRef CAS PubMed.
- E. Bormashenko, General equation describing wetting of rough surfaces, J. Colloid Interf. Sci., 2011, 360(1), 317–319 CrossRef CAS PubMed.
- D. Bratko, C. D. Daub, K. Leung and A. Luzar, Effect of field direction on electrowetting in a nanopore, J. Am. Chem. Soc., 2007, 129(9), 2504–2510 CrossRef CAS PubMed.
- H. Hu, H. F. Ji and Y. Sun, The effect of oxygen vacancies on water wettability of a ZnO surface, Phys. Chem. Chem. Phys., 2013, 15(39), 16557–16565 RSC.
- P. de Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and wetting phenomena: drops, bubbles, pearls, waves, Springer Science & Business Media, Berlin, 2013 Search PubMed.
- T. D. Blake, The physics of moving wetting lines, J. Colloid Interface Sci., 2006, 299(1), 1–13 CrossRef CAS PubMed.
- R. E. Skyner, J. L. McDonagh, C. R. Groom, T. van Mourik and J. B. O. Mitchell, A review of methods for the calculation of solution free energies and the modelling of systems in solution, Phys. Chem. Chem. Phys., 2015, 17(9), 6174–6191 RSC.
- A. Poynor, L. Hong, I. K. Robinson, S. Granick, Z. Zhang and P. A. Fenter, How water meets a hydrophobic surface, Phys. Rev. Lett., 2006, 97(26), 266101 CrossRef PubMed.
- C. Sendner, D. Horinek, L. Bocquet and R. R. Netz, Interfacial water at hydrophobic and hydrophilic surfaces: slip, viscosity, and diffusion, Langmuir, 2009, 25(18), 10768–10781 CrossRef CAS PubMed.
- F.-C. Wang and Y.-P. Zhao, Slip boundary conditions based on molecular kinetic theory: The critical shear stress and the energy dissipation at the liquid–solid interface, Soft Matter, 2011, 7(18), 8628 RSC.
- S. Gim, H.-K. Lim and H. Kim, Multiscale simulation method for quantitative prediction of surface wettability at the atomistic level, J. Phys. Chem. Lett., 2018, 9, 1750–1758 CrossRef CAS PubMed.
- D. Y. Zong, H. Hu, Y. Y. Duan and Y. Sun, Viscosity of water under electric field: Anisotropy induced by redistribution of hydrogen bonds, J. Phys. Chem. B, 2016, 120(21), 4818–4827 CrossRef CAS PubMed.
- L. Zhao and J.-T. Cheng, The mechanism and universal scaling law of the contact line friction for the Cassie-state droplets on nanostructured ultrahydrophobic surfaces, Nanoscale, 2018, 10, 6426–6436 RSC.
- A. V. Lukyanov and A. E. Likhtman, Dynamic contact angle at the nanoscale: A unified view, ACS Nano, 2016, 10(6), 6045–6053 CrossRef CAS PubMed.
- L. Chen, J. P. Yu and H. Wang, Convex nanobending at a moving contact line: The missing mesoscopic link in dynamic wetting, ACS Nano, 2014, 8(11), 11493–11498 CrossRef CAS PubMed.
- E. Spohr, Computer-Simulation of the Water Platinum Interface, J. Phys. Chem., 1989, 93(16), 6171–6180 CrossRef CAS.
- S. Shin and A. P. Willard, Three-body Hydrogen Bond Defects Contribute Significantly to the Dielectric Properties of the Liquid Water-Vapor Interface, J. Phys. Chem. Lett., 2018, 9, 1649–1654 CrossRef CAS PubMed.
- D. Houdoux, J. Houplin, L. Amiaud, A. Lafosse and C. Dablemont, Interfacial water on organic substrates at cryogenic temperatures: hydrogen bonding and quantification in the submonolayer regime, Phys. Chem. Chem. Phys., 2017, 19(3), 2313–2321 RSC.
- M. Darvas, L. Partay, P. Jedlovszky and G. Horvai, Computer simulation and ITIM analysis of the surface of water–methanol mixtures containing traces of water, J. Mol. Liq., 2010, 153(1), 88–93 CrossRef CAS.
- L. Partay, G. Horvai and P. Jedlovszky, Molecular level structure of the liquid/liquid interface. Molecular dynamics simulation and ITIM analysis of the water-CCl4 system, Phys. Chem. Chem. Phys., 2008, 10(32), 4754–4764 RSC.
- R. Vacha, S. W. Rick, P. Jungwirth, A. G. F. de Beer, H. B. de Aguiar, J. S. Samson and S. Roke, The orientation and charge of water at the hydrophobic oil droplet-water interface, J. Am. Chem. Soc., 2011, 133(26), 10204–10210 CrossRef CAS PubMed.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides, J. Phys. Chem. B, 2001, 105(28), 6474–6487 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. TiradoRives, Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids, J. Am. Chem. Soc., 1996, 118(45), 11225–11236 CrossRef CAS.
- H. Heinz, R. A. Vaia, B. L. Farmer and R. R. Naik, Accurate Simulation of Surfaces and Interfaces of Face-Centered Cubic Metals Using 12-6 and 9-6 Lennard-Jones Potentials, J. Phys. Chem. C, 2008, 112(44), 17281–17290 CrossRef CAS.
- A. Gupta, B. Boekfa, H. Sakurai, M. Ehara and U. D. Priyakumar, Structure, Interaction, and Dynamics of Au/Pd Bimetallic Nanoalloys Dispersed in Aqueous Ethylpyrrolidone, a Monomeric Moiety of Polyvinylpyrrolidone, J. Phys. Chem. C, 2016, 120(31), 17454–17464 CrossRef CAS.
- N. V. Priezjev, Relationship between induced fluid structure and boundary slip in nanoscale polymer films, Phys. Rev. E, 2010, 82(5), 051603 CrossRef PubMed.
- J. D. Wang, S. Chen and D. R. Chen, Spontaneous transition of a water droplet from the Wenzel state to the Cassie state: a molecular dynamics simulation study, Phys. Chem. Chem. Phys., 2015, 17(45), 30533–30539 RSC.
- Q. Yuan, X. Huang and Y.-P. Zhao, Dynamic spreading on pillar-arrayed surfaces: Viscous resistance versus molecular friction, Phys. Fluids, 2014, 26(9), 092104 CrossRef.
- H. Bekker, H. Berendsen, E. Dijkstra, S. Achterop, R. Van Drunen, D. Van der Spoel, A. Sijbers, H. Keegstra, B. Reitsma and M. Renardus, Gromacs: A parallel computer for molecular dynamics simulations, Physics Computing, 1993, 92, 252–256 Search PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, A Smooth Particle Mesh Ewald Method, J. Chem. Phys., 1995, 103(19), 8577–8593 CrossRef CAS.
- E. Guardia, J. Marti, L. Garcia-Tarres and D. Laria, A molecular dynamics simulation study of hydrogen bonding in aqueous ionic solutions, J. Mol. Liq., 2005, 117, 63–67 CrossRef CAS.
- F. Sedlmeier, D. Horinek and R. R. Netz, Nanoroughness, Intrinsic Density Profile, and Rigidity of the Air-Water Interface, Phys. Rev. Lett., 2009, 103(13), 136102 CrossRef PubMed.
- A. E. Ismail, G. S. Grest and M. J. Stevens, Capillary waves at the liquid-vapor interface and the surface tension of water, J. Chem. Phys., 2006, 125(1), 014702 CrossRef PubMed.
- P. A. Thompson, G. S. Grest and M. O. Robbins, Phase-Transitions and Universal Dynamics in Confined Films, Phys. Rev. Lett., 1992, 68(23), 3448–3451 CrossRef PubMed.
- M. J. de Ruijter, T. D. Blake and J. De Coninck, Dynamic wetting studied by molecular modeling simulations of droplet spreading, Langmuir, 1999, 15(22), 7836–7847 CrossRef CAS.
- K. Inoue, T. Ishiyama, S. Nihonyanagi, S. Yamaguchi, A. Morita and T. Tahara, Efficient Spectral Diffusion at the Air/Water Interface Revealed by Femtosecond Time-Resolved Heterodyne-Detected Vibrational Sum Frequency Generation Spectroscopy, J. Phys. Chem. Lett., 2016, 7(10), 1811–1815 CrossRef CAS PubMed.
- J. J. Velasco-Velez, C. H. Wu, T. A. Pascal, L. W. F. Wan, J. H. Guo, D. Prendergast and M. Salmeron, The structure of interfacial water on gold electrodes studied by x-ray absorption spectroscopy, Science, 2014, 346(6211), 831–834 CrossRef CAS PubMed.
- M. Foroutan, M. Darvishi and S. M. Fatemi, Structural and dynamical characterization of water on the Au (100) and graphene surfaces: A molecular dynamics simulation approach, Phys. Rev. E, 2017, 96(3), 033312 CrossRef PubMed.
- A. R. Nair and S. P. Sathian, A molecular dynamics study to determine the solid-liquid interfacial tension using test area simulation method (TASM), J. Chem. Phys., 2012, 137(8), 084702 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra02578b |
| This journal is © The Royal Society of Chemistry 2019 |