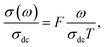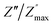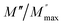DOI:
10.1039/C9RA02815C
(Paper)
RSC Adv., 2019,
9, 19285-19296
Influence of defect on the electrical and optical properties of A-site non-stoichiometry Ca0.67La0.22□0.11Ti(1−x)CrxO3−δ perovskite
Received
14th April 2019
, Accepted 21st May 2019
First published on 19th June 2019
Abstract
An investigation of the dielectric dispersion, electrical properties, scaling behavior and optical defects of Ca0.67La0.22□0.11Ti(1−x)CrxO3−δ (CLT(1−x)Crx) with x = 0 and x = 0.1 compositions is presented. The square in the formula is attributed to a vacancy in A-site. Relaxation phenomena were studied with dielectric and modulus formalism, while, the conductivity mechanism was investigated using electrical conductivity. A high permittivity of around 104, low dielectric loss and low electrical conductivity of around 10−3 S cm−1 for Ca0.67La0.22TiO3 (CLT) was observed. These values make this composition interesting for microelectric applications. A comparison between the Z′′ and M′′ indicated that the short-range carrier motion dominates at low temperature and becomes less localized at high temperature. The optical defects of CLT and Ca0.67La0.22Ti0.9Cr0.1O3 (CLT0.9Cr0.1) were studied by electron paramagnetic resonance (EPR) spectroscopy. The results suggest the formation of a [TiO6]9− center, a (Ti3+–VO) center, and 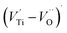 dipole defect for CLT compound and Cr3+–VO center defect for CLT0.9Cr0.1 compound. These defects are the source of the in-gap electron traps, which improve the optical properties of CLT(1−x)Crx and hence make it an interesting optical material for different applications.
dipole defect for CLT compound and Cr3+–VO center defect for CLT0.9Cr0.1 compound. These defects are the source of the in-gap electron traps, which improve the optical properties of CLT(1−x)Crx and hence make it an interesting optical material for different applications.
1. Introduction
Solid-oxide electrochemical sensors are one of the most reliable appliances whose most advantageous features are detection of toxic gases. Among these gases, nitrogen oxides NOX (nitrogen monoxide NO and nitrogen dioxide NO2), which are mainly released from automotive engines, are the most dangerous air pollutants; they are harmful to humans and the environment.1 To monitor NOX emission, lots of efforts have been made to develop high performance and compact solid electrolyte NOX type sensors with a stable, sensitive, selective and quick response.2–8 Yttrium Stabilized Zirconia Y4xZr1−4xO2−2x (YSZ) has exceptionally high ionic conductivity but only at a temperature beyond 800 °C. Its high operating temperature, however, can lead to many problems; it limits the selection of compatible electrodes and interconnect materials9 and reduces the service life of the sensor.10 Thus, it is urgent to search for an alternative oxide electrolyte material that can capture NOX at a mild temperature. In this case, several kinds of perovskite (ABO3) solid electrolytes have recently been proposed as optimal materials for NOX sensors with higher sensing performance, at low and intermediate temperature (∼400–600 °C), than that of YSZ. One of the most promising electrolyte materials proposed by Ishihara et al. and by Feng and Goodenough in 1994 is doped lanthanum gallate (LaGaO3) such as La(1−x)SrxGa(1−y)MgyO3−δ (LSGM),11,12 whose conductivity at low temperature is higher than those of YSZ.13–15 Unfortunately, the use of LSGM as a solid electrolyte has so far been hampered by several issues, such as the difficulty of obtaining pure phase materials,16 the volatility of gallium at high temperature and its high reactivity with Ni (typically used as anode), which greatly limits the application of such sensor in NOX detection, too. Later, Sinha et al.17 examined the calcium-doped GdAlO3 used for NOX sensor, whereas both response and recovery speed are still slow. Recently, a great amount of experimental data has peaked in favor of A-site non-stoichiometry perovskites notably on sodium bismuth titanate (NBT). Several researches realized by many authors18–23 explored the influence of A-site non-stoichiometry on the ionic conductivity in NBT. Li et al.24 also reported that Mg-doping Na0.5Bi0.49Ti0.98Mg0.0202.96 revealed a perfect conductivity of up to σ ∼10−2 S cm−1 at 600 °C and predicted the possible application in solid oxide fuel cell and sensor field as electrolyte material. Meyer and Albe25 discovered that the different phases of NBT have different migration barriers, and the association of oxygen vacancies with migration barriers can be used to describe the change in the activation energy. Doping bismuth with a high rate leads to the total oxygen vacancy (VO) concentration.26 In this way, already small amounts of defects are sufficient to severely influence the ionic conductivity.27–29 More than that, Yang et al.30 attributed the high level of oxide-ionic conductivity to the mobility of oxygen ions. Based on these considerations, namely the A-site non-stoichiometric perovskite, the aim of the present work is to investigate the defect chemistry and electrical properties of A-site non-stoichiometric CLT(1−x)Crx ceramics which have an important dielectric and optical behavior related to VO31 and which, furthermore, might account for the application in technology as gas sensor.
2. Experimental section
The A-site non-stoichiometry CLT(1−x)Crx ceramics with x = 0 and 0.1 are prepared from high purity (99.9%) precursors CaCO3, La2O3, TiO2 and Cr2O3 in powder by using a conventional ceramic-making technique of solid-state reaction. Polycrystalline sample synthesis and its X-ray structure determination by the Rietveld refinement were reported by us elsewhere.31 It was found that CLT(1−x)Crx crystallizes in Orthorhombic Pnma structure without any detectable secondary phase.
The dielectric measurements were performed on ceramic disks (of about 8 mm diameter and 1 mm thickness) after the deposition of gold electrodes on the circular faces by cathodic sputtering using an impedance analyzer, Wayne-Kerr 6425 (in the frequency range from 20 Hz to 1 MHz).
Electron paramagnetic resonance (EPR) measurements were performed at room temperature using an EMX X-band EPR spectrometer (Brucker EMX EPR, Germany) in which the EPR signal was acquired with 2 mW of power and a spectral width in the field range 0 < H < 8000 Gauss. From the resonance fields H, determined by the zero-crossing point (dp/dH = 0), the Landé g-factor is deduced using the relation g = hν/μBH where μB is the Bohr magneton.
3. Results and discussion
3.1. Dielectric permittivity analysis
Fig. 1(a and b) shows the frequency dependence of the permittivity for CLT(1−x)Crx ceramics from 500 K to 650 K and from 303 K to 650 K for x = 0 and x = 0.1, respectively. The value of 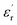 , for all the samples, increases with decreasing frequency and increasing temperature, indicating a strong dielectric dispersion. In fact, the high value of
, for all the samples, increases with decreasing frequency and increasing temperature, indicating a strong dielectric dispersion. In fact, the high value of 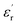 at lows frequencies is mainly attributed to the contribution of electronic, space charges, ionic, and interfacial polarization which are generally accompanied by the appearance of dielectric relaxation. However, at high frequency,
at lows frequencies is mainly attributed to the contribution of electronic, space charges, ionic, and interfacial polarization which are generally accompanied by the appearance of dielectric relaxation. However, at high frequency, 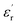 is independent of temperature and frequency. This independence is due to the inability of electric dipoles to follow the fast variation of the applied electric field. Therefore, the dielectric dispersion observed at low frequency range is due to the interfacial polarization, because the electronic and atomic polarizations persist unchanged at this frequency range.32 Furthermore, we can note that when chromium is introduced into CLT, a significant rise in the real part of permittivity is seen, suggesting that the variation of
is independent of temperature and frequency. This independence is due to the inability of electric dipoles to follow the fast variation of the applied electric field. Therefore, the dielectric dispersion observed at low frequency range is due to the interfacial polarization, because the electronic and atomic polarizations persist unchanged at this frequency range.32 Furthermore, we can note that when chromium is introduced into CLT, a significant rise in the real part of permittivity is seen, suggesting that the variation of 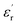 values results not only from the contribution of thermally-activated charge defects but also from the dominant effect of chromium-doping. This might be generated by the multivalent configuration of chromium ions. The variation of dielectric loss (tan
values results not only from the contribution of thermally-activated charge defects but also from the dominant effect of chromium-doping. This might be generated by the multivalent configuration of chromium ions. The variation of dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) with frequency is shown in Fig. 2. Here angle “δ” is the phase difference between the applied electric field and the induced current.33 Similar to ε′, the tan
δ) with frequency is shown in Fig. 2. Here angle “δ” is the phase difference between the applied electric field and the induced current.33 Similar to ε′, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values decrease with increasing frequency and become constant at higher frequencies. This behavior can be attributed to the decrease in polarization at an applied higher electric field. The observed tan
δ values decrease with increasing frequency and become constant at higher frequencies. This behavior can be attributed to the decrease in polarization at an applied higher electric field. The observed tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ variation with frequency can be due to the conduction mechanism which is analogous to Koop's phenomenological model.34 The tan
δ variation with frequency can be due to the conduction mechanism which is analogous to Koop's phenomenological model.34 The tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ curve is considered to be caused by domain wall resonance. At higher frequencies range, losses are found to be low if the domain wall motion is restrained as per Rezlescu model.32,35 Moreover, the tan
δ curve is considered to be caused by domain wall resonance. At higher frequencies range, losses are found to be low if the domain wall motion is restrained as per Rezlescu model.32,35 Moreover, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ rises when the polarization lags behind the applied alternating electric field. This rise in tan
δ rises when the polarization lags behind the applied alternating electric field. This rise in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ may also be caused by the grain boundaries, imperfections in the crystal lattice, and impurities.36,37 Furthermore, one can see that for the CLT0.9Cr0.1 composition the tan
δ may also be caused by the grain boundaries, imperfections in the crystal lattice, and impurities.36,37 Furthermore, one can see that for the CLT0.9Cr0.1 composition the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ curve exhibits a broad peaks with the frequency dispersion at different temperatures. These peaks shift to a higher frequency with increasing temperature, suggesting a typical characteristic of dielectric relaxation phenomenon.
δ curve exhibits a broad peaks with the frequency dispersion at different temperatures. These peaks shift to a higher frequency with increasing temperature, suggesting a typical characteristic of dielectric relaxation phenomenon.
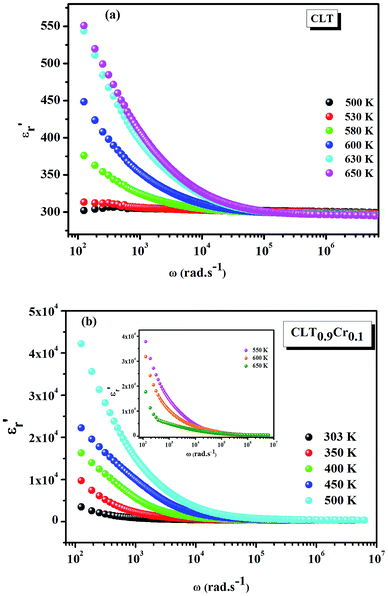 |
| | Fig. 1 Frequency and temperature dependence of the real part of permittivity for the compositions (a) x = 0 and (b) x = 0.1 solid solution CLT(1−x)Crx ceramics. | |
 |
| | Fig. 2 Frequency and temperature dependence of the dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) for compositions (a) x = 0 and (b) x = 0.1. δ) for compositions (a) x = 0 and (b) x = 0.1. | |
3.2. Conductivity analysis
The electrical conductivity is the most common representation for relating the macroscopic measurement to the microscopic movement of the ions. The conductivity of the samples was obtained using the Maxwell relation σ(ω) = jωε0ε*(ω), where 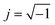 , ε0 is the vacuum permittivity, and ε*(ω) is the complex permittivity. Fundamentally, alternative conductivity (σ(ω)) originates from the migration of ions by hopping between neighboring potential wells. It provides insights into different relaxation mechanisms by investigating its frequency and/or temperature dependent response behaviors. Fig. 3(a and b) displays the frequency dependence of (σ(ω)) for CLT and CLT0.9Cr0.1 at various temperatures. The conductivity increases with increasing frequency, therefore, it starts from its dc value and eventually attains a “high frequency” plateau at about 106 Hz. More than that, (σ(ω)) exhibits a dispersion that shifts to higher frequency with increasing temperatures for all samples. Indeed, the σ(ω) spectrum can be decomposed into three parts: the low frequency (direct conductivity (σdc)) plateau regime (region I), mid-frequency dispersive regime (region II) and high frequency plateau regime (region III). These types of characteristics can be explained on the basis of the jump relaxation model (JRM)38 which states that after a hop of a central ion from an initially relaxed local position, it will be no longer in equilibrium with its neighbors.39,40 To stabilize the new position of the ion, other ions in its surroundings have to move. However, the ion can also jump back (unsuccessful hop) in order to partially relax the position after the jump. At low frequencies in region I, the frequency is low and the electric field cannot perturb the hopping conduction process of the charged particles. On the contrary, the conductivity is assigned to the successful hops from one localized site to its neighboring vacant site due to the available long time period (ω = 2πf = 2π/T), T is the time period, hence, resulting in a long-range motion of ions and conductance may be approximated to the dc value in this range. As the frequency increases, the unsuccessful hops increase, since two competing relaxation processes take place, such as; the correlated ion position related to forward backward forward, i.e., unsuccessful hopping and successful hopping wherein the localized orientation hopping in which once jumped ions become relaxed and stay in the new site. Nevertheless, every individual hop is seen when the time window is sufficiently short. This behavior is assigned to the region II. On the other hand, as the ratio of successful to unsuccessful hopping increases, it results in more dispersive conductivity and the increase of conductivity with frequency in region II is thus qualitatively explained. In region III, the rise in conductivity observed in all samples is almost proportional to frequency, resulting in near constant loss (NCL).41 Based on JRM, the frequency dependence of the conductivity data was possible to fit (Fig. 4) to a double power law38,42 σ(ω) = σdc + Aωn1 + Bωn2, where σdc assigned to dc conductivity whose translational hopping gives the long-range electrical transport in the long-time limit, (i.e., at lower frequency). The second term Aωn1, corresponding to the middle region (II) in which the exponent 0 < n1 < 1 characterizes the low frequency regime, indicates the short range translational hopping motion. The third term Bωn2, attributed to the higher frequency region (III) for which the exponent 1 < n2 < 2, corresponds to localized or reorientation hopping motion. The n1 and n2 values obtained from the fitting data are shown in Fig. 5(a and b). The n1 value exhibits a continuous increase with the temperature, while n2 decreases in the measured temperature for all samples. Early reports42,43 predict the dependence of n with the frequency and temperature, where an increase of the exponent values with increasing temperature is assigned to the small polaronic hopping, whereas a decrease in exponent values is ascribed to the large polaronic hopping. From the trend of the exponents behavior with the temperature of CLT and CLT0.9Cr0.1 compounds, the obtained value of n1 was less than 1 and increasing with temperature, which can indicate that the conduction in region II corresponding to the short translational hopping is provided by small polaronic mechanism. On the other hand, in the case of n2, the values varied between 1 and 2 and decreased with the temperature, implying that the conduction in region III ascribed to the localized orientation hopping, is assisted by large polaron mechanism. Furthermore, electrical conduction is a thermally activated process and follows the Arrhenius law σdc = σ0
, ε0 is the vacuum permittivity, and ε*(ω) is the complex permittivity. Fundamentally, alternative conductivity (σ(ω)) originates from the migration of ions by hopping between neighboring potential wells. It provides insights into different relaxation mechanisms by investigating its frequency and/or temperature dependent response behaviors. Fig. 3(a and b) displays the frequency dependence of (σ(ω)) for CLT and CLT0.9Cr0.1 at various temperatures. The conductivity increases with increasing frequency, therefore, it starts from its dc value and eventually attains a “high frequency” plateau at about 106 Hz. More than that, (σ(ω)) exhibits a dispersion that shifts to higher frequency with increasing temperatures for all samples. Indeed, the σ(ω) spectrum can be decomposed into three parts: the low frequency (direct conductivity (σdc)) plateau regime (region I), mid-frequency dispersive regime (region II) and high frequency plateau regime (region III). These types of characteristics can be explained on the basis of the jump relaxation model (JRM)38 which states that after a hop of a central ion from an initially relaxed local position, it will be no longer in equilibrium with its neighbors.39,40 To stabilize the new position of the ion, other ions in its surroundings have to move. However, the ion can also jump back (unsuccessful hop) in order to partially relax the position after the jump. At low frequencies in region I, the frequency is low and the electric field cannot perturb the hopping conduction process of the charged particles. On the contrary, the conductivity is assigned to the successful hops from one localized site to its neighboring vacant site due to the available long time period (ω = 2πf = 2π/T), T is the time period, hence, resulting in a long-range motion of ions and conductance may be approximated to the dc value in this range. As the frequency increases, the unsuccessful hops increase, since two competing relaxation processes take place, such as; the correlated ion position related to forward backward forward, i.e., unsuccessful hopping and successful hopping wherein the localized orientation hopping in which once jumped ions become relaxed and stay in the new site. Nevertheless, every individual hop is seen when the time window is sufficiently short. This behavior is assigned to the region II. On the other hand, as the ratio of successful to unsuccessful hopping increases, it results in more dispersive conductivity and the increase of conductivity with frequency in region II is thus qualitatively explained. In region III, the rise in conductivity observed in all samples is almost proportional to frequency, resulting in near constant loss (NCL).41 Based on JRM, the frequency dependence of the conductivity data was possible to fit (Fig. 4) to a double power law38,42 σ(ω) = σdc + Aωn1 + Bωn2, where σdc assigned to dc conductivity whose translational hopping gives the long-range electrical transport in the long-time limit, (i.e., at lower frequency). The second term Aωn1, corresponding to the middle region (II) in which the exponent 0 < n1 < 1 characterizes the low frequency regime, indicates the short range translational hopping motion. The third term Bωn2, attributed to the higher frequency region (III) for which the exponent 1 < n2 < 2, corresponds to localized or reorientation hopping motion. The n1 and n2 values obtained from the fitting data are shown in Fig. 5(a and b). The n1 value exhibits a continuous increase with the temperature, while n2 decreases in the measured temperature for all samples. Early reports42,43 predict the dependence of n with the frequency and temperature, where an increase of the exponent values with increasing temperature is assigned to the small polaronic hopping, whereas a decrease in exponent values is ascribed to the large polaronic hopping. From the trend of the exponents behavior with the temperature of CLT and CLT0.9Cr0.1 compounds, the obtained value of n1 was less than 1 and increasing with temperature, which can indicate that the conduction in region II corresponding to the short translational hopping is provided by small polaronic mechanism. On the other hand, in the case of n2, the values varied between 1 and 2 and decreased with the temperature, implying that the conduction in region III ascribed to the localized orientation hopping, is assisted by large polaron mechanism. Furthermore, electrical conduction is a thermally activated process and follows the Arrhenius law σdc = σ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Edc/kBT), where σ0 is the pre-exponential term and Edc represents the activation energies for dc conductivity. As shown in Fig. 6 for CLT and CLT0.9Cr0.1 compounds, a good linear fit between ln
exp(−Edc/kBT), where σ0 is the pre-exponential term and Edc represents the activation energies for dc conductivity. As shown in Fig. 6 for CLT and CLT0.9Cr0.1 compounds, a good linear fit between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σdc and 1000/T is obtained. The conduction activation energies are 1.08 eV and 0.69 eV for CLT and 0.42 eV and 0.12 eV for CLT0.9Cr0.1. It is obvious that a slight substitution of chromium for titanium in B-sites reduced the activation energy for electrical conductions in grain boundaries, indicating that it is easier to activate the conducting electrons in our compounds after Cr substitution. This corresponds to a decrease of grain boundary resistance in Cr-doped samples. More than that, Ang et al.44 proposed that in titanate perovskite, the ionization of oxygen vacancy separated two stages and created the conducting electrons, depicted as.
σdc and 1000/T is obtained. The conduction activation energies are 1.08 eV and 0.69 eV for CLT and 0.42 eV and 0.12 eV for CLT0.9Cr0.1. It is obvious that a slight substitution of chromium for titanium in B-sites reduced the activation energy for electrical conductions in grain boundaries, indicating that it is easier to activate the conducting electrons in our compounds after Cr substitution. This corresponds to a decrease of grain boundary resistance in Cr-doped samples. More than that, Ang et al.44 proposed that in titanate perovskite, the ionization of oxygen vacancy separated two stages and created the conducting electrons, depicted as.| |
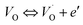 | (1) |
| |
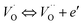 | (2) |
Or these electrons might be bonded to Ti4+ in the form of Ti4+ + e′ ⇔ Ti3+.
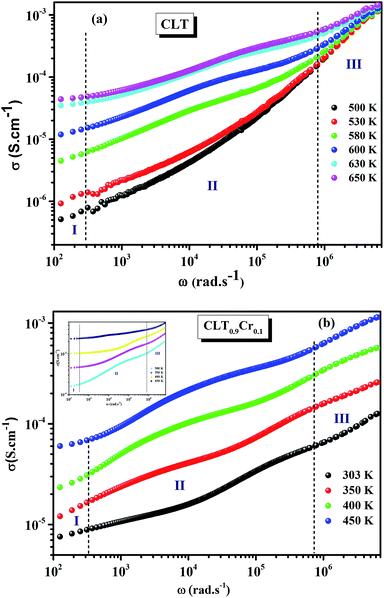 |
| | Fig. 3 Variation of conductivity σ(ω) as a function of frequency in a log–log scale at different temperature for CLT (a) and CLT0.9Cr0.1 (b) compounds. | |
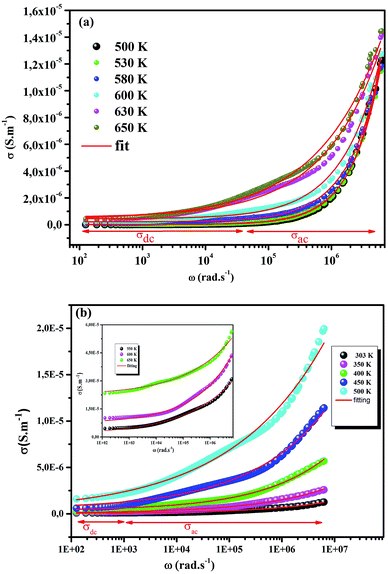 |
| | Fig. 4 Frequency dependent of σ(ω) conductivity and its continuous fitting curves using double power law. | |
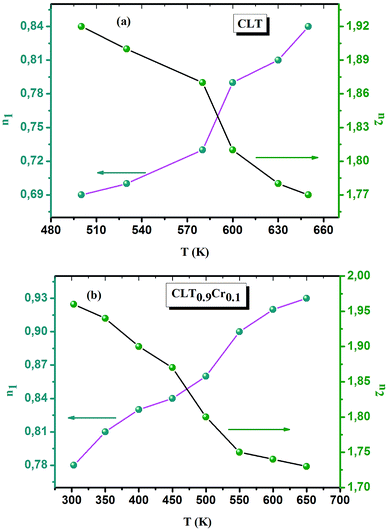 |
| | Fig. 5 Double power temperatures parameters (n1, n2) obtained from the fitting curve of σ(ω) for the compositions (a) x = 0 and (b) x = 0.1 solid solution CLT(1−x)Crx ceramics. | |
 |
| | Fig. 6 Arrhenius plots as a function of the temperature, indicating two regions with different activation energies for compositions (a) x = 0 and (b) x = 0.1. | |
The first conduction activation energies at low temperature (0.69 eV and 0.12 eV) and the second at higher temperature are (0.42 eV and 1.08 eV) for CLT and CLT0.9Cr0.1, respectively, are very close to the activation energy value of oxygen vacancies in ferroelectric oxides and the values are associated with 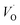 and
and  , respectively.45 At low temperatures, the Edc values indicate that the
, respectively.45 At low temperatures, the Edc values indicate that the 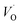 and electron hopping are responsible for conduction because these values are much less than that of the
and electron hopping are responsible for conduction because these values are much less than that of the 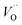 .46 At high temperatures, the Edc values increase, which shows that the electrical conduction is governed by the thermal excitation of carriers from the
.46 At high temperatures, the Edc values increase, which shows that the electrical conduction is governed by the thermal excitation of carriers from the 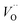 . One of the conducting electrons is created by the VO ionization and the other from the valence fluctuation between Ti3+ and Ti4+. The created electrons would be trapped at defects, such as lattice vacancies, boundaries, and dislocations. These electros might hop between the neighboring transition metal ions as Ti4+ and Ti3+. Besides, the low conductivity and high activation energy of the CLT compounds suggest that the elimination of defects, trapped in the grain boundary and electrode-interface, significantly reduces the influence of domain walls and VO can easily be released out and no space charge is built up.
. One of the conducting electrons is created by the VO ionization and the other from the valence fluctuation between Ti3+ and Ti4+. The created electrons would be trapped at defects, such as lattice vacancies, boundaries, and dislocations. These electros might hop between the neighboring transition metal ions as Ti4+ and Ti3+. Besides, the low conductivity and high activation energy of the CLT compounds suggest that the elimination of defects, trapped in the grain boundary and electrode-interface, significantly reduces the influence of domain walls and VO can easily be released out and no space charge is built up.
3.3. Conductivity scaling
From σ(ω) spectra, a strong frequency dispersion above the characteristic crossover frequency can be observed and it is found to shift towards higher values with increasing temperature. Besides, it can be seen that the frequency range of the mid frequency plateau region of σ(ω) spectra depends strongly on temperature. These two observations indicate that multiple σ(ω) isotherms can be superimposed to form a single master curve in a process known as the time–temperature superposition principal (TTSP) or scaling.47 In this case, different approaches have been proposed to carry out the TTSP and in general the scaling of conductivity spectra is determined by the following equation48,49
where F is the scaling parameter. In our study, we adopt the scaling approach, in which the scaling parameter is chosen as.50 This scaling approach implies only two directly accessible physical parameters, σdc and temperature, for the formation of the master curve. The formation of the master curve using the Summerfield scaling approach for CLT and CLT0.9Cr0.1 composition is shown in Fig. 7. The curves perfect overlap at different temperatures indicates that the ion conduction mechanism in our compounds is independent of temperature51 but with a small deviation, at high temperature and in the low-frequency range, attributed to electrode polarization effects.
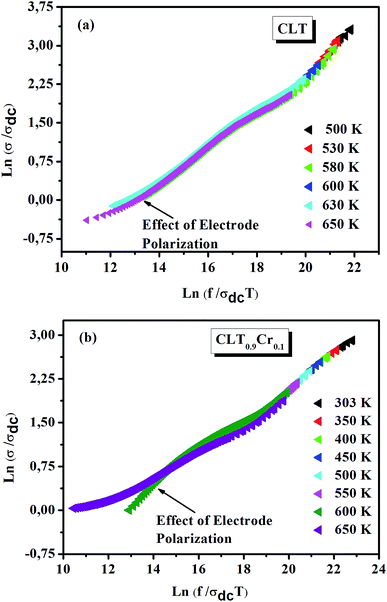 |
| | Fig. 7 Scaling behavior of conductivity at various temperatures for compositions (a) x = 0 and (b) x = 0.1. | |
3.4. Electrical modulus analysis
The electrical modulus formalism (M*) is a widely used technique to investigate the electrical relaxation phenomena as it helps in understanding the ion conduction mechanism and relaxation processes by suppressing the effects of electrode polarization essentially observed in the low frequency regions. Note that M* scales inversely to the complex permittivity; that is the more the conductivity loss contributes to the permittivity, the less the conductivity loss affects the module.52,53 M* is calculated from the dielectric permittivity using the following relation:| |
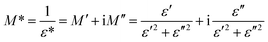 | (3) |
The frequency dependence of the real and imaginary parts of electrical module spectra M′ and M′′ at different temperatures of CLT and CLT0.9Cr0.1 are shown in Fig. 8(a and b). As can be seen M′ increases gradually with increasing frequency for all compositions. Besides, the composition with x = 0 presents a saturation even at low frequencies (103 Hz) for low temperatures (T < 580 K) and at high frequency for the other temperature range, which indicates that the electrode polarization phenomena did not contribute and may be ignored when the electric field, are analyzed in this form.54 However, for the CLT0.9Cr0.1 composition, M′ should get saturation at very high frequency, but due to the frequency limitation of the experimental setup used, we did not observe proper saturation of M′ spectra. Nonetheless, at very low temperatures and high frequency, M′ exhibited a nearly saturated behavior. In the case of M′′ spectra, we did observed a distinct peak which corresponds to the conductivity relaxation process. Hence, below the loss peak maximum, the frequency regions determine the range in which charge carriers are mobile (long-range motion). Above this range, however, the carriers are confined to potential wells, being mobile at short distances. Hence, a localized motion was detected here. The frequency region where the peak occurs is indicative of the transition from localized to non-localized mobility with the increase in frequency. This type of behavior of the electrical module is indicative of a temperature-dependent hopping type mechanism for electrical conduction (charge transport) in the system. The values of Full-Width-at-Half-Maxima (FWHM) calculated from the M′′ spectra are greater than 1.144, indicating a spread of relaxation with different time constants and a non-Debye type relaxation.55 The relaxation time (τM) can be defined as the inverse of the maximum module angular frequency 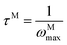 , with ωMmax being the angular frequency where the maximum M′′(ω) occurs. τM is found to obey the Arrhenius relation
, with ωMmax being the angular frequency where the maximum M′′(ω) occurs. τM is found to obey the Arrhenius relation 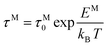 , where τM0 is the pre-exponential factor of the relaxation time and EM is the relaxation activation energy. ln
, where τM0 is the pre-exponential factor of the relaxation time and EM is the relaxation activation energy. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τM vs. (1000/T) is also plotted (inset Fig. 8). The plot exhibits one activation energy for CLT, suggesting one type of probable relaxation process in this composition. However, two activation energies above and below 550 K (Tm for x = 0.1 (ref. 31)), indicate that two relaxation processes indeed occur in CLT0.9Cr0.1. The best fittings of EM were computed for the two samples and are given in Table 1. It is observed that the activation relaxation energy is lower than the activation energy for conduction. This result is explained by the fact that the activation energy for conduction (Edc) is the sum of both the creation of charge carriers and their hopping free energy over long range. Whereas, the activation energy for relaxation (EM) is equal to the migration free energy of charge carriers and their hopping between the adjacent lattice sites.56 The difference between the conduction and relaxation activation energies may be due to the creation of free energy. Relaxation time (τ) calculated from M′′ is related to the free energy, from the Eyring theory, by the following formula.57
τM vs. (1000/T) is also plotted (inset Fig. 8). The plot exhibits one activation energy for CLT, suggesting one type of probable relaxation process in this composition. However, two activation energies above and below 550 K (Tm for x = 0.1 (ref. 31)), indicate that two relaxation processes indeed occur in CLT0.9Cr0.1. The best fittings of EM were computed for the two samples and are given in Table 1. It is observed that the activation relaxation energy is lower than the activation energy for conduction. This result is explained by the fact that the activation energy for conduction (Edc) is the sum of both the creation of charge carriers and their hopping free energy over long range. Whereas, the activation energy for relaxation (EM) is equal to the migration free energy of charge carriers and their hopping between the adjacent lattice sites.56 The difference between the conduction and relaxation activation energies may be due to the creation of free energy. Relaxation time (τ) calculated from M′′ is related to the free energy, from the Eyring theory, by the following formula.57
| |
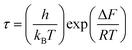 | (4) |
where Δ
F is the free energy of activation for dipole relaxation and
R is the constant of perfect gas. Indeed, the enthalpy(Δ
H) and the entropy (Δ
S) are related to (Δ
F) by the relation: Δ
F = Δ
H –
TΔ
S. This can be expressed as:
| |
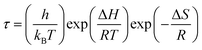 | (5) |
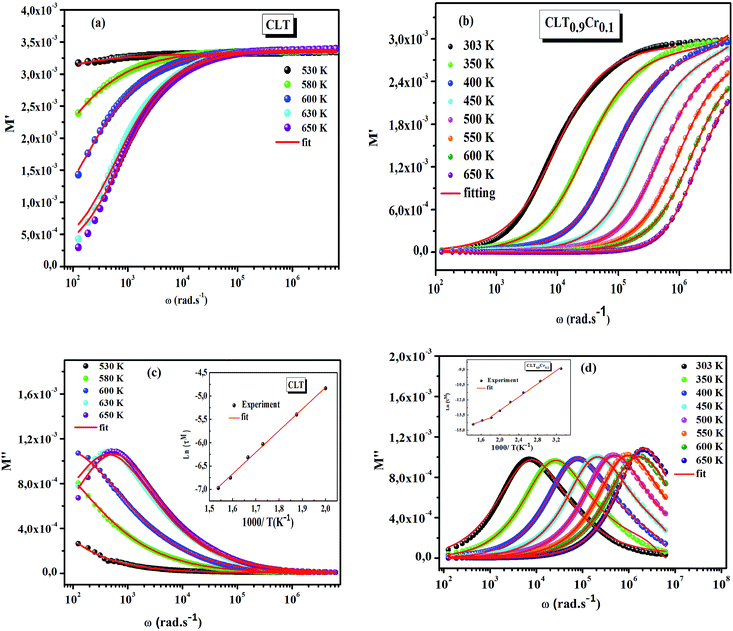 |
| | Fig. 8 (a and b) Angular frequency dependence of the real part of electric modulus at several temperatures for compositions (a) x = 0 and (b) x = 0.1. (c and d) Angular frequency dependence of the imaginary part of electric module at several temperatures for compositions (c) x = 0 and (d) x = 0.1, the inset shows their corresponding Arrhenius plot of relaxation time (τM). | |
Table 1 Activation energy values (Ea) obtained from the relaxation time plots for different functions: real part of dielectric permittivity, dc conductivity, and electrical modulus
| Compounds |
Activation energy (eV) |
Electrical modulus |
| Dielectric permittivity |
dc conductivity |
| CLT |
0.073 |
0.69 |
0.40 |
| 1.08 |
| CLT0.9Cr0.1 |
0.01 |
0.12 |
0.16 |
| 0.03 |
0.42 |
0.28 |
ln(τT) versus 1000/T (Fig. 9) was, thus, plotted. ΔH and ΔS were fitted to be 5.8428 k cal K−1 mol−1 and -29.0857 cal mol−1 K−1 for CLT0.9Cr0.1. The negative value for the change in entropy (ΔS) suggests the existence of dipole–dipole interactions. For a better understanding of the nature of the conductivity relaxation, we presented in Fig. 10 and 11 the combined plots of Z′′ and M′′ for CLT and CLT0.9Cr0.1, respectively, which allows to distinguish between the short-range (i.e. localized: dielectric relaxation) and long-range motion (i.e. non-localized: long range conductivity).58,59 We can clearly see that the frequency of the loss peak maximum in the 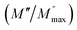 slightly shifted to a higher frequency region together with
slightly shifted to a higher frequency region together with 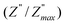 peak. Moreover, it is known that the relaxation time τZ and τM, associated to the two dielectric impedance and electric module, respectively, follows the general order τZ ≥ τM.60 That is why the Z′′ maximum appears in a frequency range lower than that of the M′′ maximum peak. The separation between the normalized M′′ and Z′′ loss peak suggests that the current relaxations are dominated by the localized hopping of charge carriers.61,62 Furthermore, the frequency gap (Δf) between
peak. Moreover, it is known that the relaxation time τZ and τM, associated to the two dielectric impedance and electric module, respectively, follows the general order τZ ≥ τM.60 That is why the Z′′ maximum appears in a frequency range lower than that of the M′′ maximum peak. The separation between the normalized M′′ and Z′′ loss peak suggests that the current relaxations are dominated by the localized hopping of charge carriers.61,62 Furthermore, the frequency gap (Δf) between 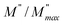 and
and 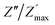 peaks decreased when temperature increased. This behavior indicates that the conduction process became less localized and translated to non-localized i.e. long-range motion. This proves that the oxygen ions or vacancies contribute to the dc conductivity at high temperatures. Fig. 12(a and b) shows the scaling behaviors of the electric module for the samples with x = 0 and x = 0.1, respectively. We can say that the peaks almost collapsed into one curve for CLT0.9Cr0.1, this shows that the dynamic process of both charge carriers for this composition is temperature independent. However, for sample with x = 0, it can be noted that the peaks almost collapsed into two curves above and below T = 600 K, suggesting that the dynamic mechanism of charge carriers for CLT is temperature dependent.
peaks decreased when temperature increased. This behavior indicates that the conduction process became less localized and translated to non-localized i.e. long-range motion. This proves that the oxygen ions or vacancies contribute to the dc conductivity at high temperatures. Fig. 12(a and b) shows the scaling behaviors of the electric module for the samples with x = 0 and x = 0.1, respectively. We can say that the peaks almost collapsed into one curve for CLT0.9Cr0.1, this shows that the dynamic process of both charge carriers for this composition is temperature independent. However, for sample with x = 0, it can be noted that the peaks almost collapsed into two curves above and below T = 600 K, suggesting that the dynamic mechanism of charge carriers for CLT is temperature dependent.
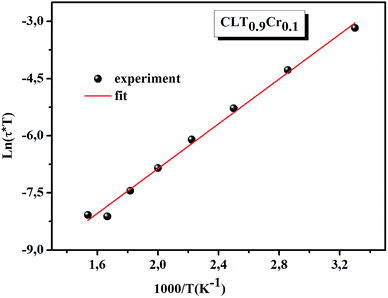 |
| | Fig. 9 The temperature dependence of ln(τT). | |
 |
| | Fig. 10 Angular frequency dependence of 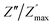 and and 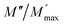 at different temperature for composition (a and b) x = 0. at different temperature for composition (a and b) x = 0. | |
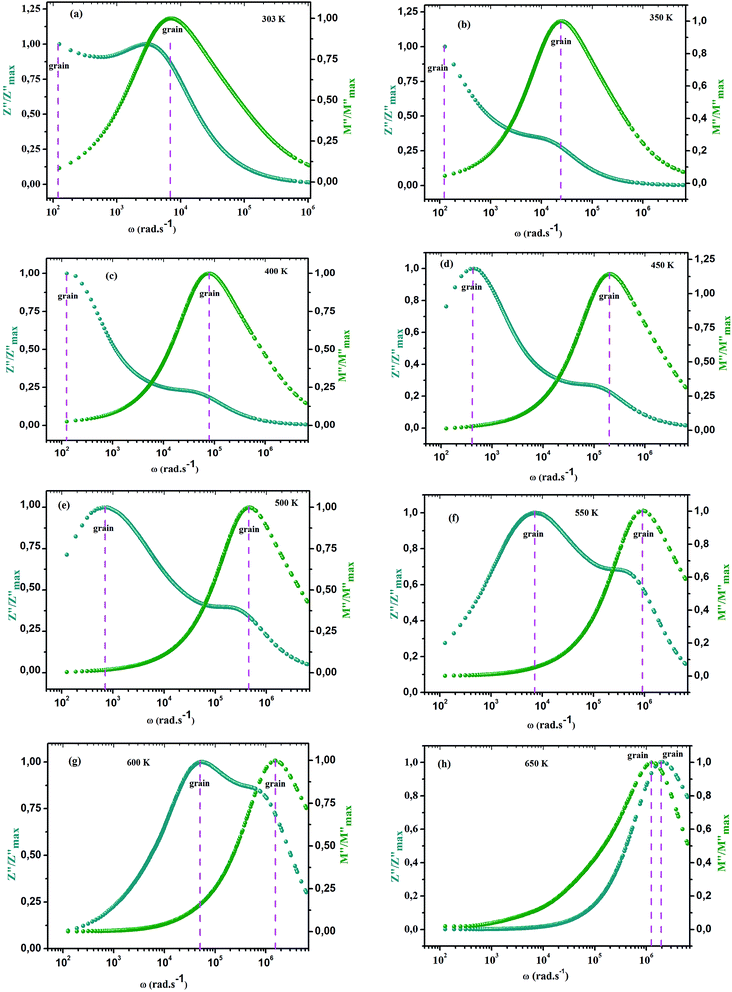 |
| | Fig. 11 Angular frequency dependence of 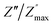 and and 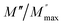 at different temperature for composition (a–h) x = 0.1. at different temperature for composition (a–h) x = 0.1. | |
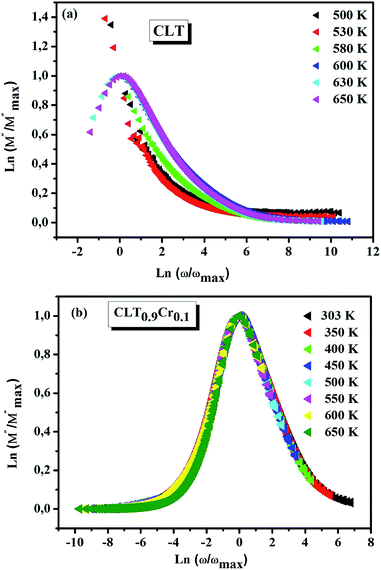 |
| | Fig. 12 Scaling behavior of imaginary part of electrical module versus ln(ω/ωmax) for compositions (a) x = 0 and (b) x = 0.1. | |
3.5. Electronic paramagnetic resonance analysis
The main focus in this work is to understand the interrelationships among A-site non-stoichiometry, defect equilibria, and transport properties in the perovskite solid solution of LT(1−x)Crx. The EPR technique was used to identify the paramagnetic center (PC) and to investigate defects species in perovskite materials. A phenomenological spin Hamiltonian for PC having an electron spin S, a nuclear spin I and the magnetic hyperfine interaction constant A is| | |
HB = μBSgB0 − gnμnB0I + SAI
| (6) |
where μB denotes the Bohr magneton, μn the nuclear magneton, B0 the external magnetic field, g is the electron g-matrix and gn the nuclear g-matrix. The first two terms describe the electronic and nuclear Zeeman interaction, respectively, and the third term represents the hyperfine interaction between electron spin and the nuclear spin.63 The resonance condition with the applied microwave field (hν) was achieved when: hν = gμBB, where h is Planck's constant (6.626 9 10−34 J s) and ν is the microwave frequency (9.815687 GHz). Fig. 13(a) shows the EPR spectrum of CLT which exhibits a resonance signal at g = 2.1265, 2.0923, 2.0755, 2.0452, 2.0257, 1.9974, 1.9761, 1.9564, 1.9288 and 1.8812. The intense resonance signal at g = 2.1265, 2.0923 and 2.0755 is bigger than that of free electron (ge = 2.0023),64,65 it originated from surface trapping site according to Shivram et al.66 Moreover, Bärner et al.67 attributed these signals (g = 2.1265, 2.0923 and 2.0755) to the trapped single electrons located in oxygen vacancies sites 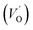 . These
. These 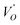 are linked to TiO5 clusters, called
are linked to TiO5 clusters, called 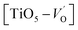 oxygen complex clusters.68 The paramagnetic center at g = 2.0452is due to O− free radical.69,70 The sharp signal at g = 2.0257 is probably attributed to an electron shared among the six octahedral oxygen orbits surrounding B-site, i.e., [TiO6]9− center.66 A similar result is observed by Boutinaud et al.71 Based on the researches realized by Kutty el al, the resonance signal associated to g = 1.9971 corresponds to the paramagnetic state due to chemistry defects (e.g. non-stoichiometric A-site).72,73 Kutty et al.73 assumed that EPR signal at g = 1.9971 is due to singly ionized A-site. The second strategy assumes that, when the ratio
oxygen complex clusters.68 The paramagnetic center at g = 2.0452is due to O− free radical.69,70 The sharp signal at g = 2.0257 is probably attributed to an electron shared among the six octahedral oxygen orbits surrounding B-site, i.e., [TiO6]9− center.66 A similar result is observed by Boutinaud et al.71 Based on the researches realized by Kutty el al, the resonance signal associated to g = 1.9971 corresponds to the paramagnetic state due to chemistry defects (e.g. non-stoichiometric A-site).72,73 Kutty et al.73 assumed that EPR signal at g = 1.9971 is due to singly ionized A-site. The second strategy assumes that, when the ratio 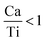 , excess Ti4+ ions occupy A-site. To satisfy the electro-neutrality, calcium vacancies should be formed in the vicinity of the Ti4+ ion at the Ca2+ site. In this case, a singlet EPR signal arises when the calcium vacancy releases one electron or the Ti4+ ion at the Ca2+ site captures one or two electrons. The paramagnetic center at g = 1.9761 is attributed to the presence of Ti3+ related defect centers (Ti3+–VO).73 These defect centers are commonly observed in BaTiO3 reducing conditions.64 In contrary, Sun et al., however, assign the signal at g = 1.976 to the presence of Ba (A-site) vacancies.74 Nevertheless, there are some important differences between the compositions in our study and those in Sun's work.74 Sun identified the defect associated with Nd-doped BaTiO3, whereas the composition in this study was lanthanum (La) doped calcium titanate (CaTiO3) on the A-site. The paramagnetic center resonance at g = 1.9464, based on the results of Eichel et al.64 which showed that >1.93, is associated with an
, excess Ti4+ ions occupy A-site. To satisfy the electro-neutrality, calcium vacancies should be formed in the vicinity of the Ti4+ ion at the Ca2+ site. In this case, a singlet EPR signal arises when the calcium vacancy releases one electron or the Ti4+ ion at the Ca2+ site captures one or two electrons. The paramagnetic center at g = 1.9761 is attributed to the presence of Ti3+ related defect centers (Ti3+–VO).73 These defect centers are commonly observed in BaTiO3 reducing conditions.64 In contrary, Sun et al., however, assign the signal at g = 1.976 to the presence of Ba (A-site) vacancies.74 Nevertheless, there are some important differences between the compositions in our study and those in Sun's work.74 Sun identified the defect associated with Nd-doped BaTiO3, whereas the composition in this study was lanthanum (La) doped calcium titanate (CaTiO3) on the A-site. The paramagnetic center resonance at g = 1.9464, based on the results of Eichel et al.64 which showed that >1.93, is associated with an 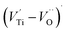 dipole defect. However, a study by Erdem et al. indicated that when g > 1.91, the paramagnetic center defect is associated with
dipole defect. However, a study by Erdem et al. indicated that when g > 1.91, the paramagnetic center defect is associated with 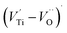 dipole defect.75 Taking into account this last result shown in ref. 45, the signal at g = 1.9288 is due to the
dipole defect.75 Taking into account this last result shown in ref. 45, the signal at g = 1.9288 is due to the 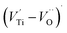 defects dipoles. Nonetheless, Scharschwerdt et al. demonstrated that the signal 1.920–1.9337 is due to Ti3+–V0.76 The last signal observed in CLT spectrum is at g = 1.8812. This paramagnetic signal is due to surface hole trapping sites.77 Fig. 13(b) shows the EPR spectrum of CLT0.9Cr0.1. The spectra can be described by the spin Hamiltonian.78
defects dipoles. Nonetheless, Scharschwerdt et al. demonstrated that the signal 1.920–1.9337 is due to Ti3+–V0.76 The last signal observed in CLT spectrum is at g = 1.8812. This paramagnetic signal is due to surface hole trapping sites.77 Fig. 13(b) shows the EPR spectrum of CLT0.9Cr0.1. The spectra can be described by the spin Hamiltonian.78| |
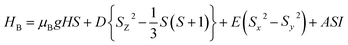 | (7) |
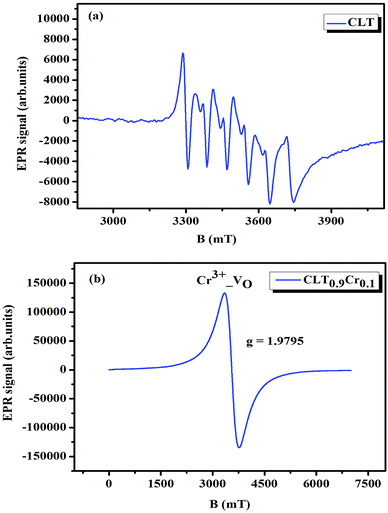 |
| | Fig. 13 Room temperature EPR spectra of CLT(1−x)Crx with (a) x= 0.0 and (b) x = 0.1. | |
With 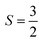 , I = 0 for Cr isotopes with even mass number, and
, I = 0 for Cr isotopes with even mass number, and 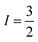 for 53Cr. It can be noted that a slight substitution of chromium for titanium in B-sites has considerable effects. Cr4+ has spin S = 1 and silent EPR.79 Moreover, all paramagnetic centers, observed in CLT disappeared, and a new resonance signal at g = 1.9795 arose. This paramagnetic center is attributed, according to La Mattina et al.80 to 3+ state of the 50Cr, 52Cr and 54Cr isotopes (I = 0), despite the absence of the signal due to the hyperfine quartet caused by the nuclear-spin coupling
for 53Cr. It can be noted that a slight substitution of chromium for titanium in B-sites has considerable effects. Cr4+ has spin S = 1 and silent EPR.79 Moreover, all paramagnetic centers, observed in CLT disappeared, and a new resonance signal at g = 1.9795 arose. This paramagnetic center is attributed, according to La Mattina et al.80 to 3+ state of the 50Cr, 52Cr and 54Cr isotopes (I = 0), despite the absence of the signal due to the hyperfine quartet caused by the nuclear-spin coupling 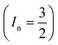 of the 53Cr isotope.80 In addition, Azamat et al. assumed that the single signal at g = 1.9788 is due to the Cr3+–VO centers.81 The slight change in the value of g in different systems is related to differences in the method of synthesis, chemical environment and heat treatment conditions.
of the 53Cr isotope.80 In addition, Azamat et al. assumed that the single signal at g = 1.9788 is due to the Cr3+–VO centers.81 The slight change in the value of g in different systems is related to differences in the method of synthesis, chemical environment and heat treatment conditions.
4. Conclusion
A descriptive report on detailed investigation of dielectric, electrical and optical properties of the lead free CLT(1−x)Crx has been presented. It was observed that the dispersion dielectric behavior was dominated in the low frequency range, whereas the resonance dielectric behavior was found to be dominating at higher frequency. Electrical conductivity was described by the jump relaxation model. Three conductivity channels were identified and were found to obey well the double power law, exponent values (n1 < 1) and (n2 < 2), indicating the different mobile charge species contribution to conductivity. A comparative study of the normalized relaxation peaks corresponding to Z′′ and M′′ showed the coexistence of localized and delocalized motion of charges carriers. Scaling behavior revealed that electrical conduction and dielectric relaxation mechanisms are temperature independent. The EPR study showed several types of paramagnetic point defects in CLT and one defect center corresponding to Cr3+–VO center in CLT0.9Cr0.1.
Conflicts of interest
There are no conflicts to declare.
References
- D. Li, L. Meng, S. Dang, D. Jiang and W. Shi, J. Alloys Compd., 2017, 690, 1–7 CrossRef CAS.
- X. Zhang, M. Ikram, Z. Liu, L. Teng, J. Xue, D. Wang, L. Li and K. Sh, RSC Adv., 2019, 9, 8768–8777 RSC.
- S. Cai, S. Yu, W. Wan, W. Wen and Y. Zhou, RSC Adv., 2017, 7, 27397–27404 RSC.
- T. Ueda, M. Sakai, K. Kai, T. Hyodo and Y. Shimizu, Sens. Actuators, B, 2016, 237, 247–255 CrossRef CAS.
- L. Wu, J. Xia, W. Shi, D. Jiang and Q. Li, Ionics, 2016, 22, 927–934 CrossRef CAS.
- L. Wang, B. Han, Z. Wang, L. Dai and H. Zhou, Sens. Actuators, B, 2015, 207, 791–800 CrossRef CAS.
- Y. Yan, S. Krishnakumar, H. Yu, S. Ramishetti, L.-W. Deng, S. Wang, L. Huang and D. Huang, J. Am. Chem. Soc., 2013, 135, 5312 CrossRef CAS PubMed.
- Y. Yan, J. Sun, K. Zhang, H. Zhu, H. Yu, M. Sun, D. Huang and S. Wang, Anal. Chem., 2015, 87, 2087 CrossRef CAS PubMed.
- J. M. Reyes, H. Tiznado, G. Soto, M. V. Bautista, D. Dominguez, E. Murillo, D. Sweeney and J. Read, J. Mater. Sci.: Mater. Electron., 2018, 29, 15349 CrossRef.
- K. Mahendraprabhu and P. Elumalai, RSC Adv., 2015, 5, 24126–24131 RSC.
- T. Ishihara, H. Matsuda and Y. Takata, J. Am. Chem. Soc., 1994, 116, 3801 CrossRef CAS.
- M. Feng and J. B. Goodenough, Eur. J. Solid State Inorg. Chem., 1994, T31, 663 Search PubMed.
- S. W. Tao, J. T. S. Irvine and J. A. Kilner, Faraday Discuss., 2007, 9, 134 Search PubMed.
- A. Orera and P. R. Slater, Chem. Mater., 2010, 22, 675 CrossRef CAS.
- R. C. Biswal and K. Biswas, Int. J. Hydrogen Energy, 2015, 40, 509 CrossRef CAS.
- A. Matraszek, L. Singheiser, D. Kobertz, K. Hilpert, M. Miller, O. Schulz and M. Martin, Solid State Ionics, 2004, 166, 343 CrossRef CAS.
- A. Sinha, B. P. Sharma and P. Gopalan, Electrochim. Acta, 2006, 51, 1184 CrossRef CAS.
- R. Zuo, S. Su, Y. Wu, J. Fu, M. Wang and L. Li, Mater. Chem. Phys., 2008, 110, 311 CrossRef CAS.
- Y. S. Sung, J. M. Kim, J. H. Cho, T. K. Song, M. H. Kim, H. H. Chong, T. G. Park, D. Do and S. S. Kim, Appl. Phys. Lett., 2010, 96, 022901 CrossRef.
- Y. S. Sung, J. M. Kim, J. H. Cho, T. K. Song, M. H. Kim and T. G. Park, Appl. Phys. Lett., 2011, 98, 012902 CrossRef.
- M. Li, M. J. Pietrowski, R. A. De Souza, H. Zhang, I. M. Reaney, S. N. Cook, J. A. Kilner and D. C. Sinclair, Nat. Mater., 2013, 13, 31 CrossRef PubMed.
- M. Naderer, T. Kainz, D. Schütz and K. Reichmann, J. Eur. Ceram. Soc., 2014, 34, 663 CrossRef CAS.
- M. Li, H. Zhang, S. N. Cook, L. Li, J. A. Kilner, I. M. Reaney and D. C. Sinclair, Chem. Mater., 2015, 27, 629 CrossRef CAS.
- M. Li, M. J. Pietrowski, R. A. De Souza, H. Zhang, I. M. Reaney, S. N. Cook, J. A. Kilner and D. C. Sinclair, Nat. Mater., 2014, 13, 31 CrossRef CAS PubMed.
- K.-C. Meyer and K. Albe, J. Mater. Chem. A, 2017, 5, 4368 RSC.
- K. Reichmann, A. Feteira and M. Li, Materials, 2015, 8, 5469 CrossRef PubMed.
- X. Liu, H. Fan, J. Shi, L. Wang and H. Du, RSC Adv., 2016, 6, 30623 RSC.
- J. Huang, F. Zhu, D. Huang, B. Wang, T. Xu, X. Li, P. Fan, F. Xia, J. Xiao and H. Zhang, Ceram. Int., 2016, 42, 16798 CrossRef CAS.
- F. Yang, P. Wu and D. C. Sinclair, Solid State Ionics, 2017, 299, 38 CrossRef CAS.
- F. Yang, M. Li, L. Li, P. Wu, E. Pradal-Velázquez and D. C. Sinclair, J. Mater. Chem. A, 2018, 6, 5243 RSC.
- A. B. Hassen, F. I. H. Rhouma, J. Dhahri and N. Abedlmoula, J. Alloys Compd., 2016, 663, 436 CrossRef.
- R. C. Kambale, P. A. Shaikh, C. H. Bhosale, K. Y. Rajpure and Y. D. Kolekar, Smart Mater. Struct., 2009, 18, 115028 CrossRef.
- Y. D. Kolekar, L. J. Sanchez and C. V. Ramana, J. Appl. Phys., 2014, 115, 144106 CrossRef.
- C. G. Koops, Phys. Rev., 1951, 83, 121 CrossRef CAS.
- A. M. Bhavikatti, S. Kulkarni and A. Lagashetty, Int. J. Eng. Sci. Technol., 2014, 3, 5985 Search PubMed.
- G. H. Jonker, J. Phys. Chem. Solids, 1959, 9, 165 CrossRef CAS.
- S. Mahalakshmi, M. K. Srinivasa and S. Nithiyanantham, J. Supercond. Novel Magn., 2014, 27, 2083 CrossRef CAS.
- N. Ortega, A. Kumar, P. Bhattacharya, S. B. Majumder and R. S. Katiyar, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 014111 CrossRef.
- A. Bettaibi, R. Jemai, M. A. Wederni, R. M'nassri, M. Barbouche, H. Rahmouni and K. Khirouni, RSC Adv., 2017, 7, 22578 RSC.
- W. Li and R. W. Schwartz, Appl. Phys. Lett., 2006, 89, 242906 CrossRef.
- A. Pelaiz-Barramco, M. P. Gutierrez-Amador, A. Huanosta and R. Valenzuela, Appl. Phys. Lett., 1998, 73, 2039 CrossRef.
- S. R. Elliott, Adv. Phys., 1987, 36, 135 CrossRef CAS.
- S. Chouchene, K. Jaoudi, T. Mhiri, N. Zouari and A. Daoud, Ionics, 2017, 23, 169 CrossRef CAS.
- C. Ang, Z. Yu and L. E. Cross, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 228 CrossRef.
- F. Rehman, H. Jin and J. Li, RSC Adv., 2016, 6, 35102 RSC.
- J. Wu and J. Wang, J. Am. Ceram. Soc., 2010, 93, 2795 CrossRef CAS.
- S. Das and A. J. Bhattacharyya, J. Phys. Chem. Lett., 2012, 3, 3550–3554 CrossRef CAS PubMed.
- S. N. Tripathy, Z. Wojnarowska, J. Knapik, H. Shirota, R. Biswas and M. Paluch, J. Chem. Phys., 2015, 142, 184504 CrossRef PubMed.
- S. Murugavel and B. Roling, Phys. Rev. Lett., 2002, 89, 195902 CrossRef CAS PubMed.
- S. Das and A. J. Bhattacharyya, J. Phys. Chem. Lett., 2012, 3, 3550 CrossRef CAS PubMed.
- A. Pan and A. Ghosh, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 12301 CrossRef.
- Q. Ke, X. Lou, Y. Wang and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 024102 CrossRef.
- A. E. Stearn and H. Hyring, J. Chem. Phys., 1937, 5, 113 CrossRef CAS.
- N. Ortega, A. Kumar, P. Bhattacharya, S. B. Majumder and R. S. Katiyar, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 014111 CrossRef.
- G. Molnár, S. Cobo, T. Mahfoud, E. J. M. Vertelman, P. J. van Koningsbruggen, P. Demont and A. Bousseksou, J. Phys. Chem. C, 2009, 113, 2586 CrossRef.
- I. W. Kim, C. W. Ahn, J. S. Kim, J. S. Bae, B. C. Choi, J. H. Jheong and J. S. Lee, Appl. Phys. Lett., 2002, 80, 4006 CrossRef CAS.
- A. V. Sarode and A. C. Kumbharkhane, J. Mol. Liq., 2011, 164, 226 CrossRef CAS.
- J. J. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 144106 CrossRef.
- M. A. L. Nobre and S. Lanfredi, J. Appl. Phys., 2003, 93, 5576 CrossRef CAS.
- W. Bai, G. Chen, J. Y. Zhu, J. Yang and T. Lin, Appl. Phys. Lett., 2012, 100, 082902 CrossRef.
- Q. Ke, X. Lou, Y. Wang and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 024102 CrossRef.
- A. E. Stearn and H. Hyring, J. Chem. Phys., 1937, 5, 113–124 CrossRef CAS.
- B. Bleaney and K. W. H. Stevens, Rep. Prog. Phys., 1953, 16, 108 CrossRef.
- R. A. Eichel, Phys. Chem. Chem. Phys., 2011, 13, 368 RSC.
- D. T. Edwards, Y. Zhang, S. J. Glaser, S. Hancd and M. S. Sherwin, Phys. Chem. Chem. Phys., 2013, 15, 5707 RSC.
- M. Shivram, R. H. Krishna, H. Nagabhushana, S. C. Sharma, B. M. Nagabhushana, B. S. Ravikumar, N. Dhananjaya, C. Shivakumara, J. L. Rao and R. P. S. Chakradhar, Mater. Res. Bull., 2013, 48, 1490 CrossRef.
- X. J. Luo, Y. S. Liu, C. P. Yang, S. S. Chen, S. L. Tang and K. Bärner, J. Eur. Ceram. Soc., 2015, 35, 2073 CrossRef CAS.
- J. Milanez, A. T. de Figueiredo, S. de Lazaro, V. M. Longo, R. Erlo, V. R. Mastelaro, R. W. A. Franco, E. longo and J. A. Varela, J. Appl. Phys., 2009, 106, 043526 CrossRef.
- E. Possenriede, P. Jacobs and O. F. Schirmer, J. Phys.: Condens. Matter, 1992, 4, 4719 CrossRef CAS.
- G. Pinarello, C. Pisani, A. D'Ercole, M. Chiesa, M. C. Paganini, E. Giamello and O. Diwald, Surf. Sci., 2001, 494, 95 CrossRef CAS.
- P. Boutinaud, E. Pinel, M. Dubois, A. P. Vink and R. Mahiou, J. Lumin., 2005, 111, 69 CrossRef CAS.
- T. R. N. Kutty, P. Murugaraj and N. S. Gajbhiye, Mater. Res. Bull., 1985, 20, 565 CrossRef CAS.
- N. S. Hari, P. Padmini and T. R. N. Kutty, J. Mater. Sci.: Mater. Electron., 1997, 8, 15 CrossRef CAS.
- Q. Sun, Q. Gu, K. Zhu, R. Jin, J. Liu, J. Wang and J. Qiu, Sci. Rep., 2017, 7, 42274 CrossRef CAS PubMed.
- E. Erdem, P. Jakes and R.-A. Eichel, Funct. Mater. Lett., 2010, 3, 65 CrossRef CAS.
- R. Scharfschwerdt, A. Mazur, O. F. Schirmer, H. Hesse and S. Mendricks, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 15284 CrossRef CAS PubMed.
- R. F. Howe and M. Gratzel, J. Phys. Chem., 1987, 91, 3906 CrossRef CAS.
- A. Abragam and M. H. L. Pryce, Proc. Phys. Soc., London, Sect. A, 1951, 205, 135 CAS.
- R. H. Hoskins and B. H. Soffer, Phys. Rev. A, 1964, 490, 133 Search PubMed.
- F. La Mattina, J. G. Bednorz, S. F. Alvarado, A. Shengelaya, K. A. Müller and H. Keller, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 075122 CrossRef.
- D. V. Azamat, A. Dejneka, J. Lancok, V. A. Trepakov, L. Jastrabik and A. G. Badalyan, J. Appl. Phys., 2013, 113, 174106 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b,
M. Daoudic,
J. Dhahri
b,
M. Daoudic,
J. Dhahri a,
M. Zaidi
a,
M. Zaidi *d and
N. Abdelmoulae
*d and
N. Abdelmoulae
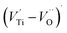 dipole defect for CLT compound and Cr3+–VO center defect for CLT0.9Cr0.1 compound. These defects are the source of the in-gap electron traps, which improve the optical properties of CLT(1−x)Crx and hence make it an interesting optical material for different applications.
dipole defect for CLT compound and Cr3+–VO center defect for CLT0.9Cr0.1 compound. These defects are the source of the in-gap electron traps, which improve the optical properties of CLT(1−x)Crx and hence make it an interesting optical material for different applications.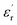 , for all the samples, increases with decreasing frequency and increasing temperature, indicating a strong dielectric dispersion. In fact, the high value of
, for all the samples, increases with decreasing frequency and increasing temperature, indicating a strong dielectric dispersion. In fact, the high value of 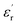 at lows frequencies is mainly attributed to the contribution of electronic, space charges, ionic, and interfacial polarization which are generally accompanied by the appearance of dielectric relaxation. However, at high frequency,
at lows frequencies is mainly attributed to the contribution of electronic, space charges, ionic, and interfacial polarization which are generally accompanied by the appearance of dielectric relaxation. However, at high frequency, 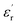 is independent of temperature and frequency. This independence is due to the inability of electric dipoles to follow the fast variation of the applied electric field. Therefore, the dielectric dispersion observed at low frequency range is due to the interfacial polarization, because the electronic and atomic polarizations persist unchanged at this frequency range.32 Furthermore, we can note that when chromium is introduced into CLT, a significant rise in the real part of permittivity is seen, suggesting that the variation of
is independent of temperature and frequency. This independence is due to the inability of electric dipoles to follow the fast variation of the applied electric field. Therefore, the dielectric dispersion observed at low frequency range is due to the interfacial polarization, because the electronic and atomic polarizations persist unchanged at this frequency range.32 Furthermore, we can note that when chromium is introduced into CLT, a significant rise in the real part of permittivity is seen, suggesting that the variation of 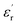 values results not only from the contribution of thermally-activated charge defects but also from the dominant effect of chromium-doping. This might be generated by the multivalent configuration of chromium ions. The variation of dielectric loss (tan
values results not only from the contribution of thermally-activated charge defects but also from the dominant effect of chromium-doping. This might be generated by the multivalent configuration of chromium ions. The variation of dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) with frequency is shown in Fig. 2. Here angle “δ” is the phase difference between the applied electric field and the induced current.33 Similar to ε′, the tan
δ) with frequency is shown in Fig. 2. Here angle “δ” is the phase difference between the applied electric field and the induced current.33 Similar to ε′, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values decrease with increasing frequency and become constant at higher frequencies. This behavior can be attributed to the decrease in polarization at an applied higher electric field. The observed tan
δ values decrease with increasing frequency and become constant at higher frequencies. This behavior can be attributed to the decrease in polarization at an applied higher electric field. The observed tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ variation with frequency can be due to the conduction mechanism which is analogous to Koop's phenomenological model.34 The tan
δ variation with frequency can be due to the conduction mechanism which is analogous to Koop's phenomenological model.34 The tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ curve is considered to be caused by domain wall resonance. At higher frequencies range, losses are found to be low if the domain wall motion is restrained as per Rezlescu model.32,35 Moreover, the tan
δ curve is considered to be caused by domain wall resonance. At higher frequencies range, losses are found to be low if the domain wall motion is restrained as per Rezlescu model.32,35 Moreover, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ rises when the polarization lags behind the applied alternating electric field. This rise in tan
δ rises when the polarization lags behind the applied alternating electric field. This rise in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ may also be caused by the grain boundaries, imperfections in the crystal lattice, and impurities.36,37 Furthermore, one can see that for the CLT0.9Cr0.1 composition the tan
δ may also be caused by the grain boundaries, imperfections in the crystal lattice, and impurities.36,37 Furthermore, one can see that for the CLT0.9Cr0.1 composition the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ curve exhibits a broad peaks with the frequency dispersion at different temperatures. These peaks shift to a higher frequency with increasing temperature, suggesting a typical characteristic of dielectric relaxation phenomenon.
δ curve exhibits a broad peaks with the frequency dispersion at different temperatures. These peaks shift to a higher frequency with increasing temperature, suggesting a typical characteristic of dielectric relaxation phenomenon.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) for compositions (a) x = 0 and (b) x = 0.1.
δ) for compositions (a) x = 0 and (b) x = 0.1.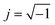 , ε0 is the vacuum permittivity, and ε*(ω) is the complex permittivity. Fundamentally, alternative conductivity (σ(ω)) originates from the migration of ions by hopping between neighboring potential wells. It provides insights into different relaxation mechanisms by investigating its frequency and/or temperature dependent response behaviors. Fig. 3(a and b) displays the frequency dependence of (σ(ω)) for CLT and CLT0.9Cr0.1 at various temperatures. The conductivity increases with increasing frequency, therefore, it starts from its dc value and eventually attains a “high frequency” plateau at about 106 Hz. More than that, (σ(ω)) exhibits a dispersion that shifts to higher frequency with increasing temperatures for all samples. Indeed, the σ(ω) spectrum can be decomposed into three parts: the low frequency (direct conductivity (σdc)) plateau regime (region I), mid-frequency dispersive regime (region II) and high frequency plateau regime (region III). These types of characteristics can be explained on the basis of the jump relaxation model (JRM)38 which states that after a hop of a central ion from an initially relaxed local position, it will be no longer in equilibrium with its neighbors.39,40 To stabilize the new position of the ion, other ions in its surroundings have to move. However, the ion can also jump back (unsuccessful hop) in order to partially relax the position after the jump. At low frequencies in region I, the frequency is low and the electric field cannot perturb the hopping conduction process of the charged particles. On the contrary, the conductivity is assigned to the successful hops from one localized site to its neighboring vacant site due to the available long time period (ω = 2πf = 2π/T), T is the time period, hence, resulting in a long-range motion of ions and conductance may be approximated to the dc value in this range. As the frequency increases, the unsuccessful hops increase, since two competing relaxation processes take place, such as; the correlated ion position related to forward backward forward, i.e., unsuccessful hopping and successful hopping wherein the localized orientation hopping in which once jumped ions become relaxed and stay in the new site. Nevertheless, every individual hop is seen when the time window is sufficiently short. This behavior is assigned to the region II. On the other hand, as the ratio of successful to unsuccessful hopping increases, it results in more dispersive conductivity and the increase of conductivity with frequency in region II is thus qualitatively explained. In region III, the rise in conductivity observed in all samples is almost proportional to frequency, resulting in near constant loss (NCL).41 Based on JRM, the frequency dependence of the conductivity data was possible to fit (Fig. 4) to a double power law38,42 σ(ω) = σdc + Aωn1 + Bωn2, where σdc assigned to dc conductivity whose translational hopping gives the long-range electrical transport in the long-time limit, (i.e., at lower frequency). The second term Aωn1, corresponding to the middle region (II) in which the exponent 0 < n1 < 1 characterizes the low frequency regime, indicates the short range translational hopping motion. The third term Bωn2, attributed to the higher frequency region (III) for which the exponent 1 < n2 < 2, corresponds to localized or reorientation hopping motion. The n1 and n2 values obtained from the fitting data are shown in Fig. 5(a and b). The n1 value exhibits a continuous increase with the temperature, while n2 decreases in the measured temperature for all samples. Early reports42,43 predict the dependence of n with the frequency and temperature, where an increase of the exponent values with increasing temperature is assigned to the small polaronic hopping, whereas a decrease in exponent values is ascribed to the large polaronic hopping. From the trend of the exponents behavior with the temperature of CLT and CLT0.9Cr0.1 compounds, the obtained value of n1 was less than 1 and increasing with temperature, which can indicate that the conduction in region II corresponding to the short translational hopping is provided by small polaronic mechanism. On the other hand, in the case of n2, the values varied between 1 and 2 and decreased with the temperature, implying that the conduction in region III ascribed to the localized orientation hopping, is assisted by large polaron mechanism. Furthermore, electrical conduction is a thermally activated process and follows the Arrhenius law σdc = σ0
, ε0 is the vacuum permittivity, and ε*(ω) is the complex permittivity. Fundamentally, alternative conductivity (σ(ω)) originates from the migration of ions by hopping between neighboring potential wells. It provides insights into different relaxation mechanisms by investigating its frequency and/or temperature dependent response behaviors. Fig. 3(a and b) displays the frequency dependence of (σ(ω)) for CLT and CLT0.9Cr0.1 at various temperatures. The conductivity increases with increasing frequency, therefore, it starts from its dc value and eventually attains a “high frequency” plateau at about 106 Hz. More than that, (σ(ω)) exhibits a dispersion that shifts to higher frequency with increasing temperatures for all samples. Indeed, the σ(ω) spectrum can be decomposed into three parts: the low frequency (direct conductivity (σdc)) plateau regime (region I), mid-frequency dispersive regime (region II) and high frequency plateau regime (region III). These types of characteristics can be explained on the basis of the jump relaxation model (JRM)38 which states that after a hop of a central ion from an initially relaxed local position, it will be no longer in equilibrium with its neighbors.39,40 To stabilize the new position of the ion, other ions in its surroundings have to move. However, the ion can also jump back (unsuccessful hop) in order to partially relax the position after the jump. At low frequencies in region I, the frequency is low and the electric field cannot perturb the hopping conduction process of the charged particles. On the contrary, the conductivity is assigned to the successful hops from one localized site to its neighboring vacant site due to the available long time period (ω = 2πf = 2π/T), T is the time period, hence, resulting in a long-range motion of ions and conductance may be approximated to the dc value in this range. As the frequency increases, the unsuccessful hops increase, since two competing relaxation processes take place, such as; the correlated ion position related to forward backward forward, i.e., unsuccessful hopping and successful hopping wherein the localized orientation hopping in which once jumped ions become relaxed and stay in the new site. Nevertheless, every individual hop is seen when the time window is sufficiently short. This behavior is assigned to the region II. On the other hand, as the ratio of successful to unsuccessful hopping increases, it results in more dispersive conductivity and the increase of conductivity with frequency in region II is thus qualitatively explained. In region III, the rise in conductivity observed in all samples is almost proportional to frequency, resulting in near constant loss (NCL).41 Based on JRM, the frequency dependence of the conductivity data was possible to fit (Fig. 4) to a double power law38,42 σ(ω) = σdc + Aωn1 + Bωn2, where σdc assigned to dc conductivity whose translational hopping gives the long-range electrical transport in the long-time limit, (i.e., at lower frequency). The second term Aωn1, corresponding to the middle region (II) in which the exponent 0 < n1 < 1 characterizes the low frequency regime, indicates the short range translational hopping motion. The third term Bωn2, attributed to the higher frequency region (III) for which the exponent 1 < n2 < 2, corresponds to localized or reorientation hopping motion. The n1 and n2 values obtained from the fitting data are shown in Fig. 5(a and b). The n1 value exhibits a continuous increase with the temperature, while n2 decreases in the measured temperature for all samples. Early reports42,43 predict the dependence of n with the frequency and temperature, where an increase of the exponent values with increasing temperature is assigned to the small polaronic hopping, whereas a decrease in exponent values is ascribed to the large polaronic hopping. From the trend of the exponents behavior with the temperature of CLT and CLT0.9Cr0.1 compounds, the obtained value of n1 was less than 1 and increasing with temperature, which can indicate that the conduction in region II corresponding to the short translational hopping is provided by small polaronic mechanism. On the other hand, in the case of n2, the values varied between 1 and 2 and decreased with the temperature, implying that the conduction in region III ascribed to the localized orientation hopping, is assisted by large polaron mechanism. Furthermore, electrical conduction is a thermally activated process and follows the Arrhenius law σdc = σ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Edc/kBT), where σ0 is the pre-exponential term and Edc represents the activation energies for dc conductivity. As shown in Fig. 6 for CLT and CLT0.9Cr0.1 compounds, a good linear fit between ln
exp(−Edc/kBT), where σ0 is the pre-exponential term and Edc represents the activation energies for dc conductivity. As shown in Fig. 6 for CLT and CLT0.9Cr0.1 compounds, a good linear fit between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σdc and 1000/T is obtained. The conduction activation energies are 1.08 eV and 0.69 eV for CLT and 0.42 eV and 0.12 eV for CLT0.9Cr0.1. It is obvious that a slight substitution of chromium for titanium in B-sites reduced the activation energy for electrical conductions in grain boundaries, indicating that it is easier to activate the conducting electrons in our compounds after Cr substitution. This corresponds to a decrease of grain boundary resistance in Cr-doped samples. More than that, Ang et al.44 proposed that in titanate perovskite, the ionization of oxygen vacancy separated two stages and created the conducting electrons, depicted as.
σdc and 1000/T is obtained. The conduction activation energies are 1.08 eV and 0.69 eV for CLT and 0.42 eV and 0.12 eV for CLT0.9Cr0.1. It is obvious that a slight substitution of chromium for titanium in B-sites reduced the activation energy for electrical conductions in grain boundaries, indicating that it is easier to activate the conducting electrons in our compounds after Cr substitution. This corresponds to a decrease of grain boundary resistance in Cr-doped samples. More than that, Ang et al.44 proposed that in titanate perovskite, the ionization of oxygen vacancy separated two stages and created the conducting electrons, depicted as.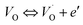
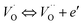




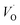 and
and  , respectively.45 At low temperatures, the Edc values indicate that the
, respectively.45 At low temperatures, the Edc values indicate that the 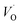 and electron hopping are responsible for conduction because these values are much less than that of the
and electron hopping are responsible for conduction because these values are much less than that of the 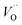 .46 At high temperatures, the Edc values increase, which shows that the electrical conduction is governed by the thermal excitation of carriers from the
.46 At high temperatures, the Edc values increase, which shows that the electrical conduction is governed by the thermal excitation of carriers from the 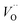 . One of the conducting electrons is created by the VO ionization and the other from the valence fluctuation between Ti3+ and Ti4+. The created electrons would be trapped at defects, such as lattice vacancies, boundaries, and dislocations. These electros might hop between the neighboring transition metal ions as Ti4+ and Ti3+. Besides, the low conductivity and high activation energy of the CLT compounds suggest that the elimination of defects, trapped in the grain boundary and electrode-interface, significantly reduces the influence of domain walls and VO can easily be released out and no space charge is built up.
. One of the conducting electrons is created by the VO ionization and the other from the valence fluctuation between Ti3+ and Ti4+. The created electrons would be trapped at defects, such as lattice vacancies, boundaries, and dislocations. These electros might hop between the neighboring transition metal ions as Ti4+ and Ti3+. Besides, the low conductivity and high activation energy of the CLT compounds suggest that the elimination of defects, trapped in the grain boundary and electrode-interface, significantly reduces the influence of domain walls and VO can easily be released out and no space charge is built up.
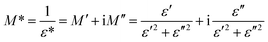
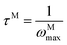 , with ωMmax being the angular frequency where the maximum M′′(ω) occurs. τM is found to obey the Arrhenius relation
, with ωMmax being the angular frequency where the maximum M′′(ω) occurs. τM is found to obey the Arrhenius relation 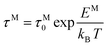 , where τM0 is the pre-exponential factor of the relaxation time and EM is the relaxation activation energy. ln
, where τM0 is the pre-exponential factor of the relaxation time and EM is the relaxation activation energy. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τM vs. (1000/T) is also plotted (inset Fig. 8). The plot exhibits one activation energy for CLT, suggesting one type of probable relaxation process in this composition. However, two activation energies above and below 550 K (Tm for x = 0.1 (ref. 31)), indicate that two relaxation processes indeed occur in CLT0.9Cr0.1. The best fittings of EM were computed for the two samples and are given in Table 1. It is observed that the activation relaxation energy is lower than the activation energy for conduction. This result is explained by the fact that the activation energy for conduction (Edc) is the sum of both the creation of charge carriers and their hopping free energy over long range. Whereas, the activation energy for relaxation (EM) is equal to the migration free energy of charge carriers and their hopping between the adjacent lattice sites.56 The difference between the conduction and relaxation activation energies may be due to the creation of free energy. Relaxation time (τ) calculated from M′′ is related to the free energy, from the Eyring theory, by the following formula.57
τM vs. (1000/T) is also plotted (inset Fig. 8). The plot exhibits one activation energy for CLT, suggesting one type of probable relaxation process in this composition. However, two activation energies above and below 550 K (Tm for x = 0.1 (ref. 31)), indicate that two relaxation processes indeed occur in CLT0.9Cr0.1. The best fittings of EM were computed for the two samples and are given in Table 1. It is observed that the activation relaxation energy is lower than the activation energy for conduction. This result is explained by the fact that the activation energy for conduction (Edc) is the sum of both the creation of charge carriers and their hopping free energy over long range. Whereas, the activation energy for relaxation (EM) is equal to the migration free energy of charge carriers and their hopping between the adjacent lattice sites.56 The difference between the conduction and relaxation activation energies may be due to the creation of free energy. Relaxation time (τ) calculated from M′′ is related to the free energy, from the Eyring theory, by the following formula.57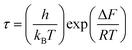
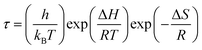
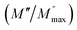 slightly shifted to a higher frequency region together with
slightly shifted to a higher frequency region together with 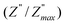 peak. Moreover, it is known that the relaxation time τZ and τM, associated to the two dielectric impedance and electric module, respectively, follows the general order τZ ≥ τM.60 That is why the Z′′ maximum appears in a frequency range lower than that of the M′′ maximum peak. The separation between the normalized M′′ and Z′′ loss peak suggests that the current relaxations are dominated by the localized hopping of charge carriers.61,62 Furthermore, the frequency gap (Δf) between
peak. Moreover, it is known that the relaxation time τZ and τM, associated to the two dielectric impedance and electric module, respectively, follows the general order τZ ≥ τM.60 That is why the Z′′ maximum appears in a frequency range lower than that of the M′′ maximum peak. The separation between the normalized M′′ and Z′′ loss peak suggests that the current relaxations are dominated by the localized hopping of charge carriers.61,62 Furthermore, the frequency gap (Δf) between 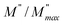 and
and 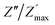 peaks decreased when temperature increased. This behavior indicates that the conduction process became less localized and translated to non-localized i.e. long-range motion. This proves that the oxygen ions or vacancies contribute to the dc conductivity at high temperatures. Fig. 12(a and b) shows the scaling behaviors of the electric module for the samples with x = 0 and x = 0.1, respectively. We can say that the peaks almost collapsed into one curve for CLT0.9Cr0.1, this shows that the dynamic process of both charge carriers for this composition is temperature independent. However, for sample with x = 0, it can be noted that the peaks almost collapsed into two curves above and below T = 600 K, suggesting that the dynamic mechanism of charge carriers for CLT is temperature dependent.
peaks decreased when temperature increased. This behavior indicates that the conduction process became less localized and translated to non-localized i.e. long-range motion. This proves that the oxygen ions or vacancies contribute to the dc conductivity at high temperatures. Fig. 12(a and b) shows the scaling behaviors of the electric module for the samples with x = 0 and x = 0.1, respectively. We can say that the peaks almost collapsed into one curve for CLT0.9Cr0.1, this shows that the dynamic process of both charge carriers for this composition is temperature independent. However, for sample with x = 0, it can be noted that the peaks almost collapsed into two curves above and below T = 600 K, suggesting that the dynamic mechanism of charge carriers for CLT is temperature dependent.
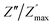 and
and 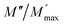 at different temperature for composition (a and b) x = 0.
at different temperature for composition (a and b) x = 0.
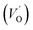 . These
. These 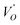 are linked to TiO5 clusters, called
are linked to TiO5 clusters, called 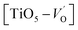 oxygen complex clusters.68 The paramagnetic center at g = 2.0452is due to O− free radical.69,70 The sharp signal at g = 2.0257 is probably attributed to an electron shared among the six octahedral oxygen orbits surrounding B-site, i.e., [TiO6]9− center.66 A similar result is observed by Boutinaud et al.71 Based on the researches realized by Kutty el al, the resonance signal associated to g = 1.9971 corresponds to the paramagnetic state due to chemistry defects (e.g. non-stoichiometric A-site).72,73 Kutty et al.73 assumed that EPR signal at g = 1.9971 is due to singly ionized A-site. The second strategy assumes that, when the ratio
oxygen complex clusters.68 The paramagnetic center at g = 2.0452is due to O− free radical.69,70 The sharp signal at g = 2.0257 is probably attributed to an electron shared among the six octahedral oxygen orbits surrounding B-site, i.e., [TiO6]9− center.66 A similar result is observed by Boutinaud et al.71 Based on the researches realized by Kutty el al, the resonance signal associated to g = 1.9971 corresponds to the paramagnetic state due to chemistry defects (e.g. non-stoichiometric A-site).72,73 Kutty et al.73 assumed that EPR signal at g = 1.9971 is due to singly ionized A-site. The second strategy assumes that, when the ratio 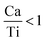 , excess Ti4+ ions occupy A-site. To satisfy the electro-neutrality, calcium vacancies should be formed in the vicinity of the Ti4+ ion at the Ca2+ site. In this case, a singlet EPR signal arises when the calcium vacancy releases one electron or the Ti4+ ion at the Ca2+ site captures one or two electrons. The paramagnetic center at g = 1.9761 is attributed to the presence of Ti3+ related defect centers (Ti3+–VO).73 These defect centers are commonly observed in BaTiO3 reducing conditions.64 In contrary, Sun et al., however, assign the signal at g = 1.976 to the presence of Ba (A-site) vacancies.74 Nevertheless, there are some important differences between the compositions in our study and those in Sun's work.74 Sun identified the defect associated with Nd-doped BaTiO3, whereas the composition in this study was lanthanum (La) doped calcium titanate (CaTiO3) on the A-site. The paramagnetic center resonance at g = 1.9464, based on the results of Eichel et al.64 which showed that >1.93, is associated with an
, excess Ti4+ ions occupy A-site. To satisfy the electro-neutrality, calcium vacancies should be formed in the vicinity of the Ti4+ ion at the Ca2+ site. In this case, a singlet EPR signal arises when the calcium vacancy releases one electron or the Ti4+ ion at the Ca2+ site captures one or two electrons. The paramagnetic center at g = 1.9761 is attributed to the presence of Ti3+ related defect centers (Ti3+–VO).73 These defect centers are commonly observed in BaTiO3 reducing conditions.64 In contrary, Sun et al., however, assign the signal at g = 1.976 to the presence of Ba (A-site) vacancies.74 Nevertheless, there are some important differences between the compositions in our study and those in Sun's work.74 Sun identified the defect associated with Nd-doped BaTiO3, whereas the composition in this study was lanthanum (La) doped calcium titanate (CaTiO3) on the A-site. The paramagnetic center resonance at g = 1.9464, based on the results of Eichel et al.64 which showed that >1.93, is associated with an 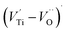 dipole defect. However, a study by Erdem et al. indicated that when g > 1.91, the paramagnetic center defect is associated with
dipole defect. However, a study by Erdem et al. indicated that when g > 1.91, the paramagnetic center defect is associated with 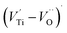 dipole defect.75 Taking into account this last result shown in ref. 45, the signal at g = 1.9288 is due to the
dipole defect.75 Taking into account this last result shown in ref. 45, the signal at g = 1.9288 is due to the 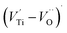 defects dipoles. Nonetheless, Scharschwerdt et al. demonstrated that the signal 1.920–1.9337 is due to Ti3+–V0.76 The last signal observed in CLT spectrum is at g = 1.8812. This paramagnetic signal is due to surface hole trapping sites.77 Fig. 13(b) shows the EPR spectrum of CLT0.9Cr0.1. The spectra can be described by the spin Hamiltonian.78
defects dipoles. Nonetheless, Scharschwerdt et al. demonstrated that the signal 1.920–1.9337 is due to Ti3+–V0.76 The last signal observed in CLT spectrum is at g = 1.8812. This paramagnetic signal is due to surface hole trapping sites.77 Fig. 13(b) shows the EPR spectrum of CLT0.9Cr0.1. The spectra can be described by the spin Hamiltonian.78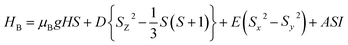
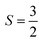 , I = 0 for Cr isotopes with even mass number, and
, I = 0 for Cr isotopes with even mass number, and 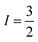 for 53Cr. It can be noted that a slight substitution of chromium for titanium in B-sites has considerable effects. Cr4+ has spin S = 1 and silent EPR.79 Moreover, all paramagnetic centers, observed in CLT disappeared, and a new resonance signal at g = 1.9795 arose. This paramagnetic center is attributed, according to La Mattina et al.80 to 3+ state of the 50Cr, 52Cr and 54Cr isotopes (I = 0), despite the absence of the signal due to the hyperfine quartet caused by the nuclear-spin coupling
for 53Cr. It can be noted that a slight substitution of chromium for titanium in B-sites has considerable effects. Cr4+ has spin S = 1 and silent EPR.79 Moreover, all paramagnetic centers, observed in CLT disappeared, and a new resonance signal at g = 1.9795 arose. This paramagnetic center is attributed, according to La Mattina et al.80 to 3+ state of the 50Cr, 52Cr and 54Cr isotopes (I = 0), despite the absence of the signal due to the hyperfine quartet caused by the nuclear-spin coupling 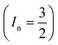 of the 53Cr isotope.80 In addition, Azamat et al. assumed that the single signal at g = 1.9788 is due to the Cr3+–VO centers.81 The slight change in the value of g in different systems is related to differences in the method of synthesis, chemical environment and heat treatment conditions.
of the 53Cr isotope.80 In addition, Azamat et al. assumed that the single signal at g = 1.9788 is due to the Cr3+–VO centers.81 The slight change in the value of g in different systems is related to differences in the method of synthesis, chemical environment and heat treatment conditions.