Open Access Article
Open Access ArticlePressure-induced hydrogen localization coupled to a semiconductor–insulator transition in a hydrogen-bonded molecular conductor†
Akira Ueda‡
 *a,
Kouki Kishimotoa,
Takayuki Isono§
a,
Shota Yamadaab,
Hiromichi Kamoa,
Kensuke Kobayashic,
Reiji Kumai
*a,
Kouki Kishimotoa,
Takayuki Isono§
a,
Shota Yamadaab,
Hiromichi Kamoa,
Kensuke Kobayashic,
Reiji Kumai c,
Youichi Murakamic,
Jun Gouchia,
Yoshiya Uwatokoa,
Yutaka Nishiob and
Hatsumi Mori
c,
Youichi Murakamic,
Jun Gouchia,
Yoshiya Uwatokoa,
Yutaka Nishiob and
Hatsumi Mori *a
*a
aThe Institute for Solid State Physics, The University of Tokyo, Kashiwa, Chiba 277-8581, Japan. E-mail: aueda@kumamoto-u.ac.jp; hmori@issp.u-tokyo.ac.jp
bDepartment of Physics, Toho University, Funabashi, Chiba 274-8510, Japan
cCondensed Matter Research Center (CMRC) and Photon Factory, Institute of Materials Structure Science, High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki 305-0801, Japan
First published on 11th June 2019
Abstract
Purely organic crystals, κ-X3(Cat-EDT-TTF)2 [X = H or D, Cat-EDT-TTF = catechol-fused tetrathiafulvalene], are a new type of molecular conductor with hydrogen dynamics. In this work, hydrostatic pressure effects on these materials were investigated in terms of the electrical resistivity and crystal structure. The results indicate that the pressure induces and promotes hydrogen (deuterium) localization in the hydrogen bond, in contrast to the case of the conventional hydrogen-bonded materials (where pressure prevents hydrogen localization), and consequently leads to a significant change in the electrical conducting properties (i.e., the occurrence of a semiconductor–insulator transition). Therefore, we have successfully found a new type of pressure-induced phase transition where the cooperation of the hydrogen dynamics and π-electron interactions plays a crucial role.
Introduction
Hydrostatic pressure is a powerful tool to modulate the structure, properties, and phase transitions of solid state materials. Its effect is more pronounced in molecular materials, because of the inherent softness of their crystal lattices. For example, in molecular conductors, such as BEDT-TTF salts [BEDT-TTF = bis(ethylenedithio)tetrathiafulvalene], the intermolecular π–π interactions (more precisely, the electron correlation U/W, where U and W are the on-site Coulomb repulsion and bandwidth, respectively) can be controlled by pressure, leading to a variety of electronic states, such as metals, superconductors, insulators, and recently quantum spin liquids.1 Also, in hydrogen-bonded (H-bonded) materials, pressure can modulate the dynamic properties of the hydrogens, which for example, results in a change in their order–disorder transition (or (anti)ferroelectric transition) temperatures Tc. In many cases, the Tc is decreased with increasing pressure (i.e., dTc/dP < 0),2 which is interpreted as the result of a decrease in the height of the double-well potential barrier by decreasing the H-bond distance.3Recently, we have successfully synthesized a new type of molecular conductor with hydrogen dynamics, κ-X3(Cat-EDT-TTF)2 [X = H or D, Cat-EDT-TTF = catechol-fused tetrathiafulvalene; hereafter abbreviated as H-TTF and D-TTF, respectively] (Fig. 1).4,5 In contrast to the conventional molecular conductors, H-TTF and D-TTF have no counter anion species, but instead, have anionic [O⋯X⋯O]−1 H-bonds [X = H: H-TTF, X = D: D-TTF] between two-dimensional (2D) conducting layers (Fig. 1a). H-TTF and D-TTF are isostructural at room temperature and the purple color in Fig. 1a represents their component molecular unit, in which two crystallographically equivalent Cat-EDT-TTF+0.5 molecules are connected by the symmetrical anionic [O⋯X⋯O]−1 H-bond (Fig. 1b). The Cat-EDT-TTF+0.5 molecules are strongly dimerized in the conducting layer, forming a dimer-Mott insulating state with a so-called κ-type molecular arrangement (Fig. 1b, right). However, due to the H/D isotope effect, the low-temperature (LT) structures and electronic properties of these analogues are greatly different from each other (Fig. 1c and d).4b,5,6 In D-TTF, the H-bonded deuterium is localized below 185 K (Fig. 1c, left), which desymmetrizes the H-bond and then induces electron transfer (charge disproportionation) between the two Cat-EDT-TTF+0.5 skeletons, to lead to a charge-ordered spin-singlet insulating state (Fig. 1c, right).4b On the other hand, in H-TTF, the “lighter” hydrogen is not localized even at 0.04 K (=quantum paraelectricity) (Fig. 1d, left),6a,c probably due to the effective single-well potential.7a This prevents H-TTF from undergoing a phase transition, resulting in keeping the uniformly-charged dimer-Mott state (=quantum spin liquid at very low temperatures) (Fig. 1d, right).6
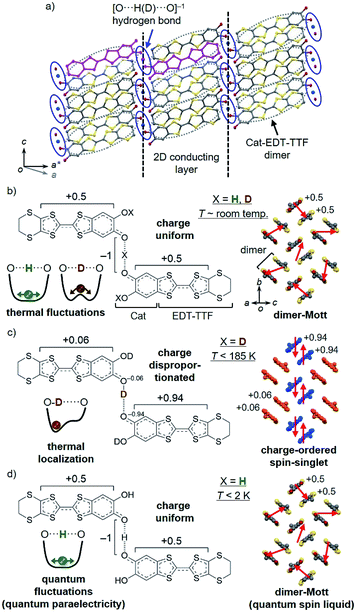 | ||
| Fig. 1 Structures of H-TTF and D-TTF. (a) Crystal structure at room temperature (purple color represents the H-bonded unit) and (b–d) chemical structures of the H-bonded molecular unit and schematic drawings of the H-bond potential curve7a and 2D conducting layer at room temperature ((b) X = H, D) and low temperatures ((c) X = D, (d) X = H). | ||
Here we report the hydrostatic pressure effects on the electrical transport properties and phase transition behavior of these new molecular conductors with hydrogen dynamics. Electrical resistivity measurements demonstrate that the pressure (1) increases the phase transition temperature (namely, the deuterium localization and charge disproportionation/ordering temperature) in D-TTF and (2) causes a semiconductor–insulator transition in H-TTF. Interestingly, X-ray diffraction measurements indicate that this pressure-induced insulating phase in H-TTF is a charge-ordered phase caused by hydrogen localization, similar to the LT charge-ordered phase in D-TTF. Therefore, we conclude that, in these systems, hydrostatic pressure induces and promotes hydrogen (or deuterium) localization in the H-bond, in contrast to the usual case.2,3 This unique phenomenon should result from that the hydrogen dynamics and π-electron interactions are strongly coupled and cooperatively modulated by pressure.
Results and discussion
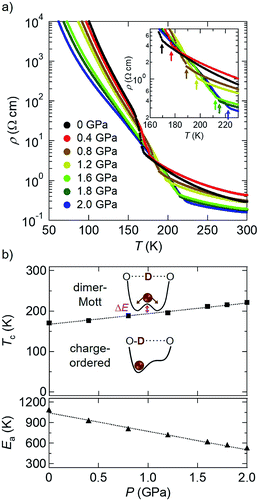
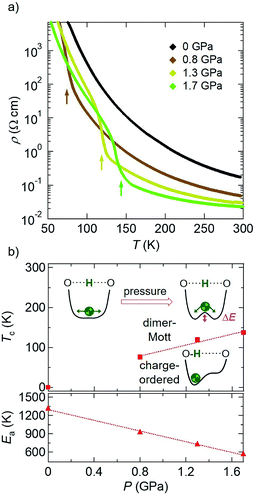
First, we show the results of electrical resistivity (ρ) measurements on a single crystal of D-TTF under hydrostatic pressure (Fig. 2; four-probe method, along the c axis).8 At ambient pressure (black circles in Fig. 2a), an abrupt increase in ρ attributable to the above-mentioned charge ordering transition (Fig. 1c) was observed at around 170 K.9 This transition temperature Tc was increased with increasing pressure (i.e., dTc/dP > 0), reaching 221 K at 2.0 GPa (blue circles in Fig. 2a). A plot of Tc versus P (Fig. 2b, top) reveals their linear relationship in this pressure region. Considering that this charge ordering is triggered by deuterium localization in the double-well potential,4b,7a this result means that its barrier height (ΔE; Fig. 2b, top) is increased with increasing pressure. Therefore, hydrostatic pressure promotes the deuterium localization or H-bond ordering in this compound,10 which is in marked contrast to the above-mentioned general trend.2,3 Also, the high-temperature (HT) phase (T > Tc) remains semiconducting even at 2.0 GPa; however, with increasing pressure the activation energy Ea11 is significantly decreased (dEa/dP < 0; Fig. 2b, bottom). This result suggests that, with increasing pressure, the intermolecular distances in the conducting layers (the bc-plane, Fig. 1) are decreased and consequently the intermolecular transfer integrals and bandwidth (W) are increased.12 In fact, such a pressure-induced decrease in Ea or enhancement in conductivity is frequently observed in molecular conductors.1,4aThen, similar electrical resistivity measurements under pressure were made on the hydrogen analogue, H-TTF (Fig. 3).8 As mentioned above, this material is a dimer-Mott insulator down to very low temperatures at ambient pressure (Fig. 1d),6 thus exhibiting a semiconducting temperature dependence as shown in black diamonds in Fig. 3a.4 However, when a hydrostatic pressure of 0.8 GPa was applied (brown diamonds in Fig. 3a), an abrupt increase in ρ appeared at around 76 K after the semiconducting behavior at higher temperatures. Importantly, the Tc to this pressure-induced insulating phase was increased with increasing pressure (red squares in the top panel of Fig. 3b), as is the case for the charge ordering transition of D-TTF (Fig. 2). Thus, this pressure-induced insulating phase in H-TTF is expected to be a charge-ordered insulating phase similar to that in D-TTF (this is in fact confirmed by the following X-ray diffraction analysis). Also, Ea in the HT semiconducting phase of H-TTF11 was found to show a linear decrease with increasing pressure (dEa/dP < 0; Fig. 3b, bottom), similar to that of D-TTF (Fig. 2b, bottom). From the linear fitting of the data (dashed lines in Fig. 2b and 3b), the dTc/dP and dEa/dP values of H-TTF (+69 K GPa−1 and −440 K GPa−1) are much larger in magnitude than those of D-TTF (+26 K GPa−1 and −270 K GPa−1).13 This suggests that H-TTF is more sensitive to pressure than D-TTF (the details are under investigation).
Therefore, in order to gain structural insight into this pressure-induced phase transition, we have performed synchrotron X-ray diffraction measurements on a H-TTF single crystal under hydrostatic pressure (see the Experimental section and Fig. S1 in the ESI†). The pressures used were 0.8 and 1.6 GPa, where the insulator transition was clearly observed (Fig. 3a). Fig. 4 shows the results obtained at 1.6 GPa (a similar kind of data obtained at 0.8 GPa is shown in Fig. S2 in the ESI†). At 160 K, diffraction spots attributable to the original semiconducting (dimer-Mott) phase were clearly observed, as shown in the far right panel of Fig. 4a.14,15 In addition to the original spots, additional weak diffraction spots were found beside them (e.g., the bottom spot in the far right panel of Fig. 4a). Such minor spots grew rapidly with decreasing temperature, and simultaneously, the original spots diminished and finally disappeared (Fig. 4a, right to left). It should be noted that these temperature-dependent changes in the diffraction peak intensity are well correlated with the temperature-dependent changes in ρ at 1.7 GPa (Fig. 4b). Namely, the rapid increase in the intensity of the diffraction peaks of the LT phase (blue symbols in Fig. 4b) occurs simultaneously with the rapid increase in ρ (black line in Fig. 4b). A similar result is observed in the measurements at 0.8 GPa (see Fig. S2 in the ESI†). Therefore, the pressure-induced semiconductor–insulator transition in H-TTF should be accompanied by a structural transition. Interestingly, analysis of the diffraction data reveals that the LT phase has a similar crystal structure to the charge-ordered phase of D-TTF (Table 1).15,16 This means that a similar charge ordering transition occurs in H-TTF under pressure, leading to the rapid increase in ρ. Importantly, considering the case of D-TTF (Fig. 1c), this charge ordering in H-TTF should also be triggered by localization of hydrogen in the H-bond. Namely, the hydrogen fluctuating in the H-bond at ambient pressure (Fig. 1d) should be localized near one of the oxygen atoms by applying pressure. Therefore, we now imagine that the original effective single-well potential is changed to a double-well potential by pressure, which induces the hydrogen localization at low temperatures, as schematically illustrated in Fig. 3b, and the following charge disproportionation/ordering. It should be noted that, although pressure-induced H-bond symmetrization is sometimes observed,2d,17 such asymmetrization or hydrogen localization is rarely observed.18
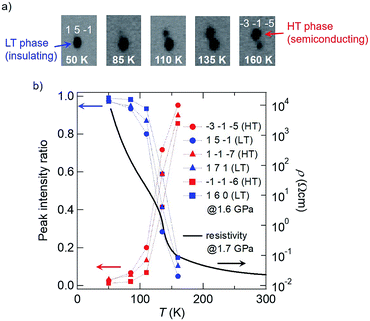 | ||
| Fig. 4 X-ray diffraction measurements on a H-TTF single crystal at 1.6 GPa. (a) Images of the diffraction spots of −3 −1 −5 in the HT phase and 1 5 −1 in the LT phase measured at several temperatures and (b) temperature dependence of the relative intensity ratios (left side) of three pairs of diffraction peaks in the HT (red symbols) and LT (blue symbols) phases. For comparison, the temperature dependence of electrical resistivity at 1.7 GPa is also shown in (b) (right side; identical to the data shown in Fig. 3a). | ||
| Compound | Crystal system | Space group | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | V (Å3) |
|---|---|---|---|---|---|---|---|---|---|
| a Fig. 4.b Fig. S2. | |||||||||
| H-TTF (1.6 GPa, 50 K)a | Triclinic | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
8.042(5) | 10.779(5) | 14.865(7) | 78.717(9) | 79.10(2) | 89.79(2) | 1240(1) |
| H-TTF (0.8 GPa, 5 K)b | Triclinic | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
8.220(7) | 10.983(8) | 14.982(11) | 78.788(12) | 78.46(3) | 89.575(18) | 1299(2) |
| D-TTF (1 atm, 50 K)4b | Triclinic | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
8.3968(7) | 11.0492(5) | 15.0735(5) | 78.892(5) | 77.53(1) | 89.288(6) | 1339.3(2) |
Thus, finally, let us discuss why this unique pressure effect appeared in the present system. Here, the H-bonds triggering the phase transition exist within the ac-plane (nearly along the c-axis), as shown in Fig. 1a and S5d.† By applying hydrostatic pressure, the c-axis length is significantly decreased (∼2% at 0.8 GPa, ∼4% at 1.6 GPa; Fig. S5c†), which would lead to compression of the H-bond (i.e., the O⋯O distance). In addition, the b-axis, vertical to the H-bond, is also significantly contracted (∼2% at 0.8 GPa, ∼4% at 1.6 GPa; Fig. S5b†), and furthermore, the a-axis is slightly contracted (∼0.05% at 0.8 GPa, ∼0.08% at 1.6 GPa; Fig. S5a†). Therefore, one can imagine that the H-bond is not simply contracted but deformed by applying the pressure, similar to the case reported by Endo et al.19 As a result, the original single-well energy potential curve in H-TTF (Fig. 1d)7a might be transformed into a double-well one, leading to the hydrogen localization at low temperatures (as schematically illustrated in the top panel of Fig. 3b) and the following charge disproportionation/ordering. In addition, there is the possibility that the increase in the intermolecular transfer integrals (Table S6 and Fig. S4 in the ESI†) might contribute to the occurrence of the phase transition in H-TTF and also to the increase in the Tc in H-TTF and D-TTF. This is because larger intermolecular π-electron interactions (especially the intradimer one) should be advantageous for the spin-singlet formation in the LT phase (Fig. 1c); thus possibly inducing and promoting the phase transition. In fact, we have previously observed that a D-TTF analogue with larger intermolecular transfer integrals has higher Tc (∼10 K) than the parent D-TTF, although their H-bond distances are similar.20 Therefore, we assume that hydrostatic pressure affects the π-electron interactions in the conducting layer and the hydrogen dynamics between the layers in cooperative manner in this kind of materials,21 which led to the above-mentioned peculiar pressure-induced phenomena and properties.
Conclusions
In conclusion, we have found that, in H-bonded molecular conductors H-TTF and D-TTF, hydrostatic pressure induces and promotes the localization of the hydrogen (or deuterium) in the H-bond in cooperation with a charge disproportionation/ordering of the π-electron system, leading to a semiconductor–insulator transition. Full structure determination of these materials under pressure will provide further insights into this peculiar hydrogen–π-electron cooperative phenomenon22 and thus is now underway. In addition, investigation of the transport properties and phase transition behavior at higher pressures is also of great interest.Experimental
Sample preparation
Single crystals of H-TTF and D-TTF were prepared according to the literatures.4a,bElectrical resistivity measurements
The temperature dependence of electrical resistivity of H-TTF and D-TTF single crystals under hydrostatic pressure was measured with a Physical Property Measurement System (PPMS, Quantum Design) by using the conventional four-probe ac method (annealed Au wires and carbon paste were used). The sample was placed in a Ni–Cr–Al piston-cylinder-type pressure cell together with lead (for pressure calibration) and Daphne 7373 (pressure medium). The applied pressure P was estimated based on the observed superconducting transition temperature of lead: dTc/dP = −0.365 K GPa−1.23X-ray diffraction measurements
X-ray diffraction measurements on a H-TTF single crystal under hydrostatic pressure were performed with a synchrotron radiation source (λ = 0.6889 Å) at the Photon Factory (PF) BL-8A in the High Energy Accelerator Research Organization (KEK), Japan. The sample was placed in a diamond anvil cell together with a NaCl single crystal (for pressure calibration at low temperatures24), a ruby chip (for pressure calibration at room temperature25), and Daphne 7373 (pressure medium). The temperature was controlled by a cryostat. The diffraction data were collected on an Imaging plate (IP) system (Rigaku), where four oscillation photographs (oscillation angle: 3°) were taken at each temperature and pressure. From these data, the space group and lattice parameters were determined (Tables 1, S1, and S2†). An overview of the experimental setup is shown in Fig. S1.†X-ray diffraction measurements on a H-TTF single crystal under ambient pressure were performed on a Rigaku MercuryII CCD X-ray diffractometer (MoKα, λ = 0.71073 Å) or with a synchrotron radiation source (λ = 0.6889 Å) at the Photon Factory (PF) BL-8A in the High Energy Accelerator Research Organization (KEK), Japan. The structures were solved by direct methods using the SIR2014 program.26 Refinements were carried out by a full-matrix least-squares method (SHELXL Version 2018/3).27 Anisotropic thermal parameters were applied to all non-hydrogen atoms. The hydrogen atoms of the benzene ring (at 270, 235, 200, and 175 K) were generated geometrically.
CCDC 1896674 (H-TTF, 150 K), 1896675 (H-TTF, 235 K), 1896676 (H-TTF, 175 K), 1896677 (H-TTF, 200 K), and 1896678 (H-TTF, 270 K) contain the supplementary crystallographic data for this paper.
Theoretical calculations
Intermolecular transfer integrals and electronic band structures were calculated by the extended Hückel method28 and the tight-binding approximation method,28 respectively. The atomic coordinates used were taken from X-ray data.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by JSPS Grants-in-Aid for Scientific Research (No. JP16K05744, JP24340074, JP16H04010, JP19K05397), MEXT Grants-in-Aid for Scientific Research on Innovative Areas “π-Figuration” (JP17H05143) and “Hydrogenomics” (JP18H05516), and the Canon Foundation. The synchrotron X-ray study was performed with the approval of the Photon Factory Program Advisory Committee (no. 2017S2-001). We thank Dr H. Sato (Rigaku Corporation) for analysis of X-ray diffraction data. We also acknowledge Prof. H. Yoshizawa (the Univ. of Tokyo) for assistance in using his Physical Property Measurement System (Quantum Design).Notes and references
- K. Kanoda, Hyperfine Interact., 1997, 104, 235 CrossRef CAS; K. Miyagawa, K. Kanoda and A. Kawamoto, Chem. Rev., 2004, 104, 5635 CrossRef PubMed; H. Mori, J. Phys. Soc. Jpn., 2006, 75, 051003 CrossRef; K. Kanoda, J. Phys. Soc. Jpn., 2006, 75, 051007 CrossRef.
- (a) G. A. Samara, Phys. Rev. Lett., 1971, 27, 103 CrossRef CAS; (b) G. A. Samara and D. Semmingsen, J. Chem. Phys., 1979, 71, 1401 CrossRef CAS; (c) G. A. Samara, Ferroelectrics, 1987, 71, 161 CrossRef CAS; (d) Y. Moritomo, Y. Tokura, H. Takahashi and N. Mōri, Phys. Rev. Lett., 1991, 67, 2041 CrossRef CAS PubMed; (e) S. Horiuchi, R. Kumai and Y. Tokura, Angew. Chem., Int. Ed., 2007, 46, 3497 CrossRef CAS PubMed.
- J. E. Tibballs, R. J. Nelmes and G. J. McIntyre, J. Phys. C: Solid State Phys., 1982, 15, 37 CrossRef CAS; A. Katrusiak and R. J. Nelmes, J. Phys. C: Solid State Phys., 1986, 19, L765 CrossRef; M. Ichikawa, J. Phys. Soc. Jpn., 1987, 56, 3748 CrossRef.
- (a) T. Isono, H. Kamo, A. Ueda, K. Takahashi, A. Nakao, R. Kumai, H. Nakao, K. Kobayashi, Y. Murakami and H. Mori, Nat. Commun., 2013, 4, 1344 CrossRef PubMed; (b) A. Ueda, S. Yamada, T. Isono, H. Kamo, A. Nakao, R. Kumai, H. Nakao, Y. Murakami, K. Yamamoto, Y. Nishio and H. Mori, J. Am. Chem. Soc., 2014, 136, 12184 CrossRef CAS PubMed.
- A. Ueda, Bull. Chem. Soc. Jpn., 2017, 90, 1181 CrossRef CAS.
- (a) T. Isono, H. Kamo, A. Ueda, K. Takahashi, M. Kimata, H. Tajima, S. Tsuchiya, T. Terashima, S. Uji and H. Mori, Phys. Rev. Lett., 2014, 112, 177201 CrossRef PubMed; (b) S. Yamashita, Y. Nakazawa, A. Ueda and H. Mori, Phys. Rev. B, 2017, 95, 184425 CrossRef; (c) M. Shimozawa, K. Hashimoto, A. Ueda, Y. Suzuki, K. Sugii, S. Yamada, Y. Imai, R. Kobayashi, K. Itoh, S. Iguchi, M. Naka, S. Ishihara, H. Mori, T. Sasaki and M. Yamashita, Nat. Commun., 2017, 8, 1821 CrossRef CAS PubMed.
- (a) K. Yamamoto, Y. Kanematsu, U. Nagashima, A. Ueda, H. Mori and M. Tachikawa, Phys. Chem. Chem. Phys., 2016, 18, 29673 RSC; (b) K. Yamamoto, Y. Kanematsu, U. Nagashima, A. Ueda, H. Mori and M. Tachikawa, Chem. Phys. Lett., 2017, 674, 168 CrossRef CAS.
- Single crystals of H-TTF and D-TTF were prepared according to ref. 4a and b..
- This Tc (170 K) is actually somewhat lower than the reported Tc (182 K; in the resistivity measurements under ambient pressure).4b This is probably due to the inclusion of a small amount of H-TTF (without transition) in this crystal. Namely, D/H exchange in the H-bond would partially occur by contacting the D-TTF crystal with air and/or a pressure medium (Daphne 7373) in the sampling process. However, the charge ordering transition is clearly observed and the degree of deuteration seems to be still high enough to evaluate the pressure effect..
- This type of “inverse” pressure effect on H-bond order-disorder transitions (dTc/dP > 0) is rarely observed. For example, see: Y. Moritomo and Y. Tokura, Jpn. J. Appl. Phys., 1993, 32, 309 CrossRef CAS . See also ref. 18..
- The activation energies Ea in the semiconducting phase (shown in the bottom panel of Fig. 2b and 3b) were calculated by the Arrhenius equation, ρ = ρ0
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ea/kBT), where ρ, kB, and T represent the electrical resistivity, Boltzmann constant, and temperature, respectively. Namely, the Ea is an indicator of the semiconducting energy gap Δ (=2Ea) between the valence and conduction bands and thus has no relationship with the barrier height (ΔE) of the double-well potential of the hydrogen bond schematically illustrated in the top panel of Fig. 2b and 3b..
exp(Ea/kBT), where ρ, kB, and T represent the electrical resistivity, Boltzmann constant, and temperature, respectively. Namely, the Ea is an indicator of the semiconducting energy gap Δ (=2Ea) between the valence and conduction bands and thus has no relationship with the barrier height (ΔE) of the double-well potential of the hydrogen bond schematically illustrated in the top panel of Fig. 2b and 3b.. - The occurrence of these crystal and electronic structure changes by pressure is supported by X-ray diffraction studies and theoretical calculations. For details, see Table S6, Fig. S4 and S5 in the ESI.†.
- The relationship of dTc/dP > 0 is an experimental evidence that the phase transition is promoted by pressure..
- Analysis of the diffraction data (the major spots) at 160 K and 135 K provided unit cell parameters similar to those of the original semiconducting (dimer-Mott) phase measured at ambient pressure.4a For details, see Tables S3–S5 in the ESI.†.
- Although the unit cell parameters under pressure were determined, the full structure determination was not successful, because the ranges of the scattering and rotation angles were limited as 2θ ∼ 45° and −15° < ω < 15° in our high-pressure measurements using a diamond anvil cell (DAC). See also the Experimental section and Fig. S1 in the ESI.†.
- The unit cell parameters of the LT phase at 110 and 85 K at 1.6 GPa were also determined. See Table S2 in the ESI.†.
- M. Benoit, D. Marx and M. Parrinello, Nature, 1998, 392, 258 CrossRef CAS; H. Bhatt, C. Murli, A. K. Mishra, A. K. Verma, N. Garg, M. N. Deo, R. Chitra and S. M. Sharma, J. Phys. Chem. B, 2016, 120, 851 CrossRef PubMed.
- J. Watanabe, M. Kasahara and T. Yagi, J. Korean Phys. Soc., 1998, 32, S559 Search PubMed; H. Furuta, S. Endo, M. Kobayashi, J. Watanabe, M. Kasahara and T. Yagi, Ferroelectrics, 2000, 242, 37 CrossRef CAS.
- S. Endo, T. Chino, S. Tsuboi and K. Koto, Nature, 1989, 340, 452 CrossRef CAS.
- A. Ueda, A. Hatakeyama, M. Enomoto, R. Kumai, Y. Murakami and H. Mori, Chem. –Eur. J., 2015, 21, 15020 CrossRef CAS PubMed.
- In the LT phase of D-TTF, the H-bonded deuteriums are ordered in an antiferroelectric manner,4b to cancel their electric dipoles.6c Thus, in addition to the spin-singlet formation, this antiferroelectric ordering (dipole–dipole interaction) might be promoted by pressure, as pointed out in ref. 10. The details are under investigation..
- By using chemical modification and electric field, we have observed other types of hydrogen–π-electron cooperative phenomena in this kind of compounds, see: J. Yoshida, A. Ueda, A. Nakao, R. Kumai, H. Nakao, Y. Murakami and H. Mori, Chem. Commun., 2014, 50, 15557 RSC; J. Yoshida, A. Ueda, R. Kumai, Y. Murakami and H. Mori, CrystEngComm, 2017, 19, 367 RSC; A. Ueda, K. Kishimoto, Y. Sunairi, J. Yoshida, H. Yamakawa, T. Miyamoto, T. Terashige, H. Okamoto and H. Mori, J. Phys. Soc. Jpn., 2019, 88, 034710 CrossRef CAS.
- A. Eiling and J. S. Schilling, J. Phys. F: Met. Phys., 1981, 11, 623 CrossRef CAS.
- J. M. Brown, J. Appl. Phys., 1999, 86, 5801 CrossRef CAS.
- H. K. Mao, P. M. Bell, J. W. Shaner and D. J. Steinberg, J. Appl. Phys., 1978, 49, 3276 CrossRef CAS.
- M. C. Burla, R. Caliandro, M. Camalli, B. Carrozzini, G. L. Cascarano, C. Cuocci, C. Giacovazzo, M. Mallamo, A. Mazzone and G. Polidori, J. Appl. Crystallogr., 2015, 48, 306 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- (a) T. Mori, A. Kobayashi, Y. Sasaki, H. Kobayashi, G. Saito and H. Inokuchi, Bull. Chem. Soc. Jpn., 1984, 57, 627 CrossRef CAS; (b) T. Mori, Energy band calculation software package, http://www.op.titech.ac.jp/lab/mori/lib/program.html Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details, theoretical calculations, and crystallographic data. CCDC 1896674–1896678. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9ra02833a |
| ‡ Present address: Department of Chemistry, Kumamoto University, Chuo-ku, Kumamoto 860-8555, Japan. |
| § Present address: Department of Physics, Gakushuin University, Toshima, Tokyo 171-8588, Japan. |
| This journal is © The Royal Society of Chemistry 2019 |