Open Access Article
Open Access ArticleHow pressure affects confine water inside different nanoslits†
Qingyin Zhang *a,
Xin Wanga,
Jipeng Lib,
Sumin Lua and
Diannan Lu
*a,
Xin Wanga,
Jipeng Lib,
Sumin Lua and
Diannan Lu *b
*b
aState Key Laboratory of Separation Membranes and Membranes Processes, School of Chemistry and Chemical Engineering, Tianjin Polytechnic University, Tianjin, 300387, China. E-mail: zhangqingyin@tjpu.edu.cn
bState Key Laboratory of Chemical Engineering, Department of Chemical Engineering, Tsinghua University, Beijing, 100084, China. E-mail: ludiannan@tsinghua.edu.cn
First published on 17th June 2019
Abstract
Nanoslits composed of different layered nanomaterials attract great attention in the theoretical and experimental investigations of nanofluidic devices due to their geometric simplicity and unique surface properties. Although many efforts have witnessed simulations of water molecules inside slit-like nanochannels formed by graphenes, the thermodynamic properties and transport behavior of water inside nanoslits formed by different two-dimensional materials are seldom investigated. In this paper, we choose nanoslits formed by graphene, boron nitride (hBN), and molybdenum disulfide (MoS2) as models, and study the water properties inside these nanoslits using traditional molecular dynamics simulations at different pressures. It is shown that water molecules can form a planar square at high pressure (10 kbar) in all three types of nanoslit. The nanoslits affect diffusion coefficient, orientation of water molecules, number of hydrogen bonds and life-time of hydrogen bonding significantly. The self-diffusion coefficients of water molecules in different nanoslits are all lower than that of bulk water. The diffusion coefficients are significantly affected by the special ordered structure of water, which is caused by the unique surface structure of the nanoslit. The results of the present work will be helpful to understand the unique behavior of confined water in nanoslits composed of different nanomaterials and provide theoretical guidance for many applications, such as desalination and nano-energy conversion.
Introduction
Recent years have witnessed rapid developments in two-dimensional (2D) materials and their applications in biochemical analysis,1 desalination2 and energy conversion.3 Thanks to a steady improvement in nano-manufacturing capacity, it is now possible to fabricate sophisticated nano-devices with precise control of the surface properties of nanoslits formed by 2D materials.4 The spacing between two layers of nanoslits is less than 100 nm, while the length and width are much larger than their spacing.5 Thus, the understanding of water structure inside these nanoslits formed by 2D materials and their influence on diffusion behavior are of fundamental importance in the field of nanofluidics.Different from the water in bulk, the structure and transfer behavior of water molecules in nanoslits have some unique properties. In nanoslit with 0.7 nm in depth, water molecules present a mono-layer distribution.6 The layered structure formed by confined water disappears when the depth of spacing is higher than 10 nm. Algara-Siller's group7 and Nair's group have found that water molecules can form ‘square ice’ structure in a nanoslit formed by graphene. Joshi's group8,9 and Huang's group10–13 have demonstrated that self-diffusion coefficients of confined water in a nanoslit are less than that in bulk. The unique properties of confined water in a nanoslit is attributed to size and surface properties of the nanoslit. That is, the interaction between the water molecule and the nanoslit with higher specific area hinders the diffusion of confined water, as well as affects the phase diagram of water.14 Molecular simulations are an effective method to study properties of confined waters.15 Previous efforts mainly focus on water phase diagram and diffusion behavior in the nanoslit formed by graphene.8,9,15–17 It is shown that both properties of surface and the width of slit significantly affect the orientation and self-diffusion dynamics properties of confined water molecules.
However, how the pressure and the surface property of nanoslits affect the structure and dynamic properties of confined water in different nanoslits are seldom investigated. In this paper, the self-diffusion behaviors of water molecules in different nanoslits were studied using traditional molecular dynamics simulations. The influence of pressure on the structure and dynamics of confined water molecules were systematically studied.
Models and methods
Models
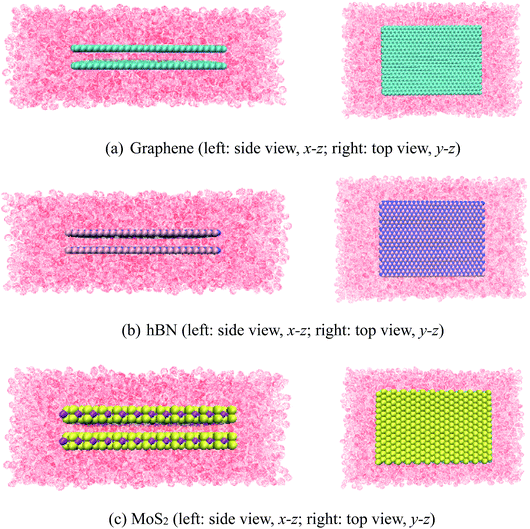
In this work, three types of nanoslits, which were composed of graphene, boron nitride (hBN), and molybdenum disulfide (MoS2), were chosen as models (Fig. 1). Graphene and hBN model were generated using VMD18 and MoS2 model was from ref. 19. The spacing distance between two plates was fixed as 0.7 nm. The length of the nanoslits were about 6 nm. The nanoslit was located in the center of simulation box. Water molecules were filled into the simulation box with the density of about 1.0 g mL−1. Solvation process also can be done using VMD.A simple point charge-extended (SPC/E) model was used for water molecules, due to its excellent description for bulky water at room temperature. Table 1 gives the number of atoms and geometric parameters of different nanoslits.
| Nanoslit | Plate size (y–z), y nm × z nm | Number of atoms | Simulation box size (at 1 bar), x nm × y nm × z nm |
|---|---|---|---|
| Graphene | 4.1 × 6.0 | C: 2000 | 4.2 × 7.3 × 11.4 |
| hBN | 4.2 × 5.9 | B: 960; N: 960 | 4.2 × 7.3 × 11.3 |
| MoS2 | 4.0 × 6.4 | Mo: 624; S: 1248 | 4.7 × 7.1 × 10.9 |
Simulation methods
MD simulations were performed using the NAMD 2.9 simulation package,20 VMD was used to visualize the system.Each simulation box contained one nanoslit as shown in Fig. 1. The 12-6 Lennard-Jones parameters and charges for the carbon, nitrogen, boron, molybdenum and sulfur atoms were listed in Table 2. All other parameters were adopted from CHARMM27 force-field. Particle mesh Ewald (PME) calculation21 was used for the treatment of the electrostatic interaction. The cutoffs for LJ and electrostatic interactions were both 1.2 nm. 20 ns NVT simulations were conducted to equilibrium systems, and additional 30 ns NPT simulations were conducted to collect data for analysis. The integration time was 1 fs and data were collected for every 0.5 ps. For NVT simulation, Langevin thermostat was incorporated to ensure a constant temperature (300 K). For NPT simulation, Langevin thermostat and Langevin pressure control were adopted to keep temperature and pressure constant, respectively.
Analytical method
The density distribution of water molecules in nanoslit was calculated according to eqn (1).
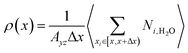 | (1) |
The 2-dimensional diffusion coefficients (Dyz) of water molecules in nanoslits were calculated through the mean square displacements (MSDyz(t)) according to eqn (2) and (3).
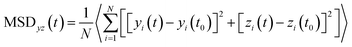 | (2) |
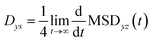 | (3) |
Hydrogen bonds were determined with cut-offs for the acceptor–donor-hydrogen angle, which is less than 30°, and the donor–acceptor distance, which is less than 0.35 nm.23,24
The stability of hydrogen bonds among confined water molecules was calculated through the intermittent time correlation function CHB(t).
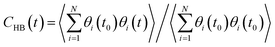 | (4) |
Results and discussion
Structural properties of confined water molecules
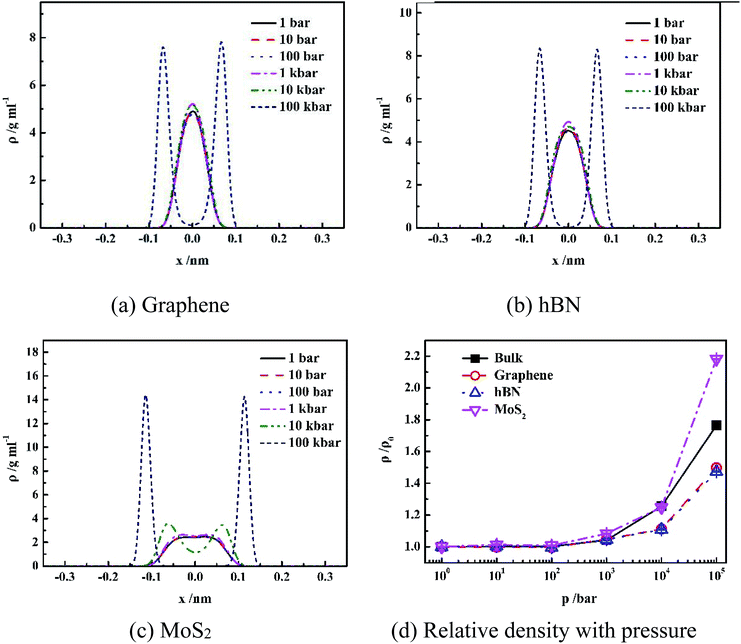
It is shown in Fig. 2(a–c) that all density distributions of the confined water in the nanoslits exhibit symmetry with respect to the center of the nanoslits. At low pressure (1 bar to 10 kbar for graphene and hBN, 1 bar to 1 kbar for MoS2), water molecules form single layer with maximum density in the center of nanoslits, which is consistent with the simulation results of the confined water in the graphene and hBN nanoslits in previous work.17,25 However, at extremely high pressure, such as 100 kbar for graphene and hBN or 10 and 100 kbar for MoS2, double-layer water forms, indicating more complex water network at high pressure. Under high system pressure, the distribution of water molecules becomes narrower with high peak value, indicating that the more uniform structure of water forms sequentially.26,27
Fig. 2(d) gives the change of relative density of water inside different nanoslits with pressure. It shown that densities of both confined water and bulk water are not sensitive to pressure until pressure is higher than 1 kbar. At extremely high pressure (100 kbar), the relative water density inside nanoslit composed of MoS2 is higher than those in bulk and other nanoslits. This is due to the unique surface properties of MoS2, which will be further discussed later.
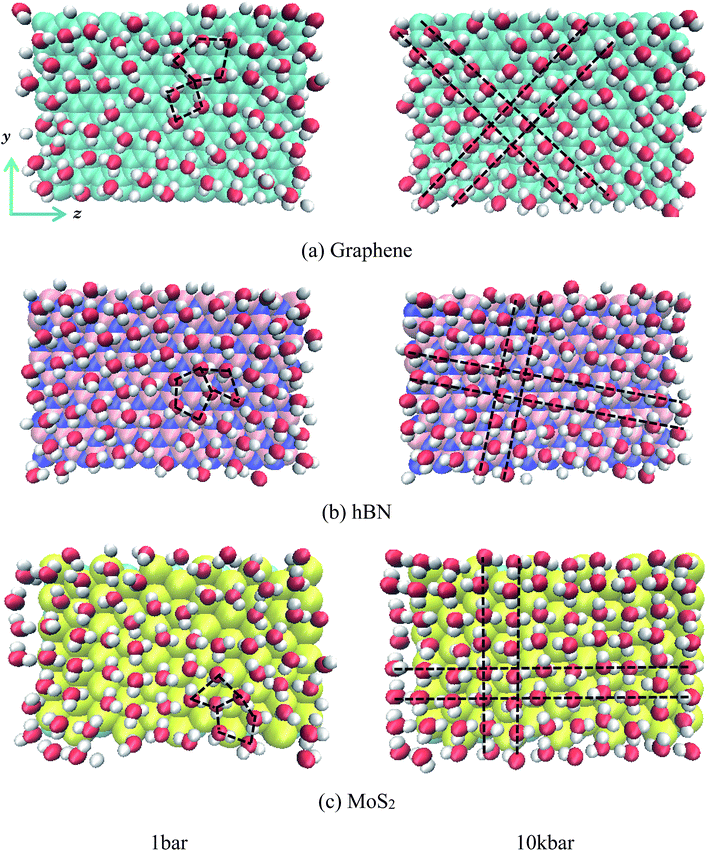
Fig. 3 gives the snapshots of water molecules inside different nanoslits at 1 bar and 100 kbar respectively.
It is shown in Fig. 3 that at low pressure (1 bar) both five-ring and four-ring water networks can be found in all nanoslits (highlighted in black dash line). At high pressure, however, only four-ring water networks exist in all nanoslits (highlighted in black dash line). It is very interesting that, although the surface properties of graphene, hBN and MoS2 are different, the four-ring water networks are well maintained inside nanoslits, indicating the structure of water layer inside nanoslit is mainly affected by the geometry of nanoslit but not by the properties of it.
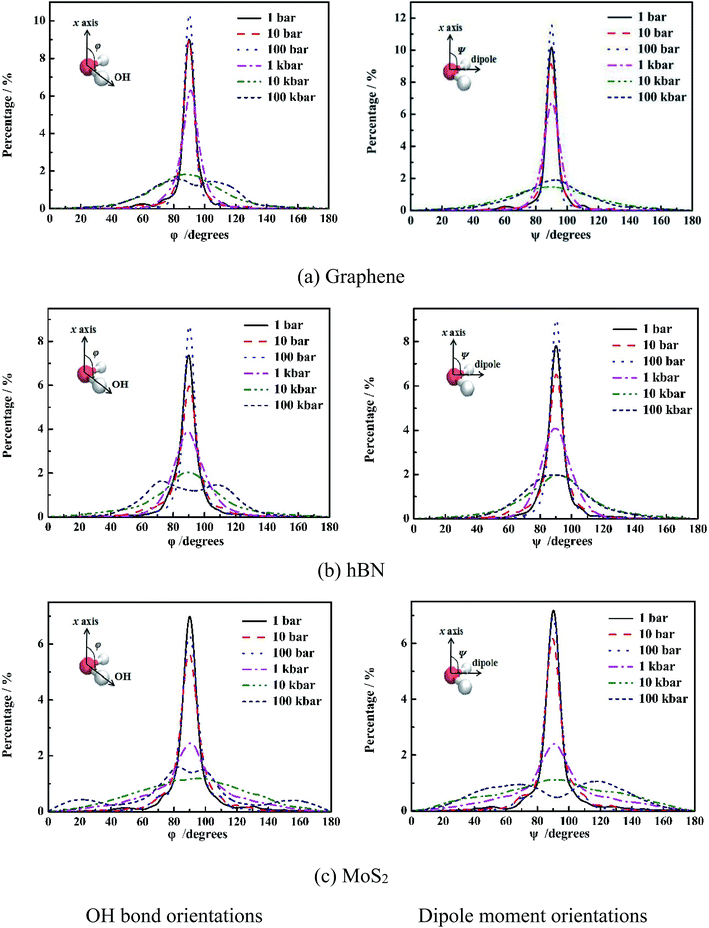
It is shown in Fig. 4 that at low pressure (1 bar to 1 kbar), both φ and ψ have one maximum population at 90°, indicating orientations of OH bond and dipole of molecules are parallel to the wall of nanoslit. This results in the formation of five-ring and four-ring water network as shown in Fig. 3. Due to only one layer of water molecules, only intra-layer hydrogen bonds among water molecules form, which is consistent with previous work.6,28,29 It is also shown that the increase of pressure results in the increase of peak width. For graphene and hBN, when the pressure is higher than 100 kbar, there are two maximum for φ, which are 70° and 110°, respectively, indicating the formation two layers of water molecules inside nanoslits as shown in Fig. 2(a) and (b). However, the maximum of ψ maintains at 90°, although the extension of peak width as shown in Fig. 3(a) and (b). For MoS2, the changes of φ and ψ is rather complex. At high pressure (100 kbar), both φ and ψ are widely distributed, indicating the orientation of water molecules becomes random and more complex structures formed inside MoS2 nanoslit.
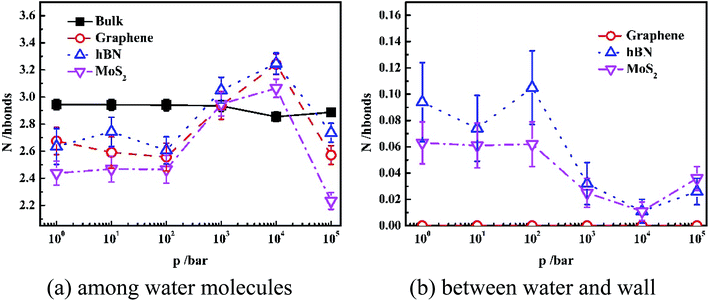
In order to interpret the orientation of water molecules inside different nanoslits, we analyzed the number of hydrogen bonding (N) among water molecules and that between water and nanoslit wall, as shown in Fig. 5.
Fig. 5(a) shows the average hydrogen bond number of both confined water and bulk water formed among the water molecules. It is shown in Fig. 5(a) that the hydrogen bond number of bulk water maintains 3.0 even when pressure is 10 kbar. The further increase of pressure results in the increase of hydrogen bond number. For water confined in nanoslit, however, the effect of pressure on hydrogen bond number is rather complicated. When pressure is lower than 100 bar, although the hydrogen number of water confined inside graphene and MoS2 is lower than that inside hBN, the pressure has little effect on hydrogen bond number, which is similar to that of bulk water. When pressure is higher than 100 bar, the hydrogen bond formed between water molecules inside all nanoslits increases significantly with pressure and reaches maximum when pressure is 10 kbar. Further increase of pressure results in the sharp decrease of hydrogen bond number. In previous work, it is shown that the strengthen of hydrogen bond network leads to the decrease of self-diffusion of water molecules.30,31 Therefore, we can predict that the diffusion behavior of water inside nanoslits is more sensitive to pressure than that in bulk.
Fig. 5(b) shows the average hydrogen bond number of confined waters formed between water and wall of nanoslits at different pressures. Due to the lack of donor and acceptor of graphene, there is no hydrogen bond formed between water and graphene. The N atom of hBN and S atom of MoS2 can provide electrons as the donor, which result in the formation of hydrogen bond at low pressure. Similar to Fig. 5(a), when pressure is lower than 100 bar, there is little effect on hydrogen bond number. The numbers of hydrogen bonds formed between water and nanoslits decrease and reach minimum at 10 kbar. Further increase of pressure results in the increase of hydrogen bond number.
It is interesting that although both hBN and MoS2 can form hydrogen bond with water molecules inside nanoslits, the average number of hydrogen bond formed among water molecules inside hBN is higher than that inside MoS2. This is caused by the more uniform structure formed inside hBN at low pressure.
Transport properties of confined water molecules in different nanoslits
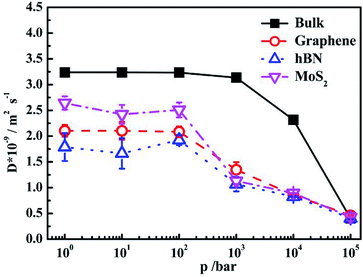
It is shown that for bulk water, the self-diffusion coefficient at 1 bar is 3.237 × 10−9/m2 s−1, which is consistent with previous work.32 The self-diffusion coefficient maintains constant when pressure increases from 1 bar to 1 kbar. Further increase of pressure leads to the decrease of self-diffusion coefficients signifyingly. The diffusion coefficients of confined water inside different nanoslits are lower than that in bulk. It is interesting that although the interaction between water and MoS2 is higher than graphene, the diffusion coefficient of water inside MoS2 nanoslit is higher than those in both graphene and hBN nanoslits. This is caused by the smaller number of hydrogen bonds formed between confined water molecules as shown in Fig. 5(a), and the less orderly orientation distribution of confined water molecule in Fig. 3.
The self-diffusion coefficients of confined water in nanoslits become decrease when the pressure is higher than 100 bar, which is significantly lower than that in bulk water (1 kbar). This indicates that the self-diffusion coefficient of confined water is more sensitive to pressure, which is relevant to the water structure in confined environment (Fig. 5(a)).
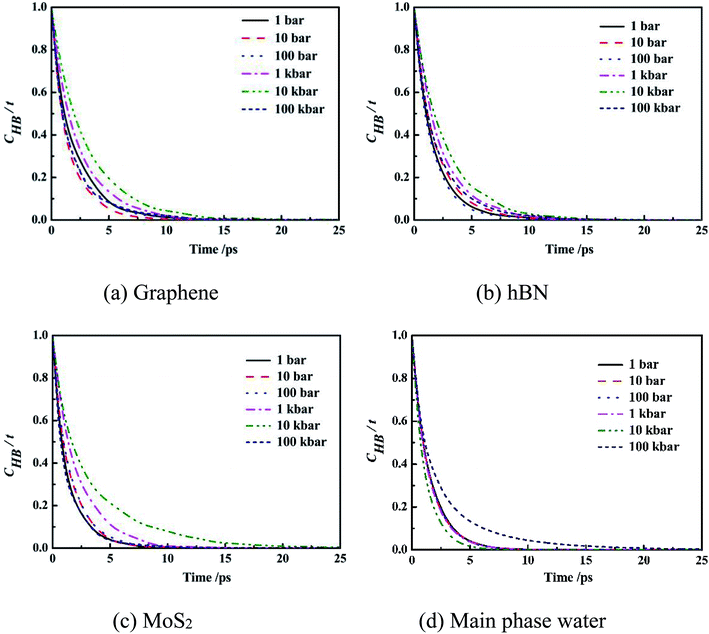 | ||
| Fig. 7 Intermittent time correlation function CHB(t) of main phase water molecules and confined water molecules in slit nanochannels. | ||
It can be seen from the figure that the CHB(t) curves of confined water molecules inside slit nanochannels decay slower than the main phase water molecules CHB(t). Three kinds of confined water molecules CHB(t) all slowed down with the increase of system pressure, mainly because under high system pressure, the fourth ring structure formed between the water molecules inside the slit nanochannels made the hydrogen bond very stable, which was also consistent with the result that the self-diffusion coefficient of the confined water molecules was small at this time. This indicates that the CHB(t) decay depends largely on the system pressure. The CHB(t) decay slower, more stable the hydrogen bonds, and disadvantage the movement of water molecules inside slit nanochannels. The system pressure has little effect on the stability and life time of main phase water hydrogen bond.
Conclusions
In this work, the confined water properties inside different nanoslits were studied by using molecular dynamics simulations. It is shown that water molecules can form a planar square at high pressure (10 kbar) in all three kinds of nanoslit. The nanoslits affect diffusion coefficient, orientation of water molecules, number of hydrogen bonding and life time of hydrogen bonding significantly. The diffusion coefficients of water molecules in different nanoslits are all lower than that of bulky water. The diffusion coefficients are significantly affected by special ordered structure of water, which is caused by unique surface structure of nanoslit. The results of present work will help us further understand the relationship between the diversity of structure properties and dynamic behavior of the water molecules in the different nanoslits. In addition, this work will also help to design and fabricate different two-dimensional nanoslits for many practical applications, such as desalination and nano-energy conversion.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Key Research and Development Program of China (2016YFD0400203) and the National Natural Science Foundation of China under Grant No. 21476172 and No. U1862204. The numerical calculations were performed at the “Exploration 100” platform supported by Tsinghua National Laboratory for Information Science and Technology.References
- W. Guan, R. Fan and M. A. Reed, Nat. Commun., 2011, 2, 506 CrossRef PubMed.
- J. Tarun, R. J. S. Guerrero, C. A. Aguilar and K. Rohit, Anal. Chem., 2013, 85, 3871–3878 CrossRef PubMed.
- C. Davidson and X. Xuan, J. Power Sources, 2008, 179, 297–300 CrossRef CAS.
- X. Peng, C. Wan, J. Gu, Z. Liu, Y. Men, Y. Huang, J. Zhang, L. Zhu and C. Tao, Adv. Funct. Mater., 2015, 25, 2428–2435 CrossRef.
- J. C. T. Eijkel and A. V. D. Berg, Microfluid. Nanofluid., 2005, 1, 249–267 CrossRef CAS.
- P. Hirunsit and P. B. Balbuena, J. Phys. Chem. C, 2007, 111, 1709–1715 CrossRef CAS.
- G. Algara-Siller, O. Lehtinen, F. C. Wang, R. R. Nair, U. Kaiser, H. A. Wu, A. K. Geim and I. V. Grigorieva, Nature, 2015, 519, 443 CrossRef CAS PubMed.
- R. K. Joshi, P. Carbone, F. C. Wang, V. G. Kravets, Y. Su, I. V. Grigorieva, H. A. Wu, A. K. Geim and R. R. Nair, Science, 2014, 343, 752–754 CrossRef CAS PubMed.
- R. R. Nair, H. A. Wu, P. N. Jayaram, I. V. Grigorieva and A. K. Geim, Science, 2012, 335, 442–444 CrossRef CAS PubMed.
- H. W. Dai, Z. J. Xu and X. N. Yang, J. Phys. Chem. C, 2016, 120, 22585–22596 CrossRef CAS.
- H. B. Huang, Z. G. Song, N. Wei, L. Shi, Y. Y. Mao, Y. L. Ying, L. W. Sun, Z. P. Xu and X. S. Peng, Nat. Commun., 2013, 4, 2979 CrossRef PubMed.
- X. P. Yang, X. N. Yang and S. Y. Liu, Chin. J. Chem. Eng., 2015, 23, 1587–1592 CrossRef CAS.
- X. Yang, H. Dai and Z. Xu, J. Phys. Chem. C, 2016, 120, 22585–22596 CrossRef.
- G. Karniadakis, A. Beşkök and N. R. Aluru, Microflows and nanoflows : fundamentals and simulation, Springer, New York, NY, 2005 Search PubMed.
- X. Liang, H. Yuan-Zhong, M. Tian-Bao and W. Hui, Nanotechnology, 2013, 24, 505504 CrossRef PubMed.
- Q. Yu, X. Xiang and L. Hui, Appl. Phys. Lett., 2013, 103, 249–267 Search PubMed.
- A. Kommu and J. K. Singh, J. Phys. Chem. C, 2017, 121, 7867–7880 CrossRef.
- J. Hsin, A. Arkhipov, Y. Ying, J. E. Stone and K. Schulten, Curr. Protoc. Bioinf., 2008 DOI:10.1002/0471250953.bi0507s24.
- J. Feng, M. Graf, K. Liu, D. Ovchinnikov, D. Dumcenco, M. Heiranian, V. Nandigana, N. R. Aluru, A. Kis and A. Radenovic, Nature, 2016, 536, 197–200 CrossRef CAS PubMed.
- L. Kalé, R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan and K. Schulten, J. Comput. Phys., 1999, 151, 283–312 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- M. Darvishi and M. Foroutan, J. Mol. Liq., 2017, 225, 1–10 CrossRef CAS.
- A. Luzar and D. Chandler, Nature, 1996, 379, 55–57 CrossRef CAS.
- R. Kumar, J. R. Schmidt and J. L. Skinner, J. Chem. Phys., 2007, 126, 204107 CrossRef CAS PubMed.
- X. Yang, X. Yang and S. Liu, Chin. J. Chem. Eng., 2015, 23, 1587–1592 CrossRef CAS.
- L. B. D. Silva, J. Nanostruct. Chem., 2014, 4, 104 CrossRef.
- Y. Nakamura and T. Ohno, Mater. Chem. Phys., 2012, 132, 682–687 CrossRef CAS.
- X. Yang, X. Yang and S. Liu, Chin. J. Chem. Eng., 2015, 23, 1587–1592 CrossRef CAS.
- A. Pertsin and M. Grunze, J. Phys. Chem. B, 2004, 108, 1357–1364 CrossRef CAS.
- H. Mosaddeghi, S. Alavi, M. H. Kowsari and B. Najafi, J. Chem. Phys., 2012, 137, 184703 CrossRef PubMed.
- A. Striolo, Nano Lett., 2006, 6, 633–639 CrossRef CAS PubMed.
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra02870f |
| This journal is © The Royal Society of Chemistry 2019 |