Open Access Article
Open Access ArticleCrystal structure, hydrogen bonding, mechanical properties and Raman spectrum of the lead uranyl silicate monohydrate mineral kasolite†
Francisco Colmenero *a,
Jakub Plášil
*a,
Jakub Plášil b,
Joaquín Cobos
b,
Joaquín Cobos c,
Jiří Sejkora
c,
Jiří Sejkora d,
Vicente Timón
d,
Vicente Timón a,
Jiří Čejka
a,
Jiří Čejka d and
Laura J. Bonales
d and
Laura J. Bonales c
c
aInstituto de Estructura de la Materia (IEM-CSIC), C/ Serrano, 113, 28006 Madrid, Spain. E-mail: francisco.colmenero@iem.cfmac.csic.es
bInstitute of Physics ASCR, v.v.i., Na Slovance 2, 182 21, Praha 8, Czech Republic
cCentro de Investigaciones Energéticas, Medioambientales y Tecnológicas (CIEMAT), Avda/Complutense, 40, 28040 – Madrid, Spain
dMineralogicko-Petrologické Oddělení, Národní Muzeum, Cirkusová 1740, 193 00 Praha 9, Czech Republic
First published on 16th May 2019
Abstract
The crystal structure, hydrogen bonding, mechanical properties and Raman spectrum of the lead uranyl silicate monohydrate mineral kasolite, Pb(UO2)(SiO4)·H2O, are investigated by means of first-principles solid-state methods based on density functional theory using plane waves and pseudopotentials. The computed unit cell parameters, bond lengths and angles and X-ray powder pattern of kasolite are found to be in very good agreement with their experimental counterparts. The calculated hydrogen atom positions and associated hydrogen bond structure in the unit cell of kasolite confirmed the hydrogen bond scheme previously determined from X-ray diffraction data. The kasolite crystal structure is formed from uranyl silicate layers having the uranophane sheet anion-topology. The lead ions and water molecules are located in the interlayer space. Water molecules belong to the coordination structure of lead interlayer ions and reinforce the structure by hydrogen bonding between the uranyl silicate sheets. The hydrogen bonding in kasolite is strong and dual, that is, the water molecules are distributed in pairs, held together by two symmetrically related hydrogen bonds, one being directed from the first water molecule to the second one and the other from the second water molecule to the first one. As a result of the full structure determination of kasolite, the determination of its mechanical properties and Raman spectrum becomes possible using theoretical methods. The mechanical properties and mechanical stability of the structure of kasolite are studied using the finite deformation technique. The bulk modulus and its pressure derivatives, the Young and shear moduli, the Poisson ratio and the ductility, hardness and anisotropy indices are reported. Kasolite is a hard and brittle mineral possessing a large bulk modulus of the order of B ∼ 71 GPa. The structure is mechanically stable and very isotropic. The large mechanical isotropy of the structure is unexpected since layered structures are commonly very anisotropic and results from the strong dual hydrogen bonding among the uranyl silicate sheets. The experimental Raman spectrum of kasolite is recorded from a natural mineral sample from the Jánská vein, Příbram base metal ore district, Czech Republic, and determined by using density functional perturbation theory. The agreement is excellent and, therefore, the theoretical calculations are employed to assign the experimental spectrum. Besides, the theoretical results are used to guide the resolution into single components of the bands from the experimental spectrum. A large number of kasolite Raman bands are reassigned. Three bands of the experimental spectrum located at the wavenumbers 1015, 977 and 813 cm−1, are identified as combination bands.
1 Introduction
Kasolite, Pb(UO2)(SiO4)·H2O, is an important hydrated uranyl silicate mineral phase which was found for the first time by Schoep in 1921.1 Its name, was coined by Schoep, emphasizing the locality in which it was found for the first time: the Kasolo mine (Katanga, Democratic Republic of the Congo).1 Uranyl silicates are the most abundant uranyl minerals in the Earth's surface and form predominantly in uranium rich aqueous solutions containing the ubiquitous silicate ion.2,3 They have been invariably found as a result of the oxidation and dissolution/precipitation processes occurring in uraninite-bearing ore deposits.4–8 Kasolite has also been documented to be a fundamental component of the paragenetic sequence of secondary phases that arises from the corrosion of spent nuclear fuel (SNF) under the final geological disposal conditions.9–13 Kasolite, the only known uranyl silicate containing lead, together with the lead uranyl oxides, such as vandendriesscheite or curite,14,15 is among the most relevant lead uranyl containing phases. The study of uranyl silicate phases is extremely important because the knowledge of their long-term stability under various environmental conditions is required to understand the complex assemblages of uranyl minerals found at uranium deposits.2,3 While the crystal structure of kasolite has long been investigated,16–21 its full structure determination, including the positions of the hydrogen atoms has been reported only recently.22One of the most important sources of lead in uranium containing minerals is via uranium radioactive decay.2,3 During this decay, uranium disintegrates through a series of daughter products finally to radiogenic lead. The content of radiogenic lead is quite variable but can reach large values in ancient uraninite.23,24 Lead may replace uranium to some extent and occupy interstitial sites within the uraninite structure.25 The accumulation of lead in uraninite induces significant strain in the structure of uraninite and it is eventually released from it. Since lead is relatively immobile in most groundwaters, may form oxides or sulfurs (as galena), but also, under oxidant conditions, may precipitate in the form of uranyl containing minerals. Accumulation of radiogenic lead may also occur in the crystal structure of uranyl containing minerals leading to the destabilization of the structure and yielding the reprecipitation of lead containing secondary phases as kasolite and curite.26,27 Kasolite may also have a non-radiogenic origin, for example from uraninite in contact with other lead containing minerals as galena under oxidant conditions.2
The knowledge of the structures of uranyl containing minerals has increased significantly in the last decades2,3 due to the generation of better analytical techniques, the most important one being the introduction of charge-coupled device (CCD) detectors for X-ray diffraction.28 These CCD detectors allow for accurate structure determinations of both small unit cell crystalline materials and of minerals with large unit cells, both types of structures being varieties frequent within the uranyl mineral groups. However, for uranyl containing materials, the resolution of the positions of the hydrogen atoms from X-ray diffraction data by structure refinement is usually not possible. Five important examples for which a full structure determination has been possible in recent times are those of the schoepite,29 metaschoepite,30 becquerelite31 and curite15 mineral phases and uranyl squarate monohydrate synthetic material (USM).32 For schoepite, metaschoepite, becquerelite and USM, the hydrogen atom positions were successfully determined using theoretical methods. These studies are extended here since the full crystal structure of kasolite is determined in this paper using the theoretical solid-state methodology. This study confirms the full crystal structure determination, including the hydrogen atom positions, performed recently by Fejfarová et al.22 While these positions may also be obtained by using other less involved methods, as the TORQUE method,33 which has been used recently to determine the hydrogen bond structure of curite mineral,15 the theoretical methodology offers a more rigorous solution, since the results can be assured to be a global minimum of hypersurface of the total energy of the material in terms of the associated lattice parameters and atomic positions. Furthermore, in turn, the availability of the energy optimized full crystal structure, including the hydrogen atom positions, permits the realization of additional theoretical studies. As an example, the mechanical and Raman spectroscopic properties of kasolite are evaluated in this paper. The calculations have been carried out using first-principles theoretical solid-state methods based on density functional theory (DFT) using large plane wave basis sets and pseudopotentials for the description of internal atomic electrons.34 At the basis of this work and a series of previous theoretical works concerning uranyl containing minerals,29–31,33,35–47 is the seminal generation of an accurate relativistic norm conserving pseudopotential specific for uranium atom.35,36
This paper is organized as follows. In Section 2, the experimental and first-principles theoretical solid state methodology used in this work is described. The main results of the present paper are contained in Section 3. Section 3.1, reports the calculated crystal structure of kasolite. The hydrogen bonding structure in kasolite is discussed in Section 3.2. The computed X-ray powder pattern is reported in Section 3.3. The mechanical properties and mechanical stability of kasolite are studied in Section 3.4. The computed Raman spectrum and the assignment of the bands in this spectrum are provided in Section 3.5. In this same section the theoretical spectrum is compared with the experimental one recorded from a natural mineral sample. Finally, Section 4 presents the main conclusions of this paper.
2 Materials and methods
2.1 Experimental
The natural mineral sample studied in this work is from the Jánská vein, Příbram base metal ore district, Czech Republic.48,49 Kasolite sample is an aggregate of lath-like to acicular crystals. This mineral sample was analyzed using Raman spectroscopy. The Raman spectrum was recorded using incident radiation perpendicular to the direction of elongation of crystals. The Raman spectrum was collected in the range 4000–45 cm−1 using a DXR dispersive Raman Spectrometer (Thermo Scientific) mounted on a confocal Olympus microscope. The Raman signal was excited by an unpolarised red 633 nm He–Ne gas laser and detected by a CCD detector. The experimental parameters were: 100× objective, 10 s exposure time, 100 exposures, 50 μm pinhole spectrograph aperture and 8 mW laser power level. The instrument was set up by a software-controlled calibration procedure using multiple neon emission lines (wavelength calibration), multiple polystyrene Raman bands (laser frequency calibration) and standardized white-light sources (intensity calibration). Spectral manipulations were performed using the Omnic 9 software (Thermo Scientific). The Raman spectrum was recorded for well-formed single-crystals of kasolite. Therefore, the possibility of the presence of impurities is very small.2.2 First-principles theoretical solid state methodology
The present theoretical study was performed using the CASTEP code,50 a module of the Materials Studio software suite.51 The specialized version of the Perdew–Burke–Ernzerhof energy-density functional,52 PBEsol,53 was used. The pseudopotentials used for H, O, Si and Pb atoms in the unit cell of kasolite mineral were standard norm-conserving pseudopotentials54 given in CASTEP code (00PBE-OP type). The relativistic norm-conserving pseudopotential employed for uranium atom was generated from first principles in previous works.35,36 This pseudopotential has been validated extensively in the research of uranyl containing materials.29–31,33,35–47 The optimization of the dimensions and shape as well as the atomic positions of the unit cell of kasolite was carried out by means of the Broyden–Fletcher–Goldfarb–Shanno (BFGS) technique.55 The plane wave kinetic energy cut-off parameter employed in the calculations was very large, ε = 1000 eV, and the k-mesh56 employed was 3 × 3 × 2. These parameters were chosen to obtain well converged crystal structures, energies and mechanical properties. The X-ray powder diffraction patterns were determined57 from the optimized crystal structures using the software REFLEX implemented in the Materials Studio package.51The computation of the Raman spectrum of kasolite was carried out using the linear response density functional perturbation theory (DFPT),58–60 in the same way as in previous papers.29,36–38,40,41,44,47,61,62 The calculated Raman shifts were not scaled to correct them for the anharmonicity and remaining approximations used in the theoretical treatment employed, such as incomplete treatment of electron correlation and basis set truncation.63 Therefore, they correspond to the harmonic approximation of the interatomic force field.
The elastic tensor elements needed to determine the mechanical properties and to study the mechanical stability of the kasolite crystal structure were calculated from stress–strain relationships using the technique of finite deformations64 as programmed in CASTEP code.50 This technique has been very satisfactorily applied in the determination of the elastic response of solid materials.29,31,33,38,39,41,44,46,65,66 The bulk modulus and its derivatives with respect to pressure were obtained by fitting the lattice volumes and associated pressures to a fourth-order Birch–Murnahan equation of state.67 The lattice volumes in the neighborhood of the optimized equilibrium geometry were determined by optimizing the kasolite crystal structure under the effect of eighteen different applied external pressures with values in the range −1.0 to 11 GPa. EOSFIT 5.2 code68 was used to adjust the results to the chosen equation of state. The corresponding crystal structure optimizations under pressure were also performed using the BFGS method. The three-dimensional representations of the mechanical properties of kasolite as a function of the orientation of the applied strain were performed with the ElAM software.69
3 Results and discussion
3.1 Crystal structure
The crystal structure of kasolite was first experimentally studied as soon as 1963 by Huynen et al.19 This study was continued by a large set of subsequent studies including those of Mokeeva,20 Rosenzweig and Ryan,16 Stohl and Smith,17 Vochten et al.,18 Chenorukov et al.21, and Fejfarová et al.22 The refined structure of Fejfarová et al.22 improved largely the previous proposed structures and provided the hydrogen atom positions in the kasolite unit cell. In the current study, based on density functional theory calculations, we confirmed the hydrogen bond model proposed in the work by Fejfarová et al.22 The calculated atomic positions resulting from our calculations are given as ESI in an independent file of CIF (Crystallographic Information File) type.†The crystal structure of kasolite has monoclinic symmetry, space group P121/c1 (no. 14). Table 1 gives the calculated lattice parameters, volume and density compared with the corresponding experimental information. As may be observed, the agreement is very good, the difference of the calculated volume and density with respect to the experimental values reported by Fejfarová et al.22 being only about 0.9%.
| Parameter | a (Å) | b (Å) | c (Å) | α (deg) | β (deg) | γ (deg) | Vol. (Å3) | Dens. (g cm−3) |
|---|---|---|---|---|---|---|---|---|
| DFT (this work) | 6.7035 | 6.8325 | 13.1795 | 90.0 | 101.92 | 90.0 | 590.6266 | 6.605 |
| Exp.22 | 6.705(3) | 6.9257(2) | 13.2857(5) | 90.0 | 105.064(4) | 90.0 | 595.74(3) | 6.548 |
| Exp.16,17 | 6.704 | 6.932 | 13.252 | 90.0 | 104.22 | 90.0 | 596.9788 | 6.535 |
| Exp.18 | 6.7030 | 6.9308 | 13.270 | 90.0 | 104.25 | 90.0 | 597.5177 | 6.529 |
| Exp.19 | 6.66 | 6.96 | 13.23 | 90.0 | 104 | 90.0 | 595.0417 | 6.556 |
| Exp.20 | 6.74 | 6.96 | 13.28 | 90.0 | 104.25 | 90.0 | 603.8019 | 6.461 |
| Exp.21 | 6.699 | 6.950 | 13.28 | 90.0 | 104.1 | 90.0 | 599.6630 | 6.505 |
| Exp.49 | 6.716 | 6.924 | 13.256 | 90.0 | 104.17 | 90.0 | 597.6694 | 6.527 |
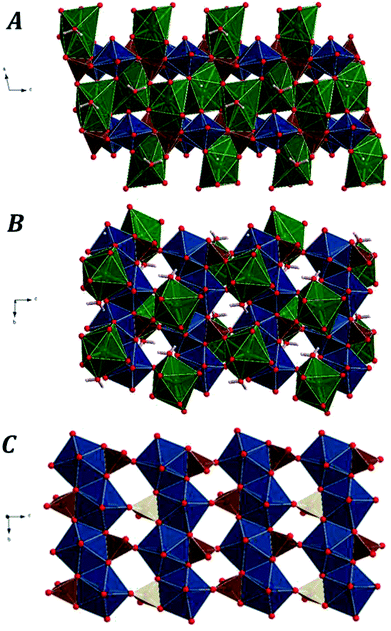
Fig. 1 displays the computed crystal structure of kasolite. As may be seen in Fig. 1, U atom in kasolite is coordinated as a pentagonal bipyramid,70 which is the most frequent coordination type among the hexavalent U structures.71 The uranyl bipyramids share two equatorial edges to form chains expanding along b axis. As shown in the Fig. 1C, the chains are connected through silicate tetrahedra to form uranyl silicate layers perpendicular to a axis. The layers are perfectly superimposed when viewed from a direction. The silicate fragments share an edge (two oxygen atoms) with one chain and a vertex with another. The three oxygen atoms in the silicate edge and vertex from a triangle which is placed within the uranyl silicate sheet. The remaining oxygen atom in the silicate fragment points towards the interlayer space. The Pb atoms and water molecules are placed within the interlayer space. If the Pb–O bond distance cutoff is taken as 3.3 Å, the coordination number of Pb to O is eight as shown in Fig. 1. The geometric shape of the Pb coordination structure is an irregular polyhedra having 16 triangular faces, 16 edges and 8 vertices (4 equatorial vertices, 2 upper apical vertices and 2 lower apical vertices), which has a square shaped equatorial plane. As can be seen in Fig. 1, the interlayer water is not free (held to the structure by hydrogen bonding only), but structural since forms part of the lead coordination structure.
A set of representative interatomic lengths and angles are given in Tables 2 and 3 compared with the corresponding experimental values.16,22 As can be seen, the experimental values reported by Rosenzweig and Ryan16 were significantly improved by Fejfarová et al.22 The values calculated in this work agree very well with the last experimental values. For example, the uranyl oxygen atoms at the apical positions of the uranyl pentagonal bipyramids have experimental22 uranium–oxygen bond lengths (U–O1 and U–O2) of 1.796 and 1.825 Å which are in good agreement with the computed values of 1.839 and 1.857 Å, respectively. The experimental average equatorial UO distance22 is 2.35 Å and the calculated one is 2.32 Å. These two values are close to the average value of 2.37 Å reported by Burns et al.71 for this kind of coordination polyhedra determined from a large set of well-defined structures of uranyl containing materials.
| Bond | Exp.16 | Exp.22 | Calc. |
|---|---|---|---|
| Uranyl-silicate sheet: U–O | |||
| U–O2 | 1.805 | 1.825(7) | 1.857 |
| U–O1 | 1.809 | 1.796(6) | 1.839 |
| U–O4 | 2.230 | 2.235(5) | 2.164 |
| U–O5 | 2.317 | 2.315(5) | 2.299 |
| U–O6 | 2.320 | 2.296(5) | 2.261 |
| U–O5# | 2.364 | 2.373(5) | 2.376 |
| U–O6# | 2.543 | 2.550(5) | 2.480 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Uranyl-silicate sheet: Si–O | |||
| Si–O3 | 1.588 | 1.603(6) | 1.635 |
| Si–O4 | 1.617 | 1.632(7) | 1.630 |
| Si–O6 | 1.636 | 1.647(5) | 1.658 |
| Si–O5 | 1.676 | 1.655(5) | 1.675 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Interlayer: Pb–O | |||
| Pb–O3 | 2.358 | 2.327(5) | 2.327 |
| Pb–O3# | 2.379 | 2.396(6) | 2.374 |
| Pb–O7w | 2.540 | 2.529(6) | 2.526 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Interlayer: water | |||
| O7w-H1 | — | 0.82(11) | 0.978 |
| O7w-H2 | — | 0.82(12) | 0.997 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Interlayer: hydrogen bonds (O–H⋯O) | |||
| O7w⋯O2 | — | 2.962(9) | 2.704 |
| H2⋯O2 | — | 2.07(13) | 1.710 |
| O7w⋯O7w# | — | 2.922(15) | 2.988 |
| H1⋯O7w# | — | 2.23(14) | 2.394 |
| O7w#···Ow7 | — | 2.922(15) | 2.988 |
| H1⋯O7w | — | 2.23(14) | 2.394 |
| Angle | Exp.16 | Exp.22 | Calc. |
|---|---|---|---|
| Uranyl-silicate sheet: O–U–O | |||
| O2–U–O1 | 175.51 | 176.17(19) | 176.29 |
| O1–U–O4 | 93.49 | 88.9(2) | 93.17 |
| O1–U–O5 | 88.80 | 89.9(2) | 87.88 |
| O1–U–O6 | 92.11 | 90.5(2) | 92.91 |
| O4–U–O5 | 78.13 | 91.1(2) | 77.25 |
| O4–U–O6 | 87.80 | 83.7(2) | 85.70 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Uranyl-silicate sheet: O–Si–O | |||
| O3–Si–O4 | 115.31 | 114.7(3) | 112.51 |
| O3–Si–O6 | 113.09 | 113.6(3) | 115.07 |
| O3–Si–O5 | 108.79 | 107.6(3) | 110.03 |
| O4–Si–O6 | 112.60 | 113.0(3) | 111.04 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Interlayer: O–Pb–O | |||
| O3–Pb–O3# | 79.33 | 78.1(2) | 77.73 |
| O3–Pb–O7 | 119.85 | 122.74(16) | 112.47 |
| O3#–Pb–O7 | 70.61 | 71.6(3) | 70.54 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Interlayer: water | |||
| H1–O7–H2 | — | 109.88 | 105.27 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Interlayer: hydrogen bonds (O–H⋯O) | |||
| O7–H2⋯O2 | — | 167(11) | 173.98 |
| O7–H1⋯O7# | — | 109(10) | 118.57 |
3.2 Hydrogen bonding
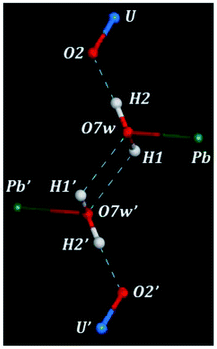
There are three hydrogen bonds in the structure of kasolite. These hydrogen bonds are shown in Fig. 2. The first is a strong nearly linear bond between the water oxygen and the uranyl O2 oxygen mediated by H2. The other two are symmetry equivalent hydrogen bonds between two water molecules mediated by H1. Each pair of water molecules are hydrogen bonded by these two hydrogen bonds as shown in Fig. 2. This kind of hydrogen bonding involving two symmetrically related bonds between each pair of water molecules should be quite strong and is very interesting. As far as we are concerned, its presence has not been reported for other solid materials. Due to the large restrictions in the structural water molecule positions, imposed by the interactions with the lead central cation and the uranyl silicate sheet, the possibility of finding a similar geometrical distribution of the water molecules in other materials is very small. Besides, the highly symmetrical and energy favored water distribution in kasolite confers to the interlayer structure a large strength and rigidity which, as shown below, is reflected in the large hardness and mechanical isotropy of kasolite structure.3.3 X-ray powder diffraction pattern
The X-ray powder diffractograms of kasolite were determined57 from the computed and experimental16 crystal structures employing the software REFLEX included in Materials Studio package of programs51 with CuKα radiation (λ = 1.540598 Å). The obtained patterns are compared in Fig. 3 in which a true experimental X-ray powder diffraction pattern of kasolite72 is also included. The agreement of the computed and experimental diffractograms is very good. This fact gives a firm support to the computed crystal structure and to the theoretical treatment used in this work.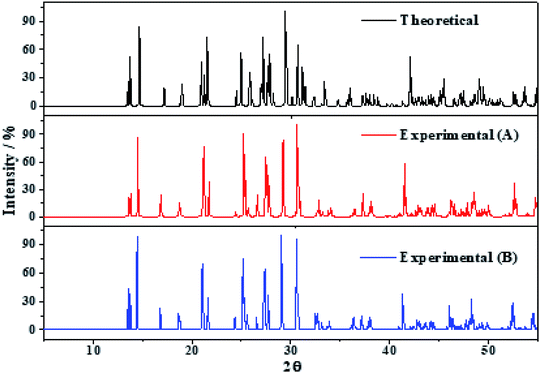 | ||
| Fig. 3 X-ray diffraction powder patterns of kasolite mineral. The upper pattern has been determined from the calculated geometry. The mid pattern was obtained from the experimental geometry16 (excluding hydrogen atom positions). Finally, the lower diffractogram is the experimental pattern of a natural mineral sample from Musonoi Extension, Shaba Province (Zaire) taken from record R060479 of the RRUFF database.72 | ||
3.4 Mechanic properties and stability
| ij | Cij |
|---|---|
| 11 | 108.02 |
| 22 | 189.96 |
| 33 | 165.58 |
| 44 | 53.02 |
| 55 | 40.35 |
| 66 | 40.08 |
| 12 | 45.86 |
| 13 | 20.05 |
| 15 | −3.22 |
| 23 | 55.65 |
| 25 | 2.97 |
| 35 | −0.53 |
| 46 | 4.24 |
The generic necessary and sufficient Born criterion for stability of a monoclinic symmetry crystal structure is that all eigenvalues of the C matrix be positive.75 Therefore, the C matrix was diagonalized numerically and all eigenvalues were found to be positive. Since the above condition was fulfilled, kasolite crystal structure is mechanically stable.
| Property | Value | |
|---|---|---|
| a The values of the bulk, shear and Young moduli (B, G and E) are given in GPa. | ||
| B | Bulk modulus | 70.94 |
| G | Shear modulus | 46.85 |
| E | Young modulus | 115.19 |
| ν | Poisson ratio | 0.23 |
| D | Ductility index | 1.51 |
| H | Hardness index | 8.68 |
| AU | Universal anisotropy | 0.39 |
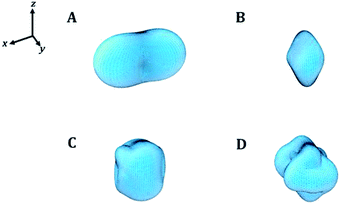
In order to visualize the dependence of the mechanical properties of kasolite as a function of the direction of the applied strain in a detailed manner, the ElAM program69 was utilized to generate detailed tridimensional representations of the most important elastic properties. The results are displayed in Fig. 4. As can be observed, the Fig. 4A–D are consistent with the previous discussion about the large mechanical isotropy of this mineral. The dependence of its elastic properties with respect to the direction of the applied strain is relatively featureless in comparison with the dependence observed for other uranyl containing materials29,31 and also non-uranyl materials.65,66 As can be seen, this dependence is very different to that of the schoepite29 and becquerelite,31 despite they are also layered uranyl containing materials.
Finally, the transverse and longitudinal elastic wave velocities in kasolite were estimated using the calculated elastic constants.44,74 The values found were VL = 4.587 km s−1 and VT = 2.701 km s−1 using the computed bulk and shear moduli and the calculated crystal density of 6.605 g cm−3 (see Table 1).
| Property | Value |
|---|---|
| a The values of the bulk modulus computed from the elastic constants are also given in the last row of the table for comparison. | |
| EOS | |
| B (GPa) | 66.08 ± 1.89 |
| B′ | 2.48 ± 1.34 |
| B′′(GPa−1) | −0.49 ± 0.29 |
| χ2 | 0.008 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Elastic constants | |
| B (GPa) | 70.94 ± 6.88 |
3.5 Raman spectroscopy
The Raman spectra of kasolite was recorded from a natural mineral sample from the Jánská vein, Příbram base metal ore district, Czech Republic.48,49 The resulting spectrum was compared with the theoretical spectrum computed by using density functional perturbation theory. The theoretical spectrum was computed at T = 298 K, λ = 532 nm, FWHM = 20 cm−1. As may be seen in Fig. 5, the experimental and theoretical spectra are in very good agreement. Pictures of the atomic motions in the Raman active vibrational modes are provided in Fig. S1 of ESI.†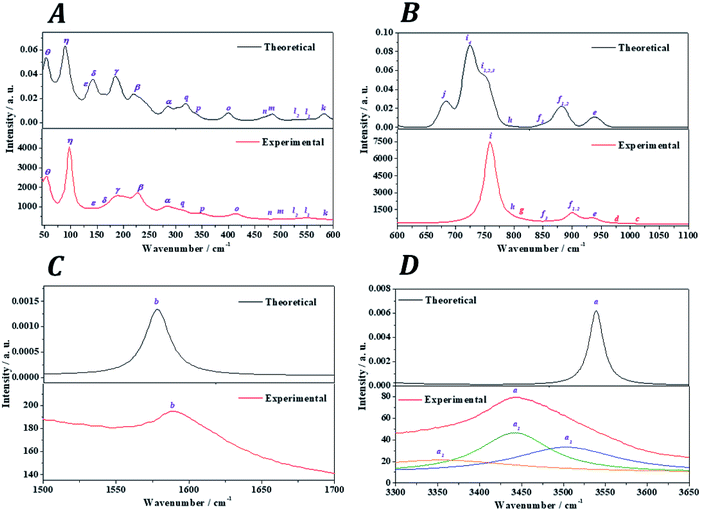 | ||
| Fig. 5 Experimental and theoretical Raman spectra of kasolite mineral: (A) region: 0–600 cm−1; (B) region: 600–1100 cm−1; (C) region: 1500–1700 cm−1; (D) region: 3300-3650 cm−1. | ||
The analysis of the Raman spectrum was performed in four different wavenumber regions: (i) OH stretching vibration region from 3300 to 3650 cm−1 (Fig. 5D); (ii) H2O bending region from 1500 to 1700 cm−1 (Fig. 5C); (iii) uranyl (UO22+) and silicate (SiO44−) fundamental vibrations region from 600 to 1100 cm−1 (Fig. 5B); and (iv) low wavenumber region from 45 to 600 cm−1 (Fig. 5A). The band wavenumbers of both spectra along with the corresponding calculated intensities and assignments are given in Table 7. The Raman band shifts and assignments performed by Frost et al.83 are also given in this table for comparison. The Raman spectrum of Frost et al.83 was recorded from a high purity natural specimen from El Sherana mine, South Alligator River, Northern Territory, Australia. The Raman spectrum was collected in the range between 100 and 4000 cm−1 at the liquid nitrogen temperature (77 K), using as excitation source a HeNe laser (633 nm). The spectral resolution achieved was 2 cm−1.
| Band name | Exp. shift (cm−1) [this work] | Exp. shift (cm−1)/assignment [Frost et al.83] | Calc. shift (cm−1) | Int. (Å4) | Assignment [this work] |
|---|---|---|---|---|---|
| a Raman shifts and assignments performed by Frost et al.83 are also given for comparison. | |||||
| OH stretching region | |||||
| a | 3503.4 | 3484.2/ν(OH) | 3555.7 | 12.11 | ν(OH) |
| 3441.7 | 3438.2/ν(OH) | 3540.6 | 174.80 | ν(OH) | |
| 3354.0 | 3411.1/ν(OH) | 3540.5 | 1362.67 | ν(OH) | |
| 3159.2 | 3166.4/ν(OH) | 3173.7 | 244.75 | ν(OH) | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| H2O bending region | |||||
| b | 1595.3 | 1593.7/δ(HOH) | 1578.3 | 88.78 | δ(HOH) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Fundamental UO22+ and SiO44− vibrations region | |||||
| c | 1015.1 | — | — | — | ν1 + ν2 = 850.8 + 163.3 = 1014.1 [f3 + δ1] |
| ν1 + ν2 = 794.9 + 223.1 = 1018.0 [h + β3] | |||||
| d | 976.6 | — | — | — | ν1 + ν2 = 794.9 + 182.4 = 977.3 [h + γ4] |
| ν1 + ν2 = 754.4 + 223.1 = 977.5 [i3 + β3] | |||||
| e | 936.6 | 939.9/νs(SiO44−) | 939.7 | 334.44 | νs(SiO44−) + νa(UO22+) |
| f | 907.7 | 903.6/νs(SiO44−) | 883.4 | 660.97 | νa(SiO44−) |
| 900.0 | 886.3/νs(SiO44−) | 882.4 | 18.05 | νa(SiO44−) | |
| 850.8 | 876.2/νa(UO22+) | 855.3 | 75.88 | νs(SiO44−) + l(H2O) | |
| g | 813.2 | 820.8/νa(UO22+) | — | — | ν1 + ν2 = 759.2 + 55.1 = 814.3 [i2 + θ] |
| ν1 + ν2 = 713.9 + 102.6 = 816.5 [i4 + η1] | |||||
| ν1 + ν2 = 529.7 + 283.8 = 813.5 [l2 + α1] | |||||
| h | 794.9 | 793.9/νs(UO22+) | 793.1 | 32.11 | νa(SiO44−) |
| i | 767.9 | 766.7/νs(UO22+) | 762.8 | 132.53 | ν(UO22+) + l(H2O) |
| 759.2 | 758.7/νs(UO22+) | 750.2 | 295.86 | ν(UO22+) + l(H2O) | |
| 754.4 | 750.0/νs(UO22+) | 750.4 | 794.50 | ν(UO22+) + l(H2O) | |
| 713.9 | 721.3/νs(UO22+) | 723.3 | 1870.19 | ν(UO22+) + l(H2O) | |
| j | — | — | 683.2 | 557.03 | l(H2O) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Low wavenumber region | |||||
| k | 574.3 | 575.9/δ(SiO44−) [ν2] | 583.5 | 100.66 | l(H2O) |
| l | 549.0 | 550.4/δ(SiO44−) [ν2] | 554.2 | 23.53 | ν(UO22+) + ν(UOeq) + γ(SiO44−) + l(H2O) |
| 529.7 | 533.3/δ(SiO44−) [ν2] | 529.5 | 17.81 | ν(UOeq) + γ(SiO44−) + l(H2O) | |
| m | 502.7 | 501.1/δ(SiO44−) [ν2] | 485.0 | 75.81 | l(H2O) |
| n | 457.4 | 454.6/δ(SiO44−) [ν2] | 467.2 | 19.21 | l(H2O) |
| o | 414.0 | 415.1/δ(SiO44−) [ν2] | 400.8 | 80.21 | δ(OSiO) + l(H2O) |
| p | 347.9 | 341.4 | 339.3 | 28.03 | ρ(UO22+) + w(OUOeq) + t(OUOeq) + γ(SiO44−) + l(H2O) |
| q | 316.2 | 319.0 | 319.7 | 71.01 | ρ(UO22+) + w(OUOeq) + t(OUOeq) + γ(SiO44−) + l(H2O) |
| r | 293.5 | 302.5 | 303.1 | 37.50 | δ(UO22+) + δop(UOeq) + γ(SiO44−) + T(H2O) |
| α | 283.8 | 285.3 | 285.9 | 30.52 | ρ(UO22+) + w(OUOeq) + t(OUOeq) + γ(SiO44−) + l(H2O) |
| 277.1 | 283.4 | 25.04 | δ(UO22+) + t(OUOeq) + l(H2O) | ||
| β | 234.7 | 234.3 | 246.3 | 29.01 | ρ(UO22+) + w(OUOeq) + l(H2O) |
| 228.9 | 231.1 | 232.9 | 37.18 | γ(UO22+) + t(SiO44−) + T(H2O) | |
| 223.1 | 217.7 | 221.0 | 33.37 | γ(UO22+) + T(H2O) | |
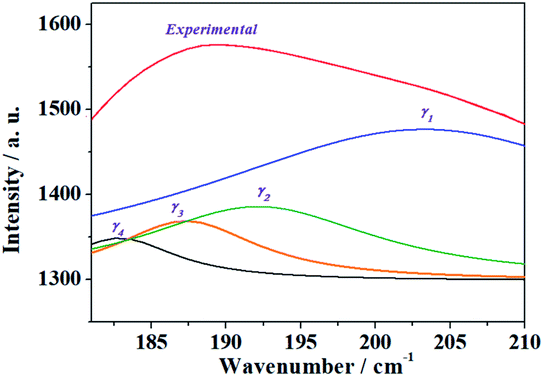
| γ | 202.8 | 184.7 | 197.9 | 24.78 | ρ(UO22+) + δ(UOSi) + T(H2O) |
| 192.2 | 191.6 | 37.87 | γ(UO22+) + δ(UOSi) + T(H2O) | ||
| 187.4 | 185.3 | 38.35 | ρ(UO22+) + w(OUOeq) + t(OUOeq) + γ(SiO44−) + T(H2O) | ||
| 182.4 | 182.9 | 40.54 | ρ(UO22+) + T(H2O) | ||
| δ | 163.3 | 165.3 | 146.1 | 25.13 | ρ(UO22+) + δop(UOeq) + T(H2O) |
| 155.6 | 153.5 | 143.8 | 19.28 | T(H2O) | |
| ε | 143.1 | 140.1 | 138.3 | 22.31 | ρ(UO22+) + δop(UOeq) + T(H2O) |
| η | 102.6 | 107.5 | 108.7 | 3.14 | ν(PbO) + T(UO22+) + T(SiO) + T(H2O) |
| 97.7 | 99.6 | 90.6 | 52.12 | ν(PbO) + T(UO22+) + T(SiO) + T(H2O) | |
| θ | 55.1 | — | 53.6 | 9.61 | ν(PbO) + γ(UO22+) + T(H2O) |
(i) OH stretching vibrations region: the experimental and theoretical Raman spectra of the hydroxyl stretching region are shown in Fig. 5D. The experimental spectrum displays a wide band having three main components located at 3503, 3442 and 3365 cm−1. A fourth very broad component is placed at 3159 cm−1. Frost et al.83 found these components at 3484, 3438, 3411 and 3166 cm−1, respectively. These components are reproduced theoretically at 3556, 3541, 3540 and 3174 cm−1.
(ii) H2O bending region: the experimental and theoretical spectra of this region are shown in Fig. 5C. The experimental spectrum displays a single band at 1595 cm−1 (found by Frost et al.83 at 1594 cm−1). This band corresponds to the theoretical water molecule bending band located at 1578 cm−1.
(iii) Uranyl (UO22+) and silicate (SiO44−) fundamental vibrations region: the experimental spectrum of this region presents two first weak bands, referred to as c and d, respectively, in Table 7 located at 1015 and 977 cm−1. These bands were not detected by Frost et al.83 and are absent in the theoretical spectrum. These two bands are identified as combination bands as indicated in Table 7. The third band located at 937 cm−1 is satisfactorily reproduced by the theoretical calculations at 940 cm−1. This band was assigned by Frost et al.83 to silicate symmetric stretching vibrations, νs(SiO44−). This assignment is confirmed here. However, as may be seen in Table 7, this band contain also significant contributions from uranyl antisymmetric stretching vibrations (see Fig. S1 of the ESI†). The next bands at 908 and 900 cm−1, correspond to the bands calculated at 883 and 882 cm−1 and are assigned to silicate asymmetric stretching vibrations, νa(SiO44−). The term asymmetric is used instead of antisymmetric because the silicate symmetry is lost in these vibrations. In this case the assignment performed by Frost et al.83 seems to be incorrect since, as the 937 cm−1 band, these bands were attributed to silicate symmetric stretching vibrations. The experimental band placed at 851 cm−1 is reproduced at 855 cm−1 and is ascribed to a combination of silicate symmetric stretching vibrations and water librations. Again, Frost et al.83 assigned this band differently to uranyl antisymmetric stretching vibrations, which, as has been noticed, appear at higher wavenumbers.
The weak band called g and placed at 813 cm−1 (found at 821 cm−1 by Frost et al.83), does not appear in the theoretical Raman spectrum and, as the bands c and d, is identified as a combination band. This identification was not recognized by Frost et al.83 which attributed this band to uranyl antisymmetric stretching vibrations. The set of five experimental bands at 795, 768, 759, 754 and 714 cm−1 correspond to the theoretical bands placed at 793, 763, 750, 750 and 723 cm−1. All these bands were assigned by Frost et al.83 to the fundamental uranyl symmetric stretching vibrations, νs(UO22+). In the present work, the assignment is the same for the last four bands. However, the first band is attributed to silicate asymmetric stretching vibrations. The band calculated at 683 cm−1, ascribed to water librations, is not observed in the present experimental spectrum and in that from Frost et al.83
(iv) Low wavenumber region: the first six bands in this spectral region observed at 574, 549, 530, 503, 457 and 414 cm−1 are very well reproduced theoretically at 583, 554, 529, 485, 467 and 401 cm−1. The first four of these bands were assigned by Frost et al.83 to ν2 silicate bending modes and the last two bands to ν4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) silicate bending modes.84 This assignment is not supported by this study. The symmetry of these vibrations is lost in kasolite. According to the normal mode analysis of the theoretical spectrum, the bands located at 574, 503 and 457 cm−1 should be attributed to water librations only. Similarly, the band placed at 549 cm−1 is ascribed to a combination of uranyl and equatorial UO stretching vibrations, silicate deformations and water librations. The band at 530 cm−1 is assigned to a combination of equatorial UO stretching vibrations, silicate deformations and water librations. Finally, the band at 414 cm−1 is assigned to OSiO bending vibrations and water librations.
silicate bending modes.84 This assignment is not supported by this study. The symmetry of these vibrations is lost in kasolite. According to the normal mode analysis of the theoretical spectrum, the bands located at 574, 503 and 457 cm−1 should be attributed to water librations only. Similarly, the band placed at 549 cm−1 is ascribed to a combination of uranyl and equatorial UO stretching vibrations, silicate deformations and water librations. The band at 530 cm−1 is assigned to a combination of equatorial UO stretching vibrations, silicate deformations and water librations. Finally, the band at 414 cm−1 is assigned to OSiO bending vibrations and water librations.
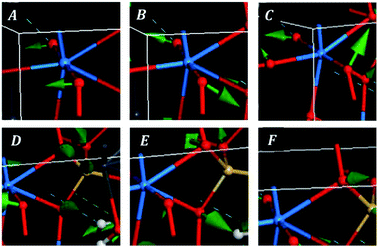
The bands at 348, 316, 294, 284, 277, 235, 229 and 223 correspond to the calculated bands at 339, 320, 303, 286, 283, 246, 233 and 221 cm−1. The whole set was assigned to uranyl bending vibrations by Frost et al.83 Again, this assignment is not supported by the theoretical work. The assignment of these bands is complicated and is given in detail in Table 7. As may be observed, the interpretation of the origin of these bands involves a large series of atomic motions as the uranyl bending, δ(UO22+), the uranyl rotation, ρ(UO22+), and the uranyl deformation, γ(UO22+), motions. The difference between these three kinds of uranyl atomic motions is illustrated in Fig. 6. As can be seen, the bending and rotation motions involve displacements of the uranyl oxygens out of the uranyl axis in the same and opposite directions. In the deformation motion, each oxygen displaces in a different direction. Since the uranyl fragment displays these three different types of motion, this spectral region should not be referred to as uranyl bending region. Other types of motions involving atomic motions in the uranyl polyhedra are the equatorial OUO wagging and twisting vibrations, w(OUOeq) and t(OUOeq) and the equatorial out of plane UO bending vibration, which are also shown in Fig. 6.
Finally, the good agreement obtained for the positions of the experimental bands at very low wavenumbers, 203, 192, 187, 182, 163, 156, 143, 103, 98 and 55 cm−1, with those determined theoretically (198, 192, 185, 183, 146, 144, 138, 109, 91 and 54 cm−1) is a very satisfactory feature due to the great difficulty of reproducing these types of bands using first-principles methods. In general, it is impossible to assign the bands of very low wavenumbers empirically and they are simply ascribed without any specification to deformation, translational and rotational motions. The excellent agreement obtained allowed to assign all these bands, providing a detailed description of the origin of these bands (see Table 7).
4 Conclusions
The crystal structure of kasolite mineral was obtained by using first-principles theoretical solid-state methods. The structure optimization was carried out by employing the PBEsol exchange–correlation energy-density functional. The computed structure confirmed the experimental observations22 since the lattice parameters, interatomic distances and angles, and X-ray powder pattern were in good agreement with the experimental information. The detailed analysis of the hydrogen bond structure revealed that the hydrogen bonding in kasolite is strong and dual. The water molecules in kasolite are distributed in pairs held together by two symmetrically related hydrogen bonds (one being directed from the first water molecule to the second one and the other from the second water molecule to the first one). The availability of the energy optimized hydrogen atom positions in kasolite permitted the theoretical computation of its mechanical properties and Raman spectrum because the application of the theoretical methodology for their calculation requires the knowledge of the optimized full crystal structure.From the calculated elasticity matrix, the mechanical stability of the kasolite crystal structure was studied and a large series of relevant mechanical data was obtained. The computed mechanical properties include the bulk modulus and its pressure derivatives, the Young and shear moduli, the Poisson ratio and the ductility, hardness and anisotropy indices. Since these properties have not been measured experimentally, their values were predicted. Kasolite is shown to be a hard and brittle mineral having a large bulk modulus of the order of B ∼71 GPa. Kasolite has a great mechanical isotropy despite of being a layered material. This property is the direct consequence of the strong hydrogen bonding between the structural uranyl silicate sheets in kasolite, which makes the bonding strength along the direction perpendicular to the layers of similar magnitude to that along the remaining directions.
Finally, the Raman spectrum of a natural sample of kasolite was recorded and compared with the computed Raman spectrum. Since the agreement was very good, the theoretical calculations were used to assign the bands of the experimental spectrum. A large number of kasolite Raman bands were reassigned. Three bands of the experimental spectrum, located at the wavenumbers 1015, 977 and 813 cm−1, were identified as combination bands. The theoretical calculations were also found to be an extremely useful tool to guide the resolution into single components of the bands of the experimental spectrum.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Supercomputer time CTI-CSIC center is greatly acknowledged. This work has been carried out in the context of a CSIC – CIEMAT collaboration agreement: “Caracterización experimental y teórica de fases secundarias y óxidos de uranio formados en condiciones de almacenamiento de combustible nuclear”. VT was supported by the Ministry of Science, Innovation and Universities within the Project FIS2016-77726-C3-1-P. JP acknowledge the support through the project no. LO1603 of the Ministry of Education, Youth and Sports National Sustainability Program I of the Czech Republic. JS was supported financially by the Ministry of Culture of the Czech Republic (long-term project DKRVO 2019-2023/1.II.a; National Museum, 00023272). We want to thank Dr A. M. Fernández for reading the manuscript and many helpful comments.References
- A. Schoep, C. R. Acad. Sci., 1922, 173, 1476–1477 Search PubMed.
- S. V. Krivovichev, J. PlášIl, in Uranium: From Cradle to Grave, ed. P. C. Burns, G. E. Sigmon, Mineralogical Association of Canada Short Courses, 2013, vol. 43, pp. 15–119 Search PubMed.
- R. J. Finch and T. Murakami, Rev. Mineral. Geochem., 1999, 38, 91–180 CAS.
- C. Frondel, Am. Mineral., 1956, 41, 539–568 CAS.
- R. M. Garrels and C. L. Christ, U.S. Geol. Surv. Prof. Pap., 1959, 320, 81–89 CAS.
- R. J. Finch and R. C. Ewing, J. Nucl. Mater., 1992, 190, 133–156 CrossRef CAS.
- I. Grenthe, J. Drozdzynski, T. Fujino, E. C. Buck, T. E. Albrecht-Schmitt and S. F. Wolf, in The Chemistry of Actinide and Transactinide Elements, ed. L. R. Morss, N. M. Edelstein and J. Fuger, Springer Science and Business Media, Berlin, 2006, ch V, vol. I, pp. 253–638 Search PubMed.
- J. Plášil, J. Geosci., 2014, 59, 99–114 CrossRef.
- R. J. Finch and R. C. Ewing, SKB Technical Report 91-15, SKB, Stockholm, 1991 Search PubMed.
- R. S. Forsyth and L. O. Werme, J. Nucl. Mater., 1992, 190, 3–19 CrossRef CAS.
- E. C. Pearcy, J. D. Prikryl, W. M. Murphy and B. W. Leslie, Appl. Geochem., 1994, 9, 713–732 CrossRef CAS.
- D. J. Wronkiewicz, J. K. Bates, T. J. Gerding, E. Veleckis and B. S. Tani, J. Nucl. Mater., 1992, 190, 107–127 CrossRef CAS.
- D. J. Wronkiewicz, J. K. Bates, S. F. Wolf and E. C. Buck, J. Nucl. Mater., 1996, 238, 78–95 CrossRef CAS.
- P. C. Burns, Am. Mineral., 1997, 82, 1176–1186 CAS.
- S. Ghazisaeed, B. Kiefer and J. Plášil, RSC Adv., 2019, 9, 10058–10063 RSC.
- A. Rosenzweig and R. R. Ryan, Cryst. Struct. Commun., 1977, 6, 617–621 CAS.
- F. V. Stohl and D. K. Smith, Am. Mineral., 1981, 66, 610–625 Search PubMed.
- R. Vochten, N. Blaton, O. Peeters, k. Van Springel and L. Van Haverbeke, Can. Mineral., 1997, 35, 735–741 CAS.
- A. M. Huynen, J. Piret-Meunier and M. Van Meerssche, Acad. R. Belg., Bull., 1963, 49, 192–201 CAS.
- V. I. Mokeeva, Sov. Phys. Crystallogr., 1965, 9, 621–622 Search PubMed.
- N. G. Chernorukov, A. V. Knyazev and O. V. Nipruk, Radiochem, 2007, 49, 340–345 CrossRef CAS.
- K. Fejfarová, M. Dušek, J. Plášil, J. Čejka, J. Sejkora and R. Škoda, J. Nucl. Mater., 2013, 434, 461–467 CrossRef.
- R. M. Berman, Am. Mineral., 1957, 42, 705–731 CAS.
- J. Janeczek and R. C. Ewing, Geochim. Cosmochim. Acta, 1995, 59, 1917–1931 CrossRef CAS.
- J. Janeczek and R. C. Ewing, J. Nucl. Mater., 1992, 190, 128–132 CrossRef CAS.
- H. Isobe, T. Murakami and R. C. Ewing, J. Nucl. Mater., 1992, 190, 174–187 CrossRef CAS.
- R. J. Finch and R. C. Ewing, Am. Mineral., 1997, 82, 607–619 CAS.
- P. C. Burns, Can. Mineral., 1998, 36, 847–853 CAS.
- F. Colmenero, J. Cobos and V. Timón, Inorg. Chem., 2018, 57, 4470–4481 CrossRef CAS PubMed.
- F. Colmenero, A. M. Fernández, J. Cobos and V. Timón, ACS Earth Space Chem., 2019, 3, 17–28 CrossRef CAS.
- F. Colmenero, A. M. Fernández, J. Cobos and V. Timón, RSC Adv., 2019, 8, 24599–24616 RSC.
- F. Colmenero, J. Cobos and V. Timón, J. Phys.: Condens. Matter, 2019, 31, 175701 CrossRef.
- S. Ghazisaeed, J. Majzlan, J. Plášil and B. Kiefer, J. Appl. Crystallogr., 2018, 51, 1116–1124 CrossRef CAS.
- M. C. Payne, M. P. Teter, D. C. Ailan, A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS.
- F. Colmenero, PhD thesis, Universidad Autónoma de Madrid, Madrid, 2017, p. 443.
- L. J. Bonales, F. Colmenero, J. Cobos and V. Timón, Phys. Chem. Chem. Phys., 2016, 18, 16575–16584 RSC.
- F. Colmenero, L. J. Bonales, J. Cobos and V. Timón, Spectrochim. Acta, Part A, 2017, 174, 245–253 CrossRef CAS PubMed.
- F. Colmenero, L. J. Bonales, J. Cobos and V. Timón, J. Solid State Chem., 2017, 253, 249–257 CrossRef CAS.
- F. Colmenero, L. J. Bonales, J. Cobos and V. Timón, J. Phys. Chem. C, 2017, 121, 5994–6001 CrossRef CAS.
- F. Colmenero, L. J. Bonales, J. Cobos and V. Timón, J. Phys. Chem. C, 2017, 121, 14507–14516 CrossRef CAS.
- F. Colmenero, L. J. Bonales, J. Cobos and V. Timón, Clay Miner., 2018, 53, 377–392 CrossRef CAS.
- F. Colmenero, A. M. Fernández, J. Cobos and V. Timón, J. Phys. Chem. C, 2018, 122, 5254–5267 CrossRef CAS.
- F. Colmenero, A. M. Fernández, J. Cobos and V. Timón, J. Phys. Chem. C, 2018, 122, 5268–5279 CrossRef CAS.
- F. Colmenero, in Minerals, ed. K. S. Essa, InTechOpen, London, 2018, ISBN: 978-953-51-6784-6 Search PubMed.
- F. Colmenero, in Density Functional Theory, ed. D. Glossman-Mitnik, InTechOpen, London, 2018, ISBN: 978-953-51-7020-4 Search PubMed.
- F. Colmenero, Appl. Sci., 2018, 8, 2281–2290 CrossRef.
- F. Colmenero, J. Cobos and V. Timón, Theor. Chem. Acc., 2019, 138, 43 Search PubMed.
- P. Škácha, V. Goliáš, J. Sejkora, J. Plášil, L. Strnad, R. Škoda and J. Ježek, J. Geosci., 2009, 54, 1–13 Search PubMed.
- J. Sejkora, J. Litochleb, J. Čejka and P. Černý, Bull. Mineral.-Petrolog. Odd. Nár. Muz., 2013, 21, 37–46 Search PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- MaterialsStudio, http://3dsbiovia.com/products/collabora-tivescience/biovia-materials-studio/, accessed April 1, 2019 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS.
- B. G. Pfrommer, M. Cote, S. G. Louie and M. L. Cohen, J. Comput. Phys., 1997, 131, 233–240 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- R. T. Downs, K. L. Bartelmehs, G. V. Gibbs and M. B. Boisen, Am. Mineral., 1993, 78, 1104 CAS.
- S. Baroni, S. de Gironcoli and A. Dal Corso, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- C. Lee and X. Gonze, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 8610–8613 CrossRef CAS.
- K. Refson, P. R. Tulip and S. J. Clark, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155114 CrossRef.
- F. Colmenero and V. Timon, J. Solid State Chem., 2018, 263, 131–140 CrossRef CAS.
- F. Colmenero, J. Phys. Chem. Solids, 2019, 125, 31–42 CrossRef CAS.
- W. J. Hehre, L. Radom, P. V. R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, Wiley, New York, 1986 Search PubMed.
- R. Yu, J. Zhu and H. Q. Ye, Comput. Phys. Commun., 2010, 181, 671–675 CrossRef CAS.
- F. Colmenero, Mater. Res. Express, 2019, 6, 045610 CrossRef.
- F. Colmenero, Phys. Chem. Chem. Phys., 2019, 21, 2673–2690 RSC.
- F. Birch, Phys. Rev., 1947, 71, 809–824 CrossRef CAS.
- (a) R. J. Angel, Rev. Mineral. Geochem., 2000, 41, 35–60 CrossRef; (b) EOSFIT 5.2 software, http://www.ccp14.ac.uk/ccp/web-mirrors/ross-angel/rja/soft/, accessed April 1, 2019 Search PubMed.
- A. Marmier, Z. A. D. Lethbridge, R. Walton, C. W. Smith, S. C. Parker and K. E. Evans, Comput. Phys. Commun., 2010, 181, 2102–2115 CrossRef CAS.
- H. T. Evans, Science, 1963, 141, 154–158 CrossRef CAS PubMed.
- P. C. Burns, R. C. Ewing and F. C. Hawthorne, Can. Mineral., 1997, 35, 1551–1570 CAS.
- R. T. Downs, Abstracts of the 19th General Meeting of the International Mineralogical Association in Kobe, Japan, 2006, O03-13; RRUFF database, http://rruff.info/kasolite, Record RRUFF-060479 Search PubMed.
- J. F. Nye, The Physical Properties of Crystals: Their Representation by Tensors and Matrices, Oxford University Press, New York, 1985 Search PubMed.
- P. F. Weck, E. Kim and E. C. Buck, RSC Adv., 2015, 5, 79090–79097 RSC.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- W. Voigt, Lehrbuch der Kristallphysik, Teubner, Leipzig, 1962 Search PubMed.
- A. Reuss, Z. Angew. Math. Mech., 1929, 9, 49–58 CrossRef CAS.
- R. Hill, Proc. Phys. Soc., London, 1952, 65, 349–354 CrossRef.
- S. F. Pugh, Philos. Mag., 1954, 45, 823–843 CAS.
- Y. Bouhadda, S. Djella, M. Bououdina, N. Fenineche and Y. Boudouma, J. Alloys Compd., 2012, 534, 20–24 CrossRef CAS.
- H. Niu, P. Wei, Y. Sun, C.-X. Chen, C. Franchini, D. Li and Y. Li, Appl. Phys. Lett., 2011, 99, 031901 CrossRef.
- S. I. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett., 2008, 101, 055504 CrossRef PubMed.
- R. L. Frost, J. Čejka, M. L. Weier and W. Martens, J. Raman Spectrosc., 2006, 37, 538–551 CrossRef CAS.
- K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, J. Wiley and Sons, New York, 1986 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Pictures of the atomic motions in the Raman active vibrational modes of kasolite mineral. CCDC 1907046. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9ra02931a |
| This journal is © The Royal Society of Chemistry 2019 |