Fluoride ion assisted growth of hierarchical flowerlike nanostructures of Co/Ni ferrites and their magnetoresistive response

Abstract

One-dimensional nanorod arrays exhibiting hierarchical flowerlike morphologies, of Co and Ni based ferrites were synthesized by hydrothermal treatment and using ammonium fluoride (NH₄F) as a mineralizing agent. The effects of NH₄F concentration and synthesis temperature were probed to control the morphology of these nanorods that were formed as a result of crystal nucleation. It was observed that a higher concentration of NH₄F leads to several other nucleation sites above these nanorods while controlled concentration of precursors and NH₄F results in the synthesis of floral patterns. The specific geometries of these nanorods leads to a shape anisotropy effect resulting in increased magnetic coercive fields. To study the effect of magnetic field on the resistance and current density, impedance spectroscopy and I–V–R characteristics, respectively, were performed. Nanorods show enhanced values for resistance with the increase in magnetic field confirming the effect of magnetoresistive coupling while a decrease in current densities with increasing magnetic field highlights the potential of these structures for magnetoresistive applications.

---

I. Introduction

One-dimensional (1D) nanostructures (NSs) have fascinated nanotechnologists because of their unique properties and potential applications in modern day technology.^1,2 With the advances in synthesis methods, these NSs have been produced with more ease, possess uniform morphology and exist as ordered aggregates. However, it is still a difficult task to synthesize self-assembled NSs with controlled morphology and high chemical stability as these properties strongly affect the physical behavior of the NSs.³

In the realm of nanomaterials, magnetic behavior of spinel ferrites has also been studied as these materials show improved properties when synthesized in nano-dimensions.⁴ Their magnetic properties greatly depend upon their synthesis conditions and composition and are modulated by shape and size.^5,6 They also show interesting magnetic and transport properties such as colossal magnetoresistance (CMR), tunnel magnetoresistance (TMR), magnetodielectric and magnetoelectric effects which are directly applicable to spintronic devices.^7–9 Among these materials, cobalt ferrite (CoFe₂O₄) with an inverse spinel structure shows attractive magnetodielectric properties with high magnetic anisotropy and chemical stability.^10,11 Nickel ferrite (NiFe₂O₄) being ferrimagnetic, on the other hand, possesses magneto-resistive nature, which is significantly influenced by variation in particle size and shapes.^12,13 The magnetoresistance (MR) defined as:¹⁴

δR/R₀ = (R_H − R₀)/R₀ ∝ (μB)² (1)

is shown to quadratically depend on the applied magnetic field enabling the detection of minute magnetic fields. Such MR devices are also employed in magnetic field sensing through the phenomenon of anisotropic magnetoresistance (AMR) effect.¹⁵ The MR effect is also valuable for spin valve devices which consist of a non-magnetic layer sandwiched between two ferromagnetic layers whose electrical resistance changes as a result of the relative alignment of magnetization in these layers.¹⁶ Furthermore, information storage technologies such as resistive-switching random access memories (RRAM), multistate devices and magnetoelectric random access memories, all requires strong magnetoelectric (ME) effect with appreciably sized MR. Although, MR effect is proved to be independent of ME effect,¹⁷ many studies have already focused on achieving MR in spinel ferrites.^18,19 Recently, these ferrites have been synthesized in various shapes and sizes such as nanoparticles, rods, wires and flakes.^20,21 However, their self-assembly into ordered 3D nanostructures is still difficult to attain which could provide enhanced magneto-resistive properties in order to expand the scope of applications of ferrites.

In this work, we report the synthesis of novel hierarchical flowerlike Co and Ni based spinel ferrites accompanying 1D nanorod (NR) arrays synthesized through ammonium fluoride mediated self-assembly process. This method has been previously adopted to synthesize nanosheet arrays of MgCo₂O₄ using hydrothermal approach.²² Hydrothermal method is one of the most facile chemicals method to synthesize NSs but generating arrays of NSs is not a simple task. Here, a small amount of an active reagent ammonium fluoride is used for the self-assembly of these NR arrays to form ordered flowerlike pattern. These structures were then investigated for the MR effect for spintronic based applications.

II. Experimental

Materials

Analytical grade iron(III) nitrate nonahydrate [Fe(NO₃)₃·9H₂O] (≥99.95%), cobalt(II) nitrate hexahydrate [Co(NO₃)₂·6H₂O] (≥98%), nickel(II) nitrate hexahydrate [Ni(NO₃)₂·6H₂O] (≥98.5%), urea [CO(NH₂)₂] (≥98%) and ammonium fluoride [NH₄F] (≥99.99%) purchased from Sigma-Aldrich, USA were utilized to prepare the ferrite NSs in this work.

Synthesis of spinel ferrite nano-rod arrays

In a typical procedure, stoichiometric molar masses of Fe(NO₃)₃·9H₂O, Co(NO₃)₂·6H₂O, CO(NH₂)₂ and NH₄F were dissolved in a mixed solution of deionized water and ethanol with a mixing ratio of 3 : 2. After 10 min of intense stirring at room temperature (RT), a homogenous pink solution was obtained which was then transferred to a 40 mL Teflon-lined stainless-steel autoclave. At this stage, two different heating treatments were done in order to optimize the temperature effect on the morphology of these ferrites. The solution in autoclave was treated at 120 °C for 4 h while another, similar solution was treated at 180 °C for 4 h. This optimization was done in accordance with the different literature available for the synthesis of these NSs using the hydrothermal technique.^22,23 These as-synthesized NSs were then taken out in the form of the powder and repeatedly washed with deionized water. Finally, the powder was heat treated at 300 °C for 2 h. The CoFe₂O₄ NRs thus produced which were heat treated at 120 °C were named as CFO-1, while the sample heat treated at 180 °C was named CFO-2. Meanwhile, similar approaches were employed to synthesize NiFe₂O₄ and Ni_0.5Co_0.5Fe₂O₄ NRs, and were named as NFO-1, NFO-2, NCF-1 and NCF-2. Afterwards, the powders were subjected for calcination to obtain highly crystalline samples at 600 °C for 3 h and then pelletized in the dimensions of 0.349 cm² area and 0.1 cm thickness. The principal reactions involving the formation of CFO are given below:

Ionization:

Co(NO₃)₂·6H₂O + Fe(NO₃)₃·6H₂O → Co²⁺ + Fe³⁺ + 5NO₃⁻ + 12(H₂O) (2)

CFO formation:

Co²⁺ + 2Fe³⁺ + 2O₂ → CoFe₂O₄ (3)

Urea combustion:

CH₄N₂O + 2O₂ → CO_2(g) + 2H₂O_(g) + N_2(g) (4)

Catalytic effect of ammonium fluoride:

NH₄F_(s) → NH_3(g) + HF_(g) (5)

NH_3(g) → 1/2(N₂)_(g) + 3/2(H₂)_(g) (6)

HF_(g) → 1/2(H₂)_(g) + F_(g) (7)

Characterization

Controlled morphologies of NRs were characterized by field emission scanning electron microscope (FESEM, Nova NanoSEM 450). Energy dispersive X-ray spectroscopy (EDX) was performed with an Oxford XAct instrument attached with the FESEM, to identify the compositional stoichiometry of ferrite NRs. Crystalline structure of the NRs was investigated by powder X-ray diffraction (XRD) using a Bruker D8 Advanced X-ray diffractometer by employing Cu K_α radiations having wavelength 1.54 Å. Magnetic hysteresis loops were obtained using a 7 T field cryogen-free measurement system (Cryogenic Limited UK) by applying a maximum field of 1 T. Resistive measurements were performed using a Wayne Kerr (6520B) impedance analyzer with an attached DC magnet (maximum field 6000 Oe) for magneto-resistive measurements. For the calculation of current density at different magnetic fields, a precision multiferroic tester (P-PMF) from Radiant Technologies, USA was used with a precision current source, CS-2.5.

III. Results and discussion

FESEM images of the as-prepared NRs synthesized by hydrothermal treatment of precursors, using NH₄F as mineralizing agent, are shown in Fig. 1. These images are obtained at a high magnification of 200 000×. It can be seen that all the ferrite samples are transformed entirely into 1D NRs after hydrothermal treatment with diameters ranging from 25 to 100 nm and lengths from 150 to 600 nm. No isolated nanoparticles can be seen from the high magnification images, further clarifying the successful synthesis of Co/Ni ferrite NRs. CFO-1, NFO-1 and NCF-1 NRs [Fig. 1(a, c and e), respectively] hydrothermally treated at 120 °C seems to be more homogeneous than ferrite NRs treated at 180 °C [Fig. 1(b, d and e)]. The surface of these NRs is apparently quite smooth and edges are round except that of the NCF-2 sample which seems to be overheated. Some cubical shaped particles were also observed in the NFO-1 and NFO-2 samples (Fig. 1(c and d)).

Fig. 1 FESEM images at 200 000× of (a and b) CFO, (c and d) NFO and (e and f) NCF NRs synthesized at reaction temperatures of 120 and 180 °C, respectively.

Initially, these NRs were tested with the concentration of NH₄F as a mineralizing agent for NFO NRs with a molar ratio of CO(NH₂)₂ and NH₄F as 1 : 1 and 1 : 2. Fig. 2(a and b) shows the morphology obtained for such samples. The sample with 1 : 1 ratio of CO(NH₂)₂ to NH₄F shows smoothed surface NRs while with at the higher concentration of NH₄F, NFO NRs show nanometric particles suspended on the surface showing supersaturation due to high nucleation rate which promotes the radial growth of these NRs. These nanoparticles attached to the surface can be regarded as new nucleation sites, emerging on the surface of NRs.²⁴

Fig. 2 NFO NRs prepared using CO(NH₂)₂ and NH₄F, having molar ratios of (a) 1 : 1 and (b) 1 : 2, respectively, flowerlike morphology of NCF 1D NRs synthesized at (c) 120 and (d) 180 °C reaction temperatures. Insets show edges of the respective NRs.

Fig. 2(c and d) confirm the flowerlike morphology of the synthesized NCF NRs. This flowerlike morphology was not observed for the individual samples of Co and Ni ferrite. Thus, it can be said that the 3D flowerlike pattern is highly concentration dependent. Other factors such as reaction time and temperature, washing cycles and calcination temperature may vary the overall morphology of the NRs. From the insets of Fig. 2, it can be seen that NCF-1 NRs are made from plenty of NCF nanoparticles giving rise to sharp edges of NRs having rectangular shape. On the other hand, NCF-2 NRs have thin walls and smooth surface with distorted boundaries.

Here, we report three different morphologies of ferrites which are compared in Fig. 3. CFO-1 NRs have acquired a stacked morphology in which the NRs are arranged in stacked arrays, one above another. Fig. 3(a) shows the schematic stacking of CFO NRs placed in both directions horizontally and vertically. NFO-1 has mostly an irregular arrangement of rods but some rods can be seen to be placed in the formation of a flower as shown in Fig. 3(c and d). However, NCF NRs have only shown flowerlike morphologies.

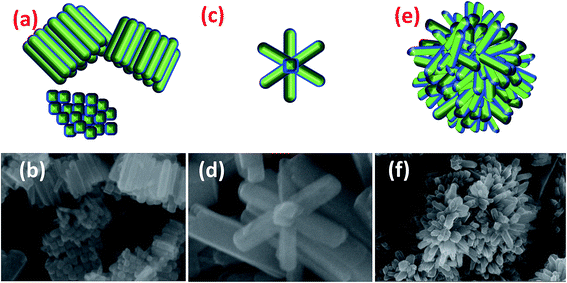Fig. 3 Schematics and original NR array formation of (a and b) CFO, (c and d) NFO and (e and f) NCF, respectively.

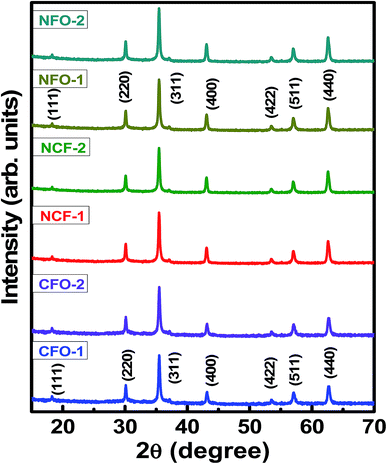
To confirm the crystalline nature of these NRs, XRD measurements were performed on the calcined samples. Fig. 4 shows the indexed XRD patterns of highly crystalline NRs. Well-defined reflected intensities were observed in the XRD patterns at 2θ angles of 18.2°, 30.12°, 35.48°, 43.13°, 53.47°, 57.12 and 62.76° for CFO NRs. These reflections were indexed in accordance with the method described by Cullity.²⁵ Accordingly, the intensities were successfully indexed as (111), (220), (311), (400), (422), (511) and (440) plane reflections for the spinel CFO structure, matched with ICSD reference no. 00-003-0864. Similarly, XRD patterns of NFO NRs were also matched with ICSD reference no. 00-010-0325 with same space group of Fd3m. No sign of any impurity phase was indicated. Lattice parameters obtained for all NRs are tabulated in Table 1. These results indicate that simple hydrothermal synthesis with NH₄F mineralizing agent is suitable for preparing transition metal oxides NRs with a high degree of crystallinity.

Fig. 4 XRD patterns of the synthesized Co/Ni ferrite NRs.

Table 1 Lattice parameter (a), saturation magnetization (M_s), remnant magnetization (M_r), coercive magnetic field (H_c) and M_r/M_s ratio for all compositions

Composition	a (Å)	Ms (emu g^−1)	Mr (emu g^−1)	Hc (Oe)	Mr/Ms
CFO-1	8.383	73	41	2470	0.56
CFO-2	8.379	64	39	2846	0.61
NFO-1	8.384	39	20	800	0.5
NFO-2	8.384	32	13	710	0.41
NCF-1	8.385	53	27	1850	0.51
NCF-2	8.385	49	24	1747	0.49

---

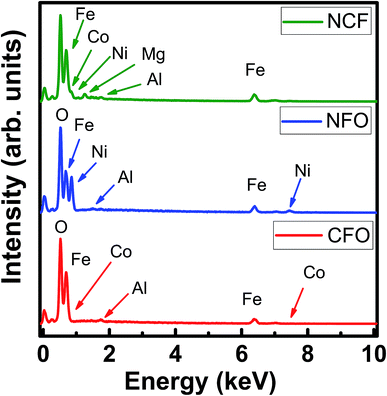
Fig. 5 shows the EDX spectra of CFO-1, NFO-1 and NCF-1 samples. The spectroscopic data obtained shows the compositional purity of the NR arrays, depicting the presence of required stoichiometric elements in each sample in accordance with their corresponding empirical formulae, thereby, confirming the synthesis of pure Co and Ni based ferrites. No impurity elements were found in the spectra, except Mg and Al which occurred due to the usage of the stage for placement of the samples inside the chamber.

Fig. 5 EDX spectra of the synthesized NRs.

Magnetic characterization was done for the ferrite samples at RT for a maximum applied magnetic field up to 1 tesla. Saturated hysteresis loops for all the ferrite samples are shown in Fig. 6. Hysteresis curve is another way to determine the synthesis of ferrite samples as the CFO being a hard-magnetic material shows high coercive fields (H_c) while NFO on the other hand being soft ferrite has low coercive value.²⁶ It can be seen from Fig. 6a that the CFO has high H_c and saturation magnetizations (M_s) as compared to NFO which shows relatively low values (Fig. 6b). However, NCF samples have midrange of these values (Fig. 6c). Trend of M_s and H_c for all the synthesized ferrites are also shown separately in Fig. 7 and tabulated in Table 1. It can be seen that the CFOs have M_s in the range of 64–73 emu g⁻¹, which is lower than the bulk ferrite due to the spin canting effect because of distorted magnetic moments at low dimensions.²⁷ A similar behavior is obtained for NFO whose reported M_s values (39 and 32 emu g⁻¹ for NFO-1 and NFO-2, respectively) are lower as compared to the bulk samples.²⁶

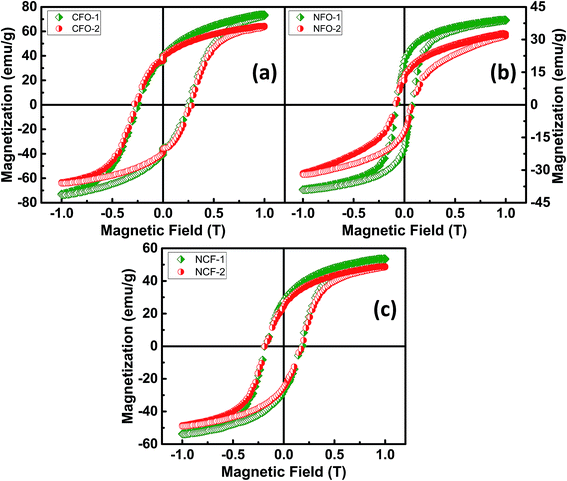Fig. 6 Room temperature M–H loops of (a) CFO, (b) NFO and (c) NCF nanorods with different reaction temperatures.

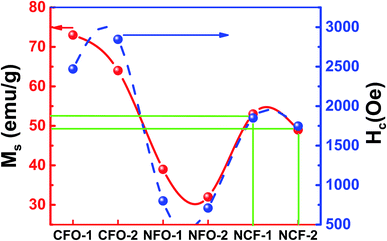Fig. 7 Saturation magnetization (M_s) and coercivity (H_c) of synthesized NRs at different reaction temperatures.

However, by far the important parameter to note is H_c, whose value for both the Co and Ni ferrite are higher than the previously reported H_c values which is ascribed to shape anisotropy.^27,28 These NRs with flat surfaces enable the surface metal cations to arrange in a more symmetric coordination as compared to the curved topology of nanocrystals. This enables fewer pinning sites because of the presence of coordinating oxygen atoms around the metal cations and thus results in enhanced coercivity.²⁹ Although, high H_c values for ferrites have been reported due to the presence of a secondary phase Fe₂O₃,³⁰ our XRD results indicate no impurity phase of Fe₂O₃ showing the high H_c is purely due to the geometry of these NRs. The CFO being highly oriented and stacked and possessing highly exposed surfaces show high M_r/M_s ratios of 0.56 and 0.61 for CFO-1 and CFO-2, respectively. The NFO and NCF NRs, have low values of M_r = 0.5 M_s and M_r = 0.49 M_s, respectively and are also shown in Table 1. For flowerlike morphology of NCF NRs, the assembly of NRs is very uniform but the surface is not highly exposed. This may have caused slightly lower values for NCF NRs but still they behave similar to hard magnets.^31,32

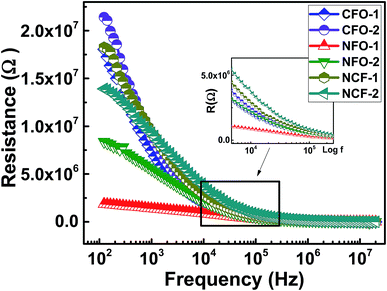
Ferrites are highly resistive materials with their resistance ranging from 10⁶ to 10⁷ Ω.³³ To determine the resistance of the synthesized NRs, the resistive curves as a function of frequency at RT are shown in Fig. 8. Resistive dispersion with frequency in Fig. 8 is similar to the dielectric dispersion which can be described by the electronic or space-charge polarization. The decreasing resistance with frequency is due to the conduction mechanism by hopping electrons.³³ The highest resistance was achieved by CFO NRs while NFO NRs provided the lowest resistance among all the synthesized ferrites. Again, the NCF samples show mid-range values for resistance, however, there relaxation frequency values are higher amongst the other ferrites. This fact can be regarded to the uniform morphology of the NCF samples which facilitates the dispersion process.

Fig. 8 Dispersion of resistance (R) vs. frequency for ferrite NRs synthesized at different reaction temperatures. Inset shows the magnified image of dispersive curve elaborating different relaxation behavior.

To determine the effect of magnetic field on the resistance of the synthesized NRs, the resistive dispersion was plotted at different applied fields for all the samples and are shown in Fig. 9. Significant and systematic changes in resistance with an increase in the applied static magnetic field indicate the presence of magneto-resistive coupling. A maximum static field of 5 kOe was applied to elicit the variation in resistance of the Co/Ni ferrites. As predicted from the RT plots of resistance, CFO NRs show a maximum of resistance. However, the increment in resistance was led by NFO as their resistance increased much strongly as compared to simple CFO or NCF NRs. This was confirmed by the magneto-resistance coupling (MRC%) plots (Fig. 10), where the maximum of MRC% value obtained was for NFO that was 68% and 75% for NFO-1 and NFO-2, respectively. Such type of giant negative magneto-resistance has been reported earlier for ferrites by many authors.^34,35 Increase in resistance due to applied magnetic field was credited to the scattering of conduction electrons as their paths diverge due to the Lorentz force.³⁶ This mechanism was supported by the quantum approach in Drude–Lorentz model where the conductivity is explained in terms of mean free time (τ) and effective mass (m*) of electrons given by:³⁷

σ = 1/ρ = e²Nτ/m² (8)

where N is the concentration of the hopping electrons. According to this theory, when a magnetic field is applied to the conducting electrons, it suppresses the wave function of these electrons thereby decreasing their jumping probability and suppresses the interference effects giving rise to negative magnetoresistance.³⁸

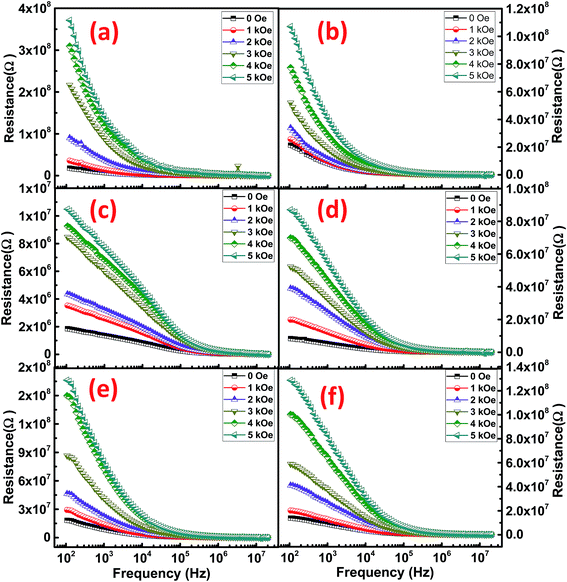Fig. 9 Variation of resistance with frequency at different magnetic fields for (a) CFO-1, (b) CFO-2, (c) NFO-1, (d) NFO-2, (e) NCF-1 and (f) NCF-2 NRs.

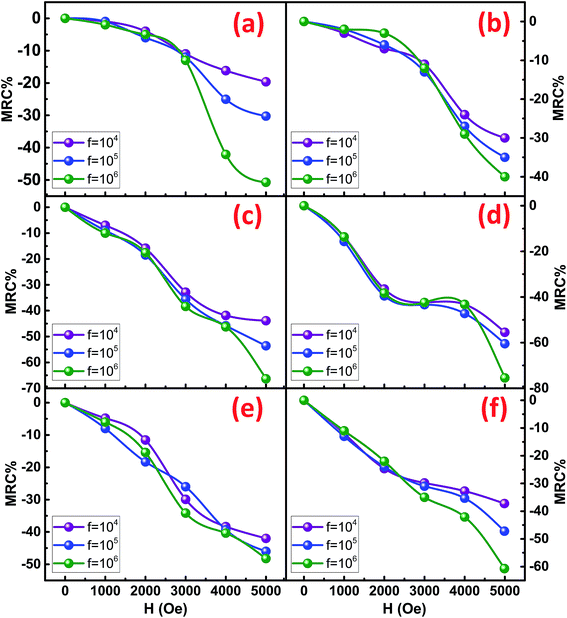Fig. 10 MRC% at different magnetic field (H) for (a) CFO-1, (b) CFO-2, (c) NFO-1, (d) NFO-2, (e) NCF-1 and (f) NCF-2 NRs.

To analyze the conduction mechanism of these ferrites, I–V–R curves were measured and shown in 3D-plotting in Fig. 11. All of the I–V–R curves were obtained at RT using a triangular waveform while the peak voltage was set to 20 V. The current and resistance dispersion with voltage shows strong dependence with electric field. These graphs lead us to calculate the current densities (J) of ferrites which highlights the conduction process inside these materials. At maximum applied electric field i.e. 20 V, CFO gives a maximum of 1.8 μA cm⁻², while that of NFO is 20.8 μA cm⁻². NCF NRs have a mid-range of J value which is 2.6 μA cm⁻². To further analyze the magnetic effect of the conduction mechanism we have measured the R–V plots (Fig. 11) at different applied magnetic fields for all the samples and then calculated the variation in current densities tabulated in Table 2. The R–V response for Co/Ni based ferrites in Fig. 12 shows strong dependence of magnetic field on the resistance of the material. Resistance tends to increase with increase in magnetic field for all the samples. The variation of resistance with voltage is also evident. For all the samples resistance decrease with the increase in voltage for both the directions and then tend to saturate at higher voltages except that for NFO NRs where resistance increase at higher voltages. This increment in resistance clarifies the dependence of conduction mechanism with electric field and the interference mechanism of electron hopping among the Ni²⁺ and Fe³⁺ sites.³⁸ This might be the reason why the MRC% of NFO is highest amongst the rest of the samples.

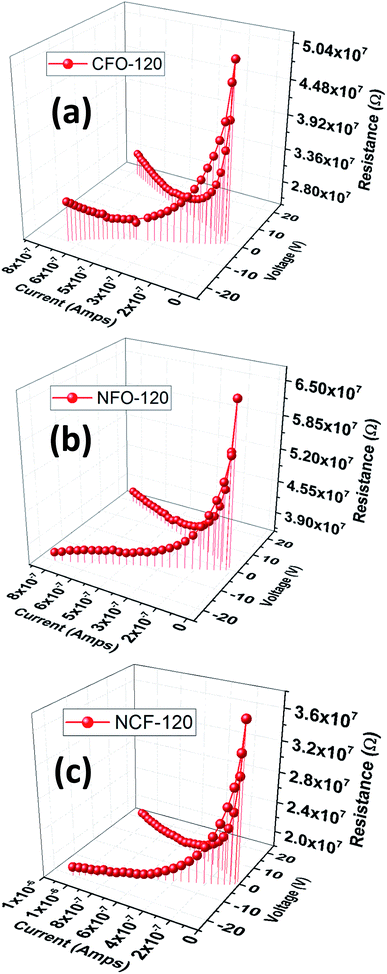Fig. 11 I–V–R 3D plots of (a) CFO, (b) NFO and (c) NCF NRs synthesized at 120 °C reaction temperature.

Table 2 Current density (J) at different applied magnetic field for all the synthesized NRs

Samples	J (μm cm^−2) @ 0 Oe	J (μm cm^−2) @ 1 kOe	J (μm cm^−2) @ 2 kOe	J (μm cm^−2) @ 3 kOe	J (μm cm^−2) @ 4 kOe	J (μm cm^−2) @ 5 kOe
CFO-1	1.82	1.35	1.25	0.73	0.41	0.14
CFO-2	2.85	2.11	1.52	1.14	0.82	0.69
NFO-1	5.63	5.12	3.35	2.47	1.79	1.38
NFO-2	4.48	3.06	2.03	1.67	1.33	1.15
NCF-1	2.15	1.45	1.25	0.79	0.59	0.46
NCF-2	1.53	1.14	0.86	0.62	0.48	0.32

---

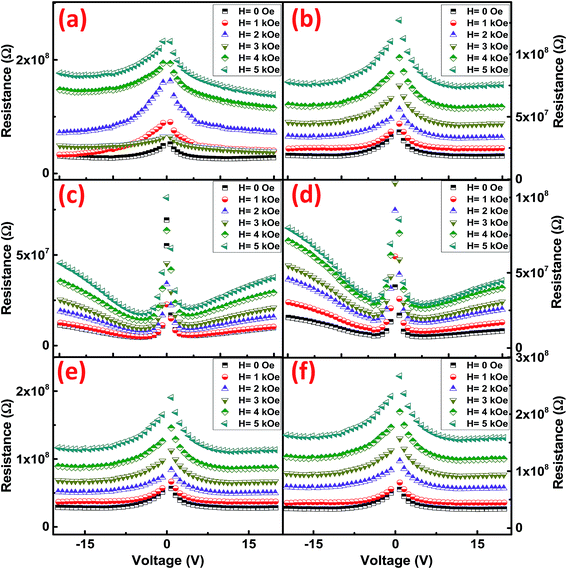Fig. 12 R–V plots at different magnetic fields for (a) CFO-1, (b) CFO-2, (c) NFO-1, (d) NFO-2, (e) NCF-1 and (f) NCF-2 NRs.

IV. Conclusion

In conclusion, we report the successful synthesis of 1D NRs arrays of Co and Ni based ferrites through hydrothermal method to form a hierarchical flowerlike morphology. With the aid of mineralizing agent NH₄F, and controlling the concentration of Co and Ni hierarchical nanostructures were obtained. Shape anisotropy leads to higher magnetic coercive fields for all the synthesized ferrite NRs. Magneto-resistive coupling was confirmed through MRC% where a maximum of 75% MRC% value was obtained for NFO at room temperature. The effect of magnetic field on the conduction mechanism was studied through R–V plots, which clarifies the interference mechanism of electrons with magnetic field during hopping between the different lattice sites.

Conflicts of interest

There are no conflicts to declare.

References

1. W. Li, C. An, H. Guo, J. Sun, M. Wang, Y. Li, L. Jiao and Y. Wang, ACS Sustainable Chem. Eng., 2019, 7, 139–146.
2. M. Tadic, S. Kralj and L. Kopanja, Mater. Charact., 2019, 148, 123–133.
3. L. S. Zhong, J. S. Hu, H. P. Liang, A. M. Cao, W. G. Song and L. J. Wan, Adv. Mater., 2006, 18(18), 2426–2431.
4. Z. Jia, D. Ren and R. Zhu, Mater. Lett., 2012, 66, 128–131.
5. J. Kim, H. S. Kim, N. Lee, T. Kim, H. Kim, T. Yu, I. C. Song, W. K. Moon and T. Hyeon, Angew. Chem., 2008, 120, 8566–8569.
6. M. Gharibshahian, M. S. Nourbakhsh and O. Mirzaee, J. Sol-Gel Sci. Technol., 2018, 85, 684–692.
7. G. Muscas, P. A. Kumar, G. Barucca, G. Concas, G. Varvaro, R. Mathieu and D. Peddis, Nanoscale, 2016, 8, 2081–2089.
8. X. Li, K. W. Lin, H. Y. Liu, D. H. Wei, G. J. Li and P. W. T. Pong, Thin Solid Films, 2014, 570, 383–389.
9. Z. Q. Lei, G. J. Li, W. F. Egelhoff, P. T. Lai and P. W. T. Pong, IEEE Trans. Magn., 2011, 47, 714–717.
10. K. Maaz, A. Mumtaz, S. K. Hasanain and A. Ceylan, J. Magn. Magn. Mater., 2007, 308, 289–295.
11. Y. Shen, J. Sun, L. Li, Y. Yao, C. Zhou, R. Su and Y. Yang, J. Mater. Chem. C, 2014, 2, 2545–2551.
12. A. K. M. Akther Hossain, M. Seki, T. Kawai and H. Tabata, J. Appl. Phys., 2004, 96(2), 1273–1275.
13. K. Nejati and R. Zabihi, Chem. Cent. J., 2012, 6, 23.
14. I. Shibasaki, and N. Kuze, Molecular Beam Epitaxy, Elsevier, 2013, pp. 697–720.
15. L. K. Quynh, B. D. Tu, C. V. Anh, N. H. Duc, A. T. Phung, T. T. Dung and D. H. Giang, J. Electron. Mater., 2019, 48, 997–1004.
16. X. Zhang, J. Tong, H. Zhu, Z. Wang, L. Zhou, S. Wang, T. Miyashita, M. Mitsuishi and G. Qin, J. Mater. Chem. C, 2017, 5, 5055–5062.
17. G. Catalan, Appl. Phys. Lett., 2006, 88, 102902.
18. H. B. Vasili, M. Gamino, J. Gàzquez, F. Sanchez, M. Valvidares, P. Gargiani, E. Pellegrin and J. Fontcuberta, ACS Appl. Mater. Interfaces, 2018, 10, 12031–12041.
19. P. Ghosh, R. N. Bhowmik, M. R. Das and P. Mitra, Phys. E, 2017, 88, 218–227.
20. K. L. Routray, S. Saha, D. Behera, N. Tripathy and S. P. Ghosh, Mater. Lett., 2019, 242, 62–65.
21. Z. Zhang, A. J. Rondinone, J. X. Ma, J. Shen and S. Dai, Adv. Mater., 2005, 17, 1415–1419.
22. Y. Teng, Y. Li, Z. Zhang, D. Yu, Y. Feng, Y. Meng, W. Tong, Y. Wu, X. Zhao and X. Liu, Chem.–Eur. J., 2018, 24, 14982–14988.
23. X. Gao, W. Wang, J. Bi, Y. Chen, X. Hao, X. Sun and J. Zhang, Electrochim. Acta, 2019, 296, 181–189.
24. J. He, Y. Hu, Z. Wang, W. Lu, S. Yang, G. Wu, Y. Wang, S. Wang, H. Gu and J. Wang, J. Mater. Chem. C, 2014, 2, 8185–8190.
25. B. D. Cullity, Elements of X-ray Diffraction, Addison-Wesley Publishing Company, Inc., Boston, 1956.
26. B. D. Cullity, and C. D. Graham Jr, Introduction to Magnetic Materials, John-Wiley and Sons, 1972.
27. L. T. Lu, N. T. Dung, L. D. Tung, C. T. Thanh, O. K. Quy, N. V. Chuc, S. Maenosono and N. T. Thanh, Nanoscale, 2015, 7, 19596–19610.
28. Y. Wu, C. Shi and W. Yang, Rare Met., 2010, 29, 385–389.
29. Q. Song and Z. J. Zhang, J. Am. Chem. Soc., 2004, 126, 6164–6168.
30. A. Aubert, V. Loyau, F. Mazeleyrat and M. LoBue, J. Eur. Ceram. Soc., 2017, 37, 3101–3105.
31. Z. Q. Liu, K. Xiao, Q. Z. Xu, N. Li, Y. Z. Su, H. J. Wang and S. Chen, RSC Adv., 2013, 3, 4372–4380.
32. Y. Soumare, C. Garcia, T. Maurer, G. Chaboussant, F. Ott, F. Fievet, J. Y. Piquemal and G. Viau, Adv. Funct. Mater., 2009, 19, 1971–1977.
33. A. H. Khan, S. Atiq, A. Mahmood, S. M. Ramay, S. K. Abbas and S. Naseem, Ceram. Int., 2018, 44, 14677–14685.
34. D. K. Pradhan, S. Kumari, V. S. Puli, P. T. Das, D. K. Pradhan, A. Kumar, J. F. Scott and R. S. Katiyar, Phys. Chem. Chem. Phys., 2017, 19, 210–218.
35. H. Gu, H. Zhang, J. Lin, Q. Shao, D. P. Young, L. Sun, T. D. Shen and Z. Guo, Polymer, 2018, 143, 324–330.
36. B. I. Shklovskii, and A. L. Efros, Electronic properties of doped semiconductors, Springer Science & Business Media, 2013.
37. J. B. Ketterson, The Physics of solids, Oxford University press, Oxford, 2016.
38. K. P. Belov, Phys.-Usp., 1994, 37, 563.

---