Open Access Article
Open Access ArticleSystematic study of the substitution effect on the tetrel bond between 1,4-diazabicyclo[2.2.2]octane and TH3X†
Mingchang Houa,
Kunyu Jina,
Qingzhong Li *a and
Shufeng Liu
*a and
Shufeng Liu b
b
aThe Laboratory of Theoretical and Computational Chemistry, School of Chemistry and Chemical Engineering, Yantai University, Yantai 264005, People's Republic of China. E-mail: liqingzhong1990@sina.com
bShandong Key Laboratory of Biochemical Analysis, College of Chemistry and Molecular Engineering, Qingdao University of Science and Technology, Qingdao 266042, PR China
First published on 11th June 2019
Abstract
A tetrel bond was characterized in the complexes of 1,4-diazabicyclo[2.2.2]octane (DABCO) with TH3X (T = C, Si, Ge; X= –Me, –H, –OH, –NH2, –F, –Cl, –Br, –I, –CN, –NO2). DABCO engages in a weak tetrel bond with CH3X but a stronger one with SiH3X and GeH3X. SiH3X is favorable to bind with DABCO relative to GeH3X, inconsistent with the magnitude of the σ-hole on the tetrel atom. The methyl group in the tetrel donor weakens the tetrel bond but an enhancing effect is found for the other substituents, particularly –NO2. The substitution effect is also related to the nature of the tetrel atom. The halogen substitution from F to I has a weakening effect in the CH3X complex but an enhancing effect in the SiH3X complex and a negligible effect in the GeH3X complex. The above abnormal results found in these complexes can be partly attributed to the charge transfer from the lone pair on the nitrogen atom of DABCO into the anti-bonding orbital σ*(T–X) of TH3X. The stability of both SiH3X and GeH3X complexes is primarily controlled by electrostatic interactions and polarization.
1. Introduction
For a long time, non-covalent interactions have attracted widespread interest because of their important roles in crystal engineering,1–3 chemical reactions4–6 and biological systems.7–9 Hydrogen bonding is one of the most important interactions and other types of interactions have also been proposed.10–12 Now these interactions are uniformly classified as σ-hole/π-hole interactions. The σ-hole refers to a region with positive electrostatic potentials along a covalent bond end13 and the π-hole is an area with positive electrostatic potentials perpendicular to a molecular plane.14 These interactions are also called halogen bond,15 chalcogen bond,16 pnicogen bond,17 and tetrel bond18 in view of the origin of these σ-holes/π-holes. These σ-holes/π-holes have an attractive interaction with electron donors such as neutral molecules with a lone pair,19–21 anions,22 radicals,23 metal hydrides,24,25 and π-molecules.26 Tetrel bonding is an attractive interaction between a group IV atom and an electron donor.18 This interaction had been explored before the name tetrel bond was proposed.27–29 For instance, Mitzel et al. reported Si⋯N interactions in the solid-state structure of Si(ONMe2)4 and related compounds27,28 and Si⋯halide contacts were described in perhalocyclohexasilane complexes.29The strength of tetrel bonding primarily determines its properties and applications since most chemical and biochemical processes are mainly accomplished by means of combination of various noncovalent interactions.30–32 Therefore, more attention was paid to the factors associated with the strength of tetrel bonding. In most cases, tetrel bonding is stronger for the heavier tetrel atom due to its smaller electronegativity and larger polarization. The magnitude of the σ-hole on the tetrel atom enlarges if this atom adjoins with electron-withdrawing atoms or groups, resulting in a stronger tetrel bond. This confirms the conclusion that most of tetrel bonds are dominated by electrostatic interaction.23 However, the bigger σ-hole may not bring out a stronger tetrel bond in some special circumstances. For instance, when N-heterocyclic carbene (NHC) acts as an electron donor, carbene tetrel bond is stronger for the Si compounds than for the Ge analogues although the latter has the bigger σ-hole.33 This shows that the dependence of tetrel bonding strength on the magnitude of σ-hole is also related to the nature of electron donor. If the electron donor is strong enough, the strength of tetrel bond is not solely determined by electrostatic and other contributions such as polarization are also important.
Substituents are also an effective method for regulating the strength of non-covalent interactions.34–43 6-OCF3-fulvene is favorable to engage in a weak H-bond with NH3 but a tetrel bond is formed when the four H atoms in 6-OCF3-fulvene are replaced by CN groups.34 The similar change was also reported for the proton effect on the interaction type between pyridine CF3/furan CF3 and NH3.44 For the tetrel-bonded complexes of formamidine with TH3F, electron-donating substituents in formamidine lead to the opposite effect on the strength of the tetrel bond: a weakening effect for –OH and –OCH3 but an enhancement for –CH3 and –NH2.41 The F substitution in TH4 (T = C–Sn) has an enhancing effect on the strength of tetrel bonding whether the H opposite to the electron donor or the three peripheral H atoms is replaced.42 Perfluorinated substitution TF4 yields the strongest tetrel bonding.42 The methyl substitution shows a reverse effect on the strength of tetrel bond to the F analogue.43 TX3+ (T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C, Ge, Sn, Pb; X
C, Ge, Sn, Pb; X![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H, F, Cl, Br) can bind with carbon monoxide and noble gas (Ng) atoms, and the nature of T-CO and T-Ng bonds is also affected by the halogen substitution.45–47 A question occurs: does the substitution in the tetrel donor on the strength of tetrel bonding depend on the electron-donating ability of an electron donor?
H, F, Cl, Br) can bind with carbon monoxide and noble gas (Ng) atoms, and the nature of T-CO and T-Ng bonds is also affected by the halogen substitution.45–47 A question occurs: does the substitution in the tetrel donor on the strength of tetrel bonding depend on the electron-donating ability of an electron donor?
1,4-Diazabicyclo[2.2.2]octane (DABCO) was often used as an organic base in organic syntheses because of its less sterically hindered nitrogen atoms. Using DABCO not only increases the yield of the Morita–Baylis–Hillman (MBH) reaction but also shows very pronounced regioselectivity.48,49 Importantly, the MBH reaction of benzaldehyde with acrylamide under DABCO catalysis can be carried out in an aqueous system.50 In addition, as a good linker, DABCO can also form structurally stable complexes with a variety of organic and organometallic compounds.51 Similarly, there are some studies on the non-covalent interactions such as hydrogen and halogen bonds involved with DABCO.52–57 A new supramolecular fluorine organic catalyst was prepared by halogen bonding between perfluorooctyl iodide and DABCO, which effectively promoted Baylis–Hillman reaction.53 DABCO participates in a stronger halogen bond than other neutral bases, indicating that DABCO is a good electron donor.57
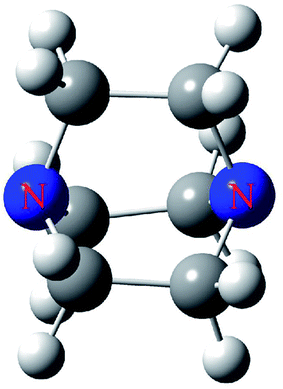
In this paper, we selected DABCO (Fig. 1) as the electron donor to bind with TH3X (T = C, Si, Ge; X= –Me, –H, –OH, –NH2, –F, –Cl, –Br, –I, –CN, –NO2). The following questions are answered. How to predict and characterize the tetrel bond between both molecules? Is the strength of tetrel bond consistent with the magnitude of σ-hole on the tetrel atom? How the substituents affect the strength of tetrel bond? Does this substitution effect depend on the nature of the tetrel atom? These tetrel-bonded complexes were studied in view of geometries, energetics, frequencies, charge transfer, orbital interaction, topological analysis and energy decomposition.
2. Methods
All calculations were performed using the Gaussian 09 software.58 First, the geometries of the complexes and monomers were optimized with the aug-cc-pVDZ basis set using the second-order Møller–Plesset perturbation theory (MP2) method. And then their frequencies were calculated at the same level to affirm that the optimized structures are minima on the potential energy surface and to analyze the frequency shifts. The interaction energy was calculated as difference between the energy of complex and the energies of monomers with their geometries in the complex, and this quantity was corrected for zero-point energy (ZPE) and basis set superposition error (BSSE) using the Boys and Bernardi method.59The electrostatic potentials of monomers were calculated on the 0.001 au isodensity using the Wave Function Analysis–Surface Analysis Suite (WFA-SAS) program.60 The AIM2000 package61 was used to assess the topological parameters at bond critical point (BCP) including electron density, its Laplacian, and energy density. Using the nature bond orbital (NBO) program,62 charge transfer and orbital interactions were obtained. In order to reveal the nature of the interaction, the GAMESS program63 was used to decompose the interaction energy into five terms with physical meaning at the MP2/aug-cc-pVDZ level using the Localized Molecular Orbital-Energy Decomposition Analysis (LMOEDA) method.64
3. Results and discussion
3.1. MEPs of monomers
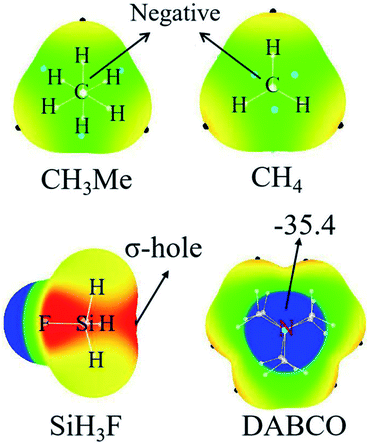
Fig. 2 represents the MEP maps of DABCO and three representative molecules of TH3X. First, there is a blue region (negative MEPs) on either side of the DABCO molecule, corresponding to the lone pair on the two nitrogen atoms in this molecule. And the most negative MEP on the two N atoms is the same with a value of −35.4 kcal mol−1. Then, let's have a look at TH3X. Considering the similarity for the MEP maps of TH3X with different X groups, we only plotted the MEP map of SiH3F, CH3Me and CH4 in Fig. 2. A σ-hole (red area) with positive MEPs is found at the X–T bond end in TH3X excluding CH3Me and CH4. In the latter two molecules, the central carbon atom is surrounded by negative MEPs. Therefore, both CH4 and CH3Me cannot form a tetrel bond with Lewis bases.Table 1 lists the extreme value of the electrostatic potential at the end of the X–T bond, which is arranged in an increasing sequence. When X is hold, the σ-hole enlarges from CH3X to SiH3X to GeH3X due to the smaller electronegativity and larger polarization. The methyl substituent results in a smaller σ-hole for T = Si and Ge or a more negative MEP on the C atom. This means that the methyl group in the tetrel donor is electron-donating. This electron-donating role of methyl group is also related to the nature of the tetrel atom and its effect is largest in SiH3Me. When X = NH2 and OH, the σ-hole is enlarged since the N/O atom has greater electronegativity than the tetrel atom and the larger enlargement is found for the –OH group with the similar reason. When X = halogen, the σ-hole is further enlarged and its enlargement increases from the heavier halogen atom to the lighter halogen atom. As expected, the stronger electron-withdrawing groups CN and NO2 lead to the much larger σ-hole.
| T = C | Vmax | T = Si | Vmax | T = Ge | Vmax |
|---|---|---|---|---|---|
| X = CH3 | −2.2 | X = CH3 | 16.0 | X = CH3 | 15.7 |
| X = H | −2.1 | X = H | 22.1 | X = H | 21.0 |
| X = NH2 | 4.1 | X = NH2 | 22.5 | X = NH2 | 25.5 |
| X = OH | 12.0 | X = OH | 32.1 | X = OH | 36.8 |
| X = I | 16.3 | X = I | 38.5 | X = I | 41.0 |
| X = Br | 19.3 | X = Br | 40.7 | X = Br | 44.3 |
| X = Cl | 20.3 | X = Cl | 41.7 | X = Cl | 45.9 |
| X = F | 24.1 | X = F | 45.0 | X = F | 50.8 |
| X = CN | 26.5 | X = CN | 47.1 | X = CN | 48.1 |
| X = NO2 | 34.9 | X = NO2 | 61.8 | X = NO2 | 63.1 |
3.2. Structures and interaction energies
Fig. S1 of ESI† shows the MP2/aug-cc-pVDZ optimized structures of all binary complexes. First, let's study the carbon-bonded complexes formed by CH3X. Since there is no σ-hole in CH3Me and CH4, the corresponding carbon-bonded complex is not obtained. In general, the N–N–T angle is arranged linearly. However, there is no such linear arrangement in the carbon-bonded complexes. The nonlinear arrangement of some C-containing complexes such as DABCO–CH3NH2 can partly attributed to its weak nature and thus it belongs to a van der Waals interaction without directionality, while more unexpected structures are mainly caused by the repulsion between the H atoms in both molecules.The corresponding binding distances of all complexes are listed in Table 2. For C-bond complexes, the binding distance is shorter than the sum of the corresponding atomic van der Waals radii (RC⋯N = 3.2 Å), except for CH3NH2 of 3.291 Å. In spite of Si and Ge with bigger atomic radii, the respective binding distance is shorter than that of C-bond analogue, and their binding distances are 2.1–2.7 Å and 2.2–2.8 Å, respectively. The relationship between the binding distance and the substituent is worth considering. In most cases, if the substituent causes a bigger σ-hole, the corresponding separation decreases. Interestingly, some exceptions are found. The methyl group elongates the Si⋯N distance but shortens the Ge⋯N distance, which is inconsistent with the σ-hole of the Ge atom. For X = halogen, with the increase of X atomic mass, the C⋯N distance prolongates, while the Si⋯N and Ge⋯N distances reduce, inconsistent with the change of the σ-hole on the Si/Ge atom. Although the NO2 substitution leads to the larger σ-hole than does the F atom, the C⋯N distance in the CH3NO2 complex is longer than that in the CH3F counterpart.
| T = C | R | T = Si | R | T = Ge | R |
|---|---|---|---|---|---|
| X = CH3 | — | X = CH3 | 2.674 | X = CH3 | 2.773 |
| X = H | — | X = H | 2.657 | X = H | 2.787 |
| X = NH2 | 3.291 | X = NH2 | 2.423 | X = NH2 | 2.550 |
| X = OH | 3.147 | X = OH | 2.304 | X = OH | 2.417 |
| X = I | 3.073 | X = I | 2.179 | X = I | 2.313 |
| X = Br | 3.036 | X = Br | 2.189 | X = Br | 2.314 |
| X = Cl | 3.058 | X = Cl | 2.200 | X = Cl | 2.317 |
| X = F | 3.013 | X = F | 2.222 | X = F | 2.325 |
| X = CN | 3.163 | X = CN | 2.247 | X = CN | 2.404 |
| X = NO2 | 3.029 | X = NO2 | 2.122 | X = NO2 | 2.241 |
Upon complexation, the T–X bond is elongated and its elongation is generally related to the strength of tetrel bond (Table S1†). Accompanied with the bond elongation, this bond stretch vibration displays a red shift and this red shift in most complexes is big enough to be observed with experiments.
The interaction energies of all complexes are listed in Table 3. Firstly, we focus on the tetrel bonding strength with different tetrel atoms. Regardless of the X substituent, the interaction energy sequentially increases from CH3X to GeH3X to SiH3X. Generally, the bigger σ-hole on the tetrel atom engages in the stronger tetrel bond. However, for the N electron donor in DABCO, the smaller σ-hole on the Si atom forms a stronger tetrel bond than the σ-hole on the Ge atom. Such abnormal result was also reported in the σ-hole tetrel-bonded complexes with NHC,33 H3ZO (Z = N, P, As),65 formamidine41 as the strong electron donors. The moderate base such as NH3 usually participates in a stronger tetrel bond with GeH3X relative to SiH3X, while an opposite result is obtained when X is 6-O-fulvene.34 This abnormality is partially ascribed to the fact that the silicon atom is more easily polarized than the Ge atom when it binds with a strong Lewis base.
| T = C | ΔE | T = Si | ΔE | T = Ge | ΔE |
|---|---|---|---|---|---|
| X = CH3 | — | X = CH3 | −3.7 | X = CH3 | −2.7 |
| X = H | — | X = H | −3.7 | X = H | −2.7 |
| X = NH2 | −0.9 | X = NH2 | −7.2 | X = NH2 | −5.5 |
| X = OH | −1.2 | X = OH | −11.2 | X = OH | −9.1 |
| X = I | −1.7 | X = I | −18.4 | X = I | −13.7 |
| X = Br | −1.8 | X = Br | −18.1 | X = Br | −13.9 |
| X = Cl | −2.0 | X = Cl | −17.5 | X = Cl | −13.9 |
| X = F | −2.0 | X = F | −16.4 | X = F | −13.7 |
| X = CN | −2.2 | X = CN | −14.9 | X = CN | −10.4 |
| X = NO2 | −2.7 | X = NO2 | −25.0 | X = NO2 | −18.9 |
Table S2† lists deformation energy of the complexes. The deformation energy is defined as the energy difference between the isolated molecules and the molecules within the geometry of the complex. This deformation energy is very small (∼0.5 kcal mol−1) in the CH3X complexes, indicating that both molecules exhibit small distortion. The difference in the deformation energy between the SiH3X and GeH3X complexes ranges from 0.5 to 3.1 kcal mol−1. The tetrel bond in the CH3X complex is much weaker than that in the SiH3X and GeH3X complexes.
Then we analyze the effect of the X substituent on the strength of tetrel bond. The methyl group in the tetrel donor weakens the tetrel bond, and this weakening effect is very slight. The role of methyl groups has been explored in different types of interactions such as OH⋯O hydrogen bond66 and halogen bond.67 Generally, the methyl group in both electron donors and acceptors plays an enhancing role in hydrogen bonds. However, the methyl group in the electron acceptor has a weakening effect on the strength of tetrel bond. For –NH2 and –OH groups, both of them enhance the tetrel bond due to their electron-withdrawing character, and this enhancing effect is larger for the –OH group with an increase of more than 200% in the interaction energy. For the halogen substitution, its effect depends on the nature of the tetrel atom. In the C-bond complex, the tetrel bond is stronger in sequence of I < Br < Cl < F, consistent with the σ-hole at the C–X bond end. In the Si-bond complex, an opposite trend is found. In the Ge-bond complex, the halogen substitution has little effect on the strength of tetrel bond. This shows that the strength of tetrel bond is not only affected by electrostatic interaction but also related to other factors. Although –CN group has the stronger electron-withdrawing ability than –F substitution, the former results in a weaker tetrel bond than the latter in the Si and Ge complexes, inconsistent with the magnitude of the σ-hole. The different in the interaction energy between the TH3CN and TH3F complexes varies from 1.5 kcal mol−1 for SiH3X to 3.3 kcal mol−1 for GeH3X. As expected, NO2 is the strongest electron-withdrawing group and results in the largest o-hole, thus the interaction energy is largest in the TH3NO2 complex.
In all, the strength of tetrel bond can be adjusted with the substituent in the tetrel donor. In general, the methyl group weakens the tetrel bond and the other groups strengthen the tetrel bond. Moreover, the influence of substituent is also related to the nature of the tetrel atom. For example, the halogen atom has a different effect on the strength of tetrel bond when the tetrel donor is varied. In addition, the X substituent has a prominent effect on the strength of tetrel bond. For instance, the –NO2 group increases the interaction energy from −3.7 kcal mol−1 in the SiH4 complex to −25.0 kcal mol−1 in the SiH3NO2 complex, increased by more than four times. Therefore, the substituent is feasible method for regulating the strength of tetrel bond.
It is interesting to compare different types of interactions involving DABCO. The interaction energy corrected for BSSE was calculated at the MP2/aug-cc-pVTZ level to be respectively −14.6, −19.6, and −26.1 kcal mol−1 in the SiH3F complexes with formamidine,41 H3NO,64 and NHC,33 which are often taken as stronger electron donors. The interaction energy corrected for BSSE and ZPE at the MP2/aug-cc-pVDZ level is −16.4 kcal mol−1 in DABCO–SiH3F. Thus DABCO is also a good electron donor in the tetrel bond. At the CCSD(T)/CBS level, the interaction energy was in a range of 9–26.5 kcal mol−1 in the halogen-bonded complexes of DABCO with dihalogen.57 Thus we think that DABCO has a comparable affinity to the halogen and tetrel atoms.
In most hydrogen bonds, both binding distance and interaction energy display a linear relationship. Fig. S2† shows the relationship between the binding distance and the interaction energy in the tetrel-bonded complexes. No relationship is found for them in the CH3X complex, while a quadratic relationship is present between them in the SiH3X and GeH3X complexes, with a correlation coefficient of 0.993 and 0.996, respectively.
3.3. AIM analyses
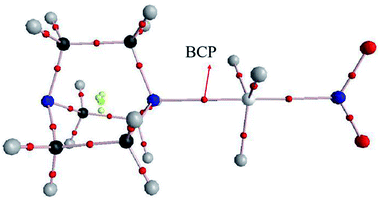
AIM analysis can provide some useful information for the existence of noncovalent interactions as well as the strength and nature of each interaction. Fig. 3 shows the AIM diagram obtained by AIM2000 software. We only plotted the AIM diagram of DABCO⋯GeH3NO2 since others are similar. Obviously, there is a Ge⋯N BCP, providing an evidence for the existence of a tetrel bond.Table 4 presents the topological parameters including the electron density (ρ), its Laplacian (∇2ρ), and total energy density (H) at the intermolecular BCP in the TH3X complexes. The electron density at the C⋯N BCP is small, less than 0.011 au, and its change is irregular. The electron densities at the Si⋯N and Ge⋯N BCPs are comparable each other and they exhibit an exponential relationship with the binding distance as shown in Fig. S3.† The corresponding correlation coefficients are 0.994 and 0.988. Both Laplacian and energy density at the C⋯N BCP are positive, confirming the weak interaction and a closed-shell interaction in the CH3X complex. However, in the SiH3X and GeH3X complexes, the energy density becomes negative though its Laplacian is still positive. This indicates that the Si⋯N and Ge⋯N tetrel bond has a partially covalent character.68–77 The stronger Si⋯N interaction has the more negative energy density than the Ge⋯N analogue.
| T = C | T = Si | T = Ge | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ρ | ∇2ρ | H | ρ | ∇2ρ | H | ρ | ∇2ρ | H | |
| X = CH3 | — | — | — | 0.024 | 0.042 | −0.003 | 0.022 | 0.052 | −0.001 |
| X = H | — | — | — | 0.025 | 0.041 | −0.004 | 0.024 | 0.050 | −0.002 |
| X = NH2 | 0.005 | 0.023 | 0.001 | 0.035 | 0.047 | −0.010 | 0.035 | 0.047 | −0.010 |
| X = OH | 0.008 | 0.029 | 0.001 | 0.042 | 0.063 | −0.015 | 0.041 | 0.100 | −0.007 |
| X = I | 0.009 | 0.034 | 0.002 | 0.048 | 0.137 | −0.014 | 0.048 | 0.136 | −0.010 |
| X = Br | 0.010 | 0.035 | 0.002 | 0.050 | 0.102 | −0.018 | 0.051 | 0.119 | −0.012 |
| X = Cl | 0.011 | 0.033 | 0.002 | 0.050 | 0.096 | −0.018 | 0.050 | 0.119 | −0.012 |
| X = F | 0.009 | 0.037 | 0.002 | 0.046 | 0.090 | −0.004 | 0.049 | 0.119 | −0.011 |
| X = CN | 0.008 | 0.029 | 0.001 | 0.046 | 0.072 | −0.017 | 0.043 | 0.100 | −0.008 |
| X = NO2 | 0.010 | 0.034 | 0.002 | 0.056 | 0.144 | −0.019 | 0.059 | 0.137 | −0.016 |
3.4. NBO analyses
The orbital interaction and charge transfer were analyzed for all complexes. For the C-bond complexes, there is only one type of orbital interaction: Lp(N) → σ*(C–X), where Lp(N) denotes the lone pair orbital of N atom and σ*(C–X) is the anti-bonding orbital of C–X bond. However, for the Si- and Ge-bond complexes, there are two types of orbital interactions. In addition to Lp(N) → σ*(T–X), there is also an orbital interaction of Lp(N) → σ*(T–H). The strength of these orbital interactions is estimated with second-order perturbation energies in Table 5, where E1(2) is for Lp(N) → σ*(T–X) and E2(2) for the sum of three Lp(N) → σ*(T–H) orbital interactions. From the table we can see that for the C-bond system, E1(2) is very small, about 0.5–2.0 kcal mol−1, consistent with the weak interaction in the C-bond complex. The Si- and Ge-bond complexes have large E(1) values, and E1(2) is larger than E2(2). Thus the Lp(N) → σ*(T–X) orbital interaction is dominant in the tetrel bond. Regardless of the orbital interaction, the value of E(2) in the Si-bond system is greater than that of the Ge-bond system, which has the same order as the interaction energy. For the halogen substitution, both types of orbital interactions show an increasing tendency from F to I, particularly for the Lp(N) → σ*(T–X) orbital interaction. Therefore, some abnormal results in the tetrel bond can be partly explained with the orbital interactions.| CT | E1(2) | E2(2) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| T = C | T = Si | T = Ge | T = C | T = Si | T = Ge | T = C | T = Si | T = Ge | |
| a E1(2) and E2(2) correspond to the Lp(N) → σ*(T–R) and Lp(N) → σ*(T–H) orbital interactions, respectively. | |||||||||
| X = CH3 | — | 0.038 | 0.030 | — | 8.0 | 7.3 | — | 2.7 | 2.3 |
| X = H | — | 0.037 | 0.027 | — | 7.5 | 6.3 | — | 2.6 | 2.2 |
| X = NH2 | 0.003 | 0.064 | 0.051 | 0.5 | 14.5 | 12.7 | — | 5.7 | 4.5 |
| X = OH | 0.003 | 0.083 | 0.071 | 1.1 | 19.1 | 17.1 | — | 7.8 | 6.5 |
| X = I | 0.004 | 0.121 | 0.100 | 1.6 | 31.0 | 27.5 | — | 10.3 | 8.4 |
| X = Br | 0.005 | 0.118 | 0.101 | 1.8 | 28.7 | 26.2 | — | 10.1 | 8.3 |
| X = Cl | 0.005 | 0.113 | 0.099 | 1.7 | 27.1 | 24.8 | — | 9.9 | 8.2 |
| X = F | 0.005 | 0.098 | 0.089 | 2.1 | 23.0 | 21.2 | — | 9.0 | 7.9 |
| X = CN | 0.002 | 0.105 | 0.081 | 0.8 | 22.3 | 18.1 | — | 9.1 | 6.7 |
| X = NO2 | 0.005 | 0.140 | 0.122 | 2.0 | 33.6 | 30.9 | — | 12.0 | 10.3 |
The formation of tetrel-bonded complexes leads to charge transfer from the Lewis base to the acid. So the amount of charge transfer can to a certain extent reflect the strength of tetrel bond. For the C-bond complexes, the value of charge transfer is very small, only between 0.002–0.005e, corresponding to the weak interaction. For the Si- and Ge-bond complexes, the amount of charge transfer is relatively large, and the Si complex has the greater charge transfer than the Ge analogue. We also made a graph of the relationship between charge transfer and interaction energy, as shown in Fig. S4.† No relationship is found in the C-bond complex, while a linear relationship is present between them for the Si and Ge complexes. The correlation coefficients are 0.973 and 0.983 for the Si and Ge systems, respectively. Therefore, charge transfer is of great important in the formation of Si- and Ge-bond complexes.
3.5. Energy decomposition analyses
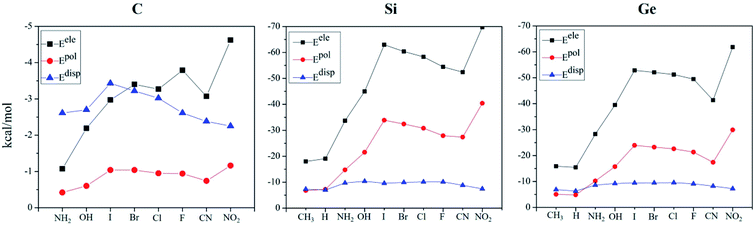
To have a deep insight into the origin of the tetrel bond, the interaction energies of all complexes were decomposed into electrostatic (Eele), exchange (Eex), repulsion (Erep), polarisation (Epol), and dispersion energies (Edisp). Both Erep and Eex are partly cancelled each other, so we only focused on three attractive terms (Eele, Epol, and Edisp). For easy comparison, these terms were plotted in Fig. 4. For the C-bond complex, Epol is smallest; Edisp dominates over Eele when the substituent is NH2, OH and I, while Eele exceeds Edisp in the case of the remaining substituents. These quantities have a similar variation in the Si- and Ge-bond complexes. Eele is greater than Epol and Edisp, confirming the electrostatic nature of tetrel bonding. For the different substituents, both Eele and Epol change uniformly, and Edisp is little changed. For the halogen substitution, both Eele and Epol increase from F to I. Fig. S5† shows the relationship between the total interaction energy and Eele/Epol in the Si- and Ge-bond complexes. Obviously, a good linear relationship is present between them. Thus the strength of tetrel bond in the TH3X (T = Si and Ge) complex is jointly controlled by electrostatic and polarization interactions.4. Conclusions
The complexes of DABCO⋯TH3X (T = C, Si, and Ge) have been studied with theoretical methods in view of the geometrics, energetics, charge transfer, orbital interactions, and AIM parameters. The main conclusions are summarized as:(1) The interaction energy of DABCO⋯TH3X is comparable with that of stronger Lewis bases such as NHC, formamidine, and H3NO, indicating that DABCO is also a good electron donor in the tetrel bond.
(2) The tetrel bond strengthens in order of C < Ge < Si, inconsistent with the magnitude of σ-hole on the tetrel atom. It is primarily attributed to the stronger orbital interaction in the SiH3X systems.
(3) The methyl group in the tetrel donor weakens the tetrel bond, while the other substituents enhance it. The substituents have a small effect on the strength of tetrel bond in the C-bond complex but a larger effect in the Si- and Ge-bond complexes. For the halogen substitution from F to I, the tetrel bond weakens a little in the C-bond complex, strengthens in the Si-bond complex, and is almost not changed in the Ge-bond complex. Thus the substitution effect on the strength of tetrel bond is also related to the nature of the tetrel atom. The strongest electron-withdrawing group NO2 results in the strongest tetrel bond.
(5) The tetrel bond is a closed-shell interaction in the C-bond complex but a partially covalent interaction in the Si- and Ge-bond complexes.
(6) Three attractive terms (Eele, Epol, and Edisp) are small and show an irregular change in the C-bond complex but a similar variation is found in the Si- and Ge-bond complexes. In the stronger tetrel bond, both Eele and Epol display a linear relationship with the interaction energy although the former has a larger contribution.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (21573188) and Open Subject of Faculty of Chemistry of QingDao University of Science and Technology (QUSTHX201807).References
- G. Mahmoudi, A. Bauzá and A. Frontera, Dalton Trans., 2016, 45, 4965–4969 RSC.
- G. Mahmoudi, A. Bauzá, M. Amini, E. Molins, J. T. Mague and A. Frontera, Dalton Trans., 2016, 45, 10708–10716 RSC.
- M. S. Gargari, V. Stilinović, A. Bauzá, A. Frontera, P. McArdle, D. V. Derveer, S. W. Ng and G. Mahmoudi, Chem.–Eur. J., 2016, 21, 17951–17958 CrossRef PubMed.
- S. J. Grabowski, Phys. Chem. Chem. Phys., 2014, 16, 1824–1834 RSC.
- M. X. Liu, J. B. Cheng, H. B. Li and Q. Z. Li, J. Chem. Phys., 2016, 145, 224310 CrossRef PubMed.
- J. Mikosch, S. Trippel, C. Eichhorn, R. Otto, U. Lourderaj, J. X. Zhang, W. L. Hase, M. Weidemüller and R. Wester, Science, 2008, 319, 183–186 CrossRef CAS PubMed.
- G. R. Desiraju, J. Am. Chem. Soc., 2001, 123, 191–192 Search PubMed.
- X. García-LLinás, A. Bauzá, S. K. Seth and A. Frontera, J. Phys. Chem. A, 2017, 121, 5371–5376 CrossRef PubMed.
- V. R. Mundlapati, D. K. Sahoo, S. Bhaumik, S. Jena, A. Chandrakar and H. S. Biswal, Angew. Chem., Int. Ed., 2018, 57, 16496–16500 CrossRef CAS PubMed.
- P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189 RSC.
- J. S. Murray, P. Lane and P. Politzer, J. Mol. Model., 2009, 15, 723–729 CrossRef CAS PubMed.
- A. Bauzá, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2015, 16, 2496–2517 CrossRef PubMed.
- T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296 CrossRef CAS PubMed.
- J. S. Murray, P. Lane, T. Clark, K. E. Riley and P. Politzer, J. Mol. Model., 2012, 18, 541–548 CrossRef CAS PubMed.
- G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713 CAS.
- W. Z. Wang, B. M. Ji and Y. Zhang, J. Phys. Chem. A, 2009, 113, 8132–8135 CrossRef CAS PubMed.
- S. Zahn, R. Frank, E. Hey-Hawkins and B. Kirchner, Chem.–Eur. J., 2011, 17, 6034–6038 CrossRef CAS PubMed.
- A. Bauzá, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2013, 52, 12317–12321 CrossRef PubMed.
- S. Scheiner, J. Phys. Chem. A, 2015, 119, 9189–9199 CrossRef CAS PubMed.
- K. J. Donald and M. Tawfik, J. Phys. Chem. A, 2013, 117, 14176–14183 CrossRef CAS PubMed.
- A. Bundhun, P. Ramasami, J. S. Murray and P. Politzer, J. Mol. Model., 2013, 19, 2739–2746 CrossRef CAS PubMed.
- S. A. C. Mcdowell and J. A. Joseph, Phys. Chem. Chem. Phys., 2014, 16, 10854–10860 RSC.
- Q. Z. Li, X. Guo, X. Yang, W. Z. Li, J. B. Cheng and H. B. Li, Phys. Chem. Chem. Phys., 2014, 16, 11617–11625 RSC.
- Q. Z. Li, H. Y. Zhuo, H. B. Li, Z. B. Liu, W. Z. Li and J. B. Cheng, J. Phys. Chem. A, 2015, 119, 2217–2224 CrossRef CAS PubMed.
- M. D. Esrafili and F. Mohammadiansabet, J. Mol. Model., 2015, 21, 1–8 CrossRef PubMed.
- D. Mani and E. Arunan, J. Phys. Chem. A, 2014, 118, 10081–10089 CrossRef CAS PubMed.
- N. W. Mitzel and U. Losehand, Angew. Chem., Int. Ed., 1997, 36, 2807–2809 CrossRef CAS.
- N. W. Mitzel, A. J. Blake and D. W. H. Rankin, J. Am. Chem. Soc., 1997, 119, 4143–4148 CrossRef CAS.
- S. B. Choi, B. K. Kim, P. Boudjouk and D. G. Grier, J. Am. Chem. Soc., 2001, 123, 8117–8118 CrossRef CAS PubMed.
- M. D. Esrafili, H. Behzadi and N. L. Hadipour, Chem. Phys., 2008, 348, 175–180 CrossRef CAS.
- I. Alkorta, F. Blanco and J. Elguero, Struct. Chem., 2009, 20, 63–71 CrossRef CAS.
- M. D. Esrafili and S. Shahabivand, Struct. Chem., 2014, 25, 403–408 CrossRef CAS.
- M. X. Liu, Q. Z. Li, W. Z. Li and J. B. Cheng, Struct. Chem., 2017, 28, 823–831 CrossRef CAS.
- M. C. Hou, S. B. Yang, Q. Z. Li, J. B. Cheng, H. B. Li and S. F. Liu, Molecules, 2019, 24, 10 CrossRef PubMed.
- K. Nakamura, T. Hatakeyama and H. Hatakeyama, Polym. J., 1983, 15, 361–366 CrossRef CAS.
- M. Yoosefian, H. Raissi, E. S. Nadim, F. Farzad, M. Fazli, E. Karimzade and A. Nowroozi, Int. J. Quantum Chem., 2011, 111, 3505–3516 CAS.
- N. Kim, H. Lee, K. Choi, J. A. Yu, C. J. Yoon, J. Park and Y. S. Choi, J. Phys. Chem. A, 2000, 104, 5572–5578 CrossRef CAS.
- M. Solimannejad, M. Malekani and I. Alkorta, J. Phys. Chem. A, 2013, 117, 5551–5557 CrossRef CAS PubMed.
- A. C. C. Carlsson, K. Mehmeti, M. Uhrbom, A. Karim, M. Bedin, R. Puttreddy, R. Kleinmaier, A. A. Neverov, B. Nekoueishahraki, J. Gräfenstein, K. Rissanen and M. Erdélyi, J. Am. Chem. Soc., 2016, 138, 9853–9863 CrossRef CAS PubMed.
- A. Bauzá, D. Quiñonero, A. Frontera and P. M. Deyà, Phys. Chem. Chem. Phys., 2011, 13, 20371–20379 RSC.
- H. L. Xu, J. B. Cheng, X. F. Yu and Q. Z. Li, ChemistrySelect, 2018, 3, 2842–2849 CrossRef CAS.
- S. Scheiner, J. Phys. Chem. A, 2017, 121, 5561–5568 CrossRef CAS PubMed.
- W. B. Dong, Q. Z. Li and S. Scheiner, Molecules, 2018, 23, 1681 CrossRef PubMed.
- M. X. Liu, Q. Z. Li and S. Scheiner, Phys. Chem. Chem. Phys., 2017, 19, 5550–5559 RSC.
- S. Pan, D. Moreno, S. Ghosh, P. K. Chattaraj and G. Merino, J. Comput. Chem., 2016, 37, 226–236 CrossRef CAS PubMed.
- M. Ghara, S. Pan, A. Kumar, G. Merino and P. K. Chattaraj, J. Comput. Chem., 2016, 37, 2202–2211 CrossRef CAS PubMed.
- S. Pan, D. Moreno, G. Merino and P. K. Chattaraj, ChemPhysChem, 2014, 15, 3554–3564 CrossRef CAS PubMed.
- F. S. Fernandes, M. T. Rodrigues Jr, L. A. Zeoly, C. Conti, C. F. F. Angolini, M. N. Eberlin and F. Coelho, J. Org. Chem., 2018, 83, 15118–15127 CrossRef CAS PubMed.
- P. T. Kaye and R. S. Robinson, Synth. Commun., 1996, 26, 2085–2097 CrossRef CAS.
- S. H. Zhao, D. Wang, M. Wang, J. Tang and L. W. Zhang, Chin. J. Org. Chem., 2015, 35, 865–874 CrossRef CAS.
- R. Saravanakumar, B. Varghese and S. Sankararaman, J. Mol. Struct., 2014, 1076, 280–284 CrossRef CAS.
- M. Shiga, S. Kawaguchi, M. Fujibayashi, S. Nishihara, K. Inoue, T. Akutagawa, S. Noro, T. Nakamura and R. Tsunashima, Dalton Trans., 2018, 47, 7656–7662 RSC.
- S. Dordonne, B. Crousse, D. Bonnet-Delpon and J. Legros, Chem. Commun., 2011, 47, 5855–5857 RSC.
- A. Peuronen, A. Valkonen, M. Kortelainen, K. Rissanen and M. Lahtinen, Cryst. Growth Des., 2012, 12, 4157–4169 CrossRef CAS.
- Y. L. Ma, H. Ke, A. Valkonen, K. Rissanen and W. Jiang, Angew. Chem., Int. Ed., 2017, 57, 709–713 CrossRef PubMed.
- T. Asaji, K. Shido and H. Fujimori, J. Mol. Struct., 2018, 1169, 81–84 CrossRef CAS.
- P. Deepa, R. Sedlak and P. Hobza, Phys. Chem. Chem. Phys., 2014, 16, 6679–6686 RSC.
- M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb,J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision A02, Gaussian Inc., Wallingford, 2009 Search PubMed.
- S. B. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- F. A. Bulat, A. Toro-Labbé, T. Brinck, J. S. Murray and P. Politzer, J. Mol. Model., 2010, 16, 1679–1691 CrossRef CAS PubMed.
- R. F. W. Bader, AIM2000 program, version 2.0, McMasterUniversity, Hamilton, Canada, 2000 Search PubMed.
- A. E. Reed, L. A. Curtiss and F. A. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- P. F. Su and H. Li, J. Chem. Phys., 2009, 13, 014102 CrossRef PubMed.
- H. L. Xu, J. B. Cheng, H. B. Li, X. Yang and Q. Z. Li, Int. J. Quantum Chem., 2018, 118, e25660 CrossRef.
- Q. Z. Li, N. N. Wang and Z. W. Yu, J. Mol. Struct.: THEOCHEM, 2008, 862, 74–79 CrossRef CAS.
- Q. Z. Li, B. Jing, Z. B. Liu, W. Z. Li, J. B. Cheng, B. Z. Gong and J. Z. Sun, J. Chem. Phys., 2010, 133, 114303 CrossRef PubMed.
- W. D. Arnold and E. Oldfield, J. Am. Chem. Soc., 2000, 122, 12835–12841 CrossRef CAS.
- S. Pan, A. Gupta, S. Mandal, D. Moreno, G. Merino and P. K. Chattaraj, Phys. Chem. Chem. Phys., 2015, 17, 972–982 RSC.
- G. Jana, R. Saha, S. Pan, A. Kumar, G. Merino and P. K. Chattaraj, ChemistrySelect, 2016, 1, 5842–5849 CrossRef CAS.
- M. Ghara, S. Pan, J. Deb, A. Kumar, U. Sarkar and P. K. Chattaraj, J. Chem. Sci., 2016, 128, 1537–1548 CrossRef CAS.
- S. Pan, R. Saha, A. Kumar, A. Gupta, G. Merino and P. K. Chattaraj, Int. J. Quantum Chem., 2016, 116, 1016–1024 CrossRef CAS.
- S. Pan, R. Saha, S. Mandal and P. K. Chattaraj, Phys. Chem. Chem. Phys., 2016, 18, 11661–11676 RSC.
- G. Jana, S. Pan, G. Merino and P. K. Chattaraj, J. Phys. Chem. A, 2017, 121, 6491–6499 CrossRef CAS PubMed.
- G. Jana, S. Pan and P. K. Chattaraj, J. Phys. Chem. A, 2017, 121, 3803–3817 CrossRef CAS PubMed.
- G. Jana, S. Pan, G. Merino and P. K. Chattaraj, J. Phys. Chem. A, 2018, 122, 7391–7401 CrossRef CAS PubMed.
- G. Jana, S. Pan, E. Osorio, L. Zhao, G. Merino and P. K. Chattaraj, Phys. Chem. Chem. Phys., 2018, 20, 18491–18502 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra03351c |
| This journal is © The Royal Society of Chemistry 2019 |