Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effects of Mo alloying on stability and diffusion of hydrogen in the Nb16H phase: a first-principles investigation
Dianhui Wang†
 a,
Yang Wu†a,
Zhenzhen Wana,
Feng Wanga,
Zhongmin Wang*ab,
Chaohao Hu
a,
Yang Wu†a,
Zhenzhen Wana,
Feng Wanga,
Zhongmin Wang*ab,
Chaohao Hu *ab,
Xiaotian Wang
*ab,
Xiaotian Wang *c and
Huaiying Zhouab
*c and
Huaiying Zhouab
aSchool of Materials Science and Engineering, Guilin University of Electronic Technology, Guilin 541004, P. R. China. E-mail: zmwang@guet.edu.cn; chaohao.hu@guet.edu.cn
bGuangxi Key Laboratory of Information Materials, Guilin University of Electronic Technology, Guilin 541004, P. R. China
cSchool of Physical Science and Technology, Southwest University, Chongqing 400715, P. R. China. E-mail: xiaotianwang@swu.edu.cn
First published on 21st June 2019
Abstract
First-principles calculations and the method of climbing-image nudged elastic band were used to investigate the effects of Mo alloying on the structural stability, mechanical properties, and hydrogen-diffusion behavior in the Nb16H phase. The Nb12Mo4H phase (26.5 at% Mo) was found to be the most thermodynamically stable structure, with a low ΔHf value (−0.26 eV) and high elastic modulus. Calculations revealed that the tetrahedral interstitial site (TIS) was the predominant location of H in both Nb16H and Nb12Mo4H phases. The calculated H-diffusion energy barrier and the diffusion coefficient of the Nb12Mo4H phase were 0.153 eV and 5.65 × 10−6 cm2 s−1 (300 K), respectively, which suggest that the addition of Mo would lead to a lower energy barrier and high diffusion coefficients for the Nb16H phase, thus improving the hydrogen-permeation properties of Nb metal.
1. Introduction
Hydrogen is not only an important raw material for chemical and petrochemical industries, but also a potential clean fuel as well as a good energy carrier. Pure hydrogen does not exist as a natural resource like coal and oil, however. Since it has to be produced from hydrogen-containing compounds, a safe, low-cost, and highly efficient separation and purification technology is always required. Hydrogen-permeable alloy membranes have been well regarded as the most important materials for hydrogen separation and purification.1–5 Currently, group V metals (vanadium, niobium, and tantalum) have attracted many investigations as promising hydrogen-separation materials owing to their lower price and higher hydrogen permeability than those of currently used Pd-based alloys.3,6 However, there is still a large barrier to practical application of these metals because of their poor resistance to hydrogen embrittlement.3,7,8 Experimental studies have verified that alloying the metals is an effective way to solve this problem.6–9Niobium is one of the most promising hydrogen-permeable candidates for membranes because it possesses a good combination of excellent high-temperature mechanical properties and corrosion resistance.10–12 Recent theoretical research performed by Watanabe et al. revealed that the addition of W could decrease the hydrogen solubility in Nb and therefore improve its resistance to hydrogen embrittlement.6,13 Hu et al. performed a similar study and found that the addition of W can improve the mechanical properties of the Nb16H phase, decrease the structural stability of the Nb15WH (tetrahedral (T)) phase, lower the diffusion barrier of H, and enhance diffusion paths for H.14 Both W and Mo are high-Z refractory metals (i.e., refractory metals containing impurities with high atomic numbers (Z)) with similar physical properties. Moreover, Mo has several characteristic properties: compared with W, Mo has a lower melting point (2883 K) and a lower erosion rate, while H has higher diffusivity and lower solubility in Mo, leading to lower H retention.15–17 These characteristics make Mo an important alloying candidate for Nb-based alloy membranes for hydrogen permeation. However, since relevant works have not been reported in the literature, it is necessary to engage in first-principles theoretical investigations that are free from any experimental limitations on the effect of Mo addition on the structure and diffusion properties of the NbH phase in a first-principles way. Such calculations will also contribute to the understanding and design of H-storage and H-separation materials based on Nb.
The effects of the addition of Mo to the electronic structure, structural stability, H diffusion, and mechanical properties of the NbH phase were investigated by first-principles calculation based on density functional theory. Nb16H was purposely selected and four Mo atoms were added to reach the equivalent of an experimental composition of 25 at% Mo in NbH.6,7,13,18 The calculated results revealed that such addition would lead to a lower energy barrier of H diffusion, a higher diffusion coefficient, and improved mechanical properties.
2. Computational method
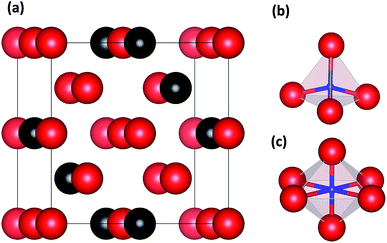
The calculations were carried out by using the Vienna Ab-initio Simulation Package (VASP).19 The interactions between core and valence electrons were described with the projector augmented wave (PAW).20 The exchange and correlation functions were generalized gradient approximations (GGAs) developed by Perdew et al.21 An energy cutoff of 360 eV was used for the plane-wave basis sets, and the K points set used in our calculations is 5 × 5 × 5 grid generated by Monkhorst–Pack schema.22 During structure relaxation of the lattice parameters, the volume and atomic positions were fully optimized with in-symmetry restrictions until the total energy converged to 10−5 eV in the self-consistent loop, and the criterion of force used in the calculations is 0.01 eV Å−1 atom−1.Accordingly, we built supercell models of basic defect structures in which a H atom was placed at the tetrahedral interstitial site (TIS) and another at the octahedral interstitial site (OIS). A unit cell of 2 × 2 × 2 (16 atoms) with a body-centered cubic (BCC) structure23 was selected for pure Nb, and a Mo atom was introduced to replace the Nb atom—a series of structures with the composition Nb16−xMox was thus obtained. One H atom was then added at the TIS and one at the OIS of BCC Nb and Nb16−xMox. Fig. 1 shows the schematic illustrations of Nb16−xMoxH (x = 4) with TIS and OIS.
To probe the diffusion properties of hydrogen in the bulk of the Nb–Mo alloy, the climbing image nudged elastic band (CI-NEB) method24 was used to determine the diffusion barriers between the initial and final positions. Four images were taken and all the images were relaxed until the maximum force on each atom was less than 0.01 eV Å−1 and the other computational parameters were the same as the above.
The diffusion coefficient (D) is also an important index that determines the diffusion velocity of H. According to the Arrhenius diffusion equation, D can be expressed by D = D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kT), where the D0, Ea, k, and T are the pre-exponential factor, diffusion energy barrier, the Boltzmann constant, and the absolute temperature, respectively. For a metal with a cubic structure, D0 can be expressed as
exp(−Ea/kT), where the D0, Ea, k, and T are the pre-exponential factor, diffusion energy barrier, the Boltzmann constant, and the absolute temperature, respectively. For a metal with a cubic structure, D0 can be expressed as 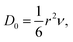 where r and ν are the jump distance and the vibration frequency, respectively. We calculated ν according to Zener and Wert's theory,25 which is approximately expressed by
where r and ν are the jump distance and the vibration frequency, respectively. We calculated ν according to Zener and Wert's theory,25 which is approximately expressed by 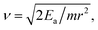 where m is the mass of the impurity atom. As it is already known that the mass of the H atom is 1.67 × 10−27 kg, the jumping distance of the TIS H in Nb was set as
where m is the mass of the impurity atom. As it is already known that the mass of the H atom is 1.67 × 10−27 kg, the jumping distance of the TIS H in Nb was set as 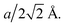
3. Results and discussion
3.1. Structure stability of Nb16−xMoxH phases
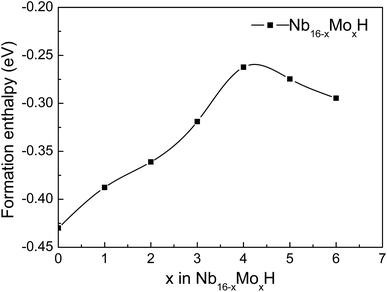
In order to investigate the effect of the amount of alloying Mo on the stability of the Nb16H phase, the heats of formation (ΔHf) of various Nb16−xMoxH (x = 0, 1, 2, 3, 4, 5, and 6) phases were calculated from the following equations:
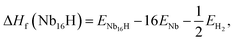 | (1) |
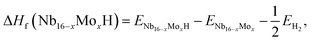 | (2) |
| Phase | Lattice constant, a (Å) | Mechanical property (GPa) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C11 | C12 | C13 | C23 | C22 | C33 | C44 | C55 | C66 | B | G | E | ||
| Nb16 | 6.60 | 244 | 139.3 | 13.7 | 174.2 | 24.3 | 69.7 | ||||||
| Nb16H (TIS) | 6.63 | 245 | 137.8 | 138 | 247.2 | 25.4 | 26.5 | 173.8 | 34.8 | 98 | |||
| Nb16H (OIS) | 6.58 | 242 | 148.3 | 128 | 274.4 | 14.5 | 13.7 | 174.1 | 26 | 74.4 | |||
| Nb12Mo4H (TIS) | 6.53 | 311 | 137.4 | 143 | 139.2 | 278.9 | 317.6 | 31.6 | 39 | 39.7 | 194.9 | 50.6 | 139.7 |
Several characteristics can be derived from Fig. 2 and Table 1. First, all of the Nb16−xMoxH phases are energetically favorable, with negative ΔHf values. The absolute values of ΔHf are very small (less than 0.2 eV), indicating that the Nb16−xMoxH phases can be stable. Second, the absolute value of the formation enthalpy of Nb16−xMoxH increases as the amount of alloying Mo increases from x = 0 to x = 4; it then decreases when x is above 4. The Nb12Mo4H phase has the highest absolute value of ΔHf, which is favorable for the dehydrogenation of the Nb16−xMoxH phase. Therefore, Nb12Mo4H was selected for further study. Third, the calculated formation enthalpy absolute values of Nb16H (TIS) and Nb16H (OIS) are 0.43 and 0.09 eV, respectively. Nb16H (TIS) has a clearly higher absolute value of 0.43 eV, which indicates that the TIS is thermodynamically more possible than the OIS for H in BCC Nb. Such results are in excellent agreement with similar experimental observations26–28 and theoretical work14 reported in the literature. Since the addition of Mo has no effect on the preferred location of H, and TIS is the predominant location of H in both Nb16H and Nb12Mo4H phases, only the Nb12Mo4H (TIS) phase was selected for further investigation of its mechanical properties. In addition, the Nb12Mo4H (TIS) phase is energetically less favorable, with higher ΔHf value than the corresponding Nb16H (TIS), suggesting that the addition of Mo would decrease the solubility of H in the TIS of Nb. A possible explanation has been offered by Yukawa et al.: the higher ΔHf basically induces an decrease in H solubility and hydrogen embrittlement.7,13,18
After the series of calculations for the supercell models, the lattice constants (a) of various Nb16H and Nb12Mo4H phases were obtained; the results are listed in Table 1. The calculated lattice constants of pure Nb, Nb16H (TIS and OIS) and Nb12Mo4H (TIS) are 6.60, 6.63, 6.58, and 6.53 Å, respectively. The values of pure Nb and Nb16H (TIS) match well with the corresponding experimental unit cell values of 6.61 and 6.63 Å.26–28 In addition, Mo has a smaller atomic radius than Nb, which may lead to a slight decrease in the lattice constant with the addition of Mo to the Nb16H phase.
3.2. Mechanical properties of Nb16H and Nb12Mo4H phases
To find out the effect of Mo alloying on the mechanical properties of Nb hydride, the elastic constants of Nb16H (TIS and OIS), Nb12Mo4H (TIS), and pure Nb were calculated for comparison. The specified elastic constant was obtained by analyzing the difference between the total energy of the original cell and that of the deformed cell under a series of small strains. For the BCC crystal of Nb, there are three independent components of elastic constants: C11, C12, and C44. Nb16H has tetragonal symmetry and possesses three more components: C13, C33, and C66. Mo doping reduces the symmetry to orthorhombic and thus adds two components: C22 and C23.29,30 The calculated elastic constants are listed in Table 1.According to the equations of elastic moduli and the criteria for mechanical stability, the mechanical stability is defined by the following restrictions for a tetragonal crystal:31,32
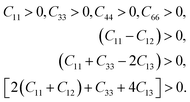 | (3) |
For an orthorhombic crystal, the criteria of mechanical stability are given by
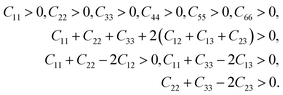 | (4) |
The results of elastic constants, Cij, indicate that both Nb16H and Nb12Mo4H phases meet the criteria for mechanical stability.
The obtained elastic constants were then used to calculate the bulk modulus (B) and shear modulus (G) from the Voigt–Reuss–Hill approximations.33,34 The Young's modulus (E) is determined using the equation E = 9BG/(3B + G).31 The values of B, G, and E of the Nb12Mo4H (TIS) phase are larger than those of the Nb16H (TIS and OIS) phase, indicating that Mo alloying improves the mechanical properties of the Nb16H phase, which possibly enhances the resistance against hydrogen embrittlement.
3.3. Electronic properties of Nb16H (TIS) and Nb12Mo4H (TIS)
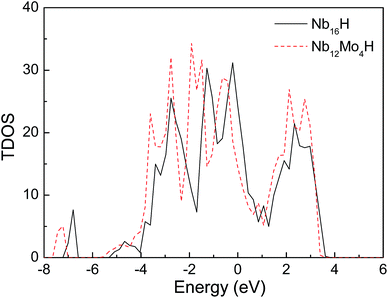
Fig. 3 displays the projected density of states (PDOS) of H atoms in the Nb16H (TIS) phase and the Nb12Mo4H (TIS) phase. It can be seen that there is an obvious difference between the PDOS of Nb16H (TIS) and that of Nb12Mo4H (TIS). The PDOS peaks at about −6.8 eV are primarily Nb d states in Nb16H (TIS), whereas the PDOS peaks of Nb12Mo4H (TIS) are dominated by the overlapping H s, Nb d, and Mo d states, indicating that the H atoms penetrated the alloy and bonded with the Nb atoms. After doping with Mo atoms, the hybridizations peaks between the H s state and the Nb d state are smaller and shifted toward lower energy. Fig. 4 shows the total density of states (TDOS) of H atoms in the Nb16H (TIS) and Nb12Mo4H phases. Compared with the TDOS of the Nb16H (TIS) phase, the TDOS of the Nb12Mo4H (TIS) below the Fermi level (EF) are shifted leftward to the positions with slightly higher binding energies. These features of electronic structures suggest that the Nb12Mo4H (TIS) phase should have a stronger chemical bonding than Nb16H (TIS), which is beneficial to hydrogen permeation and should help one understand the improved mechanical properties (B, E, and G) shown in Table 1. In addition, the PDOS peaks are energetically degenerate with the addition of Mo in all regions, which indicate that the Nb–H hybridization is remarkable and favorable for improving the stability of the corresponding system.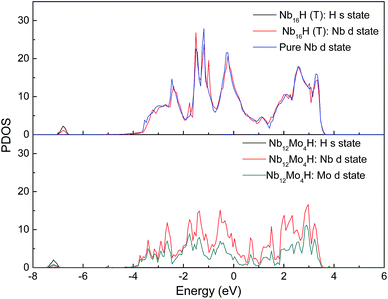 | ||
| Fig. 3 Comparison of the projected density of states (PDOS) of Nb16H (TIS) and Nb12Mo4H (TIS) phases. | ||
3.4. Diffusion and permeation of H in Nb and Nb12Mo4
Next, we investigated the effect of Mo addition on the diffusion of hydrogen in the Nb16H and Nb12Mo4H phases. The CI-NEB method was used to determine the minimum-energy path and the corresponding energy barrier for the process of H diffusion in the Nb and Nb12Mo4 phases.35–37 For both Nb and Nb12Mo4, there are three possible paths of H diffusion between TIS and OIS, namely, from TIS to TIS, from TIS to OIS, and from OIS to OIS. Since the diffusion path from OIS to OIS cannot not be realized because the TIS is just located along the path, it was excluded in our study.38–40We first investigated the pathways of H in the bulk of pure Nb. Generally, there are two pathways for H to diffuse in a BCC lattice, i.e., TIS → TIS and TIS → OIS. It can be clearly seen that the energy barrier from TIS to TIS in Nb is 0.225 eV, which is much lower than the corresponding value of 0.362 eV from TIS to OIS, suggesting that the diffusion path of H in bulk Nb should be mainly from TIS to TIS instead of TIS to OIS. For H diffusion in the Nb12Mo4 alloy, it can be clearly seen in Fig. 5 and 6 that the energy barrier from TIS to TIS (0.157 eV) is smaller than the corresponding value in Nb, and a similar observation can be seen from TIS to OIS. The above comparison demonstrates that the addition of Mo in Nb can make H diffusion easier with a smaller energy barrier.
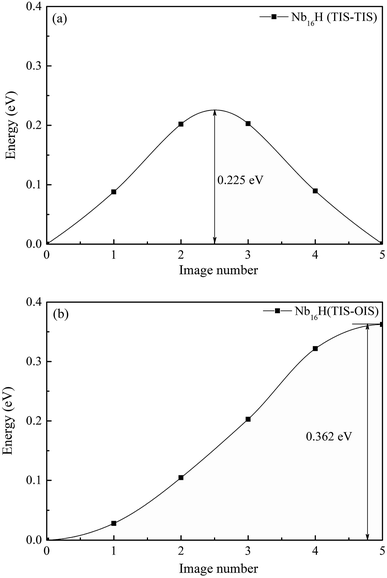 | ||
| Fig. 5 Migration barrier of H diffusion (a) from TIS to TIS and (b) from TIS to OIS in the Nb16H phase. | ||
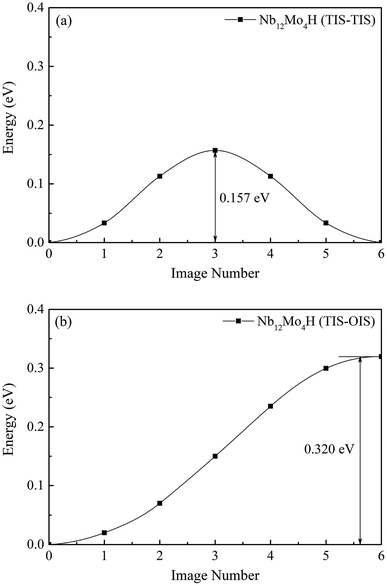 | ||
| Fig. 6 Migration barrier of H diffusion (a) from TIS to TIS and (b) from TIS to OIS in the Nb12Mo4H phase. | ||
The H-diffusion energy barrier calculated for pure Nb and the Nb12Mo4 alloy is 0.225 and 0.157 eV, respectively. The vibration frequency of pure Nb and the Nb12Mo4 alloy is 2.686 × 1013 s−1 and 2.345 × 1013 s−1, respectively. According to the Arrhenius diffusion equation, the calculated diffusion coefficient is 8.87 × 10−7 cm2 s−1 for pure Nb and 5.65 × 10−6 cm2 s−1 for the Nb12Mo4 phase at the standard room temperature of 300 K. From the above analysis, it can be deduced that the addition of Mo should have an important effect on the diffusion of H in Nb, i.e., H diffusion in the Nb12Mo4 phase should become energetically more favorable when the energy barrier is lower. These characteristics would therefore bring about an increase in the H-diffusion coefficient and an improvement in H permeability. In other words, the addition of Mo could lower the diffusion barrier of H, which would fundamentally lead to higher H diffusion and high H permeability in the Nb12Mo4H phase.
4. Conclusions
We used first-principles calculations and the CI-NEB method to perform a comprehensive study on the effects of Mo on the structural stability and mechanical properties of the Nb16H phase and the diffusion of hydrogen through the alloy. The calculations revealed that the Nb12Mo4H phase is the most thermodynamically stable structure with a low ΔHf of about −0.26 eV and a high elastic modulus. The diffusion paths of H in both Nb and Nb12Mo4 phases should be mainly from TIS to TIS. The calculated H-diffusion energy barrier and the diffusion coefficient are 0.153 eV and 5.65 × 10−6 cm2 s−1 (at 300 K), respectively. The lower energy barrier and higher diffusion coefficient of the Nb12Mo4 phase imply that the addition of a suitable amount of Mo could improve hydrogen permeation in Nb metal.Conflicts of interest
None.Acknowledgements
This work was supported by the National Natural Science Foundation of China (51471055, 51401060, and 11464008), the Natural Foundations of Guangxi Province (2016GXNSFGA380001 and 2014GXNSFGA118001), and the Guangxi Key Laboratory of Information Materials (171001-Z) and the Guangxi Postgraduate Innovation Project (YCSW2018144).References
- E. Kikuchi, Membrane reactor application to hydrogen production, Catal. Today, 2000, 56, 97–101 CrossRef CAS.
- Y. Wu, Z. M. Wang, D. H. Wang, Z. Z. Wan, Y. Zhong, C. H. Hu and H. Y. Zhou, Effects of Ni doping on various properties of NbH phases: A first-principles investigation, Sci. Rep., 2017, 7(1), 6535 CrossRef PubMed.
- S. C. Chen, C. Y. Hung, G. C. Tu and M. H. Rei, Perturbed hydrogen permeation of a hydrogen mixture-new phenomena in hydrogen permeation by Pd membrane, Int. J. Hydrogen Energy, 2008, 33(7), 1880–1889 CrossRef CAS.
- C. Y. Hao, Y. Wu, Y. J. An, B. H. Cui, J. N. Lin, X. N. Li, D. H. Wang, M. H. Jiang, Z. X. Cheng and S. Hu, Interface-coupling of CoFe-LDH on MXene as high-performance oxygen evolution catalyst, Materials Today Energy, 2019, 12, 453–462 CrossRef.
- A. Suzuki, H. Yukawa, T. Nambu, Y. Matsumoto and Y. Murata, Analysis of pressure–composition–isotherms for design of non-Pd-based alloy membranes with high hydrogen permeability and strong resistance to hydrogen embrittlement, J. Membr. Sci., 2016, 503, 110–115 CrossRef CAS.
- N. Watanabe, H. Yukawa, T. Nambu, Y. Matsumoto, G. X. Zhang and M. Morinaga, Alloying effects of Ru and W on the resistance to hydrogen embrittlement and hydrogen permeability of niobium, J. Alloys Compd., 2009, 477, 851–854 CrossRef CAS.
- G. X. Zhang, H. Yukawa, T. Nambu, Y. Matsumoto and M. Morinaga, Alloying effects of Ru and W on hydrogen diffusivity during hydrogen permeation through Nb-based hydrogen permeable membranes, Int. J. Hydrogen Energy, 2010, 35, 1245–1249 CrossRef CAS.
- J. R. Slining and D. A. Koss, Solid solution strengthening of high purity niobium alloys, Metall. Trans., 1973, 4, 1261–1264 CrossRef CAS.
- S. Kozhakhmetov, N. Sidorov, V. Piven, I. Sipatov, I. Gabis and B. Arinov, Alloys based on Group 5 metals for hydrogen purification membranes, J. Alloys Compd., 2015, 645, S36–S40 CrossRef CAS.
- Z. H. Liu and J. X. Shang, Elastic properties of Nb-based alloys by using the density functional theory, Chin. Phys. B, 2012, 21, 016202–016206 CrossRef.
- P. Khowash, S. Gowtham and R. Pandey, Electronic structure calculations of substitutional and interstitial hydrogen in Nb, Solid State Commun., 2012, 152, 788–790 CrossRef CAS.
- D. T. Peterson, A. B. Hull and B. A. Loomis, Hydrogen embrittlement considerations in niobium-base alloys for application in the ITER divertor, J. Nucl. Mater., 1992, 191–194, 430–432 CAS.
- H. Yukawa, T. Nambu, Y. Matsumoto, N. Watanabe, G. X. Zhang and M. Morinaga, Alloy design of Nb-based hydrogen permeable membrane with strong resistance to hydrogen embrittlement, Mater. Trans. JIM, 2008, 49, 2202–2207 CrossRef CAS.
- Y. T. Hu, H. Gong and L. Chen, Fundamental effects of W alloying on various properties of NbH phases, Int. J. Hydrogen Energy, 2015, 40, 12745–12749 CrossRef CAS.
- S. Nagata and K. Takahiro, J. Nucl. Mater., 2000, 283–287, 1038–1042 CrossRef CAS.
- C. Duan, Y. L. Liu, H. B. Zhou, Y. Zhang, S. Jin and G. H. Lu, et al., First-principles study on dissolution and diffusion properties of hydrogen in molybdenum, J. Nucl. Mater., 2010, 404, 109–115 CrossRef CAS.
- G. M. Wright, D. G. Whyte and B. Lipschultz, J. Nucl. Mater., 2009, 390–391, 544–549 CrossRef CAS.
- H. Yukawa, G. X. Zhang, N. Watanabe, M. Morinaga, T. Nambu and Y. Matsumoto, Analysis of hydrogen diffusion coefficient during hydrogen permeation through niobium and its alloys, J. Alloys Compd., 2009, 476, 102–106 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson and D. J. Singh, et al., Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS PubMed.
- M. Methfessel and A. T. Paxton, High-precision sampling for Brillouin-zone integration in metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed.
- J. H. Long and H. Gong, Ab initio calculation of NbH phases with low H compositions, Int. J. Hydrogen Energy, 2014, 39, 11798–11806 CrossRef CAS.
- R. Frauenfelder, Solution and Diffusion of Hydrogen in Tungsten, J. Vac. Sci. Technol., 1969, 6, 388 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901 CrossRef CAS.
- R. Lasser and K. Bickmann, Phase diagram of the Nb-T system, J. Nucl. Mater., 1985, 132, 24–28 CrossRef.
- T. Schober and H. Wenzl, The systems NbH(D), Tall(D), VH(D):structures, phase diagrams, morphologies, methods of preparation. Hydrogen in metals II, Top. Appl. Phys., 1978, 29, 11–71 CrossRef CAS.
- F. M. Mazzolai and H. K. Birnbaum, Elastic constants and ultrasonic attenuation of the a-a′ phase of the Nb-H(D) system. I: results, J. Phys. F: Met. Phys., 1985, 15, 507–523 CrossRef CAS.
- S. Q. Wang and H. Q. Ye, Ab initio elastic constants for the lonsdaleite phases of C, Si Ge, J. Phys.: Condens. Matter, 2003, 15, 5307–5314 CrossRef CAS; C. Wei, J. L. Fan and H. R. Gong, Structural, thermodynamic, and mechanical properties of bulk La and A-La2O3, J. Alloys Compd., 2015, 618, 615–622 CrossRef.
- C. P. Liang and H. R. Gong, Fundamental mechanism of tetragonal transitions in titanium hydride, Mater. Lett., 2014, 115, 252–255 CrossRef CAS.
- Z. J. Wu, E. J. Zhao and H. P. Xiang, et al., Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115 CrossRef.
- F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244 CrossRef CAS PubMed; Q. Q. Ren, J. L. Fan and H. R. Gong, Work function and cohesion properties of W-Fe interfaces, Mater. Lett., 2015, 145, 205–208 CrossRef.
- A. Reuss, Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle, Z. Angew. Math. Mech., 1929, 9, 49–58 CrossRef CAS.
- W. Voigt, Lehrbuch der Kristallphysik, B. G. Teubner, Leipzig, 1910 Search PubMed.
- G. Henkelman and B. P. Uberuaga, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113(22), 9901–9904 CrossRef CAS.
- Y. Wu, Z. M. Wang, P. F. Liu, T. Bo, C. Y. Hao, C. H. Hu, Z. X. Cheng, B. T. Wang and H. Y. Zhou, Understanding of transition metal (Ru, W) doping into Nb for improved thermodynamic stability and hydrogen permeability: density functional theory calculations, Phys. Chem. Chem. Phys., 2019 10.1039/c9cp02012h.
- J. W. Wang, Y. H. He and H. R. Gong, Various properties of Pd3Ag/TiAl membranes from density functional theory, J. Membr. Sci., 2015, 475, 406–413 CrossRef CAS.
- Y. L. Liu, Y. Zhang, G. N. Luo and G. H. Lu, Structure, stability and diffusion of hydrogen in tungsten: A first-principles study, J. Nucl. Mater., 2009, 390/391, 1032–1034 CrossRef.
- Y. L. Liu, Y. Zhang, H. B. Zhou, G. H. Lu, F. Liu and G. N. Luo, Vacancy trapping mechanism for hydrogen bubble formation in metal, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 172103 CrossRef.
- C. Duan, Y. L. Liu, H. B. Zhou, Y. Zhang, S. Jin, G. N. Luo and G. H. Lu, First-principles study on dissolution and diffusion properties of hydrogen in molybdenum, J. Nucl. Mater., 2010, 404, 109–115 CrossRef CAS.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |