Open Access Article
Open Access ArticleLaser cooling of InF, InCl and InH with an ab initio study
Rong
Yang
 *a,
Bin
Tang
b and
XiangYu
Han
ac
*a,
Bin
Tang
b and
XiangYu
Han
ac
aSchool of Mathematics and Physics, Chongqing Jiaotong University, Chongqing 400074, PR China. E-mail: cqyr88@126.com
bInstitute of Finance & Trade, Chongqing City Management College, Chongqing 401331, PR China
cInstitute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, PR China
First published on 4th October 2019
Abstract
The feasibility of laser cooling InF, InCl and InH is investigated based on ab initio quantum chemistry. To determine their suitability for laser cooling molecules, we have calculated the electronic structures, spectroscopic parameters, transition dipole moments (TDMs), radiative lifetimes, Franck–Condon factors (FCFs) and diode laser excitation wavelengths of InF, InCl and InH. Calculated spectroscopic constants of the first three electronic states for InF, InCl and InH show good agreement with available theoretical and experimental results. InF has highly diagonally distributed FCFs (f00 = 0.961, f11 = 0.909) for the C1Π → X1Σ+ transition, and the rather short lifetime of the state C1Π is computed to be 2.77 ns at the lowest vibrational level. Notable is that the 3Π → X1Σ+ transition of InF also has large diagonal FCFs and short lifetimes. Therefore, InCl and InH are not potential laser-cooling candidates because the FCFs of the 1Π → X1Σ+ transition are off-diagonal. We further propose laser cooling schemes for InF. The present results could provide a promising theoretical reference for further theoretical and experimental research on InF, InCl and InH.
1. Introduction
The production of ultracold diatomic molecules has drawn considerable interest for several years because of their wide range of prospective applications, for example, quantum computations,1 controlling chemistry2 and precision measurement.3–5 Recently, laser cooling of diatomic molecules SrF,6,7 YO,8 CaF9 and KRb10 have been experimentally performed. These successful laser cooling experiments have initiated a search for more molecules since more than 90 elements in the periodic table possibly form more than 4000 different diatomic molecules. The potential laser cooling candidates must have highly diagonal Franck–Condon factors (FCFs) and shorter lifetimes (i.e. high spontaneous-emission rates). Highly diagonal FCFs limit the number of lasers required to keep the molecule in a quasi-closed-loop cooling cycle and rapid laser cooling demands a shorter lifetime.The A2Π → X2Σ+ transition suggested by the experiments6–9 for SrF, YO and CaF has been theoretically used to establish the laser cooling schemes for RaF,4 BeF,11 MgF12 and MH13 (M = Be, Mg, Ca, Sr, and Ba). In 2015, laser cooling of LiBe molecule based on the B2Π → X2Σ+ transition has been reported by You et al.14 Interestingly, AlX (X = H,15 F,15 Cl16 and Br16) and BBr17/BCl17 molecules with an intervening state a3Π existed between the A1Π and X1Σ+ states have also been identified as potential laser-cooling candidates. The laser cooling scheme using the A1Π → X1Σ+ and a3Π → X1Σ+ transitions was theoretically suggested. In our previous works, theoretical optical schemes have been predicted for AlCl16/AlBr16 and BBr17/BCl.17 Li et al.18 propose to utilize the 1Σ–1Σ electronic transition system for direct laser cooling of AgH and AgD molecules.
The boron group molecules are of persistent interest in the investigation of cold molecules. BH19/BCl17/BBr,17 AlH15/AlF15/AlCl16/AlBr16 and GaF19 were identified as the promising laser-cooling targets theoretically. However, the study on laser cooling of indium diatomics is very limited. On the basis of previous studies, we believe InF, InCl and InH molecules are possible laser-cooling candidates. In this paper, we focus on the theoretical studies of the laser cooling of InF, InCl and InH. The electronic structure and spectroscopic properties of the low-lying electronic states of InF were given by Banerjee et al.20 from the relativistic configuration interaction calculations. They also determined the lifetime of the state C1Π was about 2.3 ns at the lowest vibrational level. Zou et al.21 obtained the potential energy curves and the spectroscopic constants on the ground and low-lying excited states of InCl using all-electron relativistic calculations. The theoretical calculations have been performed on the InH molecule based on multi-reference configuration interaction plus Davidson corrections method.22 Leininger et al.23 performed the calculations for spectroscopic constants of InH, InF, and InCl at the self-consistent-field and correlated levels. Several experimental results on the spectroscopic parameters were available in the literature for InF, InCl and InH.
Though InF, InCl and InH have been extensively investigated in previous works, as mentioned above, a systematic study of laser cooling of InF, InCl and InH is not available in the literature to the best of our knowledge. The main objective of this paper is to identify whether InF, InCl and InH are potential laser-cooling candidates and briefly design laser-cooling schemes. To determine their suitability for laser cooling molecules, we have calculated the electronic structures, spectroscopic parameters, TDMs, radiative lifetimes, FCFs and diode laser excitation wavelengths of InF, InCl and InH. Since in this work we mean to focus on the vibrational cooling, the rotational degrees of freedom can be neglected in the first approximation. Here, the C1Π → X1Σ+ transition for InF/InCl and A1Π → X1Σ+ transition for InH are the main transitions of laser cooling and the transition from intervening state 3Π to the ground state X1Σ+ is spin forbidden.
The paper is organized as follows. Section 2 details the theoretical methods and basis sets used in the calculations. Section 3 presents the results and discussions of the data, outlining the schemes for direct laser cooling. Section 4 provides a conclusion for this work.
2. Computational details
All the ab initio calculations are performed with the MOLPRO package.24 It should be noted that only the subgroup C2v point group symmetry can be adopted for InF, InCl and InH in the package. The electronic structures for the X1Σ+, C1Π and 3Π states of InF/InCl and the X1Σ+, A1Π and a3Π states of InH are calculated using the complete active space self-consistent field method (CASSCF),25,26 which is followed by MRCI plus Davidson corrections (MRCI+Q)27–29 calculations. The scalar relativistic effect is taken into account using the Douglas–Kroll–Hess (DHK)30,31 transformation of the relativistic Hamiltonian. The spectroscopic constants, including equilibrium bond distance (Re), dissociation energy (De), harmonic frequency (we), anharmonic vibrational frequency (weχe), rotational constant (Be) and electronic transition energy (Te) are evaluated by LEVEL 8.0 program.32 The TDMs of InF, InCl and InH are computed by taking the expectation and transition values using the MRCI wave functions. With the potential energy curves (PECs) and TDMs of different electronic states, we have obtained the FCFs and radiative lifetimes of the various vibrational levels from LEVEL 8.0 program.For the indium atom, being considerably heavy, we use the small-core scalar relativistic effective core potential ECP28MDF33 together with the corresponding valence basis sets. The 4s24p64d105s25p1 electrons of the In atom are kept in the valence space, while the remaining core electrons are replaced by the above mentioned pseudopotentials. The correlation consistent polarized valence quintuple zeta aug-cc-pV5Z (=AV5Z)34 is chosen for H. Meanwhile, the AVQZ35 all-electron basis sets are employed for F and Cl. That is to say, for InF, nineteen molecule orbitals (MOs) are put into active space, including 9a1, 4b1, 4b2, 1a2 symmetry (9,4,4,1), which correspond to the 1s2s2p shells of the F atom and 4s4p4d5s5p shells of the In atom; for InCl, twenty two MOs are selected as the active space, including 11a1, 5b1, 5b2, 1a2 symmetry (11,5,5,1), which correspond to the Cl 1s2s2p3s3p and In 4s4p4d5s5p shells; for InH, the active space is (7,3,3,1), which correspond with the H 1s and In 4s4p4d5s5p.
The main transitions of laser cooling for InF, InCl and InH are the 1Π → X1Σ+ transitions which are singlet states. Moreover, the excited state decays exclusively on the 1Π → X1Σ+ transition because of the selection rules for the change in parity and angular momentum in an electric dipole transition. Besides, the transition from intervening state 3Π to the ground state X1Σ+ is spin forbidden. Therefore, spin–orbit coupling effects are not considered in the calculations. Previous works on laser cooling of MH13 (M = Be, Mg, Ca, Sr, and Ba) and GaF19 also indicate that the influence of spin–orbit coupling on the spectroscopic properties is generally weak.
3. Results and discussions
3.1 PECs and spectroscopic constants
The calculated PECs of X1Σ+, 1Π and 3Π states of InF, InCl and InH acquired at the MRCI level are shown in Fig. 1. The PECs of X1Σ+ and 3Π states look surprisingly similar, implying that highly diagonal FCFs for 3Π → X1Σ+ transitions are possible. In Table 1, we report the corresponding spectroscopic constants of InF/InCl for the X1Σ+, C1Π and 3Π states and InH for the X1Σ+, A1Π and a3Π states. The experimental36 and theoretical20–23 values for these states are also listed in Table 1 for comparison.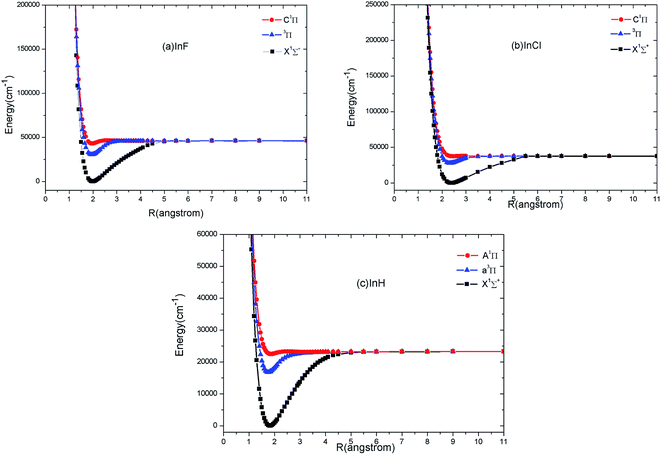 | ||
| Fig. 1 Potential energy curves of the first three electronic states of InF (a), InCl (b) and InH (c) at the MRCI level of theory. | ||
| Molecule | States | T e | R e (Å) | w e (cm−1) | w e χ e (cm−1) | B e | D e | Ref. |
|---|---|---|---|---|---|---|---|---|
| InF | X1Σ+ | 0 | 1.987 | 550.04 | 2.36 | 0.2619 | 5.45 | This work |
| 0 | 1.985 | 535.35 | — | — | 5.48 | Exp.36 | ||
| 0 | 2.010 | 564.00 | — | — | 5.37 | Ref. 20 | ||
| C1Π | 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050 050 |
1.964 | 467.05 | 16.51 | 0.2673 | 0.44 | This work | |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 809 809 |
1.966 | 463.90 | — | — | — | Exp.36 | ||
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 255 255 |
2.000 | 460.00 | — | — | — | Ref. 20 | ||
| 3Π | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 463 463 |
1.953 | 588.93 | 3.13 | 0.2727 | 1.94 | This work | |
| — | 1.946 | 575.25 | — | — | — | Exp.36 | ||
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 145 145 |
1.980 | 590.00 | — | — | — | Ref. 20 | ||
| InCl | X1Σ+ | 0 | 2.398 | 325.51 | 1.03 | 0.1094 | 4.70 | This work |
| — | 2.401 | 317.40 | — | — | 4.68 | Exp.36 | ||
| 0 | 2.431 | 313.70 | 1.38 | — | — | Ref. 21 | ||
| C1Π | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 478 478 |
2.455 | 210.06 | 14.07 | 0.1334 | 0.06 | This work | |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 484 484 |
2.473 | 177.30 | 12.60 | — | — | Exp.36 | ||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 757 757 |
2.577 | 106.90 | 2.33 | — | — | Ref. 21 | ||
| 3Π | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 802 802 |
2.335 | 350.00 | 1.90 | 0.1153 | 1.23 | This work | |
| — | 2.333 | 340.30 | — | — | — | Exp.36 | ||
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 871 871 |
2.340 | 325.20 | 1.16 | — | — | Ref. 21 | ||
| InH | X1Σ+ | 0 | 1.821 | 1537.00 | 24.83 | 4.8703 | 2.88 | This work |
| 0 | 1.838 | 1476.00 | 25.61 | 4.9945 | 2.75 | Exp.36 | ||
| — | 1.867 | 1434.00 | — | — | 2.65 | Ref. 23 | ||
| A1Π | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
1.862 | 284.30 | — | — | — | This work | |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 570 |
1.954 | — | — | — | — | Ref. 22 | ||
| a3Π | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 766 766 |
1.752 | 1523.74 | 61.55 | 5.389 | — | This work | |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 303 303 |
1.793 | 1495.85 | 63.62 | 5.270 | — | Ref. 22 |
For the ground state X1Σ+ of InF, the calculated Re and we results are only 0.002 Å and 14.69 cm−1 larger, while the De result is only 0.03 cm−1 smaller than the experimental data.36 The corresponding percentage errors in Re, we and De are 0.10%, 3.08% and 0.55%, respectively. Banerjee et al.20 provided even larger Re (1.26%) and we (5.35%), an even smaller De (2.00%) for the X1Σ+ of InF compared to the experimental data.36 The first excited state of InF is 3Π which lies well above the ground state. Our calculated Re and we of the 3Π state are in remarkably good agreement with experiment,36 and the relative errors are only 0.36% and 2.38%, respectively. While the percentage errors in Re and we given by Banerjee et al.20 are 1.74% and 2.56%, respectively. The present calculation yields a Te value for the 3Π of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 463 cm−1, and the observed A3Π0+, B3Π1–X1Σ+ transitions36 take place in the range 30
463 cm−1, and the observed A3Π0+, B3Π1–X1Σ+ transitions36 take place in the range 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400–31
400–31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1. The relativistic configuration interaction calculations by Banerjee et al.20 yielded a Te value for the 3Π of 28
300 cm−1. The relativistic configuration interaction calculations by Banerjee et al.20 yielded a Te value for the 3Π of 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 145 cm−1 which was not within the observed range. It is also encouraging to see that the present values of Re, we and Te for the C1Π state are 1.964 Å, 467.05 cm−1 and 43
145 cm−1 which was not within the observed range. It is also encouraging to see that the present values of Re, we and Te for the C1Π state are 1.964 Å, 467.05 cm−1 and 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050 cm−1, which are in very good agreement with the experimental data 1.966 Å, 463.90 cm−1 and 42
050 cm−1, which are in very good agreement with the experimental data 1.966 Å, 463.90 cm−1 and 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 809 cm−1 and the theoretical data 2000 Å, 460.00 cm−1 and 42
809 cm−1 and the theoretical data 2000 Å, 460.00 cm−1 and 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 255 cm−1.
255 cm−1.
For InCl, good agreement is found between our results and experimental data. The percentage errors of Re, we and De for the ground state X1Σ+ are 0.12%, 2.56% and 0.43%, respectively. The equilibrium bond distance Re by the available all-electron relativistic calculations21 is 2.431 Å, and the corresponding percentage error is 1.25%. The present weχe of the X1Σ+ state is 1.03 cm−1, which is slightly smaller than the previous theoretical value21 1.38 cm−1. For the C1Π, our present results compare very well with the experimental data36 (Te ∼ 6 cm−1, Re ∼ 0.018 Å, we ∼ 32.76 cm−1, weχe ∼ 1.47 cm−1). While the differences between the previous theoretical value21 and experimental data are bigger (Te ∼ 273 cm−1, Re ∼ 0.104 Å, we ∼ 70.40 cm−1, weχe ∼ 9.27 cm−1). Whereas for the 3Π, our spectroscopic constants calculated at MRCI level are in reasonable agreement with the available all-electron relativistic calculations21 (Te ∼ 69 cm−1, Re ∼ 0.005 Å, we ∼ 24.8 cm−1, weχe ∼ 0.74 cm−1). In the case of Re and we, our results (2.335 Å, 350.0 cm−1) are in good agreement with experiment36 (2.333 Å, 340.3 cm−1). The complete active space self-consistent field method (CASSCF) is used in both the previous work21 and our work. So the effects of the different active spaces (this work: 11,5,5,1) and (ref. 20: 6,3,3,1) on the spectroscopic constants of InCl can be seen from Table 1. It is obvious that the calculated spectroscopic constants of InCl for active space (11,5,5,1) are more close to the experimental values.
Concerning the X1Σ+ of InH, our calculated parameters Re, we, weχe, Be and De are also in very good agreement with experiment,36 and the relative errors are 0.92%, 4.13%, 3.05%, 2.49% and 4.73%, respectively. While the percentage errors in Re, we and De given by Leininger et al.23 are 1.58%, 2.85% and 3.64%, respectively. For the A1Π and a3Π states of InH, Table 1 shows that our present results accord with existing theoretical calculations.22,23 For example, the A1Π and a3Π states are located at 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 and 16
500 cm−1 and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 766 cm−1 in our calculations, 22
766 cm−1 in our calculations, 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 cm−1 and 16
570 cm−1 and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 303 cm−1 were reported by Zhang et al.22
303 cm−1 were reported by Zhang et al.22
In summary, our present work yield spectroscopic parameters of InF, InCl and InH for the first three electronic states that agree well with previous experimental and theoretical results.
3.2 TDM curves
Because the transition 3Π → X1Σ+ is spin forbidden at spin-free level, we only obtain the TDMs of the 1Π → X1Σ+ transition. Fig. 2 shows the computed TDMs of the dipole-allowed transitions C1Π → X1Σ+ for InF/InCl and A1Π → X1Σ+ for InH as functions of the internuclear distance. We note that the 1Π → X1Σ+ transitions for InF, InCl and InH are strong. As seen in Fig. 2, the TDM curves of InF, InCl and InH demonstrate similar behavior. The magnitude gradually increases as internuclear distance R increases, reaches a maximum (InF: 1.80 a.u., InCl: 1.40 a.u., InH: 0.92 a.u.), and drops thereafter. The TDMs of InF, InCl and InH all trend to zero at around 4.0 Å, 3.5 Å and 3.0 Å, respectively.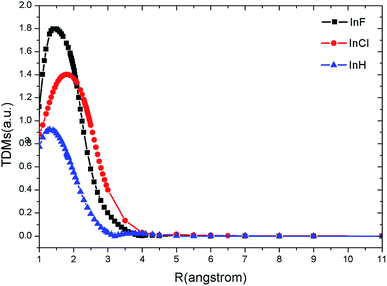 | ||
| Fig. 2 TDMs for the C1Π → X1Σ+ transitions of InF/InCl and A1Π → X1Σ+ transitions of InH at MRCI level. | ||
3.3 FCFs, spontaneous radiative lifetime and radiative width
| Molecule | Transition | f 00, f10 | f 01, f11 | f 02, f12 | f 03, f13 |
|---|---|---|---|---|---|
| InF | C1Π → X1Σ+ | 0.9606, 0.0377 | 0.0326, 0.9085 | 0.0062, 0.0369 | 0.0004, 0.0155 |
| 3Π → X1Σ+ | 0.8068, 0.1788 | 0.1670, 0.4997 | 0.0231, 0.2542 | 0.0027, 0.0565 |
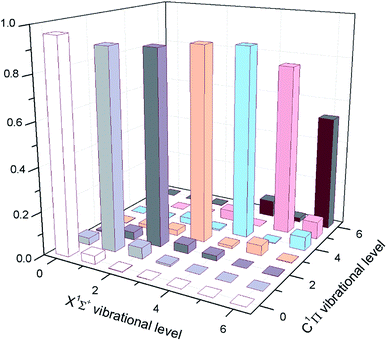 | ||
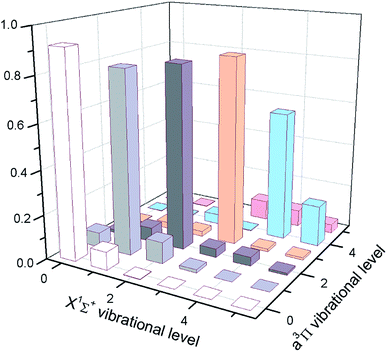
| Fig. 3 The calculated FCFs of InF for the lowest vibrational levels of the cooling transition C1Π → X1Σ+. | ||
Except for large FCFs, the potential laser cooling candidates must also have sufficiently short lifetimes. In Table 3, we have reported the computed lifetimes for the C1Π → X1Σ+ transition. Our computed lifetimes can be compared with those of the results predicted by Banerjee et al.20 The radiative lifetimes of the C1Π → X1Σ+ transition are computed to be 2.77–3.41 ns for the first five vibrational levels of InF, which shows that the C1Π of InF is a rather short lifetime state. At the same time, the radiative width for the C1Π → X1Σ+ transition are computed to be 19.15–15.53 cm−1 for the first five vibrational levels of InF. The radiative lifetimes (7.58–8.34 ns) of the 3Π are a little longer lived than these of the electronic state C1Π, which shows that the 3Π of InF is also a rather short lifetime state. As shown in Table 3, the radiative lifetimes show a slight increase with increasing vibrational level, and the radiative widths show a slight decrease with increasing vibrational level.
| Molecule | Transition | f 00, f10 | f 01, f11 | f 02, f12 | f 03, f13 |
|---|---|---|---|---|---|
| InCl | C1Π → X1Σ+ | 0.6079, 0.2912 | 0.2293, 0.0716 | 0.1010, 0.1620 | 0.0385, 0.1766 |
| 3Π → X1Σ+ | 0.5957, 0.2907 | 0.3282, 0.1437 | 0.0691, 0.3913 | 0.0067, 0.1521 |
| Molecule | Transition | f 00, f10 | f 01, f11 | f 02, f12 | f 03, f13 |
|---|---|---|---|---|---|
| InH | A1Π → X1Σ+ | 0.7897, 0.0573 | 0.1172, 0.0169 | 0.0604, 0.0372 | 0.0181, 0.0715 |
| a3Π → X1Σ+ | 0.9176, 0.0672 | 0.0809, 0.8217 | 0.0012, 0.0969 | 0.0001, 0.0014 |
3.4 Laser cooling scheme
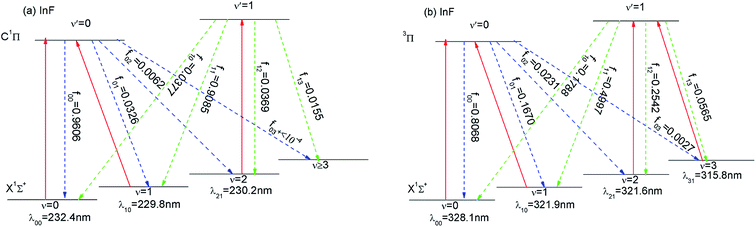
We have established the laser cooling schemes for InF, and Fig. 5 shows the proposed scheme. The corresponding computed radiative wavelengths are collected in Table 6. For InF, the main cycle is the X1Σ+(ν = 0) → C1Π(ν′ = 0) transition at wavelength λ00 = 232.4 nm. As shown in Fig. 5(a), there is a small probability of decay to the X1Σ+(ν = 1) state (≈3%), an even smaller probability of decay to the X1Σ+(ν = 2) state (≈0.6%), and a negligible probability of decay to the X1Σ+(ν ≥ 3) state (<10−4). To enhance the cooling effect, we add the X1Σ+(ν = 1) → C1Π(ν′ = 0) transition as the first vibrational pump and the X1Σ+(ν = 2) → C1Π(ν′ = 1) transition for the second pump. With this scheme, two repumping lasers λ10 = 229.8 nm and λ21 = 230.2 nm are required. The required cooling wavelengths of λ00 = 232.4 nm, λ10 = 229.8 nm and λ21 = 230.2 nm can be generated by a frequency quadrupled Ti:sapphire laser (189–235 nm). One problem with the above laser cooling scheme, is the presence of the intervening 3Π state between the two states (X1Σ+ and C1Π). Notable, the 3Π → X1Σ+ transition also have large diagonal FCFs and short lifetimes. Thus, this state 3Π could also be another option for laser cooling. We propose a four laser cyclic system involving the ν = 0–3 of the X1Σ+ state and ν′ = 0, 1 of the 3Π state. The main cycling laser at the wavelength of 328.1 nm can drive the X1Σ+(ν = 0) → 3Π(ν′ = 0) transition. Similar to the case in Fig. 5(a), a pair of repumping lasers with λ10 = 321.9 nm and λ21 = 321.6 nm are required to enhance the cooling effect. A third repumping laser with λ31 = 315.8 nm may be required on this scheme due to the non-negligible ν′ = 1 → ν = 3 transition (FCF = 0.0565). The required cooling wavelengths on this scheme are located in the ultraviolet light (UVA) range (400–320 (or 315) nm). There are similarities here to the laser cooling of AlF. Wells and Lane15 have studied on laser cooling of AlF molecules, and the X1Σ+ → C1Π and X1Σ+ → 3Π transitions of AlF had strongly FCFs. So for InF, the cooling on a strong C1Π → X1Σ+ transition may be followed by further cooling on the X1Σ+ → 3Π transition, which is similar to the laser cooling of AlF. The relatively long lifetimes of the 3Π state can be exploited to reach a much lower Doppler temperature than possible on the X1Σ+ → C1Π transition.| Molecule | λ 00 (nm) | λ 10 (nm) | λ 21 (nm) | λ 31 (nm) | Transition |
|---|---|---|---|---|---|
| InF | 232.4 | 229.8 | 230.2 | 227.8 | C1Π → X1Σ+ |
| 328.1 | 321.9 | 321.6 | 315.8 | 3Π → X1Σ+ | |
| InH | 596.9 | 549.5 | 556.3 | 525.0 | a3Π → X1Σ+ |
Compared with other potential laser-cooling candidates, diagonal FCFs f00 of InF (f00 = 0.961) is slightly larger than that predicted for BeF (f00 = 0.897), LiRb (f00 = 0.872), InH (f00 = 0.918) and KRb (f00 = 0.947). Experimentally, KRb is a typical laser-cooled molecule. Radiative lifetime τ(ν′ = 0) = 2.8 ns of InF is shorter than the one of BeF (7.9 ns), LiRb (102.6 ns), InH (205.7 ns) and KRb (229.3 ns). A shorter τ of the transition could produce a strong Doppler force, which will produce rapid laser cooling. We have identified InF is a more promising laser-cooling candidate. Not only it has bigger FCFs and shorter radiative lifetime, it also appears to attain a lower Doppler temperature on the X1Σ+ → C1Π transition followed by the weak X1Σ+ → 3Π transition. Generally, it is true that the Doppler-limit temperature is inversely proportional to the excited state lifetime. As shown in Table 3, the lifetime (7.58 ns) of the 3Π state is about three times larger than that of the C1Π state. However, the lifetime (7.58 ns) of InF is still shorter than that of KRb (229.3 ns). The short lifetime is sufficient to produce large spontaneous scattering forces.
4. Conclusions
The PECs of X1Σ+, 1Π and 3Π states of InF, InCl and InH are acquired at the MRCI level. Our present work yield spectroscopic constants (Re, De, we, weχe, Be, Te) of InF, InCl and InH for the first three electronic states that agree well with previous experimental and theoretical results. The TDMs of the dipole-allowed transitions C1Π → X1Σ+ for InF/InCl and A1Π → X1Σ+ for InH are obtained. Using the FCFs and radiative lifetimes obtained, we have identified InF is a promising candidate for laser cooling. Because of its off-diagonal FCFs, InCl is not a potential laser-cooling candidate. For InH, the A1Π state has off-diagonal FCFs and the FCFs of the a3Π → X1Σ+ transition are highly diagonal. However, this a3Π → X1Σ+ transition is very weak because it is spin-forbidden. The problem with the laser cooling scheme using the a3Π → X1Σ+ transition is that the InH molecule could not be precooled using the A1Π → X1Σ+ transition. So InH is not a promising laser-cooling candidate. The proposed laser cooling schemes of InF that drive the X1Σ+ → C1Π transition use three laser wavelength. Furthermore, the 3Π → X1Σ+ transition of InF is also strongly diagonal and the lifetimes of the excited 3Π state of InF is relatively long. So for InF, the X1Σ+ → C1Π transition may be followed by the weak X1Σ+ → 3Π transition to obtain a lower Doppler temperature. All of these three required laser-cooling wavelengths are in the visible range.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11704052).References
- A. Micheli, G. Brennen and P. Zoller, Nat. Phys., 2006, 2, 341 Search PubMed.
- R. V. Krems, Phys. Chem. Chem. Phys., 2008, 10, 4079 RSC.
- V. V. Flambaum and M. G. Kozlov, Phys. Rev. Lett., 2007, 99, 150801 CrossRef CAS PubMed.
- T. A. Isaev, S. Hoekstra and R. Berger, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 052521 CrossRef.
- J. J. Hudson, D. M. Kara, I. J. Smallman, B. E. Sauer, M. R. Tarbutt and E. A. Hinds, Nature, 2011, 473, 493 CrossRef CAS.
- E. S. Shuman, J. F. Barry and D. DeMille, Nature, 2010, 467, 820 CrossRef CAS.
- J. F. Barry, D. J. McCarron, E. B. Norrgard, M. H. Steinecker and D. DeMille, Nature, 2014, 512, 286 CrossRef CAS PubMed.
- M. T. Hummon, M. Yeo, B. K. Stuhl, A. L. Collopy, Y. Xia and J. Ye, Phys. Rev. Lett., 2013, 110, 143001 CrossRef.
- V. Zhelyazkova, A. Cournol, T. E. Wall, A. Matsushima, J. J. Hudson, E. A. Hinds, M. R. Tarbutt and B. E. Sauer, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 053416 CrossRef.
- J. Kobayashi, K. Aikawa, K. Oasa and S. Inouye, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 021401(R) CrossRef.
- I. C. Lane, Phys. Chem. Chem. Phys., 2012, 14, 15078 RSC.
- S. Y. Kang, Y. F. Gao, F. G. Kuang, T. Gao, J. G. Du and G. Jiang, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 91, 042511 CrossRef.
- Y. F. Gao and T. Gao, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 052506 CrossRef.
- Y. You, C. L. Yang, M. S. Wang, X. G. Ma and W. W. Liu, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 032502 CrossRef.
- N. Wells and I. C. Lane, Phys. Chem. Chem. Phys., 2011, 13, 19018 RSC.
- R. Yang, B. Tang and T. Gao, Chin. Phys. B, 2016, 4, 043101 CrossRef.
- R. Yang, Y. F. Gao, B. Tang and T. Gao, Phys. Chem. Chem. Phys., 2015, 17, 1900 RSC.
- C. L. Li, Y. C. Li, Z. H. Ji, X. B. Qiu, Y. Z. Lai, J. L. Wei, Y. T. Zhao, L. H. Deng, Y. Q. Chen and J. J. Liu, Phys. Rev. A, 2018, 97, 062501 CrossRef CAS.
- Y. F. Gao and T. Gao, Phys. Chem. Chem. Phys., 2015, 17, 10830 RSC.
- A. Banerjee, A. Pramanik and K. K. Das, Chem. Phys. Lett., 2006, 429, 62 CrossRef CAS.
- W. L. Zou, M. R. Lin, X. Z. Yang and B. Z. Zhang, J. Chem. Phys., 2003, 119, 3721 CrossRef CAS.
- Y. G. Zhang, H. Zhang and G. Dou, Chin. Phys. B, 2017, 9, 093101 CrossRef.
- T. Leininger, A. Nicklass, H. Stoll, M. Dolg and P. Schwerdtfeger, J. Chem. Phys., 1996, 105, 1052 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz, et al., MOLPRO, is a package of ab initio programs, version 2009.1, see http://www.molpro.net Search PubMed.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514 CrossRef CAS.
- S. R. Laughoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61 CrossRef.
- N. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89 Search PubMed.
- B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742 CrossRef CAS.
- R. J. Le Roy, LEVEL 8.0, A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasibound Levels, CPRR-663, University of Waterloo, Waterloo, ON, 2007 Search PubMed.
- I. S. Lim, H. Stoll and P. Schwerdtfeger, J. Chem. Phys., 2006, 124, 034107 CrossRef.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007 CrossRef.
- A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning Jr, J. Chem. Phys., 1999, 110, 7667 CrossRef CAS.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure IV: Constants of Diatomic Molecules, Van Nostrand, New York, 1979 Search PubMed.
| This journal is © The Royal Society of Chemistry 2019 |