Exhaustive exploration of the conformational landscape of mono- and disubstituted five-membered rings by DFT and MP2 calculations

Abstract

The conformational landscape of 22 different non, mono-, and disubstituted compounds with a five-membered ring was thoroughly explored by ab initio (MP2) and DFT (B3LYP and M06-2X) methods with the 6-311+G** basis set. Our results showed that the conformational preference of these compounds was governed mainly by the specific characteristics of the substituents, with a minor influence of the level of theory employed. After a detailed analysis of the computational data, we found an interesting preference of the electronegative substituents to take pseudo-axial positions, whereas alkyl groups preferred adopting the pseudo-equatorial locations. Such preferences were pronounced with MP2 and M06-2X and underestimated by B3LYP. Despite each level of theory affording different landscapes in many cases, as a general trend, we noticed that M06-2X afforded much higher correlation with the MP2 results than B3LYP.

---

Introduction

Conformational analysis is of central relevance to understand the chemistry and spectroscopy of organic molecules,¹ and understanding the factors controlling the conformational landscape of flexible systems has attracted the interest of generations of chemists. In a certain way, it can be considered that the history of conformational analysis is the history of organic chemistry itself. In the case of cyclic compounds, it has long been known that the molecules pucker to release the strain arising from the (hypothetical) planar structure. This was first recognized by Sachse in 1890 by postulating the chair and boat forms of cyclohexane.² This brilliant idea, eagerly confronted at that time, had to wait half a century to be finally consolidated, initially with the work of Beckett, Pitzer, and Spitzer in 1947,³ and then with the seminal publication of Barton in 1950.⁴ Ever since, extensive experimental and computational works have been carried out to understand the conformational behavior of substituted cyclohexanes or the related six-membered rings.⁵ Despite the number of different conformations being high (involving chairs, boats, skews, half-chairs, and envelopes), the conformational preference of simple systems is usually relegated to the analysis of the relative stability of the two possible chair-like conformations.

However, the situation becomes much more challenging when dealing with cyclopentanes or heterocyclic analogues due to their inherent conformational flexibility. These rings are known to exist as a combination of different puckered conformations, where each atom can assume many relative positions.^6–8 There are two extreme representative conformations, namely, envelope (E) and twist (T). In the E shape, the torsional strain is reduced dramatically by avoiding the strain that would result from the eclipsing of the hydrogens positioned in a perfect planar conformation. In this arrangement, one atom sticks out from the plane containing the other four ring atoms though this position is not fixed but rotates around the ring through the up and down motions of the methylene groups or heteroatoms. As a result of this pseudorotation, an infinite number of intermediate conformations can be found with similar energies. In the twist conformation, three adjacent atoms lie on the main plane, and the other two contiguous atoms are twisted, lying above and below the main plane. The total torsional strain of T is about 40% of the total torsional strain of the unpuckered structure.¹

The puckering of cyclopentanes has been confirmed experimentally by several methods, including entropy measurements⁹ and electron scattering.¹⁰ It is accepted that the E and T conformations show very low pseudorotational barriers (about the value of RT at room temperature or even lower), providing fast interconversion between conformers. Naturally, this idealized conformational landscape can be changed in substituted rings, depending both on the nature of the substituent and the substitution pattern.¹¹ In addition, the presence of heteroatoms at the five-membered ring also affects the conformational preference of the system.^12,13 As a result, the conformational landscape of five-membered rings cannot be easily predicted as in the case of their six-membered analogues. For this reason, this field has received some attention with respect to both theoretical¹⁴ and spectroscopical methods.¹⁵ Given the biological importance of furanoses and pyrrolidines, most of the studies have been carried out on these compounds.^13,16 The number of computational studies dealing with cyclopentane motifs are much more scarce.¹⁷ To the best of our knowledge, no quantum-based study has been carried out to systematically explore the conformational landscape of mono- and disubstituted five-membered rings. The stability of a given conformation is the result of a fine balance between different types of interactions, which can be estimated differently depending on the level of theory employed during the calculations. Among the plethora of current DFT functionals, B3LYP is undoubtedly one of the most popular and widely employed ones. However, there are many reports suggesting that it is not optimal to describe the conformational behavior of carbohydrates, indicating that the emerging M06-2X provides a better performance.¹⁸ For this reason, herein, we reported the potential energy surfaces (PESs) of a wide variety of five-membered rings computed with these two functionals. A comparison of the results with those obtained with the more computationally demanding MP2 ab initio method was also provided.

Results

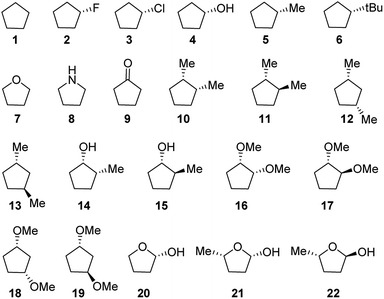
To achieve our goals, we selected a complete set of 22 compounds (Fig. 1) with different types of five-membered rings and substituents.

Fig. 1 Set of the 22 compounds studied.

The use of puckering parameters provided a substantial help to understand the pseudorotational pathways. In a pioneering work, Altona and co-workers developed a quantitative description of puckering and conformation in terms of the maximum angle of torsion (θ_m) and the “phase angle” of pseudorotation (Δ) computed from the five torsion angles in the five-membered ring; their study mainly focused on the D ring of steroids and analogues.¹⁹ Later, in 1972, Altona and Sundaralingam refined this concept for nucleosides.²⁰ Two years later, Cremer and Pople generalized the puckering calculation to any type of cyclic compound.²¹

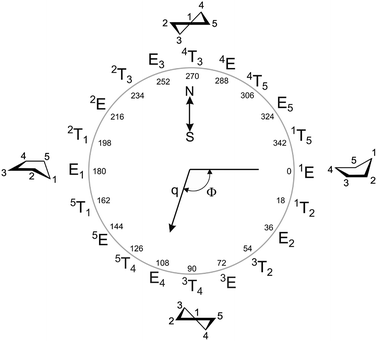
In the particular case of five-membered rings, both models (AS and CP) describe the puckering in terms of amplitude (q) and phase coordinate (Φ). The only difference between the two models is that the phase coordinates shift by a constant angle (90°). In this work, we used the CP definition, in which perfect envelope conformations were defined by Φ values as multiples of 36° (including 0°), whereas the corresponding twist conformations shifted by 18°. Other Φ values gave rise to intermediate geometries between E/T closer to one or the other depending on the specific phase shifting (Fig. 2).

Fig. 2 The Cremer–Pople (CP) rotational wheel.

Energies and stationary points

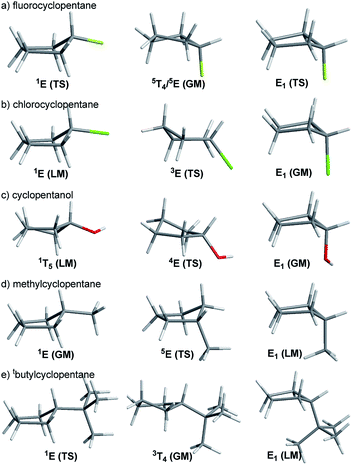
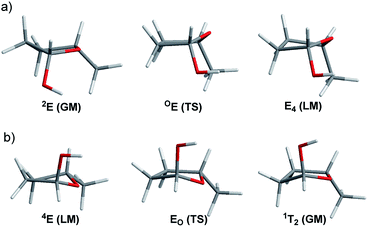
In this study, we evaluated the performance of two well-known DFT methods, namely, B3LYP and M06-2X along with that of MP2. All the stationary points were found using the 6-311+G** basis set except for larger compounds at the MP2 level. In these cases, the geometry optimizations were carried out using the 6-31+G** basis set, and the energies were recomputed at the higher level. We set tight convergence criteria and a pruned (99,590) integration grid, which were crucial for the correct exploration of the potential energy surface (PES). After the exhaustive exploration of PES for all the systems under study, we noticed three different patterns regarding the conformational landscape: a two-conformer (one minimum, one TS), a four-conformer (two minima, two TSs), and a six-conformer pattern (three minima, three TSs). It is important to point out that some molecules under study were symmetrical, making different conformations equivalent (this is indicated in Fig. 3–10 by the symmetry dotted line or lines).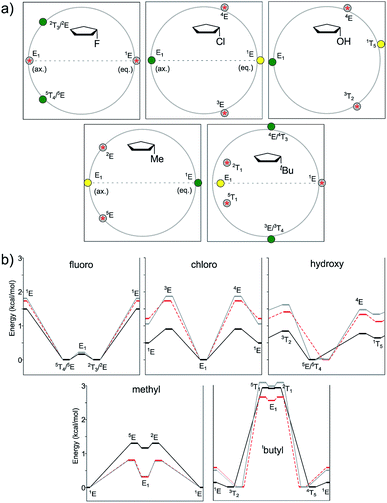

Fig. 3 (a) Geometry representations of the Cremer–Pople puckering parameters of the minima (green, global minima; yellow, local minima) and transition states (grey circle with red star) computed for compounds 2–6 at the M06-2X level. Qualitatively similar graphs were observed for the other levels of theory (see the ESI†). (b) Energies of the conformational pathways for compounds 2–6 calculated at the B3LYP (black), M06-2X (red), and MP2 (grey) levels.

Cyclopentane (1). We started our study by evaluating the performance of the three methods to explore cyclopentane. Despite it being the simplest system under study, it gave one of the most troublesome results as they were highly dependent on the method followed. This was not surprising considering the small energy differences involved. In the case of MP2, three minima of identical energies were found with E, T, and E/T shapes with the lowest frequencies close to zero (−0.5 to −2.5 cm⁻¹). In the case of B3LYP, the T shape represented the global minima, but it was very close in energy with E and E/T (0.003 kcal mol⁻¹). The E/T shape disappeared (converged to T) when using a superfine grid (96, 32, 64). As a consequence of the extremely flat PES, a switch between the local minima and saddle point occurred when changing the convergence criteria and integration prune. For instance, using Gaussian 09 default settings, the E shape was located as a minimum, whereas the T and E/T were saddle points with negative frequencies (−22.4 and −21.1 cm⁻¹, respectively); however, using tight convergence criteria and ultrafine integration, these last two became minima and the E conformation changed to TS (−12.9 cm⁻¹), whereas for the superfine integration, only the last appeared as TS (−8.3 cm⁻¹). In any case, the chemical significance of imaginary frequencies with such low magnitudes could be argued. With M06-2X, the usage of any type of grid did not qualitatively change the results: the three shapes stayed even after superfine usage, maintaining negligible energy differences (up to 2 cal mol⁻¹) between the conformers. The low energy differences, despite being beyond the precision offered by these computational methods, were in good accordance with previous results obtained by Laane and co-workers.²² The small energy differences and the low magnitude of the low frequency values for the stationary points clearly indicated a practically flat potential energy surface around the pseudorotational cycle. However, it should be noted that after adding the entropic and zero-point energies, the T shape became clearly favored (ca. 2 kcal mol⁻¹ more stable than the E shape using the superfine grid; please see the ESI†).

Fluorocyclopentane (2). The introduction of a fluorine atom modified the conformational landscape in relation to that observed for cyclopentane. Early vibrational studies recognized that fluorocyclopentane should exist as a single stable conformer.^11b Later, the CNDO/2 calculations reinforced this proposal, suggesting that it should be envelope-equatorial (¹E).²³ However, our calculations showed a different scenario (Fig. 3 and 4), with the global minima shifting towards the equivalent ⁵T₄/⁵E and ²T₃/²E conformations connected through the non-equivalent envelope-like transition structures (¹E and E₁). Notably, the E₁ conformation (showing a pseudo-axial fluorine) was 1.33–1.59 kcal mol⁻¹ more stable than the corresponding ¹E analogue, with a pseudo-equatorial F atom, which was consistent with the axiality experienced by fluorine in the global minima conformation. It was previously found that pseudo-axial fluorine stabilizes the skews and boats in the cyclohexane derivative.⁵ In addition, the energies of the lower barrier between the two minima (through ¹E) showed high similarities among the three methods under study (0.15–0.21 kcal mol⁻¹). These results were in clear agreement with the findings of During et al., who, on the basis of IR and Raman spectroscopy and MP2 calculations, proposed that fluorocyclopentane should exist exclusively as a twisted C₁ conformer, with the two envelope forms being first-order saddle points.²⁴

Fig. 4 Selected stationary points found for compounds 2–6 at the M06-2X/6-311+G** level of theory (TS: transition structure; GM: global minimum; LM: local minimum).

Chlorocyclopentane (3). The replacement of the fluorine atom by a chlorine atom generated an interesting inversion in the conformational behavior of the system. In contrast, in the case of fluorine, the ¹E and E₁ conformations were transition structures connecting the minimum; in this case, both conformations were actually the two minima (Fig. 3 and 4). The E₁ conformer (pseudo-axial chlorine) was the global minimum, with the E₁/¹E energy differences ranging from 0.49 kcal mol⁻¹ (B3LYP) to 1.21 kcal mol⁻¹ (M06-2X), which were closer to the MP2 estimation (1.05 kcal mol⁻¹). Despite the higher tendency of chlorine toward equatoriality in cyclohexane systems,⁵ in the case of cyclopentane, the pseudo-axial location of chlorine tends to stabilize the resulting geometry, which was also suggested from earlier vibrational studies.²⁵ The two local minima were connected through envelope-like transition structures (³E and the symmetry equivalent ⁴E). The B3LYP relative energy of ³E (0.90 kcal mol⁻¹) was 0.83–0.97 kcal mol⁻¹ lower than those computed with M06-2X and MP2, indicating a tendency for B3LYP to underestimate the pseudo-axial stabilization exerted by the electronegative atoms attached to the cyclopentane moiety.

Cyclopentanol (4). The conformational behavior resembled that observed for chlorocyclopentane, though with the two minima slightly shifting south (global minima) and north. The symmetry observed in previous compounds was lost as the hydrogen atom of the hydroxyl group was directed towards one side of the molecule.

With M06-2X, the global minimum was found around E₁, with a pseudo-axial orientation of the OH group; the other minimum featured the switched ¹T₅ conformation, with the OH group being pseudo-equatorial (Fig. 3 and 4). Previous vibrational studies indicated that the conformational isomerism of cyclopentanol is dictated by two representative shapes featuring equatorial and axial OH groups,^25b which is in agreement with our findings. According to B3LYP and MP2, the global minimum shifted south (around ⁵E/⁵T₄). The preference towards envelope shapes with the hydroxyl group located at an axial position at the fold of the envelope (⁵E) was previously found by Abraham et al.²⁶ The B3LYP energy difference between both conformations (0.64 kcal mol⁻¹) was lower than that observed with the other methods (1.12 kcal mol⁻¹ for M06-2X and 1.33 kcal mol⁻¹ for MP2). The transition geometries were located at ⁴E and ³T₂ (closer to ³E), with the relative energies of 0.76 kcal mol⁻¹ (B3LYP) and 1.33–1.47 (M06-2X and MP2, respectively) for the former and 0.84 kcal mol⁻¹ (B3LYP) and 1.41–1.62 kcal mol⁻¹ (M06-2X and MP2, respectively) for the latter. The tendency of B3LYP to underestimate the pseudo-axial stabilization of electronegative atoms was also reflected in these calculations. When using MP2, an additional minimum (at E₁) and the corresponding TS to reach it (around ⁵T₁) also appear. Nevertheless, PES was flat in the studied region, showing negligible energy difference (0.02 kcal mol⁻¹ between the minimum and TS, Fig. 3). All attempts to locate such conformations using B3LYP were met with no success as was observed with other common DFT functionals such as B3PW91 and PBE1PBE.

Methylcyclopentane (5). The larger steric hindrance exerted by the methyl group coupled with its low electronegativity has important conformational consequences in the conformational landscape of the corresponding cyclopentane derivative. As in the case of chlorine, the two local minima showed perfect envelope conformations (¹E and E₁). However, in this case, the global minimum was ¹E (featuring a pseudo-equatorial methyl group), reverting the trend observed for relatively small and electronegative substituents (F, Cl, and OH). The relative energy of the E₁ conformation, with the methyl group adopting a pseudo-axial position, depends largely on the level of theory employed (Fig. 3 and 4). In contrast, B3LYP predicted a relatively large energy difference between the two minima (1.16 kcal mol⁻¹); the gap was considerably lower with both M06-2X and MP2 (0.31 and 0.33 kcal mol⁻¹). An NMR study of the ³J coupling values of different deuterated methylcyclopentanes suggested that the pseudorotation path is displaced to conformations featuring equatorial methyl groups,²⁷ which was in line with a previous ¹³C NMR study of the β and γ effect.²⁸ Needless to say, a non-negligible contribution of conformations with the pseudo-axial methyl group should be expected. In spite of this, to the best of our knowledge, the ¹E/E₁ energy gap has not been measured yet, but it can be roughly estimated as 0.53 kcal mol⁻¹, which is the energy difference between cis-1,3-dimethylcyclopentane (with the two pseudo-equatorial methyl groups) and the trans-counterpart (with one pseudo-equatorial methyl group and the other one pseudo-axial, vide infra).²⁸ Our calculations also showed that the two envelopes were interconverted through a pseudorotational path involving the other envelopes (⁵E and the symmetry analogue ²E) as transition structures. The relative energy of such structures was again overestimated by B3LYP (1.30 kcal mol⁻¹ vs. 0.79 kcal mol⁻¹ computed for M06-2X and MP2).

t-Butylcyclopentane (6). A classical case of two minima, two transition structures was noticed (Fig. 3). In this case, the larger size of the t-butyl group shifted the position of the global minimum more than that observed for the smaller methyl group. When using B3LYP, 54° displacement from a perfect ¹E envelope occurred, affording ³T₂ geometry (or the symmetry equivalent ⁴T₅) with the t-butyl group close to a pseudo-equatorial position. This displacement was higher with M06-2X and MP2, leading to geometry near ³E. In all cases, the ¹E envelope was now a “soft” transition structure connecting the twisted conformers. This TS had almost the same energy as the global minima at the B3LYP level (ΔE = 0.13 kcal mol⁻¹), and it slightly increased compared to the other two model chemistries (0.57–0.68 kcal mol⁻¹). The other local minimum was located at E₁ (as in the previous case), with the t-butyl group adopting almost perfect pseudo-axiality. As expected, all the quantum methods predicted a significant energy rise in that conformation ranging from 2.55 kcal mol⁻¹ (M06-2X) to 2.90 kcal mol⁻¹ (B3LYP). The pseudorotational interconversion of E₁ occurred through a transition structure of almost the same energy with twisted ⁵T₁ (or the symmetry equivalent ²T₁) geometry. The pseudo-axial location of the bulky group accounted for the high energy content of this conformation.

Cyclopentanone (9). Our calculations showed that the only minimum found for cyclopentanone occurred at the ³T₄ conformation (or the symmetry equivalent ⁴T₃), with the carbonyl group on the main plane (Fig. 5). The other stationary points were located at perfect E₁ and ¹E envelopes, both equivalent by symmetry, corresponding to transition structures with a marked tendency to flatness (a low puckering degree, Fig. 3a). The barrier between ³T₄ and E₁ (by flattening C3) required a considerable amount of energy (2.66 kcal mol⁻¹ in the case of B3LYP), which was similar to the ³T₂/E₁ difference computed for t-butylcyclopentane. A close behavior was predicted with M06-2X and MP2 though with higher barriers (3.19 kcal mol⁻¹ and 3.57 kcal mol⁻¹, respectively). These calculations were in good agreement with the permanently twisted shape of cyclopentanone found experimentally by Kim and Gwinn using microwave spectroscopy.²⁹

Fig. 5 (a) Geometry representations of the Cremer–Pople puckering parameters of the minima (green, global minima; yellow, local minima) and transition states (grey circle with red star) computed for compounds 7–9. (b) Energies of the conformational pathways for compounds 7–9 calculated at the B3LYP (black), M06-2X (red) and MP2 (grey) levels.

Oxolane (THF, 7). Given the symmetry exerted by the oxolane ring, only three characteristic shapes could be found: two equivalent envelopes (^OE and E_O), two equivalent twists (⁴T₃ and ³T₄), and four equivalent E/T (²E/²T₃, E₅/⁴T₅, ⁵E/⁵T₄ and E₂/³T₂) geometries (Fig. 5). All these conformations exhibited negligible energy differences as a consequence of the extreme flatness of the potential energy surface (as occurred with cyclopentane). However, an interesting trend was noticed when comparing the results obtained at different levels of theory. In the case of B3LYP, the T shapes were the global minima, with the E shapes only 0.02 kcal mol⁻¹ higher in energy, and the E/T geometries were the transition structures connecting these minima (showing almost neglible energy difference as well). Interestingly, at the MP2 level, the exact opposite behavior was observed: the E/T intermediates were the global minima, and the E and T shapes corresponded to the transition structures. The dependence of PES on the level of theory employed during the calculations was consistent with the findings of Rayón and Sordo.³⁰ The relative energies were again very low (0.2 kcal mol⁻¹ and 0.04 kcal mol⁻¹). Finally, M06-2X showed intermediate results: the T shapes were the global minima, and E and E/T were the transition structures computed at 0.29 and 0.44 kcal mol⁻¹, respectively. This behavior was, however, anomalous as there was no minimum when passing from E to E/T. We speculate that this could be a calculation artifact resulting from the extremely flat energy surface.

Pyrrolidine (8). The conformational study of pyrrolidine has received considerable attention in recent years, and ambiguous conclusions have been drawn as well. Using microwave spectroscopy, Caminati et al. proposed that the most stable conformation of pyrrolidine should be envelope with the NH axial (E₁).³¹ This proposal was next verified by electron diffraction studies coupled with ab initio calculations at the HF/4-21G level.³² More than a decade later, Caminati et al. retracted their initial findings by proposing that the equatorial H(N) structure was 0.6 kcal mol⁻¹ more stable than the axial one based on rotational free jet analysis.³³ The conformational preference of the NH hydrogen was theoretically investigated by Carballeira et al. using a wide variety of Hartree–Fock, post-Hartree–Fock (MP2, CC, CI, etc.), and DFT methods.³⁴ A more recent report using femtosecond degenerate four-wave spectroscopy reinforced the higher stability of the E₁ shape but with a lower energy gap (0.08 kcal mol⁻¹) than that found by Caminati et al.³⁵ As in the case of oxolane, our calculations showed that the conformational landscape of pyrrolidine depends on the level of theory employed, which is in line with Carballeira's findings (Fig. 5).³⁴ For instance, in the case of B3LYP, the ¹E conformation (bearing an equatorial NH) was the global minimum and was 0.80 kcal mol⁻¹ more stable than the corresponding E₁ (with the axial NH) geometry. However, this trend was reversed when including the entropic component as the Gibbs free energy of ¹E was 1.95 kcal mol⁻¹ higher than that of E₁. Both MP2 and M06-2X agreed with B3LYP in finding the global minimum at ¹E, though they found the inverted E₁ shape as a low-energy transition structure connecting ¹E with a close-by minimum of almost the same energy located around ⁵E. Moreover, M06-2X free energy calculations identified this last structure as the global minimum, whereas the ¹E conformation was still the most stable one according to the free energy calculations at the MP2 level. A second transition structure around ³T₄ was located at the three levels of theory. The transition structure corresponding to nitrogen inversion was found at higher energy (3.4–4.4 kcal mol⁻¹), which was in agreement with previous observations.^34,35 Hence, according to our calculations, the stable conformers of pyrrolidine should interchange following a pseudorotational process rather than N inversion, which is exactly the opposite situation found in the case of piperidine.⁵

Dimethylcyclopentanes (10–13). Using B3LYP, the cis-1,3-, trans-1,2- and trans-1,3-dimethylcyclopentanes exhibited just one minimum and one TS located on the antipodes of the circle and given as symmetry predicts (Fig. 6a). In all cases, the axiality or equatoriality of the methyl groups defined the conformational features, as previously discussed for methylcyclopentane. The trans-1,2 compound showed the global minimum at ¹T₂, with two pseudo-equatorial methyl groups. The corresponding TS was located 2.19 kcal mol⁻¹ above with a flipped ²T₁ geometry featuring a pseudo-axial arrangement of the substituents. A similar behavior was noticed in the case of the cis-1,3 product, with the minimal conformation located at E₂, allowing the required equatoriality of the methyl groups, and the TS adopted a flipped ²E shape. Noticeably, this TS showing the two pseudo-axial methyl groups was almost 2 kcal mol⁻¹ higher in energy (relative to the global minimum) than that computed for the 1,2-trans system (Fig. 6b). In the case of the 1,3-trans compound, the preferred equatoriality of the methyl groups was better achieved at ⁴T₅, being 1.83 kcal mol⁻¹ more stable than the corresponding flipped ⁵T₄ shape found for the transition structure. The use of other model chemistry methods afforded different results. For instance, for the trans-1,2 compound, according to MP2 and M06-2X, the ²T₁ geometry is not TS connecting with the ¹T₂ global minimum but instead a local minimum located at about 1.1 kcal mol⁻¹. However, all efforts to locate any transition structure were met with no success with these levels of theory. For the trans-1,3 system, a two-minima, a two-TS scenario was produced by MP2 or M06-2X: ⁴T₅ became TS instead of a minimum, and the global minimum shifted slightly to ⁴T₃ and its “enantiomer” ¹T₅. The three methods agreed when dealing with the cis-1,2 compound, giving two equivalent minima at ¹T₂/E₂ (equivalent to ²T₁/²E), characterized by one pseudo-equatorial methyl group and the other pseudo-axial methyl group. The two non-equivalent TSs were observed at ⁴E and E₄, with the two methyl groups taking isoclinal positions.

Fig. 6 (a) Geometry representations of the Cremer–Pople puckering parameters of the minima (green, global minima; yellow, local minima) and transition states (grey circle with red star) computed for compounds 10–13 at the M06-2X level. Qualitatively similar graphs were observed for the other levels of theory (see the ESI†). (b) Energies of the conformational pathways for compounds 10–13 calculated at the B3LYP (black), M06-2X (red) and MP2 (grey) levels.

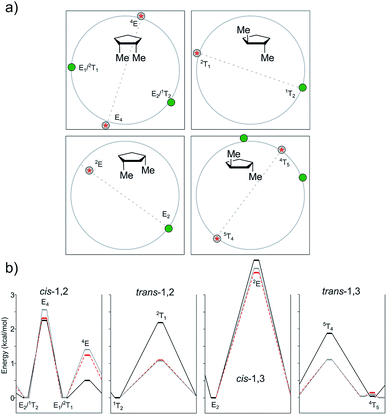
As stated above, the cis/trans energy difference was estimated experimentally as 0.53 kcal mol⁻¹ for 1,3-dimethylcyclopentane.²⁸ According to our computational results, the three levels of theory agreed with the higher stability of the cis isomer, though with lower energy gaps (0.28 kcal mol⁻¹ for B3LYP, 0.19 kcal mol⁻¹ for M06-2X, and 0.14 kcal mol⁻¹ for MP2).

2-Methylcyclopentanol (14–15). According to our results with monosubstituted cyclopentanes, the conformational preference is dictated by the trend of the electronegative and alkyl groups to become pseudo-axial and pseudo-equatorial, respectively. In an effort to explore this interesting effect, we next evaluated the conformational landscape of the cis and trans isomers of 2-methylcyclopentanol bearing one type of substituent of each kind (Fig. 7). Since the dihedral angle of the OH group imposes additional conformational freedom, we evaluated the two types of conformers resulting from the orientation of the OH group relative to the methyl fragment: “out” with OH pointing away from the methyl group and “in” with OH pointing inside. The need to consider the role of exocyclic groups when building conformational landscapes has been emphasized by Beckham and co-workers.³⁶ According to them, avoiding this effect would result in over- or underestimation of the puckering barriers.

Fig. 7 (a) Geometry representations of the Cremer–Pople puckering parameters of the minima (green, global minima; yellow, local minima) and transition states (grey circle with red star) computed for compounds 14–15 at the M06-2X level. Qualitatively similar graphs were observed for the other levels of theory (see the ESI†). (b) Energies of the conformational pathways for compounds 14–15 calculated at the B3LYP (black), M06-2X (red), and MP2 (grey) levels.

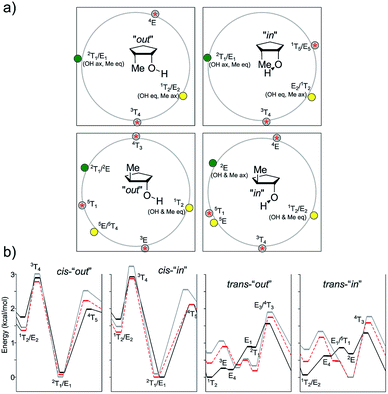
In the case of the cis isomer, several minima and TSs shifted slightly depending on the method used. In all cases, the global minimum was found near ²T₁, with pseudo-equatorial and pseudo-axial methyl and OH groups, respectively. Although the energy of the “out” conformer was lower using MP2, it was slightly higher using the DFT methods. In any case, the two-minima, two-TS pattern was observed for all the methods and OH conformers. The other minimum was located near E₂, with the exact opposite orientations of the substituents (OH pseudo-equatorial, Me pseudo-axial). The energy difference with the global minimum was quite high (1.31–1.69 kcal mol⁻¹), reinforcing our previous observations. The transition structures were located near ³T₄ and ¹T₅, the second being the most stable one. The barriers changed with the level of theory and orientation of the OH group (in vs. out). In general, the corresponding “in” TS was more stable than the analogous “out” one, with energy differences ranging up to 0.22 kcal mol⁻¹. The differences between ³T₄ and ¹T₅ were in the range of 0.67–0.81 kcal mol⁻¹ for all levels of theory.

In the case of the trans isomer, the pattern was more complicated, with three minima and three TSs, and the shapes depended on the orientation of the OH group as well. In the case of the “out” conformations, according to B3LYP, the global minima were located near ¹T₂, featuring a pseudo-equatorial arrangement of both groups. The flipped ²T₁ conformation (with pseudo-axial substituents) was 0.87 kcal mol⁻¹ higher in energy, whereas the E₄ shape with staggered groups was slightly more energetic than ¹T₂ (0.22 kcal mol⁻¹). The three transition structures connecting these minima had envelope structures (³E, E₁ and E₃) with energy gaps of 0.26 kcal mol⁻¹, 0.89 kcal mol⁻¹ and 1.56 kcal mol⁻¹, respectively. The preferred pseudo-equatorial orientation of the methyl group was also observed in TSs, with ³E (with pseudo-equatorial methyl group) being the most stable one. However, M06-2X and MP2 depicted a different scenario. In these cases, the most stable conformation (with the “out” OH group) was ²T₁ (with a trans-diaxial arrangement of the substituents), and it was 0.23 kcal mol⁻¹ (M06-2X) and 0.38 kcal mol⁻¹ (MP2) lower in energy than ¹T₂ (the global minimum according to B3LYP). In fact, this last shape was the least stable local minimum according to M06-2X and MP2. The third conformation, with the energy lying between those calculated for ¹T₂ and ²T₁, had a ⁵E/⁵T₄ shape. The lowest energy TS had the ⁵E shape, with pseudo-axial and staggered OH and methyl groups, respectively. Here, again, these results suggest that B3LYP underestimates the relative stabilization exerted by pseudo-axial electronegative substituents. The analysis of the “in” conformations allowed a similar approach. The B3LYP minimum was again ¹T₂, whereas the other two local minima slightly shifted to north (E₄ moved to ⁵T₄, and ²T₁ moved to ²E), with relative energies of 0.62 and 0.69 kcal mol⁻¹, respectively. M06-2X and MP2 showed that ²E was the global minimum, with a trans-diaxial arrangement of the substituents. The ²E/²T₁ gap was larger for MP2 (0.81 kcal mol⁻¹) than that for M06-2X (0.46 kcal mol⁻¹). TSs also slightly shifted than those computed for the “out” conformations.

1,2-Dimethoxycyclopentanes (16–17). These compounds were chosen instead of cyclopentanediols to avoid the effect of H-bond interactions. As in the previous case, two groups of conformations were available depending on the relative position of the methoxy groups: “in–out” (one OMe pointing inside, and the other outside) and “out–out” (both OMe pointing outside). However, “in–in” could not exist because of a steric clash. Moreover, “out–out” was symmetrical, whereas the former was not. Nevertheless, both types of conformations displayed similar pseudorotational behaviors and for this reason, the analysis focused on the asymmetric systems, which afforded lower energies (Fig. 8).

Fig. 8 (a) Geometry representations of the Cremer–Pople puckering parameters of the minima (green, global minima; yellow, local minima) and transition states (grey circle with red star) computed for compounds 16–17 at the M06-2X level. Qualitatively similar graphs were observed for the other levels of theory (see the ESI†). (b) Energies of the conformational pathways for compounds 16–17 calculated at the B3LYP (black), M06-2X (red) and MP2 (grey) levels.

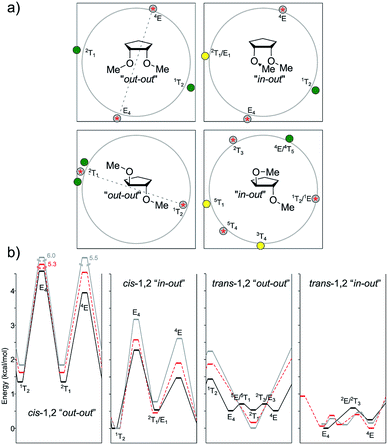
As in the case of cis-2-methylcyclopentanol, the global minimum of 1,2-cis-dimethoxycyclopentane was located at ¹T₂ (featuring one pseudo-axial methoxy group and the other pseudo-equatorial methoxy group). The other minima were found with the ²T₁ shape at 0.53–0.77 kcal mol⁻¹ at all levels of theory under study. The two transition structures connecting these minima had ⁴E and E₄ geometries (both with staggered OMe groups), with the barriers significantly increasing when passing from B3LYP to M06-2X to MP2 (1.46 kcal mol⁻¹, 1.93 kcal mol⁻¹, and 2.62 kcal mol⁻¹ for ⁴E; 2.27 kcal mol⁻¹, 2.58 kcal mol⁻¹ and 3.17 kcal mol⁻¹ for E₄). This trend could be explained on the basis of the gradual extra stabilization of the ¹T₂ shape.

The 1,2-trans isomer afforded more complex results. The symmetric conformers (“out–out”) exhibited by B3LYP afforded a six-conformation cycle, with three minima and three TSs, whereas M06-2X gave a simpler perspective (two maxima and two minima, very close in geometry). In the case of MP2, both related geometries converged into a single minimum (²T₁) and maximum in the antipodes (¹T₂). Interestingly, although sym-²T₁ was the global minimum for the MP2 calculations (with the two pseudo-axial methoxy groups), the B3LYP global minimum was around asym-E₄, with the two methoxy groups staggered. This reinforced the previous analysis regarding the underestimation of B3LYP to effectively account for the pseudo-axial stabilization exerted by electronegative groups. For the asymmetric conformations (“in–out”), the behavior was even more complex, with both B3LYP and MP2 showing a three minima-two maxima pattern (i.e., missing one transition state) and M06-2X correctly locating this TS around ¹T₂/¹E. In the case of B3LYP, the three minima were located at E₄ (global minima), ⁵T₁ (ΔE = 0.26 kcal mol⁻¹), and ⁴E (ΔE = 0.25 kcal mol⁻¹). M06-2X and MP2 showed similar patterns but with the envelope conformations displaced towards twisted ones (³T₄ and ⁴E/⁴T₅).

1,3-Dimethoxycyclopentanes (18–19). The conformational analysis of these compounds was even more complex than that discussed for the corresponding 1,2-disubstituted analogues as three different types of conformations were observed regarding the relative orientation of the two methoxy groups. Both the “out–out” and “in–in” conformations were symmetrical, whereas the “in–out” conformation was asymmetrical in nature (Fig. 9 and 10).

Fig. 9 (a) Geometry representations of the Cremer–Pople puckering parameters of the minima (green, global minima; yellow, local minima) and transition states (grey circle with red star) computed for compounds 18–19 at the M06-2X level. Qualitatively similar graphs were observed for the other levels of theory (see the ESI†). (b) Energies of the conformational pathways for compounds 18–19 calculated at the B3LYP (black), M06-2X (red), and MP2 (grey) levels.

Fig. 10 (a) Geometry representations of the Cremer–Pople puckering parameters of the minima (green, global minima; yellow, local minima) and transition states (grey circle with red star) computed for compounds 20–22 at the M06-2X level. Qualitatively similar graphs were observed for the other levels of theory (see the ESI†). (b) Energies of the conformational pathways for compounds 20–22 calculated at the B3LYP (black), M06-2X (red), and MP2 (grey) levels.

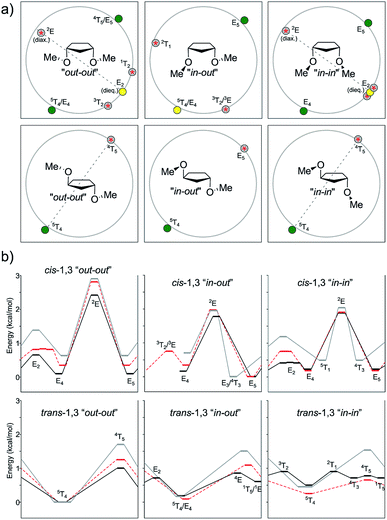
In the case of the 1,3-cis isomer, B3LYP and MP2 exhibited a classical four-conformer pattern for the “out–out” system, whereas according to M06-2X, one of the TSs became a minimum, and two close-by TSs appeared, affording a six-conformer pattern. A four-conformer pattern was also observed with B3LYP, M06-2X, and MP2 for the “in–out” conformations though one of the TSs was missing with B3LYP and MP2 (hence, it was actually a three-conformer pattern), whereas M06-2X succeeded in finding the left-out TS around ³T₂. Regarding the “in–in” type of conformations, the DFT methods encountered a six-conformer pattern, but MP2 converted the ¹T₂ minimum and its surrounding TSs into just one TS, thus conforming a four-conformer pattern. The E₅-“in–out” is usually the global minimum and it was shifted by the MP2 calculation toward E₃. In such conformations, one methoxyl group is pseudo-equatorial and the other one is staggered. The ²E conformation, featuring the two methoxy groups in a pseudo-axial position, was located as TS at a relatively high energy content for all levels of theory (2.41–2.89 kcal mol⁻¹ for “out–out” conformations, 1.77–1.97 kcal mol⁻¹ for “in–out” conformations, and 1.89–2.04 kcal mol⁻¹ for “in–in” conformations). The corresponding flipped structure (E₂) with the two pseudo-equatorial OMe groups was also found as a TS or as a relative minimum depending on the level of theory and conformation of the methoxy groups. For instance, B3LYP predicted E₂ as a TS for the “out–out” conformations and a relative minimum for the “in–in” conformations. M06-2X described a relative minimum in both cases, whereas MP2 anticipated a TS. When comparing the relative energies of ²E vs. E₂, the last ones were considerably lower (ΔE = 0.86–1.99 kcal mol⁻¹). Here, again, the ΔE values were lower for MP2 than that for B3LYP, which was consistent with our previous findings.

In the case of the trans-1,3 compound, when dealing with the “out–out” system, B3LYP gave just one minimum at ⁵T₄ and one TS at the inverted ⁴T₅ (1.00 kcal mol⁻¹ higher in energy). M06-2X afforded a similar behavior, whereas MP2 turned it into a four-conformer pattern; however, one of the TSs was very close to its surrounding minima, and they all had very low frequencies (<10 cm⁻¹). In all levels of theory, the global minima were found near ⁵T₄, with one pseudo-axial and one staggered OMe group. For “in–out”, B3LYP gave a four-conformer pattern, with the most stable conformation again near ⁵T₄ (E_rel = 0.19 kcal mol⁻¹) and the other one close in energy at ¹T₅ (E_rel = 0.60 kcal mol⁻¹). The two transition structures connecting the minima were computed at ⁴E (ΔE = 0.86 kcal mol⁻¹) and E₂ (ΔE = 0.71 kcal mol⁻¹). M06-2X and MP2 afforded a simpler two-conformer pattern, with geometries depending on the level of theory. The minimum and TS were near ⁵T₄ and E₅ according to M06-2X and shifted toward E₄ and ⁴T₅ according to MP2. Finally, for the “in–in” type of conformations, a four-conformer pattern was observed for B3LYP, with two local minima (⁵T₄ and ¹T₅) closer in energy (0.50 and 0.71 kcal mol⁻¹, respectively) and two transition structures connecting both minima at ²T₁ and ⁴T₅. MP2 also showed a four-conformer pattern, but it was completely different to that of B3LYP, with different conformers at hand (⁵T₄ and E₄/³T₄ as the local minima and E₄ and ⁴T₅ as TS). M06-2X afforded a cleaner scenario, with one minimum at ⁵T₄ and one maximum at ⁴T₅.

2-Hydroxy-THF (20). As a model structure for furanoses, the conformational landscape of 2-hydroxy-THF represents an interesting case to be disclosed. As in other compounds, the stationary points found with B3LYP slightly differed from those located with MP2 and M06-2X (Fig. 10). For instance, the former predicted a global minimum at almost perfect ²E³⁷ bearing a pseudo-axial OH group, whereas in the last two methods, a minor shift south toward ²T₁/²E was observed. In both cases, the energetic preference should be well understood considering the anomeric effect. The other minimum featured E₄ geometry with an isoclinal OH group at 0.22–0.50 kcal mol⁻¹. The most stable transition structures were located at ^OE, with low barriers (0.38–0.81 kcal mol⁻¹). Interestingly, the other transition structure featuring ¹E (B3LYP and M06-2X) or E_O/¹E_O (MP2) geometry was computed to be much higher in energy (3.36–4.17 kcal mol⁻¹), which could be explained given that the pseudo-equatorial orientation of the OH group precludes anomeric stabilization.

cis- and trans-5-Methyl-2-hydroxy-THF (21–22). The conformational analysis of furanoside-containing compounds has received considerable attention due to their relevance in different fields of chemistry and biology.¹³ Besides 2-hydroxy-THF disclosed above, we thoroughly explored the cis- and trans 5-methylated analogues as model structures for pentofuranoses (Fig. 10).

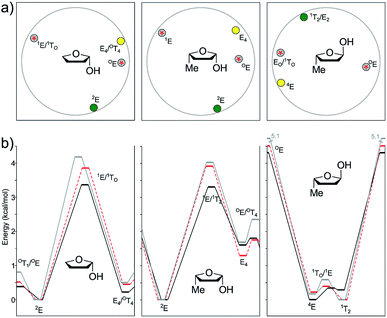
In the case of the cis isomer, the conformational landscape was quite similar to that observed for 2-hydroxy-THF disclosed above. The global minimum was located at ²E in all cases, which was consistent with the stabilization exerted by the pseudo-axial OH group as a consequence of the anomeric effect. The other minima were computed near E₄, with pseudo-axial and isoclinal methyl and hydroxyl groups, respectively. The energy difference between both minima was significant (1.29–1.69 kcal mol⁻¹), suggesting that the equilibrium should be cleanly displaced towards ²E at room temperature. The transition structures were found near those observed for 2-OH-THF, with the most stable one at ^OE and the other one at ¹E. The first TS (^OE) featured a pseudo-diaxial arrangement of the two substituents, with barriers higher than those computed for the previous related system and underestimated by the DFT methods regarding MP2 (1.77–1.80 vs. 2.36 kcal mol⁻¹). The most unstable transition structure showed ¹E geometry, with a pseudo-equatorial OH group and an isoclinal methyl group. Here, again, higher energy barriers were estimated with the three methods under study (3.30 kcal mol⁻¹ for B3LYP, 3.91 kcal mol⁻¹ for M06-2X, and 4.02 kcal mol⁻¹ for MP2).

The trans isomer reflected an excellent model study to illustrate the dependence of the conformational landscape with the relative orientation of the substituents and the level of theory employed during the calculations. The B3LYP global minimum was found at ⁴E, with a pseudo-equatorial methyl group and an isoclinal OH group. However, according to M06-2X and MP2, the global minima shifted towards ¹T₂ with a pseudo-axial OH orientation, showing once again that the stabilization exerted by pseudo-axial electronegative groups is underestimated by B3LYP. Nevertheless, the ⁴E/¹T₂ energy difference was quite low for the three levels of theory (0.17–0.29 kcal mol⁻¹), indicating that the two type of conformations should be expected to occur in real systems. Interestingly, none of the theoretical models agreed on the structure of the most stable TS connecting both minima (¹E for B3LYP, ¹T_O for M06-2X, and E_O for MP2), with similar energy barriers in all cases (0.34–0.59 kcal mol⁻¹). The relative stabilization of these structures was due to the pseudo-axial orientation of the OH group. The other TS, much higher in energy, was found at ^OE, with a pseudo-OH group. The selected stationary points of 21 and 22 found at the B3LYP/6-311+G** level of theory are shown in Fig. 11.

Fig. 11 Selected stationary points found for (a) cis-5-methyl-2-hydroxy-THF, and (b) trans-5-methyl-2-hydroxy-THF at the M06-2X/6-311+G** level of theory (TS: transition structure; GM: global minimum; LM: local minimum).

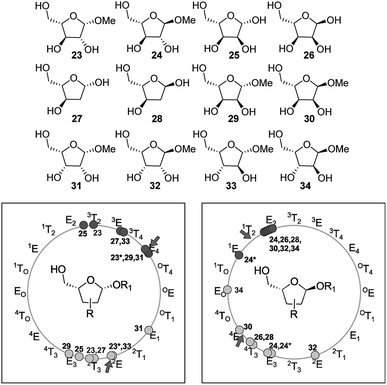
The conformational preferences calculated for these two simplified models for pentofuranoses showed good correlation with the landscape found for more complex furanosic compounds shown in Fig. 12.³⁸ For instance, Cros et al. explored methyl-β-D- and -α-L-arabinofuranosides (ent-23 and 24, respectively) with the MM3 force field.³⁹ They observed that the conformations of the two compounds were distributed in two deep low-energy wells (consistent with the two minima-two maxima reported herein). In the case of 23, the two minima were found near ³T₂ and ²T₃, whereas the stationary points of 24 were located at ¹T₂/E₂ and E₃. Later, Dowd et al. employed MM3 to build the conformational maps of the furanosyl rings of β- and α-D-ribose (ent-25 and ent-26, respectively) and their 2-deoxy counterparts (ent-27 and ent-28, respectively).⁴⁰ In the case of ribose (25 and 26), the northern (³T₂ and E₂, respectively) and southern (E₃/²T₃ and ⁴T₃, respectively) minima were located closer to the proposal made by Cros et al. for arabinofuranosides. The same trend was also noticed for the 2-deoxyribose analogues 27 (³E and ²T₃) and 28 (E₂ and ⁴T₃). More recently, Lowary and co-workers carried out a detailed examination of the stable conformations of twelve β- and α-methyl furanosides of D-arabinose (ent-23 and ent-24), D-lyxose (ent-29 and ent-30), D-ribose (ent-31 and ent-32), and D-xylose (ent-33 and ent-34) at the B3LYP/6-31+G**//B3LYP/6-31G* level of theory.⁴¹ In the cases of β-arabinose and β-ribose (23 and 31, respectively), the northern minima located at E₄ shifted by ∼50° southwest from the MM3 calculations by Cros et al. and Dowd et al. The southern minima found at ²E and E₃ slightly shifted from the MM3 results. In the case of α-series, the minima of 24 and 32 occurred at ¹E and E₃ and E₂ and ⁴E, respectively, which were again closer to the MM3 results.

Fig. 12 Scatter plot of the CP phase angle (amplitude not considered) of the local minima found for compounds 23–24 (Cros et al.), 25–28 (Dowd et al.), and 23*–24* and 29–34 (Lowary and co-workers). Light gray and dark gray circles represent the minima off the southern and northern regions, respectively, and the green arrow indicates the results of our calculations with the simplified model. The asterisks in 23 and 24 are provided to differentiate the results obtained by Cros et al. (no asterisk) from those reported by Lowary and co-workers (with asterisk).

The remaining compounds (31–34) exhibited similar trends but with some disturbances in the southern region. Taking collectively the results reported by Cros et al., Dowd et al., Lowary and coworkers, and us (Fig. 12), insightful relationships can be drawn. The conformational landscape of furanoses is governed by a 2-minima system, with one stationary point at the north and the other at the south of the rotational map. The northern region is mainly populated between ³T₂ and E₄ for the 1,4-cis isomers and between ¹E and E₂ for the 1,4-trans counterparts. In the same way, in the southern region, these conformations between E₃/²E (1,4-cis) and ⁴E/E₃ (trans) are favored. The results of our calculations on a simplified model correlated well with these interesting trends, suggesting that the conformational preference of furanoses is strongly dictated by the C-1/C-4 relative configuration. Naturally, the presence of other substituents at the ring might introduce additional steric and electronic interactions, hence affecting the location of minima. Including the solvent effect in the calculations might also generate a different outcome provided by gas phase calculations. For instance, the southern minima of 31, 32, and 34 were found at E₁, ²E, and E_O, respectively, which were slightly different from the above-mentioned range. In these cases, the formation of intramolecular H-bonds accounted for the shifts in the southern region.

Conclusions

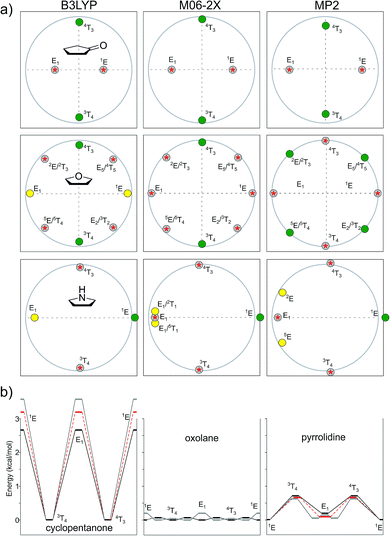
The conformational pathways of several mono- and disubstituted five-membered rings were thoroughly explored with three different quantum methods (B3LYP, M06-2X, and MP2). The results of these calculations showed that the conformational preference of a given compound is intimately linked with its own structural characteristics (type and number of substituents, substitution pattern, type of the heteroatom in the ring, etc.). Despite the case that in some systems the relative energies of different conformations fell within the limit provided by the levels of theory under study, interesting trends could be drawn. We found an interesting preference of electronegative substituents (chlorine, OH, etc.) and alkyl groups to take pseudo-axial and pseudo-equatorial positions, respectively. In addition, the conformational landscape computed for many systems showed dependence on the level of theory employed for the calculations. In this regard, we observed a higher correlation between the results provided by MP2 with M06-2X than that with B3LYP, which clearly underestimated the preferences for the pseudo-axial position of electronegative groups. In most cases, free energy calculations confirmed the results obtained using electronic energies. However, in a few cases, such as that for pyrrolidine, PES changed drastically by taking entropic effects into account.

Experimental section

Computational methods

Quantum mechanical calculations were performed using Gaussian 09W (rev. C.01)⁴² with the standard basis sets and default minimization methods and termination conditions, with the exception of the Tight keyword and the use of an Ultrafine grid for the optimizations. All the minima and transition states had zero or one imaginary frequency, respectively, as appropriate. For the transition states, it was verified that this frequency corresponded to the conformational pathway searched for. The transition states were obtained either by the traditional Berny algorithm or by using the QST2 procedure. Free energies were calculated at 298 K, as reported in the Gaussian output file, without scaling. For substituted cyclopentanes, the IUPAC numbering scheme was used, with the substituent facing down when numbering clockwise observed from above. The heterocycles were numbered following the usual carbohydrate convention, with C1 clockwise to the heteroatom (which is equivalent to atom 5).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are Research Members of the National Research Council of Argentina (CONICET). This work was supported by grants from ANPCyT (PICT-2016-0116), CONICET (PIP 298/14), UNR (BIO 316 and 500) and UBA (Q-203 and 0363).

References

1. E. Juaristi, Introduction to stereochemistry and conformational analysis, John Wiley and Sons, New York, 1991.
2. H. Sachse, Ber. Dtsch. Chem. Ges., 1890, 23, 1363–1370.
3. C. W. Beckett, K. S. Pitzer and R. Spitzer, J. Am. Chem. Soc., 1947, 69, 2488–2495.
4. D. Barton, Experientia, 1950, 6, 316–320.
5. C. A. Stortz, J. Phys. Org. Chem., 2010, 23, 1173–1186.
6. J. E. Kilpatrick, K. S. Pitzer and R. Spitzer, J. Am. Chem. Soc., 1947, 69, 2483–2488.
7. A. Wu, D. Cremer, A. A. Auer and J. Gauss, J. Phys. Chem. A, 2002, 106, 657–667.
8. K. S. Pitzer and W. E. Donath, J. Am. Chem. Soc., 1959, 81, 3213–3218.
9. (a) J. Aston, H. L. Fink and S. Schumann, J. Am. Chem. Soc., 1943, 65, 341–346; (b) J. McCullough, R. Pennington, J. Smith, I. Hossenlopp and G. Waddington, J. Am. Chem. Soc., 1959, 81, 5880–5883; (c) J. P. McCullough, J. Chem. Phys., 1958, 29, 966–967.
10. A. Almenningen, O. Bastiansen and P. Skancke, Acta Chem. Scand., 1958, 12, 5.
11. (a) D. Scott, W. Berg and J. McCullough, J. Phys. Chem., 1960, 64, 906–908; (b) D. Wertz and W. Shasky, J. Chem. Phys., 1971, 55, 2422–2425.
12. J. McCullough, D. Douslin, W. Hubbard, S. Todd, J. Messerly, I. Hossenlopp, F. Frow, J. Dawson and G. Waddington, J. Am. Chem. Soc., 1959, 81, 5884–5890.
13. H. A. Taha, M. R. Richards and T. L. Lowary, Chem. Rev., 2012, 113, 1851–1876.
14. (a) A. Golebiewski and A. Parczewski, Chem. Rev., 1974, 74, 519–530; (b) W. Cui, F. Li and N. L. Allinger, J. Am. Chem. Soc., 1993, 115, 2943–2951; (c) D. Cremer, Isr. J. Chem., 1983, 23, 72–84; (d) D. Cremer and J. A. Pople, J. Am. Chem. Soc., 1975, 97, 1358–1367.
15. (a) Z. Dzakula, M. L. Derider and J. L. Markley, J. Am. Chem. Soc., 1996, 118, 12796–12803; (b) T. J. Church, I. Carmichael and A. S. Serianni, J. Am. Chem. Soc., 1997, 119, 8946–8964; (c) J. B. Houseknecht, T. L. Lowary and C. M. Hadad, J. Phys. Chem. A, 2003, 107, 372–378; (d) J. G. Napolitano, J. A. Gavín, C. García, M. Norte, J. J. Fernández and A. Hernández Daranas, Chem.–Eur. J., 2011, 17, 6338–6347.
16. S. J. Han and Y. K. Kang, J. Mol. Struct.: THEOCHEM, 1996, 369, 157–165.
17. N. Sakhaee, S. Jalili and F. Darvish, Comput. Theor. Chem., 2016, 1090, 193–202.
18. (a) W. Sameera and D. A. Pantazis, J. Chem. Theory Comput., 2012, 8, 2630–2645; (b) M. Marianski, A. Supady, T. Ingram, M. Schneider and C. Baldauf, J. Chem. Theory Comput., 2016, 12, 6157–6168; (c) V. A. Cosenza, D. A. Navarro and C. A. Stortz, Carbohydr. Res., 2016, 426, 15–25; (d) E. A. Del Vigo, C. Marino and C. A. Stortz, Carbohydr. Res., 2017, 448, 136–147.
19. C. Altona, H. t. Geise and C. Romers, Tetrahedron, 1968, 24, 13–32.
20. C. t. Altona and M. Sundaralingam, J. Am. Chem. Soc., 1972, 94, 8205–8212.
21. D. Cremer and J. A. Pople, J. Am. Chem. Soc., 1975, 97, 1354–1358.
22. E. J. Ocola, L. E. Bauman and J. Laane, J. Phys. Chem. A, 2011, 115, 6531–6542.
23. L. Carreira, J. Chem. Phys., 1971, 55, 181–185.
24. J. R. Durig, A. M. E. Defrawy, A. Ganguly, T. K. Gounev and G. A. Guirgis, J. Phys. Chem. A, 2009, 113, 9675–9683.
25. (a) I. Ekejiuba and H. J. Hallam, J. Mol. Struct., 1970, 6, 341–357; (b) I. Ekejiuba and H. Hallam, J. Chem. Soc. B, 1970, 209–211; (c) W. Harris, J. Karriker and J. Durig, J. Mol. Struct., 1971, 9, 139–149; (d) H. M. Badawi, W. A. Herrebout, C. Zheng, T. A. Mohamed, B. Van der Veken and J. R. Durig, Struct. Chem., 2003, 14, 617–635.
26. R. J. Abraham, R. Koniotou and F. Sancassan, J. Chem. Soc., Perkin Trans. 2, 2002, 2025–2030.
27. R. L. Lipnick, J. Am. Chem. Soc., 1974, 96, 2941–2948.
28. J. D. Roberts, M. Christl and H. J. Reich, J. Am. Chem. Soc., 1971, 93, 3463–3468.
29. H. Kim and W. D. Gwinn, J. Chem. Phys., 1969, 51, 1815–1819.
30. V. M. Rayón and J. A. Sordo, J. Chem. Phys., 2005, 122, 204303.
31. W. Caminati, H. Oberhammer, G. Pfafferott, R. Filgueira and C. Gomez, J. Mol. Spectrosc., 1984, 106, 217–226.
32. G. Pfafferott, H. Oberhammer, J. E. Boggs and W. Caminati, J. Am. Chem. Soc., 1985, 107, 2305–2309.
33. W. Caminati, A. Dell'Erba, G. Maccaferri and P. G. Favero, J. Mol. Spectrosc., 1998, 191, 45–48.
34. (a) L. Carballeira and I. Pérez-Juste, J. Chem. Soc., Perkin Trans. 2, 1998, 1339–1346; (b) L. Carballeira, I. Pérez-Juste and C. Van Alsenoy, J. Phys. Chem. A, 2002, 106, 3873–3884.
35. M. Kunitski, C. Riehn, V. V. Matylitsky, P. Tarakeshwar and B. Brutschy, Phys. Chem. Chem. Phys., 2010, 12, 72–81.
36. H. B. Mayes, L. J. Broadbelt and G. T. Beckham, J. Am. Chem. Soc., 2014, 136, 1008–1022.
37. The naming of the different conformers for 2-hydroxyTHF and its 5-methylated counterparts follows the nomenclature used in sugar chemistry, i.e., C-1 for the anomeric atom, C-4 for the last carbon in the cycle, and O for the ring oxygen..
38. Most of the studies have been carried out with furanoses of D-series. However, the configurations exhibited by 21 and 22 are consistent with furanoses of L-series. Hence, to facilitate the comparison we have inverted (rotated by 180°) the results obtained for furanoses of D-series (i.e. the E₁ in D-series is identical to ¹E for L-series)..
39. S. Cros, C. H. du Penhoat, S. Pérez and A. Imberty, Carbohydr. Res., 1993, 248, 81–93.
40. M. K. Dowd, A. D. French and P. J. Reilly, J. Carbohydr. Chem., 2000, 19, 1091–1114.
41. J. B. Houseknecht, T. L. Lowary and C. M. Hadad, J. Phys. Chem. A, 2003, 107, 5763–5777.
42. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian, Inc., Wallingford CT, 2009.

---

Footnote

† Electronic supplementary information (ESI) available: Computational data associated with this paper. See DOI: 10.1039/c9ra03524a

---