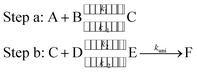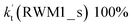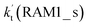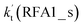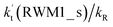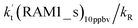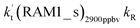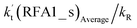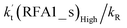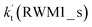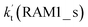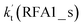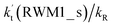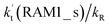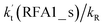Open Access Article
Open Access ArticleEffects of water, ammonia and formic acid on HO2 + Cl reactions under atmospheric conditions: competition between a stepwise route and one elementary step†
Tianlei Zhang
 *ad,
Yongqi Zhang‡ad,
Mingjie Wen‡ad,
Zhuo Tang‡a,
Bo Long
*ad,
Yongqi Zhang‡ad,
Mingjie Wen‡ad,
Zhuo Tang‡a,
Bo Long *b,
Xiaohu Yu
*b,
Xiaohu Yu a,
Caibin Zhao
a,
Caibin Zhao a and
Wenliang Wang
a and
Wenliang Wang *c
*c
aShaanxi Key Laboratory of Catalysis, School of Chemical & Environment Science, Shaanxi University of Technology, Hanzhong, Shaanxi 723001, P. R. China. E-mail: ztianlei88@l63.com; Fax: +86-0916-2641083; Tel: +86-0916-2641083
bSchool of Materials Science and Engineering, Guizhou Minzu University, Guiyang 550025, P. R. China. E-mail: longbo@gzmu.edu.cn
cKey Laboratory for Macromolecular Science of Shaanxi Province, School of Chemistry & Chemical Engineering, Shaanxi Normal University, Xi'an, Shaanxi 710062, P. R. China. E-mail: wlwang@snnu.edu.cn
dShanghai Key Laboratory of Molecular Catalysis and Innovative Materials, Fudan University, Shanghai 200433, P. R. China
First published on 10th July 2019
Abstract
Quantum chemical calculations at M06-2X and CCSD(T) levels of theory have been performed to investigate the effects of H2O, NH3, and HCOOH on the HO2 + Cl → HCl + O2 reaction. The results show that catalyzed reactions with three catalysts could proceed through two different mechanisms, namely a stepwise route and one elementary step, where the former reaction is more favorable than the latter. Meanwhile, for the stepwise route, a single hydrogen atom transfer pathway in the presence of all catalysts has more advantages than the respective double hydrogen atom transfer pathway. Then, the relative impacts of catalysts under tropospheric conditions were investigated by considering the temperature dependence of the rate constants and the altitude dependence of catalyst concentrations. The calculated results show that at 0 km altitude, the HO2 + Cl → HCl + O2 reaction with catalysts, such as H2O, NH3, or HCOOH, cannot compete with the reaction without a catalyst, as the effective rate constant with a catalyst is smaller by 2–6 orders of magnitude than the naked reaction within the temperature range 280–320 K. The calculated results also show that at altitudes of 5, 10 and 15 km, the effective rate constant of the HCOOH-catalyzed reaction increases obviously with an increase in altitude. At 15 km altitude, its value is up to 9.63 × 10−11 cm3 per molecule per s, which is close to the corresponding value of the reaction without a catalyst, showing that the contribution of HCOOH to the HO2 + Cl → HCl + O2 reaction cannot be neglected at high altitudes. The new findings in this investigation are not only of great necessity and importance for elucidating the gas-phase reaction of HO2 with Cl in the presence of acidic, neutral and basic catalysts, but are also of great interest for understanding the importance of other types of hydrogen abstraction in the atmosphere.
1. Introduction
HO2 is an important atmospheric species and plays important roles in both the troposphere and the stratosphere.1 Meanwhile, HO2 plays a significant transient intermediate role in the combustion of hydrocarbon fuels, atmospheric photolysis cycles, and biochemical processes.2,3 The chlorine radical (Cl) plays an important role in the destruction of the stratospheric ozone layer. In the stratosphere, Cl is produced by the direct photolysis of dimers of the ClOx family (ClO, ClO2 etc.).4,5 Also, Cl is mainly present in the form of reservoirs like HOCl, HCl, ClONO2, etc. in the troposphere. These reservoirs are normally formed in the stratosphere and transported back to the troposphere. Consequently, due to the higher reactivity of Cl with the majority of organic compounds etc. as compared to OH radicals,6,7 it is well known that Cl is a strong oxidant, and its reactions with atmospheric species, such as iodinated compounds and radicals, are expected to be important. Therefore, atmospheric sinks of Cl are of particular concern for fully elucidating atmospheric processes involving Cl.Previous investigations have suggested that the gas-phase oxidation reaction of HO2 by Cl (eqn (1)) is of interest in atmospheric chemistry,8–11 and is thought to play a major role in the stratosphere by trapping Cl as HCl.8,12
| HO2 + Cl → HCl + O2 | (1) |
The potential importance of the Cl reaction with the HO2 radical has led to a number of publications and, as a result, the kinetics of the HO2 + Cl reaction have been studied experimentally for a range of temperatures.8,13–16 Lee et al.16 measured the rate constant of eqn (1) in a discharge-flow system with far infrared laser magnetic resonance within the temperature range 250–420 K. Similarly, Dobis et al.8 used mass spectrometry to measure the rate constant ((4.45 ± 0.06) × 10−11 cm3 per molecule per s) of the reaction of eqn (1) in the temperature range 243–368 K. Both of these investigations showed that the rate constant in eqn (1) does not change within the measured temperature range. In another experiment, Hickson et al.9 used the discharge-flow resonance fluorescence technique coupled with infrared diode laser spectroscopy to measure the rate constant for the reaction in eqn (1) within the temperature range 226–336 K. Their results show that the rate constant in eqn (1) derived from kinetic experiments expressed in Arrhenius form was (1.6 ± 0.2) × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(249 ± 34)/T] cm3 per molecule per s. The theoretical aspect of the kinetics and mechanism for the reaction of eqn (1) have not yet been investigated. Thus, in this study, the reaction in eqn (1) has been investigated for the first time. These investigations provide meaningful information about the mechanisms and kinetics for the HO2 + Cl reaction under atmospheric conditions. However, this effort has focused only on the non-catalytic process of the HO2 + Cl reaction.
exp[(249 ± 34)/T] cm3 per molecule per s. The theoretical aspect of the kinetics and mechanism for the reaction of eqn (1) have not yet been investigated. Thus, in this study, the reaction in eqn (1) has been investigated for the first time. These investigations provide meaningful information about the mechanisms and kinetics for the HO2 + Cl reaction under atmospheric conditions. However, this effort has focused only on the non-catalytic process of the HO2 + Cl reaction.
Water has long been considered a subject of chemical interest due to its abundance and unique properties in atmospheric chemistry.17 It not only forms the hydrogen-bonded complexes (HO2⋯H2O and H2O⋯HO2) with the HO2 radical,18–22 but can also actively participate in atmospheric reactions as a catalyst,23,24 where an interesting result20 is that the HO2 self-reaction can be up to three times faster in the presence of water. Moreover, many previous studies have appeared in the literature on the electronic structure of the cluster H2O⋯Cl.25,26 These situations have stimulated our interest in modeling the gas-phase reaction of the H2O⋯HO2⋯Cl ternary system, in which a single water molecule serves as a catalyst.
Similar to the water monomer (WM), ammonia (AM) also exists widely in the atmosphere: its atmospheric concentration was found to be 30 ppb in a polluted ambient atmosphere and as high as 10 ppm in dairy farms.27,28 As the most abundant alkaline component in the atmosphere, AM can also catalyze hydrogen abstraction reactions.29,30 For example, AM plays an important role in the atmospheric formation of sulfuric acid (SA) through the hydrolysis of SO3.30 Compared to water, which is known to reduce the barrier of this reaction to 5.9 kcal mol−1, AM makes the reaction barrierless and the value of its rate constant was found theoretically to be ∼105 to 107 times that of a water catalyst. The above facts indicate that one cannot ignore AM in modeling different atmospheric hydrogen atom transfer (HAT) reactions. Meanwhile, to observe how an acid can influence the reaction in comparison to a neutral or a basic catalyst, the reaction in eqn (1) in the presence of formic acid (FA) as a catalyst has also been carried out.31 In fact, FA can remarkably decrease the energy barrier of the HAT reaction, and is the reason in eqn (1) for considering FA as an acidic catalyst. It not only has significant abundance in the atmosphere, but it has also been found that FA can decrease the energy barrier significantly for several atmospheric HAT reactions.31–35 The other issue is that it is known that a particular HAT reaction could show completely opposite temperature dependence in the presence of different catalysts. As temperature changes appreciably (by more than 100 K) within the troposphere, one needs to incorporate various types of catalysts to present a reliable picture of a particular reaction at various altitudes in the troposphere. In the troposphere, temperature decreases with increasing altitude. Therefore, with a change in altitude, the efficiency of acidic, neutral and basic catalysts on the reaction of eqn (1) should also be extensively investigated in order to provide a complete altitude dependence of the reaction.
In the present article, quantum chemical calculations have been performed to study the effect of acidic (FA), neutral (WM) and basic (AM) catalysts on the energetic and kinetic aspects of the HO2 + Cl reaction. Then, the ways in which the relative impacts of catalysts and competition between the pathways are modulated with a change in tropospheric conditions have also been investigated extensively by considering the temperature dependence of rate constants and the altitude dependence of catalyst concentrations.
2. Computational details
2.1 Electronic structure calculations
The molecular geometries of the reactants, products, pre-reactive complexes, transition states, and post-reactive complexes for the oxidation of HO2 by the Cl radical without and with catalyst molecules were optimized using the M06-2X functional36,37 with the 6-311++G(2d,2p) basis set. The M06-2X functional is one of the best functionals with which to study noncovalent interactions38,39 and has shown promising applications for estimating the thermochemistry and equilibrium structures for atmospheric reactions and molecular clusters.40–42 At the M06-2X/6-311++G(2d,2p) level, the harmonic vibrational frequencies were calculated to verify the nature of the corresponding stationary points (minima or transition state) to provide the zero-point vibrational energy (ZPE) and to determine the thermodynamic contributions to the enthalpy and free energy. In addition, intrinsic reaction coordinate (IRC)43–45 calculations were carried out to ensure that the transition states were connected to the desired reactants and products. Geometrical and frequency calculations were performed using Gaussian 09.46 The final energies were obtained by performing single-point energy calculations at the CCSD(T)-F12A/VDZ-F12 (ref. 47–49) level of theory, based on the optimized geometries at the M06-2X/6-311++G(2d,2p) level, using ORCA.50 It should be noted that the HO2 + Cl reaction is a radical–radical reaction. It is likely that there are some multireference features in the HO2 + Cl reaction. Post-CCSD(T) calculations are required for obtaining quantitative barrier heights, as has been reported in the literature.51–53 However, we mainly focus on the effects of water clusters on the HO2 + Cl reaction. Additionally, the calculated rate constant of the HO2 + Cl reaction agrees well with the experimental data. Thus, we have not considered post-CCSD(T) calculations.2.2 Rate constant calculations
To estimate the effect of the catalyst (WM, AM and FA) added, theoretical rate constants of canonical variational transition (CVT)54 state theory with small curvature tunneling (SCT) correction55 for oxidation of HO2 by a Cl radical without and with a catalyst were calculated by employing the Polyrate 8.2 program56 coupled with the steady state approximation. As described in eqn (2), all the processes for oxidation of HO2 by a Cl radical without and with a catalyst involve two major steps, as follows.Here, A and B are any two among HO2, Cl and a catalyst (WM, AM or FA), C is the binary complex formed by A and B. D is the remaining third species other than A and B. E is the ternary complex formed by HO2, Cl and a catalyst. In step a, A combines with B to form an adduct C, whereas step b consists of two elementary processes: in the first process, C reacts with D to form E and subsequently E undergoes a unimolecular transformation to produce formation F via the corresponding TS.
Assuming that intermediate E was in equilibrium with the corresponding reactants (C and D) and was at steady state,57 the rate constant for step b can be written as:
| kb = Keq2kuni | (2) |
The rate constant kuni in eqn (2) has been evaluated by employing Polyrate 8.2 programs56 in the framework of canonical variational transition state theory (CVT).54 To include the tunneling effects for motion along the reaction coordinate for the title reactions at the CCSD(T)-F12A/VDZ-F12 (ref. 47–49)//M06-2X/6-311++G(2d,2p) level, the small curvature tunneling55 (SCT) approximation has been adopted in this study. In addition, Keq2 in eqn (2) was given by eqn (3).
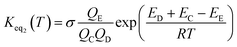 | (3) |
In eqn (3), the various Q values denote the partition functions of intermediate E, and reactants C and D, respectively. All partition functions were obtained using the M06-2X/6-311++G(2d,2p) method. ED, EC and EE stand for the energies of the species of D, C and E, respectively; σ is the symmetry factor. In the present work, kb has been used to compare the rates between the bare reaction and catalyzed reactions.
2.3 Effective rate constant calculations
If one incorporates the effect of step a, the resultant rate constant (kt) can be written as:| kt = Keq1Keq2kuni | (4) |
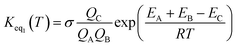 | (5) |
In eqn (5), the various Q values denote the partition functions of complex C, and reactants A and B, respectively. EA, EB and EC stand for the energies of the species A, B and C, respectively. From the above, the rate of the reaction (v) in the presence of catalysts can be written as:
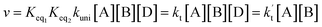 | (6) |
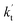 is the effective rate constant, which could be considered a measure of the relative efficiencies of the different catalysts under atmospheric conditions, as it includes the concentration as well as rate constant of a particular catalyst.
is the effective rate constant, which could be considered a measure of the relative efficiencies of the different catalysts under atmospheric conditions, as it includes the concentration as well as rate constant of a particular catalyst.
3. Results and discussion
The transition state in each reaction channel was denoted by “TS” followed by a number, and the pre-reactive complex was denoted by “IM” followed by a number. The letter “a” was used to distinguish the transition states and pre-reactive complexes which are conformers of each other and therefore have the same features; species in the presence of WM, AM and FA were respectively denoted by “WM”, “AM”, and “FA” suffixes.3.1 Uncatalyzed mechanism and kinetic for the HO2 + Cl → HCl + O2 reaction
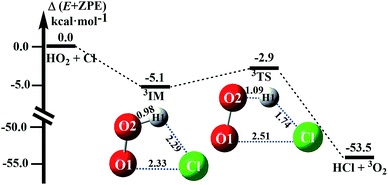
The reactions between HO2 and Cl on both singlet and triplet potential energy surfaces (PESs) have been investigated at the CCSD(T)-F12A/VDZ-F12//M06-2X/6-311++G(2d,2p) level in this study, where the channels of HCl + 1O2 formation (singlet PES) and HCl + 3O2 formation (triplet PES) have been considered, as shown in Fig. 1 and S2.† Moreover, compared with the two channels, it was found that the channel of HCl + 3O2 formation on the triplet potential energy is the most favorable channel. In this study, we reinvestigated the channel of HCl + 3O2 formation to determine the reliability of the theoretical methods used here and the catalytic effect of WM, AM and FA.In absence of any catalyst, HO2 first combines with Cl to produce a pre-reactive complex IM which is 5.1 kcal mol−1 more stable than isolated monomers (as shown in Fig. 1). Thereafter, complex IM undergoes a unimolecular transformation through cyclic TS with an energy barrier of 2.2 kcal mol−1. The ΔH (298 K) of the HO2 + Cl → HCl + O2 reaction was predicted to be −54.2 kcal mol−1, which is in good agreement with the experimental estimates of −54.4 ± 0.8 kcal mol−1.9
For the HO2 + Cl → HCl + O2 reaction without water, Table 1 lists its CVT/SCT rate constant. As given in Table 1, at 213 and 320 K the rate constant was increased by 27% and 49% due to tunneling, while the rate constant was decreased to 12% and 34% due to recrossing effects. So, similar to previous investigations,22,58,59 the tunneling transmission coefficients are very large for the hydrogen atom transfer process. Thus, herein the computed CVT/SCT rate constants have been used to estimate the catalytic effect of catalysts (WM, AM and FA). Additionally, Table 1 shows the computed CVT/SCT rate constants for Channel R1 (kR1). It is worth noting that the rate constants of the HO2 + Cl → HCl + O2 reaction increased with an increase in temperature. At 298 K, the calculated value of kR1 was 6.27 × 10−11 cm3 per molecule per s, which is in good agreement with experimental reports.8 So, this indicates that the calculations for the HO2 + Cl → HCl + O2 reaction without and with catalysts at the CCSD(T)-F12A/VDZ-F12//M06-2X/6-311++G(2d,2p) level of theory are acceptable.
| T (K) | ΓCVT | κSCT | Keq | kTST2 | kCVT2 | kCVT/SCT2 | kR | kexp |
|---|---|---|---|---|---|---|---|---|
| a kR is the rate constant of HO2 + Cl → HCl + 3O2.b The experimental value from ref. 8. | ||||||||
| 213 | 0.12 | 15.27 | 1.07 × 10−21 | 1.94 × 1011 | 2.43 × 1010 | 3.70 × 1011 | 3.98 × 10−10 | |
| 216 | 0.13 | 14.33 | 9.61 × 10−22 | 2.01 × 1011 | 2.63 × 1010 | 3.77 × 1011 | 3.62 × 10−10 | |
| 219 | 0.14 | 13.47 | 8.63 × 10−22 | 2.08 × 1011 | 2.85 × 1010 | 3.84 × 1011 | 3.31 × 10−10 | |
| 224 | 0.15 | 12.19 | 7.26 × 10−22 | 2.19 × 1011 | 3.23 × 1010 | 3.94 × 1011 | 2.86 × 10−10 | |
| 230 | 0.16 | 10.89 | 5.96 × 10−22 | 2.34 × 1011 | 3.74 × 1010 | 4.07 × 1011 | 2.43 × 10−10 | |
| 235 | 0.17 | 9.96 | 5.10 × 10−22 | 2.46 × 1011 | 4.20 × 1010 | 4.18 × 1011 | 2.13 × 10−10 | |
| 250 | 0.20 | 7.79 | 3.31 × 10−22 | 2.85 × 1011 | 5.78 × 1010 | 4.50 × 1011 | 1.49 × 10−10 | |
| 259 | 0.22 | 6.82 | 2.62 × 10−22 | 3.10 × 1011 | 6.88 × 1010 | 4.69 × 1011 | 1.23 × 10−10 | |
| 280 | 0.27 | 5.20 | 1.62 × 10−22 | 3.72 × 1011 | 9.90 × 1010 | 5.15 × 1011 | 8.32 × 10−11 | |
| 290 | 0.29 | 4.65 | 1.32 × 10−22 | 4.04 × 1011 | 1.16 × 1011 | 5.37 × 1011 | 7.08 × 10−11 | |
| 298 | 0.30 | 4.28 | 1.13 × 10−22 | 4.30 × 1011 | 1.30 × 1011 | 5.55 × 1011 | 6.27 × 10−11 | ((4.45 ± 0.06) × 10−11)b |
| 300 | 0.31 | 4.19 | 1.09 × 10−22 | 4.37 × 1011 | 1.34 × 1011 | 5.60 × 1011 | 6.09 × 10−11 | |
| 310 | 0.33 | 3.81 | 9.11 × 10−23 | 4.71 × 1011 | 1.53 × 1011 | 5.83 × 1011 | 5.32 × 10−11 | |
| 320 | 0.34 | 3.49 | 7.72 × 10−23 | 5.06 × 1011 | 1.74 × 1011 | 6.07 × 1011 | 4.69 × 10−11 | |
3.2 Mechanism and kinetics of the H2O catalyzed HO2 + Cl → HCl + O2 reaction
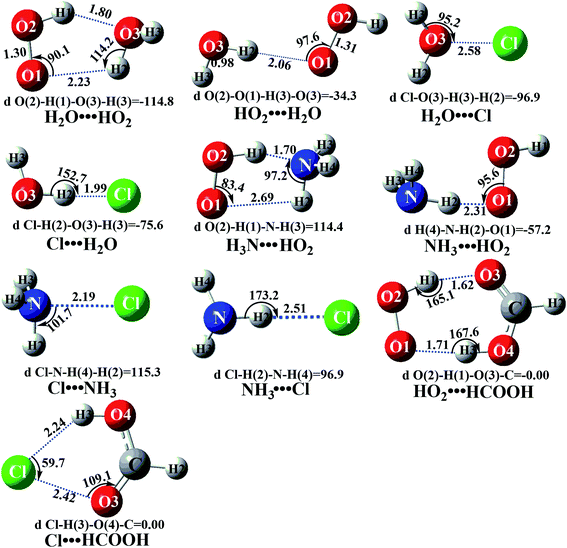
In the presence of a water molecule, both bodies of HO2 and Cl can respectively interact with water to form two-body complexes first in the entrance channels before interacting with the third body of Cl or HO2. So, it is very necessary to find the stable configurations of the two-body complexes between HO2 (or Cl) and H2O. In order to find all possible stable configurations of these complexes, global minimum searching of geometric structures was carried out using Tsinghua Global Minimum (TGMin).60,61 Then the initial structures were selected for geometrical optimization using the M06-2X/6-31G(d,p) method. The isomer structures within 5.0 kcal mol−1 of the global minimum were re-optimized by the M06-2X/6-311++G(2d,2p) method. As shown in Fig. 2 and S3,† and consistent with previous reports,62–66 a five-membered ring complex H2O⋯HO2 is much more stable than the single hydrogen bond (or van der Waals interaction) complexes HO2⋯H2O, H2O⋯Cl and Cl⋯H2O with its binding energy being larger by 5.1–6.1 kcal mol−1. Meanwhile, the equilibrium constants of these complexes at 298 K are 6.05 × 10−20, 2.60 × 10−22, 1.93 × 10−21 and 3.85 × 10−21 cm3 per molecule, respectively (Table S3†). Considering typical tropospheric concentrations of 7.64 × 1017 molecules per cm3 of H2O, 3 × 108 molecules per cm3 of HO2 (ref. 67) and 3 × 105 molecules per cm3 of Cl,68,69 the atmospheric concentration of the H2O⋯HO2 complex has been estimated to be 1.39 × 107 molecules per cm3, which is 2.33 × 102, 3.14 × 104 and 1.58 × 104 times the concentrations of HO2⋯H2O, H2O⋯Cl and Cl⋯H2O. Thus, in the four bimolecular reactions of eqn (7)–(10), we can predict that the atmospheric relevance of the bimolecular reaction of eqn (7) will be much more obvious than those reactions of eqn (8)–(10). However, for comparison, the potential energy surfaces (PESs) for all four possible types of bimolecular reactions have been considered.| H2O⋯HO2 + Cl → H2O⋯HCl + O2 | (7) |
| HO2⋯H2O + Cl → H2O + HCl + O2 | (8) |
| Cl⋯H2O + HO2 → H2O⋯HCl + O2 | (9) |
| H2O⋯Cl + HO2 → H2O⋯HCl + O2 | (10) |
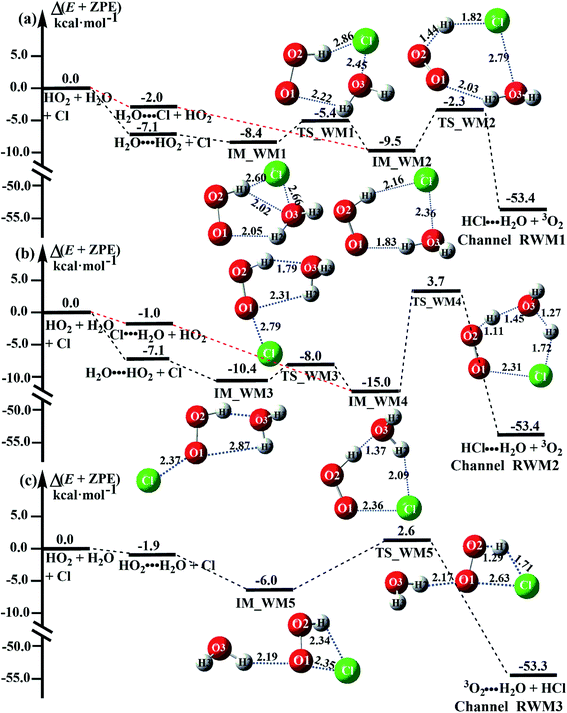
Fig. 3 presents the potential energy surfaces (PESs) for the water-catalyzed HO2 + Cl → H2O + 3O2 reaction (Channels RWM1, RWM2 and RWM3), along with the local minimum geometries on the corresponding reaction pathways. In Fig. 3, the H2O⋯HO2 + Cl reaction is mechanistically different from the three other reactions of HO2⋯H2O + Cl, Cl⋯H2O + HO2 and H2O⋯Cl + HO2, as the H2O⋯HO2 + Cl reaction involves a stepwise route, whereas the other reactions involve one elementary step. During the stepwise route reaction, the reaction occurs first via a ring enlargement, and then proceeds through a hydrogen abstraction mechanism, whereas in the case of the one elementary step reaction channel, the reaction proceeds through a hydrogen abstraction process alone.
For Channel RWM1, two kinds of reaction types can be taken (a) between H2O⋯Cl and HO2 or (b) between H2O⋯HO2 and Cl. When the H2O⋯Cl complex and HO2 act as reactants, the reaction occurs in one elementary step, which is similar to the uncatalyzed reaction of HO2 + Cl → HCl + O2 above, the HCOOH-catalyzed hydrolysis of CH3CHO and HCHO,41,70 as well as the HNO3 and HCOOH-catalyzed hydrolysis of SO3.71–73 The reaction starts with the formation of the pre-reactive complex IM_WM2, as described in Fig. 3. As shown in Fig. 3, the pre-reactive IM_WM2 complex has a six-membered ring structure, where there are two hydrogen-bonded interactions and a van der Waals interaction. The binding energy (9.5 kcal mol−1) of IM_WM2 is about 7.5 kcal mol−1 lower than that of the H2O⋯Cl and HO2 reactants at the CCSD(T)-F12A/VDZ-F12//M06-2X/6-311++G(2d,2p) level. Following the formation of the pre-reactive complex IM_WM2, the reaction proceeded through transition state TS_WM2 to produce the product of H2O⋯Cl–H + 3O2 after climbing the barrier height of 7.2 kcal mol−1. In transition state TS_WM2, the seven-membered ring structure was still conserved with the Cl radical abstracting the H atom of the HO2 moiety in the H2O⋯HO2 complex. When H2O⋯HO2 and Cl act as reactants, Channel RWM1 occurs in two steps, as depicted in Fig. 3, which is similar to the H2O-catalyzed reactions66,74 of HO2 + HO and HO2 + HS. The first step begins with the formation of the pre-reactive IM_WM1 complex, which transforms into the IM_WM2 product through the TS_WM1 transition state via a ring enlargement, while the second step is IM_WM2 isomerization into H2O⋯Cl–H + 3O2 via TS_WM2, which was discussed above. Herein, we focus on the first step because the second step has been previously discussed in the H2O⋯Cl and HO2 reaction. It should be noted that IM_WM1 has a binding energy of 8.4 kcal mol−1, which is about 1.1 kcal mol−1 higher than that of the corresponding complex IM_WM2 in the H2O⋯Cl + HO2 reaction. Furthermore, the energy barrier of IM_WM1 isomerization into IM_WM2 is very low with a value of 3.0 kcal mol−1, revealing that this process occurs facilely in the atmosphere. In order to test whether the H2O⋯Cl + HO2 reaction is more favorable than the H2O⋯HO2 + Cl reaction or not, the effective rate constants of these two routes in Channel RWM1 were calculated in Table S7,† where the effective rate constants of the H2O⋯Cl + HO2 and H2O⋯HO2 + Cl reactions were respectively labeled as 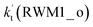 and
and 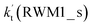 . It can be seen in Table S7† that the value of
. It can be seen in Table S7† that the value of 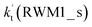 is much larger than that of
is much larger than that of 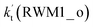 because the rate constant ratio
because the rate constant ratio 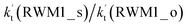 is about 5.29 × 102 to 4.91 × 101 times higher within the temperature range 280–320 K, indicating that Channel RWM1 via the interaction between H2O⋯HO2 and Cl is more favorable than that via H2O⋯Cl interacting with HO2.
is about 5.29 × 102 to 4.91 × 101 times higher within the temperature range 280–320 K, indicating that Channel RWM1 via the interaction between H2O⋯HO2 and Cl is more favorable than that via H2O⋯Cl interacting with HO2.
As for Channel RWM2, two kinds of reaction types can be taken both by (a) the stepwise mechanism (H2O⋯HO2 + Cl reaction) and (b) the one-step process (Cl⋯H2O + HO2 reaction). Similar to Channel RWM1, the stepwise mechanism in Channel RWM2 is more favorable than that of the one-step process with its effective rate constant 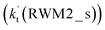 being 1087-52 times larger than the corresponding value
being 1087-52 times larger than the corresponding value 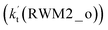 of the latter process. Thus, for Channel RWM2, only the stepwise mechanism is discussed here. Regarding the stepwise mechanism of Channel RWM2, in the first step, similar to the ring enlargement from IM_WM1 to IM_WM2 in Channel RWM1, the five-membered ring complex IM_WM3 in Channel RWM2 was rearranged into a six-membered ring complex IM_WM4 through TS_WM3 with a barrier height of 2.4 kcal mol−1. In the second step, following formation of IM_WM4, Channel RWM2 proceeded through transition state TS_WM4 to form 3O2 and H2O⋯H2O with a barrier height of 18.7 kcal mol−1. It is worth noting that the second step is the rate-determining step in both stepwise mechanisms of Channels RWM1 and RWM2. For the rate-determining step of Channels RWM1 and RWM2, unlike the transition state TS_WM2 in Channel RWM1 that involves a direct hydrogen abstraction, the transition state TS_WM4 in Channel RWM2 contains a double hydrogen transfer mechanism, where water acts as a bridge for the hydrogen transfer from the HO2 to the Cl radical, and as the WM accepts the hydrogen from HO2, it simultaneously donates another hydrogen atom to the Cl radical. Such a discrepancy in mechanism between Channels RWM1 and RWM2 may lead to the energy of transition state TS_WM2 in Channel RWM1 being 6.0 kcal mol−1 lower than that of TS_WM4 in the latter reaction. Meanwhile, for the stepwise mechanism of Channels RWM1 and RWM2, the effective rate constant of Channel RWM1
of the latter process. Thus, for Channel RWM2, only the stepwise mechanism is discussed here. Regarding the stepwise mechanism of Channel RWM2, in the first step, similar to the ring enlargement from IM_WM1 to IM_WM2 in Channel RWM1, the five-membered ring complex IM_WM3 in Channel RWM2 was rearranged into a six-membered ring complex IM_WM4 through TS_WM3 with a barrier height of 2.4 kcal mol−1. In the second step, following formation of IM_WM4, Channel RWM2 proceeded through transition state TS_WM4 to form 3O2 and H2O⋯H2O with a barrier height of 18.7 kcal mol−1. It is worth noting that the second step is the rate-determining step in both stepwise mechanisms of Channels RWM1 and RWM2. For the rate-determining step of Channels RWM1 and RWM2, unlike the transition state TS_WM2 in Channel RWM1 that involves a direct hydrogen abstraction, the transition state TS_WM4 in Channel RWM2 contains a double hydrogen transfer mechanism, where water acts as a bridge for the hydrogen transfer from the HO2 to the Cl radical, and as the WM accepts the hydrogen from HO2, it simultaneously donates another hydrogen atom to the Cl radical. Such a discrepancy in mechanism between Channels RWM1 and RWM2 may lead to the energy of transition state TS_WM2 in Channel RWM1 being 6.0 kcal mol−1 lower than that of TS_WM4 in the latter reaction. Meanwhile, for the stepwise mechanism of Channels RWM1 and RWM2, the effective rate constant of Channel RWM1 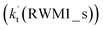 is much larger than the corresponding value
is much larger than the corresponding value 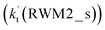 of Channel RWM2. This indicates that the double hydrogen transfer mechanism in Channel RWM2 is less favorable than the direct hydrogen abstraction involved in Channel RWM1. Such a discrepancy in mechanism between Channels RWM1 and RWM2 is consistent with our previous reports.22,65,66,75
of Channel RWM2. This indicates that the double hydrogen transfer mechanism in Channel RWM2 is less favorable than the direct hydrogen abstraction involved in Channel RWM1. Such a discrepancy in mechanism between Channels RWM1 and RWM2 is consistent with our previous reports.22,65,66,75
Unlike Channels RWM1 and RWM2 above, which mainly involve a stepwise process, the HO2⋯H2O + Cl reaction (Channel RWM3) consists of a one-step mechanism. As for Channel RWM3, the reaction started with the formation of a four-membered ring pre-reactive hydrogen bond complex IM_WM5 with a binding energy of 6.0 kcal mol−1. Starting from IM_WM5, Channel RWM3 proceeded through transition state TS_WM5 with a barrier height of 2.6 kcal mol−1, which is similar in structure to the naked transition state TS, where the Cl radical directly abstracted the hydrogen of HO2. The effective rate constant of Channel RWM3 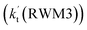 listed in Table S7† is lower by 7–8 orders than the corresponding value of
listed in Table S7† is lower by 7–8 orders than the corresponding value of 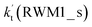 in Channel RWM1 (H2O⋯HO2 + Cl reaction). As a result of the above findings of HCl + 3O2 formation with H2O, the atmospheric relevance of the H2O⋯HO2 + Cl reaction occurring through direct hydrogen abstraction was found to be most obvious in the H2O catalyzed HO2 + Cl → HCl + 3O2 reaction.
in Channel RWM1 (H2O⋯HO2 + Cl reaction). As a result of the above findings of HCl + 3O2 formation with H2O, the atmospheric relevance of the H2O⋯HO2 + Cl reaction occurring through direct hydrogen abstraction was found to be most obvious in the H2O catalyzed HO2 + Cl → HCl + 3O2 reaction.
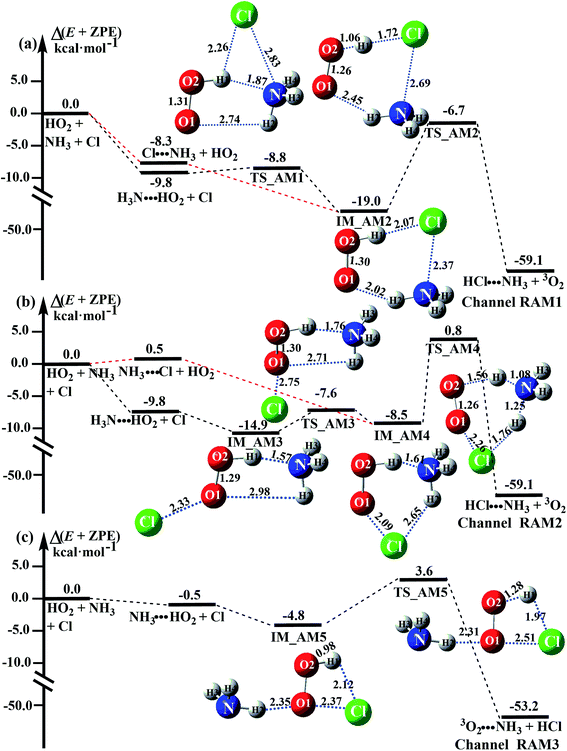
3.3 Mechanism and kinetics of the NH3 catalyzed HO2 + Cl → HCl + O2 reaction
As shown in Fig. 4, there are still four bimolecular reactions (eqn (11)–(14)) in the NH3 catalyzed HO2 + Cl → HCl + O2 reaction, where the H3N⋯HO2 + Cl reaction involves a stepwise route, and the three other reactions of Cl⋯NH3 + HO2, NH3⋯Cl + HO2 and NH3⋯HO2 + Cl occur via one elementary step. Compared with the H2O catalyzed reaction in Fig. 3, the NH3 catalyzed reaction shown in Fig. 4 has the same mechanism, with NH3 replacing H2O.| H3N⋯HO2 + Cl → HCl⋯NH3 + 3O2 | (11) |
| Cl⋯NH3 + HO2 → HCl⋯NH3 + 3O2 | (12) |
| NH3⋯Cl + HO2 → HCl⋯NH3 + 3O2 | (13) |
| NH3⋯HO2 + Cl → 3O2⋯NH3 + HCl | (14) |
Similar to the H2O⋯HO2 complex, the H3N⋯HO2 complex, as shown in Fig. 2, also forms a five-membered ring-like structure via the formation of two hydrogen bonds, where both HO2 radical and NH3 act as hydrogen donor or acceptor or both simultaneously, as shown in Fig. 2. The binding energy of H3N⋯HO2 is 9.8 kcal mol−1, which is larger by 2.7 kcal mol−1 than that of the H2O⋯HO2 complex. Single hydrogen bond (or van der Waals interaction) complexes of HO2⋯H3N, Cl⋯H3N and H3N⋯Cl are less stable than H3N⋯HO2. As shown in Table S3,† the atmospheric concentration of the H3N⋯HO2 complex is 1.26 × 105 molecules per cm3, which is 1.93 × 105, 1.83 × 103 and 1.25 × 109 times larger than the concentrations of complexes NH3⋯HO2, Cl⋯H3N and NH3⋯Cl. Thus, in the four bimolecular reactions of eqn (11)–(14), we predict that the atmospheric relevance of the bimolecular reaction of eqn (11) (H3N⋯HO2 + Cl reaction) will be much more obvious than the relevance of the reactions of eqn (12)–(14). This is similar to the water-catalyzed reactions in eqn (7)–(10) where the H2O⋯HO2 + Cl reaction is the most favorable in the H2O catalyzed HO2 + Cl → HCl + 3O2 reaction. This prediction has been proved by the calculated effective rate constants listed in Table S7,† where the effective rate constants of the H3N⋯HO2 + Cl reaction occurring through Channel RAM1 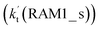 and Channel RAM2
and Channel RAM2 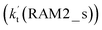 are much larger than the corresponding one-step reactions of Cl⋯NH3 + HO2
are much larger than the corresponding one-step reactions of Cl⋯NH3 + HO2 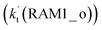 and NH3⋯Cl + HO2
and NH3⋯Cl + HO2 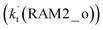 . Meanwhile, the values both
. Meanwhile, the values both 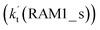 and
and 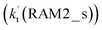 are larger than the values of
are larger than the values of 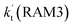 (NH3⋯HO2 + Cl reaction). Thus, only the reaction of H3N⋯HO2 + Cl has been considered here.
(NH3⋯HO2 + Cl reaction). Thus, only the reaction of H3N⋯HO2 + Cl has been considered here.
As shown in Fig. 4, for the H3N⋯HO2 + Cl reaction, the stepwise mechanism occurring through Channel RAM1 is different from that via Channel RAM2 in three aspects. First, the ring enlargement in Channel RAM1 occurs more easily than that in Channel RAM2 with its barrier lower by 1.2 kcal mol−1. Secondly, from the geometrical point of view, complexes IM_AM2 and IM_AM4 are different, because Cl and NH3 have exchanged positions in these two complexes. This is possibly the reason why complex IM_AM2 is more stable by 10.5 kcal mol−1 than complex IM_AM4. The third reason is that the barrier height of the rate-determining step in Channel RAM1 is lower by 7.5 kcal mol−1 than that in Channel RAM2. The calculated values of the effective rate constant for the H3N⋯HO2 + Cl reaction at various temperatures are given in Table S7.† As listed in Table S7,† the effective rate constant of the H3N⋯HO2 + Cl reaction occurring through Channel RAM1 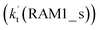 is larger by 102 to 103 times than that occurring through Channel RAM2
is larger by 102 to 103 times than that occurring through Channel RAM2 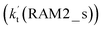 , indicating that the stepwise route of the H3N⋯HO2 + Cl reaction occurs mainly through direct hydrogen abstraction, which is similar to the H2O⋯HO2 + Cl reaction in Fig. 3.
, indicating that the stepwise route of the H3N⋯HO2 + Cl reaction occurs mainly through direct hydrogen abstraction, which is similar to the H2O⋯HO2 + Cl reaction in Fig. 3.
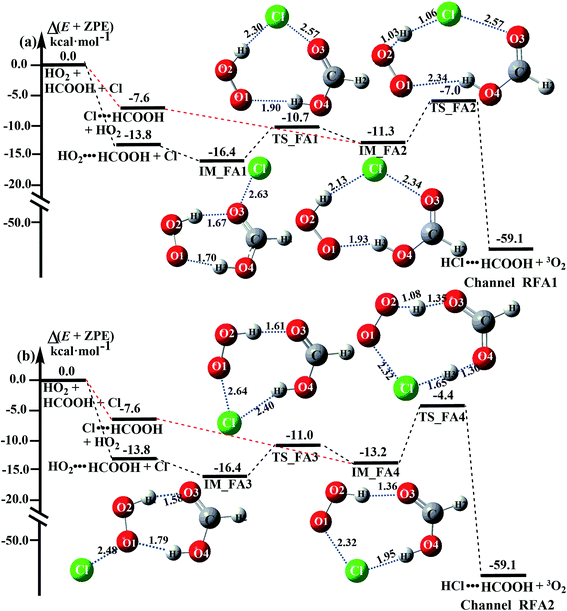
3.4 Mechanism and kinetics of the HCOOH-catalyzed HO2 + Cl → HCl + O2 reaction
The formic acid catalyzed reaction channels also follow a similar trend to that found in the cases of H2O and NH3. Depending upon the bimolecular complexes here, the two different types of reactions seen in Fig. 5 are possible. One is the reaction between the HO2⋯HCOOH complex and the Cl radical, the other is the reaction between the Cl⋯HCOOH complex and the HO2 radical. It is important to note that the HO2⋯HCOOH and Cl⋯HCOOH complexes shown in Fig. 2 are respectively the most stable complexes between HCOOH and HO2 (or Cl) with their binding energies being larger by 5.6 to 8.6 and 2.9–3.0 kcal mol−1, respectively, than those of other corresponding bimolecular complexes. Meanwhile, the atmospheric concentrations of the HO2⋯HCOOH and Cl⋯HCOOH complexes are 1.49 × 104 and 1.48 × 10−3 molecules per cm3, respectively, which are 2.03 × 103 to 2.43 × 103 and 1.32 × 101 to 3.47 × 101, respectively, times larger than the other complex between HCOOH and HO2 (or Cl). This indicates that the atmospheric relevance of the two types of reactions here will be most obvious in the HCOOH catalyzed HO2 + Cl → HCl + 3O2 reaction.As shown in Fig. 5, the HO2⋯HCOOH + Cl reaction consists of a stepwise mechanism, where the reaction occurs via a ring enlargement from the seven-membered ring complex IM_ FA1 (or IM_ FA3) to the eight-membered ring complex IM_ FA2 (or IM_ FA4) first and then it proceeds through a hydrogen abstraction mechanism; whereas the one-step route of the Cl⋯HCOOH + HO2 reaction occurs with only a hydrogen abstraction mechanism being involved. Table S7† also lists the effective rate constants of the HO2⋯HCOOH + Cl and Cl⋯HCOOH + HO2 reactions within the temperature range 280–320 K. As shown in Table S7,† for Channel RFA1, the effective rate constant of the stepwise mechanism 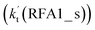 is larger by 2–4 orders of magnitude than that of the one-step route
is larger by 2–4 orders of magnitude than that of the one-step route 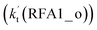 . A similar result can be obtained in Channel RFA2, where the effective rate constant of stepwise mechanism
. A similar result can be obtained in Channel RFA2, where the effective rate constant of stepwise mechanism 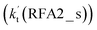 is also larger by 4–5 orders of magnitude than that of the corresponding one-step route
is also larger by 4–5 orders of magnitude than that of the corresponding one-step route 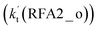 . These results suggest that the stepwise reaction of HO2⋯HCOOH + Cl is more favorable than that of the one-step route of the Cl⋯HCOOH + HO2 reaction.
. These results suggest that the stepwise reaction of HO2⋯HCOOH + Cl is more favorable than that of the one-step route of the Cl⋯HCOOH + HO2 reaction.
Similar to the H2O⋯HO2 + Cl and H3N⋯HO2 + Cl reactions above, as shown in Fig. 5, for the HO2⋯HCOOH + Cl reaction, the second step in both Channels RFA1 and RFA2 is the rate-determining step. For the rate-determining step of the HO2⋯HCOOH + Cl reaction, the barrier height of direct hydrogen abstraction in Channel RFA1 is lower by 2.6 kcal mol−1 than that of the double hydrogen transfer mechanism in Channel RFA2. Meanwhile, the effective rate constant of the HO2⋯HCOOH + Cl reaction occurring through Channel RFA1 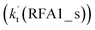 is 1.84 × 101 to 2.41 × 101 times larger than that occurring through Channel RFA2
is 1.84 × 101 to 2.41 × 101 times larger than that occurring through Channel RFA2 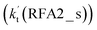 , indicating that the stepwise route of the HO2⋯HCOOH + Cl reaction occurs mainly through direct hydrogen abstraction, and the double hydrogen transfer mechanism in the HO2⋯HCOOH + Cl reaction can be neglected, which is similar to the H2O⋯HO2 + Cl reaction in Fig. 3 and the H3N⋯HO2 + Cl reaction in Fig. 4.
, indicating that the stepwise route of the HO2⋯HCOOH + Cl reaction occurs mainly through direct hydrogen abstraction, and the double hydrogen transfer mechanism in the HO2⋯HCOOH + Cl reaction can be neglected, which is similar to the H2O⋯HO2 + Cl reaction in Fig. 3 and the H3N⋯HO2 + Cl reaction in Fig. 4.
3.5 Atmospheric relevance of the HO2 + Cl → HCl + O2 reaction with H2O, NH3 and HCOOH
Since the mechanisms and kinetics mentioned above showed that the stepwise mechanism of the X⋯HO2 (X = WM, AM, and FA) + Cl reaction is the favorable route for HO2 + Cl → HCl + O2 with catalyst X, another main aim of our work was to study the influence of catalyst X on the HO2 + Cl → HCl + O2 reaction under atmospheric conditions. Thus, the rate constants for the HO2 + Cl → HCl + O2 reaction, the effective rate constant of the X⋯HO2 + Cl reaction occurring through direct hydrogen abstraction as well as the rate ratio between the reaction with a catalyst and the reaction without a catalyst have been listed in Tables 2 and 3.| T/K | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (10 ppbv) | (2900 ppbv) | Average | High | |||||||
a 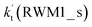 = k(RWM1_s)Keq(H2O⋯HO2)[H2O]; = k(RWM1_s)Keq(H2O⋯HO2)[H2O]; 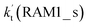 = k(RAM1_s)Keq(H3N⋯HO2)[NH3]; = k(RAM1_s)Keq(H3N⋯HO2)[NH3]; 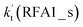 = k(RFA1_s)Keq(HO2⋯HCOOH)[HCOOH]. Keq(H2O⋯HO2), Keq(H3N⋯HO2) and Keq(HO2⋯HCOOH) are the equilibrium constants for the formation of the H2O⋯HO2, H3N⋯HO2 and HO2⋯HCOOH complexes, respectively. = k(RFA1_s)Keq(HO2⋯HCOOH)[HCOOH]. Keq(H2O⋯HO2), Keq(H3N⋯HO2) and Keq(HO2⋯HCOOH) are the equilibrium constants for the formation of the H2O⋯HO2, H3N⋯HO2 and HO2⋯HCOOH complexes, respectively. |
||||||||||
| 280 | 2.64 × 10−13 | 3.67 × 10−18 | 1.07 × 10−15 | 2.38 × 10−14 | 3.09 × 10−13 | 0.32% | 0.00% | 0.00% | 0.03% | 0.37% |
| 290 | 2.67 × 10−13 | 3.08 × 10−18 | 8.99 × 10−16 | 7.71 × 10−15 | 1.02 × 10−13 | 0.38% | 0.00% | 0.00% | 0.01% | 0.14% |
| 298 | 2.90 × 10−13 | 1.09 × 10−18 | 3.08 × 10−16 | 3.48 × 10−15 | 4.40 × 10−14 | 0.46% | 0.00% | 0.00% | 0.01% | 0.07% |
| 300 | 3.40 × 10−13 | 9.26 × 10−19 | 2.74 × 10−16 | 2.87 × 10−15 | 3.62 × 10−14 | 0.56% | 0.00% | 0.00% | 0.00% | 0.06% |
| 310 | 3.08 × 10−13 | 5.32 × 10−19 | 1.53 × 10−16 | 1.08 × 10−15 | 1.44 × 10−14 | 0.58% | 0.00% | 0.00% | 0.00% | 0.03% |
| 320 | 2.52 × 10−13 | 3.10 × 10−19 | 9.03 × 10−17 | 4.60 × 10−16 | 5.88 × 10−15 | 0.54% | 0.00% | 0.00% | 0.00% | 0.01% |
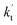 values for various catalysts at different catalyst concentrations and temperatures are listed in Table 2. It is evident from Table 2 that FA (at a high concentration limit of 10 ppbv) completely dominates over all other catalysts at 280 K, whereas water (100% RH) completely dominates within the temperature range 290–320 K. As far as the basic catalyst (AM) is concerned, it is never the most efficient catalyst under any circumstances. In fact,
values for various catalysts at different catalyst concentrations and temperatures are listed in Table 2. It is evident from Table 2 that FA (at a high concentration limit of 10 ppbv) completely dominates over all other catalysts at 280 K, whereas water (100% RH) completely dominates within the temperature range 290–320 K. As far as the basic catalyst (AM) is concerned, it is never the most efficient catalyst under any circumstances. In fact, 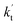 for AM at 2900 ppbv concentration is lower than that for FA (average). As shown in Table S8,† this means that AM would not make any significant contribution in catalyzing the HO2 + Cl → HCl + O2 reaction. In order to quantitatively assess the impact of FA (at a high concentration limit of 10 ppbv) and WM at 100% RH on the HO2 + Cl → HCl + O2 reaction, the rate ratio between the reaction with a catalyst and without a catalyst is also listed in Table 2. The calculated results in Table 2 show that the rate ratio of
for AM at 2900 ppbv concentration is lower than that for FA (average). As shown in Table S8,† this means that AM would not make any significant contribution in catalyzing the HO2 + Cl → HCl + O2 reaction. In order to quantitatively assess the impact of FA (at a high concentration limit of 10 ppbv) and WM at 100% RH on the HO2 + Cl → HCl + O2 reaction, the rate ratio between the reaction with a catalyst and without a catalyst is also listed in Table 2. The calculated results in Table 2 show that the rate ratio of 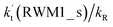 and
and 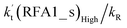 is less than 0.6% within the temperature range 280–320 K, indicating that the HO2 + Cl → HCl + O2 reaction with catalysts of H2O, NH3, and HCOOH cannot compete with the reaction without a catalyst.
is less than 0.6% within the temperature range 280–320 K, indicating that the HO2 + Cl → HCl + O2 reaction with catalysts of H2O, NH3, and HCOOH cannot compete with the reaction without a catalyst.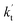 values were calculated for all the catalysts using the above-mentioned concentration and temperature values for altitudes up to 15 km and are given in Table 3. It is evident from Table 3 that at altitudes of 5, 10 and 15 km, neutral (WM) and basic catalysts (AM) do not match their acidic counterparts at higher altitudes and the gap between them increases monotonically with increasing altitude. This showed that at altitudes of 5, 10 and 15 km, the catalytic effect of FA is higher those of catalysts of WM and AM, respectively. For catalyst FA, as
values were calculated for all the catalysts using the above-mentioned concentration and temperature values for altitudes up to 15 km and are given in Table 3. It is evident from Table 3 that at altitudes of 5, 10 and 15 km, neutral (WM) and basic catalysts (AM) do not match their acidic counterparts at higher altitudes and the gap between them increases monotonically with increasing altitude. This showed that at altitudes of 5, 10 and 15 km, the catalytic effect of FA is higher those of catalysts of WM and AM, respectively. For catalyst FA, as 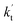 incorporates both rate coefficient (termolecular rate coefficients (kt), as seen in Table S5†) and catalyst concentration (as seen in Table S8†) within it, we found that its
incorporates both rate coefficient (termolecular rate coefficients (kt), as seen in Table S5†) and catalyst concentration (as seen in Table S8†) within it, we found that its 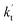 value increased rapidly with altitude as the concentration of FA decreases by ∼6 times and kt value increases by 3 orders of magnitude with increasing altitude from 5 km to 15 km. Besides, compared with the value of kR, we found that the rate ratio of
value increased rapidly with altitude as the concentration of FA decreases by ∼6 times and kt value increases by 3 orders of magnitude with increasing altitude from 5 km to 15 km. Besides, compared with the value of kR, we found that the rate ratio of 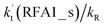 increased from 0.03% at 0 km to 24.2% at 15 km. This implies that, as we move towards higher altitude, the contribution of HCOOH to the HO2 + Cl → HCl + O2 reaction cannot be neglected at high altitude.
increased from 0.03% at 0 km to 24.2% at 15 km. This implies that, as we move towards higher altitude, the contribution of HCOOH to the HO2 + Cl → HCl + O2 reaction cannot be neglected at high altitude.4. Summary and conclusions
In this work, the hydrogen abstraction of the HO2 + Cl → HCl + 3O2 reaction catalyzed by H2O, NH3 and HCOOH has been investigated theoretically using the CCSD(T)-F12A/VDZ-F12//M06-2X/6-311++G(2d,2p) method and canonical vibrational transition (CVT) state theory with the small curvature tunneling (SCT) correction. The conclusions obtained in this investigation are summarized as follows:As for the three catalytic reactions, there are two entry channels: namely a stepwise route and a one elementary step, and this article has discovered that the stepwise route is more favorable than the corresponding one elementary step. Meanwhile, for the stepwise route, single and double hydrogen atom transfer pathways are involved, and the calculation results indicate that the former pathway has more advantages than the latter in all three catalytic reactions.
For the stepwise process of X⋯HO2 (X = H2O, NH3 and HCOOH) + Cl reaction, at 0 km altitude, none of the HO2 + Cl → HCl + O2 reactions with catalysts of H2O, NH3, and HCOOH can compete with the reaction without a catalyst, as all the rate ratios between reaction with a catalyst and without a catalyst are less than 0.6% within the temperature range 280–320 K. In addition, at higher altitudes in the troposphere, it was shown that at altitudes of 5, 10 and 15 km, the catalytic effect of HCOOH for the gas-phase oxidation reaction of HO2 by Cl is larger than those of H2O or NH3. Furthermore, the rate ratio of 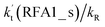 increases from 0.03% at 0 km to 24.2% at 15 km. This implies that the contribution of HCOOH to the HO2 + Cl → HCl + O2 reaction cannot be neglected at high altitudes. This present study presents a new mechanism for understanding the gas-phase oxidation reaction of HO2 by Cl via H2O, NH3 and HCOOH catalysis. Moreover, the new mechanisms have wide applications in investigating gas-phase hydrogen abstraction. Therefore, the present results could also be of great importance for elucidating and understanding other atmospheric oxidation processes with neutral, basic, and acidic catalysts.
increases from 0.03% at 0 km to 24.2% at 15 km. This implies that the contribution of HCOOH to the HO2 + Cl → HCl + O2 reaction cannot be neglected at high altitudes. This present study presents a new mechanism for understanding the gas-phase oxidation reaction of HO2 by Cl via H2O, NH3 and HCOOH catalysis. Moreover, the new mechanisms have wide applications in investigating gas-phase hydrogen abstraction. Therefore, the present results could also be of great importance for elucidating and understanding other atmospheric oxidation processes with neutral, basic, and acidic catalysts.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 21603132, 21473108), the Funds of Research Programs of Shaanxi University of Technology (No. SLGQD13(2)-3, SLGQD13(2)-4), the Shanghai Science and Technology Committee (16DZ2270100), and the Shaanxi Provincial Natural Science Foundation (No. 2019JM-336).References
- Y. Tang, G. S. Tyndall and J. J. Orlando, J. Phys. Chem. A, 2010, 114, 369–378 CrossRef CAS.
- P. D. Lightfoot, R. A. Cox, J. N. Crowley, M. Destriau, G. D. Hayman, M. E. Jenkin, G. K. Moortgat and F. Zabel, Atmos. Environ., 1992, 26, 1805–1961 CrossRef.
- D. Stone, L. K. Whalley and D. E. Heard, Chem. Soc. Rev., 2012, 41, 6348–6404 RSC.
- S. S. Prasad, R. L. Jaffe, R. C. Whitten and R. P. Turco, Planet. Space Sci., 1978, 26, 1017–1026 CrossRef CAS.
- S. C. Wofsy, Eos, Transactions American Geophysical Union, 1999, 80, 468 CrossRef.
- W. C. Keene, J. Stutz, A. A. P. Pszenny, J. R. Maben, E. V. Fischer, A. M. Smith, R. V. Glasow, S. Pechtl, B. C. Sive and R. K. Varner, J. Geophys. Res.: Atmos., 2007, 112, D10S12 CrossRef.
- C. W. Spicer, E. G. Chapman, B. J. Finlaysonpitts, R. A. Plastridge, J. M. Hubbe, J. D. Fast and C. M. Berkowitz, Nature, 1998, 394, 353–356 CrossRef CAS.
- O. Dobis and S. W. Benson, J. Am. Chem. Soc., 1993, 115, 8798–8809 CrossRef CAS.
- K. M. Hickson and L. F. Keyser, J. Phys. Chem. A, 2005, 109, 6887–6900 CrossRef CAS PubMed.
- R. Riffault, Y. Bedjanian and G. L. Bras, Int. J. Chem. Kinet., 2001, 33, 317–327 CrossRef.
- M. Weissman, L. G. S. Shum, S. P. Heneghan and S. W. Benson, J. Phys. Chem., 1981, 85, 2863–2866 CrossRef CAS.
- R. Atkinson, D. Baulch, R. Cox, J. Crowley, R. Hampson Jr, J. Kerr, M. Rossi and J. Troe, IUPAC Subcommittee on gas kinetic data evaluation for atmospheric chemistry, 2001, vol. 20 Search PubMed.
- J. Burrows, D. Cliff, G. W. Harris, B. A. Thrush and J. Wilkinson, Proc. R. Soc. London, Ser. A, 1979, 368, 463–481 CrossRef CAS.
- F. C. Cattell and R. A. Cox, J. Chem. Soc., Faraday Trans. 2, 1986, 82, 1413–1426 RSC.
- R. A. Cox, Int. J. Chem. Kinet., 1980, 12, 649–660 CrossRef CAS.
- Y. P. Lee and C. J. Howard, J. Chem. Phys., 1982, 77, 756–763 CrossRef CAS.
- R. J. Buszek, J. S. Francisco and J. M. Anglada, Int. Rev. Phys. Chem., 2011, 30, 335–369 Search PubMed.
- R. J. Buszek, M. Torrent-Sucarrat, J. M. Anglada and J. S. Francisco, J. Phys. Chem. A, 2012, 116, 5821–5829 CrossRef CAS.
- N. Butkovskaya, M. T. Rayez, J. C. Rayez, A. Kukui and G. L. Bras, J. Phys. Chem. A, 2009, 113, 11327–11342 CrossRef CAS.
- N. Kanno, K. Tonokura, A. Tezaki and M. Koshi, J. Phys. Chem. A, 2005, 109, 3153–3158 CrossRef CAS.
- K. Suma, Y. Sumiyoshi and Y. Endo, Science, 2006, 311, 1278–1281 CrossRef CAS.
- T. Zhang, W. Wang, P. Zhang, J. Lü and Y. Zhang, Phys. Chem. Chem. Phys., 2011, 13, 20794–20805 RSC.
- J. C. Hansen and J. S. Francisco, ChemPhysChem, 2002, 3, 833–840 CrossRef CAS PubMed.
- V. Vaida, H. G. Kjaergaard, P. E. Hintze and D. J. Donaldson, Science, 2003, 299, 1566–1568 CrossRef CAS.
- J. Zuo, Y. Li, H. Guo and D. Xie, J. Phys. Chem. A, 2016, 120, 3433–3440 CrossRef CAS.
- S. Mallick and P. Kumar, J. Phys. Chem. A, 2018, 122, 7151–7159 CrossRef CAS.
- G. H. Mount, B. Rumburg, J. Havig, B. Lamb, H. Westberg, D. Yonge, K. Johnson and R. Kincaid, Atmos. Environ., 2002, 36, 1799–1810 CrossRef CAS.
- S. M. Wilson and M. L. Serre, Atmos. Environ., 2007, 41, 4977–4987 CrossRef CAS.
- B. Bandyopadhyay, P. Biswas and P. Kumar, Phys. Chem. Chem. Phys., 2016, 18, 15995–16004 RSC.
- B. Bandyopadhyay, P. Kumar and P. Biswas, J. Phys. Chem. A, 2017, 121, 3101–3108 CrossRef CAS.
- R. J. Buszek, A. Sinha and J. S. Francisco, J. Am. Chem. Soc., 2011, 133, 2013–2015 CrossRef CAS.
- S. G. Da, Angew. Chem., Int. Ed., 2010, 49, 7523–7525 CrossRef.
- S. Ghoshal and M. K. Hazra, RSC Adv., 2015, 5, 17623–17635 RSC.
- M. K. Hazra and T. Chakraborty, J. Phys. Chem. A, 2005, 109, 7621–7625 CrossRef CAS.
- M. K. Hazra and T. Chakraborty, J. Phys. Chem. A, 2006, 110, 9130–9136 CrossRef CAS.
- D. Josa, J. Rodríguez-Otero, E. M. Cabaleiro-Lago and M. Rellán-Piñeiro, Chem. Phys. Lett., 2013, 557, 170–175 CrossRef CAS.
- M. Walker, A. J. Harvey, A. Sen and C. E. Dessent, J. Phys. Chem. A, 2013, 117, 12590–12600 CrossRef CAS.
- N. Bork, L. Du, H. Reiman, T. Kurtén and H. G. Kjaergaard, J. Phys. Chem. A, 2014, 118, 5316–5322 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 119, 525 Search PubMed.
- J. Elm, M. Bilde and K. V. Mikkelsen, J. Chem. Theory Comput., 2012, 8, 2071–2077 CrossRef CAS.
- F. Y. Liu, X. F. Tan, Z. W. Long, B. Long and W. J. Zhang, RSC Adv., 2015, 5, 32941–32949 RSC.
- B. Long, X. F. Tan, C. R. Chang, W. X. Zhao, Z. W. Long, D. S. Ren and W. J. Zhang, J. Phys. Chem. A, 2013, 117, 5106–5116 CrossRef CAS.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS.
- M. Page and J. W. McIver Jr, J. Chem. Phys., 1988, 88, 922–935 CrossRef CAS.
- M. J. Frisch, G. Trucks and J. A. Pople, et al., Gaussian 09, Revision A.01, Gaussian Inc, Pittsburgh, PA, 2009 Search PubMed.
- N. Bork, J. Elm, T. Olenius and H. Vehkamäki, Atmos. Chem. Phys., 2014, 14, 12023–12030 CrossRef.
- J. Elm and K. Kristensen, Phys. Chem. Chem. Phys., 2017, 19, 1122–1133 RSC.
- N. Myllys, J. Elm, R. Halonen, T. Kurtén and H. Vehkamäki, J. Phys. Chem. A, 2016, 120, 621–630 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- B. Long, J. L. Bao and D. G. Truhlar, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6135–6140 CrossRef CAS.
- B. Long, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2018, 141, 611–617 CrossRef.
- B. Long, J. L. Bao and D. G. Truhlar, Nat. Commun., 2019, 10, 2003 CrossRef.
- B. C. Garrett, D. G. Truhlar, R. S. Grev and A. W. Magnuson, J. Phys. Chem., 1980, 84, 1730–1748 CrossRef CAS.
- Y. P. Liu, G. C. Lynch, T. N. Truong, D. H. Lu, D. G. Truhlar and B. C. Garrett, J. Am. Chem. Soc., 1993, 115, 2408–2415 CrossRef CAS.
- Y. Chuang, J. Corchado, P. Fast, J. Villa, E. Coitino, W. Hu, Y. Liu, G. Lynch, K. Nguyen and C. Jackels, Polyrate-version 8.2, University of Minnesota, Minneapolis [CP], 1999 Search PubMed.
- D. L. Singleton and R. J. Cvetanovic, J. Am. Chem. Soc., 1976, 98, 6812–6819 CrossRef CAS.
- J. L. Bao, P. Seal and D. G. Truhlar, Phys. Chem. Chem. Phys., 2015, 17, 15928–15935 RSC.
- M. L. Wei, X. F. Tan, Z. W. Long and B. Long, RSC Adv., 2017, 7, 56211–56219 RSC.
- X. Chen, Y. F. Zhao, L. S. Wang and J. Li, Comput. Theor. Chem., 2017, 1107, 57–65 CrossRef CAS.
- Y. Zhao, X. Chen and J. Li, Nano Res., 2017, 10, 3407–3420 CrossRef CAS.
- X. Chen, C. Tao, L. Zhong, Y. Gao, W. Yao and S. Li, Chem. Phys. Lett., 2014, 608, 272–276 CrossRef CAS.
- B. Long, X. Tan, Z. Long, Y. Wang, D. Ren and W. Zhang, J. Phys. Chem. A, 2011, 115, 6559–6567 CrossRef CAS.
- T. Zhang, R. Wang, H. Chen, S. Min, Z. Wang, C. Zhao, Q. Xu, L. Jin, W. Wang and Z. Wang, Phys. Chem. Chem. Phys., 2015, 17, 15046–15055 RSC.
- T. Zhang, R. Wang, W. Wang, S. Min, Q. Xu, Z. Wang, C. Zhao and Z. Wang, Comput. Theor. Chem., 2014, 1045, 135–144 CrossRef CAS.
- T. Zhang, C. Yang, X. Feng, J. Kang, L. Song, Y. Lu, Z. Wang, Q. Xu, W. Wang and Z. Wang, Phys. Chem. Chem. Phys., 2016, 18, 17414–17427 RSC.
- J. Gonzalez, M. Torrent-Sucarrat and J. M. Anglada, Phys. Chem. Chem. Phys., 2010, 12, 2116–2125 RSC.
- C. T. Chang, T. H. Liu and F. T. Jeng, Environ. Res., 2004, 94, 67–74 CrossRef CAS.
- J. M. Anglada, R. Crehuet and A. Solé, Mol. Phys., 2019, 1–12 Search PubMed.
- H. A. Rypkema, A. Sinha and J. S. Francisco, J. Phys. Chem. A, 2015, 119, 4581–4588 CrossRef CAS.
- M. K. Hazra and S. Amitabha, J. Am. Chem. Soc., 2011, 133, 17444–17453 CrossRef CAS.
- B. Long, Z. Long, Y. Wang, X. Tan, Y. Han, C. Long, S. Qin and W. Zhang, ChemPhysChem, 2012, 13, 323–329 CrossRef CAS PubMed.
- B. Long, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2016, 138, 14409–14422 CrossRef CAS.
- T. Zhang, X. Lan, Z. Qiao, R. Wang, X. Yu, Q. Xu, Z. Wang, L. Jin and Z. Wang, Phys. Chem. Chem. Phys., 2018, 20, 8152–8165 RSC.
- T. Zhang, W. Wang, C. Li, Y. Du and J. Lü, RSC Adv., 2013, 3, 7381–7391 RSC.
- S. Sarkar, S. Mallick, D. Kaushik, P. Kumar and B. Bandyopadhyay, Phys. Chem. Chem. Phys., 2017, 19, 27848–27858 RSC.
- V. P. Aneja, D. R. Nelson, P. A. Roelle, J. T. Walker and W. Battye, J. Geophys. Res.: Atmos., 2003, 108, 2156–2202 CrossRef.
- G. Brasseur, J. J. Orlando and G. S. Tyndall, Atmospheric chemistry and global change, Oxford University Press, 1999 Search PubMed.
- J. X. Warner, Z. Wei, L. L. Strow, R. Dickerson and J. Nowak, Atmos. Chem. Phys. Discuss., 2015, 15, 35823–35856 CrossRef.
- N. Hiranuma, S. D. Brooks, D. C. Thornton and B. W. Auvermann, J. Air Waste Manag. Assoc., 2010, 60, 210–218 CrossRef CAS.
- A. Razavi, F. Karagulian, L. Clarisse, D. Hurtmans, P. F. Coheur, C. Clerbaux, J. F. Müller and T. Stavrakou, Atmos. Chem. Phys., 2010, 10, 857–872 Search PubMed.
- M. W. Shephard, A. Goldman, S. A. Clough and E. J. Mlawer, J. Quant. Spectrosc. Radiat. Transf., 2003, 82, 383–390 CrossRef CAS.
- J. M. Anglada, G. J. Hoffman, L. V. Slipchenko, M. M. Costa, M. F. Ruiz-Lopez and J. S. Francisco, J. Phys. Chem. A, 2013, 117, 10381–10396 CrossRef CAS.
- S. Mallick, S. Sarkar, B. Bandyopadhyay and P. Kumar, J. Phys. Chem. A, 2017, 122, 350–363 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra03541a |
| ‡ Yongqi Zhang, Mingjie Wen, and Zhuo Tang contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |