Computational assessments of diastereoselective [4+2] cycloaddition and 1,3-borotopic shift of a dearomatized tertiary boronic ester intermediate: reactivities explained through transition-state distortion energies

Abstract

Interception of a dearomatized tertiary boronic ester, formed through a kinetically and thermodynamically favorable 1,2-metalate rearrangement/anti-S_N2′ elimination of an activated ortho-lithiated benzyl amine, in a [4+2] cycloaddition or 1,3-borotopic shift has been investigated by density functional theory (DFT). Although superacitvated “naked” Li⁺ was found to greatly promote 1,3-borotopic shift, the diastereoselective [4+2] cycloaddition was favored. It was revealed that the factor that controls the diastereoselectivity was the steric bulk provided by the diene, which is in agreement with experimental diastereoselectivity. A comparison of unreactive dienophiles such as maleic anhydride, diethyl maleate, and others with 4-phenyl-3H-1,2,4-triazole-3,5(4H)-dione (PTAD) was found to be in an excellent agreement with the experiments; where their lack of reactivity is attributed to the high deformation energies of the interacting components to achieve the transition state structure which was pronounced with the high energy of LUMO orbitals.

---

Introduction

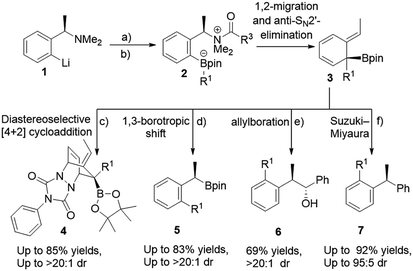
The use of boronic esters in asymmetric synthesis is a highly versatile and robust approach, due to the important stereospecific transformations through stereoinvertive or stereoretentive pathways into many functionalities that lead to complex structures.¹ For instance, bortezomib, which is a treatment for relapsed and refractory multiple myeloma, is an α-amino boronic acid that possess potent inhibitors of a serine protease.² Thus, advancing pertinent novel methods to synthesize enantiopure alkyl boronic esters with structurally complex functionalities is exceedingly favorable.³ Accordingly, an extensive endeavour to access an enantiospecific coupling of secondary and tertiary boronic esters to aromatics through transition-metal catalyzed processes has been made, though it is practically still challenging and not generally applicable.^4–6 Quite recently, Aggarwal and co-workers reported a considerable scope of stereospecific transition metal-free sp²–sp³ coupling of chiral secondary and tertiary boronic esters with electron-rich aryl lithium reagents.⁷ Subsequently, they demonstrated an enantiospecific synthesis of ortho-substituted benzylic boronic esters via a 1,2-metalate rearrangement/anti-S_N2′ elimination/1,3-borotropic shift reaction sequence starting from enantioenriched α-substituted benzylamines (Scheme 1).^8a The essential part of this sequence is that it progresses through a dearomatized tertiary boronic ester intermediate 3, followed by 1,3-borotropic shift or participating in allylboration, or allylic Suzuki–Miyaura cross-coupling reactions to provide complex enantioenriched products (Scheme 1).⁸ Importantly, they have stated that the favorable rearomatization is a driving force for these transformations, although an 1,3-brotopic shift is an exceedingly slow process (formation of 5, 6, and 7, Scheme 1). Regarding this, it has been reported that using a Lewis acid promotes an 1,3-shift at a faster rate.⁹ Aggarwal and co-workers were then intrigued in diverting reactivity of intermediate 3 through the interception in a Diels–Alder cycloaddition reaction (Scheme 1). Very recently, they published a simple one-pot procedure through the interception of the dearomatized intermediate 3 with a dienophile (PTAD) in a diastereoselective [4+2] cycloaddition to generate highly complex three-dimensional boron-containing molecular structures (Scheme 1-c).¹⁰ This intermediate has been used in total syntheses¹¹ and different transition metal-catalyzed transformations.¹²

Scheme 1 Rearomatizing transformations of ortho-lithiated benzylamine. (a) R₂Bpin, THF, −78 °C to rt; (b) ClCO₂CMe₂CCl₃, −78 °C to rt; (c) PTAD, THF, −78 °C to rt; (d) NaBPh₄, CDCl₃, 50 °C; (e) PhCHO; (f) Ag₂CO₃, rt then 5 mol% of Pd(dba)₂ and 10 mol% of RuPhos.

We were then captivated in a number of issues arising from these transformations; (1) realizing the formation of this intermediate in a compelling mechanism, (2) understanding the facial selectivity in the Diels–Alder cycloaddition which should give us a clue to rationalize the origin behind high diastereoselectivity, (3) realizing the reactivity of cycloaddition and 1,3-borotopic in the absence and presence of a Lewis acid, and (3) due to the notably limited reactivity of cyclohexadienes evaluation of the other dienophiles in [4+2] cycloaddition have raised further questions corresponding to the demand of matched/mismatched reactivities between the HOMO and LUMO orbitals. Herein, we interpret a DFT study on the diastereoselective [4+2] cycloaddition of the dearomatized tertiary boronic ester, explaining the formation of such a stable dearomatized intermediate, comparing reactivity of 1,3-borotopic shift with and without a Lewis acid, and highlighting the important role of a bulk group in producing three-dimensional boron-containing molecular structures diastereoselectivily. Furthermore, we will rationalize reactivities of different dienophiles from the point of frontier molecular orbital (FMO) analysis and distortion/interaction energies.

Results and discussion

All our simulations were obtained by means of DFT calculations using the ωB97XD/6-311+G(2d,3pd) level of theory in both the gas phase and tetrahydrofuran (THF) as a representative solvent (SMD solvation model) otherwise mentioned based on gas-phase optimized geometries by ωB97XD/6-31G(d). Generally, we have not seen noticeable discrepancies between calculations in the gas phase and implicit solvent, so all our discussions and comparisons will be based on gas phase otherwise mentioned.

Reaction mechanism

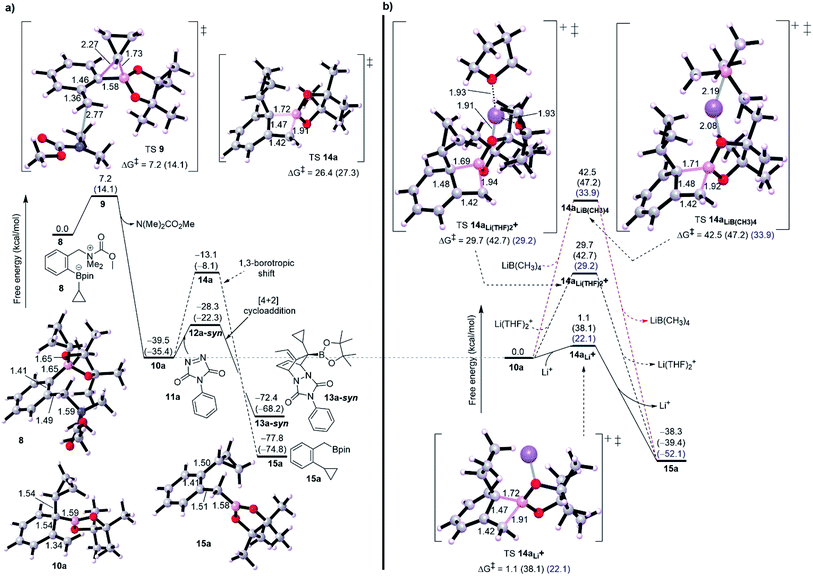
Initially, we started our investigation with the formation of dearomatized tertiary boronic ester 10, from the activated intermediate 8 (Fig. 1-a). Here, we have used acetyl chloride (MeCOCl) as an activated group instead of ClCO₂CMe₂CCl₃ to reduce computational demand. DFT simulations show that formation of 10a by 1,2-migration and anti-S_N2′-elimination mechanism needs a barrier of 7.2 kcal mol⁻¹ as a favorable exergonic reaction (−39.5 kcal mol⁻¹), where R¹ is cyclopropyl group. This would explain the desirable formation of intermediate 10a according to the experimental observations reported by Aggarwal and co-worker.^8a,10 Aggarwal et al. showed that 1,3-shift occurs only when a Lewis acid like NaBPh₄ was added to the reaction.^8a They performed an in situ salt metathesis with NaBPh₄ in noncoordinating chloroform to accordingly give “naked” Li⁺BPh₄⁻ and the latter efficiently catalyzed the reaction to afford the benzylic boronate. In this regard, the “naked” lithium cation with very weakly coordinating anions (BPh₄⁻) has been shown to be a superactivated lithium cation, substantially enhancing a Lewis acidic character and mediating various organic reactions.¹³ Thus, we were then interested in investigating the 1,3-borotopic shift in the presence and absence of a “naked” Lewis acid.

Fig. 1 (a) Free energy profile showing the mechanism of cycloadduct formation compared with 1,3-borotopic shift in the absence of Lewis acid, and for [4+2] cycloaddition only syn pathway was chosen for comparison. (b) Effect of Lewis acid on 1,3-borotopic shift, showing effect of noncoordinating “naked” Li⁺ (solid black line), THF-coordinated “naked” Li⁺ (Li(THF)₂⁺, dashed black line), and noncoordinating non-naked Li⁺ (lithium salt, LiB(CH₃)₄, dashed red line). Energies between brackets are calculated in THF/SMD and CHCl₃/SMD (blue text). Geometries of TS 12a-syn and intermediate 13a-syn are shown below. We replaced LiBPh₄ by LiB(CH₃)₄ to reduce the computational complexity.

On one hand, and in the absence of Lewis acid (Fig. 2-a), a substantial barrier of 26.4 kcal mol⁻¹ is required to overcome TS 14a to release benzylic boronate product 15a although this shift is a thermodynamically favorable step (−38.3 kcal mol⁻¹).^8a,9a The calculated activation of rearomatization (26.4 kcal mol⁻¹, k = 2.8 × 10⁻⁷) is in line with the experimental observation that this process is exceedingly slow in the absence of NaBPh₄.⁹ In comparison, the addition of such a good dienophile like PTAD, a reduced barrier [4+2] cycloaddition reaction takes place via TS 12a-syn with barrier of just 11.1 kcal mol⁻¹ as an exergonic step (13a-syn, −32.9 kcal mol⁻¹) (Fig. 2-a). The low barrier for cycloaddition totally outpaces 1,3-shift when a Lewis acid is absent, and a good dienophile is present.

Fig. 2 Computed energetic comparison between syn and ant pathway for [4+2] cycloaddition reaction of intermediate diene 11b with PTDA 12a. Energies between brackets are calculated in THF/SMD. Spacefilling model for diene 11b is shown in box.

On the other hand, when the superactivated Lewis acid was involved, the barrier of 1,3-shift varies based on the proposed TS (Fig. 2-b). Here, we have proposed three TSs to understand how Lewis acid catalyzes the reaction. When the noncoordinating “naked” Li⁺ was used, a barrierless shift of 1.1 kcal mol⁻¹ in gas phase was obtained via TS 14a_Li⁺, and this barrier increases to 22.1 kcal mol⁻¹ in CHCl₃ and to 38.1 kcal mol⁻¹ in THF. To match the experimental conditions, the difference in barrier between THF and CHCl₃ is reasonable and in accord with the fact that using CHCl₃ was the choice to promote the 1,3-shift. Coordinating two THF solvents to the “naked” Li⁺ has effectively increased the barrier to around 29.0 kcal mol⁻¹ in both gas phase and chloroform (see TS 14a_Li(THF)2⁺, Fig. 2-b) whereas 42.7 kcal mol⁻¹ in THF. Furthermore, using a “non-naked” lithium salt, LiB(CH₃)₄, led to the highest barrier for 1,3-shift (see TS 14a_LiB(CH3)4, Fig. 2-b). Finally, these results confirm the reality that the need for a superactivated Lewis acid with a noncoordinating solvent is tremendously necessary to facilitate the 1,3-borotopic shift, however this is still disfavored compared to [4+2] cycloaddition in THF or CHCl₃, plausibly consistent with the experimental observations.

Rationalization of diastereoselectivity of the [4+2] cycloaddition

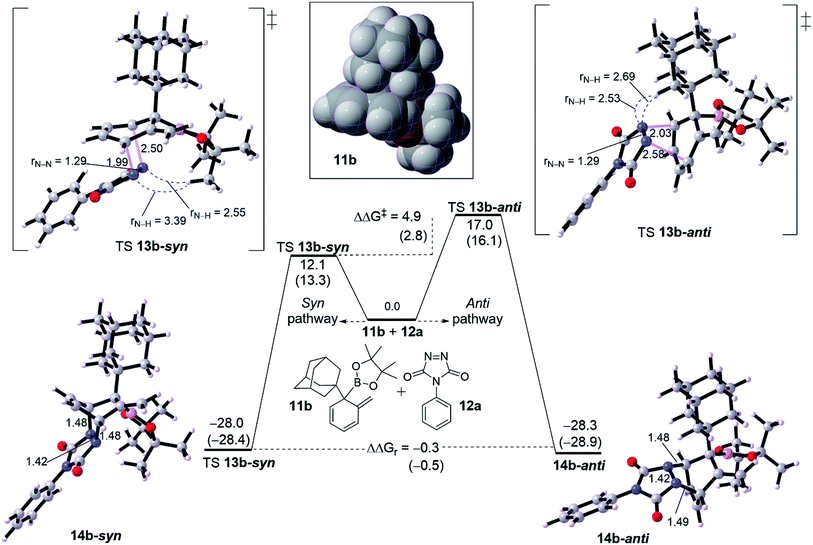
We turned out our eyes into a rationalization of the diastereoselectivity of cycloadduct formation. DFT calculations were performed with two examples of dearomatized intermediate 10. These dienes were chosen based on the size of the α-position (R¹ group). Fig. 2 shows a diastereoselective bifurcation of [4+2] cycloaddition for intermediate 10b and dienophile 11a leading to syn and anti-product, where R¹ is an and α-branched large group. Interception of the diene 10b with 11a has been found to proceed through an asynchronous concerted TS 12b-syn with a free energy barrier of 12.1 kcal mol⁻¹ as an exergonic reaction (13b-syn, −28.0 kcal mol⁻¹). Here, the N1–C1 bond in TS 12b-syn is 1.99 Å whereas N2–C2 bond is 2.50 Å, resulting in an asynchronousity of 0.51 Å between the two bonds growing along the TS.

The anti pathway, 10b → 13b-anti, proceeds with higher barrier of 17.0 kcal mol⁻¹ (ΔΔG^‡ = 4.9 kcal mol⁻¹) in a slightly similar exergonic step (ΔΔG_r = −0.5 kcal mol⁻¹). This would explain that the syn is the kinetic product whereas the anti is the thermodynamic product. The asynchronousity along TS 12b-anti increases into 0.55 Å. This activation energy difference between the isomeric pathways would reflect the experimental diastereoselectivity (>20 : 1 d.r.).¹⁰ Computational evaluations about the origin behind the high selectivity indicate that, along TS, the bulk steric between the dienophile and quaternary substituted group is responsible for the isomeric preference. Along TS 12b-syn the steric distance between CH₃ group in the Bpin of the diene moiety and N–N moiety in the dienophile (PTAD) is 3.39 Å and 2.55 Å for N1–H[CH₃]Bpin and N2–H[CH₃]Bpin respectively. However, the TS 12b-anti has shorter steric distances of 2.53 Å and 2.69 Å for N1–H[R¹] and N2–H[R¹] respectively, where R¹ is adamantyl group. This means that steric hindered provided by the Bpin moiety is less effective than adamantly group, and consequently leading to highly syn selectivity (>20 : 1 d.r.).

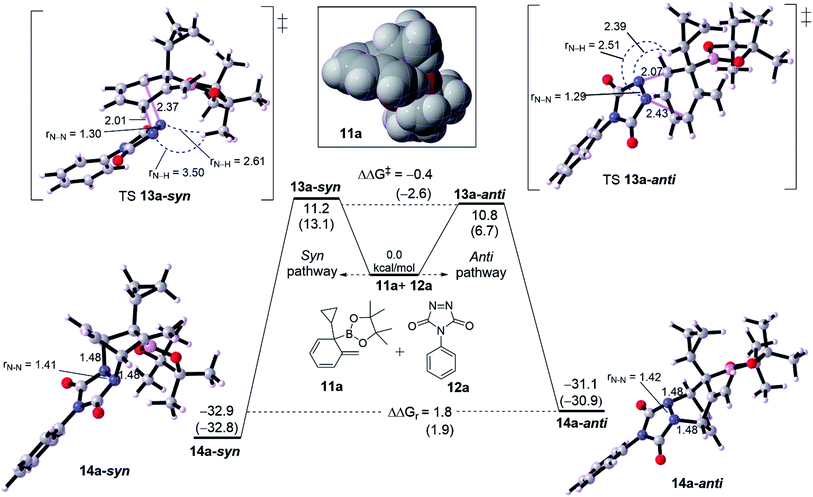
We then probed the computational diastereoselectivity when R¹ is small such as cyclopropyl, the dearomatized intermediate 10a, to rationalize the experimental observations (Fig. 3). Experimentally, low diastereoselectivity for cyclohexadiene 10a was obtained (1 : 1.6 d.r.).¹⁰ DFT calculations show that cycloaddition of 10a with 11a on both pathways are energetically similar although the effect of solvent on calculation was somewhat different. The formation of syn product 13a-syn via an asynchronous concerted TS 12a-syn needs 11.2 kcal mol⁻¹ whereas a slightly lower barrier of 10.8 kcal mol⁻¹ (TS 12a-anti, ΔΔG^‡ = −0.4 kcal mol⁻¹) was seen for the anti product 13a-anti. Thermodynamically, 13a-anti has a thermodynamic preference of ΔΔG_r = 1.8 kcal mol⁻¹. The calculated difference in activation energy between both TSs 12a-syn and 12a-anti reflects the obtained diastereoselectivity (1 : 1.6) with the inconsiderable preference for the anti over syn product. The asynchronousity of both TSs is lower than for those with adamantly-substituted TSs (see Fig. 2). Noticeably, the steric distance between the N–N moiety and cyclopropyl along the TS 12a-anti is relatively shorter than in 12b-anti, correspondingly TS 12a-anti has a lower barrier than TS 12b-anti by around 6.2 kcal mol⁻¹. This would reveal that the steric distance between N=N moiety of PTAD is not only the case in determining the preferability, but the steric bulk is effective too (see the spacefilling model for the dearomatized intermediates 10a and 10b in Fig. 2 and 3). Although PTAD 11a represents an excellent dienophile to react with cyclohexadiene, scoping other dienophiles is highly favorable (see below).

Fig. 3 Computed energetic comparison between syn and anti pathway for [4+2] cycloaddition reaction of intermediate diene 11a with PTDA 12a. Energies between brackets are calculated in THF/SMD. Spacefilling model for diene 11a is shown in box.

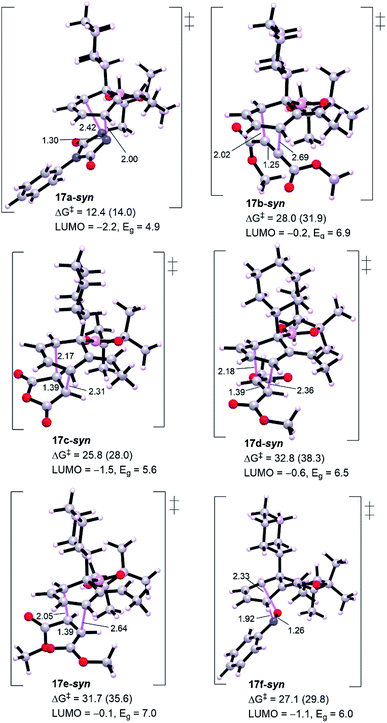
Exploring other dienophiles: we decided to perform a broader computational search for other 2π-components that could react with cyclohexadiene intermediate in a similar fashion and analogy with the cycloaddition processes. Although Aggarwal and co-workers¹⁰ chose PTAD 11a to be the dienophile based on the reported studies that addressed the poor reactivity of cyclohexadienes towards cycloaddition reactions,¹¹ other dienophiles (11b–11f) were also tested (Scheme 2). Indeed, all these dienophiles were unreactive towards cycloaddition,¹⁰ therefore, we then turned our attention into understanding their lack of reactivity by means of DFT calculations (Fig. 4).

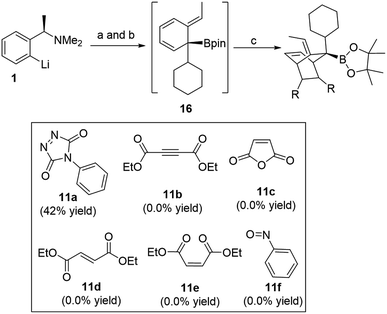Scheme 2 Other dienophiles investigated by Aggarwal and co-workers. (a) CyBpin, THF, −78 °C to rt; (b) ClCO₂CMe₂CCl₃, −78 °C to rt; (c) dienophile, THF, −78 °C to rt or 50 °C.

Fig. 4 Optimized geometries for [4+2] cycloaddition of intermediate 15 with other dienophiles. Gas phase LUMO energy of the corresponding dienophile and energy gap (E_g) are in eV. HOMO energy of diene 15 is −7.1 eV. Energies between brackets are calculated in THF/SMD. Free energies of activation are in kcal mol⁻¹. All diethyl groups in dienophiles were replaced with dimethyl groups to reduce the computational demand.

Generally, from Fig. 3 all the dienophiles except PTAD revealed high energy barriers (25.8–32.8 kcal mol⁻¹) with the lowest calculated one for maleic anhydride 11c (TS 17c-syn, ΔG^‡ = 25.8 kcal mol⁻¹) and the highest one for diethyl fumarate (TS 17d-syn, ΔG^‡ = 32.8 kcal mol⁻¹), much too high to be observed under the reaction conditions in comparison to triply-reduced barrier for PTAD (TS 17a-syn, ΔG^‡ = 12.4 kcal mol⁻¹). Diethyl maleate (11e) and nitrosobenzene (11f) display a comparable barrier to diethyl fumarate (11d) and diethyl acetylenedicarboxylate (11b), respectively. Our DFT simulations show that these barriers are in accord with the energy gaps calculated for the intermediate diene 16 and corresponding dienophiles, the lowest molecular orbital (LUMO) energy of the dienophile the lowest barrier for cycloaddition. Thus, the interception of cyclohexadiene with PTAD will be exceptionally more reactive than other dienophiles. It has been reported that cyclobutenone and cyclopropenone are 1000 to 100 000 times more reactive than cyclohexanone, at room temperature, toward cycloaddition process.^14,15 The high barriers would primarily explain the unsuccessful cycloadditions, and to assess the origin behind this failure we have performed distortion/interaction analysis to estimate the contributions of interaction and distortion energies of the geometrical deformation to the activation energy that achieve the transition state (Table 1). This approach was described by Houk and co-workers.¹⁶ The approach involves separating the TS into its components (diene and dienophile) which is followed by single point energy calculations of the obtained separated reactive components with their respective TS geometries preserved. The difference in energy between the distorted fragments and optimized ground state geometries is the distortion energy (ΔE^‡,t_dis) of the diene and the dienophile, whereas the interaction energy is the difference between the activation energy and the distortion energy (ΔE^‡_int = ΔE^‡ − ΔE^‡_dis).

Table 1 Computed energies for [4+2] cycloadditions of the reactive and unreactive dienophiles in kcal mol⁻¹. Energies between are calculated in THF/SMD^a

TS	ΔE^‡	ΔE^‡,tdis	ΔE^‡,1dis	ΔE^‡,2dis	ΔE^‡int
a ΔE^‡,tdis, ΔE^‡,1dis and ΔE^‡,2dis represents the total, diene, and dienophile distortion energies respectively.
17a-syn	−2.4 (−0.5)	19.8 (19.5)	15.7 (16.2)	4.1 (3.3)	−22.2 (−20.0)
17b-syn	10.3 (14.2)	29.2 (30.2)	13.3 (14.1)	15.9 (16.1)	−18.9 (−16.0)
17c-syn	10.0 (12.2)	30.9 (31.2)	21.4 (22.0)	9.5 (9.2)	−20.9 (−19.0)
17d-syn	12.4 (17.9)	35.4 (36.6)	24.1 (24.9)	11.3 (11.7)	−23.0 (−16.7)
17e-syn	14.2 (18.1)	35.6 (34.8)	17.7 (18.3)	17.9 (16.5)	−21.4 (−16.7)
17f-syn	10.7 (13.4)	20.6 (21.0)	17.6 (18.1)	3.0 (2.9)	−9.9 (−7.6)

---

Table 1 shows a good understandable correlation between activation energies and reactant distortion energies. Due to the high distortion energies associated with accessing the transition state geometry, the reactivity of these dienophiles is then decreased compared with PTAD. Studies by Houk and co-workers investigated the superior reactivity of PTAD as a dienophile for such systems.¹⁷ For all TSs shown in Table 1, except TS 17f-syn that depicts lower interaction energy because of its dienophile nitrosobenzene has a reduced distortion energy of around 3.0 kcal mol⁻¹, the calculated interaction energies are nearly comparable (−18.9 to −23.0 kcal mol⁻¹). This is believed to be consistent with the fact that all these dienophiles and diene have essentially constant interacting frontier molecular orbitals.¹⁴

Conclusions

We have exhibited a DFT study, using the ωB97XD/6-311+G(2d,3pd)//6-31G(d) level of theory in both the gas phase and THF/SMD, on the diastereoselective [4+2] cycloaddition of the dearomatized tertiary boronic ester intermediate with a profoundly reactive dienophile PTAD. The reaction mechanism of this intermediate formation was disclosed to follow 1,2-metalate rearrangement/anti-S_N2′ elimination from an activated ortho-lithiated benzylamine, displayed as a depressed barrier and thermodynamically exergonic step. Competition between [4+2] cycloaddition and 1,3-borotopic shift was calculated to be in an immense preference for the cycloaddition pathway either in the presence of absence of superactivated “naked” Li⁺, wherein the absence of a Lewis acid 1,3-borotopic is exceedingly slow consistent with the experimental conditions. Simulations speculate the aspect that is controlling the diastereoselectivity in producing three-dimensional boron-containing molecular structures was divulged to be the steric bulk, adamantyl group provides an α-branched broad steric bulk compared with a compact cyclopropyl. Finally, we have compared the lack of reactivity of other dienophiles (11b–11f) with PTAD (11a), where the unlikely energy barriers (25.8–32.8 kcal mol⁻¹) are attributed to the high distortion energies of the interacting components that form the TS structure and this was conspicuous with the high LUMO energies.

Computational details

All mechanical quantum calculations were performed using Gaussian 09.¹⁸ The geometries were fully optimized at the hybrid meta-generalized gradient dispersion-corrected approximation ωB97XD,¹⁹ with the basis set 6-31G(d).²⁰ All minima intermediates were verified by the absence of negative eigenvalues in the vibrational frequency analysis. Transition state structures were found using the Berny algorithm,²¹ and verified by vibrational analysis. The transition states were visualized by animating the negative eigenvector coordinate. Single-point energies of the optimized geometries were evaluated using larger basis set 6-311+G(2d,3pd).²⁰ The thermal corrections evaluated from the unscaled vibrational frequencies at the ωB97XD/6-31G(d) level of theory were then added to the ωB97XD/6-311+G(2d,3pd) electronic energies to obtain the free energies. The effect of solvent was included via the solvation model based on density (IEFPCM-SMD) using tetrahydrofuran (THF) or chloroform (CHCl₃) as a representative solvent medium.²² In order to determine the minimum energy path (MEP) on the potential energy surface (PES), intrinsic reaction coordinate (IRC) calculations, by defining the phase for the transition vector motion along the path, were performed for the identified transition states using the Hessian-based Predictor–Corrector integrator to confirm the reaction path proceeding in both directions (reactant and product), in which the Hessian was recomputed every 3 predictor steps with a step size along the reaction path of 0.05 bohr.²³ All energies reported in this paper are Gibbs free energies at 298.15 K using unscaled frequencies. All activation free energies are quoted relative to infinitely separated reagents. Optimized structures are illustrated using CYLview.²⁴

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the computational resources from the iridis4 supercomputer supported by the University of Southampton. AAH acknowledges the University of Southampton/School of Chemistry for providing the visitor-status research position (2717441/EB00-VISIT). Many thanks to the referees for their valuable comments and suggestions.

References

1. For review boron chemistry see: (a) D. S. Matteson, J. Org. Chem., 2013, 78, 10009–10023; (b) D. G. Hall, Boronic Acids, Vol 2: Preparation and Applications in Organic Synthesis, Medicine and Materials, 2nd edn, 2011, pp. 1–701; (c) D. S. Matteson,Stereodirected Synthesis with Organoboranes, Springer, Berlin, 1995; (d) C. Sandford and V. K. Aggarwal, Chem. Commun., 2017, 53, 5481–5494; (e) D. Leonori and V. K. Aggarwal, Acc. Chem. Res., 2014, 47, 3174–3183.
2. (a) D. S. Matteson, Med. Res. Rev., 2008, 28, 233–246; (b) R. Smoum, A. Rubinstein, V. M. Dembitsky and M. Srebnik, Chem. Rev., 2012, 112, 4156–4220.
3. B. S. L. Collins, C. M. Wilson, E. L. Myers and V. K. Aggarwal, Angew. Chem., Int. Ed., 2017, 56, 11700–11733.
4. (a) D. Leonori and V. K. Aggarwal, Angew. Chem., Int. Ed., 2015, 54, 1082–1096; (b) C. Y. Wang, J. Derosa and M. R. Biscoe, Chem. Sci., 2015, 6, 5105–5113; (c) A. H. Cherney, N. T. Kadunce and S. E. Reisman, Chem. Rev., 2015, 115, 9587–9652.
5. (a) S. M. Zhou, M. Z. Deng, L. J. Xia and M. H. Tang, Angew. Chem., Int. Ed., 1998, 37, 2845–2847; (b) M. Rubina, M. Rubin and V. Gevorgyan, J. Am. Chem. Soc., 2003, 125, 7198–7199; (c) T. Ohmura, T. Awano and M. Suginome, J. Am. Chem. Soc., 2010, 132, 13191–13193; (d) T. Awano, T. Ohmura and M. Suginome, J. Am. Chem. Soc., 2011, 133, 20738–20741; (e) B. W. Glasspoole, M. S. Oderinde, B. D. Moore, A. Antoft-Finch and C. M. Crudden, Synthesis, 2013, 45, 1759–1763; (f) D. Imao, B. W. Glasspoole, V. S. Laberge and C. M. Crudden, J. Am. Chem. Soc., 2009, 131, 5024–5025; (g) S. C. Matthew, B. W. Glasspoole, P. Eisenberger and C. M. Crudden, J. Am. Chem. Soc., 2014, 136, 5828–5831.
6. For related trifluoroborates see: (a) G.-H. Fang, Z.-J. Yan and M.-Z. Deng, Org. Lett., 2004, 6, 357–360; (b) D. L. Sandrock, L. Jean-Gérard, C.-y. Chen, S. D. Dreher and G. A. Molander, J. Am. Chem. Soc., 2010, 132, 17108–17110; (c) J. C. H. Lee, R. McDonald and D. G. Hall, Nat. Chem., 2011, 3, 894; (d) G. A. Molander and S. R. Wisniewski, J. Am. Chem. Soc., 2012, 134, 16856–16868; (e) L. Li, S. Zhao, A. Joshi-Pangu, M. Diane and M. R. Biscoe, J. Am. Chem. Soc., 2014, 136, 14027–14030; (f) Y. Z. Lou, P. Cao, T. Jia, Y. L. Zhang, M. Wang and J. Liao, Angew. Chem., Int. Ed., 2015, 54, 12134–12138.
7. For coupling of chiral secondary and tertiary boronic esters with electron-rich aryl lithium reagents see: (a) A. Bonet, M. Odachowski, D. Leonori, S. Essafi and V. K. Aggarwal, Nat. Chem., 2014, 6, 584; (b) M. Odachowski, A. Bonet, S. Essafi, P. Conti-Ramsden, J. N. Harvey, D. Leonori and V. K. Aggarwal, J. Am. Chem. Soc., 2016, 138, 9521–9532.
8. (a) S. Aichhorn, R. Bigler, E. L. Myers and V. K. Aggarwal, J. Am. Chem. Soc., 2017, 139, 9519–9522; (b) B. Rubial, B. S. L. Collins, R. Bigler, S. Aichhorn, A. Noble and V. K. Aggarwal, Angew. Chem., Int. Ed., 2019, 58, 1366–1370.
9. For the use of a Lewis acid in 1,3-borotopic see: (a) F. W. van der Mei, H. Miyamoto, D. L. Silverio and A. H. Hoveyda, Angew. Chem., Int. Ed., 2016, 55, 4701–4706; (b) Y. Kitazawa, R. Takita, K. Yoshida, A. Muranaka, S. Matsubara and M. Uchiyama, J.of Org. Chem., 2017, 82, 1931–1935.
10. C. Tillin, R. Bigler, R. Calo-Lapido, B. S. L. Collins, A. Noble and V. K. Aggarwal, Synlett, 2019, 30, 449–453.
11. S. P. Roche and J. A. Porco, Angew. Chem., Int. Ed., 2011, 50, 4068–4093.
12. For transition metal-catalyzed transformations of the dearomatized boronic ester see: (a) M. Okumura, A. S. Shved and D. Sarlah, J. Am. Chem. Soc., 2017, 139, 17787–17790; (b) M. Okumura and D. Sarlah, Synlett, 2018, 29, 845–855; (c) L. W. Hernandez, U. Klöckner, J. Pospech, L. Hauss and D. Sarlah, J. Am. Chem. Soc., 2018, 140, 4503–4507.
13. (a) Y. Kitazawa, R. Takita, K. Yoshida, A. Muranaka, S. Matsubara and M. Uchiyama, J. Org. Chem., 2017, 82, 1931–1935; (b) K. Fujiki, S.-y. Ikeda, H. Kobayashi, A. Mori, A. Nagira, J. Nie, T. Sonoda and Y. Yagupolskii, Chem. Lett., 2000, 29, 62–63.
14. R. S. Paton, S. Kim, A. G. Ross, S. J. Danishefsky and K. N. Houk, Angew. Chem., Int. Ed., 2011, 50, 10366–10368.
15. For reactivity of other dienes see: (a) R. Sustmann, M. Böhm and J. Sauer, Ber. Dtsch. Chem. Ges., 1979, 112, 883–889; (b) J. Sauer and R. Sustmann, Angew. Chem., 1980, 92, 773–801; (c) J. Sauer and R. Sustmann, Angew. Chem., Int. Ed. Engl., 1980, 19, 779–807.
16. For distortion/interaction model see: (a) K. N. Houk, F. Liu, Y.-F. Yang, & X. Hong The Distortion/Interaction Model for Analysis of Activation Energies of Organic Reactions, Appl. Theor. Org. Chem., 2018, pp. 371–402; (b) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086.
17. For reactivity of PTAD towards other systems see: (a) J. S. Chen, K. N. Houk and C. S. Foote, J. Am. Chem. Soc., 1998, 120, 12303–12309; (b) B. J. Levandowski and K. N. Houk, J. Org. Chem., 2015, 80, 3530–3537.
18. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009.
19. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
20. (a) T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301; (b) M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269; (c) R. C. Binning and L. A. Curtiss, J. Comput. Chem., 1990, 11, 1206–1216; (d) M. P. McGrath and L. Radom, J. Chem. Phys., 1991, 94, 511–516.
21. (a) H. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218; (b) X. Li and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 835–839.
22. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
23. (a) H. P. Hratchian and H. B. Schlegel, J. Chem. Phys., 2004, 120, 9918–9924; (b) M. A. Collins, Theor. Chem. Acc., 2002, 108, 313–324; (c) K. Fukui, Acc. Chem. Res., 1981, 14, 363–368.
24. C. C. Y. Legault, 1.0b, Universitéde Sherbrooke, Canada, 2009, http://www.cylview.org.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra03820e

---