Open Access Article
Open Access ArticleRole of electron in intramolecular vibrational energy redistribution: a simulation of time- and frequency-resolved CARS spectrum
Zanhao Wang†
 a,
Honglin Wu†
a,
Honglin Wu† b,
Xiaosong Liu
b,
Xiaosong Liu a,
Yunfei Songb and
Yanqiang Yang*ab
a,
Yunfei Songb and
Yanqiang Yang*ab
aDepartment of Physics, Harbin Institute of Technology, Harbin, 150001, P. R. China. E-mail: yqyang@hit.edu.cn
bNational Key Laboratory of Shock Wave and Detonation Physics, Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang, 621900, P. R. China
First published on 19th August 2019
Abstract
A coupled oscillator model with special attention to the electron is employed to simulate the time- and frequency-resolved coherent anti-Stokes Raman scattering (TFR-CARS) spectrum of benzene, where the electronic contribution is introduced as an oscillator as well as molecular vibration, and both the coupling between molecular vibrations and the coupling between electron and molecular vibration are involved. Through the simulation, the intramolecular vibrational energy redistribution (IVR) process is confirmed to occur more readily between the molecular vibrations with the same vibrational symmetry. Moreover, it is found that the electron plays a mediator role in the IVR process, and the coupling between electron and molecular vibration significantly increases the intramolecular vibrational energy transfer efficiency.
1 Introduction
Intramolecular vibrational energy redistribution (IVR) processes significantly influence the localization of vibrational energy in molecules.1 The determination of the paths of vibrational energy flow after a chemical bond is selectively excited, is very important for the control of chemical reactions. Several vibrational spectroscopic methods, such as, IR-Raman2–4 and coherent anti-Stokes Raman Scattering (CARS),5–7 have been established to track the IVR dynamics. With femtosecond time- and frequency-resolved CARS (TFR-CARS) technique, the vibrational modes can be coherently excited.8 The detection process consequently avoids the thermal population flow and will reflect the energy redistribution processes inside molecules.Recently, TFR-CARS experiments have been performed in our laboratory to track the coherent intramolecular vibrational energy transfer in liquid benzene9 and a series of structurally relevant monosubstituted benzenes.10 Take the experimental results of liquid benzene for instance, when the C–H stretching vibrational modes of benzene at about 3000 cm−1 (parent modes) were selectively excited, vibrational modes around 1000 cm−1 (daughter modes) far away from the direct excitation region were observed. The experimental results manifest the existence of IVR and the practicability of tracking IVR by CARS. However, only qualitative interpretation was given in the previous work. In order to get an insight into the physical mechanism of the observed IVR processes, further theoretical analyses are necessary.
The theories of TFR-CARS have been proposed for a long time involving both classical11,12 and quantum13,14 approaches. No matter which approach was used, for simplification, the vibrational modes were usually assumed to be independent, which means that the simulated CARS spectrum will not display the energy transfer process between different vibrational modes. When the IVR process is concerned, the coupling between different modes should be involved into the theoretical models. Besides, in CARS spectra, the electronic contribution was always considered as the non-resonant (NR) background,15 which was usually treated as a Gaussian envelope in time domain and simply added with the simulated vibrational dynamics. However, the properties of a molecular system are determined by the motion of the nuclei and electrons and the interaction between them, hence the electronic contribution to CARS spectrum was always underestimated in previous theories.
In this work, the electronic contribution is paid special attention to. Electron is considered as oscillator and introduced to the oscillator model for simulating TFR-CARS. The electron-vibration coupling and the vibration–vibration coupling are simultaneously considered in our model. The theoretical simulation based on this coupled oscillator model is carried out, taking the CARS of benzene as the object, to acquire the respective contribution from electron and molecular vibration and the related coupling effects.
2 Theoretical basis
A molecule is composed of atomic cores and valence electrons, and here, we assume that the molecular vibration is dominated by the motion of atomic cores, and the electronic vibration is dominated by the motion of valence electrons. Both the molecular vibration and the electronic vibration are considered as oscillators.16 The quadratic couplings are considered between different vibrational modes, and the interaction between electron and molecular vibrational mode is described by the Coulomb interaction. Involving the interaction with the electric field component of light, the Hamiltonian can be written as
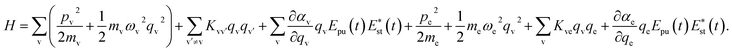 | (1) |
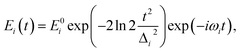 | (2) |
The ensemble averaged coherent vibrational excitation of the molecule in the CARS experiment is described by coherence amplitude q, the expectation value of displacement, which contains the amplitude and phase. Using the Hamilton's equations,17 the following coupled difference equations for the Raman-active vibrational modes and electron are obtained
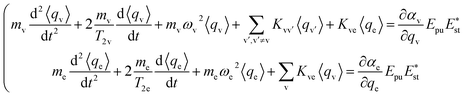 | (3) |
The damping of the molecular vibration is phenomenologically involved as the second terms in the equations of motion, where T2 is the dephasing time. Then, eqn (3) can be numerically solved with the four-order Runge–Kutta–Merson method.18
In CARS process, the coherence amplitude 〈q〉 produced by the driving force of synchronous pump and Stokes laser pair is detected by a delayed probe pulse, and the corresponding third-order polarization is
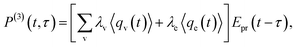 | (4) |
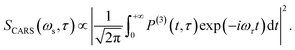 | (5) |
The corresponding Fourier transform (FT) spectrum of CARS can be obtained by performing Fourier transformation along the delay time τ axis
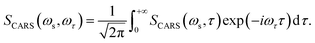 | (6) |
The FT spectrum of CARS will be used to analyze the coherent coupling between the relevant vibrations.
It should be noted that the electronic contribution, which typically dominates only when the three incident laser pulses (Raman pump, Stokes and probe pulses) overlap temporally, is naturally involved into the CARS spectrum by introducing electronic oscillator into eqn (3).
3 Results
3.1 Simulation configuration
The simulation parameters are set according to the experimental results in ref. 9. In this previous experimental work, five fundamental modes, labelled as ν1–5, have been identified participating in the IVR process. The two parent modes around 3000 cm−1 (ν1 and ν2) were directly excited, and the three daughter modes around 1000 cm−1 (ν3–5) emerged due to the vibrational energy transfer from parent modes. A directly excited combination mode at about 3165 cm−1, labelled as ν6, was identified as 2ν4 + ν3. This combination mode did not participate in the IVR process, but contributed to the polarization beats in the high-frequency region. Besides, electron is also considered as an oscillator (νe), with the oscillating frequency set to be 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 677 cm−1 corresponding to the transition frequency from the electronic ground state to the first excited electronic singlet state S1.19 The reduced mass of electron is set to be 0.023, and all the reduced masses of these vibrational modes are got from the Gaussian calculation (using the density functional b3lyp and basis set 6-311g).20
677 cm−1 corresponding to the transition frequency from the electronic ground state to the first excited electronic singlet state S1.19 The reduced mass of electron is set to be 0.023, and all the reduced masses of these vibrational modes are got from the Gaussian calculation (using the density functional b3lyp and basis set 6-311g).20
The dephasing time is determined from the experimental time-domain CARS spectrum. It is worth mentioning that both the energy of the incident light beams and the energy difference between any two laser beams are not resonant with the electron transition, then the electron is undergoing forced oscillation and the dephasing time is consequently very short, which is set to be 0.01 ps in the simulation. All the relevant information is listed in Table 1.
| ν1 | ν2 | ν3 | ν4 | ν5 | ν6 | |
|---|---|---|---|---|---|---|
| Mode | C–H stretching | C–H stretching | C–H bending | Ring breathing | C–H wagging | Combination mode |
| Symmetry | A1g | E2g | E2g | A1g | E1g | E2g |
| Frequency/cm−1 | 3074 | 3056 | 1181 | 992 | 855 | 3165 |
| Reduced mass/amu | 1.10 | 1.09 | 1.14 | 6.03 | 1.25 | 0.96 |
| Dephasing time/ps | 1.50 | 1.50 | 0.50 | 0.50 | 0.80 | 1.50 |
The parameters of the incident laser pulses are set according to the experimental conditions, the central wavelengths of pump, Stokes and probe pulse are respectively set as 640 nm, 800 nm and 640 nm, and the FWHMs of all pulses are set as 100 fs.
As mentioned above, the coupling effects between a pair of molecular vibrations and between molecular vibration and electron are both included, whose strengths are described by Kij. In order to determine the coupling strengths, some qualitative relationship was summarized from the experimental results. Firstly, coherent vibrational energy transfer is more likely to occur between vibrational modes with the same symmetry, resulting in a larger coupling strength. Secondly, the role of electron in the IVR process cannot be ignored. In the present work, all the coupling strength will be used as adjustable parameters in the simulation process. Through reproducing the experimental spectrum by simulation, the coupling strength between different modes (including electron and vibrations) can be quantitatively determined.
3.2 Simulation results
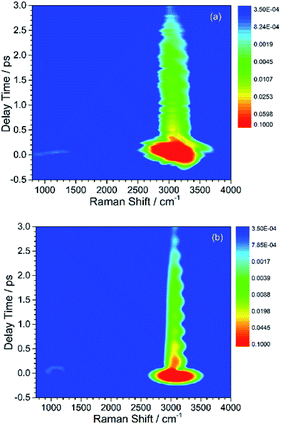
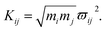 Here, the subscript numbers are corresponding to the vibrational modes listed in Table 1. To get the best simulation result, the couplings between different oscillators are listed in Table 2. It should be mentioned that only three couplings between vibrational modes are set to be nonzero, which are adopted corresponding to the conjecture in ref. 9. The physical meanings of these coupling strengths will be discussed in the Discussion section. The experimental CARS spectrum of benzene is given in Fig. 1(a). The corresponding simulated CARS spectrum of benzene, as shown in Fig. 1(b), is obtained by successively solving eqn (3)–(5) with the parameters given in Tables 1 and 2.
Here, the subscript numbers are corresponding to the vibrational modes listed in Table 1. To get the best simulation result, the couplings between different oscillators are listed in Table 2. It should be mentioned that only three couplings between vibrational modes are set to be nonzero, which are adopted corresponding to the conjecture in ref. 9. The physical meanings of these coupling strengths will be discussed in the Discussion section. The experimental CARS spectrum of benzene is given in Fig. 1(a). The corresponding simulated CARS spectrum of benzene, as shown in Fig. 1(b), is obtained by successively solving eqn (3)–(5) with the parameters given in Tables 1 and 2.
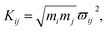 refer to Table 4
refer to Table 4
| ϖ14 | ϖ23 | ϖ45 | ϖe1 | ϖe2 | ϖe3 | ϖe4 | ϖe5 |
|---|---|---|---|---|---|---|---|
| 400 | 325 | 220 | 600 | 350 | 940 | 1200 | 100 |
By comparing Fig. 1(a) and (b), it can be seen that the simulated spectrum reproduces the main features of the experimental result. For example, there is a slowly damped oscillating signal around 3000 cm−1 after ∼0.2 ps, which mainly arises from the interference of ν2 and ν6. Besides, a weak and quickly decayed signal emerges in the region around 1000 cm−1 far away from the directly excitation region, which was assigned to be a result of IVR from parent modes. Moreover, a NR background signal several orders higher than the damped signal also appears, which mainly originates from the electronic contribution. Both of NR electronic contribution and the interference of involved molecular vibrational modes show up in the simulated and experimental pattern. For comparison, the intensity maxima of the simulated and the experiment spectrum are normalized to 1. Besides the electronic contributions at zero delay time, the other features all have comparable magnitudes, as shown in Fig. 1(a) and (b).
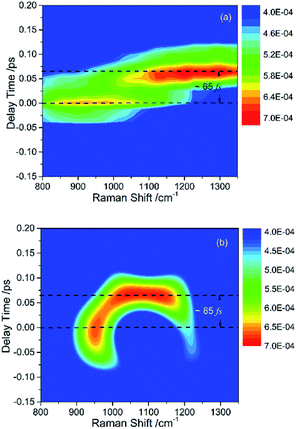
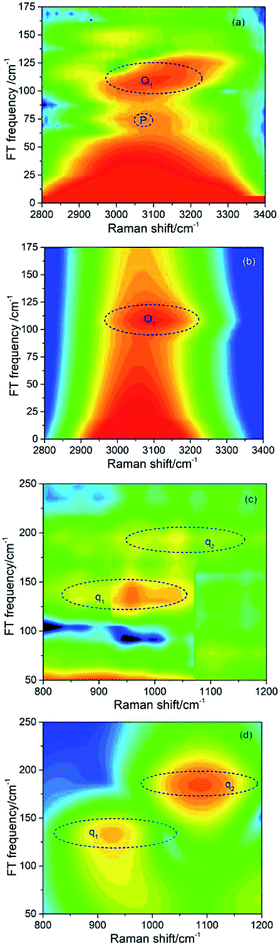
The peak intensities in the low-frequency region around ∼1000 cm−1, as a result of coherent vibrational energy transfer, are far lower than that in the high-frequency region. The part of the low-frequency region of both experimental and simulated contour map is redrawn in Fig. 2(a) and (b) for clarity. Two spectral components with a time difference of about 65 fs appear in both the two contour maps. The component around zero delay time originates from the coupling of ν4 and ν5, while the other component at around 65 fs delay time originates from the interference of ν3 and ν4.9 The time difference of 65 fs originates from the phase difference among these three daughter modes. One may notice that there are some differences in position and bandwidth between the simulated and the experimental results. There are two main reasons for the differences. On one hand, in principle, only Raman-active vibrations can be observed in CARS experiment, so only three vibrational modes around 1000 cm−1 with obvious Raman activity were taken into account in the simulation. But liquid benzene has a fundamental vibration (∼1350 cm−1)21 and some sum frequency vibrations with no Raman activity. In the case when IVR occurs, these vibrational modes around 1300 cm−1 will take part in and interference with the polarization of the 1181 cm−1 mode, which will makes a blueshift of the signal at about 65 fs and shows a broadening appearance. But we cannot determine which vibrational mode it is and its coupling with other oscillators, so we did not add any vibration mode in the simulation process. On the other hand, the simulation conditions are relatively ideal compared with the experimental conditions. First, the laser in the experiment is not the transform limit pulse as used in the simulation. The spectral width of the pulses in experiment is actually wider than that used in the simulation. Second, the tilt of the signal around 1000 cm−1 reflects the chirp of the laser pulse, which is also not taken into account in the simulation. All of these factors will influence the pattern of vibrational spectrum. The phase fluctuation and/or nonideal signal-to-noise ratio in the experiment could also result in distortion of spectral pattern in the time domain. But for all this, the simulation still reproduces the main features of the experimental results.
 | ||
| Fig. 3 Fourier transform (FT) spectra of CARS in different frequency regions. (a) and (c) show the FT spectra from experimental results, and (b) and (d) are the corresponding simulated results. | ||
| Coherent peak | Beat frequency/cm−1 | The modes involved |
|---|---|---|
| Q1 | 109 | ν2 and ν6 |
| q1 | 137 | ν4 and ν5 |
| q2 | 189 | ν3 and ν4 |
It should be noted that a peak marked by P located at about 70 cm−1 appears in the experimental FT spectrum in Fig. 3(a), but there is no corresponding peak in simulated spectrum. This peak arises from an intermolecular collective mode as reported by Shohei Kakinuma,22 which is not considered in the present simulation model.
From the above comparisons, it can be seen that the simulated CARS spectra well reproduce the experimental spectra. The reliability of the simulation results is demonstrated in both time and frequency domains. Although the simulation is carried out based on a simple coupled oscillator model, it can reasonably describe some features about the coupling between vibrational modes and between electron and vibrational modes.
4 Discussion
4.1 Electron-vibration coupling
In the previous experimental work,9 the appearance of vibrational signals in the low-frequency region was attributed to the vibrational coupling between parent modes and daughter modes. In fact, since the vibrational modes are surrounded by the electron, the IVR process should also be affected by electron. However, it is difficult to directly obtain the electronic contribution from the experimental spectra alone. The theoretical simulation introduced in this paper is really much helpful for analyzing the contribution of electron in IVR process.Since the intensity of the daughter mode is a landmark of IVR process, it can reflect the effect of the electron-vibration coupling on the IVR process. The influence of electron-coupling on IVR can be preliminarily estimated by considering the two cases when all the electron-vibration coupling parameters are set to be zero and when all the vibrational coupling parameters are set to be zero. Fig. 4(a) shows the result of considering the vibrational coupling but ignoring the electron-vibration coupling. Although the signal maintains the similar pattern as Fig. 2(b), the intensity of the signal is two orders of magnitude lower. Fig. 4(b) is the result of only considering the electron-vibration coupling but ignoring the vibrational coupling. Compared with Fig. 2(b), the signal intensity is slightly lower, but the pattern has changed significantly. When only the electron-vibration coupling is considered, energy can transfer to the daughter modes without the vibrational coupling, but not all the other vibrational modes can get energy from the parent modes. It can also be seen from the experimental CARS spectrum in Fig. 1 that only a few low-frequency daughter modes coupled with C–H stretching vibrations, while the absence of other modes outside of daughter mode region indicates that electron is not coupled with them or the coupling strength is very week. Thus, electron seems not to equally couple with all vibrations. We also found that a simple superposition of the two results shown in Fig. 4 could not reproduce the same signal pattern as that shown in Fig. 2(b). Therefore, in the IVR process, electron-vibration coupling and vibration–vibration coupling are not two isolated mechanisms. Electron will be involved in the vibrational mode coupling, and significantly changes the efficiency of vibrational energy transfer. This means that the electron, acting as a mediator, plays a key role in the coupling between the parent and daughter vibrational modes.
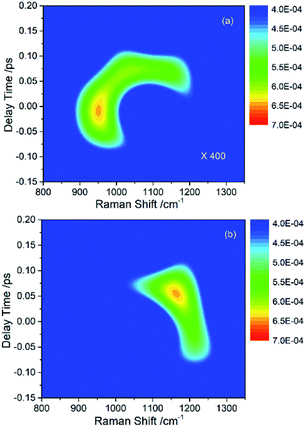 | ||
| Fig. 4 (a) The simulated signal of daughter modes only considering the vibrational coupling but ignoring the electron-vibration coupling. The intensity of this signal is two orders of magnitude lower than that in Fig. 2(b). (b) The simulated signal of daughter modes only considering the electron-vibration coupling but ignoring the vibrational coupling. The pattern is distorted severely comparing with Fig. 2(b). | ||
4.2 The coupling strength
In this coupled oscillator model, Kij is employed to represent the coupling strength between different oscillators, as expressed in eqn (1). Comparing with the experimental result, when the simulation result matches best with the experimental result, the coupling strengths between different oscillators can be obtained, as listed in Table 4. Even though the experimental signal-to-noise ratio of daughter modes is not good, the values of coupling strength cannot be precisely determined, but the magnitudes for various coupling can still be obtained.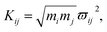 refer to Table 2
refer to Table 2
| K14 | K23 | K45 | Ke1 | Ke2 | Ke3 | Ke4 | Ke5 |
|---|---|---|---|---|---|---|---|
| 0.61 | 0.18 | 0.19 | 0.08 | 0.03 | 0.21 | 0.80 | 0.003 |
Firstly, we consider the coupling between different vibrational modes. The coupling between ν1 and ν4 causing the vibrational energy transfer originates from their same symmetry, which is the same case for ν2 and ν3. Though the symmetries of ν4 and ν5 are different, the vibrational energy transfer also occurs. As the frequency difference between the two vibrational modes is very small, we deduce that the vibrational energy transfer happens with the help of intermolecular collective modes. It should be noticed that the frequency difference is almost twice the frequency of the collective mode mentioned in Section 3.2(b). Hence it is reasonable to infer that this coupling between ν4 and ν5 is related to the participation of the intermolecular collective mode. The simulation, which well reproduces the experimental CARS spectrum of benzene, confirms the reasonability of the parameter setting of vibrational coupling.
Secondly considering the contribution of electron, it is clear that the couplings between electron and different vibrational modes are different. Considering the symmetry, electron will couple with the vibrational modes with A1g (ν1 and ν4) and E2g (ν2 and ν3) symmetry for benzene.23 The coupling strength between electron and ν5 is very weak. The value 0.003 listed in Table 3 is the maximum possible value, and any value below 0.003 will hardly influence the simulated result. So the coupling between electron and ν5 is small enough to be neglected, which is reasonable considering the symmetry. There is another experimental phenomenon that no signals from other vibrational modes with E2g symmetry were observed in the experiment, which means electrons does not couple other E2g symmetric vibrations of benzene. It is because, in the IVR process observed by CARS, electron only couples and couples simultaneously with the parent and daughter modes who have the same symmetry and the vibrational energy transfer between whom is permitted. This can be proved from the simulation result shown in Fig. 4 that the signal intensity of daughter modes will be two orders of magnitude greater when electronic contribution is involved.
5 Conclusions
A coupled oscillator model is established in order to get further understanding about the vibrational energy transfer observed in previous CARS experiment of liquid benzene. In this model, the electronic contribution is treated as an oscillator, and both molecular vibrational coupling and electronic and molecular vibration coupling are involved. The numerical simulated results well reproduce the experimental results, confirming the reliability of the simulation. The simulation results show that, there is strong coupling between the molecular vibrations with the same symmetry, which is in agreement with the experimental results. Beyond this, electron is found to play a mediator role in the IVR process through the theoretical simulation. When energy transfer occurs between two vibrational modes with the same symmetry, electron couples with the two modes simultaneously, which significantly increases the energy transfer efficiency.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 21673211), and the Science Challenging Program (Grant No. TZ2016001).Notes and references
- D. J. Nesbitt and R. W. Field, J. Phys. Chem., 1996, 100, 12735–12756 CrossRef CAS.
- B. C. Pein and D. D. Dlott, J. Phys. Chem. A, 2014, 118, 965–973 CrossRef CAS PubMed.
- B. C. Pein, Y. Sun and D. D. Dlott, J. Phys. Chem. B, 2013, 117, 10898–10904 CrossRef CAS PubMed.
- L. K. Iwaki, J. C. Deàk, S. T. Rhea and D. D. Dlott, Chem. Phys. Lett., 1999, 303, 176–182 CrossRef CAS.
- E. L. Chronister and D. D. Dlott, J. Chem. Phys., 1983, 79, 5286–5291 CrossRef CAS.
- A. M. Brodnikovsky, S. M. Gladkov and N. I. Koroteev, Opt. Commun., 1982, 40, 312–316 CrossRef.
- M. Lütgens, S. Chatzipapadopoulos and S. Lochbrunner, Opt. Express, 2012, 20, 6478–6487 CrossRef PubMed.
- X. Du, M. Zhang, X. He, Q. Meng, Y. Song, Y. Yang and J. Han, Chin. Phys. B, 2011, 20, 126301 CrossRef.
- X. Liu, W. Zhang, Y. Song, G. Yu, Z. Zheng, Y. Zeng, Z. Lv, H. Song and Y. Yang, J. Phys. Chem. A, 2017, 121, 4948–4952 CrossRef CAS PubMed.
- X. Liu, Y. Song, W. Zhang, G. Zhu, Z. Lv, W. Liu and Y. Yang, RSC Adv., 2018, 8, 29775–29780 RSC.
- D. C. Urbanek and M. A. Berg, J. Chem. Phys., 2007, 127, 044306 CrossRef PubMed.
- W. M. Tolles, J. W. Nibler, J. R. Mcdonald and A. B. Harvey, Appl. Spectrosc., 1977, 31, 253–271 CrossRef CAS.
- H. U. Stauffer, J. D. Miller, M. N. Slipchenko, T. R. Meyer, B. D. Prince, S. Roy and J. R. Gord, J. Chem. Phys., 2014, 140, 024316 CrossRef PubMed.
- K. Niu and S. Y. Lee, J. Chem. Phys., 2012, 136, 064504 CrossRef PubMed.
- F. M. Kamga and M. G. Sceats, Opt. Lett., 1980, 5, 126–128 CrossRef CAS PubMed.
- A. S. Barker JR and R. Loudon, Rev. Mod. Phys., 1972, 44, 18–47 CrossRef.
- J. R. Ray, Am. J. Phys., 1973, 41, 1188–1190 CrossRef.
- H. R. Martens, Simulation, 1969, 12, 87–94 CrossRef.
- D. S. N. Parker, R. S. Minns, T. J. Penfold, G. A. Worth and H. H. Fielding, Chem. Phys. Lett., 2009, 469, 43–47 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. heeseman, J. A. Montgomery, et al., Gaussian 03, Revision E.01, Gaussian Inc., Wallingford, CT, 2004 Search PubMed.
- C. H. Nicholas, E. M. Paul, D. A. Roger, S. A. Jamie, W. M. Christopher and J. L. Gregory, Chem. Phys. Lett., 1992, 197, 506–515 CrossRef.
- S. Kakinuma and H. Shirota, J. Phys. Chem. B, 2015, 119, 4713–4724 CrossRef CAS PubMed.
- C. B. Duke, N. O. Lipari and L. Pietronero, Chem. Phys. Lett., 1975, 30, 415–420 CrossRef CAS.
Footnote |
| † These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |