Open Access Article
Open Access ArticleTemplate-free preparation of anthracite-based nitrogen-doped porous carbons for high-performance supercapacitors and efficient electrocatalysts for the oxygen reduction reaction†
Jiawei Qi,
Bolin Jin,
Peiyao Bai,
Wendu Zhang and
Lang Xu *
*
MOE Key Laboratory of Coal Processing and Efficient Utilization, School of Chemical Engineering and Technology, China University of Mining and Technology, 1 Daxue Road, Xuzhou, Jiangsu 221116, China. E-mail: lang.xu@cumt.edu.cn
First published on 6th August 2019
Abstract
The conversion of coal into high-performance electrochemical energy materials, exemplified by electrodes and electrocatalysts for supercapacitors and fuel cells, is currently crucial to the advancement of high value-added, clean and non-fuel utilization of coal resources. In this work, anthracite-based nitrogen-doped porous carbon (ANPC) materials with well-defined pore architectures and adjustable nitrogen concentrations were prepared without any template: ANPC-1 by a one-step activation/doping process and ANPC-2 by a two-step process. The specific capacitance value of the ANPC-1 materials could attain a maximum of 346.0 F g−1 at the current density of 0.5 A g−1 in 6 M KOH. Supercapacitors composed of the ANPC-1 electrodes were able to achieve high energy densities up to 10.3 W h kg−1 and 20.8 W h kg−1, together with good charge/discharge stabilities of 95.4% and 91.3% after 5000 cycles, in KOH and Na2SO4 aqueous electrolytes, respectively. The ANPC-2 materials are more associated with the oxygen reduction reaction (ORR): one possessed a comparable ORR electrocatalytic activity to the commercial JM Pt/C (20% Pt) catalyst, and, moreover, its onset potential (0.96 V vs. RHE), half-wave potential (0.85 V vs. RHE), catalyst durability (95.9% activity retained after 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s) and methanol tolerance were all superior to the benchmark electrocatalyst. This study provides a feasible route to rational design of coal-based multifunctional materials towards electrochemical energy storage and conversion.
000 s) and methanol tolerance were all superior to the benchmark electrocatalyst. This study provides a feasible route to rational design of coal-based multifunctional materials towards electrochemical energy storage and conversion.
Introduction
The exploitation of multifunctional energy materials derived from earth-abundant and inexpensive resources in Nature is a positive measure to reduce the energy and environmental pressure.1–3 Instead of acting as fuels, high-maturation coals can be refined and processed into high value-added functional carbon materials for the electrochemical energy storage and conversion fields, such as supercapacitors and fuel cells, which not only enhances non-fuel properties of value and clean utilization of coals, but also is in accordance with environmental protection requirements.4,5 As advanced energy storage devices, carbon-based supercapacitors have attracted extensive attention owing to their superior stable chemical attributes, high power density and favourable cycling life.6–8 However, their relatively low energy density is a bottleneck hindering their wider applications.9–11 Pt-based materials have occupied the dominant position as cathodic catalysts of the oxygen reduction reaction (ORR) in proton-exchange membrane fuel cells, but there are still some disadvantages, as exemplified by high cost, scarce reserves, poor resistance to impurities and unsatisfactory stability of Pt.12–14 Therefore, developing coal-based carbon materials with good electrochemical performance is of great significance to the development of supercapacitors and fuel cells.Considerable efforts have recently been made to prepare various porous carbon materials with high surface areas and well-developed porosities for improving the performance of electrochemical energy storage and conversion devices.15–20 Porous carbons with hierarchical micro/mesopore structures have unique advantages to be promising energy materials. A large number of micropores with pore size of <2 nm are able to increase specific surface area and provide as many reaction sites as possible for capacitance formation and catalytic processes, whereas mesopores can serve as efficient transport pathways to improve ion transport kinetics.21,22 Such hierarchical pore structure is capable of supplying carbon materials with high specific capacitance and rate capability for supercapacitors and high electrocatalytic activity for the ORR.23,24 Nevertheless, porous carbon materials are very prone to penetration limitation because many micropores deeply buried in the internal carbon materials are not accessible to electrolyte ions and catalytic triple phase boundaries.25,26 Consequently, pore width distributions of materials need to be optimized by modulating the activation/doping process.
In recent years, doping nitrogen atoms into a carbon framework so as to improve electrochemical performance of carbonaceous materials has been studied extensively. It is considered that nitrogen doping can reconfigure the local electronic density and thereby readjust the physiochemical properties of carbon and its adjacent atoms.27,28 Moreover, nitrogen functional groups can improve the hydrophilicity and conductivity of carbon materials.29,30 The types of nitrogen atoms in N-doped carbon materials usually include pyridinic N, pyrrolic N, graphitic N and oxidized N, among which, pyridinic N and graphitic N were reported to be closely related to capacitive capabilities and catalytic activities.31–33 One of the major synthetic methods for N-doped carbons is post heat treatment of carbon sources under the atmosphere of a N-containing gas (usually NH3).16,18,24 In comparison, direct doping using N-containing solid-state precursors, such as melamine and urea, is another feasible way with high security and reliability.17,34 Melamine is a nitrogen-enriched, inexpensive and abundant compound with an excellent doping effect.35 Despite this, there have been precious few works on the use of melamine as a nitrogen dopant in the preparation of coal-based N-doped carbons.
Porous carbons derived from coal products, including coal, coal tar and coal tar pitch, have been routinely fabricated by using sophisticated treatments, such as freeze-drying, hydrothermal carbonization and templates.36–38 In addition, several new templates (e.g. nano-MgO, nano-ZnO, nano-Fe2O3 and salt templates) have been employed to obtain porous carbons.38–41 Nonetheless, the development of simple and sustainable preparation methods that dispense with any templates is of great necessity for the cost-effective preparation of coal-based N-doped porous carbons. Anthracite is a kind of high-grade coal with high carbon content, low volatile yield, low impurities and high density, and it can be readily transformed into energy-oriented carbonaceous materials with well-controlled pore structures under the chemical activation.42,43 In view of environmental hazards and misallocation of resources for the conventional coal usage, the efficient non-fuel utilization of anthracite as an abundant carbon source is a very promising path leading to novel and green energy-related materials.
In this research, we developed a facile and effective route to the template-free preparation of anthracite-based nitrogen-doped porous carbon (ANPC) with large specific surface area and moderate nitrogen content. The ANPC materials, functioning as high-performance supercapacitor electrodes and efficient ORR electrocatalysts, were made by the one-step (ANPC-1) and two-step (ANPC-2) activation/doping processes. A large specific surface area and suitable nitrogen content strike a controllable balance in favour of electrochemical behaviours by regulating the heat treatment temperatures and the mass ratios of melamine to carbon precursors. One ANPC-1 material exhibits an outstanding capacitive performance with a high specific capacitance. The supercapacitor composed of the two ANPC-1 electrodes delivers a high energy density and a long-term capacitance retention. Further, one ANPC-2 material exhibits a superior ORR catalytic activity to the benchmark 20% Pt/C in terms of onset potential, half-wave potential, cycling stability and methanol tolerance. Our study opens up an effective avenue towards high-activity and cost-effective coal-based multifunctional energy materials by a simple and green strategy.
Experimental
Materials
Anthracite was obtained from Henan Yongcheng Coal Mine, China. Polytetrafluoroethylene (PTFE) dispersion (60 wt%) and Nafion perfluorinated resin solution (5 wt%) were bought from Aldrich, graphite powder was bought from Acros, melamine was bought from Adamas-beta, potassium hydroxide and sodium sulfate were bought from General Reagent, the JM Pt/C (20% Pt) catalyst was bought from Shanghai Hesen, ethanol, isopropanol and hydrochloric acid were bought from Sinopharm. High-purity O2 and N2 (99.999%) were bought from Xuzhou Special Gases. Deionized water from a Satorius arium ultrapure water system (18 MΩ cm) was used to prepare all aqueous solutions.Preparations
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The mixture was transferred to a corundum crucible, which was then placed into the tube furnace and heated to 800 °C at a heating rate of 3 °C min−1 for 2 h under the continuous nitrogen flow (80 cm3 min−1). The product was washed in 1 M HCl for 2 h, and then filtered and rinsed with deionized water until the filtrate became neutral. Finally, the black product was obtained after drying overnight in the oven at 80 °C. To further investigate the effects of melamine doses and activation/doping temperatures, a series of the ANPC-1 materials were prepared by varying the mass ratios of melamine to the pretreated anthracite and the activation/doping temperatures, denoted by ANPC-1-t-x, where 1 represents the one-step synthetic procedure, t represents the activation/doping temperature and x represents the mass ratio of melamine to the pretreated anthracite. The ANPC-1 materials include ANPC-1-800-0, ANPC-1-800-0.25, ANPC-1-800-1, ANPC-1-700-0.25 and ANPC-1-900-0.25.
1. The mixture was transferred to a corundum crucible, which was then placed into the tube furnace and heated to 800 °C at a heating rate of 3 °C min−1 for 2 h under the continuous nitrogen flow (80 cm3 min−1). The product was washed in 1 M HCl for 2 h, and then filtered and rinsed with deionized water until the filtrate became neutral. Finally, the black product was obtained after drying overnight in the oven at 80 °C. To further investigate the effects of melamine doses and activation/doping temperatures, a series of the ANPC-1 materials were prepared by varying the mass ratios of melamine to the pretreated anthracite and the activation/doping temperatures, denoted by ANPC-1-t-x, where 1 represents the one-step synthetic procedure, t represents the activation/doping temperature and x represents the mass ratio of melamine to the pretreated anthracite. The ANPC-1 materials include ANPC-1-800-0, ANPC-1-800-0.25, ANPC-1-800-1, ANPC-1-700-0.25 and ANPC-1-900-0.25.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in view of the construction of adequate porous carbon structure and large specific surface area for the subsequent effective nitrogen doping. The corundum crucible containing the mixture was positioned in the tube furnace for the thermal treatment at 800 °C for 2 h with a heating rate of 5 °C min−1 under the continuous nitrogen flow (80 cm3 min−1). The product was washed in 1 M HCl for 2 h, followed by being filtered and washed with deionized water until the filtrate became neutral. The obtained product was then dried in the oven at 80 °C overnight, obtaining anthracite-based porous carbon (APC). Afterwards, the APC (0.3 g) and melamine (1.8 g) were mixed by rotating for 15 min at 400 rpm clockwise and 15 min at 400 rpm anticlockwise in the ball milling machine. Subsequently, the mixture was heated at 900 °C for 2 h with a heating rate of 2 °C min−1 under the continuous nitrogen flow (80 cm3 min−1). The black product was successively treated by acid washing, water washing and drying, as mentioned above. In order to study the effects of the melamine/APC ratios and the secondary heat treatment temperatures, a series of the ANPC-2 materials were prepared by changing the mass ratios of melamine to APC and the secondary heat treatment temperatures, designated as ANPC-2-t-x, where 2 denotes the two-step synthetic procedure, t denotes the secondary heat treatment temperature and x denotes the mass ratio of melamine to APC. The ANPC-2 materials include ANPC-2-900-4, ANPC-2-900-6, ANPC-2-900-8, ANPC-2-800-6 and ANPC-2-1000-6.
1 in view of the construction of adequate porous carbon structure and large specific surface area for the subsequent effective nitrogen doping. The corundum crucible containing the mixture was positioned in the tube furnace for the thermal treatment at 800 °C for 2 h with a heating rate of 5 °C min−1 under the continuous nitrogen flow (80 cm3 min−1). The product was washed in 1 M HCl for 2 h, followed by being filtered and washed with deionized water until the filtrate became neutral. The obtained product was then dried in the oven at 80 °C overnight, obtaining anthracite-based porous carbon (APC). Afterwards, the APC (0.3 g) and melamine (1.8 g) were mixed by rotating for 15 min at 400 rpm clockwise and 15 min at 400 rpm anticlockwise in the ball milling machine. Subsequently, the mixture was heated at 900 °C for 2 h with a heating rate of 2 °C min−1 under the continuous nitrogen flow (80 cm3 min−1). The black product was successively treated by acid washing, water washing and drying, as mentioned above. In order to study the effects of the melamine/APC ratios and the secondary heat treatment temperatures, a series of the ANPC-2 materials were prepared by changing the mass ratios of melamine to APC and the secondary heat treatment temperatures, designated as ANPC-2-t-x, where 2 denotes the two-step synthetic procedure, t denotes the secondary heat treatment temperature and x denotes the mass ratio of melamine to APC. The ANPC-2 materials include ANPC-2-900-4, ANPC-2-900-6, ANPC-2-900-8, ANPC-2-800-6 and ANPC-2-1000-6.Characterizations
N2 adsorption/desorption isotherms were measured on a Quantachrome autosorb-iQ at 77 K. Brunauer–Emmett–Teller (BET) specific surface areas of the ANPC materials were calculated according to the linear ranges of BET plots from the corresponding physisorption isotherms. Pore width distribution curves of the ANPC materials were acquired based on the quenched solid density functional theory (DFT) method. The microstructures and morphologies of the ANPC materials were observed on an FEI Tecnai field-emission transmission electron microscope (TEM) and an FEI Quanta TM 250 scanning electron microscope (SEM). Raman spectra were obtained on a Bruker Senterra confocal Raman spectrometer (laser excitation wavelength: 532 nm). X-ray photoelectron spectroscopy (XPS) spectra were collected on a Thermo Fisher ESCALAB 250Xi spectroscope equipped with an excitation source of Al Kα radiation (1486.6 eV).Capacitive measurements
The method for making a working electrode is as follows: an ANPC-1 material, graphite and PTFE dispersion (60 wt%) with a weight ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 were mixed in a small centrifuge tube under ultrasonic irradiation for 20 min to form a viscous slurry. The mixture was then coated onto a nickel-foam current collector, followed by being dried in the oven at 80 °C for 1 h and being then pressed at 15 MPa for 1 min by a hydraulic press. The working electrode was finally obtained by being dried at 80 °C for 12 h in a vacuum oven. A three-electrode system was completed by using a Ag/AgCl reference electrode and a Pt counter electrode in an electrochemical cell containing 6 M KOH aqueous solution. A two-electrode system, i.e., a supercapacitor, was assembled by employing the two identical working electrodes, which were separated by a distance of 1.5 cm and immersed in either 6 M KOH or 1 M Na2SO4 aqueous solution. Cyclic voltammetry (CV), galvanostatic charge/discharge (GCD) and electrochemical impedance spectroscopy (EIS) measurements were carried out on an Ivium potentiostat (Vertex.C.EIS, Ivium Technologies) at 25 °C. The EIS experiments were performed within the frequency range of 105 to 10−2 Hz with the amplitude of 10 mV at an open circuit voltage in the two-electrode configuration. Prior to all the electrochemical measurements, the alkaline or neutral aqueous electrolyte was purged for 30 min using N2.
10 were mixed in a small centrifuge tube under ultrasonic irradiation for 20 min to form a viscous slurry. The mixture was then coated onto a nickel-foam current collector, followed by being dried in the oven at 80 °C for 1 h and being then pressed at 15 MPa for 1 min by a hydraulic press. The working electrode was finally obtained by being dried at 80 °C for 12 h in a vacuum oven. A three-electrode system was completed by using a Ag/AgCl reference electrode and a Pt counter electrode in an electrochemical cell containing 6 M KOH aqueous solution. A two-electrode system, i.e., a supercapacitor, was assembled by employing the two identical working electrodes, which were separated by a distance of 1.5 cm and immersed in either 6 M KOH or 1 M Na2SO4 aqueous solution. Cyclic voltammetry (CV), galvanostatic charge/discharge (GCD) and electrochemical impedance spectroscopy (EIS) measurements were carried out on an Ivium potentiostat (Vertex.C.EIS, Ivium Technologies) at 25 °C. The EIS experiments were performed within the frequency range of 105 to 10−2 Hz with the amplitude of 10 mV at an open circuit voltage in the two-electrode configuration. Prior to all the electrochemical measurements, the alkaline or neutral aqueous electrolyte was purged for 30 min using N2.
The specific capacitance value of a single ANPC-1 electrode (CS) in the three-electrode configuration was calculated from the GCD curves based on the following equation:
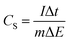 | (1) |
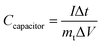 | (2) |
 | (3) |
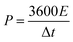 | (4) |
ORR measurements
The three-electrode configuration – (1) a glassy carbon rotating disk electrode (GCRDE) connected to an electrode rotator (AFMSRCE, Pine Research), (2) a Ag/AgCl reference electrode (3.5 M KCl, 0.205 V vs. SHE) positioned in a tube and connected to the main cell via a Luggin capillary, and (3) a platinum coil counter electrode were set up in a gas-tight glass electrochemical cell that contained 0.1 M KOH aqueous solution, which was water-jacketed to keep the temperature at 25 °C. Linear sweep voltammetry (LSV) and chronoamperometry were carried out on an Ivium potentiostat (IviumStat.h, Ivium Technologies). The working electrode was prepared by the following steps: the surface of each GCRDE was sequentially polished with 1.5 μm and 50 nm alumina slurries, followed by being washed with water and ethanol. At the same time, 3 mg of an ANPC-2 sample or 1 mg of Pt/C catalyst was dispersed in a mixed solution containing 240 μL of deionized water, 100 μL of isopropanol and 10 μL of Nafion solution (5 wt%) under ultrasonic irradiation for 30 min. Afterwards, the catalyst suspension (8 μL) was dropped onto the polished GCRDE surface by a pipette, finally obtaining the working electrode after the suspension became dry at room temperature. The N2 and O2 flows (80 cm3 min−1) supplied to the electrochemical cell were controlled by mass flow controllers (Smart-Trak 100, Sierra Instruments). The gas flows were first aerated into the electrolyte solution for 30 min and then above the solution level during the entire electrochemical experiments. The current densities recorded in the N2-saturated electrolyte solution were deducted from those in the O2-saturated solution in order to remove the capacitive contributions from the ANPC-2 catalysts. Herein the measured potentials were converted to the reversible hydrogen electrode (RHE) scale based on the Nernst equation: ERHE = EAg/AgCl + 0.059 × pH + 0.205 V (25 °C).14 The electron-transfer number values were calculated according to the Koutecky–Levich (K–L) equation.13
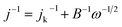 | (5) |
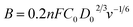 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485C mol−1), n is electron-transfer number value per mole of O2, D0 is the diffusion coefficient of O2 in 0.1 M KOH at 25 °C (1.9 × 10−5 cm2 s−1), C0 is the bulk concentration of O2 in 0.1 M KOH at 25 °C (1.2 × 10−3 mol L−1), and v is the kinetic viscosity of 0.1 M KOH at 25 °C (0.01 cm2 s−1).
485C mol−1), n is electron-transfer number value per mole of O2, D0 is the diffusion coefficient of O2 in 0.1 M KOH at 25 °C (1.9 × 10−5 cm2 s−1), C0 is the bulk concentration of O2 in 0.1 M KOH at 25 °C (1.2 × 10−3 mol L−1), and v is the kinetic viscosity of 0.1 M KOH at 25 °C (0.01 cm2 s−1).
For the rotating ring-disk electrode (RRDE) measurement, the electron-transfer number and peroxide yield (H2O2%) were calculated according to the following equations:44
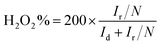 | (7) |
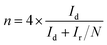 | (8) |
Results and discussion
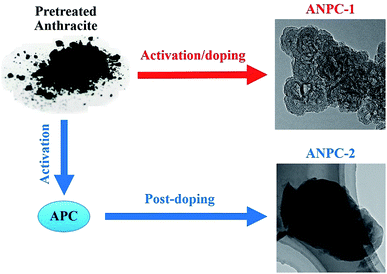
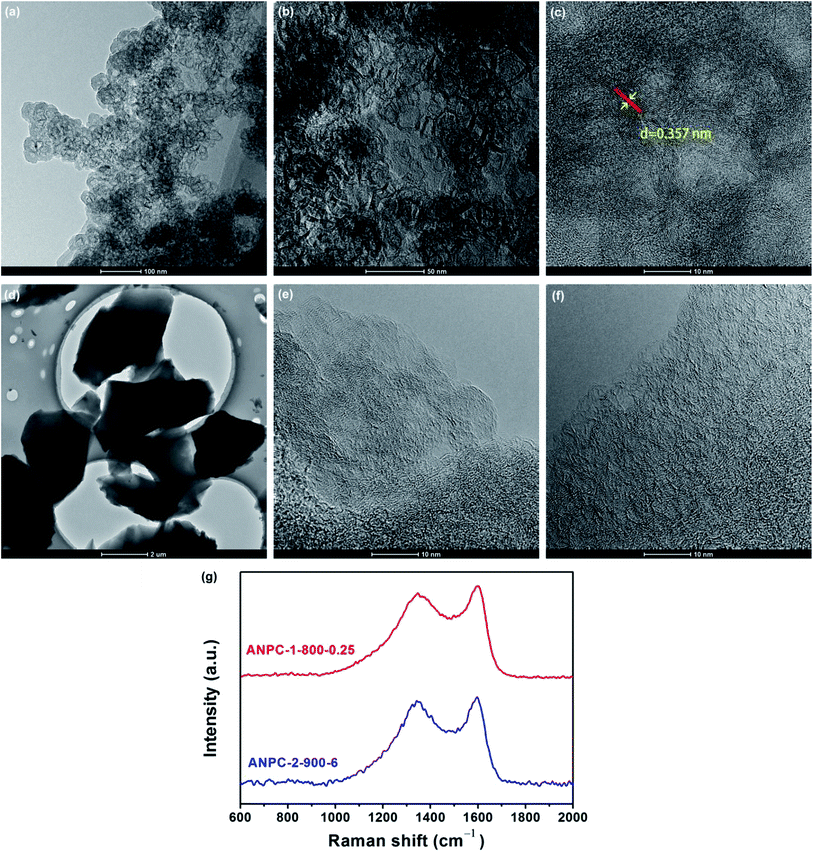
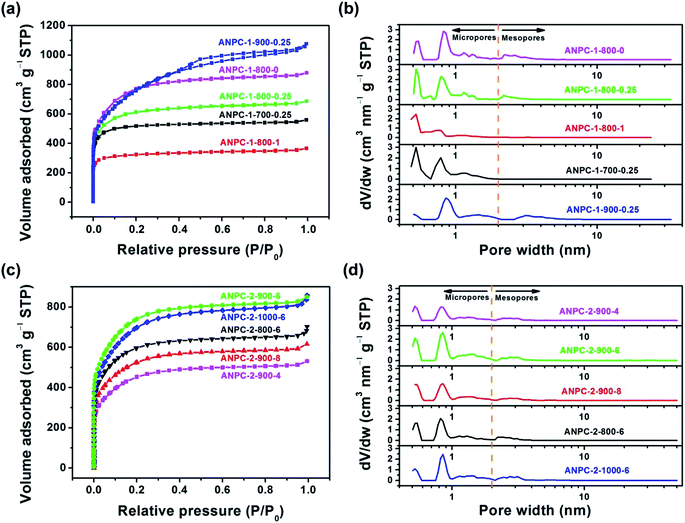
Fig. 1 shows the schematic diagram of the preparation processes of ANPC-1 and ANPC-2 – the ANPC-1 materials that are more associated with supercapacitor electrodes were made by the one-step activation/doping process whereas the ANPC-2 materials that are closely related to ORR electrocatalysts were prepared by the two-step activation/doping process via the intermediate APC. Fig. 2a–f show a set of TEM images of the two representative materials of ANPC-1 and ANPC-2. Fig. 2a and b represents the morphologies and microstructures of ANPC-1-800-0.25 with different magnifications. It could be observed that ANPC-1-800-0.25 has a hollow quasi-cubic nanostructure with size of 5–30 nm. The high-resolution TEM image of ANPC-1-800-0.25 (Fig. 2c) markedly exhibits the nanopore structures that are conducive to the increase in charge storage and rapid diffusion of electrolyte ions, as well as the lattice fringes with interplanar spacing of 0.357 nm, which could be assigned to the (002) plane of graphitic carbon, indicating ANPC-1-800-0.25 possesses a certain degree of graphitization.23 On the other hand, ANPC-2-900-6 owns a different microstructure: as shown in Fig. 2d, it has a micrometer-scale lamellar morphology with irregular shapes. Fig. 2e and f show the high-resolution TEM images of ANPC-2-900-6 in different regions. Nanopores and rough surface could be observed throughout ANPC-2-900-6, together with a few lattice fringes on the edges of the material. Compared to ANPC-1-800-0.25, the number of lattice fringes of ANPC-2-900-6 is much reduced, indicating that the graphitization of ANPC-2-900-6 becomes weak as a result of its greater degree of roughness and disorder (larger specific surface area and more nanopores) and its higher nitrogen doping concentration. SEM observations were undertaken to further examine the microscopic structures of the two typical ANPC materials. Evidently, ANPC-1-800-0.25 possesses a Swiss cheese-like, chunk structure (Fig. S1a–c†). The SEM image with the high magnification (10k) exhibits that ANPC-1-800-0.25 has holes on its rugged surface (Fig. S1c†). It is interesting to find that markedly bulky granules feature prominently in the SEM images of ANPC-1-800-0.25 by comparison with ANPC-2-900-6 at the same magnifications (1k, 5k and 10k), mainly because the preparation of the latter undergoes the one more ball-milling processing. As shown in Fig. S1d–f,† ANPC-2-900-6 owns a lumpy, block structure with irregular edges and rough surface, resulting from the mechanochemical force, which are capable of providing large specific surface areas and exposing active sites. The degree of graphitization of the ANPC-1 and ANPC-2 materials could be further examined by Raman analyses. Fig. 2g shows the Raman spectra of ANPC-1-800-0.25 and ANPC-2-900-6. Each Raman spectrum has the two marked bands: one centered at 1345 cm−1, which is known as the D (disordered) band, is relevant to the disordered and defective features of carbon, whereas the other centered at 1596 cm−1, which is known as the G (graphitic) band, is linked with the vibration of in-plane carbon atoms of graphite; therefore, the intensity ratio between the D and G bands (ID/IG) could characterize the degree of disorder or graphitization of carbonaceous materials.22 The ID/IG values of ANPC-1-800-0.25 and ANPC-2-900-6 were calculated to be 0.93 and 0.96, respectively, confirming that ANPC-1-800-0.25 has a higher degree of graphitization than ANPC-2-900-6, which is consistent with the above-mentioned high-resolution TEM observations. Comprehensively, the Raman spectra of all the ANPC-1 and ANPC-2 materials were shown in Fig. S1g and h.† Regarding the one-step activation/doping process (ANPC-1), the ID/IG values of ANPC-1-800-0, ANPC-1-800-0.25, ANPC-1-800-1, ANPC-1-700-0.25 and ANPC-1-900-0.25 were calculated to be 0.92, 0.93, 1.01, 0.94 and 0.91, respectively, indicating that increasing nitrogen doses and/or decreasing pyrolysis temperatures could intensify the disorder degree of the ANPC-1 materials. For ANPC-2, the ID/IG values of ANPC-2-900-4, ANPC-2-900-6, ANPC-2-900-8, ANPC-2-800-6 and ANPC-2-1000-6 were calculated to be 0.96, 0.96, 0.94, 0.92 and 0.95, respectively. Such similar values suggest that their common precursor APC (produced at the first step – activation) plays an important role in the degree of graphitization or disorder rather than nitrogen dosage or doping temperature (relating to the second step – doping) among the ANPC-2 materials that were prepared via the two-step activation/doping way.Fig. 3a shows the N2 adsorption/desorption isotherms of the five ANPC-1 materials. All the physisorption isotherms exhibit the steep uptakes at the very low relative pressure range (P/P0 < 0.01), indicating the presence of abundant micropores, whereas the isotherm of ANPC-1-900-0.25 has an evident hysteresis loop at the medium-to-high relative pressure range (P/P0 = 0.40–0.95), suggesting the presence of many mesopores in ANPC-1-900-0.25; hence, the N2 adsorption/desorption isotherms of ANPC-1-800-0, ANPC-1-800-0.25, ANPC-1-800-1 and ANPC-1-700-0.25 fall into the category of the Type I isotherm, while the isotherm of ANPC-1-900-0.25 belongs to the Type I isotherm with the Type H4 hysteresis loop.45,46 Fig. 3b shows the pore width distribution curves of the five ANPC-1 materials based on the DFT model. Apart from ANPC-1-800-1, the other four ANPC-1 materials possess a substantial number of micropores: the micropores of ANPC-1-800-0, ANPC-1-800-0.25 and ANPC-1-700-0.25 are mainly distributed within the two ranges of 0.7–1 nm and <0.6 nm, while the micropores of ANPC-1-900-0.25 are primarily distributed between 0.7 and 1 nm, indicating that higher temperature helps intensify the activation process and thus results in the enlargement of pore width. ANPC-1-800-1 has the smallest micropore volume among these five ANPC-1 materials, due largely to the pore blocking by the undue nitrogen dopant.47 As regards mesopores, ANPC-1-800-1 and ANPC-1-700-0.25 have the smallest quantities of mesopores whereas ANPC-1-900-0.25 owns the largest quantities of mesopores. It could be deduced that the activation/doping temperature and the mass ratio between the carbon and nitrogen precursors significantly affect the pore width distributions of the materials. Fig. 3c shows the N2 adsorption/desorption isotherms of the ANPC-2 materials. These isotherms each exhibit the characteristic Type I curves, indicating the existence of a good many micropores in all the five ANPC-2 materials.20 ANPC-2-900-6 has the maximum N2 uptake amongst the five materials, implying that ANPC-2-900-6 possesses the largest specific surface area.30 Fig. 3d exhibits the pore width distribution curves of the five ANPC-2 materials based on the DFT model. The five materials have the similar pore width distribution profiles, albeit with various values. Obviously, the specific surface areas and pore width distributions of the ANPC-2 materials are dependent upon both the secondary heat treatment temperatures and the mass ratios of melamine to APC.
To further examine the effects of temperature and melamine on surface area and porosity, the surface and pore properties of the ANPC-1 and ANPC-2 materials based upon the corresponding adsorption/desorption isotherms are listed in Table S1.† With respect to the five ANPC-1 materials, the BET specific surface areas and pore volumes of ANPC-1-800-0, ANPC-1-800-0.25 and ANPC-1-800-1 decrease with the increase in the mass ratio of melamine to anthracite (0 → 0.25 → 1) at the same activation/doping temperature (800 °C). Based upon the t-plot method, the changes in the micropore surface areas/volumes of the three materials present the same trend, indicating melamine tends to block up micropore structures and therefore reduces surface area and porosity.35 Under the fixed mass ratio of melamine to anthracite (0.25), the BET specific surface areas and pore volumes of ANPC-1-700-0.25, ANPC-1-800-0.25 and ANPC-1-900-0.25 increase with the increase in the activation/doping temperature (700 → 800 → 900 °C). ANPC-1-800-0.25 has the maximum micropore surface area/volume, whereas the micropore surface area and micropore volume of ANPC-1-900-0.25 decrease to approximately 1/2 and 1/3 of its BET specific surface area and pore volume, respectively, indicating that the micropore network tends towards collapse and undergoes conversion into the mesopore morphology owing to the excessively high activation/doping temperature.8 In regard to the five ANPC-2 materials, the BET specific surface areas, pore volumes and micropore surface areas/volumes of the materials vary according to the secondary heat treatment temperature (800–1000 °C) and the mass ratio of melamine to APC (4–8) and reach the maximum at the medium temperature (900 °C) and the medium mass ratio (6). During the two-step activation/doping process, the first step towards APC leads to the construction of a highly exposed nanopore structure with large specific surface area, which provides abundant sites for accommodating nitrogen-containing functional groups. The second step, moreover, combining the ball milling method with the high-temperature doping treatment, allows the pyrolysis of melamine to take place within the high-surface-area nanopore framework. The mechanochemical ball milling could motivate the atomic rearrangement of material surface,19 resulting in the intense interaction between melamine molecules and APC in the first place. Subsequently, melamine decomposed and generated numerous nitrogen-containing species that reacted with carbon at the raising temperature, thereby effectively doping nitrogen atoms into the carbon matrix.48 Accordingly, this two-step process allows for much more melamine employed for doping without causing marked pore shrinkage than the one-step process, which is favourable for some applications that demand high nitrogen concentrations such as ORR. On the contrary, the one-step activation/doping process, in which materials are deficient in nanopore structures prior to doping, could lead to poor pore development and pore blockage if melamine is overdose (ANPC-1-800-1).
Not all the surface area or pore structure of materials play a part in an electrochemical process since the size of electrolyte ions is the key. Given that the hydrated diameters of common electrolyte ions K+, OH− and SO42− are 0.6–0.7 nm,49,50 only pores with width >0.7 nm are accessible to these electrolyte ions, thus forming double-layer capacitance or triple phase boundaries. In other words, the micropores having the width exceeding 0.7 nm could be termed effective micropores.51 Table 1 gives the segmented specific surface areas and pore volumes of the ANPC-1 and ANPC-2 materials based on the DFT model. In comparison to Table S1,† the calculated values of specific surface areas and pore volumes obtained from the BET and DFT models are slightly different, but the change tendencies are consistent between the two models. In the case of ANPC-1, the specific surface areas and pore volumes of the effective micropores (width: 0.7–2 nm) and mesopores (width: 2–50 nm) have the positive correlation with the activation/doping temperature yet the negative correlation with the mass ratio of melamine to anthracite: ANPC-1-900-0.25 > ANPC-1-800-0 > ANPC-1-800-0.25 > ANPC-1-700-0.25 ≫ ANPC-1-800-1. Among the five ANPC-2 materials, ANPC-2-900-6 has the largest specific surface area and pore volume of the effective micropores while ANPC-2-1000-6 has the largest specific surface area and pore volume of mesopores. Specific surface areas and pore volumes of the effective micropores and mesopores determine the availability and potentiality of charge storage capacity, reaction sites and mass transport pathways, thereby acting as decisive factors in the electrochemical performance of supercapacitors and electrocatalysts.
| Material | SDFT (m2 g−1) | S0–0.7nm (m2 g−1) | S0.7–2nm (m2 g−1) | S2–50nm (m2 g−1) | VDFT (cm3 g−1) | V0–0.7nm (cm3 g−1) | V0.7–2nm (cm3 g−1) | V2–50nm (cm3 g−1) |
|---|---|---|---|---|---|---|---|---|
| a SDFT: DFT specific surface area; S0–0.7nm: specific surface area of micropores with width of 0–0.7 nm; S0.7–2nm: specific surface area of micropores with width of 0.7–2 nm; S2–50nm: specific surface area of mesopores; VDFT: DFT total pore volume; V0–0.7nm: pore volume of micropores with width of 0–0.7 nm; V0.7–2nm: pore volume of micropores with width of 0.7–2 nm; V2–50nm: pore volume of mesopores. | ||||||||
| ANPC-1-800-0 | 2356.73 | 386.33 | 1269.87 | 700.53 | 1.239 | 0.103 | 0.635 | 0.501 |
| ANPC-1-800-0.25 | 2074.85 | 575.25 | 1078.05 | 421.55 | 0.962 | 0.158 | 0.508 | 0.296 |
| ANPC-1-800-1 | 1396.43 | 924.94 | 380.16 | 91.33 | 0.507 | 0.253 | 0.172 | 0.082 |
| ANPC-1-700-0.25 | 1958.58 | 786.98 | 1007.32 | 164.28 | 0.778 | 0.210 | 0.461 | 0.107 |
| ANPC-1-900-0.25 | 2306.74 | 325.44 | 1242.36 | 738.94 | 1.505 | 0.076 | 0.670 | 0.759 |
| ANPC-2-900-4 | 1397.75 | 319.05 | 705.65 | 373.05 | 0.740 | 0.084 | 0.372 | 0.284 |
| ANPC-2-900-6 | 2263.23 | 505.28 | 1308.52 | 449.43 | 1.190 | 0.133 | 0.707 | 0.350 |
| ANPC-2-900-8 | 1672.08 | 463.28 | 846.62 | 362.18 | 0.856 | 0.123 | 0.448 | 0.285 |
| ANPC-2-800-6 | 1919.27 | 483.13 | 965.27 | 470.87 | 0.948 | 0.125 | 0.489 | 0.334 |
| ANPC-2-1000-6 | 2165.34 | 488.74 | 1060.76 | 615.84 | 1.172 | 0.120 | 0.568 | 0.484 |
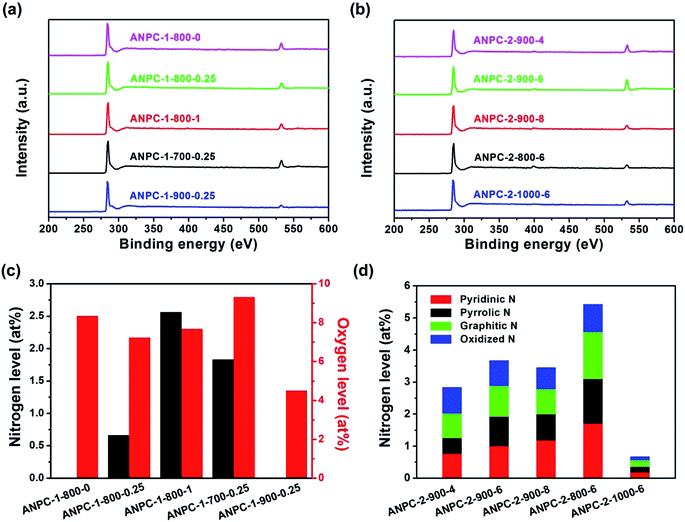
In addition to surface roughness and pore width distributions, surface chemical compositions and states, which could be investigated by XPS, also exert a considerable influence on the electrochemical capabilities of materials. Fig. 4a and b show the XPS survey spectra of the ANPC-1 and ANPC-2 materials, respectively. The XPS spectra of all the materials exhibit strong C peaks (centered at ∼285 eV) and relatively weak O peaks (centered at ∼532 eV), whereas the very weak N peaks (centered at ∼400 eV) could only be observed in the XPS spectra of ANPC-1-800-1 and the ANPC-2 materials (except ANPC-2-1000-6), indicating that melamine dosage and heating temperature have a major impact on the nitrogen doping concentrations. Fig. 4c shows the nitrogen and oxygen levels of the ANPC-1 materials. Among the five materials, ANPC-1-800-1 (the largest mass ratio of melamine to anthracite) has the highest nitrogen level (2.56 at%), while ANPC-1-800-0 that dispenses with melamine and ANPC-1-900-0.25 have no detectable nitrogen content. The high-resolution XPS N 1s spectra of the ANPC-1 materials that contain detectable nitrogen concentrations (i.e. ANPC-1-800-0.25, ANPC-1-800-1 and ANPC-1-700-0.25) could be all deconvoluted into four peaks corresponding to pyridinic, pyrrolic, graphitic and oxidized nitrogens (Fig. S2†). The nitrogen levels of ANPC-1-700-0.25, ANPC-1-800-0.25 and ANPC-1-900-0.25 are 1.83, 0.66 and 0 at%, respectively, showing that the high activation/doping temperature gives rise to the dissipation of nitrogen. Likewise, the oxygen levels of the ANPC-1 materials decrease (9.32 → 7.68 → 4.50 at%) with the increase in the activation/doping temperature (700 → 800 → 900 °C). Heteroatoms are capable of bringing about faradaic pseudocapacitances, which, together with double-layer capacitances, contribute to the overall capacitances of the ANPC-1 materials.34 Fig. 4d shows the nitrogen levels and the atomic percentages of different types of nitrogen of the ANPC-2 materials. Consistently, the overall nitrogen doping concentrations of the ANPC-2 materials decrease (5.42 → 3.67 → 0.67 at%) with the increase in the secondary heat treatment temperature (800 → 900 → 1000 °C). The atomic percentages of different types of nitrogen in each material are obtained from the respective high-resolution XPS spectra. As shown in Fig. S3,† all of the high-resolution XPS N 1s spectra of the five ANPC-2 materials could be deconvoluted into four peaks, corresponding to pyridinic N (398.5 eV), pyrrolic N (400.1 eV), graphitic N (401.0 eV) and oxidized N (403.5 eV).7 As mentioned above, pyridinic N and graphitic N are closely associated with capacitive capabilities and ORR electrocatalytic activities of N-doped carbons.32,33
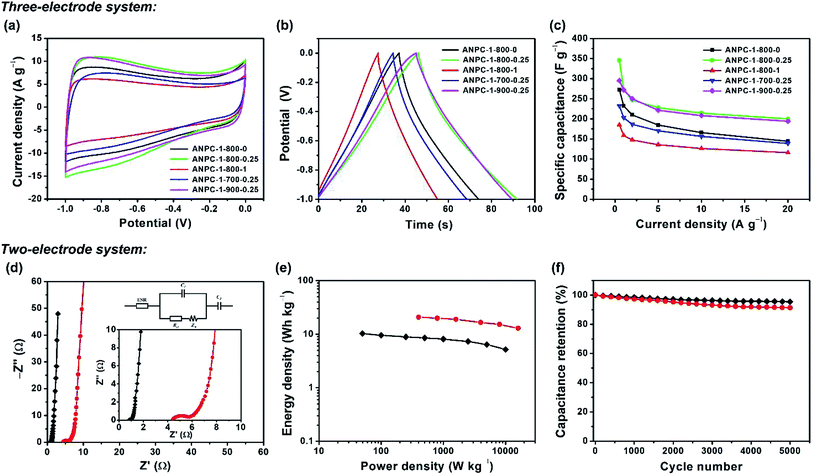
In light of the superior surface and pore properties, the capacitive capabilities of the ANPC-1 materials as supercapacitor electrodes are determined in a three-electrode system (using an alkaline aqueous electrolyte – KOH) and a two-electrode system (using both KOH and a neutral aqueous electrolyte – Na2SO4). Fig. 5a shows the CV curves of the five ANPC-1 materials at a scan rate of 50 mV s−1 within the potential window between −1.0 and 0 V. All the CV curves present quasi-rectangular shapes, which are characteristic of electrostatic double-layer capacitance. Fig. 5b shows the GCD curves of the ANPC-1 materials at a charge/discharge current density of 5.0 A g−1 between −1.0 and 0 V. All the GCD curves exhibit quasi-symmetric triangular shapes that are indicative of good charge/discharge reversibility. At the scan rate of 50 mV s−1 or the current density of 5.0 A g−1, ANPC-1-800-0.25 has the largest area encircled by its CV curve or the longest discharging time, ANPC-1-900-0.25 comes second while ANPC-1-800-1 owns the smallest encircled area or the shortest discharging time according to their respective CV and GCD curves, indicating that ANPC-1-800-0.25 has the largest specific capacitance and yet ANPC-1-800-1 has the smallest value at the aforesaid scan rate or current density. The respective CV and GCD curves of each ANPC-1 material at six other scan rates (5, 10, 20, 80, 100 and 200 mV s−1) and five other charge/discharge current densities (0.5, 1.0, 2.0, 10 and 20 A g−1) are shown in Fig. S4.† All the CV curves could keep quasi-rectangular forms even though the scan rate reaches as high as 200 mV s−1, implying the rapid ionic diffusion and efficient charge transport existing within the nanopore structures of the five ANPC-1 materials. The specific capacitance values of each ANPC-1 material at different charge/discharge current densities could be calculated based on the discharging time from the corresponding GCD curves (eqn (1)), as exhibited in Fig. 5c. The specific capacitance of ANPC-1-800-0.25 attains a maximum of 346.0 F g−1 at the current density of 0.5 A g−1 and is capable of maintaining above 200.0 F g−1 at a high current density of 20 A g−1, presenting a good rate capability of ANPC-1-800-0.25. Compared to other coal-based or bio-derived porous carbonaceous materials (Table S2†), ANPC-1-800-0.25 has a superior capacitive capability. At the charge/discharge current densities other than 0.5 A g−1, there is very little difference in specific capacitance between ANPC-1-800-0.25 and ANPC-1-900-0.25. It is worth noting that ANPC-1-800-0.25 has the higher heteroatom level than ANPC-1-900-0.25 (Fig. 4c) whereas ANPC-1-900-0.25 has the larger specific surface area and pore volume of effective micropores and mesopores than ANPC-1-800-0.25 (Table 1), but these discrepancies between the two materials are not large; as a consequence, a balance is achieved between the psudocapacitive contribution (from the heteroatom doping) and the double-layer capacitive contribution (from the interface roughness). By comparison, ANPC-1-800-1 owns the smallest specific capacitance value at every charge/discharge current density among the five ANPC-1 materials. Despite the fact that ANPC-1-800-1 possesses the second highest heteroatom level (Fig. 4c), its combined specific surface area (471.49 cm2 g−1) of the effective micropores and mesopores is merely 31.4% of that (1499.60 cm2 g−1) of ANPC-1-800-0.25 and 23.8% of that (1981.30 cm2 g−1) of ANPC-1-900-0.25 (Table 1). It follows that the rising overall specific capacitance of ANPC-1-800-1 due to the extra pseudocapacitance is seriously suppressed by its deficient double-layer capacitance. Hence, in the one-step activation/doping process (i.e. the preparation of ANPC-1), a moderate amount of melamine could contribute to additional pseudocapacitance without significantly sacrificing specific surface area and pore volume, while more-than moderate melamine could cause pore blockage and greatly undermine the pseudocapacitance contribution. So does temperature: the activation/doping temperature at 900 °C results in the nearly complete loss (undetectable amount) of nitrogen atoms of ANPC-1-900-0.25 (Fig. 4c). As a consequence, larger quantities of melamine or higher activation/doping temperatures were not explored for the ANPC-1 materials.
To evaluate the electrochemical performance of the ANPC-1 materials in a supercapacitor, ANPC-1-800-0.25 was selected to set up the two-electrode system, using 6 M KOH and 1 M Na2SO4 solutions separately as aqueous electrolytes. Fig. S5a† shows the CV curves of the ANPC-1-800-0.25//ANPC-1-800-0.25 supercapacitor at different scan rates in 6 M KOH. All the CV curves, regardless of scan rates, are capable of retaining quasi-rectangular shapes, establishing that the supercapacitor composed of ANPC-1-800-0.25 is typical of double-layer capacitance with a rapid charging/discharging capability. Fig. S5b† shows the GCD curves of the ANPC-1-800-0.25//ANPC-1-800-0.25 supercapacitor at different charge/discharge current densities in 6 M KOH. The GCD curves of the supercapacitor ranging from the low to high current densities all present isosceles triangular forms, which are indicative of its ideal electrostatic double-layer capacitive behaviour, high reversibility and low charge transport resistance. According to eqn (2), the specific capacitance values of the ANPC-1-800-0.25//ANPC-1-800-0.25 supercapacitor were calculated to be 68.2, 64.0, 61.0, 58.0, 52.3 and 46.3 F g−1 at current densities of 0.2, 0.5, 1.0, 2.0, 5.0 and 10 A g−1 in 6 M KOH, respectively, as presented in Fig. S5c.† The specific capacitance at 10 A g−1 makes up 67.9% of that at 0.2 A g−1, exhibiting the fine rate capability of the supercapacitor.
Supercapacitors are able to acquire wider voltage windows by employing Na2SO4 as an aqueous electrolyte because the stronger solvation energy of Na+ cations and SO42− anions can bring about the higher voltage for water splitting in Na2SO4 than in KOH.10 Fig. S6a† shows the CV curves of the ANPC-1-800-0.25//ANPC-1-800-0.25 supercapacitor with various voltage windows at a scan rate of 50 mV s−1. The CV curves can maintain the quasi-rectangular shapes beyond the voltage window of 1 V, indicating the electrostatic double-layer capacitance still dominates in the supercapacitor. When the voltage increases to 1.8 V, however, both the anodic and cathodic current densities increase markedly as the water splitting reaction occurs rapidly.41 For this reason, the voltage window of the supercapacitor using 1 M Na2SO4 as the electrolyte is selected as 1.6 V. Fig. S6b† shows the CV curves of the ANPC-1-800-0.25//ANPC-1-800-0.25 supercapacitor at different scan rates, all being able to present quasi-rectangular forms. Fig. S6c† exhibits the GCD curves of the ANPC-1-800-0.25//ANPC-1-800-0.25 supercapacitor at different charge/discharge current densities. The GCD curves are quasi-symmetrical, with the obvious iR drops, suggesting that the intrinsic charge-transfer resistance using the Na2SO4 aqueous electrolyte is relatively high.9 Based on eqn (2), the specific capacitances of the ANPC-1-800-0.25//ANPC-1-800-0.25 supercapacitor in 1 M Na2SO4 were calculated to be 58.4, 55.9, 53.1, 46.3 and 42.7 F g−1 at current densities of 0.5, 1.0, 2.0, 5.0 and 10 A g−1, respectively (Fig. S6d†), each being smaller than its counterpart in 6 M KOH. In addition to the higher interface resistance, the decrease in specific capacitance in Na2SO4 arises out of less accessible surface area due to the larger hydrated diameter of Na+ ions (0.72–0.9 nm).49,50
EIS experiments were conducted to further investigate the charge-transfer resistance of the supercapacitor in both the alkaline and neutral electrolytes. Fig. 5d shows the Nyquist plot of the ANPC-1-800-0.25//ANPC-1-800-0.25 supercapacitor over the frequency range of 105 to 10−2 Hz in 6 M KOH and 1 M Na2SO4. The equivalent circuit model (Fig. 5d inset) contains equivalent series resistance (ESR), charge transfer resistance Rct, Warburg impedance ZW, and double-layer capacitance C.52–54 Almost vertical lines in the low-frequency regions reflect the distinguishing characteristics of capacitive behaviours in both the electrolytes.9 In the high-frequency regions, as magnified in the inset of Fig. 5d, it can be noted that Na2SO4 has an obviously bigger quasi-semicircle in contrast to KOH, indicating the charge-transfer resistance at the interface between the Na2SO4 electrolyte and the ANPC-1 electrode is higher, which is consistent with the comparison between the iR drops of the two electrolytes (Fig. S5b and c†).9 Based on the real axial intercepts of the Nyquist plot,29 the ESR values of the supercapacitor using 6 M KOH and 1 M Na2SO4 are 0.81 and 4.41 Ω, respectively, further confirming that the intrinsic ohmic resistance in Na2SO4 is higher than in KOH. In spite of the higher internal resistance and the lower specific capacitance, the voltage window of the supercapacitor employing Na2SO4 is larger and therefore its energy density is markedly higher than when KOH is used because energy density is directly proportional to square of voltage change (eqn (3)). Fig. 5e shows the dependence of energy densities on power densities, i.e., the Ragone plot, of the supercapacitor using 6 M KOH and 1 M Na2SO4. At the power density of 0.5 kW kg−1, the energy densities of the supercapacitor in Na2SO4 and KOH were calculated to be 20.5 and 8.5 W h kg−1, respectively. Notably, the energy densities at the corresponding power densities of the supercapacitor in 1 M Na2SO4 are all higher than in 6 M KOH. Fig. 5f show the cycling stabilities of the ANPC-1-800-0.25//ANPC-1-800-0.25 supercapacitor at a constant current density of 5 A g−1 in 6 M KOH and 1 M Na2SO4. The specific capacitances can retain 95.4% and 91.3% of the starting values after 5000 charge/discharge cycles in KOH and Na2SO4, respectively, proving good cycling stability of the supercapacitor in both electrolytes.
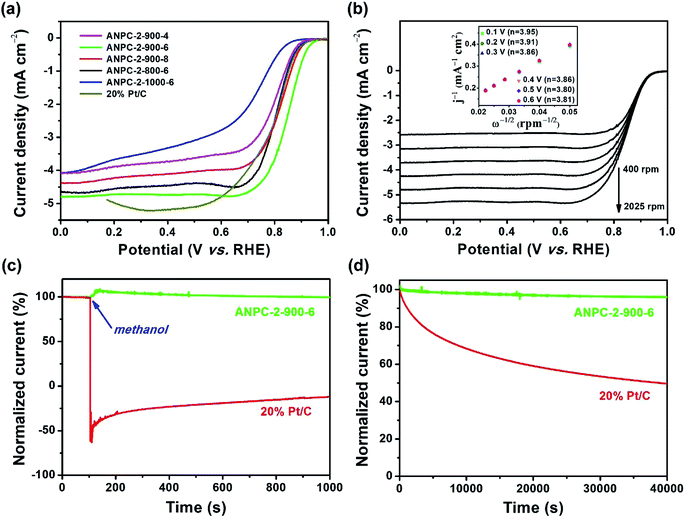
With relatively high doping concentrations of nitrogen and large surface areas/pore volumes, the ANPC-2 materials can act as potential ORR electrocatalysts. Fig. 6a shows the LSV curves of ANPC-2-900-4, ANPC-2-900-6, ANPC-2-900-8, ANPC-2-800-6 and ANPC-2-1000-6 at a rotation rate of 1600 rpm in O2 saturated 0.1 M KOH, for comparison with the benchmark JM 20% Pt/C catalyst. Among the five ANPC-2 materials, ANPC-2-900-6 presents the highest ORR electrocatalytic activity in terms of onset potential (0.96 V vs. RHE), half-wave potential (0.85 V vs. RHE) and limiting current density (4.80 mA cm−2), which is also a noticeable improvement on previous reports on coal-based ORR electrocatalysts55,56 and becomes comparable to some metal/nitrogen/carbon composite catalysts.57–59 Compared to the Pt/C catalyst, the onset and half-wave potentials of ANPC-2-900-6 are superior to those of Pt/C, whereas the limiting current density of ANPC-2-900-6 is slightly lower than that of the benchmark electrocatalyst in the potential range from 0.2 to 0.6 V vs. RHE. It could be indicated that either the smaller (ANPC-2-900-4) or the larger (ANPC-2-900-8) amount of melamine could not reach the optimal number of active sites while the excessively high temperature (ANPC-2-1000-6) would cause a dramatic decrease in the nitrogen concentration, resulting in the inferior ORR electrocatalytic performance. Fig. 6b shows the LSV curves of ANPC-2-900-6 at different rotation rates in O2 saturated 0.1 M KOH. According to the K–L equation (eqn (5)), the electron-transfer numbers of the ANPC-2-900-6-catalyzed ORR were calculated to be 3.95, 3.91, 3.86, 3.86, 3.80 and 3.81 at potentials of 0.1, 0.2, 0.3, 0.4, 0.5 and 0.6 V vs. RHE, respectively, as shown in the inset of Fig. 6b. Therefore, the average electron-transfer number is 3.87, showing that the ORR catalyzed by ANPC-2-900-6 predominantly undergoes the efficient four-electron pathway. Fig. S7† shows the electron-transfer numbers and peroxide yields of ANPC-2-900-6 and 20% Pt/C obtained from the RRDE measurements. The peroxide yield of ANPC-2-900-6 was calculated to be less than 10% across the overall potentials (0–1.0 V). The electron-transfer number of ANPC-2-900-6 surpasses 3.80 at the potentials ranging from 0 to 1.0 V vs. RHE, which is consistent with the K–L result. Fig. 6c and d show the chronoamperograms of ANPC-2-900-6 and 20% Pt/C at an applied constant potential of 0.7 V vs. RHE. To compare the methanol-tolerant capabilities of ANPC-2-900-6 and Pt/C, 1 M methanol is added at 100 s (Fig. 6c), after which the current generated by Pt/C immediately plummets to zero and continues increasing towards the opposite direction, indicating the ORR is replaced with the methanol oxidation reaction, whereas the current produced by ANPC-2-900-6 remains almost unchanged, showing that methanol cannot interfere with the ORR catalyzed by ANPC-2-900-6. This result can be further substantiated by comparing the CV curves before and after the addition of methanol, as shown in Fig. S8.† After adding methanol, the CV shape of ANPC-2-900-6, with the anodic peak (at ∼0.8 V vs. RHE) ascribable to the ORR, keeps nearly invariable, while the overwhelming cathodic peak current appears in the CV curve of the Pt/C catalyst, which could be attributed to the methanol oxidation. Current retention, a measure of activity durability of catalysts, was investigated by taking the chronoamperometric experiments (Fig. 6d). After the continuous operations over 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s, 95.9% and 49.6% of the currents were retained for ANPC-2-1000-6 and Pt/C, respectively, showing the good working stability of the former catalyst.
000 s, 95.9% and 49.6% of the currents were retained for ANPC-2-1000-6 and Pt/C, respectively, showing the good working stability of the former catalyst.
Conclusions
We have carried out a systematic study of the template-free preparation of anthracite-based nitrogen-doped nanoporous carbons by the one-step or two-step activation/doping process. By regulating heating temperature and nitrogen dosage, pore width distributions and nitrogen concentrations could be optimized. The improved electrochemical performance of the carbonaceous materials can expand the ‘repertoire’ in terms of supercapacitor electrodes and fuel cell cathodic catalysts. At least, we have seen the coal-based carbons prepared by this synthetic strategy can produce superior current/power/energy/stability capabilities to many other analogous materials. This study can, therefore, advance the clean non-fuel utilization of earth-abundant coals that are being applied to the low-carbon energy storage and conversion.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research has been supported by the National Natural Science Foundation of China (51702358) and the Natural Science Foundation of Jiangsu Province (BK20170281). We thank the Advanced Analysis and Computation Center (AACC) of China University of Mining and Technology (CUMT) for the TEM, SEM, Raman and XPS characterizations. J.Q., P.B. and W.Z. receive the ESI doctoral studentships of CUMT. L.X. holds the Jiangsu Specially-Appointed Professorship.References
- C. Hu and L. Dai, Adv. Mater., 2017, 29, 1604942 CrossRef PubMed.
- A. A. Gewirth, J. A. Varnell and A. M. DiAscro, Chem. Rev., 2018, 118, 2313–2339 CrossRef CAS PubMed.
- M. H. Sun, S. Z. Huang, L. H. Chen, Y. Li, X. Y. Yang, Z. Y. Yuan and B. L. Su, Chem. Soc. Rev., 2016, 45, 3479–3563 RSC.
- Q. Yi, W. Li, J. Feng and K. Xie, Chem. Soc. Rev., 2015, 44, 5409–5445 RSC.
- F. Tong, W. Jia, Y. Pan, J. Guo, L. Ding, J. Chen and D. Jia, RSC Adv., 2019, 9, 6184–6192 RSC.
- F. Wang, X. Wu, X. Yuan, Z. Liu, Y. Zhang, L. Fu, Y. Zhu, Q. Zhou, Y. Wu and W. Huang, Chem. Soc. Rev., 2017, 46, 6816–6854 RSC.
- L. Xie, G. Sun, F. Su, X. Guo, Q. Kong, X. Li, X. Huang, L. Wan, W. Song, K. Li, C. Lv and C. M. Chen, J. Mater. Chem. A, 2016, 4, 1637–1646 RSC.
- Q. Zhang, K. Han, S. Li, M. Li, J. Li and K. Ren, Nanoscale, 2018, 10, 2427–2437 RSC.
- G. Zhao, C. Chen, D. Yu, L. Sun, C. Yang, H. Zhang, Y. Sun, F. Besenbacher and M. Yu, Nano Energy, 2018, 47, 547–555 CrossRef CAS.
- K. Fic, G. Lota, M. Meller and E. Frackowiak, Energy Environ. Sci., 2012, 5, 5842–5850 RSC.
- B. Krüner, A. Schreiber, A. Tolosa, A. Quade, F. Badaczewski, T. Pfaff, B. M. Smarsly and V. Presser, Carbon, 2018, 132, 220–231 CrossRef.
- M. Shao, Q. Chang, J. P. Dodelet and R. Chenitz, Chem. Rev., 2016, 116, 3594–3657 CrossRef CAS PubMed.
- C. Zhang, N. Mahmood, H. Yin, F. Liu and Y. Hou, Adv. Mater., 2013, 25, 4932–4937 CrossRef CAS PubMed.
- G. Han, Y. Liu, J. Gao, L. Han, H. Cao, X. Wang, X. Wu and B. Li, ACS Sustainable Chem. Eng., 2018, 7, 2107–2115 CrossRef.
- J. Zhang, Z. Zhao, Z. Xia and L. Dai, Nat. Nanotechnol., 2015, 10, 444–452 CrossRef CAS PubMed.
- M. K. Hoque, J. A. Behan, S. N. Stamatin, F. Zen, T. S. Perova and P. E. Colavita, RSC Adv., 2019, 9, 4063–4071 RSC.
- L. Chen, Z. Chen, Y. Kuang, C. Xu, L. Yang, M. Zhou, B. He, M. Jing, Z. Li, F. Li, Z. Chen and Z. Hou, ACS Appl. Mater. Interfaces, 2018, 10, 27047–27055 CrossRef CAS PubMed.
- Z. Tang, Z. Pei, Z. Wang, H. Li, J. Zeng, Z. Ruan, Y. Huang, M. Zhu, Q. Xue, J. Yu and C. Zhi, Carbon, 2018, 130, 532–543 CrossRef CAS.
- J. Qi, W. Zhang and L. Xu, Chem.–Eur. J., 2018, 24, 18097–18105 CrossRef CAS PubMed.
- E. Hao, W. Liu, S. Liu, Y. Zhang, H. Wang, S. Chen, F. Cheng, S. Zhao and H. Yang, J. Mater. Chem. A, 2017, 5, 2204–2214 RSC.
- J. B. Xu and T. S. Zhao, RSC Adv., 2013, 5, 16–24 RSC.
- M. Liu, J. Niu, Z. Zhang, M. Dou and F. Wang, Nano Energy, 2018, 51, 366–372 CrossRef CAS.
- T. Pei, F. Sun, J. Gao, L. Wang, X. Pi, Z. Qie and G. Zhao, RSC Adv., 2018, 8, 37880–37889 RSC.
- L. Liu, G. Zeng, J. Chen, L. Bi, L. Dai and Z. Wen, Nano Energy, 2018, 49, 393–402 CrossRef CAS.
- S. Dutta, A. Bhaumik and K. C. W. Wu, Energy Environ. Sci., 2014, 7, 3574–3592 RSC.
- J. Chmiola, G. Yushin, R. Dash and Y. Gogotsi, J. Power Sources, 2006, 158, 765–772 CrossRef CAS.
- J. Wu, Z. Pan, Y. Zhang, B. Wang and H. Peng, J. Mater. Chem. A, 2018, 6, 12932–12944 RSC.
- K. Gong, F. Du, Z. Xia, M. Durstock and L. Dai, Science, 2009, 323, 760–764 CrossRef CAS PubMed.
- Y. Li, G. Wang, T. Wei, Z. Fan and P. Yan, Nano Energy, 2016, 19, 165–175 CrossRef CAS.
- F. H. Kuok, H. H. Chien, C. C. Lee, Y. C. Hao, I. S. Yu, C. C. Hsu, I. C. Cheng and J. Z. Chen, RSC Adv., 2018, 8, 2851–2857 RSC.
- D. Guo, R. Shibuya, C. Akiba, S. Saji, T. Kondo and J. Nakamura, Science, 2016, 351, 361–365 CrossRef CAS PubMed.
- Q. Lv, W. Si, J. He, L. Sun, C. Zhang, N. Wang, Z. Yang, X. Li, X. Wang, W. Deng, Y. Long, C. Huang and Y. Li, Nat. Commun., 2018, 9, 3376 CrossRef PubMed.
- N. Wang, B. Lu, L. Li, W. Niu, Z. Tang, X. Kang and S. Chen, ACS Catal., 2018, 8, 6827–6836 CrossRef CAS.
- Y. Wang, H. Xuan, G. Lin, F. Wang, Z. Chen and X. Dong, J. Power Sources, 2016, 319, 262–270 CrossRef CAS.
- X. L. Yan, H. F. Li, C. Wang, B. B. Jiang, H. Y. Hu, N. Xie, M. H. Wu, K. Vinodgopal and G. P. Dai, RSC Adv., 2018, 8, 12157–12164 RSC.
- S. Gao, Y. Tang, L. Wang, L. Liu, Z. Sun, S. Wang, H. Zhao, L. Kong and D. Jia, ACS Sustainable Chem. Eng., 2018, 6, 3255–3263 CrossRef CAS.
- Y. Wu, J. P. Cao, X. Y. Zhao, Z. Q. Hao, Q. Q. Zhuang, J. S. Zhu, X. Y. Wang and X. Y. Wei, Electrochim. Acta, 2017, 252, 397–407 CrossRef CAS.
- X. He, H. Ma, J. Wang, Y. Xie, N. Xiao and J. Qiu, J. Power Sources, 2017, 357, 41–46 CrossRef CAS.
- Q. Wang, J. Yan, Y. Wang, T. Wei, M. Zhang, X. Jing and Z. Fan, Carbon, 2014, 67, 119–127 CrossRef CAS.
- X. He, N. Zhao, J. Qiu, N. Xiao, M. Yu, C. Yu, X. Zhang and M. Zheng, J. Mater. Chem. A, 2013, 1, 9440–9448 RSC.
- L. Pan, Y. Wang, H. Hu, X. Li, J. Liu, L. Guan, W. Tian, X. Wang, Y. Li and M. Wu, Carbon, 2018, 134, 345–353 CrossRef CAS.
- M. A. Lillo-Ródenas, D. Cazorla-Amorós and A. Linares-Solano, Carbon, 2003, 41, 267–275 CrossRef.
- H. C. Lee, N. Byamba-Ochir, W. G. Shim, M. S. Balathanigaimani and H. Moon, J. Power Sources, 2015, 275, 668–674 CrossRef CAS.
- P. Chen, L. K. Wang, G. Wang, M. R. Gao, J. Ge, W. J. Yuan, Y. H. Shen, A. J. Xie and S. H. Yu, Energy Environ. Sci., 2014, 7, 4095–4103 RSC.
- M. Kruk and M. Jaroniec, Chem. Mater., 2001, 13, 3169–3183 CrossRef CAS.
- M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. W. Sing, Pure Appl. Chem., 2015, 87, 1051–1069 CAS.
- Y. Xia, G. S. Walker, D. M. Grant and R. Mokaya, J. Am. Chem. Soc., 2009, 131, 16493–16499 CrossRef CAS PubMed.
- G. A. Ferrero, A. B. Fuertes, M. Sevilla and M. M. Titirici, Carbon, 2016, 106, 179–187 CrossRef CAS.
- A. G. Volkov, S. Paula and D. W. Deamer, Bioelectrochem. Bioenerg., 1997, 42, 153–160 CrossRef CAS.
- M. Barczak, Y. Elsayed, J. Jagiello and T. J. Bandosz, Electrochim. Acta, 2018, 275, 236–247 CrossRef CAS.
- W. Zhang, J. Qi, P. Bai, H. Wang and L. Xu, New J. Chem., 2019, 43, 10878–10886 RSC.
- C. Wang, D. Wu, H. Wang, Z. Gao, F. Xu and K. Jiang, J. Colloid Interface Sci., 2018, 523, 133–143 CrossRef CAS PubMed.
- Z. Li, D. Zhao, C. Xu, J. Ning, Y. Zhong, Z. Zhang, Y. Wang and Y. Hu, Electrochim. Acta, 2018, 278, 33–41 CrossRef CAS.
- W. Lu, Z. Yuan, C. Xu, J. Ning, Y. Zhong, Z. Zhang and Y. Hu, J. Mater. Chem. A, 2019, 7, 5333–5343 RSC.
- X. Chen, X. Huang, T. Wang, S. Barwe, K. Xie, Y. U. Kayran, D. Wintrich, W. Schuhmann and J. Masa, Electrochim. Acta, 2016, 211, 568–575 CrossRef CAS.
- X. Chen, J. Wang, X. N. Huang, X. F. Zhao, P. G. Liu, B. C. He, T. Wang and J. Masa, Catal. Sci. Technol., 2018, 8, 1104–1112 RSC.
- E. Hu, J. Ning, B. He, Z. Li, C. Zheng, Y. Zhong, Z. Zhang and Y. Hu, J. Mater. Chem. A, 2017, 5, 2271–2279 RSC.
- E. Hu, X. Y. Yu, F. Chen, Y. Wu, Y. Hu and X. W. Lou, Adv. Energy Mater., 2018, 8, 1702476 CrossRef.
- C. Xu, Z. Lin, D. Zhao, Y. Sun, Y. Zhong, J. Ning, C. Zheng, Z. Zhang and Y. Hu, J. Mater. Sci., 2019, 54, 5412–5423 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra04791c |
| This journal is © The Royal Society of Chemistry 2019 |