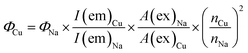Synthesis, characterization, and photoluminescent studies of three-coordinate Cu(I)–NHC complexes bearing unsymmetrically-substituted dipyridylamine ligands

Abstract

A series of heteroleptic three-coordinate Cu(I) complexes bearing monodentate N-heterocyclic carbene (NHC) ligands of the type 1,3-bis(2,6-diisopropylphenyl)imidazol-2-ylidene (IPr) and 1,3-bis(2,6-diisopropylphenyl)imidazolidin-2-ylidene (SIPr), and bidentate N-donor ligands of the type unsymmetrically-substituted dimethyl dipyridylamine (Me₂Hdpa) and bis(mesityl)biazanaphthenequinone (mesBIAN) have been synthesized. The complexes [Cu(IPr)(3,4′-Me₂Hdpa)]PF₆, 1; [Cu(IPr)(3,5′-Me₂Hdpa)]PF₆, 2; [Cu(IPr)(3,6′-Me₂Hdpa)]PF₆, 3; [Cu(IPr)(mesBIAN)]PF₆, 6; [Cu(SIPr)(3,4′-Me₂Hdpa)]PF₆, 7; [Cu(SIPr)(3,5′-Me₂Hdpa)]PF₆, 8; and [Cu(SIPr)(3,3′-Me₂Hdpa)]PF₆, 11 have been characterized by ¹H and ¹³C NMR spectroscopies, elemental analysis, cyclic voltammetry, and photophysical studies in solid and solution phase. Single crystal X-ray structures were obtained for all complexes except 11. The crystallographic data reveal a mononuclear structure for all complexes with the copper atom ligated by one C and two N atoms. The UV-Vis absorption spectra of all dipyridylamine complexes in CH₂Cl₂ show a strong ligand-centered absorption band around 250 nm and a strong metal-to-ligand charge transfer (MLCT) band around 300 nm. When irradiated with UV light, the complexes exhibit strong emission maxima at 453–482 nm with photoluminescence quantum yields (PLQY) ranging from 0.21 to 0.87 in solid state. While the PLQY values are comparable to those of the symmetrical [Cu(IPr)(Me₂Hdpa)]PF₆ complexes, a stabilizing CH–π interaction has been reduced in the current systems. In particular, complex 3 lacks any strong CH–π interaction, but emits more efficiently than 1 and 2 wherein the interactions exist. Structural data analysis was performed to clarify the role of ligands' plane angle and the NH/CH⋯F interactions to the observed light interaction of unsymmetrical [Cu(NHC)(Me₂Hdpa)]PF₆ complexes. DFT calculations were performed to assist in the assignment of the electronic structure and excited state behavior of the complexes.

---

Introduction

Photoluminescent (PL) complexes containing precious transition metals (Ru(II), Ir(III), Pt(II), etc.) have been extensively studied due to their potential application in electroluminescent devices, photochemical catalysis, OLED light displays, and solar energy conversion.^1–9 However, owing to their limited availability, toxicity, and relative cost, the substitution of these metals by more abundant alternatives is desired. In this context, d¹⁰ metals such as Cu(I) are of considerable interest. Over the last several decades, a great variety of Cu(I) complexes have been developed aiming to improve the emissive properties of Cu luminophores towards strong emission and long-lived excited states. Majority of these efforts have focused on the four-coordinate tetrahedral Cu(I) complexes with bisimine and phosphine ligands to block their non-radiative decay pathways. The flattening of the photoexcited Cu(II) complexes via a Jahn–Teller distortion promotes the formation of a five-coordinate exciplex with solvent molecules or other nucleophiles that often leads to a radiationless deactivation of the excited state.^10–16 A useful strategy to prevent the excited state configurational changes, first examined by McMillin,¹⁷ is by increasing the steric bulk of ligands at the coordination site. There has been an extensive work on the effect of bulky substituents around the tetrahedral Cu(I) coordination sphere, leading to highly emissive luminophores with long-lived excited state.^18–24 Another useful approach towards blocking the four-coordinate geometry is via bridging halides or other potential linkers in bi- and polynuclear complexes that will not be discussed in this text.^25–27

Recently, emissive three-coordinate heteroleptic Cu(I) complexes supported by bulky phosphine ligands have been reported by groups of Peters and others.^28,29 While the possibility of Jahn–Teller distortion in the excited state is eliminated in the three-coordinate geometry, the exciplex formation can still occur especially in coordinating solvents. Alternatively, Thompson,^30–33 Gaillard^34–36 and their co-workers have investigated three-coordinate mononuclear Cu(I) complexes bound to sterically challenged NHC and bidentate N-donor ligands. The choice of the ligand, guided by the high stability of Cu(I)–NHC complexes and easy modulation of the nitrogen ligand, has led to [Cu(NHC)(N^N)]X complexes (N^N = dipyridylamine and its geometrically symmetrical derivatives) with very promising luminescent properties. In their work, Gaillard and co-workers had synthesized a series of Cu(I) complexes using symmetrically-substituted Hdpa ligands bearing methyl groups on two pyridyl rings. Interestingly, the position of the methyl groups plays an important role in the luminescent properties of the complexes, with the highest and lowest quantum yields obtained using 3,3′-Me₂Hdpa and 4,4′-Me₂Hdpa ligands, respectively.

The strong emissive properties of these complexes have been assigned partly to their stable excited-state geometry that resulted from the stabilizing CH–π system interactions between the NHC and the Hdpa ligands. It could be envisioned that disrupting such stabilizing interactions in the [Cu(NHC)(Hdpa)]X complexes would affect their emissive properties. However, knowledge about the extent of their contribution to the observed photophysical activity has yet to be developed. We report herein the synthesis of a new series of cationic Cu(I) complexes bearing bulky NHC ligands (IPr, SIPr) and Me₂Hdpa ligands with methyl groups positioned unsymmetrically on two pyridyl rings (Chart 1, L1–L3). Also, we have prepared Cu(I)–NHC complexes containing Hdpa (L4) and 3,3′-Me₂Hdpa (L5) for direct comparison of chemical and photophysical properties to the unsymmetrically-substituted analogues under the same conditions. To illustrate the effect of steric challenge and rigidity on the coordination chemistry and photophysical properties of Cu(I) complexes, the bulky mesBIAN (L6) ligand has also been synthesized. The extent of stabilizing CH–π and other long-range interactions are examined by analyzing the structural parameters from single-crystal X-ray diffraction. The electrochemical and photophysical properties of these complexes are examined and compared to the Cu(I) complexes bearing unsubstituted Hdpa and symmetrically substituted Me₂Hdpa ligands. In addition, density functional theory (DFT) calculations are performed to rationalize the relationship between the electronic structure and photophysical property in these complexes.

Chart 1 Symmetrical and unsymmetrical Me₂Hdpa and NHC ligands used in this study.

Results and discussion

Synthesis of heteroleptic Cu(I) complexes

The [Cu(NHC)(N^N)]PF₆ complexes (1–12) were synthesized in a single-step reaction using [Cu(NHC)Cl], the N-donor ligand, and KPF₆ under an inert atmosphere at room temperature (Scheme 1). Both [Cu(IPr)Cl] and [Cu(SIPr)Cl] precursors were prepared according to a slightly modified Cazin–Nolan procedure using CuCl, the imidazolium/imidazolinium salt, and K₂CO₃ as a base.³⁷ Dipyridylamine ligands were obtained using a Buchwald–Hartwig coupling reaction between 2-bromopyridine and 2-aminopyridine derivatives. The optimal amount of Pd₂(dba)₃ catalyst for these syntheses was found to be 1.0 mol%, half of the amount used previously for the symmetrical Me₂Hdpa ligands.³⁴ Interestingly, some ligands such as L2 and L3 were obtained only at 20% or lower yields using 2.0 mol% catalyst loading, whereas the reduced amount of the catalyst provided great to excellent yields of all ligands.

Scheme 1 The formation of heteroleptic Cu(I) complexes via a mono-coordinate Cu–NHC intermediate.

Regarding [Cu(NHC)(N^N)]PF₆ complexes, the yield is dependent on the steric hindrance of the N-donor ligands as depicted in Table 1. However, the effect appears to be less pronounced than what is found for the symmetrical Me₂Hdpa analogues as shown by a close yield of [Cu(IPr)(L1)]PF₆ (1) and [Cu(IPr)(L2)]PF₆ (2) complexes. A clear deviation from the expected trend based on steric hindrance was found for [Cu(NHC)(L2)]PF₆ complexes that were isolated at a higher yield than those with L4 and L5 ligands. Also, the formation of [Cu(NHC)(N^N)]PF₆ complexes with bulky N-donor ligands appears to be dependent on the nature of the carbene's backbone, i.e. saturated vs. unsaturated. While both [Cu(IPr)(L3)]PF₆ (3) and [Cu(IPr)(L6)]PF₆ (6) complexes were obtained at adequate yields, no [Cu(SIPr)(L3)]PF₆ (9) and only 10% [Cu(SIPr)(L6)]PF₆ (12) formed after a two-day reaction as confirmed by ¹HNMR analysis. The synthesis of the heteroleptic Cu(I) complexes is expected to follow a two-step mechanism, wherein a mono-coordinate [Cu(NHC)]PF₆ forms initially from the removal of Cl⁻ with tenfold excess KPF₆ (Scheme 1). This was confirmed by a white solid isolated from the [Cu(IPr)Cl] and KPF₆ reaction that shows a different composition from the starting material by elemental analysis (ESI†).

Table 1 Isolated yields of heteroleptic Cu(I) complexes

Entry^a	Complex	Yield^b
a Reaction conditions: [Cu(NHC)Cl] (1 equiv.), N^N ligand (1 equiv.), KPF6 (10 equiv.), THF, stir at r.t.b Isolated yield.c Calculated from the ^1H NMR spectrum of the reaction mixture containing the product and [Cu(IPr)Cl].
1	[Cu(IPr)(L1)]PF6 (1)	77
2	[Cu(IPr)(L2)]PF6 (2)	83
3	[Cu(IPr)(L3)]PF6 (3)	62
4	[Cu(IPr)(L4)]PF6 (4)	70
5	[Cu(IPr)(L5)]PF6 (5)	53
6	[Cu(IPr)(L6)]PF6 (6)	68
7	[Cu(SIPr)(L1)]PF6 (7)	69
8	[Cu(SIPr)(L2)]PF6 (8)	85
9	[Cu(SIPr)(L3)]PF6 (9)	0
10	[Cu(SIPr)(L4)]PF6 (10)	63
11	[Cu(SIPr)(L5)]PF6 (11)	78
12	[Cu(SIPr)(L6)]PF6 (12)	∼10^c

---

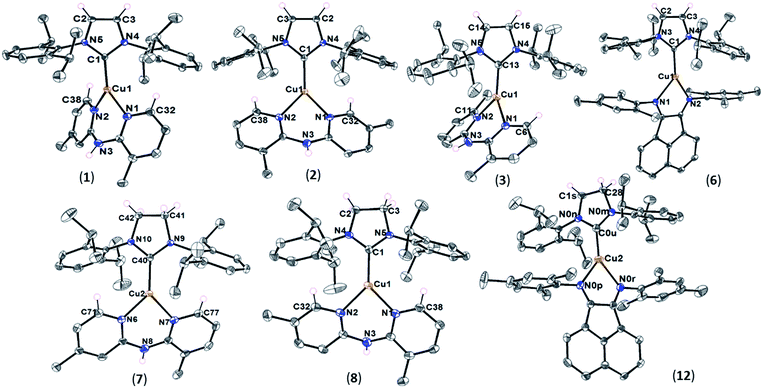
X-ray crystallography of Cu(I) complexes

Single crystals of complexes 1–3, 6–8, and 12 were obtained by slow diffusion of hexane into a solution of copper complexes in dichloromethane at room temperature. The red crystals of 12 were isolated carefully from a mixture of the complex and starting precursor, [Cu(SIPr)Cl], to further verify its formation and structure by X-ray crystallography. Also, we obtained single crystals of [Cu(SIPr)Cl] precursor from a mixture of tetrahydrofuran and hexane solution and report its crystal structure here (Fig. S1†). ORTEP diagrams of IPr- and SIPr-based complexes are shown in Fig. 1. A collection of distances and angles are presented in Table 2 with crystallographic data collection parameters summarized in Tables S1 and S2.†

Fig. 1 ORTEP diagrams of [Cu(IPr)(L1)]PF₆ (1), [Cu(IPr)(L2)]PF₆ (2), [Cu(IPr)(L3)]PF₆ (3), [Cu(IPr)(L6)]PF₆ (6), [Cu(SIPr)(L1)]PF₆ (7), [Cu(SIPr)(L2)]PF₆ (8), and [Cu(SIPr)(L6)]PF₆ (12). Only one of the cationic complexes in the unit cell are shown for 1, 7, and 12. Anions and some hydrogens are omitted for clarity. Ellipsoids are shown at the 55% probability level.

Table 2 Selected bond lengths and angles for [Cu(NHC)(N^N)]PF₆ complexes

Complex	Cu–CNHC (Å)		Cu–NN^N (Å)		CH⋯π (Å)		NH/CH⋯F^a (Å)		CNHC–Cu–NN^N (°)		Plane angle θ (deg)
a The distances have been determined only for the asymmetric unit.b The CH⋯π distances are shown only for one of the cationic complexes (Cu1) in the asymmetric unit.
[Cu(IPr)(L1)]PF6 (1)	Cu1	1.891(2)	Cu1	2.019(2)	Cu1	2.78	Cu1	2.25 (NH)	Cu1	138.23(7)	Cu1	35.52
	Cu2	1.906(2)		2.038(2)	Cu2	2.45		2.48, 2.54 (CH)		131.94(7)	Cu2	59.76
			Cu2	2.015(2)		2.70	Cu2	2.25 (NH)	Cu2	134.08(7)
				2.044(2)				2.31(CH)		135.24(7)
[Cu(IPr)(L2)]PF6 (2)		1.900(2)		2.032(2)		2.58		2.43 (NH)		136.22(7)		47.13
				2.041(2)		2.95		2.43 (CH)		134.21(7)
[Cu(IPr)(L3)]PF6 (3)		1.887(2)		2.020(2)				2.68 (CH)		134.44(7)		76.06
				2.029(2)						134.02(7)
[Cu(IPr)(L6)]PF6 (6)		1.922(3)		2.231(3)		2.53 (CHiPr)		2.32 (CHNHC)		133.86(6)		45.89
				2.062(2)		2.74 (CHMe)		2.47 (CHNHC)		147.70(6)
						2.77 (CHiPr)
						2.94 (CHace)
						2.98 (CHace)
[Cu(SIPr)(L1)]PF6 (7)	Cu1	1.893(2)	Cu1	2.026(2)	Cu1	2.74		2.26 (NH)	Cu1	130.70(8)	Cu1	38.77
	Cu2	1.917(2)		2.020(2)	Cu2	2.42		2.50 (CH)		139.25(8)	Cu2	59.59
			Cu2	2.021(2)		2.74		2.28 (CH)	Cu2	134.27(9)
				2.052(2)					Cu2	135.30(9)
[Cu(SIPr)(L2)]PF6 (8)		1.918(2)		2.045(2)		2.46		2.24 (NH)		134.13(7)		45.04
				2.046(2)		2.94		2.61 (CH)		135.57(7)
[Cu(SIPr)(L6)]PF6 (12)	Cu1	1.914(4)	Cu1	2.126(3)		2.65 (CHiPr)^b		2.26 (NH)	Cu1	138.4(1)	Cu1	48.46
	Cu2	1.914(4)		2.137(3)		2.71 (CHMe)		2.65 (CHNHC)		142.5(1)	Cu2	49.74
			Cu2	2.087(3)		2.76 (CHiPr)			Cu2	138.4(1)
				2.155(3)		2.87 (CHace)				142.7(1)
						2.92 (CHace)

---

As expected for the heteroleptic Cu(I) complexes, each Cu center is bound to the NHC and the bidentate N-donor ligand in a three-coordinate geometry. The dipyridylamine ligation in complexes 1–3, 7, and 8 results in a 6-membered chelate unlike mesBIAN that forms a 5-membered ring with Cu in 6 and 12. A common feature among the heteroleptic Cu(I) complexes in this study is the presence of long-distance interactions in their solid state. This includes, but is not limited to, the non-bonding CH⋯π interactions between the hydrogen atom(s) at the α position of the pyridyl rings and the π system of the diisopropylphenyl groups on the NHC ligands. The structures in which the calculated distance between the α hydrogen atom and the center of the NHC aromatic ring is shorter than 3.05 Å are identified to possess this interaction.³⁸ As shown in Table 2, all the dipyridylamine complexes present this interaction, except 3 that has a much longer CH⋯π distance than the cut-off. The sp²-CH⋯π interactions were considered crucial for the formation of complexes with symmetrical Me₂Hdpa ligands to an extent that [Cu(IPr)(6,6′-Me₂Hdpa)]PF₆ could not form due to the lack of α hydrogen atoms on the Hdpa ligand.³⁴ Our findings support the significance of CH⋯π interactions to the stability of the Cu(I) complexes bearing unsymmetrical Me₂Hdpa ligands as well. Nonetheless, the synthesis of [Cu(IPr)(3,6′-Me₂Hdpa)]PF₆ (3) with no sp²-CH⋯π interaction at a good yield (Table 1) indicates the contribution of other parameters to its stability.

Not surprisingly, due to the lack of α hydrogen atom with respect to nitrogen in the mesBIAN ligand, the interligand sp²-CH⋯π interactions do not exist in complexes 6 and 12. However, the presence of several aromatic rings may facilitate the sp³-CH⋯π interactions between the aliphatic hydrogens and the π systems of the NHC and diimine ligands in these complexes. Furthermore, 12 benefits from an intermolecular sp²-CH⋯π interaction between the CH groups at position 6 of the BIAN ring and the π system of the phenyl ring in SIPr (Fig. S2†). The sp³-CH⋯π interactions in 6 occur between the isopropyl groups of IPr and the aromatic mesityl substituents of mesBIAN as well as the methyl groups of mesBIAN and aromatic phenyl ring of IPr (Fig. S3†). The complexes 6 and 12, also, benefit from an intraligand interaction between the sp²-CH at positions 5 and 10 of the BIAN ring and the aromatic ring of the mesityl substituents (Fig. S2 and S3†). Additionally, the effect of NH⋯F and CH⋯F hydrogen-bonding interactions on the stability of the current heteroleptic Cu(I) systems should not be disregarded. For all the complexes in Table 2, the H⋯F distance between the F atoms of PF₆⁻ anion and the NH or sp²-CH groups of Hdpa falls within the range 2.24–2.72 Å. Since the distance is shorter than the sum of van der Waals radii of H and F (2.76 Å), the interaction can be classified as a legitimate hydrogen bond.³⁹ It should also be noted that 3 is the only Hdpa-based complex in the table in which no NH⋯F interaction was found. The significance of hydrogen-bonding to the shaping, stability, and self-assembly of organic molecules has been extensively investigated,^39–41 however, their effect on the transition metal-containing structures is far less understood. In this work, the interplay between the long-range interactions, the plan angle θ, and the light-emitting properties of the copper complexes will be elucidated via structural analysis and photophysical studies (vide infra). The θ parameter in the table describes the angle between the NHC ring and the plane formed by three nitrogen atoms in the Hdpa ligand or the plane of the mesBIAN ligand (Fig. S4†). There seem to be no direct correlation between θ and the ligand type, e.g. saturated NHC vs. unsaturated NHC or substituted Hdpa vs. unsubstituted derivatives.

Electrochemical study of Cu(I) complexes

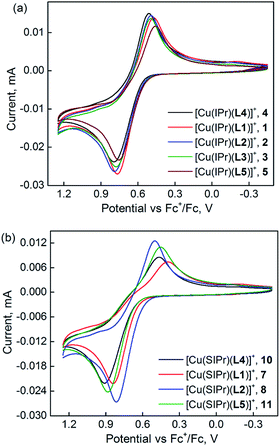
The cyclic voltammetry (CV) data were measured to investigate the electrochemical features and to estimate the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energy levels of the complexes 1–11. The electrochemical data are summarized in Table 3. As shown in Fig. 2a, all Cu–IPr complexes bearing Hdpa and its derivatives display an electrochemically quasi-reversible/reversible oxidation at 0.61–0.65 V (vs. Fc⁺/Fc), assigned to the Cu(II)/Cu(I) couple. The reversibility of this event is more prevalent for 4 and its unsymmetrical analogs shown by a linear plot of current versus the square root of scan rate (Fig. S5†). The partial reversibility was confirmed by a shift of the reduction or oxidation potentials at varying scan rates for all the Cu–IPr complexes, but is more distinct for complex 5 (Fig. S6†). On the other hand, all the Cu–SIPr complexes containing Hdpa ligand and its derivatives reveal a predominantly quasi-reversible Cu(II)/Cu(I) couple (Fig. 2b). The shape of the first oxidation peak of 4, 5, and 10 appears different in our work from that reported earlier.³⁴ While this event was irreversible and attributed to the oxidation of NH group of Hdpa ligands, we have determined a reversible/quasi-reversible couple and assigned it to a metal-centered oxidation feature. In addition to the presented data in Fig. S5 and S6,† the comparative cyclic voltammograms of the solvent and the Hdpa ligand support the assignment (Fig. S7†). A metal-based oxidation is also more consistent with a similar feature observed in the CV studies of [Ru(Hdpa)_n(bpy)_3−n]²⁺ (n = 3–0) and [Ni(Hdpa)₂(salo)]Cl complexes and with the HOMO composition in the DFT calculations (vide infra).^42,43 Nonetheless, our assessment of the irreversible reduction features at around −2.3 V and −2.5 V vs. Fc⁺/Fc in the CV of the Hdpa/Me₂Hdpa complexes is in line with the previous assignments to the Cu(I)/Cu(0) and Hdpa reduction.^34,44

Table 3 Photophysical and electrochemical data for [Cu(NHC)(N^N)]PF₆ complexes

Complex	λ^absmax^a (nm)	λ^emmax^b (nm)	E^ox1/2, ΔEp^c (V)	EPc, Epa^d (V)	HOMO/LUMO^d^,^g (eV)	PLQY/ΦPL^e	TPL^e (μs)
a Data obtained in CH2Cl2 at room temperature.b Data obtained in solid state at room temperature.c Recorded in CH2Cl2 containing 2 mM Cu(I) complexes and 0.1 M TBAPF6 at 50 mV s^−1 scan rate and 22 °C.d Recorded at 100 mV s^−1 scan rate and 22 °C.e Estimated errors ±5%.f The half-wave potential of 0 and ΔEp = Epc − Epa = 0.174 V was determined for ferrocene under the same conditions.g The values in () were calculated by the difference between the HOMO levels and the HOMO–LUMO gap obtained from the absorption edge of the UV/Vis spectra.
[Cu(IPr)(L1)]PF6 (1)	253, 302	468	0.62, 0.276^f	−2.29, 0.524	−5.32/−2.51 (−2.04)	0.48	18
[Cu(IPr)(L2)]PF6 (2)	254, 306	475	0.63, 0.278	−2.20, 0.530	−5.33/−2.60 (−2.04)	0.49	19
[Cu(IPr)(L3)]PF6 (3)	254, 307	482	0.63, 0.266	−2.22, 0.502	−5.30/−2.58 (2.03)	0.64	23
[Cu(IPr)(L4)]PF6 (4)	252, 305	453	0.65, 0.244	−2.35, 0.546	−5.35/−2.45 (−2.03)	0.21	15
[Cu(IPr)(L5)]PF6 (5)	251, 303	458	0.61, 0.267	−2.35, 0.514	−5.31/−2.45 (−1.99)	0.87	35
[Cu(IPr)(L6)]PF6 (6)	241, 321, 336	∼490	1.07, 0.364	−1.27, 1.03	−5.83/−3.53 (−3.3)	0
[Cu(SIPr)(L1)]PF6 (7)	254, 307	472	0.61, 0.425	−2.15, 0.603	−5.40/−2.65 (−2.20)	0.55	24
[Cu(SIPr)(L2)]PF6 (8)	254, 309	471	0.65, 0.294	−2.16, 0.562	−5.36/−2.64 (−2.19)	0.33	19
[Cu(SIPr)(L4)]PF6 (10)	254, 307	466	0.67, 0.298	−2.29, 0.629	−5.43/−2.51 (−2.13)	0.85	15
[Cu(SIPr)(L5)]PF6 (11)	254, 304	473	0.68, 0.376	−2.25, 0.601	−5.40/−2.55 (−2.25)	0.83	25

---

Fig. 2 Cyclic voltammogram of (a) [Cu(IPr)(Me₂Hdpa)]PF₆ and (b) [Cu(SIPr)(Me₂Hdpa)]PF₆ complexes (2.0 mM) in deaerated CH₂Cl₂/ⁿBu₄NPF₆ (0.1 M) at a scan rate of 100 mV s⁻¹ indicating Cu(II)/Cu(I) redox couple.

As expected the electron-transfer behavior of complex 6 is different from the Hdpa-containing analogs. The CV of this complex (Fig. S8†) presents a quasi-reversible Cu(II)/Cu(I) couple at 1.30 V (vs. Fc⁺/Fc) resembling the same oxidation event in the CV of Cu(I)–(aryl-BIAN) complexes bearing nitrile and phosphine co-ligands.⁴⁵ The quite large difference (0.4 V) between the oxidation and reduction waves of this couple and the substantial decrease in the cathodic peak current is likely due to some rearrangements or chemical processes during the oxidation. When continuing the cathodic scan of complex 6, two quasi-reversible reduction waves appear at −1.41 and −2.03 V (vs. Fc⁺/Fc) assigned to the Cu(I)/Cu(0) and mesBIAN/mesBIAN⁻˙ couples. The reduction potential of the ligand to its radical anion form is reasonably close to that of the free ligand reported under similar conditions.⁴⁵ While the authors did not observe this reduction couple in the cathodic scan of the bis-chelate Cu(I)–aryl-BIAN complexes, this could be due to a shorter potential window utilized than that for 6 in this study.

The onset oxidation and reduction potentials of complexes 1–11 were used to calculate the HOMO and LUMO levels according to the equation E_HOMO/LUMO = −(E_{[onset, ox/red vs. Fc⁺/Fc]} + 4.8) eV.^46,47 Since the reduction potential of the dipyridylamine complexes is close to the onset of solvent reduction, erroneous reading of the onset potential might occur. Thus, the LUMO levels were also calculated by considering the difference between their HOMO levels and the corresponding HOMO–LUMO gap determined from the absorption edge of their UV-Vis spectra. The calculated HOMO and LUMO values for complexes 1–11 in solution are listed in Table 3.

Photophysical study of Cu(I) complexes

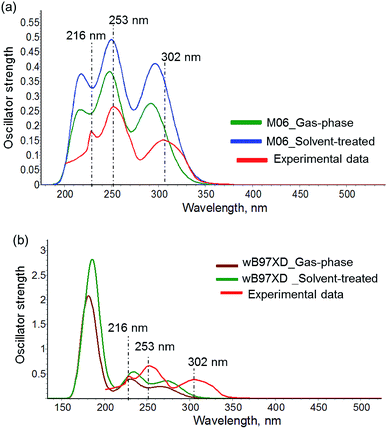
The UV-Vis absorption spectra, recorded in CH₂Cl₂, and the solid-state emission spectra of complexes 1–11 are shown in Fig. 3, S9,† and Table 3. The intense absorption bands around 251–254 nm (ε = (2.4–4.3) × 10⁴ L mol⁻¹ cm⁻¹) in the Hdpa-based complexes are attributed to the π–π* ligand-centered (LC) transitions. The relatively weaker bands around 302–309 nm (ε = (1.4–1.9) × 10⁴ L mol⁻¹ cm⁻¹) in these complexes are ascribed to the metal-to-ligand charge transfer (MLCT) transitions.³⁴ In complex 6, the π–π* LC transitions result in an intense shoulder below 250 nm beside the two equal-intensity bands at 321 nm and 336 nm (ε = 1.8 × 10⁴ L mol⁻¹ cm⁻¹) due to the spin-allowed MLCT transitions (Fig. S9a†).⁴⁸ Additionally, the broad band between 350 and 480 nm could be assigned to the intraligand π–π* charge transfer (ILCT) from the aryl groups to the naphthyl backbone and/or a low-energy MLCT band.^48,49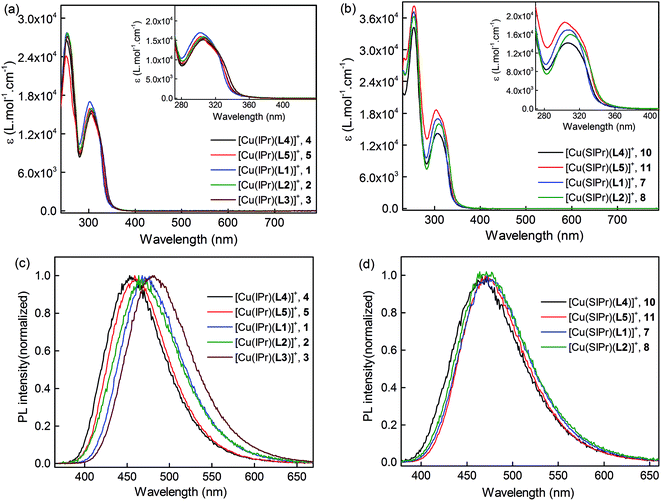

Fig. 3 (a and b) Absorption spectra of complexes 1–11 (except 6) in CH₂Cl₂ solution at room temperature. (c and d) Photoluminescent (PL) spectra of the complexes in the solid state.

The PL spectra of the complexes were recorded in solid state at room temperature using an excitation of 340 nm. As shown in Fig. 3, the Hdpa-bound complexes display broad emission spectra with PL maxima in the range of 453–482 nm. In contrast, the PL spectrum of complex 6 shows a very weak emission around 490 nm (Fig. S9†). Furthermore, the methyl substitution of the Hdpa ligands leads to the red-shifted emission maxima in Cu–IPr complexes in the order L4 < L5 < L1 < L2 < L3. In contrast, the emission pattern and PL maxima of the substituted Cu–SIPr complexes are very similar indicating that the position of methyl groups has a minimal effect on the emissive energy of these complexes. Exploring the emission and absorption profiles of 1–11, the PL quantum yields (PLQY) were estimated between 21% and 87% with emission lifetimes in the range 15–35 μs (Table 3). In this series, complex 4 exhibits the lowest yield and complexes 5, 10, and 11 show the highest quantum yields with 87% (T = 35 μs), 85% (T = 15 μs), and 83% (T = 25 μs), respectively. The calculated QY values for 4, 5, and 10 are consistent with the previous report,³⁴ however, the emission lifetime of 10 is substantially different.

Structure and light interaction relationship

Regarding the structure effect on the emission profile, different trends were found for the Cu–IPr and Cu–SIPr complexes bearing the same Hdpa ligands. While 4 is the weakest emitter among the [Cu(IPr)(N^N)]⁺ complexes, 10 has the highest QY in the [Cu(SIPr)(N^N)]⁺ series. The difference cannot be simply attributed to the greater electron-donating ability of SIPr than IPr given the reverse order of the quantum yields for 2 vs. 8 and 5 vs. 11 (Table 3). Given the PL profile of these complexes in solid state, close attention should be paid to the long-range interactions within the solid matrix. Three structural parameters relevant to the emissive properties of the Hdpa-based copper complexes are listed in Table S3.† Of these parameters, the NH/CH⋯F interactions are detrimental to PL, most likely due to inhibiting the planarization of the central nitrogen atom and change of its hybridization from sp³ to sp² during the photoexcitation. This change is necessary to access a stable triplet state and an effective emissive system. On the other hand, the CH⋯π interactions are in favor of the PL property, possibly due to enhancing the π–π* character of electronic transitions, e.g. T₁ → S₀ via the interligand CT (vide infra). Finally, the large plane angle θ has a positive impact on the emission yield by breaking the symmetry in the solid matrix and allowing the symmetry-forbidden transitions to intensify. This parameter is mostly prominent in 3, with no favorable CH⋯π interaction and with relatively long CH⋯F distances. Complex 3 displays PL with a QY of 0.64 (T = 23 s), making it the third highly emissive [Cu(IPr)(N^N)]PF₆ complex after [Cu(IPr)(3,3′-Me₂Hdp)]PF₆ and [Cu(^MeIPr^OMe)(Hdpa)]PF₆ reported by Gaillard and coworkers.^34,36 It is also worth noting that 3 possesses the largest plane angle θ among the reported [Cu(NHC)(N^N)]PF₆ complexes and those presented here (Table S3†).

Computational study of Cu(I) complexes

Density functional theory (DFT) and time-dependent DFT (TD-DFT) were used to rationalize the fundamental properties of these copper complexes and provide a theoretical foundation to explain the experimentally detected luminesce behavior. The details of the theoretical calculations are described in the ESI.† Despite the diverse range of functionals and basis sets used for copper complexes in literature that often provide good results,^50–53 the functional sensitivity of TD-DFT, especially for CT systems,⁵⁴ requires their careful screening in the luminescence studies.

Geometry optimization. The prediction of structures is always the first and most important step in computational studies, since the subsequent steps depend on its accuracy. The full geometrical optimization of complexes 1–8 and 10 was performed using three levels of theory, UB3LYP, M06, and wB97XD, and two basis sets, LANL2DZ and 6-31+G(d,p). We have avoided using the combination of effective core potential basis sets, e.g. SDD on the metal and 6-31+G(d,p) on the other elements due to a possible overestimation of binding energy.⁵³ To assess the reliability of the theoretical methods, the calculated structural parameters were compared to those obtained experimentally from X-ray crystallography. It should be noted that in comparing the crystal structure data to the gas-phase optimized DFT results the matrix effect of the solid state is neglected. This includes the long-range interactions with the PF₆ anion, possible π–π stacking, and the interactions with the solvent molecule trapped in the solid form. The quality of describing the complex's structure at a certain DFT level was evaluated by subtracting the theoretically determined bond parameter (b.p.) from its experimental counterpart using (b.p._calc − b.p._exp)/b.p._exp × 100 (Table S4†). The bond lengths and angles of the dipyridylamine-linked Cu–IPr and Cu–SIPr complexes are estimated reasonably within 5.0% using all the six functionals/basis sets combinations. The lowest over- or underestimation of the Cu–C_NHC bonds was obtained with wB97XD/6-31+G(d,p) with values between 0.2 and 1.9%, while the lowest Cu–N_N^N bond's deviation was calculated between 0.1 and 1.7% using M06/LANL2DZ. Remarkably, the CH⋯π distances were estimated with deviations ranging from 0.2 to 11.9% for all the complex ions except 3. This distance in 3 is underestimated with values between 20.0 to 34.5% using all the functionals and basis sets indicating the sensitivity of this interaction to the matrix effect in solid state (Fig. S10†). The CH⋯F hydrogen-bonding interactions between the phenyl rings of IPr or the β hydrogen atoms of pyridyl rings and F atoms seem to contribute greatly to the matrix effect and lengthening of the CH⋯π distance in complex 3 (Fig. S10†). These interactions are disregarded in the gas-phase DFT calculations, thus leading to a closer CH⋯π distances than those determined experimentally.

Electronic structure. The ground-state electronic structures of complexes 1–8, and 10 were calculated to determine the energies and composition of HOMO and LUMO. The HOMO–LUMO levels and gaps are greatly affected by the DFT methods, with hybrid functionals, UB3LYP and M06, providing smaller gaps than those obtained with dispersion-including methods such as wB97XD (Fig. S11†). The orbital energies, the HOMO–LUMO gaps, and the composition of frontier and other close lying orbitals in copper complexes are listed in Tables S5 and S6.† Different contributions from copper and Hdpa ligand to the HOMO orbitals of complexes were predicted using the three DFT methods. While UB3LYP predicts a great contribution (61–73%) from the d orbitals of copper to the HOMO, this orbital is largely distributed (58–80%) over the π* orbitals of the Hdpa ligand in complexes 2, 3, 5, 7, and 8 at wB97XD level. For the rest of the complexes, 1, 4, and 10, the Hdpa orbitals contribute substantially (35–40%) to the HOMO frontier orbital despite the copper dominance. The composition of the molecular orbitals predicted at M06 level are generally close to that obtained at UB3LYP except for 2 and 8, wherein copper contribution has reduced significantly. Additionally, the LUMO frontier orbitals of all complexes are mostly localized on the π orbitals of the Hdpa ligand (>95%) as predicted by all methods.

For the HOMO of complex 6, a major contribution (68–78%) from the π* orbitals of mesBIAN and a much smaller distribution (20–25%) over copper orbitals were calculated at three levels. Fig. 4 depicts the electron density distributions of the HOMO and LUMO of complexes 1 and 6 at wB97XD/6-31+G(d,p) level.

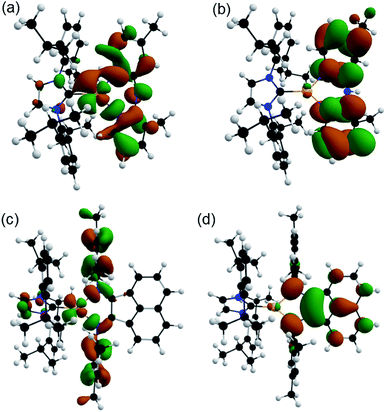Fig. 4 (a) HOMO and (b) LUMO of [Cu(IPr)(3,4′-Me₂Hdpa)]⁺ (1), and (c) HOMO and (d) LUMO of [Cu(IPr)(mesBIAN)]⁺ (6) calculated at wB97XD/6-31+G (d,p) level.

Regarding the effect of methyl groups on the HOMO–LUMO gap, there are marginal differences between unsubstituted and substituted Hdpa complexes at three theory levels. Furthermore, all saturated SIPr complexes have a slightly larger HOMO–LUMO gap than their unsaturated IPr analog due to the more electron-donating carbene and a more stabilized HOMO level. A comparative HOMO–LUMO level energy diagram of all the complexes is shown in Fig. S12.†

Excited state. TD-DFT calculations were performed to rationalize the nature of the electronic transitions in the absorption and emission spectroscopy of the copper complexes. Given the different HOMO–LUMO gap and MO composition of the frontier orbitals obtained with hybrid and non-hybrid functionals, we have performed TD-DFT at both wB97XD and M06 levels. In these calculations, both singlet–singlet and singlet–triplet transitions were considered due to the experimentally detected emissive properties and relatively long emission lifetimes (from 15 to 35 μs). Assignment of the character for each excited state was based on the compositions of the occupied and virtual MO of the dominant excitation of the excited state. Thus, if the occupied orbital is metal-based, and the virtual orbital is mainly localized on the N^N or NHC ligand, the transition is designated as metal-to-ligand charge transfer (MLCT). In this context, three singlet–singlet transitions, S₀ → S₁, S₀ → S₂, and S₀ → S₃, and the first singlet–triplet transition (S₀ → T₁) in copper complexes are listed in Tables S7 and S8,† calculated at wB97XD and M06 level, respectively. The very weak oscillator strength (f) of the first two singlet–singlet transitions has been attributed to them being inhibited by symmetry in the gas-phase DFT calculations.³⁴ In solid state, the symmetry breaks down due to the counter anion allowing these transitions to happen.

Regardless of the different excitation energy and the main MO contributor to the S₀ → S₁ transition, both wB97XD and M06 exhibit comparable emission energy and transition weight for the S₀ → T₁ transition (Table 4). Furthermore, both methods describe distinct characters for these transitions in the Hdpa-based complexes from those in complex 6. For 1–5 and 7–10, the S₀ → S₁ transition is primarily MLCT in nature, whereas the S₀ → T₁ transition is a complex mixture of MLCT and ligand-based charge transfer (LCCT). In contrast, both S₀ → S₁ and S₀ → T₁ in 6 are spatially identical and have predominantly LCCT character due to the H → L transition being the main MO contributor (Tables S9 and S10†).

Table 4 Vertical transition energies, absorption wavelength (λ in nm), oscillator strengths (f), and main MO contribution for the first singlet–singlet (S₀ → S₁) and singlet–triplet (S₀ → T₁) transitions calculated with wB97XD/6-31+G(d,p) and M06/6-31+G(d,p)

Complex	S0 → S1				S0 → T1^a			Method
	Transition type^b (weight, %)	E (eV)	λ (nm)	f	Transition type (weight, %)	E (eV)	λ (nm)
a The oscillator strength for the singlet to triplet transitions is 0 due to them being forbidden by the spin selection rule.b For each excitation energy, the corresponding most relevant molecular orbital transitions are shown with the relative weight.
[Cu(IPr)(L1)]^+ (1)	H → L + 1 (45)	4.25	291.8	0.003	H − 1 → L (40)	3.52	351.8	wB97XD
	H → L (88)	3.80	326.5	0.003	H − 1 → L (46)	3.56	369.5	M06
[Cu(IPr)(L2)]^+ (2)	H − 1 → L (29)	4.23	293.0	0.002	H → L (43)	3.49	355.7	wB97XD
	H → L (78)	3.76	329.8	0.001	H − 1 → L (38)	3.31	375.2	M06
[Cu(IPr)(L3)]^+ (3)	H − 1 → L (32)	4.29	289.2	0.012	H → L (38)	3.51	353.7	wB97XD
	H → L (86)	3.83	323.9	0.004	H − 1 → L (46)	3.36	369.2	M06
[Cu(IPr)(L4)]^+ (4)	H → L + 1 (58)	4.24	292.4	0.001	H − 1 → L (37)	3.55	349.7	wB97XD
	H → L (97)	3.77	328.9	0.000	H − 1 → L (54)	3.39	365.8	M06
[Cu(IPr)(L5)]^+ (5)	H − 1 → L + 1 (41)	4.23	292.8	0.000	H → L (39)	3.49	355.5	wB97XD
	H → L (97)	3.77	328.7	0.002	H − 1 → L (54)	3.31	374.8	M06
[Cu(IPr)(L6)]^+ (6)	H → L (87)	2.42	511.4	0.001	H → L (85)	2.23	556.5	wB97XD
	H → L (95)	2.04	608.8	0.001	H → L (93)	1.90	654.0	M06
[Cu(SIPr)(L1)]^+ (7)	H − 1 → L + 1 (36)	4.14	299.3	0.001	H → L (34)	3.53	351.8	wB97XD
	H → L (60)	3.83	324.1	0.002	H − 1 → L (44)	3.35	370.1	M06
[Cu(SIPr)(L2)]^+ (8)	H − 1 → L + 1 (40)	4.15	299.1	0.002	H → L (50)	3.49	354.8	wB97XD
	H − 1 → L + 1 (56)	3.86	320.9	0.004	H → L (52)	3.30	375.8	M06
[Cu(SIPr)(L4)]^+ (10)	H → L + 1 (49)	4.15	298.7	0.001	H − 1 → L (36)	3.56	348.5	wB97XD
	H → L (98)	3.80	326.6	0.001	H − 1 → L (53)	3.40	364.9	M06

---

Comparison with experimental data. To further clarify the agreement between the theoretical calculations and experiments, the absorption spectra of 1, 4, and 10, as exemplary complexes, were simulated with TD-DFT. The calculations were performed both in gas-phase and in the presence of a solvent (CH₂Cl₂) within M06 and wB97XD methods. To simulate the absorption spectra, a superposition of Gaussian peaks centered at the excitation energies were considered, with height equal to the oscillator strength and a width of 0.25 eV. The theoretically predicted UV-Vis spectrum of complex 4 at M06 level shows three peaks at 297, 250, and 216 nm, in good agreement with the experimental data. When simulated at wB97XD level, the absorption peaks are shifted to shorter wavelengths at 275, 234, and 186 nm, making the calculations with M06 method a better fit to the experimental data (Fig. 5). It is worth noting that the simulated spectrum in the gas phase resembles the same features but at slightly red-shifted areas at both DFT levels (Fig. 5). Furthermore, a good agreement with the experimental data was found for the simulated UV-Vis spectra of 1 and 10 at M06 level, as examples of methyl-substituted dipyridylamine and saturated NHC complexes (Fig. S13†). According to TD-DFT, the lowest-energy absorption at 294 nm in 1 arises predominantly from the HOMO − 1 → LUMO electronic transition which can be described as a mixture of MLCT and LCCT transitions (Fig. S14†). Interestingly, no shift was observed in the location of this peak when the spectrum was recorded in CH₃CN, a more polar solvent (Fig. S15†). This can be rationalized by the sum of two contrary solvent effects, hypsochromic and bathochromic, on the MLCT and LCCT transitions that results in no change in the energy of the band arising from their mixture. This is further validated by the red shift of the absorption band at 250 nm in CH₂Cl₂ to 260 nm in CH₃CN, consistent with the π → π* character of this electronic transition. The TD-DFT calculations describes a predominantly interligand transition character for this band arising from the π orbitals of IPr to the π* orbitals of 3,4′-Me₂Hdpa (HOMO − 5 → LUMO).

Fig. 5 Experimental and TD-DFT simulated UV-Vis absorption spectra of [Cu(IPr)(L4)]⁺ in gas-phase and in CH₂Cl₂ at (a) M06 level and (b) wB97XD level.

Experimental methods

General procedure

The Cu(I) complex syntheses were performed using standard Schlenk techniques or in an MBraun glove box under Ar atmosphere. Imidazolium salts, IPr·HCl and SIPr·HCl were purchased from TCI America. [Cu(IPr)Cl] and [Cu(SIPr)Cl] precursor complexes were prepared according to our modified version of Cazin–Nolan's procedure.³⁷ The ligands, Me₂Hdpa and mesBAIN, were synthesized according to the modified literature procedure (ESI†). The solvents used for the syntheses and analytical studies of copper complexes were purified and distilled under N₂ atmosphere before being stored over activated molecular sieves (4 Å) in the glovebox. Tetrahydrofuran and diethylether were purified by distillation over Na/benzophenone under N₂ atmosphere. Acetonitrile, dichloromethane, and hexane were distilled from CaH₂ under N₂. Potassium tert-butoxide (97%) was obtained from Sigma-Aldrich and crystallized from THF. Tetrabutylammonium hexafluorophosphate for electrochemical studies was doubly recrystallized from dichloromethane and diethylether. NMR samples were prepared under Ar in CDCl₃, containing 0.05% TMS as internal standard. NMR spectra were measured using a 400 MHz Bruker Avance III spectrometer. Chemical shifts (δ) for ¹H and ¹³C NMR spectra were referenced to the resonance of TMS or the residual protio solvent. Elemental analyses were performed by Atlantic Microlabs, Inc. (Norcross, Georgia). UV-visible spectra were measured at room temperature in CH₂Cl₂ and CH₃CN on a CARY 100 Bio UV-Vis spectrometer. Steady state emission spectra and emission lifetimes were recorded in solid state on a CARY ECLIPSE fluorescence spectrophotometer. For measuring absolute solid-state emission quantum yield, a solid sample holder accessory was equipped to the CARY ECLIPSE spectrofluorometer.

Synthesis of [Cu(NHC)(N^N)]PF₆ complexes

Under Ar atmosphere, [Cu(IPr)Cl] (1 equiv.) and N^N ligand (1 equiv.) were combined using 4 ml THF in a 20 ml reaction vial. The solution was stirred for 1.5 hours and then charged with KPF₆ (10 equiv.) providing a white suspension. The reaction mixture was kept stirring for 22.5 hours at room temperature, except for complex 3, after which time it was filtered through a plug of Celite and washed with THF and CH₂Cl₂. The filtrate was placed under vacuum to remove the solvent and the resultant solid was recrystallized from a mixture of dichloromethane and hexane.

Solid state quantum yield measurements

The quantum yield measurements were performed after calibrating the incident light to strike at the center of a custom-designed sample holder. The holder was made from a pair of quartz cover glasses, glued together in a squared area (0.5 × 0.5 cm) after sample placement. A 5 mg portion of a finely-ground powder was placed inside the area and distributed evenly using a flat-head spatula to cover the entire surface. For quantum yield measurements, sodium salicylate was used as the reference with quantum yield (Φ) of 0.53. The excitation wavelength of 340 nm was used to obtain phosphorescence spectra for each compound ranging from 370 nm to 650 nm. Quantum yields were calculated using the formula:⁵⁵
where I, A, and n refer to the integrated emission, the absorbance at excitation wavelength, and the refractive index, respectively. The integrated emissions were obtained from the emission spectra. The absorbance values of the reference and the sample solutions were used at the same wavelength to calculate the second term in the formula. For refractive indices, the n values of CH₂Cl₂ (n = 1.424) and CH₃OH (n = 1.331) were used as the solvents that dissolve the complexes and the reference, respectively. The emission measurements were repeated at least three times and an average of three close peak areas were used to calculate the integrated emission values. The compatibility of this method and solid samples was assessed by comparing the quantum yields of complexes 4, 5, and 11 to those obtained using integrating sphere equipment. The difference in the QY values was determined to be ±3%.

Electrochemistry

Cyclic voltammetry studies of complexes 1–11 and ferrocene at 2 mM concentration were performed using 0.1 M ⁿBu₄PF₆/CH₂Cl₂ as the supporting electrolyte under nitrogen. The electrochemistry experiment set-up consisted of a three-electrode cell connected to an external CHI 730C potentiostat run by a personal computer with CHI software. A glassy carbon electrode (0.5 mm diameter) was employed as the working electrode, with Ag/AgNO₃ (0.01 M) as the reference and Pt wire as the counter electrode. The working electrode was cleaned between experiments using a polishing pad and carefully dried. All potentials are reported versus [Fe(C₅H₅)₂]⁺/[Fe(C₅H₅)₂] by subtracting 0.252 V from the measured value versus Ag/AgNO₃ electrode.

Conclusions

A new series of heteroleptic three-coordinate Cu–IPr and Cu–SIPr complexes bearing unsymmetrically-substituted Me₂Hdpa and mesBIAN ligands were prepared and characterized by solid- and solution-phase analytical techniques. The solid-state analyses indicate the CH⋯π interactions between the center of the diisopropylphenyl groups of NHC and the α hydrogen atoms of Hdpa in the 3,4′-Me₂Hdpa and 3,5′-Me₂Hdpa complexes, like their symmetrically substituted analogs. In contrast, no such interaction was found for the 3,6′-Me₂Hdpa version within a reasonable distance. While the lack of α-hydrogen atoms in 6,6′-Me₂Hdpa and thus, the absence of CH–π interaction was reasoned for the complexation failure previously, a decent yield was obtained for [Cu(IPr)(3,6′-Me₂Hdpa)]PF₆ in our work. The stability of this complex was attributed to the large plane angle between the IPr ring and the 3,6-Me₂Hdpa ligand reducing the repulsive interactions and allowing its formation. The large plane angle was also identified as an important parameter towards improving the emissive properties of these copper complexes in solid state. This finding and the solid state luminescent properties of the complexes are consistent with their analogs bearing modified IPr and Hdpa ligands.

Furthermore, the character of the electronic states involved in light absorption and emission were elucidated via DFT and TD-DFT calculations at three theory levels. The data obtained using M06, a hybrid functional, and wB97XD, a non-hybrid functional, support the dominance of MLCT character in S₀ → S₁ transitions and a combination of MLCT and LLCT in S₀ → T₁ transitions for the Hdpa-based complexes. The simulated UV-Vis absorption spectra indicate a close match with the experimental data in solution at M06 level. While the wB97XD level calculation was adopted previously to rationalize the photophysical properties of the [Cu(NHC)(N^N)]⁺ complexes, our work supports the competency of M06 functional in these types of calculations as well. The combined experimental and theoretical findings offer a deeper understanding of the structure and light-interaction relationship in [Cu(IPr)(N^N)]⁺ and [Cu(SIPr)(N^N)]⁺ complexes and a more rational-based approach towards efficient copper-based luminophores.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge Oklahoma State University start-up funding (LT), the National Science Foundation REU program through the grant CHE-1559874 (BN), the OSU fund (Single Crystal X-ray Diffraction in the OSU core facility center), and the computing at the OSU High Performance Computing Center (HPCC) supported in part through the NSF grant OAC–1531128.

References

1. M. H. Keefe, K. D. Benkstein and J. T. Hupp, Coord. Chem. Rev., 2000, 205, 201–228.
2. J. A. Gareth Williams, S. Develay, D. L. Rochester and L. Murphy, Coord. Chem. Rev., 2008, 252, 2596–2611.
3. K. M.-C. Wong and V. W.-W. Yam, Coord. Chem. Rev., 2007, 251, 2477–2488.
4. M. S. Lowry and S. Bernhard, Chem.–Eur. J., 2006, 12, 7970–7977.
5. Z. Liu, Z. Bian and C. Huang, in Molecular Organometallic Materials for Optics, ed. H. Bozec and V. Guerchais, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, pp. 113–142,  DOI:10.1007/978-3-642-01866-4_4.
6. Y. You and W. Nam, Chem. Soc. Rev., 2012, 41, 7061–7084.
7. K. E. Erkkila, D. T. Odom and J. K. Barton, Chem. Rev., 1999, 99, 2777–2796.
8. G. M. Brown, B. S. Brunschwig, C. Creutz, J. F. Endicott and N. Sutin, J. Am. Chem. Soc., 1979, 101, 1298–1300.
9. N. Robertson, ChemSusChem, 2008, 1, 977–979.
10. M. Iwamura, S. Takeuchi and T. Tahara, Acc. Chem. Res., 2015, 48, 782–791.
11. G. Capano, U. Rothlisberger, I. Tavernelli and T. J. Penfold, J. Phys. Chem. A, 2015, 119, 7026–7037.
12. G. B. Shaw, C. D. Grant, H. Shirota, E. W. Castner, G. J. Meyer and L. X. Chen, J. Am. Chem. Soc., 2007, 129, 2147–2160.
13. M. Iwamura, H. Watanabe, K. Ishii, S. Takeuchi and T. Tahara, J. Am. Chem. Soc., 2011, 133, 7728–7736.
14. L. X. Chen, G. B. Shaw, I. Novozhilova, T. Liu, G. Jennings, K. Attenkofer, G. J. Meyer and P. Coppens, J. Am. Chem. Soc., 2003, 125, 7022–7034.
15. Z. A. Siddique, Y. Yamamoto, T. Ohno and K. Nozaki, Inorg. Chem., 2003, 42, 6366–6378.
16. E. M. Stacy and D. R. McMillin, Inorg. Chem., 1990, 29, 393–396.
17. M. W. Blaskie and D. R. McMillin, Inorg. Chem., 1980, 19, 3519–3522.
18. M. Nishikawa, Y. Wakita, T. Nishi, T. Miura and T. Tsubomura, Dalton Trans., 2015, 44, 9170–9181.
19. N. Armaroli, Chem. Soc. Rev., 2001, 30, 113–124.
20. A. J. M. Miller, J. L. Dempsey and J. C. Peters, Inorg. Chem., 2007, 46, 7244–7246.
21. M. K. Eggleston, D. R. McMillin, K. S. Koenig and A. J. Pallenberg, Inorg. Chem., 1997, 36, 172–176.
22. A. Lavie-Cambot, M. Cantuel, Y. Leydet, G. Jonusauskas, D. M. Bassani and N. D. McClenaghan, Coord. Chem. Rev., 2008, 252, 2572–2584.
23. D. V. Scaltrito, D. W. Thompson, J. A. O'Callaghan and G. J. Meyer, Coord. Chem. Rev., 2000, 208, 243–266.
24. J. Huang, M. W. Mara, A. B. Stickrath, O. Kokhan, M. R. Harpham, K. Haldrup, M. L. Shelby, X. Zhang, R. Ruppert, J. P. Sauvage and L. X. Chen, Dalton Trans., 2014, 43, 17615–17623.
25. C. Bizzarri, C. Strabler, J. Prock, B. Trettenbrein, M. Ruggenthaler, C.-H. Yang, F. Polo, A. Iordache, P. Brüggeller and L. D. Cola, Inorg. Chem., 2014, 53, 10944–10951.
26. T. Hofbeck, U. Monkowius and H. Yersin, J. Am. Chem. Soc., 2015, 137, 399–404.
27. S. B. Harkins and J. C. Peters, J. Am. Chem. Soc., 2005, 127, 2030–2031.
28. K. J. Lotito and J. C. Peters, Chem. Commun., 2010, 46, 3690–3692.
29. M. Hashimoto, S. Igawa, M. Yashima, I. Kawata, M. Hoshino and M. Osawa, J. Am. Chem. Soc., 2011, 133, 10348–10351.
30. V. A. Krylova, P. I. Djurovich, M. T. Whited and M. E. Thompson, Chem. Commun., 2010, 46, 6696–6698.
31. V. A. Krylova, P. I. Djurovich, J. W. Aronson, R. Haiges, M. T. Whited and M. E. Thompson, Organometallics, 2012, 31, 7983–7993.
32. V. A. Krylova, P. I. Djurovich, B. L. Conley, R. Haiges, M. T. Whited, T. J. Williams and M. E. Thompson, Chem. Commun., 2014, 50, 7176–7179.
33. M. J. Leitl, V. A. Krylova, P. I. Djurovich, M. E. Thompson and H. Yersin, J. Am. Chem. Soc., 2014, 136, 16032–16038.
34. R. Marion, F. Sguerra, F. Di Meo, E. Sauvageot, J.-F. Lohier, R. Daniellou, J.-L. Renaud, M. Linares, M. Hamel and S. Gaillard, Inorg. Chem., 2014, 53, 9181–9191.
35. R. Marion, F. Sguerra, F. Di Meo, E. Sauvageot, J.-F. Lohier, R. Daniellou, J.-L. Renaud, M. Linares, M. Hamel and S. Gaillard, Inorg. Chem., 2016, 55, 4068.
36. M. Elie, F. Sguerra, F. Di Meo, M. D. Weber, R. Marion, A. Grimault, J.-F. Lohier, A. Stallivieri, A. Brosseau, R. B. Pansu, J.-L. Renaud, M. Linares, M. Hamel, R. D. Costa and S. Gaillard, ACS Appl. Mater. Interfaces, 2016, 8, 14678–14691.
37. J. L. Minnick, D. Domyati, R. Ammons and L. Tahsini, Front. Chem., 2019, 17, 12.
38. H. Suezawa, T. Yoshida, Y. Umezawa, S. Tsuboyama and M. Nishio, Eur. J. Inorg. Chem., 2002, 2002, 3148–3155.
39. E. Kryachko and S. Scheiner, J. Phys. Chem. A, 2004, 108, 2527–2535.
40. T. Steiner, J. Chem. Crystallogr., 1997, 27, 673–675.
41. B. Tolnai, J. T. Kiss, K. Felföldi and I. Pálinkó, J. Mol. Struct., 2009, 924–926, 27–31.
42. D. E. Morris, Y. Ohsawa, D. P. Segers, M. K. DeArmond and K. W. Hanck, Inorg. Chem., 1984, 23, 3010–3017.
43. A. Zianna, G. Psomas, A. Hatzidimitriou and M. Lalia-Kantouri, J. Inorg. Biochem., 2016, 163, 131–142.
44. F. Franco, C. Cometto, F. Sordello, C. Minero, L. Nencini, J. Fiedler, R. Gobetto and C. Nervi, ChemElectroChem, 2015, 2, 1372–1379.
45. L. Li, P. S. Lopes, V. Rosa, C. A. Figueira, M. A. N. D. A. Lemos, M. T. Duarte, T. Avilés and P. T. Gomes, Dalton Trans., 2012, 41, 5144–5154.
46. S. Wang, Z. Cheng, X. Song, X. Yan, K. Ye, Y. Liu, G. Yang and Y. Wang, ACS Appl. Mater. Interfaces, 2017, 9, 9892–9901.
47. D. M. de Leeuw, M. M. J. Simenon, A. R. Brown and R. E. F. Einerhand, Synth. Met., 1997, 87, 53–59.
48. J. W. Kee, Y. Y. Ng, S. A. Kulkarni, S. K. Muduli, K. Xu, R. Ganguly, Y. Lu, H. Hirao and H. S. Soo, Inorg. Chem. Front., 2016, 3, 651–662.
49. P. Papanikolaou, P. D. Akrivos, A. Czapik, B. Wicher, M. Gdaniec and N. Tkachenko, Eur. J. Inorg. Chem., 2013, 2013, 2418–2431.
50. T. Lu, J.-Y. Wang, D. Tu, Z.-N. Chen, X.-T. Chen and Z.-L. Xue, Inorg. Chem., 2018, 57, 13618–13630.
51. T. Gneuß, M. J. Leitl, L. H. Finger, N. Rau, H. Yersin and J. Sundermeyer, Dalton Trans., 2015, 44, 8506–8520.
52. D. M. Zink, T. Grab, T. Baumann, M. Nieger, E. C. Barnes, W. Klopper and S. Bräse, Organometallics, 2011, 30, 3275–3283.
53. P. R. Varadwaj and H. M. Marques, Theor. Chem. Acc., 2010, 127, 711–725.
54. F. Neese, JBIC, J. Biol. Inorg. Chem., 2006, 11, 702–711.
55. G. A. Crosby and J. N. Demas, J. Phys. Chem., 1971, 75, 991–1024.

---

Footnote

† Electronic supplementary information (ESI) available: Crystallographic information files (CIF) for 1–3, 6–8, and 12, crystallographic data collection table, ¹H and ¹³C{¹H} NMR spectra for ligands, Cu precursors, and complexes 1–12 (Fig. S16–S51), ORTEP diagrams of [Cu(SIPr)Cl] and 6 and 12 with long-distance interactions, CV of complexes 4 and 5 at varying scan rates and CV of the free Hdpa (Fig. S5–S7), and further details of ligand and Cu complexes synthesis. CCDC 1861502, 1865893, 1865901, 1866337, 1866344, 1866360, 1556652 and 1918545. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9ra04886c

---