 Open Access Article
Open Access ArticleA model for the chemomechanical coupling of myosin-V molecular motors†
Ping Xie *
*
Key Laboratory of Soft Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China. E-mail: pxie@aphy.iphy.ac.cn
First published on 27th August 2019
Abstract
Herein, a model for the chemomechanical coupling of dimeric myosin-V motors is presented. Based on this model and the proposal that the rate constants of the ATPase activity of the two heads are independent of an external force in a range smaller than the stall force, we analytically studied the dynamics of the motor, such as the stepping ratio, dwell time between two mechanical steps, and velocity, under varying force and ATP concentrations. The theoretical results well reproduce the diverse available single-molecule experimental data. In particular, the experimental data showing that at a low ATP concentration, the dwell time and velocity have less force dependency than at a high ATP concentration is explained quantitatively. Moreover, the dependency of the chemomechanical coupling ratio on the force and ATP concentration was studied.
1. Introduction
Myosin-V is an ATP-dependent motor protein that can move processively on actin filaments from their pointed (minus) to barbed (positive) ends with an average step size of about 36 nm, which is responsible for intracellular transport.1,2 This motor is composed of two identical heavy chains, each consisting of a motor domain (head) and a neck domain that has 6 IQ motifs bound with 6 light chains.2 The two neck domains are connected by a coiled-coil stalk. Using various experimental techniques, diverse aspects of the motor dynamics have been elucidated. For example, using single molecule fluorescence imaging,3 single-molecule fluorescence polarization4 and high-speed atomic force microscopy,5 it was well-determined that myosin-V walks on actin filaments in a hand-over-hand manner. Using high-resolution single-molecule interferometric scattering microscopy, Andrecka et al.6 found that consecutive steps of myosin-V follow identical paths to the same side of actin, in a symmetric hand-over-hand manner. By visualizing the binding and dissociation of single fluorescently labelled nucleotide molecules and simultaneously observing the stepping motion of the fluorescently labelled myosin-V, it was revealed that under no load this motor exhibits nearly tight chemomechanical coupling.7 The tight coupling refers to a mechanical step (either a forward or backward step), which is closely associated with the hydrolysis of an ATP molecule. In particular, using single-molecule optical trapping methods, the dependence of the forward to backward stepping ratio (simply called stepping ratio), dwell time between two mechanical steps and velocity upon force and ATP concentration was determined.8–12 The single-molecule optical trapping data revealed that although myosin-V shows a steep increase in dwell time under a force larger than ∼1 pN at high ATP concentrations, it shows a less or nearly no force dependence at low ATP concentrations.8,9From a theoretical point of view, a large number of different models and methods has been presented to study the dynamics of myosin-V.13–24 In most of the theoretical studies, the dependence of dwell time and velocity on the external force was proposed to arise from the dependence of the ATPase activity on the force. Although based on the proposal of the force-dependent rate constants of the ATPase activity, most of the available experimental data was explained well. However, to date, the single-molecule data showing that at high ATP concentrations the dwell time increases steeply under a force larger than ∼1 pN, whereas at low ATP concentrations the dwell time has a less or nearly no force dependence8,9 has not been explained well. In addition, during processive stepping of myosin-V on actin, how consecutive steps follow identical paths to the same side of the actin6 is unclear. This seems to result in a coiled-coil stalk, which joins two heads together and rotates unidirectionally. Thus, it is expected that the torsion arising from the unidirectional rotation of the coiled-coil stalk increases gradually as the motor steps forward processively. However, it is puzzling how the torsion is released. Another unclear issue is while myosin-V exhibits nearly tight chemomechanical coupling under no external force,7 can it still retain the nearly tight coupling under high forces.
In this work, a new model for the chemomechanical coupling of myosin-V motors is presented, addressing the above unclear issues. We propose that the rate constants of the ATPase activity of their two heads are independent of the external force in the range smaller than the stall force. Based on this model and proposal, the dynamics of the motor under varying force and ATP concentrations were studied analytically, explaining the available single-molecule data. The results show that in general, at a low ATP concentration and under any force, the motor exhibits nearly tight chemomechanical coupling, while at a high ATP concentration and under high force, the motor evidently exhibits non-tight chemomechanical coupling.
2. Model
The model for the chemomechanical coupling of myosin-V dimers was built based mainly on the following experimental evidence and arguments.(i) A myosin head in the nucleotide-free (ϕ) or ADP state has a high affinity to actin, whereas in the ATP or ADP·Pi state, it has a low affinity.25–29 Moreover, it is argued that upon ATP binding, the affinity of the ATP-head to the local binding site on actin (denoted by Ew1) is temporarily weaker than that to other binding sites (denoted by Ew2), as done previously.30 This can be understood as follows. The strong interaction of the ADP-head or ϕ-head with actin induces a structural change in the local actin monomer.31–33 Thus, it is expected that the interaction of the local binding site on actin with the ATP-head should be different from that of other unperturbed actin monomers. It is reasonable to argue that the ATP-head has a weaker interaction with the local binding site than with other unperturbed binding sites. In time tr (in the order of μs), the changed conformation of the local monomer relaxes to the normal form, with the affinity of the ATP-head to the local binding site becoming the same as that to other unperturbed binding sites. Note here that this argument for the interaction of myosin with actin is similar to that for the interaction of kinesin with microtubules (MT).34–37 For the case of kinesin, the argument that the conformational change of the local MT tubulin induced by the strong interaction with the kinesin head in the strong MT-binding state results in the local tubulin having a further weaker interaction with the head in the weak MT-binding state than other unperturbed tubulins was supported by recent all-atom molecular dynamics simulations.38
(ii) The relative orientation of the neck domain of myosin with respect to its motor domain bound to actin depends on its nucleotide state. In the ATP or ADP·Pi state, the neck domain has random orientations,39–45 as schematically shown in Fig. 1a′ (inset box). After Pi release (in ADP state), the neck domain has a fixed orientation, tilting toward the actin-plus end or tilting forward,28,40,45–49 as schematically shown in Fig. 1b′ (inset box). After ADP release (in ϕ state), the neck domain tilts forward further,47–49 as schematically shown in Fig. 1c′ (inset box).
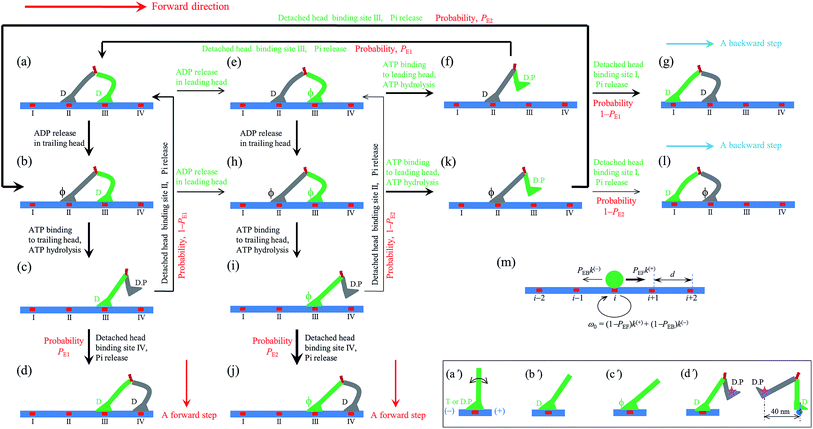 | ||
| Fig. 1 Model of myosin-V motor moving on actin at low ATP. (a)–(l) Schematic illustrations of the pathway for the chemomechanical coupling (see text for detailed description). The thickness of the arrow represents the magnitude of the transition rate or probability under low backward force. (m) Simplified model derived from the pathway shown in (a)–(l), where k(+) and k(−) are the ATPase rates of the trailing and leading heads, respectively. The green circle represents the center of mass of the motor. The positions of binding sites on actin filament are denoted by …, (i − 1), i, (i + 1), …. The motor can step forward and backward with rates PEFk(+) and PEBk(−), respectively. Inset box: (a′)–(c′) show the orientations of the neck domain relative to its motor domain bound to actin filament in different nucleotide states, and (d′) shows the relative orientation of the two heads in the intermediate state with one head bound to actin and the other head detached from the actin, with the right panel corresponding to the side view of the left panel. Stars represent the position of the gold particle labeled to the head used in the experiments of Andrecka et al.6 | ||
(iii) It is proposed that the residue elements connecting the neck domain and coiled-coil stalk behave elastically, with a small nonzero torsional/bendable elastic stiffness, as done before,17 rather than as completely flexible elements of nearly zero torsional/bendable stiffness. In the absence of actin, the nonzero torsional/bendable elastic stiffness of the residue elements would keep the two heads in a definite relative position and orientation (the equilibrium state), where the myosin-V dimer has the minimum free energy. This implies that when one head is detached from actin, the detached head will fluctuate in a limited range around its equilibrium position and orientation relative to the other actin-bound head. As discussed elsewhere,17 the existence of the equilibrium state, where the myosin-V dimer has the minimum free energy, is consistent with numerous available experimental and structural data.50–55 It is also consistent with the recent structural data of Takagi et al.56 for myosin-10. Furthermore, here, it is argued that in the equilibrium state, the relative orientation of the two heads is that schematically illustrated in Fig. 1d′ (inset box), with the right panel being the side view of the left panel. This conformation of the dimer with one head bound to the actin filament dictates that the detached head will fluctuate on the left side of the actin filament, implying that during processive stepping when one head detaches from the actin filament, it always fluctuates temporarily on the left side of the actin filament, which is in agreement with the single-molecule experimental data of Andrecka et al.6 (see later).
2.1. The pathway at low ATP concentration
Based on the above evidence or arguments, the model of the chemomechanical coupling of myosin-V at low ATP is schematically shown in Fig. 1a–l. Since ATP hydrolysis and actin-stimulated Pi release are much faster than ADP release, at low ATP, the rate-limiting steps of the ATPase activity are ADP release and ATP binding. We began the chemomechanical coupling cycle with both heads in the ADP state, with the trailing head binding strongly to binding site II on actin and the leading head binding strongly to site III (Fig. 1a). It is argued that the rate constant of ADP release from the trailing head is much larger than that from the leading head (see later).First, consider releasing ADP from the trailing head (Fig. 1b). Upon ATP binding, the trailing head detaches readily from site II by overcoming the very weak binding energy, Ew1, and then moves to the intermediate equilibrium position (Fig. 1c). From the intermediate position, by overcoming the energy (EE) for retaining the detached head in the equilibrium position and orientation relative to the actin-bound head, the detached head can bind (with probability PE1) to the forward site IV with binding energy Ew2 and then release Pi (Fig. 1d). From the intermediate position, by overcoming both energy EE and energy (EB) of bending the neck of the actin-bound ADP-head, the detached head can also rebind (with probability 1 − PE1) to site II with the binding energy Ew2 and then release Pi (Fig. 1a) (noting that after the head detaches, site II relaxes rapidly to the unchanged conformation in the order of μs). The state of Fig. 1d is the same as that of Fig. 1a except that a forward step was made.
Secondly, in Fig. 1a, ADP release from the leading head was considered (Fig. 1e). Upon ATP binding, the leading head detaches from site III by overcoming Ew1 and moves to the intermediate equilibrium position (Fig. 1f). From the intermediate position, by overcoming energy EE, the detached head can rebind (with probability PE1) to site III with the binding energy Ew2 and then release Pi (Fig. 1a). From the intermediate position, by overcoming both energy EE and energy EB, the detached head can also bind (with probability 1 − PE1) to site I with the binding energy Ew2 and then release Pi (Fig. 1g). The state of Fig. 1g is the same as that of Fig. 1a except that a backward step was made.
Note that in Fig. 1b, ADP can also be released from the leading head before ATP binding to the trailing head, becoming the state of Fig. 1h. In Fig. 1e, ADP can also be released from the trailing head before ATP binding to the leading head, also becoming the state of Fig. 1h. From Fig. 1h, upon ATP binding to the trailing head, the head detaches rapidly from site II by overcoming Ew1 and then moves to the intermediate equilibrium position (Fig. 1i). From the intermediate position, by overcoming energy EE, the detached head can bind (with probability PE2) to site IV with the binding energy Ew2 and then release Pi (Fig. 1a). From the intermediate position, by overcoming both energy EE and energy 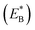 of bending the neck of the actin-bound ϕ-head, the detached head can also rebind (with probability 1 − PE2) to site II with the binding energy Ew2 and then release Pi (Fig. 1e). Note here that
of bending the neck of the actin-bound ϕ-head, the detached head can also rebind (with probability 1 − PE2) to site II with the binding energy Ew2 and then release Pi (Fig. 1e). Note here that 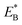 , which is the bending energy of the neck domain of the actin-bound ϕ-head when the detached head binds to the rear binding site on actin, is larger than EB, which is the bending energy of the neck domain of the actin-bound ADP-head when the detached head binds to the rear binding site on actin. The state of Fig. 1j is the same as that of Fig. 1b except that a forward step was made.
, which is the bending energy of the neck domain of the actin-bound ϕ-head when the detached head binds to the rear binding site on actin, is larger than EB, which is the bending energy of the neck domain of the actin-bound ADP-head when the detached head binds to the rear binding site on actin. The state of Fig. 1j is the same as that of Fig. 1b except that a forward step was made.
From Fig. 1h, upon ATP binding to the leading head, the head detaches rapidly from site III by overcoming Ew1 and then moves to the intermediate equilibrium position (Fig. 1k). From the intermediate position, by overcoming energy EE, the detached head can rebind (with probability PE2) to site III with the binding energy Ew2 and then release Pi (Fig. 1b). From the intermediate position, by overcoming both energy EE and energy 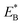 , the detached head can also bind (with probability 1 − PE2) to site I with the binding energy Ew2 and then release Pi (Fig. 1l). The state of Fig. 1l is the same as that of Fig. 1b except that a backward step was made.
, the detached head can also bind (with probability 1 − PE2) to site I with the binding energy Ew2 and then release Pi (Fig. 1l). The state of Fig. 1l is the same as that of Fig. 1b except that a backward step was made.
Since after detaching from actin, the time for the head to diffuse from the binding site on actin to the intermediate position and the time for the detached head to diffuse from the intermediate position to the binding site on actin are much shorter than the inverse of the ATPase rates, for an approximation, the velocity of the motor was determined solely by the ATPase rates of the two heads. Thus, the pathway shown in Fig. 1a–l can be described simply as follows. k(+) and k(−) denote the rate constants of ATPase activity of the trailing and leading heads, respectively. The total ATPase rate of the motor is k(+) + k(−). If ATPase activity with rate constant k(+) takes place, the motor makes either a forward step with a probability PEF or no movement with a probability (1 − PEF) (the relation of PEF with PE1 and PE2 will be presented later). If the ATPase activity with rate constant k(−) takes place, the motor makes either a backward step with a probability PEB or no movement with a probability (1 − PEB) (the relation of PEB with PE1 and PE2 will be presented later). Hence, the overall forward stepping rate of the motor is PEFk(+), the backward stepping rate is PEBk(−), and the ATPase rate with no stepping is ω0 = (1 − PEF)k(+) + (1 − PEB)k(−), as schematically shown in Fig. 1m.
2.2. The pathway at saturated ATP concentration
At saturated ATP, the pathway shown in Fig. 1a–l can be reduced to that shown in Fig. 2a–e. The chemomechanical coupling cycle was still started with the trailing head in the ADP state binding strongly to binding site II on actin and the leading head in the ADP state binding strongly to binding site III (Fig. 2a).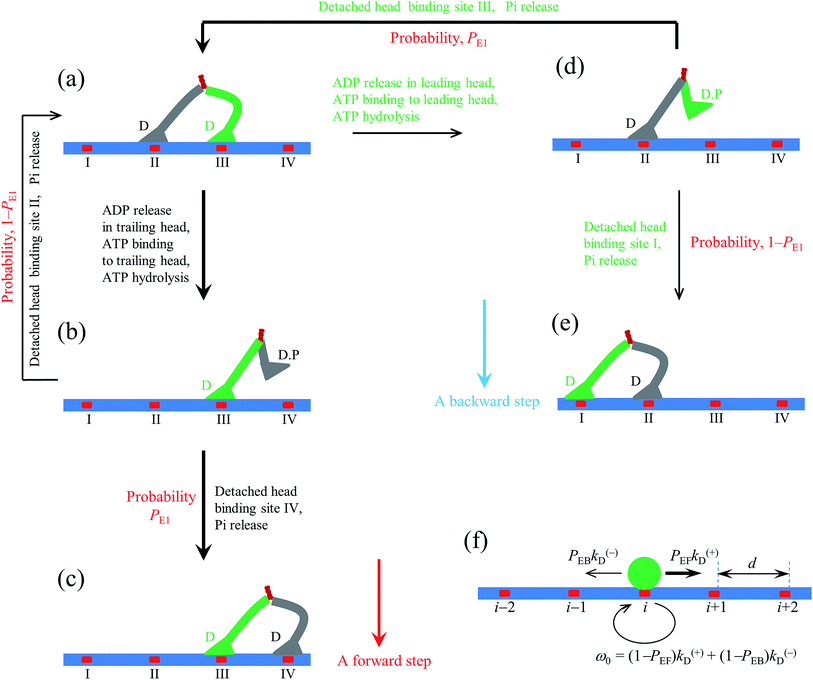 | ||
| Fig. 2 Model of myosin-V motor moving on actin at saturated ATP. The model is simplified from that in Fig. 1. (a)–(e) Schematic illustrations of the pathway for the chemomechanical coupling (see text for detailed description). The thickness of the arrow represents the magnitude of the transition rate or probability under low backward force. (f) Simplified model derived from the pathway shown in (a)–(e), where kD(+) and kD(−) are the rate constants of ADP release from the trailing and leading heads, respectively. The green circle represents the center of mass of the motor. The positions of binding sites on actin filament are denoted by …, (i − 1), i, (i + 1), …. The motor can step forward and backward with rates PEFkD(+) and PEBkD(−), respectively. | ||
Firstly, ADP release from the trailing head was considered, followed immediately by ATP binding. The trailing head detaches rapidly from site II and moves to the intermediate equilibrium position (Fig. 2b). From the intermediate position, the detached head can either bind (with probability PE1) to the forward site IV and then release Pi (Fig. 2c) or rebind (with probability 1 − PE1) to site II and then release Pi (Fig. 2a). From Fig. 2a to b to c, a forward step was made.
Secondly, ADP release from the leading head was considered, followed immediately by ATP binding. The leading head detaches rapidly from site III and moves to the intermediate equilibrium position (Fig. 2d). From the intermediate position, the detached head can either rebind (with probability PE1) to site III and then release Pi (Fig. 2a) or bind (with probability 1 − PE1) to site I and then release Pi (Fig. 2e). From Fig. 2a to d to e, a backward step was made.
At saturated ATP, the ATPase rate of the myosin-V head is approximately determined solely by the rate constants of ADP release from the two heads. Thus, as in the case of low ATP (Fig. 1m), the pathway shown in Fig. 2a–e can be simplified to that schematically shown in Fig. 2f, where kD(+) and kD(−) are rate constants of ADP release from the trailing and leading heads, respectively.
2.3. The ATPase activity is independent of external force in the small range
As done in the single-molecule optical trapping assays,8–12 an external force, F, acting on the coiled-coil stalk that connects the two neck domains of the two heads of myosin-V was considered. In this work, only the external force, F, that resists the forward movement of the motor was considered (called backward force).For kinesin dimers, it was proposed that the external force has no effect on the rate constant of the rate-limiting step of ATPase activity of the kinesin head,36,37,57,58 which is consistent with the available experimental data.59 However, the ATPase rate of the kinesin head is dependent on the orientation of its neck linker, where the trailing head with the forward orientation of the neck liner has a much higher ATPase rate than the leading head with the backward orientation.36,37,57,58
Similarly, for dimeric myosin-V, we also propose that the external force, F, which is in the small range of 0–3 pN (when the two heads are bound to actin, each head experiences a force of only 0–1.5 pN, resulting from the external force, F), has no effect on the ATPase activity of the myosin head. Specifically, the rate constants of the ATPase activity of the two heads are independent of F in the small range of 0–3 pN. However, the orientations of the two neck domains have a large effect on the rate constants of ATPase activity. In the D–D state (e.g., Fig. 1a), with both heads in the ADP state, the orientations of the two neck domains result in severe deformations of the leading head and its nucleotide-binding site. Thus, it is argued that the rate constant of ADP release in the leading head (denoted by kD(−)) is much smaller than that in the trailing head (denoted by kD(+)), which has little deformation. In the ϕ–D state (e.g., Fig. 1b), with the trailing head in the ϕ state and the leading head in the ADP state, the orientations of the two neck domains alleviate the deformation of the leading head relative to that in the D–D state. Thus, here, it is argued that the rate constant of ADP release from the leading head in the ϕ–D state (denoted by kD*(−)) is larger than kD(−) in the D–D state but is smaller than kD(+).
3. Results and discussion
3.1. Explanations for the consecutive steps following identical paths to the same side of actin and foot stomping
In the pathway (e.g., Fig. 1), the occurrence of the intermediate equilibrium state (Fig. 1c, f, i and k) implies that during processive stepping, when one head detaches from the actin filament the head always fluctuates temporarily on the left side of the actin filament, which is consistent with the single-molecule experimental data of Andrecka et al.6 In the model, the forward stepping of one head relative to the other actin-bound head is composed of two substeps. The second substep (from Fig. 1c to d or from 1i to j) induces the torsion of residue elements connecting the neck and coiled-coil stalk, while the first substep (from Fig. 1b to c or from 1h to i) releases the torsion. By contrast, if the neck domain of the detached head is argued to rotate freely around the joint of the two neck domains, the detached head will fluctuate temporarily on both sides of the actin filament with equal probability.In the pathway (e.g., Fig. 1), the occurrence of rebinding of the detached head to the previous site from which the head has just been detached (the transition from Fig. 1f to a, from 1k to b, from 1c to a, or from 1i to e) is consistent with the so-called “foot stomping” observation.5 Since under no load PE1 and PE2 are close to 1 (see later), it is expected that the foot stomp should be more frequently observed at the leading head than at the trailing head, which is also consistent with the high-speed atomic force microscopic observation.5
3.2. Dynamics at saturated ATP concentration
In this section, the dynamics of the motor for the simple case of saturated ATP were studied. The dynamics for the more complicated case of non-saturated ATP will be studied in the next section.At saturated ATP, the pathway is shown in Fig. 2a–e and the simplified model is shown in Fig. 2f. Thus, we note that PEF = PE1 and PEB = 1 − PE1. The equation of PE1 can be derived as follows. The force dependence of the rate for the detached head to transit from the intermediate state to the state binding to the front binding site on actin can be calculated as kF = C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βFd(+)), where C is a constant as a function of EE but independent of F, β−1 = kBT, with kB being the Boltzmann constant and T the absolute temperature, and d(+) is the characteristic distance for the transition. The force dependence of the rate for the detached head to transit from the intermediate state to the state binding to the rear binding site on actin can be calculated as kR = C
exp(−βFd(+)), where C is a constant as a function of EE but independent of F, β−1 = kBT, with kB being the Boltzmann constant and T the absolute temperature, and d(+) is the characteristic distance for the transition. The force dependence of the rate for the detached head to transit from the intermediate state to the state binding to the rear binding site on actin can be calculated as kR = C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βEB)exp(βFd(−)), where EB is the bending energy of the neck domain of the actin-bound ADP-head when the detached head binds to the rear binding site on actin, as defined above, and d(−) is the characteristic distance for the transition. With the above kF and kR, the probability PE1 = kF/(kF + kR) can be written as
exp(−βEB)exp(βFd(−)), where EB is the bending energy of the neck domain of the actin-bound ADP-head when the detached head binds to the rear binding site on actin, as defined above, and d(−) is the characteristic distance for the transition. With the above kF and kR, the probability PE1 = kF/(kF + kR) can be written as
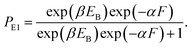 | (1) |
From Fig. 2f, the force dependence of the stepping ratio of the motor can be calculated as r = PEFkD(+)/(PEBkD(−)) = PE1kD(+)/[(1 − PE1)kD(−)]. Substituting eqn (1) into the above equation gives
| r = r0(1−F/FS), | (2) |
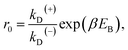 | (3) |
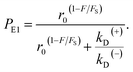 | (4) |
The velocity of the motor can be calculated as
| v = [PE1kD(+) − (1 − PE1)kD(−)]d, | (5) |
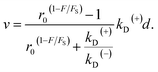 | (6) |
The equation of the dwell time between two mechanical steps can be derived as follows. Assuming that i (i ≥ 1 is an integer) ATP molecules are consumed for the motor to make a mechanical step (either a forward or backward step), the mean dwell time before the step can be calculated by i/(kD(+) + kD(−)). The probability for the motor to make a mechanical step after consuming i ATP molecules can be calculated by {[kD(+)PE1 + kD(−)(1 − PE1)]/(kD(+) + kD(−))}{[kD(+)(1 − PE1) + kD(−)PE1]/(kD(+) + kD(−))}i−1. Thus, the mean dwell time between two mechanical steps can be calculated by
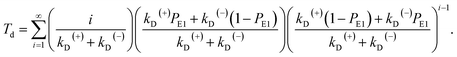 | (7) |
Simplification of eqn (7) gives
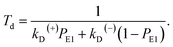 | (8) |
Substitution of eqn (4) into (8) gives
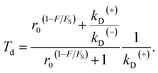 | (9) |
As seen from eqn (2), (6) and (9), only four adjustable parameters r0, FS, kD(+) and kD(−) are needed to reproduce the available single-molecule data on the dependence of the stepping ratio, velocity and dwell time upon external force at saturated ATP. The four parameters have clear physical meanings, with r0 being the stepping ratio under no external force, FS being the stall force, kD(+) being the ATPase rate of the trailing head and kD(−) being the ATPase rate of the leading head.
With eqn (2) and by adjusting r0 = 6000 and FS = 2.75 pN (see Table 1), the available single-molecule data of the stepping ratio versus force for chick brain myosin-V at saturated ATP (1 mM) measured by Uemura et al.9 and Sasaki et al.60 can be fitted well (Fig. 3a). With the above values of r0 and FS, by adjusting kD(+) = 14 s−1 and kD(−) = 0.16 s−1 (see Table 1) and using eqn (9), the available single-molecule data of the dwell time versus force for chick brain myosin-V at saturated ATP (1 mM) measured by Uemura et al.9 can also be fitted well (Fig. 3b). With eqn (6) and the parameter values given above (see Table 1), the calculated results of the velocity versus force are also in good agreement with the experimental data of Uemura et al.9 for chick brain myosin-V at 1 mM ATP (Fig. 3c).
| Parameter | Description | Value | |
|---|---|---|---|
| Under condition of Uemura et al.9 | Under condition Mehta et al.8 | ||
| a Symbol “—” denotes that the value is not required in the calculation in this work. | |||
| r0 | Stepping ratio under no load at saturated ATP | 6000 | 6000 |
| FS (pN) | Stall force at saturated ATP | 2.75 | 3 |
| kD(+) (s−1) | ADP release rate of trailing head | 14 | 11 |
| kD(−) (s−1) | ADP release rate of leading head when trailing head is in ADP state | 0.16 | 0.2 |
| CD | Ratio of ADP release rate of leading head when trailing head is in ϕ state to that when trailing head is in ADP state | 6 | 20 |
| kbT (μM−1 s−1) | Second-order rate constant of ATP binding | 0.25 | 0.7 |
| kbD(+) (μM−1 s−1) | Second-order rate constant of ADP binding to trailing head | 1.3 | — |
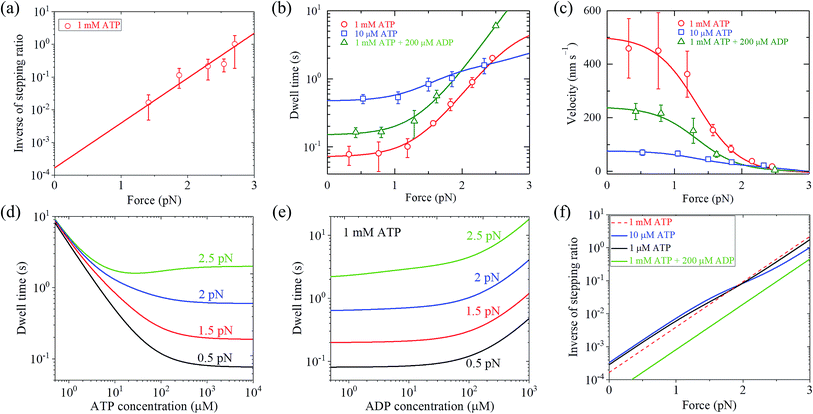 | ||
| Fig. 3 Results for dynamics of chick brain myosin-V. Lines are theoretical data calculated with parameter values given in Table 1 under the experimental conditions of Uemura et al.,9 and symbols are experimental data taken from Uemura et al.9,60 (a) Inverse of stepping ratio versus force at saturated ATP (1 mM). (b) Dwell time versus force. (c) Velocity versus force. (d) Dwell time versus ATP concentration at no additional ADP in buffer solution and for different force values. (e) Dwell time versus ADP concentration at 1 mM ATP and for different force values. (f) Inverse of stepping ratio versus force at different ATP and ADP concentrations. | ||
From eqn (3), it can be seen that the large stepping ratio under no force, r0, is attributed to both the difference in the ATPase rate between the trailing and leading heads and the bending energy (EB) of the neck domain of the actin-bound ADP-head, with the former enhancing r0 by kD(+)/kD(−)-fold while the latter enhancing r0 by exp(βEB)-fold. With the above fitted values of r0 = 6000, kD(+) = 14 s−1 and kD(−) = 0.16 s−1, it was calculated that the former makes about 56% while the latter makes about 44% contribution to r0, implying that both have comparable contributions.
Similarly, using eqn (9) and adjusting r0 = 6000, FS = 3 pN, kD(+) = 11 s−1 and kD(−) = 0.2 s−1 (see Table 1) under the experimental conditions of Mehta et al.8 (see Table 1), the calculated results of the dwell time versus the external force for chick brain myosin-V at saturated ATP are in agreement with the experimental data at 2 mM ATP8 (Fig. 4a). Note here that the four fitted parameter values under the experimental conditions of Mehta et al.8 are close to that under the experimental conditions of Uemura et al.9 (see Table 1). With the above parameter values under the experimental conditions of Mehta et al.8 (see Table 1), using eqn (6), the velocity versus the external force at saturated ATP was calculated (Fig. 4b, 2 mM). These predicted results can be tested easily using single-molecule optical trapping methods. In addition, with all the parameters having the same values as that under the experimental conditions of Mehta et al.8 except for kD(+) = 8 s−1, the calculated results of the velocity versus external force at saturated ATP (2 mM) are in agreement with the experimental data of Clemen et al.10 for chick brain myosin-V at 2 mM ATP, as shown in Fig. 4b. The difference in the values of kD(+) fitted for the experimental data of Mehta et al.8 and fitted for the experimental data of Clemen et al.10 may be due to the different buffer conditions used by the different research groups.
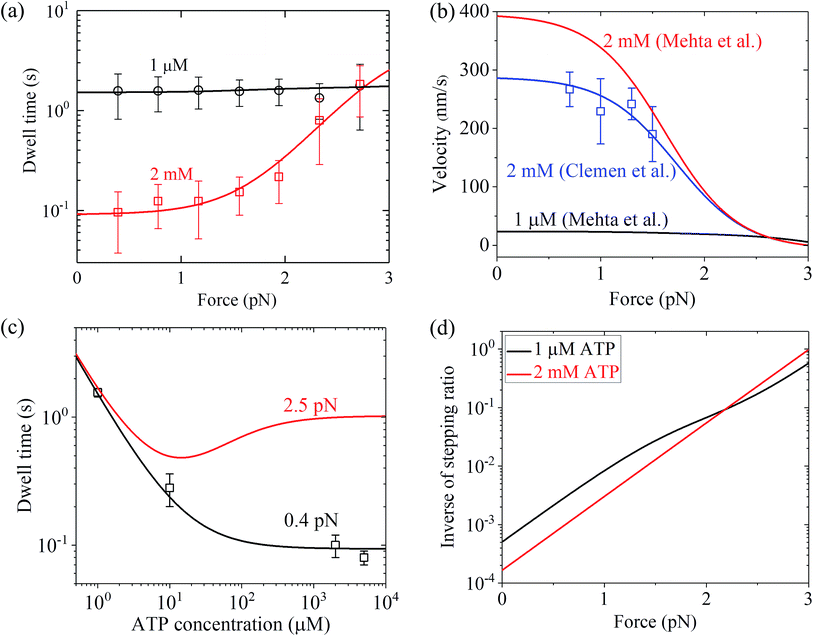 | ||
| Fig. 4 Results for dynamics of chick brain myosin-V. (a) Dwell time versus force at different ATP concentrations. Lines are theoretical data calculated with parameter values given in Table 1 under the experimental conditions of Mehta et al.,8 and symbols are experimental data taken from Mehta et al.8 (b) Velocity versus force at different ATP concentrations. Black and red lines are theoretical data calculated with parameter values given in Table 1 under the experimental conditions of Mehta et al.,8 blue line represents the theoretical data calculated with all parameters having the same values as that under the experimental conditions of Mehta et al.8 except for kD(+) = 8 s−1, and blue squares are experimental data taken from Clemen et al.10 (c) Dwell time versus ATP concentration for different force values. Lines are theoretical data calculated with parameter values given in Table 1 under the experimental conditions of Mehta et al.,8 and symbols are experimental data taken from Mehta et al.8 (d) Inverse of stepping ratio versus force at different ATP concentrations. The theoretical data was calculated with the parameter values given in Table 1 under the experimental conditions of Mehta et al.8 | ||
3.3. Dynamics at non-saturated ATP concentration
At non-saturated ATP, the pathway is shown in Fig. 1a–l and the simplified model is shown in Fig. 1m. As derived in the above section, the probability PE1 can be calculated using eqn (4). Similar to the derivation of eqn (1), the probability PE2 was derived to have following form:
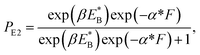 | (10) |
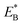 is the bending energy of the neck domain of the actin-bound ϕ-head when the detached head binds to the rear binding site on actin, as defined above, and α* = β(d*(+) + d*(−)) is independent of F, with d*(+) and d*(−) being the characteristic distances for the detached head to transit from the intermediate state (Fig. 1i or k) to the states binding to the front and rear binding sites on actin, respectively. For an approximation, d*(+) + d*(−) ≈ d(+) + d(−), and thus α* ≈ α. Then, from eqn (1)–(3) and (10), the probability PE2 can be written in another form
is the bending energy of the neck domain of the actin-bound ϕ-head when the detached head binds to the rear binding site on actin, as defined above, and α* = β(d*(+) + d*(−)) is independent of F, with d*(+) and d*(−) being the characteristic distances for the detached head to transit from the intermediate state (Fig. 1i or k) to the states binding to the front and rear binding sites on actin, respectively. For an approximation, d*(+) + d*(−) ≈ d(+) + d(−), and thus α* ≈ α. Then, from eqn (1)–(3) and (10), the probability PE2 can be written in another form
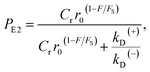 | (11) |
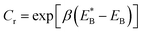 . Since
. Since 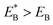 , Cr ≫ 1. Throughout, Cr = 100 was fixed, equivalent to
, Cr ≫ 1. Throughout, Cr = 100 was fixed, equivalent to 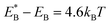 .
.
Denote by kbT(+) and kbT(−) the second-order rate constant of ATP binding to the trailing and leading heads, respectively. Throughout, kbT(+) = kbT(−) = kbT was used. The ATPase rate of the trailing head can be calculated as:
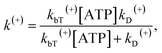 | (12) |
The occurrence probability of ADP release from the leading head with the trailing head in the ϕ state can be calculated as
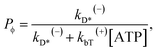 | (13) |
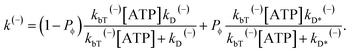 | (14) |
When an ATP molecule binds to the trailing head, the occurrence probability of the intermediate state of Fig. 1c, with the actin-bound head in ADP state, can be calculated as
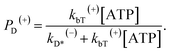 | (15) |
When an ATP molecule binds to the trailing head, the occurrence probability of the intermediate state of Fig. 1i, with the actin-bound head in the ϕ state, can then be calculated as 1 − PD(+).
When an ATP molecule binds to the leading head, the occurrence probability of the intermediate state of Fig. 1f, with the actin-bound head in the ADP state, can be calculated as
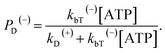 | (16) |
When an ATP molecule binds to the leading head, the occurrence probability of the intermediate state of Fig. 1k, with the actin-bound head in the ϕ state, can then be calculated as 1 − PD(−).
From the pathway shown in Fig. 1a–l, PEF = PD(+)PE1 + (1 − PD(+))PE2 and PEB = PD(−)(1 − PE1) + (1 − PD(−))(1 − PE2). Thus, the velocity of the motor can be calculated as v = (PEFk(+) − PEBk(−))d, which can be rewritten as
| v = {[PD(+)PE1 + (1 − PD(+))PE2]k(+) − [PD(−)(1 − PE1) + (1 − PD(−))(1 − PE2)]k(−)}d. | (17) |
Similar to the derivation of eqn (8) at saturated ATP, at non-saturated ATP, the following equation was finally derived for the dwell time between two mechanical steps, Td = 1/(PEFk(+) + PEBk(−)), which can be rewritten as
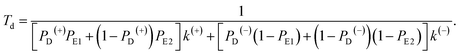 | (18) |
As expected, from eqn (12)–(18) it is noted that at saturated ATP, i.e., at [ATP] → ∞, eqn (17) and (18) are reduced to eqn (5) and (8), respectively.
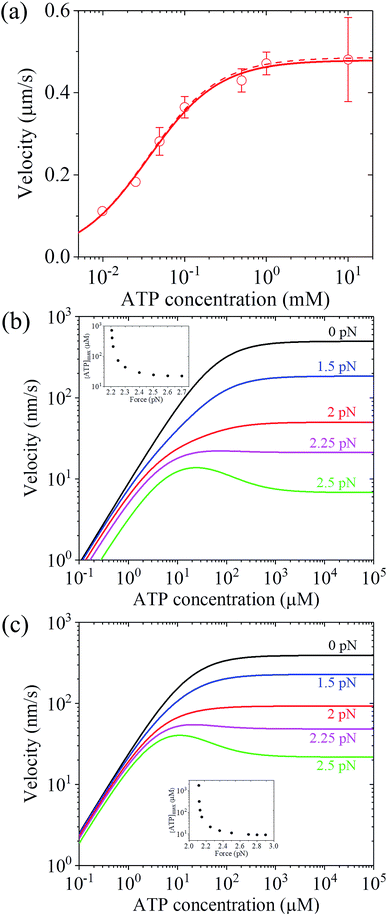
The above equations are applicable to the case of no additional ADP molecules in buffer solution. In the presence of additional ADP in buffer solution, the ADP-release rates kD(+), kD(−) and kD*(−) were replaced by κD(+), κD(−) and κD*(−), respectively. The rates κD(+), κD(−) and κD*(−) can be calculated as
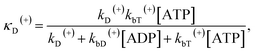 | (19) |
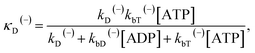 | (20) |
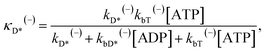 | (21) |
As seen from eqn (10)–(21), to fit the available single-molecule data on the force dependence of velocity and dwell time at non-saturated ATP, besides the four parameters r0, FS, kD(+) and kD(−), as determined in the above section for the case of saturated ATP, two additional parameters kbT and CD are needed to adjust at non-saturated ATP and no additional ADP. In the presence of additional ADP, another parameter kbD(+) is also needed for the adjustment.
With eqn (18), the values of the parameters r0, FS, kD(+) and kD(−) for chick brain myosin-V under the experimental conditions of Uemura et al.,9 as given in the above section, and by additionally adjusting kbT = 0.25 μM−1 s−1 and CD = 6 (see Table 1), the calculated results of the dwell time versus external force at 10 μM ATP and no additional ADP are in good agreement with the experimental data of Uemura et al.,9 as shown in Fig. 3b. Using eqn (17), the calculated results of the velocity versus external force at 10 μM ATP and no additional ADP are also in good agreement with the experimental data of Uemura et al.,9 as shown in Fig. 3c. In the presence of 200 μM ADP, by additionally adjusting kbD(+) = 1.3 μM−1 s−1 (see Table 1), the calculated results of both the dwell time and velocity versus external force at 1 mM ATP are also in good agreement with the experimental data of Uemura et al.,9 as shown in Fig. 3b and c. Taken together, with seven adjustable parameters (see Table 1), seven experimental curves on diverse aspects of the dynamics of chick brain myosin-V shown in Fig. 3a–c can be reproduced quantitatively.
Moreover, with the parameter values under the experimental conditions of Uemura et al.,9 as given in Table 1, the predicted results on the dependence of the dwell time upon ATP concentration under different values of the external force and no additional ADP (Fig. 3d), on the force dependence of the dwell time under different ADP concentrations and 1 mM ATP (Fig. 3e), and on the force dependence of stepping ratio under different ATP and ADP concentrations (Fig. 3f) are provided. These predicted results can be tested easily using single-molecule optical trapping.
Similarly, with eqn (18), the values of the parameters r0, FS, kD(+) and kD(−) for chick brain myosin-V under the experimental conditions of Mehta et al.,8 as given in the above section, and by additionally adjusting kbT = 0.7 μM−1 s−1 and CD = 20 (see Table 1), the calculated results of the dwell time versus external force at 1 μM ATP are in good agreement with the single-molecule data of Mehta et al.8 (Fig. 4a). The calculated results of the dwell time versus ATP concentration under a low force of 0.4 pN are also in quantitative agreement with the single-molecule data of Mehta et al.8 (Fig. 4c). Moreover, under the experimental conditions of Mehta et al.,8 the predicted results on the force dependence of the velocity at 1 μM ATP (Fig. 4b), on the dependence of dwell time upon ATP concentration under a high force of 2.5 pN (Fig. 4c) and on the force dependence of stepping ratio under different ATP concentrations (Fig. 4d) are provided.
From Fig. 3b, c and 4a, b it is interesting to see that both the theoretical and experimental data show that for myosin-V, at low ATP, the dwell time and velocity have less force dependence than at high ATP. In particular, under the experimental conditions of Mehta et al.,8 at 1 μM ATP, the dwell time is nearly independent of the force, whereas at 2 mM ATP the dwell time increases sensitively with an increase in the force (Fig. 4a). Under the large force near the stall force, the dwell time at 2 mM ATP becomes nearly equal to and even larger than that at 1 μM ATP (Fig. 4a). For comparison, the model of tight chemomechanical coupling (see Section S1 in the ESI†) was considered, where the force dependence of the dwell time at saturated ATP was assumed to result from the force dependence of the ADP-release rate. It is shown that even with the argument of the second-order rate constant of ATP binding being independent of F, under any F, the dwell time at low ATP is always evidently larger than that at high ATP (Fig. S1,† lines). For example, under F = 2.7 pN the dwell time at 1 μM ATP is about 2-fold larger than that at 2 mM ATP (Fig. S1,† lines), which is contrary to the single-molecule data showing that under F = 2.7 pN the dwell time at 1 μM ATP is nearly equal to or slightly smaller than that at 2 mM ATP (Fig. S1† or Fig. 4a, symbols).
Up to here, the dependence of dwell time on force and ATP concentration, dependence of stepping ratio on force, and dependence of velocity on force (Fig. 3 and 4) have been the focus. Thus, here, the dependence of velocity on ATP concentration using eqn (17) is discussed. Under F = 0, since r0 ≫ kD(+)/kD(−) (see Table 1), from eqn (4) and (11), PE1 ≈ 1 and PE2 ≈ 1. Thus, from eqn (17) v ≈ k(+)d. Hence, only two parameters kD(+) and kbT are required to calculate v versus ATP concentration under F = 0. For example, by adjusting kD(+) = 13.5 s−1 and kbT = 0.38 μM−1 s−1, the available experimental data for the velocity versus ATP concentration under F = 0 for murine myosin-V measured by Zhang et al.61 can be fitted well (red dashed line, Fig. 5a). For comparison, Fig. 5a (red solid line) also shows the results under F = 0 calculated using eqn (17) and the parameter values given in Table 1 under the experimental conditions of Uemura et al.9 except for kD(+) = 13.5 s−1 and kbT = 0.38 μM−1 s−1. As expected, the two curves are nearly identical.
 | ||
| Fig. 5 Results for the dependence of velocity of myosin-V on ATP concentration. (a) Under no force. Dashed line represents the theoretical data calculated using v = k(+)d and kD(+) = 13.5 s−1 and kbT = 0.38 μM−1 s−1. Solid line represents the theoretical data calculated using eqn (17) and parameter values given in Table 1 under the experimental conditions of Uemura et al.9 except for kD(+) = 13.5 s−1 and kbT = 0.38 μM−1 s−1, and circles represent experimental data taken from Zhang et al.61 (b) Under force with different values. Lines are theoretical data calculated using eqn (17) and parameter values given in Table 1 under the experimental conditions of Uemura et al.9 Inset shows the ATP concentration, [ATP]max, at which the maximum velocity occurs, versus force. (c) Under force with different values. Lines are theoretical data calculated using eqn (17) and parameter values given in Table 1 under the experimental conditions of Mehta et al.8 Inset shows the ATP concentration, [ATP]max, at which the maximum velocity occurs, versus force. | ||
To see the dependence of velocity on ATP concentration under an external force, calculations were performed using eqn (17) and the parameter values given in Table 1 under the experimental conditions of Uemura et al.9 and under the experimental conditions of Mehta et al.,8 with the calculated results shown in Fig. 5b and c, respectively. From Fig. 5b and c, it can be seen that under a low force, the velocity increases with an increase in ATP concentration and saturates at high ATP concentrations, as expected. Interestingly, under a high force, the velocity does not increase monotonously with an increase in ATP concentration and the maximum velocity occurs at an intermediate ATP concentration. The ATP concentration, [ATP]max, at which the maximum velocity occurs, levels out at high forces and increases significantly with a decrease in the force, with [ATP]max becoming infinite at a force of about 2.2 pN and 2.11 pN under the experimental conditions of Uemura et al.9 (inset of Fig. 5b) and Mehta et al.8 (inset of Fig. 5c), respectively. These predicted results can be tested easily with single-molecule optical trapping methods.
3.4. Number of ATP molecules hydrolyzed per mechanical step
In this section, the number of ATP molecules hydrolyzed per mechanical step (either a forward or backward step) is studied, which is equal to the inverse of the chemomechanical coupling ratio. Based on the simplified model (Fig. 1m), the number of ATP molecules hydrolyzed per unit time is k(+) + k(−), while the number of mechanical steps (including both the forward and backward steps) per unit time is PEFk(+) + PEBk(−), where, PEF = PD(+)PE1 + (1 − PD(+))PE2 and PEB = PD(−)(1 − PE1) + (1 − PD(−))(1 − PE2). The mean number of ATP molecules hydrolyzed per mechanical step can be calculated as N = (k(+) + k(−))/(PEFk(+) + PEBk(−)), which can be rewritten as
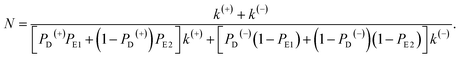 | (22) |
Using eqn (22) and the parameter values given in Table 1 under the experimental conditions of Uemura et al.9 and Mehta et al.,8 N was calculated as a function of force and ATP concentration. The results are shown in Fig. 6. From Fig. 6a and c, it can be seen that at low ATP (e.g., 1 μM), N is insensitive to the force, with N being close to 1, implying nearly tight chemomechanical coupling. As the ATP concentration increases, N becomes more and more sensitive to the force, with N increasing with an increase in force. From Fig. 6b and d, it can be seen that under low force (e.g., 0.5 pN), N is close to 1. Under high force, N increases significantly with an increase in ATP concentration. N ≫ 1 under large force implies evidently non-tight chemomechanical coupling. Consequently, it can be concluded that in general, at low ATP and under any force, the motor exhibits nearly tight chemomechanical coupling, and at high ATP and under high force, the motor exhibits evidently non-tight chemomechanical coupling.
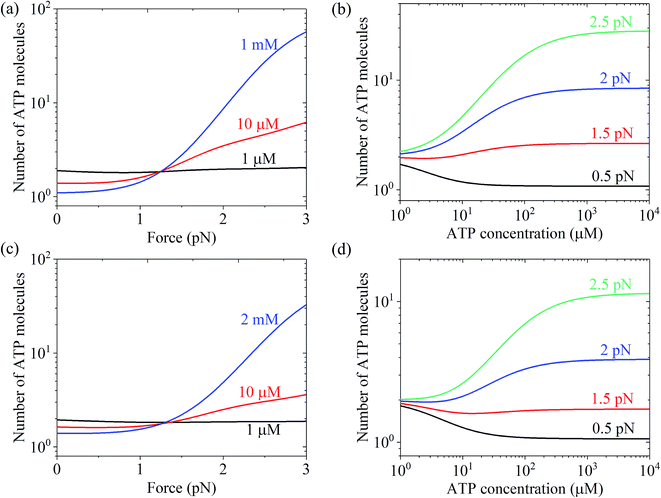 | ||
| Fig. 6 Results of the mean number of ATP molecules consumed per mechanical step for chick brain myosin-V. (a) Number versus force at different ATP concentrations. The data was calculated using the parameter values given in Table 1 under the experimental conditions of Uemura et al.9 (b) Number versus ATP concentration for different values of the force. The data are calculated with parameter values given in Table 1 under the experimental condition of Uemura et al.9 (c) Number versus force at different ATP concentrations. The data was calculated with parameter values given in Table 1 under the experimental conditions of Mehta et al.8 (d) Number versus ATP concentration for different force values. The data was calculated using the parameter values given in Table 1 under the experimental conditions of Mehta et al.8 | ||
4. Concluding remarks
Herein, a model for the chemomechanical coupling of myosin-V motors was proposed. In this model, the forward tilting of the neck domain of the actin-bound head in the ADP or ϕ state plays a role in the biased binding of the detached head to the front binding site on actin. By contrast, in the previously proposed models, it was proposed that the forward tilting of the neck domain of the actin-bound head acts as a power stroke that drives the detached head moving forward. Moreover, it was proposed here that the rate constants of ATPase activity are independent of the external force in a range smaller than the stall force, which is contrary to the previous proposal that the rate constants of the ATPase activity depends sensitively on the external force. Based on the current model and proposal, the dynamics of myosin-V motor was studied analytically. The theoretical data quantitatively reproduced the available single-molecule data on the force and ATP dependence of stepping ratio, dwell time and velocity. In particular, the experimental data showing that at low ATP, the dwell time and velocity have less force dependence than at high ATP are explained well.It was noted that the model of myosin-V proposed here is similar to that of kinesin presented before.58 In the latter, the neck linker docking of the MT-bound head in the ATP or ADP·Pi state plays a role in biased diffusing of the detached head from the intermediate position to the front binding site on MT rather than as a power stroke that drives the detached head moving forward. The rate constants of kinesin ATPase activity are also independent of the external force. Since the two models are similar, the dynamics of myosin-V and that of kinesin can be described by similar equations at saturated ATP. However, at non-saturated ATP, the two motors behave differently in the ATP-dependent dynamics. The reason for this difference is as follows. For myosin-V, the lifetime of the intermediate state with one head bound to actin is very short at any ATP concentration. When the actin-bound head is in the ADP state, the probability for the detached head to move from the intermediate position to the front binding site on actin is different from that when the actin-bound head is in the ϕ state. By contrast, for kinesin, the lifetime of the intermediate state with one head bound to MT is dependent on the ATP concentration, and when the MT-bound head is in the ϕ state the detached head is not allowed to bind MT.58
Finally, it should be mentioned that only the forward and backward stepping of the myosin-V motor resulting from the ATPase activity under a backward force smaller than the stall force were considered. Specifically, only the ATP-dependent stepping was considered. The single-molecule data of Gebhardt et al.12 showed that under a high backward force, myosin-V can also make ATP-independent backward stepping. This can be explained as follows. Under the experimental conditions of Gebhardt et al.,12 the backward force can drive the leading head in the ϕ or ADP state bound strongly to actin (called strongly-binding state) to detach from actin. In our model, if the detachment of the leading head from actin in the strongly-binding state was considered, the force dependence of velocity can still be calculated using eqn (17), but with k(−) being replaced with k(−) + ε0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(F/Fd) (see Section S2 in the ESI†), where ε0 is the detachment rate of the leading head in the strongly-binding state under F = 0 and Fd is the characteristic detachment force. By adjusting ε0 = 1.3 s−1 and Fd = 4.5 pN and taking the values of the parameters related to ATPase activity and ATP-dependent stepping under the experimental conditions of Uemura et al.9 (see Table 1) except for kbT = 2 μM−1 s−1, the available single-molecule data of Gebhardt et al.12 at 1 μM ATP can be fitted very well, as shown in Fig. 7 (black line). For comparison, the calculated data without considering ATP-independent backward stepping (i.e., taking ε0 = 0) is also shown in Fig. 7 (red line). Note that different experimental conditions give different values of ε0.
exp(F/Fd) (see Section S2 in the ESI†), where ε0 is the detachment rate of the leading head in the strongly-binding state under F = 0 and Fd is the characteristic detachment force. By adjusting ε0 = 1.3 s−1 and Fd = 4.5 pN and taking the values of the parameters related to ATPase activity and ATP-dependent stepping under the experimental conditions of Uemura et al.9 (see Table 1) except for kbT = 2 μM−1 s−1, the available single-molecule data of Gebhardt et al.12 at 1 μM ATP can be fitted very well, as shown in Fig. 7 (black line). For comparison, the calculated data without considering ATP-independent backward stepping (i.e., taking ε0 = 0) is also shown in Fig. 7 (red line). Note that different experimental conditions give different values of ε0.
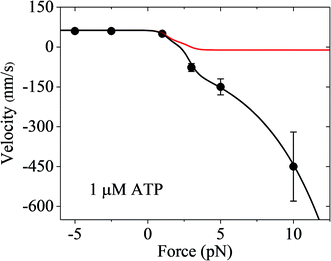 | ||
| Fig. 7 Results of the force dependence of velocity for chick brain myosin-V with the inclusion of ATP-independent backward stepping under the experimental conditions of Gebhardt et al.12 Lines are theoretical data calculated using the parameter values given in Table 1 under the experimental conditions of Uemura et al.9 except for kbT = 2 μM−1 s−1. Circles are experimental data at 1 μM ATP taken from Gebhardt et al.12 Black line is the case with the inclusion of ATP-independent backward stepping (ε0 = 1.3 s−1 and Fd = 4.5 pN). Red line is the case without inclusion of ATP-independent backward stepping (ε0 = 0). | ||
Conflicts of interest
No conflict of interest exists.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11775301).References
- S. Reck-Peterson, D. W. Provance, M. S. Mooseker and J. A. Mercer, Biochim. Biophys. Acta, 2000, 1496, 36–51 CrossRef CAS.
- R. D. Vale, Cell, 2003, 112, 467–480 CrossRef CAS PubMed.
- A. Yildiz, J. N. Forkey, S. A. McKinney, T. Ha, Y. E. Goldman and P. R. Selvin, Science, 2003, 300, 2061–2065 CrossRef CAS PubMed.
- J. N. Forkey, M. E. Quinlan, M. A. Shaw, J. E. T. Corrie and Y. E. Goldman, Nature, 2003, 422, 399–404 CrossRef CAS PubMed.
- N. Kodera, D. Yamamoto, R. Ishikawa and T. Ando, Nature, 2010, 468, 72–76 CrossRef CAS PubMed.
- J. Andrecka, J. O. Arroyo, Y. Takagi, G. de Wit, A. Fineberg, L. MacKinnon, G. Young, J. R. Sellers and P. Kukura, eLife, 2015, 4, e05413 CrossRef PubMed.
- T. Sakamoto, M. R. Webb, E. Forgacs, H. D. White and J. R. Sellers, Nature, 2008, 455, 128–132 CrossRef CAS PubMed.
- A. D. Mehta, R. S. Rock, M. Rief, J. A. Spudich, M. S. Mooseker and R. E. Cheney, Nature, 1999, 400, 590–593 CrossRef CAS PubMed.
- S. Uemura, H. Higuchi, A. O. Olivares, E. M. De La Cruz and S. Ishiwata, Nat. Struct. Mol. Biol., 2004, 11, 877–883 CrossRef CAS PubMed.
- A. E. M. Clemen, M. Vilfan, J. Jaud, J. Zhang, M. Barmann and M. Rief, Biophys. J., 2005, 88, 4402–4410 CrossRef CAS PubMed.
- N. M. Kad, K. M. Trybus and D. M. Warshaw, J. Biol. Chem., 2008, 283, 17477–17484 CrossRef CAS PubMed.
- J. C. M. Gebhardt, A. E. M. Clemen, J. Jaud and M. Rief, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 8680–8685 CrossRef CAS PubMed.
- A. B. Kolomeisky and M. E. Fisher, Biophys. J., 2003, 84, 1642–1650 CrossRef CAS PubMed.
- A. Vilfan, Biophys. J., 2005, 88, 3792–3805 CrossRef CAS PubMed.
- G. H. Lan and S. X. Sun, Biophys. J., 2005, 88, 999–1008 CrossRef CAS PubMed.
- K. I. Skau, R. B. Hoyle and M. S. Turner, Biophys. J., 2006, 91, 2475–2489 CrossRef CAS PubMed.
- P. Xie, S.-X. Dou and P.-Y. Wang, Biophys. Chem., 2006, 120, 225–236 CrossRef CAS PubMed.
- E. M. Craig and H. Linke, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18261–18266 CrossRef CAS PubMed.
- V. Bierbaum and R. Lipowsky, Biophys. J., 2011, 100, 1747–1755 CrossRef CAS PubMed.
- W. Zheng, Proteins, 2011, 79, 2291–2305 CrossRef CAS PubMed.
- M. Hinczewski, R. Tehver and D. Thirumalai, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E4059–E4068 CrossRef CAS PubMed.
- S. Mukherjee, R. Alhadeff and A. Warshel, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2259–2264 CrossRef CAS PubMed.
- T. Sumi, Sci. Rep., 2017, 7, 13489 CrossRef PubMed.
- Y. C. Chou, Phys. A, 2019, 521, 399–405 CrossRef.
- M. A. Geeves and K. C. Holmes, Annu. Rev. Biochem., 1999, 68, 687–728 CrossRef CAS PubMed.
- S. Highsmith, Biochemistry, 1999, 38, 9791–9797 CrossRef CAS PubMed.
- A. Houdusse and H. L. Sweeney, Curr. Opin. Struct. Biol., 2001, 11, 182–194 CrossRef CAS PubMed.
- J. A. Spudich, Nat. Rev. Mol. Cell Biol., 2001, 2, 387–392 CrossRef CAS PubMed.
- M. A. Geeves, R. Fedorov and D. J. Manstein, Cell. Mol. Life Sci., 2005, 62, 1462–1477 CrossRef CAS PubMed.
- P. Xie, Biophys. Chem., 2010, 151, 71–80 CrossRef CAS PubMed.
- A. Orlova and E. H. Egelman, J. Mol. Biol., 1997, 265, 469–474 CrossRef CAS PubMed.
- E. Prochniewicz, T. F. Walseth and D. D. Thomas, Biochemistry, 2004, 43, 10642–10652 CrossRef CAS PubMed.
- J. von der Ecken, S. M. Heissler, S. Pathan-Chhatbar, D. J. Manstein and S. Raunser, Nature, 2016, 534, 724–728 CrossRef PubMed.
- P. Xie, Biochim. Biophys. Acta, 2008, 1777, 1195–1202 CrossRef CAS PubMed.
- P. Xie, Int. J. Biol. Sci., 2010, 6, 665–674 CrossRef CAS PubMed.
- S.-K. Guo, P.-Y. Wang and P. Xie, J. Theor. Biol., 2017, 414, 62–75 CrossRef CAS PubMed.
- S.-K. Guo, P.-Y. Wang and P. Xie, Int. J. Biol. Macromol., 2017, 105, 1126–1137 CrossRef CAS PubMed.
- X.-X. Shi, Y.-B. Fu, S.-K. Guo, P.-Y. Wang, H. Chen and P. Xie, Proteins, 2018, 86, 1127–1139 CrossRef CAS PubMed.
- J. E. Baker, I. Brust-Mascher, S. Ramachandran, L. E. W. LaConte and D. D. Thomas, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 2944–2949 CrossRef CAS PubMed.
- Y. E. Goldman, Cell, 1998, 93, 1–4 CrossRef CAS PubMed.
- O. Roopnarine, A. G. Szent-Györgyi and D. D. Thomas, Biochemistry, 1998, 37, 14428–14436 CrossRef CAS PubMed.
- D. M. Warshaw, E. Hayes, D. Gaffney, A. M. Lauzon, J. Wu, G. Kennedy, K. Trybus, S. Lowey and C. Berger, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 8034–8039 CrossRef CAS PubMed.
- M. Walker, X.-Z. Zhang, W. Jiang, J. Trinick and H. D. White, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 465–470 CrossRef CAS PubMed.
- N. Volkmann and D. Hanein, Curr. Opin. Cell Biol., 2000, 12, 26–34 CrossRef CAS PubMed.
- J. Xu and D. D. Root, Biophys. J., 2000, 79, 1498–1510 CrossRef CAS PubMed.
- R. Cooke, Physiol. Rev., 1997, 77, 671–697 CrossRef CAS PubMed.
- M. Whitaker, E. M. Wilson-Kubalek, J. E. Smith, L. Faust, R. A. Milligan and H. L. Sweeney, Nature, 1995, 378, 748–751 CrossRef PubMed.
- J. D. Jontes, E. M. Wilson-Kubalek and R. A. Milligan, Nature, 1995, 378, 751–753 CrossRef CAS PubMed.
- S. F. Wulf, V. Ropars, S. Fujita-Becker, M. Oster, G. Hofhaus, L. G. Trabuco, O. Pylypenko, H. L. Sweeney, A. M. Houdusse and R. R. Schröder, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E1844–E1852 CrossRef CAS PubMed.
- N. B. Becker, S. M. Altmann, T. Scholz, J. K. H. Hörber, E. H. K. Stelzer and A. Rohrbach, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 021907 CrossRef PubMed.
- R. A. Mendelson and P. H. Cheung, Biochemistry, 1978, 17, 2139–2148 CrossRef CAS PubMed.
- S. Ishiwata, K. Kinosita Jr, H. Yoshimura and A. Ikegami, J. Biol. Chem., 1987, 262, 8314–8317 CAS.
- T. Sakamoto, F. Wang, S. Schmitz, Y. Xu, Q. Xu, J. E. Molloy, C. Veigel and J. R. Sellers, J. Biol. Chem., 2003, 278, 29201–29207 CrossRef CAS PubMed.
- F. Wang, L. Chen, O. Arcucci, E. V. Harvey, B. Bowers, Y. Xu, J. A. Hammer III and J. R. Sellers, J. Biol. Chem., 2000, 275, 4329–4335 CrossRef CAS PubMed.
- E. Katayama, J. Mol. Biol., 1998, 278, 349–367 CrossRef CAS PubMed.
- Y. Takagi, R. E. Farrow, N. Billington, A. Nagy, C. Batters, Y. Yang, J. R. Sellers and J. E. Molloy, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E1833–E1842 CrossRef CAS PubMed.
- P. Xie and H. Chen, Phys. Chem. Chem. Phys., 2018, 20, 4752–4759 RSC.
- P. Xie, S.-K. Guo and H. Chen, J. Chem. Inf. Model., 2019, 59, 360–372 CrossRef CAS PubMed.
- A. Yildiz, M. Tomishige, A. Gennerich and R. D. Vale, Cell, 2008, 134, 1030–1041 CrossRef CAS PubMed.
- K. Sasaki, M. Kaya and H. Higuchi, Biophys. J., 2018, 115, 1–12 Search PubMed.
- C. Zhang, M. Y. Ali, D. M. Warshaw and N. M. Kad, Biophys. J., 2012, 103, 728–737 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra05072h |
| This journal is © The Royal Society of Chemistry 2019 |
