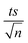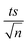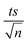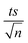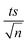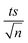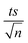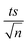DOI:
10.1039/C9RA05362J
(Paper)
RSC Adv., 2019,
9, 33472-33485
Chemically and thermally activated persulfate for theophylline degradation and application to pharmaceutical factory effluent†
Received
13th July 2019
, Accepted 26th September 2019
First published on 18th October 2019
Abstract
Degradation of PPCPs by AOPs has gained major interest in the past decade. In this work, theophylline (TP) oxidation was studied in thermally (TAP) and chemically (CAP) activated persulfate systems, separately and in combination (TCAP). For [TP]0 = 10 mg L−1, (i) TAP resulted in 60% TP degradation at [PS]0 = 5 mM and T = 60 °C after 60 min of reaction and (ii) CAP showed slight degradation at room temperature; however, (iii) TCAP resulted in complete TP degradation for [PS]0 = [Fe2+]0 = 2 mM at T = 60 °C following a pseudo-first order reaction rate with calculated kobs = 5.6 (±0.4) × 10−2 min−1. In the TCAP system, the [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 1
[Fe2+]0 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 presented the best results. A positive correlation was obtained between the TP degradation rate and increasing temperature and [PS]0, and a negative correlation was obtained with increasing pH. Both chloride and humic acid inhibited the degradation process, while nitrates enhanced it. TP dissolved in spring, sea and waste water simulating real effluents showed lower degradation rates than in DI water. Waste water caused the highest inhibition (kobs = 2.6 (±0.6) × 10−4 min−1). Finally, the TCAP system was tested on a real factory effluent highly charged with TP, e.g. [TP]0 = 160 mg L−1, with successful degradation under the conditions of 60 °C and [PS]0 = [Fe2+]0 = 50 mM.
1 presented the best results. A positive correlation was obtained between the TP degradation rate and increasing temperature and [PS]0, and a negative correlation was obtained with increasing pH. Both chloride and humic acid inhibited the degradation process, while nitrates enhanced it. TP dissolved in spring, sea and waste water simulating real effluents showed lower degradation rates than in DI water. Waste water caused the highest inhibition (kobs = 2.6 (±0.6) × 10−4 min−1). Finally, the TCAP system was tested on a real factory effluent highly charged with TP, e.g. [TP]0 = 160 mg L−1, with successful degradation under the conditions of 60 °C and [PS]0 = [Fe2+]0 = 50 mM.
1. Introduction
Theophylline (TP), or 1,3-dimethyl-7H-purine-2,6-dione, is a crystalline compound that is used in the treatment of respiratory diseases such as asthma and wheezing; it is also found in trace amounts in normal diet foods, such as tea and cocoa beans.1,2 TP belongs to the pharmaceuticals and personal care products (PPCPs) family, whose members have gained global attention in the past few decades as emerging contaminants. This increased attention is attributed to the discovery of PPCPs in ground and surface water, aided by advancements in analytical techniques which enable their detection at previously undetectable concentrations.3 The presence of PPCPs in water, even at low concentrations, poses environmental hazards and possible public health risks. Among these risks are bioaccumulation, such as the accumulation of lipophilic PPCPs in aquatic organisms4,5 and the development of antibiotic resistance,6 in addition to uncertain synergistic/antagonist effects of long term exposure to mixtures of pharmaceuticals at low concentrations.7 TP is introduced into nature by several pathways, such as from untreated pharmaceutical production plant wastewater effluents, in addition to domestic wastewater, which can contain TP from direct disposal of the drug and from urine excretion; this contributes to the pollution of water bodies by TP.8,9
To solve the problem of water contamination by several pollutants, water treatment plants are integrated to treat wastewater discharges from domestic, agricultural and industrial sources. Conventional water treatment methods include, but are not limited to, carbon adsorption, chemical precipitation, evaporation and ion exchange.10 It has been shown that conventional methods do not treat PPCPs efficiently; PPCPs are resistant to such treatment and have been detected in drinking water.11–13 One of the pharmaceuticals detected in water is TP. It was found in spring water in Lebanon, possibly due to the discharge of untreated waste water.14 TP degradation has been studied during the past decades by several methods, including degradation by means of ferrate(VI)15 and a metal organic framework (Pd@MIL-100(Fe)) with visible light (λ ≥ 420 nm),16 UV/H2O2,17,18 and UV/TiO2 nanobelts.19 Novel water treatment methods include advanced oxidation processes (AOPs), which have been proved to be significantly efficient in removing persistent organic compounds. A wide variety of techniques involving different oxidants and different methods of activation are used in AOPs; examples include Fenton,20 photo-Fenton,21 UV/PS,22,23 Fe/PS,24,25 and heat/PS26–29 systems, in addition to alkaline/PS and alkaline/peroxymonosulfate30 systems. PS and H2O2 are the two most commonly used effective oxidants in AOPs; however, PS poses some advantages over H2O2 in terms of cost, safety in handling, and ease of access in some regions. PS is effective in degrading several pharmaceuticals;31–34 however, to our knowledge, it has not been tested by other research groups to treat TP. The main PS activation methods are UV, chemical, and heat activation, which generate highly reactive sulfate radicals (SRs) (eqn (1)–(3)).22–29,34,35 Our research group has recently studied TP degradation by UV-activated PS.36
In this study, TP degradation by thermally activated PS (TAP) and chemically activated PS (CAP) was studied separately as well as in a combined thermally and chemically activated PS (TCAP) system. The combination of activation techniques was applied, for the first time, to simulated effluents and to a real highly concentrated pharmaceutical effluent collected from a local pharmaceutical factory. The degradation process was optimized by testing several parameters in order to obtain efficient degradation within a reasonable time at an affordable cost. Finally, charge distribution and frontier orbital calculations were investigated in order to better elucidate the TP degradation mechanism by oxidative radical species in solution.
| | |
S2O82− → 2SO4˙− (thermal activation) 30 °C < T < 99 °C
| (1) |
| | |
S2O82− + Fe2+ → SO42− + SO4˙− + Fe3+ (chemical activation)
| (2) |
| | |
S2O82− + hν → 2SO4˙− (UV activation)
| (3) |
2. Materials and methods
2.1. Chemicals
Theophylline (C7H8N4O2) (C7H8N4O2, ≥99%) and sodium persulfate (PS) (Na2S2O8, ≥99.0%), were obtained from Sigma-Aldrich (China and France, respectively). Methanol (MeOH, CH4O) and tertiary butyl alcohol (TBA) of HPLC grade were purchased from Sigma-Aldrich (Germany). MeOH was used as the mobile phase for chromatographic analysis in combination with deionized water (DI). Ferrous chloride tetrahydrate (FeCl2·4H2O), used as a chemical activator for PS, was obtained from Fluka (Switzerland). HCl (37%) was obtained from Fluka (Netherlands) and used to dissolve FeCl2 in the preparation of stock solutions. To evaluate the effects of ionic additives, sodium chloride (NaCl) was purchased from Fluka (Netherlands), and sodium nitrate (NaNO3) was obtained from Sigma-Aldrich (Germany). DI water was used for the preparation of all solutions in this study.
2.2. Chemical analysis: TP quantification and identification
High performance liquid chromatography (HPLC, Agilent 1100 series) was used for TP quantification. The HPLC was equipped with a thermo-electrically cooled autosampler unit, a quaternary pump, a vacuum degasser, and a thermally controlled column. Separation of TP from other by-products was enabled by the use of a C-18 reverse phase column (Discovery® HS, 5 μm; 4.6 mm internal diameter × 250 mm length) connected to a guard column (HS C-18, 5 μm; 4.0 mm internal diameter, 20 mm length) (Pennsylvania, USA). The temperature of the column was set at 30 °C, while that of the autosampler compartment was set at 4 °C. A column flow rate of 0.5 mL min−1 was used with a mobile phase consisting of water and MeOH (70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 ratio) maintained in isocratic mode. The injection volume was set at 80 μL. A diode-array detector for the quantification of TP was coupled to the HPLC. For the aforementioned conditions, the TP retention time was observed to be 12 min. All samples were filtered using 0.45 μm PTFE 13 mm disc filters (Jaytee Biosciences Ltd., UK) before HPLC analysis. Selected TP chemical properties in addition to the calibration curve and the corresponding LINEST output are summarized in ESI Fig. 1S(a–c).† Identification of the degradation and transformation products of TP was performed on an Ultimate 3000 RSLC Thermo Scientific HPLC-MS/MS connected to a Q Exactive Orbitrap. A Hypersil GOLD C18 150 column (100 × 2.1 mm, 1.9 μm) was used for separation. The injection volume was set as 2 μL and the elution process was performed at a flow rate of 0.3 mL min−1 using DI water (containing 0.1% formic acid) as eluent A and methanol as eluent B. The mass spectrometer was operated in positive ionization mode. The auxiliary gas heater temperature was set as 350 °C and the capillary temperature was 320 °C.
30 ratio) maintained in isocratic mode. The injection volume was set at 80 μL. A diode-array detector for the quantification of TP was coupled to the HPLC. For the aforementioned conditions, the TP retention time was observed to be 12 min. All samples were filtered using 0.45 μm PTFE 13 mm disc filters (Jaytee Biosciences Ltd., UK) before HPLC analysis. Selected TP chemical properties in addition to the calibration curve and the corresponding LINEST output are summarized in ESI Fig. 1S(a–c).† Identification of the degradation and transformation products of TP was performed on an Ultimate 3000 RSLC Thermo Scientific HPLC-MS/MS connected to a Q Exactive Orbitrap. A Hypersil GOLD C18 150 column (100 × 2.1 mm, 1.9 μm) was used for separation. The injection volume was set as 2 μL and the elution process was performed at a flow rate of 0.3 mL min−1 using DI water (containing 0.1% formic acid) as eluent A and methanol as eluent B. The mass spectrometer was operated in positive ionization mode. The auxiliary gas heater temperature was set as 350 °C and the capillary temperature was 320 °C.
2.3. Experimental setup
The experimental setup consisted of 200 mL Erlenmeyer flasks used as reactors and immersed in a controlled-temperature water bath. The latter was equipped with an orbital shaker (Wise Bath WSB-30) and amended with a homemade Plexiglas cover plate with the capacity to hold all the Erlenmeyer flasks by their necks in order to prevent the reactors from falling (Fig. 2S†). The experimental setup could accommodate up to 12 reactors at a time, and all experiments were performed in triplicate. The reactors were efficiently submerged in the water bath to ensure that their temperatures matched that of the surrounding water. This was further guaranteed by the measurement of the inner temperature of the reactor using a thermometer. The temperatures tested were room temperature in addition to 40 °C to 75 °C. To ensure proper homogenization and heat distribution, the orbital shaker was set at 70 revolutions per minute throughout the experiments.
2.4. Experimental procedure
The stock solutions were prepared as follows: TP (100 mg L−1) was prepared by dissolving 100 mg of dry TP powder in 1 L of DI water; PS (100 mM) was prepared by dissolving 2.38 g of sodium persulfate in 100 mL of DI; FeCl2 (80 mM) was prepared by dissolving 3.1808 g of FeCl2·4H2O in concentrated HCl (37%) in a 250 mL volumetric flask, followed by the addition of DI. The stock solutions were prepared weekly and stored in the dark at 4 °C. The water bath was turned on before the experiments to attain the required temperature. The reactors outside the water bath were each filled with predetermined amounts of prepared concentrated stock solutions of TP and matrix solution when required, in addition to DI water. Each obtained solution was mixed and preheated in the water bath to reach the desired temperature. Finally, the experiment was initiated by adding FeCl2 (20 mM) and PS (100 mM) stock solutions, reaching a final reactor volume of 200 mL. Samples were withdrawn using a clean 1 mL syringe from every reactor, then filtered using a 0.45 μm PTFE 13 mm disc filter and stored in 2 mL HPLC vials. To quench any further oxidation reactions after sample withdrawal, vials were placed in an ice bath to prevent further thermal activation of PS26 and spiked with 0.5 mL of methanol to prevent further chemical activation of PS.34 Waste water used in real water sample experiments was pre-filtered using a 1 μm ashless glass fiber filter.
2.5. Calculation of charge distributions and frontier orbitals
The theoretical calculations were performed using the Gaussian 09 program37 with density functional theory. The Becke 3-parameter Lee–Yang–Parr (B3LYP)38,39 functional was used with the 6-311++(2d,2p) basis set. First, the molecular parameters of theophylline molecule were optimized using the mentioned level of theory. Second, at the same level of theory, the frontier electron densities and Mulliken charge distributions were obtained utilizing the optimized parameters.
3. Results and discussion
3.1. Thermal activation of PS (TAP system)
3.1.1. Thermal stability of TP and effects of [PS]0. To test the stability and behaviour of TP molecules under thermal stress, control experiments were conducted in a PS-free medium with [TP]0 = 10 mg L−1 at different temperatures (40–75 °C) for a total reaction time of 60 min.As can be noted in Fig. 3S,† heat did not significantly affect the stability of TP in aqueous solutions. In fact, a slight decline in the concentration of TP was observed, with a maximum of about 5% for T = 40–75 °C, demonstrating the thermal stability of TP.
Thermal activation was tested by spiking a [TP]0 = 10 mg L−1 solution with different concentrations of PS at 60 °C. Table 1 and Fig. 4S† show that the TP degradation increased from 3% to 60% with increasing [PS]0 from 0.25 mM to 5 mM, respectively, after a period of 60 min. This increase in the % degradation is attributed to the production of more SO4˙− in the more PS-concentrated solution, as per eqn (1).
Table 1 % TP degradation in the TAP system at T = 55–75 °C and different [PS]0, and in the CAP system at room temperature. Experimental conditions: [PS]0 = 0.25–5 mM, [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios = 1
[Fe2+]0 ratios = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, 1
10, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and 1
5 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and [TP]0 = 10 mg L−1 for all studied cases
1, and [TP]0 = 10 mg L−1 for all studied cases
| Activation method |
[TP]0 (mg L−1) |
T (°C) |
[PS]0 (mM) |
[Fe2+]0 (mM) |
% degradation at t = 60 min |
pHi/pHf |
| Check Fig. 4S, Fig. 1a. Check Fig. 5S |
| TAa |
10 |
55 |
2 |
— |
14 |
3.83/3.69 |
| 60 |
0.25 |
3 |
4.30/4.56 |
| 1 |
12 |
3.87/3.75 |
| 2 |
28 |
3.83/3.58 |
| 5 |
60 |
3.41/3.05 |
| 65 |
2 |
45 |
3.57/3.46 |
| 70 |
100 |
3.57/3.22 |
| 75 |
100 |
3.50/3.22 |
| CAb |
10 |
20 |
0.25 |
0.025 |
0.5 |
3.48/3.83 |
| 0.125 |
— |
2.97/2.84 |
| 0.25 |
5 |
2.81/2.54 |
| 1 |
0.1 |
4 |
2.96/3.18 |
| 0.05 |
— |
2.43/2.30 |
| 1 |
2 |
2.23/2.12 |
| 5 |
0.5 |
4 |
2.59/2.76 |
| 0.25 |
1 |
1.84/1.79 |
| |
|
5 |
2 |
1.65/1.54 |
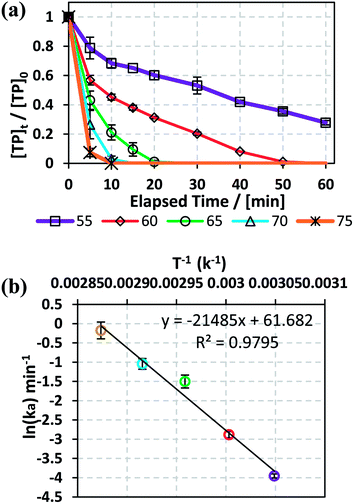
3.1.2. Effects of temperature and determination of activation energy. The effects of temperature on TP degradation by the TAP system were studied under the following conditions: [TP]0 = 10 mg L−1, [PS]0 = 2 mM and T = 55–75 °C. Fig. 1a shows that increasing the temperature resulted in improved TP degradation. For example, when temperature increased from 55 °C to 75 °C, the % TP degradation increased from 10% to 100% at t = 40 min. This observed trend has been found in several studies of TAP systems.26,28 This can be explained by the increase in the energy provided to the system upon heating, which in its turn favors increasing numbers of collisions between the reacting TP and SRs.
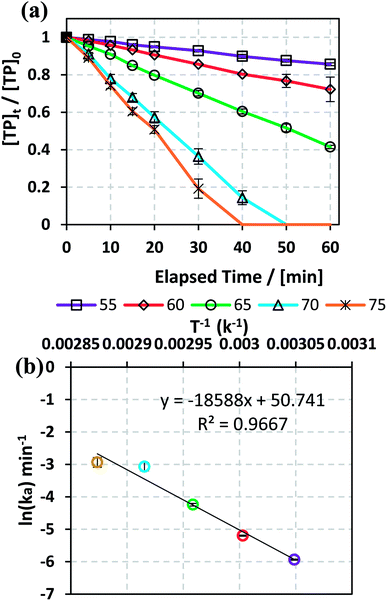 |
| | Fig. 1 (a) Effects of temperature on TP degradation in a TAP system. (b) The corresponding Arrhenius plot of ln(ka) vs. (1/T), showing the equation for linear best fit. Experimental conditions: [TP]0 = 10 mg L−1, [PS]0 = 2 mM and T = 55–75 °C. Error bars are calculated as 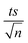 , where absent bars fall within the symbols. , where absent bars fall within the symbols. | |
The observed degradation rate constant (kobs) was calculated according to the pseudo-first order kinetics model using eqn (4), which showed good fit (Text S2†). Additionally, the activation energy (EA) of the TP degradation reaction in the TAP system was determined using the Arrhenius equation (eqn (5)), where T is the temperature in K, kobs is the observed degradation rate constant calculated at different temperatures in min−1, A is the Arrhenius constant, and R is the gas constant (8.314 J mol−1 K−1). eqn (5) was plotted, and the slope obtained represents 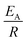 (Fig. 1b). EA and ln(A) were determined to be 154 (±16) kJ mol−1 and 50 (±5) kJ mol−1, respectively. The EA value is close to those reported by Ghauch et al. for ibuprofen, EA = 168 (±9) kJ mol−1, and naproxen, EA = 155.03 (±26.4) kJ mol−1, both using a TAP system; however, they used half the [PS]0 used in this work, e.g. 1 mM.26,28 The uncertainties reported for ln(A) and EA were determined using the LINEST function of Microsoft Excel.
(Fig. 1b). EA and ln(A) were determined to be 154 (±16) kJ mol−1 and 50 (±5) kJ mol−1, respectively. The EA value is close to those reported by Ghauch et al. for ibuprofen, EA = 168 (±9) kJ mol−1, and naproxen, EA = 155.03 (±26.4) kJ mol−1, both using a TAP system; however, they used half the [PS]0 used in this work, e.g. 1 mM.26,28 The uncertainties reported for ln(A) and EA were determined using the LINEST function of Microsoft Excel.
| |
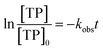 | (4) |
| |
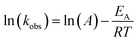 | (5) |
3.2. Chemical activation of PS (CAP system)
To test the effectiveness of CAP for TP degradation at room temperature, a solution of [TP]0 = 10 mg L−1 was subjected to [PS]0 = 0.25, 1 and 5 mM activated by Fe2+ with [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios of 10
[Fe2+]0 ratios of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at favorable acidic pH to ensure Fe2+ solubility. Under all conditions tested, only negligible degradation of TP was observed (Fig. 5S†), with a maximum of 5% TP degradation noted at 60 min for the case of [PS]0 = 0.25 mM and a [PS]0
1 at favorable acidic pH to ensure Fe2+ solubility. Under all conditions tested, only negligible degradation of TP was observed (Fig. 5S†), with a maximum of 5% TP degradation noted at 60 min for the case of [PS]0 = 0.25 mM and a [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 1
[Fe2+]0 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, as summarized in Table 1. Thus, TP is demonstrated to be relatively resistant to the CAP system at room temperature compared to other organic contaminants. For example, Oh et al. obtained incomplete degradation of polyvinyl alcohol utilizing Fe2+-based CAP at room temperature and used a higher reaction temperature to secure significant degradation of the contaminant.40 This can be explained by the common scavenging effect of SO4˙− by Fe2+ to form the less effective Fe3+ ion (eqn (6))24,41 in addition to the recalcitrant character of the TP molecule.
1, as summarized in Table 1. Thus, TP is demonstrated to be relatively resistant to the CAP system at room temperature compared to other organic contaminants. For example, Oh et al. obtained incomplete degradation of polyvinyl alcohol utilizing Fe2+-based CAP at room temperature and used a higher reaction temperature to secure significant degradation of the contaminant.40 This can be explained by the common scavenging effect of SO4˙− by Fe2+ to form the less effective Fe3+ ion (eqn (6))24,41 in addition to the recalcitrant character of the TP molecule.| | |
SO4˙− + Fe2+ → SO42− + Fe3+
| (6) |
3.3. Combined thermal and chemical activation of PS (TCAP system)
Because both TAP and CAP systems showed low to negligible performance in degrading TP in aqueous solutions, both activation methods were combined into a thermally and chemically activated PS (TCAP) system. This system was tested for different [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios, [PS]0 values and temperatures in order to positively or negatively confirm any synergistic effect that can be obtained upon combination of both PS activation techniques.
[Fe2+]0 ratios, [PS]0 values and temperatures in order to positively or negatively confirm any synergistic effect that can be obtained upon combination of both PS activation techniques.
3.3.1. Effects of [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) [Fe2+]0 ratio and [PS]0. TP degradation was studied at different [PS]0
[Fe2+]0 ratio and [PS]0. TP degradation was studied at different [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios and [PS]0 values. [PS]0
[Fe2+]0 ratios and [PS]0 values. [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios of 10
[Fe2+]0 ratios of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were tested at [PS]0 = 0.25, 1 and 5 mM, [TP]0 = 10 mg L−1 and T = 60 °C. kobs was calculated for the pseudo-first order kinetics model according to eqn (4), as demonstrated in previous work (Text S3,† Table 3). In fact, the reaction at the early stage can be considered to be zero order in the first five minutes;25 however, as the reaction proceeds, degradation by-products form and the reaction follows pseudo-first order kinetics. As depicted in Fig. 2 and Table 2, the 1
1 were tested at [PS]0 = 0.25, 1 and 5 mM, [TP]0 = 10 mg L−1 and T = 60 °C. kobs was calculated for the pseudo-first order kinetics model according to eqn (4), as demonstrated in previous work (Text S3,† Table 3). In fact, the reaction at the early stage can be considered to be zero order in the first five minutes;25 however, as the reaction proceeds, degradation by-products form and the reaction follows pseudo-first order kinetics. As depicted in Fig. 2 and Table 2, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [PS]0
1 [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio showed the highest degradation rate in the three tested [PS]0 conditions, followed by the 2
[Fe2+]0 ratio showed the highest degradation rate in the three tested [PS]0 conditions, followed by the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 10
1 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratios.
1 ratios.
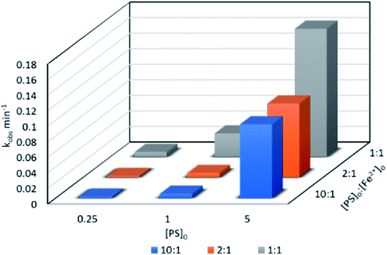 |
| | Fig. 2 Effects of the [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio on TP degradation in a TCAP system. Experimental conditions: [PS]0 = 0.25, 1 and 5 mM, [PS]0 [Fe2+]0 ratio on TP degradation in a TCAP system. Experimental conditions: [PS]0 = 0.25, 1 and 5 mM, [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios of 1 [Fe2+]0 ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2 1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 10 1 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and T = 60 °C. 1, and T = 60 °C. | |
Table 2 Effects of the [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio on TP degradation in a TCAP system. Initial and final pH values are presented for every case. Experimental conditions: [PS]0 = 0.25, 1 and 5 mM, [PS]0
[Fe2+]0 ratio on TP degradation in a TCAP system. Initial and final pH values are presented for every case. Experimental conditions: [PS]0 = 0.25, 1 and 5 mM, [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios of 1
[Fe2+]0 ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 10
1 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and T = 60 °C
1, and T = 60 °C
[PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 [Fe2+]0 |
[PS]0 mM |
[Fe2+]0 mM |
pHi/pHf |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0.25 |
0.025 |
3.50/3.30 |
| 1 |
0.1 |
2.79/2.7 |
| 5 |
0.5 |
2.19/2.07 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0.25 |
0.125 |
2.97/2.85 |
| 1 |
0.5 |
2.53/2.9 |
| 5 |
0.25 |
1.84/1.79 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0.25 |
0.25 |
2.81/2.54 |
| 1 |
1 |
2.23/2.12 |
| 5 |
5 |
1.63/1.54 |
Different studies have showed the effectiveness of different [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios. The optimum ratio obtained varies depending on different parameters, such as the target analyte, the method of iron addition, and the state/morphology of the added iron.42 For example, a study by Oh et al. showed that 1
[Fe2+]0 ratios. The optimum ratio obtained varies depending on different parameters, such as the target analyte, the method of iron addition, and the state/morphology of the added iron.42 For example, a study by Oh et al. showed that 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [PS]0
1 [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 was the optimum ratio for the degradation of polyvinyl alcohol by CAP.40 Also, Naim and Ghauch (2016) showed that 1
[Fe2+]0 was the optimum ratio for the degradation of polyvinyl alcohol by CAP.40 Also, Naim and Ghauch (2016) showed that 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [PS]0
1 [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 was the most effective ratio to yield full ranitidine degradation in almost 10 min.24 On the other hand, Shang et al. obtained 10
[Fe2+]0 was the most effective ratio to yield full ranitidine degradation in almost 10 min.24 On the other hand, Shang et al. obtained 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [PS]0
1 [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 as the optimum ratio for degrading diatrizoate in a CAP system.43
[Fe2+]0 as the optimum ratio for degrading diatrizoate in a CAP system.43
In order to study the effects of [PS]0 on TP degradation, different [PS]0 concentrations were used (0.25 to 5 mM) while maintaining a constant [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 1
[Fe2+]0 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and [TP]0 = 10 mg L−1 at T = 60 °C. Fig. 3 and Table 3 show that the higher the [PS]0, the greater the observed rate constant kobs. For example, kobs increased by 32 fold when [PS]0 increased from 0.25 mM to 5.0 mM with good correlation (R2 = 0.9879), as shown in the inset of Fig. 3. This observation can be explained by the production of a greater amount of SO4˙− upon increasing [PS]0 (Fig. 3).
1 and [TP]0 = 10 mg L−1 at T = 60 °C. Fig. 3 and Table 3 show that the higher the [PS]0, the greater the observed rate constant kobs. For example, kobs increased by 32 fold when [PS]0 increased from 0.25 mM to 5.0 mM with good correlation (R2 = 0.9879), as shown in the inset of Fig. 3. This observation can be explained by the production of a greater amount of SO4˙− upon increasing [PS]0 (Fig. 3).
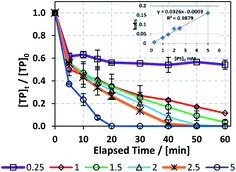 |
| | Fig. 3 Optimization of reaction conditions for the TCAP system: effects of [PS]0 = 0.25–5 mM on the degradation of TP at a [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 1 [Fe2+]0 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. [TP]0 = 10 mg L−1 for all experiments and T = 60 °C. Error bars are calculated as 1. [TP]0 = 10 mg L−1 for all experiments and T = 60 °C. Error bars are calculated as 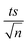 , where absent bars fall within the symbols. , where absent bars fall within the symbols. | |
Table 3 Optimization of [PS]0 for the TCAP system. The kobs values and linearity constants of the pseudo-first order equation plot are presented. [TP]0 = 10 mg L−1 for all experiments and T = 60 °C
| [PS]0 (mM) |
[Fe2+]0 (mM) |
kobs × 10−1 (min−1) |
R2 |
| 0.25 |
0.25 |
0.05 (±0.02) |
0.41 |
| 1 |
1 |
0.29 (±0.02) |
0.93 |
| 1.5 |
1.5 |
0.47 (±0.03) |
0.96 |
| 2 |
2 |
0.56 (±0.04) |
0.96 |
| 2.5 |
1.5 |
0.8 (±0.1) |
0.93 |
| 5 |
5 |
1.6 (±0.1) |
0.98 |
3.3.2. Effects of temperature and determination of the activation energy. To study the effects of temperature on TP degradation in TCAP systems, the same conditions as before (Section 3.3.1) were adopted; however, in addition to the temperature reaction variation: [TP]0 = 10 mg L−1, [PS]0 = [Fe2+]0 = 2 mM and T = 55 °C to 75 °C. As can be noted in Fig. 4a, complete TP degradation occurred in only 10 min at 75 °C, while up to 50 min were required at 60 °C. However, at 55 °C, only partial TP degradation, e.g. 83%, was obtained after 1 h of reaction. The results also showed that as the temperature increased from 55 °C to 75 °C, kobs increased by 44 fold from 1.9 (±0.1) × 10−2 min−1 to 8.3 (±0.1) × 10−1 min−1.
 |
| | Fig. 4 (a) Effects of temperature on TP degradation in TCAP systems. (b) The corresponding Arrhenius plot of ln(ka) vs. 1/T, showing the equation of linear best fit. Experimental conditions: [TP]0 = 10 mg L−1, [PS]0 = [Fe2+]0 = 2 mM and T = 50–75 °C. Error bars are calculated as 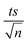 , where absent bars fall within the symbols. , where absent bars fall within the symbols. | |
The TCAP system, like the investigated TAP system (Section 3.1.2), showed excellent fitting with the Arrhenius equation, where the calculated ln(A) and the apparent activation energy EA were greater than those calculated in the absence of Fe2+, e.g. 61 (±5) kJ mol−1 and 178 (±14) kJ mol−1, respectively (Fig. 4b). This should not be surprising, as one might expect a lower activation energy in the presence of Fe2+. In fact, Fe2+ does not play the role of a catalyst to decrease EA, nor is it involved in the TP degradation reaction directly. Rather, it plays the role of speeding the production of SO4˙− from PS upon the chemical activation process (eqn (2)). Additional experiments were carried out at a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [PS]0
1 [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio at different temperatures (40 °C, 50 °C and 60 °C), and the obtained results showed the same outputs. For example, as the reaction temperature increased from 40 °C to 50 °C and 60 °C, the % degradation of TP improved from 29% to 45% and 100%, respectively, at 60 min for [PS]0 = 5 mM (Fig. 6S†). A similar trend was observed for aniline degradation, where [PS]0 = 2.5 mM and zero valent iron [ZVI]0 = 0.3 g L−1 resulted in the total elimination of [aniline]0 = 0.05 mM in periods of 1 and 2 h at T = 80 °C and 60 °C, respectively.44
[Fe2+]0 ratio at different temperatures (40 °C, 50 °C and 60 °C), and the obtained results showed the same outputs. For example, as the reaction temperature increased from 40 °C to 50 °C and 60 °C, the % degradation of TP improved from 29% to 45% and 100%, respectively, at 60 min for [PS]0 = 5 mM (Fig. 6S†). A similar trend was observed for aniline degradation, where [PS]0 = 2.5 mM and zero valent iron [ZVI]0 = 0.3 g L−1 resulted in the total elimination of [aniline]0 = 0.05 mM in periods of 1 and 2 h at T = 80 °C and 60 °C, respectively.44
3.4. Effects of pH adjustment of the TCAP system
To study the effects of pH on the TP degradation process in the TCAP system, the initial pH (pHi) was adjusted to values of around 3, 5 and 7 using NaOH solution before the addition of PS. The subsequent PS addition caused a further decrease in pH (pHPS) (Fig. 5 and Table 4). The use of a buffer solution was not possible because an organic buffer would compete with TP on the PS present in the solution; on the other hand, an inorganic buffer, such as phosphate buffer, would cause interference by complexing with Fe2+.25,34 The effect of initial pH is important to study because the effluent to be treated may contain traces of acid or base from the reactor cleaning process; however, most pharmaceutical production plants use deionized water for preliminary washing of their equipment, so the effluent should contain the highest [TP] at acidic pH.
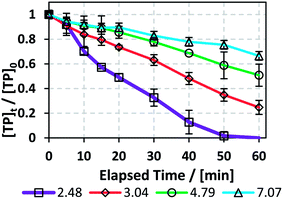 |
| | Fig. 5 Effects of pH adjustment on the degradation of TP in the TCAP system. The pH values adjusted before PS addition are presented. Experimental conditions: [TP]0 = 10 mg L−1, [PS]0 = [Fe2+]0 = 2 mM and T = 60 °C. Error bars are calculated as 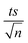 , where absent bars fall within the symbols. , where absent bars fall within the symbols. | |
Table 4 Effects of pH adjustment on the degradation of TP in the TCAP system. pHi represents the pH adjusted before PS addition, i.e. the pH value of the solution before treatment, pHPS is the pH after PS addition, and pHf is final pH at t = 60 min. kobs is calculated from the pseudo-first order equation plot. Experimental conditions: [TP]0 = 10 mg L−1, [PS]0 = [Fe2+]0 = 2 mM and T = 60 °C
| pH adjustment |
pHia |
pHPSb |
pHf |
kobs (min−1) |
| pHi is measured before PS addition. pHPS is measured after PS addition. |
| − |
2.48 |
2.01 |
2.20 |
4.9 (±0.4) × 10−2 |
| + |
3.04 |
2.19 |
2.39 |
1.7 (±0.1) ×10−2 |
| + |
4.79 |
2.23 |
2.93 |
1.09 (±0.6) × 10−2 |
| + |
7.07 |
2.81 |
5.06 |
6.0 (±0.3) × 10−3 |
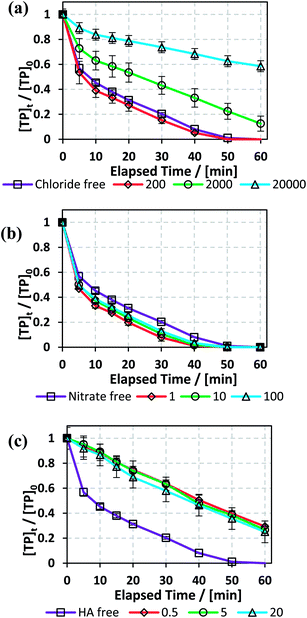
It should be noted that the decrease in pH in the case of the un-adjusted solution is due to two main factors. First, the added Fe2+ solution contains HCl, which was used to increase its solubility. Second, PS causes acidification of the medium, as per eqn (7) and (8):25
| |
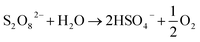 | (7) |
| | |
HSO4− → SO42− + H+, (pKa = 1.92)
| (8) |
The results showed that the initial pH value significantly impacts the degradation process, where kobs decreased with increasing pHi from 4.9 (±0.4) × 10−2 min−1 in the case of pHi = 2.48 to 6.0 (±0.3) × 10−3 min−1 for pHi = 7.07 (Fig. 5 and Table 4). This can be explained by the fact that at increasing pH, e.g. pH above 4, the free iron species in the solution decrease, probably as a result of the formation of Fe(II) complexes.45 This was proved experimentally by the formation of a visible precipitate upon pH increase, e.g. formation of Fe(OH)2 precipitate. As a result, a decrease in the amount of soluble Fe2+ occurs, thereby decreasing the reaction rate between Fe2+ and PS for SO4˙− production. This was further clarified by comparing the case of pHi adjusted to pH 7 in the TCAP system to that of the TAP system at the same [PS]0 = 2 mM. In fact, kobs is 6.0 (±0.3) × 10−3 for the former and 5.52 (±0.08) × 10−3 min−1 for the latter (Table 1S†). These values can be explained by the insignificant effects of Fe2+ in the TCAP system adjusted initially to neutral pH. Thus, the studied TCAP system is very sensitive to pH variations. These results can be compared to a solar/Fe2+/PS system investigated by Nie et al.46 In fact, the authors found a decrease in the degradation rate of chloramphenicol by around 70% when the reaction pH increased from 3 to 9.
3.5. Additive and matrix effects in the TCAP system
In order to test the effects of Cl−, NO3−, and HA additives on the degradation rate of TP, the experimental conditions that yielded full TP degradation in 1 h at 60 °C were chosen as previously determined (Fig. 3).
3.5.1. Effects of sodium chloride. Different concentrations of saline solutions spiked with TP were investigated in the TCAP system. The resulting TP solutions had NaCl concentrations of 0, 200, 2000 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg L−1 to mimic the conditions of distilled, fresh, brackish and saline water, respectively, according to Gorrell et al. and EPA data.47,48 It should be noted that chloride was present in all solutions at a concentration of 4 mM from FeCl2 (Fe2+ source) because FeCl2 was used as a source of Fe2+.
000 mg L−1 to mimic the conditions of distilled, fresh, brackish and saline water, respectively, according to Gorrell et al. and EPA data.47,48 It should be noted that chloride was present in all solutions at a concentration of 4 mM from FeCl2 (Fe2+ source) because FeCl2 was used as a source of Fe2+.As can be noted from Fig. 6, the calculated kobs for the cases of DI and fresh water were almost equal, showing a very slight positive effect of low [NaCl]0 in solution. However, the results also showed that higher [NaCl]0 caused inhibition of the degradation process, where kobs decreased from 5.6 (±0.4) × 10−2 min−1 in the case of DI water to 3.0 (±0.2) × 10−2 min−1 and 8.0 (±0.5) × 10−3 min−1 in the cases of brackish and saline water, respectively (Fig. 6a and Table 5). Moreover, although a decrease in kobs was noticed for fresh water, almost complete TP degradation was achieved in 60 min. The decrease in kobs is attributed to the quenching of SO4˙− (E° = 2.437 (±0.019) V) by Cl− to produce Cl˙ (E° = 2.432 (±0.018) V), which in turn reacts to produce Cl2˙− (E° = 2.126 (± 0.017) V) (eqn (9) and (10)). The latter radical formed has lower redox potential and is thus less effective in terms of oxidation of TP and its transformation products compared to SO4˙−.49–51
 |
| | Fig. 6 Effects of (a) [NaCl] = 200–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg L−1, (b) [NO3−] = 1–100 mg L−1, and (c) [HA] = 0.5–20 mg L−1 on TP degradation in the TCAP system. Experimental conditions: [PS]0 = [Fe2+]0 = 2 mM and [TP]0 = 10 mg L−1 for all conditions tested. Error bars are calculated as 000 mg L−1, (b) [NO3−] = 1–100 mg L−1, and (c) [HA] = 0.5–20 mg L−1 on TP degradation in the TCAP system. Experimental conditions: [PS]0 = [Fe2+]0 = 2 mM and [TP]0 = 10 mg L−1 for all conditions tested. Error bars are calculated as  , where absent bars fall within the symbols. , where absent bars fall within the symbols. | |
Table 5 Effects of [NaCl] = 200–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg L−1, [NO3−] = 1–100 mg L−1, and [HA] = 0.5–20 mg L−1 on TP degradation in a TCAP system. Experimental conditions: [PS]0 = [Fe2+]0 = 2 mM and [TP]0 = 10 mg L−1 for all conditions tested. kobs is obtained as per the pseudo-first order reaction rate model
000 mg L−1, [NO3−] = 1–100 mg L−1, and [HA] = 0.5–20 mg L−1 on TP degradation in a TCAP system. Experimental conditions: [PS]0 = [Fe2+]0 = 2 mM and [TP]0 = 10 mg L−1 for all conditions tested. kobs is obtained as per the pseudo-first order reaction rate model
| Matrix |
Unit |
kobs × 10−2 (min−1) |
pHi/pHf |
| No additive |
mg L−1 |
5.6 (±0.4) |
1.85/1.53 |
| [NaCl] = 200 |
6.5 (±0.5) |
1.85/1.56 |
| [NaCl] = 2000 |
3.0 (±0.2) |
1.81/1.62 |
[NaCl] = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.8 (±0.05) |
1.78/1.56 |
| [NO3−] = 1 |
10.0 (±0.1) |
1.81/1.71 |
| [NO3−] = 10 |
9.0 (±0.1) |
1.79/1.71 |
| [NO3−] = 100 |
7.6 (±0.7) |
1.78/1.70 |
| [HA] = 0.5 |
1.68 (±0.07) |
1.84/1.97 |
| [HA] = 5 |
2.1 (±0.1) |
1.83/1.95 |
| [HA] = 20 |
2.2 (±0.1) |
1.81/1.94 |
Different studies have showed varied effects of Cl− on degradation processes. For example, Fan et al. observed enhancement in the degradation of sulfamethazine,52 whereas Norzaee et al. observed inhibition of penicillin G degradation,53 both in TAP systems. Wang et al. observed inhibition of acetaminophen degradation at low chloride concentrations and enhancement at high concentrations, while Amasha et al. noted inhibition of ketoprofen degradation, both in Fe2+/PS systems.34,54 The increased degradation in the presence of Cl− can be explained by the formation of Cl˙, which has a redox potential close to that of SO4˙−, in addition to the formation of reactive HO˙ (eqn (9) and (11)–(13)).50,51
| | |
SO4˙− + Cl− ⇆ Cl˙ + SO42−, kf = 4.7 × 108, kb = 2.5 × 108 M−1 s−1
| (9) |
| | |
Cl˙ + Cl− ⇆ Cl2˙−, kf = 8 × 109 M−1 s−1, kb = 4.2 × 104 s−1
| (10) |
| | |
Cl− + H2O ⇆ ClOH˙− + H+, kf[H2O] = 1.6 × 105 s−1, kb = 2.6 × 1010 M−1 s−1
| (11) |
| | |
HOCl˙− ⇆ HO˙ + Cl−, kf = 6.1 × 109 s−1, kb = 4.3 × 109 M−1 s−1
| (12) |
| | |
HOCl˙− + H+ ⇆ H2O + Cl˙, kf = 2.1 × 1010, kb = 1.3 × 103 M−1 s−1
| (13) |
3.5.2. Effects of nitrates. Nitrate is one of the most commonly present ions in different water bodies, such as groundwater, due to the excessive use of fertilizers.55 Accordingly, the effects of [NO3−] = 1, 10 and 100 mg L−1 on TP degradation in the TCAP system were tested. The results showed that the reaction rate increased in the presence of [NO3−], where kobs increased by 6 fold from 5.6 (±0.4) × 10−2 min−1 to 1.0 (±0.1) × 10−1 min−1 in DI media and [NO3−] = 1 mg L−1, respectively, and then slightly decreased for [NO3−] = 10 and 100 mg L−1 to values of 9.0 (±0.1) × 10−2 min−1 and 7.6 (±0.7) × 10−2 min−1, respectively (Fig. 6b and Table 5).The increase in TP degradation in the presence of nitrates can be attributed to the formation of NO3˙, which is considered to have significant oxidation redox potential (Ered1/2 = 2.50 V) and can react with TP.22 Therefore, although nitrates react with SO4˙− and quench them, the formation of NO3˙ appears to compensate for the decrease in [SO4˙−] (eqn (14)). However, the increase in [NO−3] also results in an increase of [NO3˙], which can subsequently undergo self-quenching reactions; this decreases [NO3˙] and, as a result, decreases the degradation rate. Ghauch et al. also noted an increase in the naproxen degradation rate by 154.3% in the presence of [NO−3] = 5 mg L−1 in a TAP system.26
| | |
SO4˙− + NO−3 → SO42− + NO3˙
| (14) |
3.5.3. Effects of humic acid (HA). One widely present type of natural organic matter (NOM) is humic acid (HA).45 TP degradation in the TCAP system was studied in the presence of [HA]0 = 0.5, 5 and 20 mg L−1, which are in the typical naturally existing range.56 The results show that HA inhibited the degradation rate, where kobs decreased by almost 3 fold when [HA]0 = 0.5 mg L−1 compared to HA-free medium. After that, the increase in [HA]0 caused no significant change in kobs (Fig. 6c and Table 5). The inhibition in TP degradation can be explained by the competitiveness of active radicals, where NOM quenches SO4˙− due to the presence of electron-rich sites.57 Liu et al. noted a significant decrease in reaction rate with increasing [HA] during sulfachloropyridazine degradation in a TAP system.57 Amasha et al. noted enhanced ketoprofen degradation in a CAP system at [HA]0 = 0.5, which was explained by the possible reductive ability of HA towards transition metals which, in the case of a CAP system, can regenerate Fe2+ from Fe3+.34,58 Thus, for the case of TP degradation in the TCAP system, the cease in the decrease in kobs with increasing [HA]0 can be explained by the counter effects of HA; at higher concentrations, HA contributes more to the re-generation of Fe2+, which counteracts its radical-quenching properties.
3.6. Case of natural water matrices: spring, sea, and waste water in the TCAP system
The degradation of TP was studied in media of natural sea, spring and waste water (SW, SpW and WW) obtained from locations at coordinates of 33°44′17.9′′N 35°34′12.5′′E, 33°54′11.1′′N 35°28′44.8′′E and 33°54′08.2′′N 35°29′05.0′′E, respectively. The experimental conditions are as follows: [PS]0 = 5 mM, [Fe2+]0 = 0.5 mM, and TP were added in adequate amounts to each water medium so that [TP]0 = 10 mg L−1. A [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 10
[Fe2+]0 ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was used instead of the optimum obtained ratio of 1
1 was used instead of the optimum obtained ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
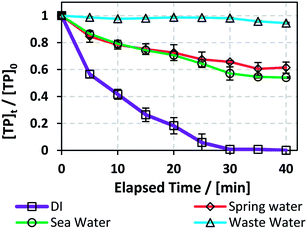
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in order to decrease the use of Fe2+, e.g. Fe(OH)2 in neutral media.45 These conditions were adopted because natural water matrices are buffered to around neutral pH (Table 6), mainly because of the presence of bicarbonate. The results showed that TP degradation was inhibited in the three tested cases compared to the DI matrix case, where kobs = 1.5 (±0.1) × 10−1 min−1, with WW showing ∼570 fold inhibition in terms of kobs = 2.6 (±0.6) × 10−4 min−1, followed by SpW ∼ 14 fold and SW ∼ 10 fold, kobs = 1.1 (±0.1) × 10−2 and 1.54 (±0.09) × 10−2 min−1, respectively (Fig. 7).
1 in order to decrease the use of Fe2+, e.g. Fe(OH)2 in neutral media.45 These conditions were adopted because natural water matrices are buffered to around neutral pH (Table 6), mainly because of the presence of bicarbonate. The results showed that TP degradation was inhibited in the three tested cases compared to the DI matrix case, where kobs = 1.5 (±0.1) × 10−1 min−1, with WW showing ∼570 fold inhibition in terms of kobs = 2.6 (±0.6) × 10−4 min−1, followed by SpW ∼ 14 fold and SW ∼ 10 fold, kobs = 1.1 (±0.1) × 10−2 and 1.54 (±0.09) × 10−2 min−1, respectively (Fig. 7).
Table 6 Physical parameters of the natural water matrices used before and after treatment in the TCAP system. Experimental conditions: [TP]0 = 10 mg L−1, [PS]0 = 5 mM and [Fe2+]0 = 0.5 mM
| Parameters |
Units |
Spring water |
Sea water |
Waste water |
| Before treatment |
After treatment |
Before treatment |
After treatment |
Before treatment |
After treatment |
| Colony forming unit. Nephelometric turbidity unit. Too numerous to count. |
| pH |
— |
7 |
3.14 |
8 |
2.84 |
8.2 |
4.12 |
| Total coliforms |
CFUa |
NA |
NA |
76 |
NA |
TNTCc |
NA |
| Fecal coliforms |
|
NA |
NA |
4 |
NA |
TNTC |
NA |
| Turbidity |
NTUb |
0.63 |
8.52 |
1 |
6.9 |
9.5 |
4.68 |
| TSS |
mg L−1 |
9 |
3 |
88 |
125 |
425 |
15 |
| TDS |
|
350 |
1460 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
4400 |
6140 |
| Sulfate |
|
16 |
300 |
3500 |
3300 |
420 |
590 |
| Chloride |
|
42.6 |
450 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 250 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
3375 |
2265 |
 |
| | Fig. 7 Degradation of TP in real water samples: spring, sea and waste water. Experimental conditions: [TP]0 = 10 mg L−1, [PS]0 = 5 mM and [Fe2+]0 = 0.5 mM. Error bars are calculated as 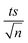 , where absent bars fall within the symbols. , where absent bars fall within the symbols. | |
One reason for the inhibition of the degradation of TP in the three investigated cases is the neutral to slightly basic pH values (7 to 8.2); this pH range causes the complexation and precipitation of Fe2+, e.g. as Fe(OH)2, where natural water media act as buffer solutions compared to DI medium, which becomes acidic (pHi ≈ 2) immediately after the addition of PS and Fe2+ solutions. The inhibition was the highest in the case of the WW matrix, where WW possessed the highest values of total and fecal coliforms, chlorides, turbidity and total suspended and dissolved solids among the three studied matrices. The organic and inorganic material present in WW competes with TP in reacting with SO4˙−, thus inhibiting TP degradation. Additionally, chlorides acted as quenchers in the studied TCAP system (Section 3.5.1), and WW showed the highest [Cl−]. It should be noted that total elimination of coliforms was observed in the WW and SW (Table 6) systems; this is probably due to the heat factor in addition to the activity of the SO4˙− present. Effluents of pharmaceutical production plants, after discharge, may be mixed with several water matrices with different properties. In addition, the water used for initial cleaning operations may be of natural origin and not DI water. The results presented in this section show that it is crucial to clean mixing reactors in pharmaceutical production facilities with distilled water whenever possible and to treat the effluent mixture before its release into the environment. A great decrease in degradation rates in waste water was also observed by Ghauch's research group upon degradation of chloramphenicol and ketoprofen in UV/PS systems.22,34
3.7. Case study: real factory effluent
3.7.1. Effects of [PS]0. The efficiency of the TCAP system was tested on a real pharmaceutical factory effluent solution containing TP in addition to other excipients. The effluent samples were collected from a local production facility that produces a syrup containing TP. The production process consists of mixing TP and other excipients in a 1000 L 316 SS container, after which the mixture is pumped through a filter press into 100 L 316 SS containers. Waste water samples were collected by washing the SS reactor and the filter press with distilled water. The resulting factory effluent solution contained [TP]0 = 160 mg L−1 (Fig. 8S†). To account for the high [TP]0 effluent content, [PS]0 was tested at 25, 50, 75 and 100 mM utilizing the optimum [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 1
[Fe2+]0 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and T = 60 °C.
1 and T = 60 °C.The results showed that a higher [PS]0 caused faster degradation, where total TP elimination was observed within 40 min in the case of [PS]0 = [Fe2+]0 = 100 mM and within 180 min for [PS]0 = [Fe2+]0 = 25 mM (Fig. 8 and Table 7). To compare the degradation of TP in DI and in the factory effluent mixture, kobs can be compared in cases of similar [PS]0/[TP]0 molar ratios. As such, for the case of [TP]0 = 10 mg L−1 (0.0555 mM) and [PS]0 = [Fe2+]0 = 1.5 mM in DI, [PS]0/[TP]0 = 27, while for the case of [TP]0 = 160 mg L−1 and [PS]0 = [Fe2+]0 = 25 mM in factory effluent, [PS]0/[TP]0 = 28. The corresponding kobs decreased by 2 fold from 0.29 (±0.02) 10−1 to 1.4 (±0.1) × 10−2 min−1. Thus, the TP degradation in factory effluent is less efficient than in DI medium. This can be attributed to the presence of excipients, such as potassium sorbate, sorbitol, ethanol, vanillin and saccharine, as provided by the manufacturer. Those can compete with TP in reacting with the active SRs. It should be noted that the efficiency of the TCAP system would have decreased if natural water was used to rinse the mixing reactor instead of DI water (Section 3.3.5); thus, it is crucial for industries to utilize adequate amounts of distilled (DI) water in rinsing apparatuses and tools used during syntheses and mixing processes for efficient and cost-effective effluent treatment.
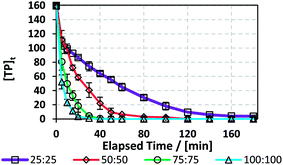 |
| | Fig. 8 Degradation of TP by TCAP in real pharmaceutical effluent containing [TP]0 = 160 mg L−1. Experimental conditions: [PS]0 = 25, 50, 75 and 100 mM, [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio = 1 [Fe2+]0 ratio = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and T = 60 °C. Error bars are calculated as 1, and T = 60 °C. Error bars are calculated as 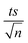 , where absent bars fall within the symbols. , where absent bars fall within the symbols. | |
Table 7 Degradation of TP by TCAP in real pharmaceutical effluent containing [TP]0 = 160 mg L−1. Experimental conditions: [PS]0 = 25–100 mM, [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 1
[Fe2+]0 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and T = 60 °C. kobs is calculated for the pseudo-first order reaction rate
1, and T = 60 °C. kobs is calculated for the pseudo-first order reaction rate
| [PS]0 mM |
[Fe2+]0 mM |
T °C |
kobs min−1 |
pHi/pHf |
| 25 |
25 |
60 |
1.4 (±0.1) × 10−2 |
1.17/1.08 |
| 50 |
50 |
4.5 (±0.2) × 10−2 |
0.85/0.78 |
| 75 |
75 |
1.16 (±0.05) × 10−1 |
0.67/0.60 |
| 100 |
100 |
1.65 (±0.09) × 10−1 |
0.58/0.48 |
3.7.2. Economic study. The cost of factory effluent treatment utilizing the TCAP system was estimated. The electric energy required to heat the solution in addition to the reagent price were considered to be the main contributors to the total cost of operation (eqn (15)).| | |
Total system cost ($ per m3) = electrical energy cost + reagent cost
| (15) |
Electric energy per order (EEO) was defined as the electric energy required to degrade contaminants by one order of magnitude, for example from 10 mg L−1 to 1 mg L−1, in one cubic meter of contaminated water or air; this was calculated using eqn (16) for a batch system.59
| |
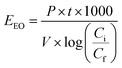 | (16) |
where
P is the power supplied to the system in kW,
t is the duration of the treatment in hours,
V is the volume treated in L,
Ci and
Cf are the initial and final concentrations, respectively, and 1000 is a conversion factor from L to m
3. Thus,
EEO is obtained in kW h per m
3 per order. Additionally,
eqn (16) was simplified by substituting the first-order reaction rate
eqn (17) in
eqn (16) and changing the unit of time. Thus, the following simplification was performed (
eqn (16)–(19)):
| |
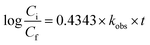 | (17) |
| |
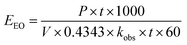 | (18) |
| |
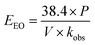 | (19) |
The resulting simplified eqn (19) shows P in kW, V in L, and kobs in min−1.59 Power was calculated based on the energy and time needed to heat the reactors. The energy required for this heating was calculated using eqn (20), where Q is the energy in J, m is the mass of water in g (200 g), C is the specific heat capacity of water (4.186 J g−1 °C−1), and ΔT (35 °C) is the temperature difference for heating from 25 °C to 60 °C. Q was found to be 29.3 kJ.
Power was calculated utilizing eqn (21), where t is the time in seconds needed to heat the solution to the desired temperature. Experimentally, 12 min were required to heat the 200 mL reactor from room temperature to 60 °C. Thus, P = 0.122 kW.
| |
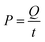 | (21) |
The EEO was calculated for each of the four different [PS]0 values, and the results are presented in Table 8. The electrical energy cost was estimated utilizing electricity cost rates in Lebanon, with the Electricité du Liban (EDL) average rate of 255 LBP per kW per h equivalent to 0.169 $ per kW per h at the current conversion rate,60,61 as well as in the US, where the average electricity cost rate for the industrial sector is 0.0709 $ per kW per h. The costs of the reagents were calculated using wholesale prices in every case (Table S1†). The total system cost can thus be obtained (eqn (15)) and is presented in detail in Fig. 9. It was observed that as [PS]0 increases, the reagent cost increases, while the electric cost due to heating decreases. Consequently, the choice of [PS]0 for the treatment of factory effluent can be based on the estimated total cost, where the case of [PS]0 = 50 mM gave the lowest total cost of 56.8 and 73.8 $ per m3 based on electricity prices in the US and in Lebanon, respectively (Fig. 9 and Table 8).
Table 8 Treatment costs of pharmaceutical effluent contaminated with TP using a TCAP system. The calculations of total system cost for different TP degradation conditions in pharmaceutical effluent are based on electricity price rates in the US and in Lebanon. Experimental conditions: [TP]0 = 160 mg L−1, [PS]0 = 25, 50, 75 and 100 mM, [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 1
[Fe2+]0 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and T = 60 °C
1, and T = 60 °C
| [PS]0, mM |
kobs, min−1 |
EEO, kW h per m3 per order |
Electricity cost (US), $ per m3 per order |
Electricity cost (Lebanon), $ per m3 per order |
Reagent costa, $ per m3 |
Total cost (US), $ m−3 |
Total cost (Lebanon), $ per m3 |
| Check Table 1S. |
| 25 |
1.4 (±0.1) × 10−2 |
558 |
39.6 |
94.4 |
22.2 |
61.8 |
116.6 |
| 50 |
4.5 (±0.2) × 10−2 |
174 |
12.3 |
29.4 |
44.5 |
56.8 |
73.8 |
| 75 |
1.16 (±0.05) × 10−1 |
67.4 |
4.8 |
11.4 |
66.7 |
71.5 |
78.1 |
| 100 |
1.65 (±0.09) × 10−1 |
47.4 |
3.4 |
8.0 |
88.9 |
92.3 |
96.9 |
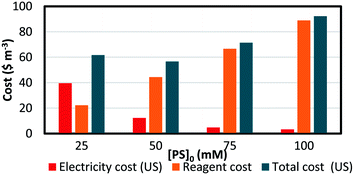 |
| | Fig. 9 Treatment cost of pharmaceutical effluent contaminated with TP using a TCAP system. The electricity, reagent and total costs are presented (based on US electricity cost). Experimental conditions: [TP]0 = 160 mg L−1, [PS]0 = 25–100 mM, [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 1 [Fe2+]0 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and T = 60 °C. 1 and T = 60 °C. | |
Amasha et al. obtained a total cost of 44.414 $ per m3 for degradation of ketoprofen (7.87 μM, 2.00 mg L−1) in a TAP system, with [PS]0 = 1 mM and T = 60 °C.34 The lower total cost obtained by the mentioned study can be attributed to the fact that no Fe2+ was used, so the reagent price was lower; in addition, the degradation was performed in DI and not in factory effluent, where competitive reactions take place between SO4˙− and the excipients present (Section 3.7.1).
3.8. Effects of MeOH and TBA quenchers
Radical scavenging by methanol (MeOH) and tert-butyl-alcohol (TBA) was tested in the TCAP system to determine the effectiveness of the produced SO4˙− and HO˙ in the degradation of TP. Different concentrations of MeOH and TBA (400, 800 mM) were added separately to reactors containing [TP]0 = 10 mg L−1 and [PS]0 = [Fe2+]0 = 2 mM. The experiments were conducted in tight reactors using rubber stoppers in order to prevent substantial loss of MeOH 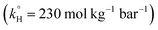 and TBA
and TBA 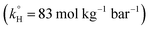 from the reactor due to heat.62 It is known that MeOH quenches both SO4˙− and HO˙ radicals, whereas TBA mainly quenches OH˙.22
from the reactor due to heat.62 It is known that MeOH quenches both SO4˙− and HO˙ radicals, whereas TBA mainly quenches OH˙.22
Fig. 10 shows that MeOH and TBA caused increased inhibition as their concentrations increased. This is due to the increase in competition between the quenchers and TP to react with the radicals present in the medium. Wang et al. also obtained a positive correlation between inhibition extent and the concentrations of TBA and MeOH used in a TAP system.63 In the case of 800 mM quenchers used (quencher/PS: 400/1), TBA and MeOH caused almost total quenching due to their high concentrations. However, when 400 mM quenchers were used (Quencher/PS: 200/1), MeOH caused slightly more quenching than TBA. We can deduce that HO˙ is the major reactive species when degrading TP in a TCAP system.
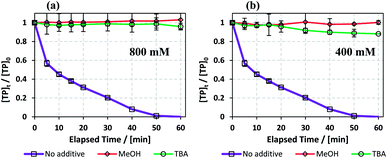 |
| | Fig. 10 (a) Effects of MeOH and TBA quenchers on TP degradation in the TCAP system. Experimental conditions: [TP]0 = 10 mg L−1, [PS]0 = [Fe2+]0 = 2 mM. [MeOH] = [TBA] = (a) 800 and (b) 400 mM and T = 60 °C. Error bars are calculated as 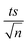 , where absent bars fall within the symbols. , where absent bars fall within the symbols. | |
3.9. Suggested degradation pathway
A theoretical study of the degradation pathway utilizing frontier orbitals and charge distribution was conducted. Frontier molecular orbital theory shows that electrophilic reactions are more likely to occur for atoms with higher values of the highest occupied molecular orbital (HOMO), while nucleophilic reactions are prone to occur for atoms with higher values of the lowest unoccupied molecular orbital (LUMO).64 Consequently, several studies suggest that atoms with a higher 2FEDHOMO2 are more easily oxidized, and those with a higher FEDHOMO2 + FEDLUMO2 are more susceptible to addition reactions.65–67 The 2FEDHOMO2, 2FEDHOMO2, and Mulliken charge distributions were calculated for TP and are presented along with the atom numbering and the isodensity surfaces of frontier molecular orbital theory in Fig. 11 and Table 9. For TP, 1C showed the highest 2FEDHOMO2, followed by 9N, 8O, 2C, 19C, 3C and 7O. Therefore, attack by oxidants is expected to occur readily on 1C, 9N and 8O. Also, 3C showed the highest FEDHOMO2 + FEDLUMO2, followed by 19C, 1C, 9N, 2C, 7O and 4N. Thus, addition reactions will mostly take place at 1C, 19C and 3C; however, it was noted that 19C is the least sterically hindered of the three atoms. Thus, addition reactions are expected to occur more readily at 19C, such as the formation of hydroxylated products at this site. It is known that HO˙ performs H abstraction and SO4˙− acts selectively as an electron transfer reactant.68 According to the obtained Mulliken charge distributions, electrons are mostly abstracted from 7O and 8O because they show the most negative charges (Table 9). These results were used to suggest a degradation mechanism (Fig. 12).
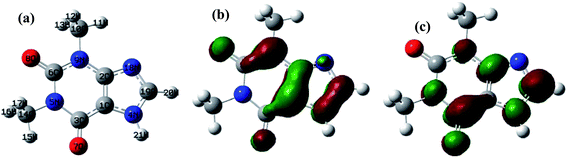 |
| | Fig. 11 (a) TP atomic labeling and numbering. Isodensity surfaces of the (b) HOMO and (c) LUMO of TP with isovalues of 0.05. | |
Table 9 The computed values of the FEDs for the HOMO and LUMO in addition to the Mulliken charge distributions
| Atom |
FEDHOMO2 + FEDLUMO2 |
2FEDHOMO2 |
2FEDLUMO2 |
Mulliken charge |
| 1C |
0.27 |
0.45 |
0.08 |
0.35 |
| 2C |
0.23 |
0.19 |
0.27 |
0.11 |
| 3C |
0.38 |
0.17 |
0.58 |
0.25 |
| 4N |
0.17 |
0.13 |
0.21 |
−0.21 |
| 5N |
0.05 |
0.01 |
0.10 |
−0.25 |
| 6C |
0.02 |
0.04 |
0.01 |
0.56 |
| 7O |
0.18 |
0.17 |
0.19 |
−0.66 |
| 8O |
0.10 |
0.20 |
0.00 |
−0.67 |
| 9N |
0.25 |
0.38 |
0.11 |
−0.26 |
| 10C |
0.01 |
0.01 |
0.01 |
−0.21 |
| 11H |
0.00 |
0.00 |
0.00 |
0.14 |
| 12H |
0.01 |
0.02 |
0.00 |
0.14 |
| 13H |
0.01 |
0.02 |
0.00 |
0.14 |
| 14C |
0.00 |
0.00 |
0.00 |
−0.15 |
| 15H |
0.00 |
0.00 |
0.00 |
0.15 |
| 16H |
0.01 |
0.00 |
0.02 |
0.14 |
| 17H |
0.01 |
0.00 |
0.02 |
0.14 |
| 18N |
0.01 |
0.01 |
0.01 |
−0.47 |
| 19C |
0.28 |
0.19 |
0.36 |
0.29 |
| 20H |
0.00 |
0.00 |
0.00 |
0.23 |
| 21H |
0.00 |
0.00 |
0.00 |
0.25 |
| 22H |
— |
— |
— |
— |
 |
| | Fig. 12 Suggested TP degradation pathway by SO4˙− and HO˙. Two detected by-products, BP1 and BP2, are included. | |
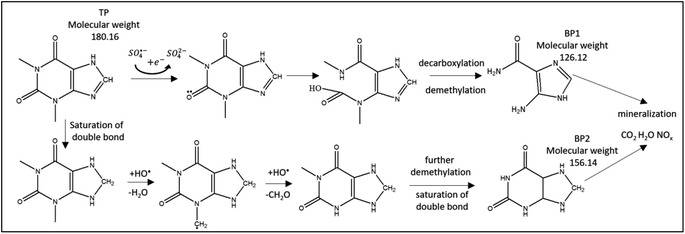
LC/MS/MS was used to identify the by-products of TP degradation. Fig. 8S† shows two identified by-products termed BP1 (molecular weight 126.12 g mol−1) and BP2 (molecular weight 156.14 g mol−1). The extracted ion chromatograms of BP1 and BP2 showed that the intensities of their peaks constantly increased with time, which proves that these by-products are formed throughout the degradation reaction (Fig. 8S†). It was noted that the intensity of BP1 is higher, which suggests that it is more prevalent than BP2.
Fig. 12 presents the suggested degradation pathway based on the results obtained from theoretical studies and LC/MS/MS results. Electron abstraction is expected on the oxygen group (8O, Fig. 11) by SO4˙−. Attack of SO4˙− and HO˙ is expected on the 6-membered ring, where ring opening occurs with the formation of carboxylic groups. This is followed by loss of CO2 and de-methylation on the 5N and 9N sites. As a result, BP1 is obtained.
Demethylation is initiated by hydrogen abstraction at 10C and 14C, which is followed by HO˙ attack. BP2 is formed through demethylation and saturation of double bonds. Ultimately, mineralization is expected, which was obtained in similar AOP studies.69,70
4. Conclusions
In this study, TP degradation was tested in systems of TAP, CAP and TCAP. TAP resulted in incomplete (60%) TP degradation at t = 60 min for [PS]0 = 5 mM and T = 60 °C. The CAP system was not effective at room temperature, where a maximum of 5% TP degradation was observed at t = 60 min for [PS]0 = [Fe2+]0 = 0.25 mM. To obtain better efficiency, the two methods of PS activation were combined in a TCAP system, which resulted in complete TP degradation at T = 60 °C and [PS]0 = [Fe2+]0 = 2 mM. The reaction followed a pseudo-first order reaction rate, with kobs = 5.6 (±0.4) × 10−2 min−1. The effects of [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio, [PS]0 and temperature were tested, where the 1
[Fe2+]0 ratio, [PS]0 and temperature were tested, where the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio gave optimum results, and the degradation rate increased with increasing [PS]0 and temperature. Salinity inhibited the degradation process, while nitrates slightly enhanced the process. The presence of HAs inhibited TP degradation. TP was dissolved in real water samples of spring, sea and waste water, which showed lower degradation rates in comparison with DI water medium. Real factory effluent containing TP was obtained and showed total degradation of [TP]0 = 160 mg L−1 within 180 and 40 min for [PS]0 = [Fe2+]0 = 25 and 100 mM, respectively. The degradation cost was estimated to 56.8 $ per m3, for electricity price rates in the US at [PS]0 = [Fe2+]0 = 50 mM. A degradation mechanism involving in situ evolved reactive oxidative species, mainly sulfate and hydroxyl radicals, was also suggested based on LC/MS/MS HRAM analyses supported by frontier molecular orbital theory calculations.
1 ratio gave optimum results, and the degradation rate increased with increasing [PS]0 and temperature. Salinity inhibited the degradation process, while nitrates slightly enhanced the process. The presence of HAs inhibited TP degradation. TP was dissolved in real water samples of spring, sea and waste water, which showed lower degradation rates in comparison with DI water medium. Real factory effluent containing TP was obtained and showed total degradation of [TP]0 = 160 mg L−1 within 180 and 40 min for [PS]0 = [Fe2+]0 = 25 and 100 mM, respectively. The degradation cost was estimated to 56.8 $ per m3, for electricity price rates in the US at [PS]0 = [Fe2+]0 = 50 mM. A degradation mechanism involving in situ evolved reactive oxidative species, mainly sulfate and hydroxyl radicals, was also suggested based on LC/MS/MS HRAM analyses supported by frontier molecular orbital theory calculations.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This research was funded in part by the Lebanese National Council for Scientific Research (Award Number 103250), the K Shair CRSL fund (Award Number 103599), and the University Research Board (Award Number 103603) of the American University of Beirut and USAID-Lebanon through The National Academy of Sciences under PEER project 5-18 (Award number 103262). The authors are thankful to Prof. Faraj Hasanayn for his kind assistance in obtaining the theoretical study data. Additionally, the authors are thankful to Eng. Joan Younes, senior technician Simon Al-Ghawi and the glass blower at the chemistry department, Boutros Sawaya, for their technical assistance and the personnel of the K. Shair CRSL for their kind help.
References
- American Society of Health-System Pharmacists, Theophylline, https://medlineplus.gov/druginfo/meds/a681006.html, 2017 Search PubMed.
- C. A. Shively and S. M. Tarka, Prog. Clin. Biol. Res., 1984, 158, 149–178 CAS.
- K. Noguera-Oviedo and D. S. Aga, J. Hazard. Mater., 2016, 316, 242–251 CrossRef CAS PubMed.
- A. Wennmalm and S. C. Council, in Encyclopedia of Environmental Health, 2011, pp. 462–471 Search PubMed.
- A. Zenker, M. R. Cicero, F. Prestinaci, P. Bottoni and M. Carere, J. Environ. Manage., 2014, 378–387 CrossRef CAS.
- T. U. Berendonk, C. M. Manaia, C. Merlin, D. Fatta-Kassinos, E. Cytryn, F. Walsh, H. Bürgmann, H. Sørum, M. Norström, M. N. Pons, N. Kreuzinger, P. Huovinen, S. Stefani, T. Schwartz, V. Kisand, F. Baquero and J. L. Martinez, Nat. Rev. Microbiol., 2015, 310 CrossRef CAS.
- O. A. Jones, J. N. Lester and N. Voulvoulis, Trends Biotechnol., 2005, 163–167 CrossRef CAS.
- T. Heberer, Toxicol. Lett., 2002, 131, 5–17 CrossRef CAS.
- M. E. Rybak, M. R. Sternberg, C.-I. Pao, N. Ahluwalia and C. M. Pfeiffer, J. Nutr., 2015, 145, 766–774 CrossRef CAS.
- P. Rajasulochana and V. Preethy, Resour.-Effic. Technol., 2016, 2, 175–184 Search PubMed.
- Y. Luo, W. Guo, H. H. Ngo, L. D. Nghiem, F. I. Hai, J. Zhang, S. Liang and X. C. Wang, Sci. Total Environ., 2014, 473–474, 619–641 CrossRef CAS.
- Y. Yang, Y. S. Ok, K.-H. Kim, E. E. Kwon and Y. F. Tsang, Sci. Total Environ., 2017, 596–597, 303–320 CrossRef CAS.
- S. A. Snyder, Ozone: Sci. Eng., 2008, 30, 65–69 CrossRef CAS.
- J. Doummar, K. Nödler, T. Geyer and M. Sauter, Assessment and Analysis of Micropollutants 2010–2011 Search PubMed.
- S. Sun, J. Jiang, S. Pang, J. Ma, M. Xue, J. Li, Y. Liu and Y. Yuan, Sep. Purif. Technol., 2018, 201, 283–290 CrossRef CAS.
- R. Liang, S. Luo, F. Jing, L. Shen, N. Qin and L. Wu, Appl. Catal., B, 2015, 176–177, 240–248 CrossRef CAS.
- M. M. Sunil Paul, U. K. Aravind, G. Pramod, A. Saha and C. T. Aravindakumar, Org. Biomol. Chem., 2014, 12, 5611–5620 RSC.
- I. Kim, N. Yamashita and H. Tanaka, Chemosphere, 2009, 77, 518–525 CrossRef CAS.
- R. Liang, A. Hu, W. Li and Y. N. Zhou, J. Nanopart. Res., 2013, 15, 1990 CrossRef.
- N. S. Shah, A. D. Rizwan, J. A. Khan, M. Sayed, Z. U. H. Khan, B. Murtaza, J. Iqbal, S. U. Din, M. Imran, M. Nadeem, A. H. Al-Muhtaseb, N. Muhammad, H. M. Khan, M. Ghauri and G. Zaman, Process Saf. Environ. Prot., 2018, 117, 473–482 CrossRef CAS.
- F. Ali, J. A. Khan, N. S. Shah, M. Sayed and H. M. Khan, Process Saf. Environ. Prot., 2018, 307–314 CrossRef CAS.
- A. Ghauch, A. Baalbaki, M. Amasha, R. El Asmar, O. Tantawi, R. El Asmar and O. Tantawi, Chem. Eng. J., 2017, 317, 1012–1025 CrossRef CAS.
- M. Amasha, A. Baalbaki, S. Al Hakim, R. El Asmar and A. Ghauch, J. Adv. Oxid. Technol., 2018, 21, 261–273 CrossRef.
- S. Naim and A. Ghauch, Chem. Eng. J., 2016, 288, 276–288 CrossRef CAS.
- A. Ghauch, G. Ayoub and S. Naim, Chem. Eng. J., 2013, 228, 1168–1181 CrossRef CAS.
- A. Ghauch, A. M. Tuqan and N. Kibbi, Chem. Eng. J., 2015, 279, 861–873 CrossRef CAS.
- A. Ghauch, A. M. Tuqan, N. Kibbi and S. Geryes, Chem. Eng. J., 2012, 213, 259–271 CrossRef CAS.
- A. Ghauch, A. M. Tuqan and N. Kibbi, Chem. Eng. J., 2012, 197, 483–492 CrossRef CAS.
- A. Ghauch and A. M. Tuqan, Chem. Eng. J., 2012, 183, 162–171 CrossRef CAS.
- A. Fernandes, P. Makoś and G. Boczkaj, J. Cleaner Prod., 2018, 195, 374–384 CrossRef CAS.
- Y. Gao, N. Gao, Y. Deng, Y. Yang and Y. Ma, Chem. Eng. J., 2012, 195, 248–253 CrossRef.
- L. Bu, S. Zhou, Z. Shi, L. Deng, G. Li, Q. Yi and N. Gao, Environ. Sci. Pollut. Res., 2016, 23, 2848–2855 CrossRef CAS.
- C. Tan, N. Gao, S. Zhou, Y. Xiao and Z. Zhuang, Chem. Eng. J., 2014, 253, 229–236 CrossRef CAS.
- M. Amasha, A. Baalbaki and A. Ghauch, Chem. Eng. J., 2018, 350, 395–410 CrossRef CAS.
- G. Mark, M. N. Schuchmann, H. P. Schuchmann and C. von Sonntag, J. Photochem. Photobiol., A, 1990, 55(2), 157–168 CrossRef CAS.
- S. Al Hakim, S. Jaber, N. Zein Eddine, A. Baalbaki and A. Ghauch, Chem. Eng. J., 2020, 380, 122478 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford CT, 2013.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- S. Y. Oh, H. W. Kim, J. M. Park, H. S. Park and C. Yoon, J. Hazard. Mater., 2009, 168, 346–351 CrossRef CAS.
- I. M. Kolthoff, A. I. Medalia and H. P. Raaen, J. Am. Chem. Soc., 1951, 73, 1733–1739 CrossRef CAS.
- L. W. Matzek and K. E. Carter, Chemosphere, 2016, 151, 178–188 CrossRef CAS.
- W. Shang, Z. Dong, M. Li, X. Song, M. Zhang, C. Jiang and S. Feiyun, Chem. Eng. J., 2019, 361, 1333–1344 CrossRef CAS.
- I. Hussain, Y. Zhang and S. Huang, RSC Adv., 2014, 4(7), 3502–3511 RSC.
- D. Wu, X. Li, J. Zhang, W. Chen, P. Lu, Y. Tang and L. Li, Sep. Purif. Technol., 2018, 207, 255–261 CrossRef CAS.
- M. Nie, C. Yan, X. Xiong, X. Wen, X. Yang, Z. lv and W. Dong, Chem. Eng. J., 2018, 348, 455–463 CrossRef CAS.
- H. A. Gorrell, Am. Assoc. Pet. Geol. Bull., 1958, 42, 2513 Search PubMed.
- Environment Protection Authority (EPA), in South Australia, Salinity, http://www.epa.sa.gov.au/environmental_info/water_quality/threats/salinity, accessed 15 June 2017 Search PubMed.
- D. A. Armstronga, R. E. Huie, S. Lymar, W. H. Koppenol, G. Merényi, P. Neta, D. M. Stanbury, S. Steenken and P. Wardman, BioInorg. React. Mech., 2013, 9(1–4), 59–61 Search PubMed.
- C. Liang, Z.-S. Wang and N. Mohanty, Sci. Total Environ., 2006, 370, 271–277 CrossRef CAS.
- K. Hasegawa and P. Neta, J. Phys. Chem., 1978, 82, 854–857 CrossRef CAS.
- Y. Fan, Y. Ji, D. Kong, J. Lu and Q. Zhou, J. Hazard. Mater., 2015, 300, 39–47 CrossRef CAS.
- S. Norzaee, M. Taghavi, B. Djahed and F. K. Mostafapour, J. Environ. Manage., 2018, 215, 316–323 CrossRef CAS.
- S. Wang, J. Wu, X. Lu, W. Xu, Q. Gong, J. Ding, B. Dan and P. Xie, Chem. Eng. J., 2019, 358, 1091–1100 CrossRef CAS.
- D. Keeney and R. A. Olson, Crit. Rev. Environ. Control, 1986, 16, 257–304 CrossRef CAS.
- S. J. Boggs, D. Livermore and M. G. Seitz, Humic substances in natural waters and their complexation with trace metals and radionuclides: a review, 129 references, 1985 Search PubMed.
- L. Liu, S. Lin, W. Zhang, U. Farooq, G. Shen and S. Hu, Chem. Eng. J., 2018, 346, 515–524 CrossRef CAS.
- M. D. Paciolla, S. Kolla and S. A. Jansen, Adv. Environ. Res., 2002, 7(1), 169–178 CrossRef CAS.
- J. R. Bolton, K. G. Bircher, W. Tumas and C. A. Tolman, Pure Appl. Chem., 2001, 73(4), 627–637 CAS.
- F. Fardoun, O. Ibrahim, R. Younes and H. Louahlia-Gualous, Energy Procedia, 2012, 19, 310–320 CrossRef.
- XE Currency Converter: LBP to USD, https://www.xe.com/currencyconverter/convert/?Amount=225%26From=LBP%26To=USD, .
- J. A. V. Butler, C. N. Ramchandani and D. W. Thomson, J. Chem. Soc., 1935, 280–285 RSC.
- Q. Wang, X. Lu, Y. Cao, J. Ma, J. Jiang, X. Bai and T. Hu, Chem. Eng. J., 2017, 328, 236–245 CrossRef CAS.
- K. Fukui, T. Yonezawa and H. Shingu, J. Chem. Phys., 1952, 20(4), 722–725 CrossRef CAS.
- H. Yang, S. Zhou, H. Liu, W. Yan, L. Yang and B. Yi, J. Environ. Sci., 2013, 25(8), 1680–1686 CrossRef CAS.
- D. Miao, J. Peng, X. Zhou, L. Qian, M. Wang, L. Zhai and S. Gao, Chemosphere, 2018, 207, 174–182 CrossRef CAS.
- H. Liu, P. Sun, M. Feng, H. Liu, S. Yang, L. Wang and Z. Wang, Appl. Catal., B, 2016, 187, 1–10 CrossRef CAS.
- E. Lipczynska-Kochany, G. Sprah and S. Harms, Chemosphere, 1995, 30, 9–20 CrossRef CAS.
- J. M. Monteagudo, A. Durán, J. Latorre and A. J. Expósito, J. Hazard. Mater., 2016, 306, 77–86 CrossRef CAS.
- X. Xu, G. Pliego, J. A. Zazo, J. A. Casas and J. J. Rodriguez, J. Hazard. Mater., 2016, 318, 355–362 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra05362j |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 1
[Fe2+]0 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 presented the best results. A positive correlation was obtained between the TP degradation rate and increasing temperature and [PS]0, and a negative correlation was obtained with increasing pH. Both chloride and humic acid inhibited the degradation process, while nitrates enhanced it. TP dissolved in spring, sea and waste water simulating real effluents showed lower degradation rates than in DI water. Waste water caused the highest inhibition (kobs = 2.6 (±0.6) × 10−4 min−1). Finally, the TCAP system was tested on a real factory effluent highly charged with TP, e.g. [TP]0 = 160 mg L−1, with successful degradation under the conditions of 60 °C and [PS]0 = [Fe2+]0 = 50 mM.
1 presented the best results. A positive correlation was obtained between the TP degradation rate and increasing temperature and [PS]0, and a negative correlation was obtained with increasing pH. Both chloride and humic acid inhibited the degradation process, while nitrates enhanced it. TP dissolved in spring, sea and waste water simulating real effluents showed lower degradation rates than in DI water. Waste water caused the highest inhibition (kobs = 2.6 (±0.6) × 10−4 min−1). Finally, the TCAP system was tested on a real factory effluent highly charged with TP, e.g. [TP]0 = 160 mg L−1, with successful degradation under the conditions of 60 °C and [PS]0 = [Fe2+]0 = 50 mM.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 ratio) maintained in isocratic mode. The injection volume was set at 80 μL. A diode-array detector for the quantification of TP was coupled to the HPLC. For the aforementioned conditions, the TP retention time was observed to be 12 min. All samples were filtered using 0.45 μm PTFE 13 mm disc filters (Jaytee Biosciences Ltd., UK) before HPLC analysis. Selected TP chemical properties in addition to the calibration curve and the corresponding LINEST output are summarized in ESI Fig. 1S(a–c).† Identification of the degradation and transformation products of TP was performed on an Ultimate 3000 RSLC Thermo Scientific HPLC-MS/MS connected to a Q Exactive Orbitrap. A Hypersil GOLD C18 150 column (100 × 2.1 mm, 1.9 μm) was used for separation. The injection volume was set as 2 μL and the elution process was performed at a flow rate of 0.3 mL min−1 using DI water (containing 0.1% formic acid) as eluent A and methanol as eluent B. The mass spectrometer was operated in positive ionization mode. The auxiliary gas heater temperature was set as 350 °C and the capillary temperature was 320 °C.
30 ratio) maintained in isocratic mode. The injection volume was set at 80 μL. A diode-array detector for the quantification of TP was coupled to the HPLC. For the aforementioned conditions, the TP retention time was observed to be 12 min. All samples were filtered using 0.45 μm PTFE 13 mm disc filters (Jaytee Biosciences Ltd., UK) before HPLC analysis. Selected TP chemical properties in addition to the calibration curve and the corresponding LINEST output are summarized in ESI Fig. 1S(a–c).† Identification of the degradation and transformation products of TP was performed on an Ultimate 3000 RSLC Thermo Scientific HPLC-MS/MS connected to a Q Exactive Orbitrap. A Hypersil GOLD C18 150 column (100 × 2.1 mm, 1.9 μm) was used for separation. The injection volume was set as 2 μL and the elution process was performed at a flow rate of 0.3 mL min−1 using DI water (containing 0.1% formic acid) as eluent A and methanol as eluent B. The mass spectrometer was operated in positive ionization mode. The auxiliary gas heater temperature was set as 350 °C and the capillary temperature was 320 °C.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios = 1
[Fe2+]0 ratios = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, 1
10, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and 1
5 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and [TP]0 = 10 mg L−1 for all studied cases
1, and [TP]0 = 10 mg L−1 for all studied cases
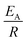 (Fig. 1b). EA and ln(A) were determined to be 154 (±16) kJ mol−1 and 50 (±5) kJ mol−1, respectively. The EA value is close to those reported by Ghauch et al. for ibuprofen, EA = 168 (±9) kJ mol−1, and naproxen, EA = 155.03 (±26.4) kJ mol−1, both using a TAP system; however, they used half the [PS]0 used in this work, e.g. 1 mM.26,28 The uncertainties reported for ln(A) and EA were determined using the LINEST function of Microsoft Excel.
(Fig. 1b). EA and ln(A) were determined to be 154 (±16) kJ mol−1 and 50 (±5) kJ mol−1, respectively. The EA value is close to those reported by Ghauch et al. for ibuprofen, EA = 168 (±9) kJ mol−1, and naproxen, EA = 155.03 (±26.4) kJ mol−1, both using a TAP system; however, they used half the [PS]0 used in this work, e.g. 1 mM.26,28 The uncertainties reported for ln(A) and EA were determined using the LINEST function of Microsoft Excel.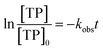
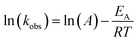
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios of 10
[Fe2+]0 ratios of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at favorable acidic pH to ensure Fe2+ solubility. Under all conditions tested, only negligible degradation of TP was observed (Fig. 5S†), with a maximum of 5% TP degradation noted at 60 min for the case of [PS]0 = 0.25 mM and a [PS]0
1 at favorable acidic pH to ensure Fe2+ solubility. Under all conditions tested, only negligible degradation of TP was observed (Fig. 5S†), with a maximum of 5% TP degradation noted at 60 min for the case of [PS]0 = 0.25 mM and a [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 1
[Fe2+]0 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, as summarized in Table 1. Thus, TP is demonstrated to be relatively resistant to the CAP system at room temperature compared to other organic contaminants. For example, Oh et al. obtained incomplete degradation of polyvinyl alcohol utilizing Fe2+-based CAP at room temperature and used a higher reaction temperature to secure significant degradation of the contaminant.40 This can be explained by the common scavenging effect of SO4˙− by Fe2+ to form the less effective Fe3+ ion (eqn (6))24,41 in addition to the recalcitrant character of the TP molecule.
1, as summarized in Table 1. Thus, TP is demonstrated to be relatively resistant to the CAP system at room temperature compared to other organic contaminants. For example, Oh et al. obtained incomplete degradation of polyvinyl alcohol utilizing Fe2+-based CAP at room temperature and used a higher reaction temperature to secure significant degradation of the contaminant.40 This can be explained by the common scavenging effect of SO4˙− by Fe2+ to form the less effective Fe3+ ion (eqn (6))24,41 in addition to the recalcitrant character of the TP molecule.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios, [PS]0 values and temperatures in order to positively or negatively confirm any synergistic effect that can be obtained upon combination of both PS activation techniques.
[Fe2+]0 ratios, [PS]0 values and temperatures in order to positively or negatively confirm any synergistic effect that can be obtained upon combination of both PS activation techniques.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) [Fe2+]0 ratio and [PS]0. TP degradation was studied at different [PS]0
[Fe2+]0 ratio and [PS]0. TP degradation was studied at different [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios and [PS]0 values. [PS]0
[Fe2+]0 ratios and [PS]0 values. [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios of 10
[Fe2+]0 ratios of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were tested at [PS]0 = 0.25, 1 and 5 mM, [TP]0 = 10 mg L−1 and T = 60 °C. kobs was calculated for the pseudo-first order kinetics model according to eqn (4), as demonstrated in previous work (Text S3,† Table 3). In fact, the reaction at the early stage can be considered to be zero order in the first five minutes;25 however, as the reaction proceeds, degradation by-products form and the reaction follows pseudo-first order kinetics. As depicted in Fig. 2 and Table 2, the 1
1 were tested at [PS]0 = 0.25, 1 and 5 mM, [TP]0 = 10 mg L−1 and T = 60 °C. kobs was calculated for the pseudo-first order kinetics model according to eqn (4), as demonstrated in previous work (Text S3,† Table 3). In fact, the reaction at the early stage can be considered to be zero order in the first five minutes;25 however, as the reaction proceeds, degradation by-products form and the reaction follows pseudo-first order kinetics. As depicted in Fig. 2 and Table 2, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [PS]0
1 [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio showed the highest degradation rate in the three tested [PS]0 conditions, followed by the 2
[Fe2+]0 ratio showed the highest degradation rate in the three tested [PS]0 conditions, followed by the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 10
1 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratios.
1 ratios.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio on TP degradation in a TCAP system. Experimental conditions: [PS]0 = 0.25, 1 and 5 mM, [PS]0
[Fe2+]0 ratio on TP degradation in a TCAP system. Experimental conditions: [PS]0 = 0.25, 1 and 5 mM, [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios of 1
[Fe2+]0 ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 10
1 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and T = 60 °C.
1, and T = 60 °C.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio on TP degradation in a TCAP system. Initial and final pH values are presented for every case. Experimental conditions: [PS]0 = 0.25, 1 and 5 mM, [PS]0
[Fe2+]0 ratio on TP degradation in a TCAP system. Initial and final pH values are presented for every case. Experimental conditions: [PS]0 = 0.25, 1 and 5 mM, [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios of 1
[Fe2+]0 ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 10
1 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and T = 60 °C
1, and T = 60 °C
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0
[Fe2+]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratios. The optimum ratio obtained varies depending on different parameters, such as the target analyte, the method of iron addition, and the state/morphology of the added iron.42 For example, a study by Oh et al. showed that 1
[Fe2+]0 ratios. The optimum ratio obtained varies depending on different parameters, such as the target analyte, the method of iron addition, and the state/morphology of the added iron.42 For example, a study by Oh et al. showed that 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [PS]0
1 [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 was the optimum ratio for the degradation of polyvinyl alcohol by CAP.40 Also, Naim and Ghauch (2016) showed that 1
[Fe2+]0 was the optimum ratio for the degradation of polyvinyl alcohol by CAP.40 Also, Naim and Ghauch (2016) showed that 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [PS]0
1 [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 was the most effective ratio to yield full ranitidine degradation in almost 10 min.24 On the other hand, Shang et al. obtained 10
[Fe2+]0 was the most effective ratio to yield full ranitidine degradation in almost 10 min.24 On the other hand, Shang et al. obtained 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [PS]0
1 [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 as the optimum ratio for degrading diatrizoate in a CAP system.43
[Fe2+]0 as the optimum ratio for degrading diatrizoate in a CAP system.43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 1
[Fe2+]0 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and [TP]0 = 10 mg L−1 at T = 60 °C. Fig. 3 and Table 3 show that the higher the [PS]0, the greater the observed rate constant kobs. For example, kobs increased by 32 fold when [PS]0 increased from 0.25 mM to 5.0 mM with good correlation (R2 = 0.9879), as shown in the inset of Fig. 3. This observation can be explained by the production of a greater amount of SO4˙− upon increasing [PS]0 (Fig. 3).
1 and [TP]0 = 10 mg L−1 at T = 60 °C. Fig. 3 and Table 3 show that the higher the [PS]0, the greater the observed rate constant kobs. For example, kobs increased by 32 fold when [PS]0 increased from 0.25 mM to 5.0 mM with good correlation (R2 = 0.9879), as shown in the inset of Fig. 3. This observation can be explained by the production of a greater amount of SO4˙− upon increasing [PS]0 (Fig. 3).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [PS]0
1 [PS]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio at different temperatures (40 °C, 50 °C and 60 °C), and the obtained results showed the same outputs. For example, as the reaction temperature increased from 40 °C to 50 °C and 60 °C, the % degradation of TP improved from 29% to 45% and 100%, respectively, at 60 min for [PS]0 = 5 mM (Fig. 6S†). A similar trend was observed for aniline degradation, where [PS]0 = 2.5 mM and zero valent iron [ZVI]0 = 0.3 g L−1 resulted in the total elimination of [aniline]0 = 0.05 mM in periods of 1 and 2 h at T = 80 °C and 60 °C, respectively.44
[Fe2+]0 ratio at different temperatures (40 °C, 50 °C and 60 °C), and the obtained results showed the same outputs. For example, as the reaction temperature increased from 40 °C to 50 °C and 60 °C, the % degradation of TP improved from 29% to 45% and 100%, respectively, at 60 min for [PS]0 = 5 mM (Fig. 6S†). A similar trend was observed for aniline degradation, where [PS]0 = 2.5 mM and zero valent iron [ZVI]0 = 0.3 g L−1 resulted in the total elimination of [aniline]0 = 0.05 mM in periods of 1 and 2 h at T = 80 °C and 60 °C, respectively.44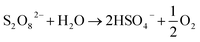
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg L−1 to mimic the conditions of distilled, fresh, brackish and saline water, respectively, according to Gorrell et al. and EPA data.47,48 It should be noted that chloride was present in all solutions at a concentration of 4 mM from FeCl2 (Fe2+ source) because FeCl2 was used as a source of Fe2+.
000 mg L−1 to mimic the conditions of distilled, fresh, brackish and saline water, respectively, according to Gorrell et al. and EPA data.47,48 It should be noted that chloride was present in all solutions at a concentration of 4 mM from FeCl2 (Fe2+ source) because FeCl2 was used as a source of Fe2+.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg L−1, [NO3−] = 1–100 mg L−1, and [HA] = 0.5–20 mg L−1 on TP degradation in a TCAP system. Experimental conditions: [PS]0 = [Fe2+]0 = 2 mM and [TP]0 = 10 mg L−1 for all conditions tested. kobs is obtained as per the pseudo-first order reaction rate model
000 mg L−1, [NO3−] = 1–100 mg L−1, and [HA] = 0.5–20 mg L−1 on TP degradation in a TCAP system. Experimental conditions: [PS]0 = [Fe2+]0 = 2 mM and [TP]0 = 10 mg L−1 for all conditions tested. kobs is obtained as per the pseudo-first order reaction rate model
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 10
[Fe2+]0 ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was used instead of the optimum obtained ratio of 1
1 was used instead of the optimum obtained ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in order to decrease the use of Fe2+, e.g. Fe(OH)2 in neutral media.45 These conditions were adopted because natural water matrices are buffered to around neutral pH (Table 6), mainly because of the presence of bicarbonate. The results showed that TP degradation was inhibited in the three tested cases compared to the DI matrix case, where kobs = 1.5 (±0.1) × 10−1 min−1, with WW showing ∼570 fold inhibition in terms of kobs = 2.6 (±0.6) × 10−4 min−1, followed by SpW ∼ 14 fold and SW ∼ 10 fold, kobs = 1.1 (±0.1) × 10−2 and 1.54 (±0.09) × 10−2 min−1, respectively (Fig. 7).
1 in order to decrease the use of Fe2+, e.g. Fe(OH)2 in neutral media.45 These conditions were adopted because natural water matrices are buffered to around neutral pH (Table 6), mainly because of the presence of bicarbonate. The results showed that TP degradation was inhibited in the three tested cases compared to the DI matrix case, where kobs = 1.5 (±0.1) × 10−1 min−1, with WW showing ∼570 fold inhibition in terms of kobs = 2.6 (±0.6) × 10−4 min−1, followed by SpW ∼ 14 fold and SW ∼ 10 fold, kobs = 1.1 (±0.1) × 10−2 and 1.54 (±0.09) × 10−2 min−1, respectively (Fig. 7).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500
500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400
400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250
250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500
500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 1
[Fe2+]0 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and T = 60 °C.
1 and T = 60 °C.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 1
[Fe2+]0 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and T = 60 °C. kobs is calculated for the pseudo-first order reaction rate
1, and T = 60 °C. kobs is calculated for the pseudo-first order reaction rate
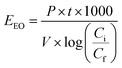
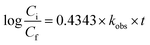
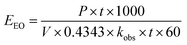
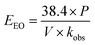
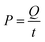
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio of 1
[Fe2+]0 ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and T = 60 °C
1, and T = 60 °C
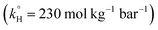 and TBA
and TBA 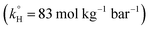 from the reactor due to heat.62 It is known that MeOH quenches both SO4˙− and HO˙ radicals, whereas TBA mainly quenches OH˙.22
from the reactor due to heat.62 It is known that MeOH quenches both SO4˙− and HO˙ radicals, whereas TBA mainly quenches OH˙.22


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Fe2+]0 ratio, [PS]0 and temperature were tested, where the 1
[Fe2+]0 ratio, [PS]0 and temperature were tested, where the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio gave optimum results, and the degradation rate increased with increasing [PS]0 and temperature. Salinity inhibited the degradation process, while nitrates slightly enhanced the process. The presence of HAs inhibited TP degradation. TP was dissolved in real water samples of spring, sea and waste water, which showed lower degradation rates in comparison with DI water medium. Real factory effluent containing TP was obtained and showed total degradation of [TP]0 = 160 mg L−1 within 180 and 40 min for [PS]0 = [Fe2+]0 = 25 and 100 mM, respectively. The degradation cost was estimated to 56.8 $ per m3, for electricity price rates in the US at [PS]0 = [Fe2+]0 = 50 mM. A degradation mechanism involving in situ evolved reactive oxidative species, mainly sulfate and hydroxyl radicals, was also suggested based on LC/MS/MS HRAM analyses supported by frontier molecular orbital theory calculations.
1 ratio gave optimum results, and the degradation rate increased with increasing [PS]0 and temperature. Salinity inhibited the degradation process, while nitrates slightly enhanced the process. The presence of HAs inhibited TP degradation. TP was dissolved in real water samples of spring, sea and waste water, which showed lower degradation rates in comparison with DI water medium. Real factory effluent containing TP was obtained and showed total degradation of [TP]0 = 160 mg L−1 within 180 and 40 min for [PS]0 = [Fe2+]0 = 25 and 100 mM, respectively. The degradation cost was estimated to 56.8 $ per m3, for electricity price rates in the US at [PS]0 = [Fe2+]0 = 50 mM. A degradation mechanism involving in situ evolved reactive oxidative species, mainly sulfate and hydroxyl radicals, was also suggested based on LC/MS/MS HRAM analyses supported by frontier molecular orbital theory calculations.