Open Access Article
Open Access ArticleLSGSP: a novel miRNA–disease association prediction model using a Laplacian score of the graphs and space projection federated method
Yi Zhang†
a,
Min Chen† *b,
Xiaohui Chenga and
Zheng Chenb
*b,
Xiaohui Chenga and
Zheng Chenb
aSchool of Information Science and Engineering, Guilin University of Technology, 541004 Guilin, China
bSchool of Computer Science and Technology, Hunan Institute of Technology, 421002 Hengyang, China. E-mail: chenmin@hnit.edu.cn
First published on 20th September 2019
Abstract
Lots of research findings have indicated that miRNAs (microRNAs) are involved in many important biological processes; their mutations and disorders are closely related to diseases, therefore, determining the associations between human diseases and miRNAs is key to understand pathogenic mechanisms. Existing biological experimental methods for identifying miRNA–disease associations are usually expensive and time consuming. Therefore, the development of efficient and reliable computational methods for identifying disease-related miRNAs has become an important topic in the field of biological research in recent years. In this study, we developed a novel miRNA–disease association prediction model using a Laplacian score of the graphs and space projection federated method (LSGSP). This integrates experimentally validated miRNA–disease associations, disease semantic similarity scores, miRNA functional scores, and miRNA family information to build a new disease similarity network and miRNA similarity network, and then obtains the global similarities of these networks through calculating the Laplacian score of the graphs, based on which the miRNA–disease weighted network can be constructed through combination with the miRNA–disease Boolean network. Finally, the miRNA–disease score was obtained via projecting the miRNA space and disease space onto the miRNA–disease weighted network. Compared with several other state-of-the-art methods, using leave-one-out cross validation (LOOCV) to evaluate the accuracy of LSGSP with respect to a benchmark dataset, prediction dataset and compare dataset, LSGSP showed excellent predictive performance with high AUC values of 0.9221, 0.9745 and 0.9194, respectively. In addition, for prostate neoplasms and lung neoplasms, the consistencies between the top 50 predicted miRNAs (obtained from LSGSP) and the results (confirmed from the updated HMDD, miR2Disease, and dbDEMC databases) reached 96% and 100%, respectively. Similarly, for isolated diseases (diseases not associated with any miRNAs), the consistencies between the top 50 predicted miRNAs (obtained from LSGSP) and the results (confirmed from the above-mentioned three databases) reached 98% and 100%, respectively. These results further indicate that LSGSP can effectively predict potential associations between miRNAs and diseases.
Introduction
MiRNAs are non-coding RNAs of about 20–25 nucleotides,1 which are widely found in eukaryotes. MiRNAs can account for 1–4% of human genes.2 MiRNAs normally regulate gene expression at the post-transcriptional level through targeting mRNAs for cleavage or translational inhibition.3 Many life processes, such as cell growth,4,5 differentiation,3 proliferation,6 aging7 and signal transduction,8 have been found to be associated with miRNAs. There is increasing evidence showing that miRNAs are closely related to complex diseases in humans, and can be regarded as tumor genes or tumor suppressor genes. For example, Mussnich et al.9 found that miR-199a and miR-375 affect the sensitivity of colon cancer cells to cetuximab through targeting PHLPP1, and that mir-106b-25 is related to esophageal neoplastic progression and proliferation via the suppression of 2 target genes: p21 and Bim.10 MiR-367 exerts a tumor-promoting effect through negatively regulating FBXW7 in non-small cell lung cancer (NSCLC), and it could be a potential therapeutic target for NSCLC intervention.11 MiR-100 and miR-125b are associated with lymph node metastasis in early colorectal cancer, and may be novel biomarkers for the lymph node metastasis of early colorectal cancers with submucosal invasion.12 Therefore, studying disease-related miRNAs is helpful for analyzing pathogenesis and exploring the rules related to diseases.The biological experiments, such as qRT-PCR and microarray profiling, used for discovering the associations between miRNAs and diseases are time consuming and labor intensive.13,14 Moreover, evidence relating to the associations between miRNAs and diseases discovered through biological experiments is only the tip of the iceberg, meaning that our understanding of the biological functions of miRNAs has a long way to go, although lots of miRNA–disease associations have been explored by scientists. It is an extremely urgent requirement to develop rapid and efficient computational methods to predict disease-related miRNAs to guide biological experiments.15,16
Based on the hypothesis that miRNAs with similar functions are often associated with diseases of similar phenotypes,17–19 Jiang et al.20 used a hypergeometric distribution to predict the associations between miRNAs and diseases. Based on the weighted-k-most-similar-neighbour method, Xuan et al.21 proposed HDMP to predict the relationship between miRNA and disease. On the basis of the method proposed be Xuan et al., Han et al.22 proposed DismiPred, which used topology information between nodes. Chen et al.23,24 designed two KNN-based disease association ranking algorithms (RKNNMDA and BLHARMDA). Chen et al.25 used random walks to predict disease-related miRNAs. However, these methods cannot predict diseases without any known related miRNAs. To solve this problem, Chen et al.26 used disease semantic similarity, miRNA similarity, Gaussian interaction profile kernel similarity and experimentally validated miRNA–disease associations to construct a heterogeneous graph approach, named HGIMDA, for revealing potential miRNA–disease associations. Shi et al.27 further integrated miRNA–gene relationships and random walks to predict miRNA–disease associations. Liao et al.28 proposed a new prediction method for disease-related miRNAs using the Laplacian score of the graphs and a random walk method. Chen et al.29 also proposed a new computational method named WBSMDA to uncover potential miRNAs related to multiple complex diseases through integrating known miRNA–disease association, semantic disease similarity, miRNA functional similarity, Gauss's nuclear spectrum of disease and miRNA to obtain final relevance scores for unconfirmed miRNA–disease associations. These methods have achieved good predictive performance and can be used for the prediction of isolated diseases.
Sun et al.30 proposed a method, named NTSMDA, using network topology to predict disease–miRNA associations. Nalluri et al.31 designed DISMIRA, a prediction method for disease-related miRNAs, from the two aspects of a maximum weighted matching model and motif-based analyses, respectively. You et al.32 proposed a path-based prediction method named PBMDA through integrating different biological data. Chen et al.33 proposed a bipartite heterogeneous network link prediction method (BHCN) based on bipartite network co-neighbours to predict miRNA–disease associations. Chen et al.34 proposed a method named NetCBI to predict disease-associated miRNAs using consistency of disease networks. Gu et al.35 and Chen et al.36 predicted potential miRNA–disease associations using bipartite network projections. Le et al.37 applied RWR, PRINCE, PRP and KSM to correlation analysis for predicting miRNA–disease associations. Chen et al.38 used network distance analysis. Yu et al.39 used global linear neighbours to predict miRNA–disease associations.
Machine learning methods have also entered the field of bioinformatics research.40–42 Support vector machines (SVMs) were used by Jiang et al.,43 Xu et al.,44 Zeng et al.45 and Wang et al.,46 a logistic model tree was used by Wang et al.,47 and a decision tree was used by Zhao et al.;48 these are excellent classification tools with global optimality and better generalization abilities to predict potential disease-related candidate miRNAs, but such methods require known negative sample information related to disease-related miRNAs that is difficult to obtain. In order to solve the problem of negative sample acquisition, Chen et al.49 used a regularized least squares approach to optimize similarity networks of miRNAs and diseases, respectively, and the final miRNA–disease associations were linear weightings of miRNA similarity scores and disease similarity scores. Restricted Boltzmann machine,50 auto-encoder,51 extreme gradient boosting machine,52 convolutional neural network,53 kernelized Bayesian matrix factorization,54,55 non-negative matrix factorization,56,57 singular value decomposition,58 Kronecker regularized least squares,59,60 Laplacian regularized sparse subspace learning,61 regularized least squares62 and semi-supervised link integrated prediction methods all were used to infer the relationships between potential diseases and miRNAs with good prediction results. Jiang et al.63 proposed a novel similarity kernel fusion (MDA-SKF) method via integrating multiple similarity kernels (three miRNA similarity kernels and three disease similarity kernels) to overcome the limitations through which some initial information may be lost in the process and some noise may exist in the integrated similarity kernel. SKF as an accurate network similarity construction method for MDA-SKF utilized the Laplacian regularized least squares method to uncover potential miRNA–disease associations, and it can be used as an accurate and efficient computational tool for guiding traditional experiments. Zou et al.64 utilized two methods of social network analysis (KATZ and CATAPULT) to predict potential disease-related candidate miRNAs. Li et al.65 utilized recommendation systems to predict associations between environmental factors, miRNAs and diseases. Peng et al.66 combined negative-aware and rating-based recommendation algorithms to predict miRNA–disease associations. Chen et al.67 constructed a similarity network and utilized ensemble learning to combine ranked results, called ensemble learning and link prediction for miRNA–disease association prediction. Chen et al.68 presented a HAMDA model that considered not only the network structure and information propagation but also field-related information to reveal miRNA–disease associations through mixing graph-based recommendation algorithms, and it obtained satisfactory prediction results.
For experimentally verified less well-known miRNA–disease associations and hard-to-obtain negative samples of miRNA–disease associations, Zeng et al.,69 Li et al.,70 Chen et al.71 and Peng et al.72 utilized matrix completion to estimate potential miRNA–disease associations. Chen et al.73 combined a sparse learning method with a heterogeneous graph inference method for miRNA–disease association predictions. Tang et al.74 fully exploited miRNA functional similarity and disease semantic similarity to achieve the matrix completion of miRNA–disease association through using a dual Laplacian regularization term, which transformed miRNA–disease association prediction into a matrix completion problem. This achieved good prediction effects, only needing experimentally validated miRNA–disease associations, and it provided new ideas for solving the problems that occur when miRNA–disease association data is insufficient.
Although existing computational methods have made outstanding contributions to the field of miRNA–disease association prediction, they still have the following defects:
(1) These prediction methods are not accurate enough;
(2) Isolated diseases and new miRNAs (miRNAs not associated with any disease) cannot be predicted; and
(3) Negative samples of miRNA–disease associations are required.
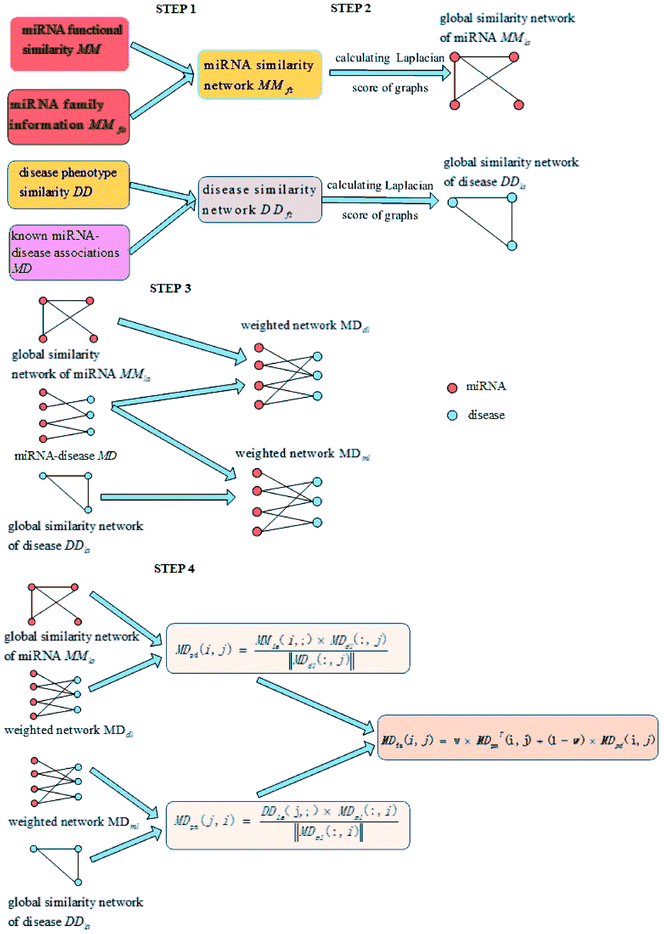
In order to overcome these defects, our proposed LSGSP model mainly consists of the following four steps to predict miRNA–disease associations:
(1) Reconstructing similarity networks for diseases and miRNAs, using known miRNA–disease associations, disease semantic similarity, miRNA family information and miRNA functional similarity, respectively;
(2) Obtaining the global similarity scores of the disease similarity networks and miRNA similarity networks through calculating the Laplacian scores of the graphs;
(3) Constructing miRNA–disease weight networks on the basis of experimentally verified miRNA–disease Boolean networks combined with global disease similarity networks and global miRNA similarity networks;
(4) Representing the miRNA–disease association scores using vector projections.
Therefore, LSGSP, as a global approach that does not require negative samples, can simultaneously predict all miRNA–disease associations, and can be used to predict isolated diseases and new miRNAs with good prediction effects in LOOCV and case analysis.
Materials and methods
Data preparation
We used three datasets, known as the benchmark dataset, prediction dataset and compare dataset, in this paper. The benchmark dataset, obtained from the ESI in ref. 20, is composed by processed 99 miRNAs, 51 diseases and 225 miRNA–disease associations from an original 271 miRNA–disease associations verified by experiments. The prediction dataset, obtained from the ESI in ref. 19, is composed by processed of 271 miRNAs, 137 diseases and 1395 miRNA–disease associations. The compare dataset,75 obtained from the HMDDv2.0 database, is composed by processed 495 miRNAs, 383 diseases and 5430 miRNA–disease associations. The matrix MD was used to represent the miRNA–disease associations, and the corresponding value of MD(i,j) is set to 1 if the miRNA node mi is associated with the disease node dj, otherwise it is set to 0.Functional similarity scores between miRNAs obtained from the ESI in ref. 19 were represented by the matrix MM. MiRNA family information obtained from the miRBase database76 was represented by the matrix MMfa. MMfa(i,j) is set to 1 if the miRNA node mi is associated with the miRNA node mj, otherwise it is set to 0. We used the matrix DD to represent the semantic similarity scores between diseases obtained from the ESI in ref. 66.
Firstly, we used the known matrix MD to calculate the disease similarity information DDas, which can be represented by:
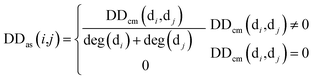 | (1) |
| DDfs(i,j) = μ × DD(i,j) + (1 − μ) × DDas(i,j) | (2) |
| MMfs(i,j) = θ × MM(i,j) + (1 − θ) × MMfa(i,j) | (3) |
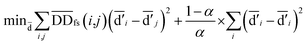 | (4) |
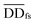 denotes the normalized matrix of the disease similarity matrix DDfs, and α is an equilibrium factor with a range of α ∈ (0,1). The approximate solution of formula (4) is as follows:77
denotes the normalized matrix of the disease similarity matrix DDfs, and α is an equilibrium factor with a range of α ∈ (0,1). The approximate solution of formula (4) is as follows:77
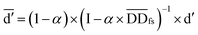 | (5) |
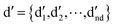 denotes the initial vector used for representing the similarity between the disease node dk(k = 1,2,…,nd) and other disease nodes, where the corresponding element value of
denotes the initial vector used for representing the similarity between the disease node dk(k = 1,2,…,nd) and other disease nodes, where the corresponding element value of 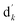 is 1 when querying the kth position in this vector, and the other elements are 0. The Laplacian scores of the graphs between all diseases are represented by the matrix DDla, which is the collection of vectors
is 1 when querying the kth position in this vector, and the other elements are 0. The Laplacian scores of the graphs between all diseases are represented by the matrix DDla, which is the collection of vectors 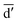 .
.Similarly, the Laplacian score of the graphs between all miRNAs is represented by MMla, which is as follows:
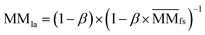 | (6) |
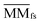 denotes the normalized matrix of MMfs, and β denotes an equilibrium factor with a range of β ∈ (0,1).
denotes the normalized matrix of MMfs, and β denotes an equilibrium factor with a range of β ∈ (0,1).
By integrating the global similarity matrix of disease DDla and the experimentally verified Boolean network MD of miRNA–disease associations, the weighted network MDdl of miRNA–disease associations was constructed based on the global similarity information of diseases.
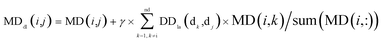 | (7) |
Through integrating the global similarity matrix of miRNAs MMla and the experimentally verified Boolean network MD of miRNA–disease associations, the weighted network MDml of miRNA–disease associations was constructed based on the global similarity information from miRNAs.
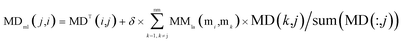 | (8) |
(1) Spatial projection scores based on the Laplacian similarities of diseases:
We used the projected scores of the disease similarity networks in the weighted network MDml of miRNA–disease associations to represent the miRNA–disease association scores; the calculation is as follows:
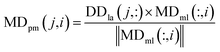 | (9) |
(2) spatial projection scores based on the Laplacian similarities of miRNAs:
We used the projected scores of miRNA similarity networks in the weighted network MDdl to represent the miRNA–disease scores; the calculation is as follows:
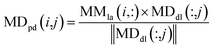 | (10) |
(3) Final integrated spatial projection scores based on Laplacian similarities of diseases and miRNAs:
Finally, we integrated the spatial projection scores based on the Laplacian similarities of diseases and spatial projection scores based on Laplacian similarities of miRNAs to calculate the final prediction scores, as shown below:
| MDfs(i,j) = ω×MDTpm(i,j) + (1 − ω) × MDpd(i,j) | (11) |
Although many researchers have used Laplacian regularization to identify miRNA–disease associations (such as LRSSLMDA,61 MDA-SKF,63 and DLRMC74), our proposed LSGSP differs from these research approaches in the following three aspects:
Firstly, it differs in terms of the data preparation process. MDA-SKF used miRNA sequence similarity, but others (LSGSP, LRSSLMDA and DLRMC) did not. LSGSP uses miRNA family information, but others (MDA-SKF, LRSSLMDA and DLRMC) do not.
Secondly, it differs in terms of the purposes of Laplacian regularization utilization. LRSSLMDA, MDA-SKF and DLRMC used Laplacian regularization in the classification decision stage. LRSSLMDA built an objective function from the common miRNA/disease subspace for miRNA/disease feature spaces, an L1-norm constraint and Laplacian regularization, and finally combined these optimization results to attain the final prediction outcomes. MDA-SKF optimized objective Laplacian regularized least squares functions to obtain a predicted association matrix, which uncovered potential miRNA–disease associations. DLRMC used a matrix completion model to calculate the potential missing entries of the miRNA–disease association matrix, and then used dual Laplacian regularization to regularize the miRNA–disease association matrix. The purpose of using Laplacian scores of the graphs in LSGSP is to obtain global network similarity, and for missing miRNA–disease association calculations, a network projection method was used.
Thirdly, it differs in the type of model used. From a classifier perspective, LRSSLMDA, DLRMC and MDA-SKF all utilized a machine learning-based model for miRNA–disease association prediction, which needed to optimize objective functions to obtain prediction results. However, our LSGSP is a network analysis-based computable model, whose missing miRNA–disease association calculations do not need the optimal solution to obtain an objective function. The implementation process of LSGSP is simple, and the prediction results of LSGSP are intuitive and easy to interpret.
Results
Parameter selection method
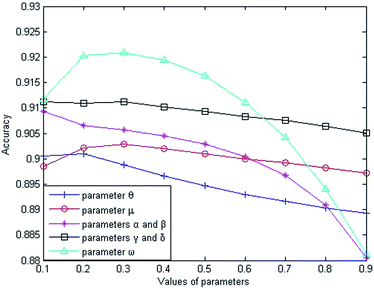
This section mainly discusses the influences of different types of parameters (the weighting parameters θ and μ, equilibrium parameters α and β, equilibrium parameters γ and δ, and weighting parameter ω) on the prediction performance of LSGSP.(1) The weight parameters θ and μ for similarity network construction.
The weight parameter θ represents the proportion of the functional similarity scores from Wang et al.19 used for constructing the miRNA similarity network. In order to find the optimal θ value, we first set the parameters to fixed values (μ = α = β = γ = δ = ω = 0.5), and changed the value of θ from 0.1 to 0.9. Through experiments involving cross-validating and calculating AUC values from the benchmark dataset, we found that the AUC value increased gradually from 0.9006 to 0.9010 when θ went from 0.1 to 0.2 and the AUC value decreased gradually from 0.9010 to 0.8892 when θ went from 0.2 to 0.9. From the changing curve shown in Fig. 2, the AUC value reached a maximum when θ = 0.2; therefore, we set θ = 0.2 to obtain good prediction performance.
The weight parameter μ from the disease similarity network indicates the semantic similarity score proportion in the constructed network. On the basis of θ = 0.2, we set the rest of the parameters to 0.5 (θ = 0.2, α = β = γ = δ = ω = 0.5). By taking 0.1 as the step size to increase the μ value, we found that the AUC value reached a maximum when μ = 0.3 and the AUC value decreased gradually when μ went from 0.3 to 0.9, as shown in Fig. 2. Therefore, we set μ = 0.3 for good prediction performance.
(2) The equilibrium parameters α and β for the global similarity network.
The Laplacian similarity equilibrium factor α, used for the disease similarity network, and the Laplacian similarity equilibrium factor β, used for the miRNA similarity network, were initially set to 0.1 and gradually changed to the same value using a step size of 0.1. The other three types of parameter values were set to fixed values (θ = 0.2, μ = 0.3, γ = δ = ω = 0.5) at the same time. When α and β increased gradually, the AUC value decreased from 0.9093 to 0.8805 gradually in the experiment; therefore the AUC value was optimal when α and β were set to 0.1.
(3) The equilibrium parameters γ and δ for miRNA–disease weight network construction.
Similarly, the third type of parameter included the equilibrium parameters γ and δ, used for miRNA–disease weight network construction; their values were set to the same value. The effects of the equilibrium parameters γ and δ on LSGSP were tested in the same way as before, and the AUC value reached an optimal value of 0.9113 when γ andδ were set to 0.1.
(4) The weight parameterω for spatial projection scores.
Finally, in order to obtain the optimal ω value, we gradually increased the value of ω, taking 0.1 as the step size. Through experiment, we found that the AUC value increased gradually from 0.9113 to 0.9221 when the value of ω was increased from 0.1 to 0.3. When the value of ω was increased from 0.3 to 0.9, the AUC value decreased from 0.9221 to 0.8812. Therefore, we set ω = 0.3 to obtain the optimal AUC value, which indicated that our prediction results depended more on the spatial projection scores based on the Laplacian similarities of miRNAs.
In summary, our parameter selections from the benchmark dataset were: θ = 0.2; μ = 0.3; α = β = 0.1; γ = δ = 0.1; ω = 0.3. By using the same method, the parameter selections from the prediction dataset were: θ = 0.2; μ = 0.1; α = β = 0.1; γ = δ = 0.9; ω = 0.9. For the compare dataset, the parameter θ was set to 1 because family information was not used. From the same method as used before, the parameter selections from the compare dataset were: θ = 1; μ = 0.1; α = β = 0.1; γ = δ = 0.9; ω = 0.3.
Comparison of the prediction performance in different situations
In this paper, the proposed LSGSP predicted the association scores of miRNAs and diseases using the spatial projection scores of Laplacian similarity. The execution process of LSGSP was as follows:(1) Reconstructing the miRNA network using family information;
(2) Reconstructing the disease network using miRNA–disease association pairs;
(3) Obtaining the global similarity network using the Laplacian scores;
(4) Constructing the miRNA–disease weighted network using the global disease similarity network, the global miRNA similarity network and miRNA–disease association information;
(5) Obtaining the prediction scores using vector space projection.
We evaluate the predictive performance of LSGSP in the following five situations:
(1) The predictive performance without considering miRNA network reconstruction and disease network reconstruction (LSGSP without NR);
(2) The predictive performance in the case of reconstructing the miRNA network (LSGSP with MNR);
(3) The predictive performance in the case of reconstructing the disease network (LSGSP with DNR);
(4) The predictive performance in the case of reconstructing the miRNA network and disease network without reconstructing the miRNA–disease weight network (LSGSP without MDWN); and
(5) The predictive performance with all relevant information (LSGSP with all information).
From the results from performing LOOCV shown in Fig. 3, it can be found that the worst predictive performance occurred in the situation of LSGSP without MDWN, where the AUC value was only 0.7809. However, once the miRNA–disease weighted network was constructed, even without considering the reconstruction of the miRNA network and disease network (LSGSP without NR), the AUC value reached 0.8973, which indicated that miRNA–disease weighted network construction had a significant effect on the improvement of prediction performance. In the situation of LSGSP with MNR, the AUC value increased from 0.8973 to 0.9135. After reconstructing the disease network through adding structural information relating to the known association network (LSGSP with DNR), the AUC value increased from 0.8973 to 0.9049, and the AUC value in the situation of LSGSP with all information was increased to 0.9221. This shows that LSGSP is commendable at predicting the associations between miRNAs and diseases.
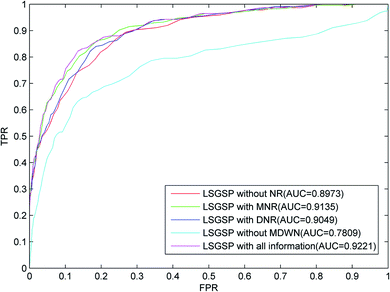 | ||
| Fig. 3 ROC curves and AUC values based on LOOCV in different situations, using the benchmark dataset. | ||
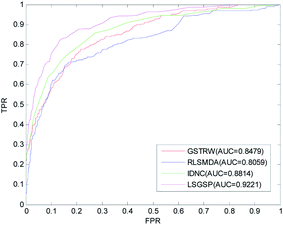
Comparison with other methods
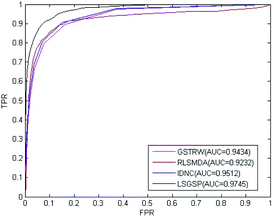
To further evaluate the predictive performance of LSGSP, we compared it with three classical methods, RLSMDA,49 IDNC78 and GSTRW,79 with the same parameter selection as described in the respective papers. From the results of performing LOOCV on the benchmark dataset, as shown in Fig. 4, the AUC values of RLSMDA, IDNC, GSTRW and LSGSP were 0.8059, 0.8479, 0.8814 and 0.9221, respectively, which showed that LSGSP achieved the best predictive performance, with a value 12.60%, 8.05% and 4.41% higher, respectively, than RLSMDA, IDNC and GSTRW.To avoid data dependence, the prediction dataset was used to further compare the four methods mentioned above. According to the prediction dataset, with more known associations than the benchmark dataset, the accuracy of all four methods greatly improved. The AUC values of RLSMDA, IDNC, GSTRW and LSGSP for the prediction dataset were 0.9232, 0.9434, 0.9512 and 0.9745, respectively, as shown in Fig. 5. The AUC value of LSGSP using the prediction dataset was the highest, with a value 5.26%, 3.19% and 2.39% higher, respectively, than those of RLSMDA, IDNC and GSTRW. The prediction results showed the excellent predictive abilities of LSGSP, mainly due to the use of Laplacian scores and network projection, and LSGSP showed more outstanding advantages with less experimentally verified miRNA–disease associations.
So far, LRSSLMDA,61 MDA-SKF63 and DLRMC74 have obtained good predictive results from the compare dataset using Laplacian regularization to identify miRNA-disease associations. To compare LSGSP with the above-mentioned three methods equally, the AUC values from LSGSP, LRSSLMDA, MDA-SKF and DLRMC given from the compare dataset in Table 1 are the optimal values described in the papers that they belong to. When using the same available experimental data without any family information for LSGSP, LRSSLMDA and DLRMC equally, the AUC value of LSGSP was 0.9194, which was higher than those of LRSSLMDA and DLRMC, as shown in Table 1. MDA-SKF showed the best prediction results, with an optimal AUC value of 0.9576, which were attributed to its accurate SKF network construction method. However, it is unfair to compare the prediction results of MDA-SKF with those from LSGSP directly, because MDA-SKF used extra miRNA sequence similarity information but LSGSP did not. Using SKF for network reconstruction with LSGSP (named LSGSP-SKF) to compare with MDA-SKF under the same experimental conditions, the AUC value was 0.9675, shown as LSGSP-SKF in Table 1; this value was the highest among all methods.
| No. | Method | AUC |
|---|---|---|
| 1 | LSGSP | 0.9194 |
| 2 | LRSSLMDA | 0.9178 |
| 3 | DLRMC | 0.9174 |
| 4 | MDA-SKF | 0.9576 |
| 5 | LSGSP-SKF | 0.9675 |
The prediction of new miRNAs and isolated diseases
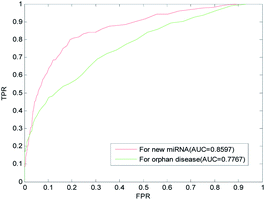
The term isolated disease refers to associations between a disease and all miRNAs that are unknown, and the term new miRNA refers to a miRNA with unknown association information related to diseases. The prediction of isolated diseases and new miRNAs can further help scientists to understand the molecular mechanisms of diseases and further reveal the mechanisms behind the occurrences of diseases. Recently, more and more miRNAs have been found with unknown disease-related information. It is urgent to develop efficient calculation methods to predict the associations between new miRNAs and isolated diseases, to reduce the blindness of subsequent biological experiments, to help scientists understand the regulation mechanisms of miRNAs, and to analyze the pathogenesis of diseases at the molecular level.We implemented LOOCV on the benchmark dataset to evaluate the predictive performance of LSGSP for new miRNAs and isolated diseases. For each new miRNA verified, the associations between the miRNA and all diseases were removed to simulate a new miRNA. The ROC curves and AUC values predicted by LSGSP using the benchmark dataset are shown in Fig. 6, in which the AUC of LSGSP was 0.8597. Similarly, the associations between the disease and all miRNAs were removed to simulate an isolated disease, and the AUC value from the benchmark dataset was 0.7767. According to the prediction results, LSGSP showed excellent predictive performance in predicting new miRNA-related diseases and isolated disease-related miRNAs.
Case studies
Lots of research evidence has indicated that miRNA mutations and disorders are important causes of disease; thus, the further evaluation of the LSGSP performance for miRNA–disease association prediction is necessary. We selected prostate neoplasms and lung neoplasms as case studies with model training and prediction using the prediction dataset, and then validated all predictions using the updated HMDD, miR2Disease, and dbDEMC databases, respectively. After that, the predictive abilities of LSGSP for potential miRNA–disease associations and associations between isolated diseases and miRNAs were analyzed.Potential miRNA–disease prediction
Prostate neoplasms are a disease occurring in the male reproductive system, especially common in countries with a severely aging population.80 Biological experiments have proved some important associations between prostate cancer and miRNAs, such as the epigenetically altered mir-193b target cyclin D1.81 Rauhala et al.82 found that mir-193b is an epigenetically regulated putative tumor for prostate cancer. Yang et al.83 found that the downregulation of mir-221 and mir-222, which inhibited prostate neoplasm cell proliferation and migration, was mediated in part by SIRT1 activation. Recognizing prostate neoplasm related miRNAs helps to understand the pathogenic mechanism of prostate neoplasms, so as to start treatment at the early stages of the disease.We used LSGSP for training and prediction, using 34 known associations between prostate neoplasms and miRNAs from the prediction dataset. Only 2 of the top 50 miRNAs predicted to be associated with prostate neoplasms were not confirmed from the updated HMDD, miR2Disease, and dbDEMC databases (shown in Table 2), which were hsa-mir-429 and hsa-mir-7 (ranked 23rd and 50th in predictive results, respectively). However, we found evidence of associations between these two miRNAs and prostate neoplasms upon searching the latest literature. Ouyang et al.84 found that the down-regulation of hsa-mir-429 inhibited the proliferation of prostate cancer cells. Zhou et al.85 identified a total of 130 differentially expressed miRNAs via miRNA microarray studies and found that hsa-mir-7-1 was up-regulated. Sánchez et al.86 proposed synergy between miR-21-5p and miR-7p in the regulation of prostate carcinogenesis. However, the dates of publication for these literature studies were all after the last updates of the three databases, further confirming the effectiveness of LSGSP.
| Rank | miRNA name | Evidence | Rank | miRNA name | Evidence |
|---|---|---|---|---|---|
| 1 | hsa-mir-18a | dbDEMC | 26 | hsa-mir-9 | dbDEMC |
| 2 | hsa-mir-19b | HMDD, dbDEMC, miR2Disease | 27 | hsa-mir-30d | HMDD, dbDEMC |
| 3 | hsa-let-7a | dbDEMC, miR2Disease | 28 | hsa-mir-15b | dbDEMC |
| 4 | hsa-mir-19a | dbDEMC | 29 | hsa-mir-30b | dbDEMC |
| 5 | hsa-mir-34a | HMDD, dbDEMC, miR2Disease | 30 | hsa-mir-302a | dbDEMC |
| 6 | hsa-let-7d | HMDD, dbDEMC, miR2Disease | 31 | hsa-mir-143 | HMDD, dbDEMC, miR2Disease |
| 7 | hsa-let-7e | dbDEMC, miR2Disease | 32 | hsa-mir-218 | dbDEMC, miR2Disease |
| 8 | hsa-mir-155 | dbDEMC | 33 | hsa-mir-92b | dbDEMC |
| 9 | hsa-let-7f | dbDEMC, miR2Disease | 34 | hsa-mir-302b | dbDEMC |
| 10 | hsa-mir-200b | HMDD, dbDEMC | 35 | hsa-mir-372 | dbDEMC |
| 11 | hsa-let-7b | HMDD, dbDEMC, miR2Disease | 36 | hsa-mir-200c | dbDEMC |
| 12 | hsa-let-7c | HMDD, dbDEMC, miR2Disease | 37 | hsa-mir-24 | dbDEMC, miR2Disease |
| 13 | hsa-mir-20b | dbDEMC | 38 | hsa-mir-181a | dbDEMC |
| 14 | hsa-let-7i | dbDEMC | 39 | hsa-mir-339 | hsa-miR-339-5p |
| 15 | hsa-mir-92a | dbDEMC | 40 | hsa-mir-302c | dbDEMC, miR2Disease |
| 16 | hsa-mir-34b | HMDD, dbDEMC | 41 | hsa-mir-151 | dbDEMC |
| 17 | hsa-mir-29a | HMDD, dbDEMC, miR2Disease | 42 | hsa-mir-27a | HMDD, dbDEMC, miR2Disease |
| 18 | hsa-mir-141 | HMDD, dbDEMC, miR2Disease | 43 | hsa-mir-215 | dbDEMC |
| 19 | hsa-mir-18b | dbDEMC | 44 | hsa-mir-320 | dbDEMC, miR2Disease |
| 20 | hsa-mir-126 | HMDD, dbDEMC, miR2Disease | 45 | hsa-mir-1 | dbDEMC |
| 21 | hsa-mir-200a | HMDD, dbDEMC | 46 | hsa-mir-29c | dbDEMC |
| 22 | hsa-mir-125a | dbDEMC, miR2Disease | 47 | hsa-mir-196a | dbDEMC |
| 23 | hsa-mir-429 | Unconfirmed | 48 | hsa-mir-383 | dbDEMC |
| 24 | hsa-let-7g | dbDEMC, miR2Disease | 49 | hsa-mir-195 | HMDD, dbDEMC, miR2Disease |
| 25 | hsa-mir-125b | dbDEMC, miR2Disease | 50 | hsa-mir-7 | Unconfirmed |
Due to the low detection rate of lung neoplasms, a common lethal disease, they pose a great threat to people's lives,87,88 especially in developing countries. Recent studies have found that miRNA dysregulation can be considered a diagnostic biomarker for lung neoplasms, such as the expression of mir-1246 and mir-1290, which can be a key driving factor promoting tumor initiation and progression in human non-small cell lung cancer89. Lin et al.90 confirmed that mir-324-5p and mir-324-3p play carcinogenic roles with respect to lung cancer. MiR-101 represses lung cancer via down-regulating CXCL12.91 With the discovery of more and more lung neoplasm-related miRNA functions, their study can provide more help for the early detection of lung neoplasms.
We used 72 lung neoplasm–miRNA associations from the prediction dataset to train LSGSP and then predicted the remaining unknown associations. We found supporting evidence for all the first 50 miRNAs related to lung neoplasms predicted by LSGSP using the above-mentioned three databases (as shown in Table 3).
| Rank | miRNA name | Evidence | Rank | miRNA name | Evidence |
|---|---|---|---|---|---|
| 1 | hsa-mir-106b | dbDEMC | 26 | hsa-mir-302b | dbDEMC, miR2Disease |
| 2 | hsa-mir-93 | dbDEMC | 27 | hsa-mir-27a | HMDD, dbDEMC |
| 3 | hsa-mir-200b | HMDD, dbDEMC | 28 | hsa-mir-215 | dbDEMC |
| 4 | hsa-mir-20b | HMDD, dbDEMC | 29 | hsa-mir-151 | dbDEMC |
| 5 | hsa-mir-25 | dbDEMC | 30 | hsa-mir-339 | dbDEMC, miR2Disease |
| 6 | hsa-mir-127 | HMDD, dbDEMC | 31 | hsa-mir-373 | dbDEMC |
| 7 | hsa-mir-429 | dbDEMC | 32 | hsa-mir-302a | dbDEMC |
| 8 | hsa-mir-141 | dbDEMC | 33 | hsa-mir-367 | HMDD, dbDEMC, miR2Disease |
| 9 | hsa-mir-92b | HMDD, dbDEMC | 34 | hsa-mir-181a | dbDEMC, miR2Disease |
| 10 | hsa-mir-18b | dbDEMC | 35 | hsa-mir-148a | dbDEMC |
| 11 | hsa-mir-98 | HMDD, dbDEMC, miR2Disease | 36 | hsa-mir-15a | dbDEMC |
| 12 | hsa-mir-221 | HMDD, dbDEMC, miR2Disease | 37 | hsa-mir-520b | dbDEMC |
| 13 | hsa-mir-200a | dbDEMC | 38 | hsa-mir-103 | dbDEMC |
| 14 | hsa-mir-200c | dbDEMC, miR2Disease | 39 | hsa-mir-133a | dbDEMC |
| 15 | hsa-mir-222 | dbDEMC | 40 | hsa-mir-372 | HMDD, dbDEMC, miR2Disease |
| 16 | hsa-mir-16 | HMDD | 41 | hsa-mir-107 | HMDD, dbDEMC |
| 17 | hsa-mir-10b | HMDD, dbDEMC, miR2Disease | 42 | hsa-mir-99b | dbDEMC |
| 18 | hsa-mir-194 | HMDD, dbDEMC, miR2Disease | 43 | hsa-mir-130a | dbDEMC, miR2Disease |
| 19 | hsa-mir-195 | dbDEMC, miR2Disease | 44 | hsa-mir-451 | dbDEMC |
| 20 | hsa-mir-7 | dbDEMC | 45 | hsa-mir-15b | dbDEMC, miR2Disease |
| 21 | hsa-mir-181b | dbDEMC | 46 | hsa-mir-499 | dbDEMC, miR2Disease |
| 22 | hsa-mir-320 | HMDD, dbDEMC, miR2Disease | 47 | hsa-mir-204 | dbDEMC, miR2Disease |
| 23 | hsa-mir-296 | dbDEMC | 48 | hsa-mir-23b | dbDEMC |
| 24 | hsa-mir-135b | dbDEMC | 49 | hsa-mir-302d | dbDEMC |
| 25 | hsa-mir-302c | dbDEMC | 50 | hsa-mir-153 | dbDEMC |
Isolated disease-related miRNA prediction
Next we validated the predictive ability of LSGSP for isolated diseases, through simulating isolated diseases by removing all known miRNA associations with verified diseases. The predicted results from LSGSP relating to prostate neoplasms and lung neoplasms from an isolated disease perspective are listed in Table 4 and 5; they were obtained under the conditions of removing the 34 known prostate neoplasm–miRNA associations, where only hsa-mir-302d from the predicted top 50 prostate neoplasm-related miRNAs was not found. Of the predicted top 50 lung neoplasm-related miRNAs, all were found in the above three databases. However, Aghanoori et al.92 found that hsa-mir-302d was down-regulated in lung cancer tissue. Therefore, supporting evidence for the prediction capabilities of LSGSP for potential disease–miRNA associations and isolated disease–miRNA associations was found from the databases and was validated by the latest literature studies, which means that LSGSP has excellent predictive performance.| Rank | miRNA name | Evidence | Rank | miRNA name | Evidence |
|---|---|---|---|---|---|
| 1 | hsa-mir-21 | HMDD, dbDEMC, miR2Disease | 26 | hsa-mir-146a | HMDD, dbDEMC, miR2Disease |
| 2 | hsa-mir-155 | HMDD, dbDEMC, miR2Disease | 27 | hsa-mir-137 | dbDEMC |
| 3 | hsa-mir-15a | HMDD, dbDEMC, miR2Disease | 28 | hsa-let-7a | HMDD, miR2Disease |
| 4 | hsa-mir-377 | HMDD | 29 | hsa-mir-205 | dbDEMC |
| 5 | hsa-mir-373 | HMDD, dbDEMC | 30 | hsa-mir-141 | dbDEMC |
| 6 | hsa-mir-372 | HMDD, dbDEMC, miR2Disease | 31 | hsa-mir-302a | dbDEMC |
| 7 | hsa-mir-29c | HMDD, dbDEMC, miR2Disease | 32 | hsa-mir-181a | dbDEMC, miR2Disease |
| 8 | hsa-mir-34a | dbDEMC | 33 | hsa-mir-200b | HMDD, dbDEMC |
| 9 | hsa-mir-302b | dbDEMC | 34 | hsa-mir-30a | dbDEMC |
| 10 | hsa-mir-451 | HMDD, dbDEMC, miR2Disease | 35 | hsa-mir-143 | HMDD, dbDEMC, miR2Disease |
| 11 | hsa-mir-184 | dbDEMC, miR2Disease | 36 | hsa-let-7e | dbDEMC |
| 12 | hsa-mir-29a | HMDD | 37 | hsa-let-7b | HMDD, dbDEMC, miR2Disease |
| 13 | hsa-mir-16 | HMDD, dbDEMC, miR2Disease | 38 | hsa-mir-223 | HMDD, dbDEMC, miR2Disease |
| 14 | hsa-mir-19a | dbDEMC | 39 | hsa-let-7d | HMDD, dbDEMC, miR2Disease |
| 15 | hsa-mir-17 | HMDD, dbDEMC, miR2Disease | 40 | hsa-let-7c | HMDD, dbDEMC, miR2Disease |
| 16 | hsa-mir-211 | dbDEMC | 41 | hsa-let-7f | dbDEMC, miR2Disease |
| 17 | hsa-mir-20a | HMDD, dbDEMC, miR2Disease | 42 | hsa-let-7i | dbDEMC |
| 18 | hsa-mir-125b | dbDEMC | 43 | hsa-let-7g | dbDEMC, miR2Disease |
| 19 | hsa-mir-18a | HMDD, dbDEMC, miR2Disease | 44 | hsa-mir-9 | dbDEMC |
| 20 | hsa-mir-10a | dbDEMC, miR2Disease | 45 | hsa-mir-302c | dbDEMC |
| 21 | hsa-mir-221 | HMDD, dbDEMC, miR2Disease | 46 | hsa-mir-15b | HMDD, dbDEMC |
| 22 | hsa-mir-19b | dbDEMC | 47 | hsa-mir-145 | HMDD, dbDEMC |
| 23 | hsa-mir-92a | HMDD, dbDEMC | 48 | hsa-mir-92b | dbDEMC |
| 24 | hsa-mir-222 | HMDD, dbDEMC, miR2Disease | 49 | hsa-mir-302d | Unconfirmed |
| 25 | hsa-mir-181b | HMDD, dbDEMC, miR2Disease | 50 | hsa-mir-127 | dbDEMC |
| Rank | miRNA name | Evidence | Rank | miRNA name | Evidence |
|---|---|---|---|---|---|
| 1 | hsa-mir-21 | HMDD, dbDEMC, miR2Disease | 26 | hsa-mir-18a | HMDD, dbDEMC |
| 2 | hsa-mir-373 | dbDEMC | 27 | hsa-mir-137 | HMDD, dbDEMC |
| 3 | hsa-mir-29c | HMDD, dbDEMC, miR2Disease | 28 | hsa-mir-146a | HMDD, dbDEMC, miR2Disease |
| 4 | hsa-mir-302b | dbDEMC | 29 | hsa-mir-19b | HMDD, dbDEMC, miR2Disease |
| 5 | hsa-mir-451 | dbDEMC, miR2Disease | 30 | hsa-mir-92a | HMDD, dbDEMC |
| 6 | hsa-mir-34a | HMDD, dbDEMC | 31 | hsa-let-7a | HMDD, dbDEMC, miR2Disease |
| 7 | hsa-mir-184 | dbDEMC | 32 | hsa-mir-141 | dbDEMC, miR2Disease |
| 8 | hsa-mir-29a | HMDD, dbDEMC | 33 | hsa-mir-181a | HMDD, dbDEMC |
| 9 | hsa-mir-16 | dbDEMC, miR2Disease | 34 | hsa-mir-30a | HMDD, dbDEMC, miR2Disease |
| 10 | hsa-mir-372 | dbDEMC | 35 | hsa-mir-200b | HMDD, dbDEMC |
| 11 | hsa-mir-155 | HMDD, dbDEMC, miR2Disease | 36 | hsa-mir-223 | HMDD, dbDEMC |
| 12 | hsa-mir-148a | HMDD, dbDEMC, miR2Disease | 37 | hsa-let-7e | HMDD, dbDEMC, miR2Disease |
| 13 | hsa-mir-211 | dbDEMC | 38 | hsa-let-7b | HMDD, dbDEMC, miR2Disease |
| 14 | hsa-mir-148b | dbDEMC | 39 | hsa-let-7d | HMDD, dbDEMC, miR2Disease |
| 15 | hsa-mir-152 | dbDEMC | 40 | hsa-let-7c | HMDD, dbDEMC, miR2Disease |
| 16 | hsa-mir-15a | dbDEMC | 41 | hsa-let-7i | HMDD, dbDEMC |
| 17 | hsa-mir-125b | HMDD, dbDEMC, miR2Disease | 42 | hsa-let-7f | HMDD, dbDEMC, miR2Disease |
| 18 | hsa-mir-17 | HMDD, dbDEMC, miR2Disease | 43 | hsa-let-7g | HMDD, dbDEMC, miR2Disease |
| 19 | hsa-mir-19a | HMDD, dbDEMC, miR2Disease | 44 | hsa-mir-143 | HMDD, dbDEMC, miR2Disease |
| 20 | hsa-mir-221 | HMDD, dbDEMC, miR2Disease | 45 | hsa-mir-9 | HMDD, dbDEMC |
| 21 | hsa-mir-10a | dbDEMC | 46 | hsa-mir-302c | dbDEMC |
| 22 | hsa-mir-20a | HMDD, dbDEMC, miR2Disease | 47 | hsa-mir-302a | dbDEMC |
| 23 | hsa-mir-222 | HMDD, dbDEMC | 48 | hsa-mir-92b | HMDD, dbDEMC |
| 24 | hsa-mir-205 | HMDD, dbDEMC, miR2Disease | 49 | hsa-mir-302d | dbDEMC |
| 25 | hsa-mir-181b | HMDD, dbDEMC | 50 | hsa-mir-145 | HMDD, dbDEMC, miR2Disease |
Discussion and conclusions
MiRNAs play a crucial role in the occurrence and development of diseases, therefore studying disease-related miRNAs can help people to understand pathogenesis and explore the rules related to diseases. In recent years, many calculation methods have emerged to extract useful information from massive biomolecular datasets.93–95 Our proposed LSGSP is one such calculation methods for predicting miRNA–disease associations with some good attributes (such as being easy to implement, being able to predict isolated diseases and new miRNAs, and not requiring negative samples of miRNA–disease associations). Through implementing LOOCV on a benchmark dataset, prediction dataset and compare dataset, AUC values were obtained of 0.9221, 0.9745 and 0.9194, respectively, which proved that the predictive performance of LSGSP was significantly better than other existing methods.In a case study, LSGSP, when used in selected prostate neoplasm and lung neoplasm cases, achieved 96% and 100% accuracy in potential disease-related miRNA prediction, and 98% and 100% accuracy for isolated disease prediction, respectively, further demonstrating the excellent predictive performance of LSGSP; it also provided supporting evidence for the top 50 predicted disease–miRNA associations in the updated HMDD, mir2Disease and dbDEMC databases. Supporting evidence for the other miRNA–disease associations not verified in the above three databases was found in the latest literature studies; this demonstrated that LSGSP shows excellent predictive performance for potential associations between miRNAs and diseases. This is helpful for understanding pathogenic mechanisms at the level of miRNAs and finding disease-related miRNAs.
The excellent predictive performance of LSGSP is mainly attributed to the following factors. (1) The good construction of the relationship networks: we reconstructed the disease similarity network and the miRNA similarity network using known miRNA–disease association information, disease semantic similarity, miRNA family information and miRNA functional similarity. (2) The full utilization of network topology characteristics; we used Laplacian scores of the graphs to obtain the global similarities of the miRNA network and the disease network. (3) The accurate construction of weighted networks; we integrated the global similarities of diseases, global similarities of miRNAs and the experimentally validated miRNA–disease Boolean network to construct the miRNA–disease weighted network with a more accurately portrayed miRNA–disease relationship. (4) The use of a calculable projection of network space; we used vector projection to represent the miRNA–disease association degree.
Although LSGSP has achieved creditable predictive results, there are still some capabilities that need to be improved in the future to make the model more efficient and general: (1) the time for selecting the optimal parameters needs to be shortened; and (2) the accuracy of the representation of miRNA–miRNA similarities needs to be improved further through using biological information data, such as lncRNA–miRNA interactions and miRNA expression profiles.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research in this paper has been sponsored by the National Natural Science Foundation of China (Grant No. 61772192, 61672223, 61662017), the Natural Science Foundation of Hunan Province, China (Grant No. 2018JJ2085, 2019JJ40064, 2019JJ40063), the Major Cultivation Projects of Hunan Institute of Technology (Grant No. 2017HGPY001), and the Science and Technology Innovative Research Team of Hunan Institute of Technology (Grant No. TD18005).References
- M. V. Iorio, M. Ferracin, C.-G. Liu, A. Veronese, R. Spizzo, S. Sabbioni, E. Magri, M. Pedriali, M. Fabbri and M. Campiglio, Cancer Res., 2005, 65, 7065–7070 CrossRef CAS PubMed.
- G. Meister and T. Tuschi, Nature, 2004, 431, 343 CrossRef CAS PubMed.
- E. A. Miska, Curr. Opin. Genet. Dev., 2005, 15, 563–568 CrossRef CAS PubMed.
- L. Zhu, J. Zhao, J. Wang, C. Hu, J. Peng, R. Luo, C. Zhou, J. Liu, J. Lin and Y. Jin, PLoS Pathog., 2016, 12, e1005423 CrossRef PubMed.
- T. R. Fernando, N. I. Rodriguez-Malave and D. S. Rao, J. Hematol. Oncol., 2012, 5, 7 CrossRef CAS.
- A. M. Cheng, M. W. Byrom, J. Shelton and L. P. Ford, Nucleic Acids Res., 2005, 33, 1290–1297 CrossRef CAS.
- P. Xu, M. Guo and B. A. Hay, Trends Genet., 2004, 20, 617–624 CrossRef CAS PubMed.
- R. W. Carthew and E. J. Sontheimer, Cell, 2009, 136, 642–655 CrossRef CAS PubMed.
- P. Mussnich, R. Ros, R. Bianco, A. Fusco and D. D'Angelo, Expert Opin. Ther. Targets, 2015, 19, 1017–1026 CrossRef CAS PubMed.
- T. Kan, F. Sato, T. Ito, N. Matsumura, S. David, Y. Cheng, R. Agarwal, B. C. Paun, Z. Jin and A. V. Olaru, Gastroenterology, 2009, 136, 1689–1700 CrossRef CAS PubMed.
- G. Xiao, X. Gao, X. Sun, C. Yang, B. Zhang, R. Sun, G. Huang, X. Li, J. Liu and N. Du, Oncol. Rep., 2017, 38, 1190–1198 CrossRef CAS PubMed.
- Y. Fujino, S. Takeishi, K. Nishida, K. Okamoto, N. Muguruma, T. Kimura, S. Kitamura, H. Miyamoto, A. Fujimoto and J. Higashijima, Cancer Sci., 2017, 108, 390–397 CrossRef CAS.
- C. C. Pritchard, H. H. Cheng and M. Tewari, Nat. Rev. Genet., 2012, 13, 358 CrossRef CAS.
- H. Dong, J. Lei, L. Ding, Y. Wen, H. Ju and X. Zhang, Chem. Rev., 2013, 113, 6207 CrossRef CAS PubMed.
- X. Zeng, X. Zhang and Q. Zou, Briefings Bioinf., 2016, 17, 193–203 CrossRef CAS PubMed.
- X. Chen, D. Xie, Q. Zhao and Z.-H. You, Briefings Bioinf., 2019, 20, 515–539 CrossRef PubMed.
- M. Lu, Q. Zhang, M. Deng, J. Miao, Y. Guo, W. Gao and Q. Cui, PLoS One, 2008, 3, e3420 CrossRef PubMed.
- S. Bandyopadhyay, R. Mitra, U. Maulik and M. Q. Zhang, Silence, 2010, 1, 6 CrossRef.
- D. Wang, J. Wang, M. Lu, F. Song and Q. Cui, Bioinformatics, 2010, 26, 1644–1650 CrossRef CAS PubMed.
- Q. Jiang, Y. Hao, G. Wang, L. Juan, T. Zhang, M. Teng, Y. Liu and Y. Wang, BMC Syst. Biol., 2010, 4(Supp.1), S2 CrossRef.
- P. Xuan, K. Han, M. Guo, Y. Guo, J. Li, J. Ding, Y. Liu, Q. Dai, J. Li and Z. Teng, PLoS One, 2013, 8, e70204 CrossRef CAS.
- K. Han, P. Xuan, J. Ding, Z. Zhao, L. Hui and Y. Zhong, Genet. Mol. Res., 2014, 13, 2009–2019 CrossRef CAS.
- X. Chen, Q.-F. Wu and G.-Y. Yan, RNA Biol., 2017, 14, 952–962 CrossRef PubMed.
- X. Chen, J.-Y. Cheng and J. Yin, RNA Biol., 2018, 15, 1192–1205 CrossRef.
- X. Chen, M.-X. Liu and G.-Y. Yan, Mol. BioSyst., 2012, 8, 2792–2798 RSC.
- X. Chen, C. C. Yan, Z. Xu, Z. H. You, H. Yuan and G. Y. Yan, Oncotarget, 2016, 7, 65257–65269 Search PubMed.
- H. Shi, J. Xu, G. Zhang, L. Xu, C. Li, L. Wang, Z. Zhao, W. Jiang, Z. Guo and X. Li, BMC Syst. Biol., 2013, 7, 101 CrossRef PubMed.
- M. Chen, X. Lu, B. Liao, Z. Li, L. Cai and C. Gu, PLoS One, 2016, 11, e0166509 CrossRef PubMed.
- X. Chen, C. C. Yan, X. Zhang, Z. H. You, L. Deng, Y. Liu, Y. Zhang and Q. Dai, Sci. Rep., 2016, 6, 21106 CrossRef CAS.
- D. Sun, A. Li, H. Feng and M. Wang, Mol. BioSyst., 2016, 12, 2224–2232 RSC.
- J. J. Nalluri, B. K. Kamapantula, D. Barh, N. Jain, A. Bhattacharya, S. S. de Almeida, R. T. Juca Ramos, A. Silva, V. Azevedo and P. Ghosh, BMC Genomics, 2015, 16, S12 CrossRef.
- Z. H. You, Z. A. Huang, Z. Zhu, G. Y. Yan, Z. W. Li, Z. Wen and X. Chen, PLoS Comput. Biol., 2017, 13, e1005455 CrossRef.
- M. Chen, Y. Zhang, A. Li, Z. Li, W. Liu and Z. Chen, Front. Genet., 2019, 10, 385 CrossRef.
- H. Chen and Z. Zhang, BMC Med. Genomics, 2013, 6, 12 CrossRef CAS.
- C. Gu, L. Bo, X. Li and K. Li, Sci. Rep., 2016, 6, 36054 CrossRef CAS.
- X. Chen, D. Xie, L. Wang, Q. Zhao, Z.-H. You and H. Liu, Bioinformatics, 2018, 34, 3178–3186 CrossRef CAS.
- D. H. Le, Comput. Biol. Chem., 2015, 58, 139–148 CrossRef CAS.
- X. Chen, L. Y. Wang and L. Huang, J. Cell. Mol. Med., 2018, 22, 2884–2895 CrossRef CAS PubMed.
- S.-P. Yu, C. Liang, Q. Xiao, G.-H. Li, P.-J. Ding and J.-W. Luo, RNA Biol., 2018, 15, 1215–1227 CrossRef.
- M. Chen, M. Zhong, Z. Li, X. Li and A. Li, J. Comput. Theor. Nanosci., 2015, 12, 4036–4042 CrossRef CAS.
- M. Chen, Z. Li, Y. Zhang, X. Chen and A. Li, J. Comput. Theor. Nanosci., 2015, 12, 4890–4894 CrossRef CAS.
- M. Chen, X. He, S. Duan and Y. Deng, Comb. Chem. High Throughput Screening, 2017, 20, 158–163 CAS.
- Q. Jiang, G. Wang, T. Zhang and Y. Wang, Predicting human microRNA-disease associations based on support vector machine, in 2010 IEEE International Conference On Bioinformatics and Biomedicine (BIBM), 2010, pp. 467–472 Search PubMed.
- J. Xu, C.-X. Li, J.-Y. Lv, Y.-S. Li, Y. Xiao, T.-T. Shao, X. Huo, X. Li, Y. Zou and Q.-L. Han, Mol. Cancer Ther., 2011, 10, 1857–1866 CrossRef CAS PubMed.
- X. Zeng, Z. Xuan, Y. Liao and L. Pan, Biochim. Biophys. Acta, 2016, 1860, 2735–2739 CrossRef CAS PubMed.
- C.-C. Wang, X. Chen, J. Yin and J. Qu, RNA Biol., 2019, 16, 257–269 CrossRef PubMed.
- L. Wang, Z.-H. You, X. Chen, Y.-M. Li, Y.-N. Dong, L.-P. Li and K. Zheng, PLoS Comput. Biol., 2019, 15, e1006865 CrossRef PubMed.
- Y. Zhao, X. Chen and J. Yin, Bioinformatics, 2019, 1, 9 Search PubMed.
- X. Chen and G.-Y. Yan, Sci. Rep., 2014, 4, 5501 CrossRef CAS PubMed.
- X. Chen, C. C. Yan, X. Zhang, Z. Li, L. Deng, Y. Zhang and Q. Dai, Sci. Rep., 2015, 5, 13877 CrossRef PubMed.
- L. Fu and Q. Peng, Sci. Rep., 2017, 7, 14482 CrossRef PubMed.
- X. Chen, L. Huang, D. Xie and Q. Zhao, Cell Death Dis., 2018, 9, 3 CrossRef PubMed.
- P. Xuan, Y. Dong, Y. Guo, T. Zhang and Y. Liu, Int. J. Mol. Sci., 2018, 19, 3732 CrossRef PubMed.
- W. Lan, J. Wang, M. Li, J. Liu, F. X. Wu and Y. Pan, IEEE/ACM Trans. Comput. Biol. Bioinf., 2016, 1 CAS.
- W. Lan, J. Wang, M. Li, J. Liu and Y. Pan, Predicting microRNA-disease associations by integrating multiple biological information, in IEEE International Conference on Bioinformatics and Biomedicine, 2015, pp. 183–188 Search PubMed.
- Q. Xiao, J. Luo, C. Liang, J. Cai and P. Ding, Bioinformatics, 2018, 34, 239–248 CrossRef CAS.
- Y. Zhong, P. Xuan, X. Wang, T. Zhang, J. Li, Y. Liu and W. Zhang, Bioinformatics, 2018, 34, 267–277 CrossRef CAS PubMed.
- C. Pasquier and J. Gardès, Sci. Rep., 2016, 6, 27036 CrossRef CAS.
- X. Chen, Y. W. Niu, G. H. Wang and G. Y. Yan, J. Transl. Med., 2017, 15, 251 CrossRef CAS PubMed.
- J. Luo, Q. Xiao, C. Liang and P. Ding, IEEE Access, 2017, 5, 2503–2513 Search PubMed.
- X. Chen and L. Huang, PLoS Comput. Biol., 2017, 13, e1005912 CrossRef.
- L. Peng, M. Peng, B. Liao, Q. Xiao, W. Liu, G. Huang and K. Li, RSC Adv., 2017, 7, 44447–44455 RSC.
- M. Chen, B. Liao and Z. Li, Sci. Rep., 2018, 8, 6481 CrossRef.
- Q. Zou, J. Li, Q. Hong, Z. Lin, Y. Wu, H. Shi and Y. Ju, BioMed Res. Int., 2015, 2015, 8105 Search PubMed.
- J. Li, Z. Wu, F. Cheng, W. Li, G. Liu and Y. Tang, Sci. Rep., 2014, 4, 5576 CrossRef CAS PubMed.
- L. Peng, Y. Chen, N. Ma and X. Chen, Mol. BioSyst., 2017, 13, 2650–2659 RSC.
- X. Chen, Z. Zhou and Y. Zhao, RNA Biol., 2018, 15, 807–818 Search PubMed.
- X. Chen, Y. W. Niu, G. H. Wang and G. Y. Yan, J. Biomed. Inf., 2017, 76, 50–58 CrossRef PubMed.
- X. Zeng, N. Ding, A. Rodríguez-Patón, Z. Lin and Y. Ju, Curr. Proteomics, 2016, 13, 151–157 CrossRef CAS.
- J. Q. Li, Z. H. Rong, X. Chen, G. Y. Yan and Z. H. You, Oncotarget, 2017, 8, 21187–21199 Search PubMed.
- X. Chen, L. Wang, J. Qu, N.-N. Guan and J.-Q. Li, Bioinformatics, 2018, 34, 4256–4265 CAS.
- L. Peng, M. Peng, B. Liao, G. Huang, W. Liang and K. Li, Sci. Rep., 2017, 7 Search PubMed.
- X. Chen, J. Yin, J. Qu and L. Huang, PLoS Comput. Biol., 2018, 14, e1006418 CrossRef PubMed.
- C. Tang, H. Zhou, X. Zheng, Y. Zhang and X. Sha, RNA Biol., 2019, 16, 601–611 CrossRef PubMed.
- Y. Li, C. Qiu, J. Tu, B. Geng, J. Yang, T. Jiang and Q. Cui, Nucleic Acids Res., 2013, 42, D1070–D1074 CrossRef PubMed.
- A. Kozomara and S. Griffithsjones, Nucleic Acids Res., 2011, 39, D152–D157 CrossRef CAS PubMed.
- D. Zhou, O. Bousquet, T. N. Lal, J. Weston and B. Schölkopf, Learning with local and global consistency, in Advances in neural information processing systems, 2004 Search PubMed.
- M. Chen, Y. Peng, A. Li, Z. Li, Y. Deng, W. Liu, B. Liao and C. Dai, RSC Adv., 2018, 8, 36675–36690 RSC.
- L. Jiang, Y. Ding, J. Tang and F. Guo, Front. Genet., 2018, 9, 618 CrossRef PubMed.
- K. Lefort, G. P. Ostano, M. Mello-Grand, V. Calpini, M. Scatolini, A. Farsetti, G. P. Dotto and G. Chiorino, Oncotarget, 2016, 7, 48011 CrossRef PubMed.
- K. M. Kaukoniemi, H. E. Rauhala, M. Scaravilli, L. Latonen, M. Annala, R. L. Vessella, M. Nykter, T. L. Tammela and T. Visakorpi, Cancer Med., 2015, 4, 1417–1425 CrossRef CAS PubMed.
- H. E. Rauhala, S. E. Jalava, J. Isotalo, H. Bracken, S. Lehmusvaara, T. L. Tammela, H. Oja and T. Visakorpi, Int. J. Cancer, 2010, 127, 1363–1372 CrossRef CAS PubMed.
- X. Yang, Y. Yang, R. Gan, L. Zhao, W. Li, H. Zhou, X. Wang, J. Lu and Q. H. Meng, PLoS One, 2014, 9, e98833 CrossRef PubMed.
- Y. Ouyang, P. Gao, B. Zhu, X. Chen, F. Lin, X. Wang, J. Wei and H. Zhang, Mol. Med. Rep., 2015, 11, 1435–1441 CrossRef CAS PubMed.
- W. Zhou and D. Wu, Int. J. Clin. Exp. Med., 2016, 9, 8713–8718 CAS.
- C. A. Sánchez, E. I. Andahur, R. Valenzuela, E. A. Castellon, J. A. Fulla, C. G. Ramos and J. C. Triviño, Oncotarget, 2016, 7, 3993 CrossRef PubMed.
- S. Temraz, M. Charafeddine, D. Mukherji and A. Shamseddine, Journal of epidemiology and global health, 2017, 7, 161 CrossRef PubMed.
- L. A. Torre, R. L. Siegel and A. Jemal, in Lung cancer and personalized medicine, Springer, 2016, pp. 1–19 Search PubMed.
- W. C. Zhang, T. M. Chin, H. Yang, M. E. Nga, D. P. Lunny, E. K. H. Lim, L. L. Sun, Y. H. Pang, Y. N. Leow and S. R. Y. Malusay, Nat. Commun., 2016, 7, 11702 CrossRef CAS PubMed.
- M. H. Lin, Y. Z. Chen, M. Y. Lee, K. P. Weng, H. T. Chang, S. Y. Yu, B. J. Dong, F. R. Kuo, L. T. Hung and L. F. Liu, Oncol. Lett., 2018, 15, 9818–9826 Search PubMed.
- J. Zhang, J. Liu, Y. Liu, W. Wu, X. Li, Y. Wu, H. Chen, K. Zhang and L. Gu, Biomed. Pharmacother., 2015, 74, 215–221 CrossRef CAS PubMed.
- M.-R. Aghanoori, B. Mirzaei and M. Tavallaei, Asian Pac. J. Cancer Prev., 2014, 15, 9557–9565 CrossRef PubMed.
- G. Huang, F. Yan and D. Tan, Curr. Protein Pept. Sci., 2018, 19, 562–572 CrossRef CAS PubMed.
- G. Huang, K. Feng, X. Li and Y. Peng, Comb. Chem. High Throughput Screening, 2016, 19, 121–128 CrossRef CAS.
- G. Huang and W. Zeng, MATCH Commun. Math. Comput. Chem., 2016, 75, 717–730 Search PubMed.
Footnote |
| † The authors wish it to be known that, in their opinion, the first two authors should be regarded as joint first authors. |
| This journal is © The Royal Society of Chemistry 2019 |